Ерөнхий Фурье цуврал. Фурье цуврал: шинжлэх ухааны хөгжилд математик механизмын түүх ба нөлөө

Аль хэдийн нэлээд залхсан. Мөн онолын стратегийн нөөцөөс шинэ лаазалсан хүнс гаргаж авах цаг ирсэн гэдгийг би мэдэрч байна. Функцийг өөр аргаар цуврал болгон өргөжүүлэх боломжтой юу? Жишээлбэл, шулуун шугамын сегментийг синус ба косинусаар илэрхийлэх үү? Энэ нь гайхалтай юм шиг санагдаж байгаа ч ийм хол мэт санагдах функцууд нь өөрсдийгөө зээлдүүлдэг
"дахин нэгдэх". Онол, практикийн танил зэрэглэлээс гадна функцийг цуврал болгон өргөжүүлэх өөр аргууд байдаг.

Энэ хичээлээр бид тригонометрийн Фурье цувралтай танилцаж, түүний нийлбэр ба нийлбэрийн асуудлыг хөндөж, мэдээжийн хэрэг функцийг Фурьегийн цуврал болгон өргөжүүлэх олон жишээнд дүн шинжилгээ хийх болно. Би нийтлэлийг "Даммигийн Фурье цуврал" гэж нэрлэхийг чин сэтгэлээсээ хүсч байсан ч энэ нь зальтай байх болно, учир нь асуудлыг шийдвэрлэхэд математикийн шинжилгээний бусад хэсгүүдийн мэдлэг, зарим практик туршлага шаардлагатай болно. Тиймээс оршил нь сансрын нисгэгчдийн сургалттай төстэй байх болно =)

Нэгдүгээрт, хуудасны материалыг судлахдаа маш сайн хэлбэрээр хандах хэрэгтэй. Нойрмог, амарч, сэрүүн. Хагарсан шишүүхэй хөлний тухай хүчтэй сэтгэл хөдлөл, амьдралын хүнд хэцүү байдлын талаархи бодол санаагүйгээр аквариумын загас. Фурье цуврал нь ойлгох үүднээс тийм ч хэцүү биш боловч практик даалгаврууд нь анхаарал төвлөрүүлэхийг шаарддаг - хамгийн тохиромжтой нь гадны өдөөгчийг бүрэн орхих хэрэгтэй. Шийдэл, хариултыг шалгах амаргүй арга байхгүй нь нөхцөл байдлыг улам хүндрүүлж байна. Тиймээс, хэрэв таны эрүүл мэнд дунджаас доогуур байвал илүү энгийн зүйл хийх нь дээр. Үнэн.

Хоёрдугаарт, сансарт нисэхээсээ өмнө хяналтын самбарыг судлах хэрэгтэй сансрын хөлөг. Машин дээр товших ёстой функцүүдийн утгуудаас эхэлцгээе.

Аливаа байгалийн үнэ цэнийн хувьд:

нэг). Үнэн хэрэгтээ синусоид нь "pi" тус бүрээр x тэнхлэгийг "анивчдаг":
. Аргументийн сөрөг утгуудын хувьд үр дүн нь мэдээж ижил байх болно: .

2). Гэхдээ хүн бүр үүнийг мэддэггүй байсан. "Pi en" косинус нь "анивчсан гэрэл"-тэй тэнцүү байна:

Сөрөг аргумент нь хэргийг өөрчлөхгүй: .

Магадгүй хангалттай.

Гуравдугаарт, эрхэм сансрын нисэгчдийн корпус, та чадвартай байх хэрэгтэй ... нэгтгэх.
Ялангуяа, мэдээж дифференциал тэмдгийн дор функцийг авчрах, хэсгүүдээр нэгтгэхмөн сайн харилцаатай байх Ньютон-Лейбницийн томъёо. Нислэгийн өмнөх чухал дасгалуудыг эхлүүлцгээе. Би үүнийг алгасахыг зөвлөдөггүй, ингэснээр та таталцлын үндсэн дээр тэгшлэхгүй байх болно.

Жишээ 1

Тодорхой интегралыг тооцоолох

байгалийн үнэт зүйлсийг хаанаас авдаг.

Шийдэл: интеграцчлалыг "x" хувьсагч дээр гүйцэтгэдэг бөгөөд энэ үе шатанд "en" дискрет хувьсагчийг тогтмол гэж үзнэ. Бүх интегралд функцийг дифференциалын тэмдгийн дор авчирна:

Буудахад тохиромжтой шийдлийн богино хувилбар нь дараах байдалтай байна.

Дассан:

Үлдсэн дөрвөн оноо нь дангаараа байна. Даалгаврыг ухамсартайгаар хийж, интегралуудыг богино хугацаанд зохион байгуулахыг хичээ. Хичээлийн төгсгөлд шийдлийн жишээ.

ЧАНАРТАЙ дасгал хийсний дараа скафандр өмслөө
мөн эхлэхэд бэлдэж байна!

Фурье цуврал дахь функцийг интервал дээр өргөтгөх

Ийм функцийг авч үзье тодорхойлсоннаад зах нь интервал дээр (мөн магадгүй илүү том интервал дээр). Хэрэв энэ функц сегмент дээр интегралдах боломжтой бол үүнийг тригонометр болгон өргөжүүлж болно Фурье цуврал:
, гэж нэрлэгддэг зүйл хаана байна Фурье коэффициентүүд.

Энэ тохиолдолд дугаарыг дуудна задралын хугацаа, мөн тоо нь байна хагас задралын задрал.

Мэдээжийн хэрэг, ерөнхий тохиолдолд Фурье цуврал нь синус ба косинусуудаас бүрддэг.

Үнэхээр үүнийг дэлгэрэнгүй бичье:

Цувралын тэг гишүүнийг ихэвчлэн гэж бичдэг.

Фурье коэффициентийг дараахь томъёогоор тооцоолно.

Шинэ нэр томьёо нь эхлэгчдэд энэ сэдвийг судлахад бүрхэг хэвээр байгааг би маш сайн ойлгож байна. задралын хугацаа, хагас мөчлөг, Фурье коэффициентүүдгэх мэт сандрах хэрэггүй, энэ нь явахын өмнөх сэтгэл хөдлөлтэй харьцуулах аргагүй юм Гадаад орон зай. Хамгийн ойрын жишээн дээр бүх зүйлийг олж мэдье, хэрэгжүүлэхээсээ өмнө практик асуултуудыг асуух нь логик юм.

Дараах ажлуудад юу хийх хэрэгтэй вэ?

Функцийг Фурье цуврал болгон өргөжүүл. Нэмж дурдахад функцийн график, цувралын нийлбэрийн график, хэсэгчилсэн нийлбэр зурах, нарийн мэргэжлийн профессорын уран зөгнөлийн хувьд өөр зүйл хийх шаардлагатай болдог.

Функцийг Фурье цуврал болгон хэрхэн өргөжүүлэх вэ?

Үндсэндээ та олох хэрэгтэй Фурье коэффициентүүд, өөрөөр хэлбэл гурвыг зохиож, тооцоол тодорхой интеграл.

Фурье цувралын ерөнхий хэлбэр болон ажлын гурван томьёог дэвтэртээ хуулж авна уу. Сайтын зарим зочдод сансрын нисгэгч болох хүүхэд насны мөрөөдөл миний нүдэн дээр биелж байгаад маш их баяртай байна =)

Жишээ 2

Функцийг интервал дээр Фурье цуврал болгон өргөжүүл. График, цуваа болон хэсэгчилсэн нийлбэрийн нийлбэрийн графикийг байгуул.

Шийдэл: даалгаврын эхний хэсэг нь функцийг Фурье цуврал болгон өргөжүүлэх явдал юм.

Эхлэл нь стандарт тул дараах зүйлийг бичихээ мартуузай.

Энэ асуудалд тэлэлтийн үе , хагас .

Бид функцийг Фурье цувралын интервал дээр өргөжүүлнэ.

Тохирох томъёог ашиглан бид олдог Фурье коэффициентүүд. Одоо бид гурвыг зохиож, тооцоолох хэрэгтэй тодорхой интеграл. Тохиромжтой болгох үүднээс би оноог дугаарлах болно:

1) Эхний интеграл нь хамгийн энгийн боловч нүд, нүдийг аль хэдийн шаарддаг.

2) Бид хоёр дахь томьёог ашигладаг:

Энэ интеграл нь сайн мэддэг бөгөөд тэр үүнийг хэсэгчлэн авдаг:

Ашигласан олдвол функцийг дифференциал тэмдгийн дор оруулах арга.

Харж байгаа ажилд нэн даруй ашиглах нь илүү тохиромжтой тодорхой интегралд хэсгүүдээр нэгтгэх томъёо :

Хэд хэдэн техникийн тэмдэглэл. Эхлээд томъёог хэрэглэсний дараа илэрхийлэл бүхэлдээ том хаалтанд байх ёстой, анхны интегралын өмнө тогтмол байдаг тул. Үүнийг алдахгүй байцгаая! Цаашид аль ч алхамд хаалт нээж болно, би үүнийг хамгийн сүүлчийн ээлжинд хийсэн. Эхний "хэсэгт" Бид орлуулахдаа туйлын нарийвчлалыг харуулж байна, таны харж байгаагаар тогтмол нь ажиллахгүй, интеграцийн хязгаарыг бүтээгдэхүүнд орлуулж байна. Энэ үйлдлийг дөрвөлжин хаалтаар тэмдэглэв. За тэгээд томьёоны хоёр дахь "хэсэг"-ийн интегралыг сургалтын даалгавраас сайн мэдэж байгаа ;-)

Хамгийн гол нь анхаарлын хамгийн дээд төвлөрөл!

3) Бид гурав дахь Фурье коэффициентийг хайж байна:

Өмнөх интегралын харьцангуйг олж авсан бөгөөд энэ нь мөн адил юм хэсгүүдээр нэгтгэсэн:

Энэ жишээ нь арай илүү төвөгтэй тул би дараагийн алхамуудыг алхам алхмаар тайлбарлах болно:

(1) Илэрхийлэл бүхэлдээ том хаалтанд байна.. Би уйтгартай мэт санагдахыг хүсээгүй, тэд байнга тогтмол байдлаа алддаг.

(2) Энэ тохиолдолд би тэр даруй том хаалтуудыг өргөжүүлсэн. Онцгой анхаарал Бид эхний "хэсэг" -д зориулдаг: байнгын тамхи татдаг бөгөөд бүтээгдэхүүнд нэгтгэх ( ба ) хязгаарыг орлуулахад оролцдоггүй. Бичлэгийн эмх замбараагүй байдлыг харгалзан энэ үйлдлийг дөрвөлжин хаалтанд дахин тэмдэглэхийг зөвлөж байна. Хоёр дахь "хэсэг" -ээр Бүх зүйл илүү энгийн: энд том хаалт нээгдсэний дараа бутархай гарч ирсэн ба тогтмол нь танил болсон интегралыг нэгтгэсний үр дүнд гарч ирэв ;-)

(3) Дөрвөлжин хаалтанд бид хувиргалтыг хийж, баруун интегралд интегралын хязгаарыг орлуулна.

(4) Бид дөрвөлжин хаалтаас "гэрэлтүүлэгч" -ийг гаргаж авсны дараа дотоод хаалтыг нээнэ: .

(5) Бид хаалтанд байгаа 1 ба -1-ийг цуцалж, эцсийн хялбаршуулалтыг хийдэг.

Эцэст нь бүх гурван Фурье коэффициентийг олов:

Тэдгээрийг томъёонд орлуулна уу :

Хагас хувахаа бүү мартаарай. Сүүлийн шатанд "en" -ээс хамаарахгүй тогтмол ("хасах хоёр") нийлбэрээс хасагдана.

Тиймээс бид Фурье цуврал дахь функцийн өргөтгөлийг дараах интервал дээр олж авлаа.

Фурье цувралын нийлмэл байдлын асуултыг судалж үзье. Би онолыг ялангуяа тайлбарлах болно Дирихлетийн теорем, шууд утгаараа "хуруунд" байгаа тул хэрэв танд хатуу томъёолол хэрэгтэй бол тооцооллын сурах бичгийг үзнэ үү. (жишээлбэл, Боханы 2-р боть эсвэл Фихтенхольцын 3-р боть, гэхдээ энэ нь илүү хэцүү байдаг).

Даалгаврын хоёр дахь хэсэгт график, цуврал нийлбэрийн график, хэсэгчилсэн нийлбэрийн график зурах шаардлагатай.

Функцийн график нь ердийнх юм хавтгай дээрх шулуун шугам, хар тасархай шугамаар зурсан:

Бид цувралын нийлбэрийг авч үздэг. Та бүхний мэдэж байгаагаар функциональ цуваа функцүүдэд нийлдэг. Манай тохиолдолд баригдсан Фурье цуврал "x"-ийн дурын утгын хувьдулаанаар харуулсан функцэд нийлдэг. Энэ функцэд хамаарна 1-р төрлийн завсарлагацэгээр , гэхдээ мөн тэдгээрт тодорхойлогдсон (зураг дээрх улаан цэгүүд)

Энэ замаар: . Энэ нь анхны функцээс эрс ялгаатай болохыг хялбархан харж болно, тиймээс тэмдэглэгээнд байна Тэнцүү тэмдгийн оронд тильд ашигладаг.

Цувралын нийлбэрийг бүтээхэд тохиромжтой алгоритмыг судалцгаая.

Төвийн интервал дээр Фурье цуваа функц өөрөө нийлдэг (төв улаан сегмент нь шугаман функцийн хар тасархай шугамтай давхцдаг).

Одоо тригонометрийн тэлэлтийн шинж чанарын талаар бага зэрэг яръя. Фурье цуврал зөвхөн үечилсэн функцийг (тогтмол, синус ба косинус) багтаасан тул цувралын нийлбэр мөн үечилсэн функц юм.

Энэ нь манайд юу гэсэн үг вэ тодорхой жишээ? Мөн энэ нь цувралын нийлбэр гэсэн үг юм –заавал үе үемөн интервалын улаан сегмент зүүн ба баруун талд хязгааргүй давтагдах ёстой.

Одоо "задралын үе" гэсэн хэллэгийн утга нь эцэстээ тодорхой болсон гэж би бодож байна. Энгийнээр хэлэхэд нөхцөл байдал дахин дахин давтагдах бүртээ.

Практикт зураг дээр үзүүлсэн шиг гурван задралын үеийг дүрслэх нь ихэвчлэн хангалттай байдаг. За, мөн хөрш зэргэлдээ үеийн "хожуул" - график үргэлжилж байгааг тодорхой болгохын тулд.

Ялангуяа сонирхолтой байдаг 1-р төрлийн тасалдалтын цэгүүд. Ийм цэгүүдэд Фурье цуврал нь тусгаарлагдсан утгууд руу нийлдэг бөгөөд тэдгээр нь тасалдал "үсрэлт" (зураг дээрх улаан цэгүүд) яг дунд хэсэгт байрладаг. Эдгээр цэгүүдийн ординатыг хэрхэн олох вэ? Эхлээд "дээд давхрын" ординатыг олъё: үүний тулд бид төвийн тэлэлтийн үеийн хамгийн баруун цэг дэх функцийн утгыг тооцоолно: . "Доод давхрын" ординатыг тооцоолохын тулд хамгийн хялбар арга бол тухайн үеийн хамгийн зүүн талын утгыг авах явдал юм. . Дундаж утгын ординат нь "дээд ба доод"-ын нийлбэрийн арифметик дундаж юм: . Зургийг бүтээхдээ дунд нь зөв эсвэл буруу тооцоолсон эсэхийг шууд харах болно гэдэг сайхан хэрэг юм.

Цувралын хэсэгчилсэн нийлбэрийг бүтээж, нэгэн зэрэг "нийцэх" гэсэн нэр томъёоны утгыг давтъя. Хичээлээс сэдэл нь мэдэгддэг тооны цувралын нийлбэр. Бид өөрсдийн баялгийг дэлгэрэнгүй тайлбарлая:

Хэсэгчилсэн нийлбэр гаргахын тулд та тэг + цувралын өөр хоёр гишүүнийг бичих хэрэгтэй. өөрөөр хэлбэл,

Зураг дээр функцийн графикийг үзүүлэв ногоон өнгөтэй, мөн таны харж байгаагаар энэ нь бүхэлдээ нийлбэрийг нэлээд нягт "боодог". Хэрэв бид цувралын таван гишүүний хэсэгчилсэн нийлбэрийг авч үзвэл энэ функцийн график нь улаан шугамыг илүү нарийвчлалтай ойртуулах болно, хэрэв зуун гишүүн байвал "ногоон могой" нь улаан сегментүүдтэй бүрэн нийлнэ. гэх мэт. Ийнхүү Фурье цуваа нийлбэртээ нийлдэг.

Аливаа хэсэгчилсэн нийлбэр нь гэдгийг тэмдэглэх нь сонирхолтой юм тасралтгүй функц, гэхдээ цувралын нийт нийлбэр тасархай хэвээр байна.

Практикт хэсэгчилсэн нийлбэрийн график байгуулах нь ердийн зүйл биш юм. Үүнийг хэрхэн хийх вэ? Манай тохиолдолд сегмент дээрх функцийг авч үзэх, сегментийн төгсгөл ба завсрын цэгүүдэд түүний утгыг тооцоолох шаардлагатай (илүү олон оноо авч үзэх тусам график илүү нарийвчлалтай байх болно). Дараа нь та эдгээр цэгүүдийг зурган дээр тэмдэглэж, тухайн үеийн графикийг анхааралтай зурж, дараа нь зэргэлдээх интервалд "хуулбарлах" хэрэгтэй. Өөр яаж? Эцсийн эцэст ойртох нь бас үечилсэн функц юм ... ... түүний график нь эмнэлгийн төхөөрөмжийн дэлгэц дээрх зүрхний жигд хэмнэлийг ямар нэгэн байдлаар санагдуулдаг.

Мэдээжийн хэрэг, барилгын ажлыг гүйцэтгэх нь тийм ч тохиромжтой биш юм, учир нь та хагас миллиметрээс багагүй нарийвчлалыг хадгалахын тулд маш болгоомжтой байх хэрэгтэй. Гэсэн хэдий ч, би зураг зурахтай зөрчилдөж буй уншигчдад таалагдах болно - "бодит" даалгаварт зураг зурах нь үргэлж шаардлагатай байдаггүй, хаа нэгтээ 50% тохиолдолд функцийг Фурье цуврал болгон өргөжүүлэх шаардлагатай байдаг. тэр.

Зургийг дуусгасны дараа бид даалгаврыг гүйцэтгэнэ.

Хариулах:

Олон үүрэг даалгаврын хувьд функц нь зовдог 1-р төрлийн хагаралшууд задралын хугацаанд:

Жишээ 3

Интервал дээр өгөгдсөн функцийг Фурьегийн цувралд өргөжүүл. Функцийн график болон цувралын нийт нийлбэрийг зур.

Санал болгож буй функцийг хэсэгчлэн өгнө (зөвхөн сегмент дээр анхаараарай)мөн тэвчих 1-р төрлийн хагаралцэг дээр. Фурье коэффициентийг тооцоолох боломжтой юу? Асуудалгүй. Функцийн зүүн ба баруун хэсэг хоёулаа интервалаараа интегралдах боломжтой тул гурван томьёо тус бүрийн интегралыг хоёр интегралын нийлбэрээр илэрхийлэх ёстой. Жишээлбэл, тэг коэффициентийн хувьд үүнийг хэрхэн хийхийг харцгаая.

Хоёр дахь интеграл нь тэгтэй тэнцүү болж, энэ нь ажлыг багасгасан боловч энэ нь үргэлж тийм биш юм.

Бусад хоёр Фурье коэффициентийг ижил төстэй байдлаар бичсэн.

Цувралын нийлбэрийг хэрхэн харуулах вэ? Зүүн интервал дээр бид шулуун шугамын сегментийг зурж, интервал дээр - шулуун шугамын сегментийг (тэнхлэгийн хэсгийг тод, тодоор тодруулна). Өөрөөр хэлбэл, өргөтгөлийн интервал дээр цувралын нийлбэр нь гурван "муу" цэгээс бусад бүх функцтэй давхцдаг. Функцийн тасалдлын цэг дээр Фурье цуваа нь тусгаарлагдсан утгад нийлдэг бөгөөд энэ нь тасалдалын "үсрэлт"-ийн яг дунд байрладаг. Үүнийг амаар харахад хэцүү биш: зүүн талын хязгаар:, баруун гар талын хязгаар: мөн дунд цэгийн ординат нь 0.5 байх нь ойлгомжтой.

Нийлбэрийн үечилсэн байдлаас шалтгаалан зургийг зэргэлдээх үеүүдэд "үржүүлж", тухайлбал, ижил зүйлийг интервал дээр дүрсэлсэн байх ёстой. Энэ тохиолдолд цэгүүд дээр Фурье цуваа медиан утгуудад нийлдэг.

Үнэндээ энд шинэ зүйл алга.

Энэ асуудлыг өөрөө шийдэхийг хичээ. Хичээлийн төгсгөлд нарийн дизайн, зургийн ойролцоо жишээ.

Фурье цуврал дахь функцийг дурын хугацаанд өргөтгөх

"el" нь дурын эерэг тоо байх дурын өргөтгөлийн хугацааны хувьд Фурье цуврал ба Фурье коэффициентүүдийн томъёо нь бага зэрэг төвөгтэй синус ба косинусын аргументаар ялгаатай байна.

Хэрэв бол бид эхэлсэн интервалын томъёог авна.

Асуудлыг шийдвэрлэх алгоритм, зарчмууд бүрэн хадгалагдан үлдсэн боловч тооцооллын техникийн нарийн төвөгтэй байдал нэмэгддэг.

Жишээ 4

Функцийг Фурье цуврал болгон өргөжүүлж, нийлбэрийг зур.

Шийдэл: үнэн хэрэгтээ жишээ No3-ын аналог 1-р төрлийн хагаралцэг дээр. Энэ асуудалд тэлэлтийн үе , хагас . Функц нь зөвхөн хагас интервал дээр тодорхойлогддог боловч энэ нь ямар ч зүйлийг өөрчлөхгүй - функцийн хоёр хэсэг нь интегралдах боломжтой байх нь чухал юм.

Функцийг Фурье цуврал болгон өргөжүүлье.

Функц нь эхэнд тасархай тул Фурье коэффициент бүрийг хоёр интегралын нийлбэрээр бичих нь ойлгомжтой.

1) Би эхний интегралыг аль болох нарийвчлан бичих болно.

2) Сарны гадаргуу руу анхааралтай ажигла:

Хоёр дахь интеграл хэсэгчлэн авна:

Уусмалын үргэлжлэлийг одоор нээсний дараа та юуг анхаарах ёстой вэ?

Нэгдүгээрт, бид эхний интегралыг алдахгүй , бид нэн даруй гүйцэтгэх газар дифференциалын тэмдгийн дор авчрах. Хоёрдугаарт, том хаалт болон өмнө нь муу хувь заяаны тогтмолыг мартаж болохгүй тэмдгүүдэд бүү андууртомъёог ашиглах үед . Эцсийн эцэст том хаалт нь дараагийн алхамд нэн даруй нээхэд илүү тохиромжтой.

Үлдсэн хэсэг нь техникийн асуудал, зөвхөн интегралыг шийдвэрлэх туршлага хангалтгүй байх нь хүндрэл үүсгэдэг.

Тийм ээ, Францын математикч Фурьегийн нэр хүндтэй хамтрагчид уурлаж бухимдсан нь дэмий хоосон байсангүй - тэр функцүүдийг тригонометрийн цуврал болгон задалж зүрхлэв үү? =) Дашрамд хэлэхэд, магадгүй хүн бүр тухайн даалгаврын практик утгыг сонирхож байгаа байх. Фурье өөрөө дулаан дамжуулалтын математик загвар дээр ажиллаж байсан бөгөөд дараа нь түүний нэрээр нэрлэгдсэн цуврал нь гадаад ертөнцөд үл үзэгдэх олон үечилсэн процессуудыг судлахад ашиглагдаж эхэлсэн. Одоо, дашрамд хэлэхэд, хоёр дахь жишээний графикийг үе үе зүрхний хэмнэлтэй харьцуулсан нь санамсаргүй хэрэг биш гэж өөрийгөө барьж авав. Хүссэн хүмүүс танилцаж болно практик хэрэглээ Фурье хувиргалтгуравдагч талын эх сурвалжаас. ... Хэдий тэгээгүй нь дээр ч гэсэн анхны хайр гэж дурсагдах болно =)

3) Дахин дурдсан сул холбоосуудыг харгалзан бид гурав дахь коэффициентийг авч үздэг.

Хэсэг хэсгүүдээр нэгтгэх:

Бид олсон Фурье коэффициентийг томъёонд орлуулна , тэг коэффициентийг хагасаар хувахаа мартаж болохгүй.

Цувралын нийлбэрийг зуръя. Процедурыг товчхон давтъя: интервал дээр бид шугам, интервал дээр шугамыг барина. "Х"-ийн тэг утгаараа бид завсарын "үсрэлт" -ийн дунд цэг тавьж, хөрш зэргэлдээх үеүүдийн графикийг "хуулбарлана".


Үеүүдийн "уулзвар" дээр нийлбэр нь мөн ялгааны "үсрэлтийн" дунд цэгүүдтэй тэнцүү байх болно.

Бэлэн. Функц нь өөрөө зөвхөн хагас интервал дээр нөхцөлт байдлаар тодорхойлогддог бөгөөд мэдээжийн хэрэг интервал дээрх цувралын нийлбэртэй давхцаж байгааг би танд сануулж байна.

Хариулах:

Заримдаа хэсэгчлэн өгөгдсөн функц нь өргөтгөлийн хугацаанд үргэлжилдэг. Хамгийн энгийн жишээ: . Шийдэл (Бохан 2-р ботийг үзнэ үү)өмнөх хоёр жишээтэй ижил байна: үл хамааран функцын тасралтгүй байдалцэг дээр Фурье коэффициент бүрийг хоёр интегралын нийлбэрээр илэрхийлнэ.

Салалтын интервалд 1-р төрлийн тасалдалтын цэгүүдба / эсвэл графикийн "уулзвар" цэгүүд илүү байж болно (хоёр, гурав, ерөнхийдөө аль ч эцсийнтоо). Хэрэв функц хэсэг бүр дээр интегралдах боломжтой бол Фурье цувралд мөн өргөтгөх боломжтой. Гэхдээ практик туршлагаас харахад би ийм цагаан тугалга санахгүй байна. Гэсэн хэдий ч зүгээр л авч үзэхээс илүү хэцүү даалгаварууд байдаг бөгөөд нийтлэлийн төгсгөлд хүн бүрт зориулсан Фурье цувралын нарийн төвөгтэй байдлыг нэмэгдүүлэх холбоосууд байдаг.

Энэ хооронд тайвширч, сандал дээрээ тулан оддын төгсгөлгүй далайг эргэцүүлэн бодоцгооё:

Жишээ 5

Функцийг интервал дээр Фурье цуврал болгон өргөжүүлж, цувааны нийлбэрийг зур.

Энэ даалгаварт функц Үргэлжилсэншийдлийг хялбаршуулдаг задралын хагас интервал дээр. Бүх зүйл №2-р жишээтэй маш төстэй. Та сансрын хөлгөөс холдох боломжгүй - та шийдэх хэрэгтэй болно =) Хичээлийн төгсгөлд загвар дизайны загвар, хуваарийг хавсаргав.

Тэгш ба сондгой функцүүдийн Фурье цувралын өргөтгөл

Тэгш ба сондгой функцүүдийн тусламжтайгаар асуудлыг шийдэх үйл явц мэдэгдэхүйц хялбаршсан болно. Тийм ч учраас. "Хоёр пи" хугацааны Фурье цуврал дахь функцийн өргөтгөл рүү буцъя. болон дурын хугацаа "хоёр але" .

Бидний функц тэгш байна гэж бодъё. Цувралын ерөнхий нэр томьёо нь таны харж байгаагаар тэгш косинус, сондгой синусуудыг агуулна. Хэрэв бид ТЭГШ функцийг задлах юм бол яагаад сондгой синусууд хэрэгтэй вэ?! Шаардлагагүй коэффициентийг дахин тохируулъя: .

Энэ замаар, тэгш функц нь зөвхөн косинусаар Фурьегийн цуваа болж өргөждөг:

Үүний хэрээр тэгш функцүүдийн интегралуудТэгтэй харьцуулахад тэгш хэмтэй интеграцийн сегментийг хоёр дахин нэмэгдүүлэх боломжтой бол Фурьегийн бусад коэффициентийг мөн хялбаршуулна.

Хүрээний хувьд:

Дурын интервалын хувьд:

Тооцооллын бараг бүх сурах бичигт байдаг сурах бичгийн жишээнд тэгш функцүүдийн өргөтгөлүүд багтсан болно . Нэмж дурдахад тэд миний хувийн практикт олон удаа уулзаж байсан.

Жишээ 6

Функц өгсөн. Шаардлагатай:

1) функцийг үетэй Фурье цуврал болгон өргөжүүлэх, энд дурын эерэг тоо;

2) тэлэлтийг интервал дээр бичиж, функц байгуулж, цувралын нийт нийлбэрийн графикийг зур.

Шийдэл: эхний догол мөрөнд асуудлыг ерөнхий байдлаар шийдэхийг санал болгож байгаа бөгөөд энэ нь маш тохиромжтой! Хэрэгцээ бий болно - зүгээр л өөрийнхөө үнэ цэнийг орлуулаарай.

1) Энэ асуудалд тэлэлтийн үе , хагас үе . Цаашдын үйл ажиллагааны явцад, ялангуяа интеграцийн үед "el" нь тогтмол гэж тооцогддог

Функц нь тэгш бөгөөд энэ нь зөвхөн косинусуудаар Фурьегийн цуваа болж өргөсдөг гэсэн үг юм: .

Фурье коэффициентийг томъёогоор хайж байна . Тэдэнд анхаарлаа хандуулаарай болзолгүй давуу тал. Нэгдүгээрт, интеграци нь өргөтгөлийн эерэг сегмент дээр хийгддэг бөгөөд энэ нь бид модулийг аюулгүйгээр арилгана гэсэн үг юм. , хоёр хэсгээс зөвхөн "x"-г авч үзвэл. Хоёрдугаарт, интеграци нь мэдэгдэхүйц хялбаршуулсан.

Хоёр:

Хэсэг хэсгүүдээр нэгтгэх:

Энэ замаар:
, харин "en"-ээс хамаарахгүй тогтмол нь нийлбэрээс хасагдсан.

Хариулах:

2) Бид өргөтгөлийг интервал дээр бичдэг бөгөөд үүний тулд хагас хугацааны хүссэн утгыг ерөнхий томъёонд орлуулна.

Фурье цуваа нь дур мэдэн авсан функцийг тодорхой үетэй цуваа хэлбэрээр дүрслэх явдал юм. Ерөнхийдөө энэ шийдвэрортогональ суурь дээр элементийн задрал гэж нэрлэдэг. Фурьегийн цувралын функцүүдийн өргөтгөл нь аргумент, хувиргалт дахь илэрхийлэлийг нэгтгэх, ялгах, шилжүүлэх үед энэхүү хувиргалтын шинж чанараас шалтгаалан янз бүрийн асуудлыг шийдвэрлэх нэлээд хүчирхэг хэрэгсэл юм.

Танихгүй хүн дээд математик, мөн Францын эрдэмтэн Фурьегийн бүтээлүүдээс харахад эдгээр "цуврал" нь юу болохыг, юунд зориулагдсан болохыг ойлгохгүй байх магадлалтай. Үүний зэрэгцээ энэхүү өөрчлөлт нь бидний амьдралд нэлээд нягт болсон. Үүнийг зөвхөн математикчид төдийгүй физикч, химич, эмч, одон орон судлаач, газар хөдлөлт судлаач, далай судлаачид болон бусад олон хүмүүс ашигладаг. Мөн цаг үеэсээ түрүүлж нээлт хийсэн францын агуу эрдэмтний бүтээлүүдийг дэлгэрэнгүй сонирхоцгооё.

Хүн ба Фурье өөрчлөгддөг

Фурье цуврал нь аргуудын нэг юм (шинжилгээ болон бусадтай хамт) Энэ үйл явц нь хүн ямар ч дууг сонсох бүрт тохиолддог. Бидний чих нь автоматаар энгийн хэсгүүдийг уян харимхай орчинд хувиргадаг бөгөөд тэдгээр нь янз бүрийн өндөртэй дууны түвшний дууны түвшний дараалсан утгуудын эгнээнд (спектрийн дагуу) задардаг. Дараа нь тархи энэ өгөгдлийг бидэнд танил дуу болгон хувиргадаг. Энэ бүхэн бидний хүсэл, ухамсараас гадна өөрөө тохиолддог боловч эдгээр үйл явцыг ойлгохын тулд дээд математикийг судлахад хэдэн жил шаардагдана.

Фурье хувирлын талаар дэлгэрэнгүй

Фурье хувиргалтыг аналитик, тоон болон бусад аргаар хийж болно. Фурье цуваа нь далайн түрлэг, гэрлийн долгионоос эхлээд нарны (болон бусад одон орны объектуудын) үйл ажиллагааны мөчлөг хүртэлх аливаа хэлбэлзлийн процессыг задлах тоон аргыг хэлдэг. Эдгээр математикийн аргуудыг ашиглан аливаа хэлбэлзлийн процессыг хамгийн багааас хамгийн их ба эсрэгээр чиглэсэн синусоид бүрэлдэхүүн хэсгүүдийн цуваа хэлбэрээр илэрхийлэх функцүүдэд дүн шинжилгээ хийх боломжтой. Фурье хувиргалт нь тодорхой давтамжтай харгалзах синусоидуудын фаз ба далайцыг тодорхойлдог функц юм. Энэ процессыг дулаан, гэрэл эсвэл цахилгаан энергийн нөлөөн дор явагддаг динамик процессыг дүрсэлсэн маш нарийн төвөгтэй тэгшитгэлийг шийдвэрлэхэд ашиглаж болно. Мөн Фурье цуврал нь нарийн төвөгтэй хэлбэлзлийн дохионы тогтмол бүрэлдэхүүн хэсгүүдийг тусгаарлах боломжийг олгодог бөгөөд энэ нь анагаах ухаан, хими, одон орон судлалын олж авсан туршилтын ажиглалтыг зөв тайлбарлах боломжийг олгосон.

Түүхийн лавлагаа

Энэ онолыг үндэслэгч нь Францын математикч Жан Батист Жозеф Фурье юм. Энэ өөрчлөлтийг дараа нь түүний нэрээр нэрлэжээ. Эрдэмтэн эхэндээ дулаан дамжуулах механизм - хатуу биет дэх дулааны тархалтыг судлах, тайлбарлахдаа өөрийн аргыг ашигласан. Фурье анхны жигд бус тархалтыг хамгийн энгийн синусоид болгон задалж болно гэж санал болгосон бөгөөд тэдгээр нь тус бүр өөрийн температурын хамгийн бага ба максимум, мөн өөрийн үе шаттай байх болно. Энэ тохиолдолд ийм бүрэлдэхүүн хэсэг бүрийг хамгийн багааас дээд тал руу, эсрэгээр нь хэмжинэ. Муруйн дээд ба доод оргилууд, түүнчлэн гармоник бүрийн үе шатыг тодорхойлдог математик функцийг температурын тархалтын илэрхийлэлийн Фурье хувиргалт гэж нэрлэдэг. Онолын зохиогч ерөнхий функцМатематикийн хувьд тайлбарлахад хэцүү тархалтыг косинус ба синусын маш тохиромжтой цуврал болгон нэгтгэж, анхны тархалтыг өгдөг.

Өөрчлөлтийн зарчим ба орчин үеийн хүмүүсийн үзэл бодол

Эрдэмтний үеийнхэн - XIX зууны эхэн үеийн тэргүүлэх математикчид энэ онолыг хүлээн зөвшөөрөөгүй. Гол эсэргүүцэл нь шулуун эсвэл тасархай муруйг дүрсэлсэн тасархай функцийг үргэлжилсэн синусоид илэрхийллийн нийлбэр хэлбэрээр илэрхийлж болно гэсэн Фурьегийн нотолгоо байв. Жишээлбэл, Heaviside-ийн "алхам" -ыг авч үзье: түүний утга нь завсарын зүүн талд тэг, баруун талд нэг байна. Энэ функц нь хамаарлыг тодорхойлдог цахилгаан гүйдэлхэлхээг хаах үед түр зуурын хувьсагчаас. Тасархай илэрхийлэл нь экспоненциал, синусоид, шугаман эсвэл квадрат гэх мэт тасралтгүй, энгийн функцүүдийн хослолоор тодорхойлогддог ийм нөхцөл байдалтай тухайн үеийн онолын орчин үеийн хүмүүс хэзээ ч тулгарч байгаагүй.

Францын математикчдыг Фурьегийн онолд юу будилуулсан бэ?

Эцсийн эцэст, хэрэв математикч хэлсэн үгэндээ зөв байсан бол хязгааргүй тригонометрийн Фурье цувралыг нэгтгэн дүгнэж үзвэл, ижил төстэй олон үе шаттай байсан ч алхам алхмаар илэрхийллийн яг тодорхой дүрслэлийг олж авах боломжтой. 19-р зууны эхэн үед ийм мэдэгдэл нь утгагүй мэт санагдаж байв. Гэхдээ бүх эргэлзээтэй байсан ч олон математикчид энэ үзэгдлийг судлах хүрээг өргөжүүлж, дулаан дамжилтын илтгэлцүүрийг судлах хүрээнээс хэтрүүлсэн. Гэсэн хэдий ч ихэнх эрдэмтдийг "Синусоид цувааны нийлбэр нь нийлдэг үү" гэсэн асуултад зовж шаналж байв. яг үнэ цэнэтасархай функц?"

Фурье цувралын нэгдэл: жишээ

Төгсгөлгүй тооны цуваа нийлбэр хийх шаардлагатай үед нэгдэх тухай асуулт гарч ирдэг. Энэ үзэгдлийг ойлгохын тулд сонгодог жишээг авч үзье. Хэрэв дараалсан алхам бүр өмнөх алхамынхаа хагастай тэнцүү байвал та хананд хүрч чадах уу? Зорилгодоо хоёр метрийн зайд байна гэж бодъё, эхний алхам нь таныг замын хагаст ойртуулж, дараагийн алхам нь дөрөвний гурвын тэмдэг рүү ойртуулж, тав дахь алхмын дараа та замын бараг 97 хувийг туулах болно. Гэсэн хэдий ч та хичнээн алхам хийсэн ч математикийн хатуу утгаараа зорьсон зорилгодоо хүрч чадахгүй. Тоон тооцооллыг ашиглан эцэст нь дур мэдэн бага өгөгдсөн зайд ойртох боломжтой гэдгийг харуулж болно. Энэ нотолгоо нь хагас, дөрөвний нэг гэх мэтийн нийт үнэ цэнэ нэг рүү чиглэх болно гэдгийг нотлохтой тэнцүү юм.

Нэгдлийн тухай асуулт: Хоёр дахь ирэлт буюу Лорд Келвиний хэрэгсэл

19-р зууны төгсгөлд Фурьегийн цувралыг урсацын эрчмийг урьдчилан таамаглахад ашиглахыг оролдох үед энэ асуулт дахин гарч ирэв. Энэ үед Лорд Келвин цэргийн болон худалдааны флотын далайчдад үүнийг хянах боломжийг олгодог аналог тооцоолох төхөөрөмжийг зохион бүтээжээ. байгалийн үзэгдэл. Энэхүү механизм нь тухайн усан боомтод жилийн турш анхааралтай хэмжсэн далайн түрлэгийн өндрийн хүснэгтээс үе шат ба далайцын багцыг тодорхойлсон. Параметр бүр нь түрлэгийн өндрийн илэрхийллийн синусоид бүрэлдэхүүн хэсэг байсан бөгөөд ердийн бүрэлдэхүүн хэсгүүдийн нэг байв. Хэмжилтийн үр дүнг Лорд Келвиний тооцоолуурт оруулсан бөгөөд энэ нь усны өндрийг цаг хугацааны функцээр таамагласан муруйг нэгтгэсэн. дараа жил. Удалгүй дэлхийн бүх боомтуудад ижил төстэй муруйг зурав.

Хэрэв процесс нь тасалдсан функцээр эвдэрсэн бол?

Тэр үед далайн түрлэгийн давалгааг урьдчилан таамаглах нь ойлгомжтой байсан их хэмжээнийдансны элементүүдийг тооцоолж болно олон тооныүе шат ба далайц зэрэг нь илүү үнэн зөв таамаглалыг өгдөг. Гэсэн хэдий ч синтез хийх ёстой түрлэгийн илэрхийлэл нь огцом үсрэлт агуулсан, өөрөөр хэлбэл тасалдсан тохиолдолд ийм тогтмол байдал ажиглагддаггүй. Хугацааны моментийн хүснэгтээс өгөгдлийг төхөөрөмжид оруулсан тохиолдолд хэд хэдэн Фурье коэффициентийг тооцоолно. Синусоидын бүрэлдэхүүн хэсгүүдийн ачаар анхны функц сэргээгддэг (олдсон коэффициентүүдийн дагуу). Анхны болон сэргээгдсэн илэрхийлэл хоорондын зөрүүг ямар ч үед хэмжиж болно. Давтан тооцоолол, харьцуулалт хийх үед хамгийн том алдааны утга буурахгүй байгааг харж болно. Гэсэн хэдий ч тэдгээр нь тасалдсан цэгт харгалзах бүс нутагт нутагшсан бөгөөд бусад цэгүүдэд тэглэх хандлагатай байдаг. 1899 онд энэ үр дүнг Йелийн их сургуулийн Жошуа Виллард Гиббс онолын хувьд баталжээ.

Фурье цувралын нэгдэл ба математикийн ерөнхий хөгжил

Фурье шинжилгээ нь тодорхой интервалд хязгааргүй тооны тэсрэлт агуулсан илэрхийлэлд хамаарахгүй. Ерөнхийдөө Фурье цуваа, хэрэв анхны функц нь бодит үр дүнгээр дүрслэгдсэн бол физик хэмжээс, үргэлж нийлдэг. Функцийн тодорхой ангиудын хувьд энэ үйл явцыг нэгтгэх тухай асуултууд нь математикийн шинэ хэсгүүд, жишээлбэл, ерөнхий функцүүдийн онолууд гарч ирэхэд хүргэсэн. Энэ нь Л.Шварц, Ж.Микусинский, Ж.Темпл зэрэг нэртэй холбоотой. Энэ онолын хүрээнд тодорхой бөгөөд тодорхой онолын суурьДирак дельта функц (энэ нь нэг цэгийн хязгааргүй жижиг орчимд төвлөрсөн нэг талбайн мужийг дүрсэлдэг) болон Хевисайдын "алхам" гэх мэт илэрхийллийн дор. Энэхүү ажлын ачаар Фурье цуврал нь цэгийн цэнэг, цэгийн масс, соронзон диполь, мөн цацраг дээрх төвлөрсөн ачаалал зэрэг зөн совингийн ойлголтууд гарч ирдэг тэгшитгэл, асуудлыг шийдвэрлэхэд хэрэглэгдэх болсон.

Фурье арга

Интерференцийн зарчмуудын дагуу Фурье цуврал нь өргөтгөлөөс эхэлдэг нарийн төвөгтэй хэлбэрүүдилүү энгийн хүмүүст. Жишээлбэл, дулааны урсгалын өөрчлөлтийг дулаан тусгаарлагч материалаас янз бүрийн саад тотгороор дамжин өнгөрөх замаар тайлбарладаг. жигд бус хэлбэрэсвэл дэлхийн гадаргуугийн өөрчлөлт - газар хөдлөлт, тойрог замд өөрчлөлт орох тэнгэрийн бие- гаригуудын нөлөө. Дүрмээр бол энгийн сонгодог системийг дүрсэлсэн ижил төстэй тэгшитгэлийг долгион бүрийн хувьд энгийн байдлаар шийддэг. Фурье үүнийг харуулсан энгийн шийдлүүдмөн илүү олон шийдлийг олж авахын тулд нэгтгэж болно сорилттой даалгаварууд. Математикийн хэлээр илэрхийлсэн Фурье цуврал нь илэрхийлэлийг гармоник - косинус ба синусоидуудын нийлбэр хэлбэрээр илэрхийлэх арга юм. Тиймээс энэ шинжилгээг "гармоник анализ" гэж бас нэрлэдэг.

Фурье цуврал бол "компьютерийн эрин үе"-ийн өмнөх хамгийн тохиромжтой техник юм.

Компьютерийн технологийг бий болгохоос өмнө Фурье техник нь манай дэлхийн долгионы шинж чанартай ажиллахад эрдэмтдийн зэвсэглэлд байсан хамгийн шилдэг зэвсэг байсан. Фурье цуврал нь нарийн төвөгтэй хэлбэрээр Ньютоны механикийн хуулиудад шууд хэрэглэгдэх энгийн асуудлуудыг шийдвэрлэх боломжийг олгодог. үндсэн тэгшитгэл. 19-р зууны Ньютоны шинжлэх ухааны ихэнх нээлтүүд зөвхөн Фурьегийн техникээр л боломжтой болсон.

Өнөөдөр Фурье цуврал

Компьютер хөгжихийн хэрээр Фурьегийн хувиргалт нь чанарын шинэ түвшинд гарсан. Энэхүү техник нь шинжлэх ухаан, технологийн бараг бүх салбарт бат бөх нэвтэрсэн. Жишээ нь дижитал аудио болон видео дохио юм. Үүнийг хэрэгжүүлэх нь зөвхөн боловсруулсан онолын ачаар л боломжтой болсон Францын математикч XIX зууны эхээр. Ийнхүү Фурье цуврал нь нарийн төвөгтэй хэлбэрээр сансар огторгуйн судалгаанд нээлт хийх боломжтой болсон. Үүнээс гадна энэ нь хагас дамжуулагч материал ба плазмын физик, богино долгионы акустик, далай судлал, радар, газар хөдлөлт судлалын судалгаанд нөлөөлсөн.

Тригонометрийн Фурье цуврал

Математикийн хувьд Фурье цуврал нь дур зоргоороо илэрхийлэх арга юм нарийн төвөгтэй функцуудэнгийн нийлбэр. IN нийтлэг тохиолдлуудийм илэрхийллийн тоо хязгааргүй байж болно. Түүгээр ч зогсохгүй тэдний тоог тооцоололд харгалзан үзэх тусам эцсийн үр дүн илүү нарийвчлалтай болно. Ихэнхдээ хамгийн энгийн байдлаар ашиглагддаг тригонометрийн функцуудкосинус эсвэл синус. Энэ тохиолдолд Фурье цувааг тригонометр гэж нэрлэдэг ба ийм илэрхийллийн шийдлийг гармоникийн тэлэлт гэж нэрлэдэг. Энэ арга нь тоглодог чухал үүрэгматематикт. Юуны өмнө тригонометрийн цуваа нь дүрслэх хэрэгсэл болохоос гадна функцийг судлах боломжийг олгодог бөгөөд энэ нь онолын үндсэн аппарат юм. Нэмж дурдахад энэ нь математикийн физикийн хэд хэдэн асуудлыг шийдвэрлэх боломжийг олгодог. Эцэст нь энэ онол нь математикийн шинжлэх ухааны хэд хэдэн маш чухал хэсгийг (интегралын онол, үечилсэн функцын онол) хөгжүүлэхэд хувь нэмэр оруулж, амьдралд авчирсан. Нэмж дурдахад энэ нь бодит хувьсагчийн дараах функцуудыг хөгжүүлэх эхлэлийн цэг болж, гармоник шинжилгээний эхлэлийг тавьсан юм.

2π үетэй үечилсэн функцүүдийн Фурье цуврал.

Фурье цуврал нь үечилсэн функцийг бүрэлдэхүүн хэсгүүдэд задлах замаар судлах боломжийг олгодог. хувьсах гүйдэлба хүчдэл, шилжилт хөдөлгөөн, тахир механизмын хурд, хурдатгал, акустик долгион нь ердийн зүйл юм практик жишээүечилсэн функцийг инженерийн тооцоонд ашиглах.

Фурье цувралын өргөтгөл нь бүх гэсэн таамаглал дээр суурилдаг практик үнэ цэнэ-π ≤x≤ π интервал дахь функцуудыг нэгтгэсэн тригонометрийн цуваагаар илэрхийлж болно (хэрэв гишүүдээс бүрдсэн хэсэгчилсэн нийлбэрүүдийн дараалал нийлдэг бол цувралыг нийлсэн гэж үзнэ):

Sinx болон cosx-ийн нийлбэрээр дамжуулан стандарт (=ердийн) тэмдэглэгээ

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

Энд a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. нь бодит тогтмолууд, өөрөөр хэлбэл.

Энд -π-ээс π хүртэлх мужид Фурье цувралын коэффициентүүдийг дараах томъёогоор тооцоолно.

a o ,a n ба b n коэффициентүүдийг нэрлэнэ Фурье коэффициентүүд, хэрэв тэдгээрийг олж чадвал (1) цувралыг дуудна Фурьегийн ойролцоо, f(x) функцтэй харгалзах. Цуврал (1)-ийн хувьд (a 1 cosx+b 1 sinx) нэр томъёог эхний буюу гэж нэрлэдэг гол гармоник,

Цуврал бичих өөр нэг арга бол acosx+bsinx=csin(x+α) хамаарлыг ашиглах явдал юм.

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

ao нь тогтмол бол c 1 \u003d (a 1 2 +b 1 2) 1/2, cn \u003d (2 +bn 2) 1/2 нь янз бүрийн бүрэлдэхүүн хэсгүүдийн далайц бөгөөд \-тэй тэнцүү байна. u003d arctg an /b n.

(1) цувралын хувьд (a 1 cosx + b 1 sinx) эсвэл c 1 sin (x + α 1) нэр томъёог эхний буюу гол гармоник,(a 2 cos2x+b 2 sin2x) эсвэл c 2 sin(2x+α 2)-ийг гэнэ. хоёр дахь гармоникгэх мэт.

Нарийн төвөгтэй дохиог үнэн зөв илэрхийлэхийн тулд ихэвчлэн хязгааргүй тооны нэр томъёо шаардлагатай байдаг. Гэсэн хэдий ч олон практик асуудалд зөвхөн эхний хэдэн нэр томъёог авч үзэх нь хангалттай юм.

2π үетэй үечилсэн бус функцүүдийн Фурье цуваа.

Тогтмол бус функцүүдийн задрал.

Хэрэв f(x) функц нь үечилсэн бус байвал x-ийн бүх утгыг Фурье цувралд өргөтгөх боломжгүй. Гэсэн хэдий ч 2π өргөнтэй аль ч муж дахь функцийг илэрхийлэх Фурье цувралыг тодорхойлох боломжтой.

Тогтмол бус функцийг өгөгдсөн тохиолдолд тодорхой муж доторх f(x) утгуудыг сонгож, энэ мужаас гадуур 2π интервалаар давтах замаар шинэ функц үүсгэж болно. Шинэ функц нь 2π-ийн үетэй үе үе байдаг тул x-ийн бүх утгыг Фурье цувралд өргөжүүлж болно. Жишээлбэл, f(x)=x функц нь үечилсэн биш юм. Гэхдээ хэрэв 0-ээс 2π хүртэлх интервалаар Фурьегийн цуваа болгон өргөтгөх шаардлагатай бол энэ интервалаас гадуур 2π хугацаатай үечилсэн функцийг байгуулна (доорх зурагт үзүүлэв).

f(x)=x гэх мэт үечилсэн бус функцүүдийн хувьд Фурье цувааны нийлбэр нь өгөгдсөн муж дахь бүх цэг дэх f(x)-ийн утгатай тэнцүү боловч цэгүүдийн хувьд f(x)-тэй тэнцүү биш байна. хүрээнээс гадуур. 2π муж дахь үечилсэн бус функцийн Фурье цувралыг олохын тулд Фурьегийн коэффициентүүдийн ижил томъёог ашиглана.

Тэгш ба сондгой функцууд.

Тэд y=f(x) функцийг хэлдэг. бүрХэрэв x-ийн бүх утгын хувьд f(-x)=f(x) байвал. Тэгш функцүүдийн графикууд нь y тэнхлэгт үргэлж тэгш хэмтэй байдаг (өөрөөр хэлбэл тэдгээр нь толин тусгалтай байдаг). Тэгш функцүүдийн хоёр жишээ: y=x 2 ба y=cosx.

Тэд y=f(x) функц гэж хэлдэг. хачин,Хэрэв x-ийн бүх утгын хувьд f(-x)=-f(x) байвал. Хачирхалтай функцүүдийн графикууд нь гарал үүслийн хувьд үргэлж тэгш хэмтэй байдаг.

Олон функц тэгш, сондгой ч биш.

Косинус дахь Фурье цувралын өргөтгөл.

2π үетэй тэгш үечилсэн функцийн Фурье цуврал f(x) нь зөвхөн косинусын гишүүн (өөрөөр хэлбэл синус гишүүн агуулаагүй) бөгөөд тогтмол гишүүнийг агуулж болно. Үүний үр дүнд,

Фурье цувралын коэффициентүүд хаана байна,

2π үетэй f(x) сондгой үечилсэн функцийн Фурье цуваа нь зөвхөн синустай гишүүдийг агуулна (өөрөөр хэлбэл косинустай гишүүнчлэлийг агуулаагүй).

Үүний үр дүнд,

Фурье цувралын коэффициентүүд хаана байна,

Хагас мөчлөгийн Фурье цуврал.

Хэрэв функц нь зөвхөн 0-ээс 2π хүртэл биш, 0-ээс π хүртэлх мужид тодорхойлогдсон бол түүнийг зөвхөн синусуудын хувьд эсвэл зөвхөн косинусын хувьд цуврал болгон өргөжүүлж болно. Үр дүнд нь Фурье цуврал гэж нэрлэдэг Хагас мөчлөг дээр Фурьегийн ойролцоо.

Хэрэв та задралыг авахыг хүсвэл Косинусын хагас цикл дээр Фурье f(x) функц 0-ээс π хүртэлх зайд байвал тэгш үечилсэн функц зохиох шаардлагатай. Зураг дээр. доор f(x)=x функц нь x=0-ээс x=π хүртэлх интервал дээр бүтээгдсэн байна. Тэгш функц нь f(x) тэнхлэгт тэгш хэмтэй байдаг тул бид AB шугамыг зурж үзүүлсний дагуу зурна. доор. Хэрэв бид авч үзсэн интервалаас гадуур үүссэн гурвалжин хэлбэр нь 2π үетэй үе үе байна гэж үзвэл эцсийн график нь дэлгэцийн хэлбэртэй байна. Зураг дээр. доор. Косинус дахь Фурье тэлэлтийг олж авах шаардлагатай тул өмнөх шигээ Фурьегийн a o ба a n коэффициентийг тооцоолно.

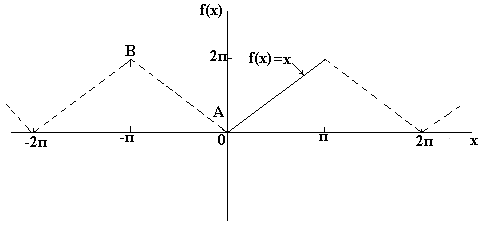
Хэрэв та авах шаардлагатай бол синус хагас цикл Фурье тэлэлт f(x) функц 0-ээс π хүртэлх зайд байвал сондгой үечилсэн функц зохиох шаардлагатай. Зураг дээр. доор f(x)=x функц нь x=0-ээс x=π хүртэлх интервал дээр бүтээгдсэн байна. Сондгой функц нь гарал үүслийн хувьд тэгш хэмтэй тул бид CD шугамыг Зураг дээр үзүүлсэн шиг байгуулна. Хэрэв бид авч үзсэн интервалаас гадуур хүлээн авсан хөрөөний дохио нь 2π-ийн үетэй үе үе байна гэж үзвэл эцсийн график нь Зураг дээр үзүүлсэн хэлбэртэй байна. Фурье тэлэлтийг синусын хувьд хагас мөчлөгт авах шаардлагатай тул өмнөх шигээ Фурьегийн коэффициентийг тооцоолно. б

Дурын интервалд зориулсан Фурье цуваа.

L үетэй үечилсэн функцийг өргөтгөх.

Тогтмол функц f(x) нь x нь L-ээр нэмэгдэхэд давтагдана, i.e. f(x+L)=f(x). Өмнө нь авч үзсэн 2π үетэй функцээс L үетэй функц руу шилжих нь хувьсагчийн өөрчлөлтийг ашиглан хийх боломжтой тул маш энгийн.

-L/2≤x≤L/2 муж дахь f(x) функцийн Фурьегийн цувааг олохын тулд бид шинэ u хувьсагчийг оруулснаар f(x) функц нь u-тай харьцуулахад 2π үетэй байна. u=2πx/L бол u=-π-ийн хувьд x=-L/2, u=π-ийн хувьд x=L/2. Мөн f(x)=f(Lu/2π)=F(u) гэж үзье. Фурье цуврал F(u) хэлбэртэй байна

(Интеграцийн хязгаарыг L урттай дурын интервалаар сольж болно, жишээлбэл, 0-ээс L хүртэл)

L≠2π интервалд өгөгдсөн функцүүдийн хагас цикл дээрх Фурье цуваа.

u=πx/L орлуулалтын хувьд x=0-ээс x=L хүртэлх интервал нь u=0-ээс u=π хүртэлх интервалтай тохирч байна. Тиймээс функцийг зөвхөн косинусын хувьд эсвэл зөвхөн синусын хувьд цуврал болгон өргөжүүлж болно, i.e. in Хагас цикл дээрх Фурье цуврал.

0-ээс L хүртэлх косинусын тэлэлт нь хэлбэртэй байна

Ерөнхий мэргэжлийн боловсролын яам

Сочи Улсын их сургуульаялал жуулчлал

мөн амралтын газрын бизнес

Сурган хүмүүжүүлэх дээд сургууль

Математикийн факультет

Ерөнхий математикийн тэнхим

ДИПЛОМС

Фурье цуврал ба тэдгээрийн хэрэглээ

математик физикийн чиглэлээр.

Гүйцэтгэсэн: 5-р курсын оюутан

өдрийн гарын үсэг

Мэргэжил 010100

"Математик"

Касперова Н.С.

Оюутны үнэмлэх No95471

Эрдэм шинжилгээний зөвлөх: дэд профессор, Ph.D.

техникийн гарын үсэг. Шинжлэх ухаан

Позин П.А.

Сочи, 2000 он

1. Танилцуулга.

2. Фурье цувралын тухай ойлголт.

2.1. Фурье цувралын коэффициентийг тодорхойлох.

2.2. Тогтмол функцүүдийн интегралууд.

3. Фурье цувралын нийлмэл байдлын шалгуур.

3.1. Фурье цуврал дахь функцүүдийн өргөтгөлийн жишээ.

4. Фурье цуврал дахь үечилсэн функцийн өргөтгөлийн тухай тэмдэглэл

5. Тэгш сондгой функцийн Фурье цуваа.

6. 2-р үетэй функцүүдийн Фурье цуваа л .

7. Үелэх бус функцийн Фурье тэлэлт.

Танилцуулга.

Жан Батист Жозеф Фурье - Францын математикч, Парисын Шинжлэх ухааны академийн гишүүн (1817).

Фурьегийн анхны бүтээлүүд нь алгебртай холбоотой. 1796 оны лекцүүд дээр тэрээр бодит язгуурын тооны тухай теоремыг аль хэдийн хэлсэн. алгебрийн тэгшитгэлэдгээр хилийн хооронд хэвтэж (1820 оны хэвлэл), түүний нэрээр нэрлэгдсэн; алгебрийн тэгшитгэлийн бодит язгуурын тооны бүрэн шийдлийг 1829 онд Ж.Ш.Ф. Шуурга. 1818 онд Фурье 1768 онд Францын математикч Ж.Р.-ийн олж авсан ижил төстэй үр дүнгийн талаар мэдээгүй байсан тэгшитгэлийн тоон шийдэлд Ньютоны боловсруулсан аргыг хэрэглэх нөхцөлийн талаархи асуултыг судалжээ. Мурайл. Фурьегийн тэгшитгэлийг шийдвэрлэх тоон аргын талаархи ажлын үр дүн нь нас барсны дараа 1831 онд хэвлэгдсэн "Тодорхой тэгшитгэлийн шинжилгээ" юм.

Фурьегийн судалгааны гол чиглэл нь математик физик байв. 1807, 1811 онд тэрээр хатуу биет дэх дулааны тархалтын онолын талаархи анхны нээлтээ Парисын Шинжлэх ухааны академид танилцуулж, 1822 онд "Дулааны аналитик онол" хэмээх алдартай бүтээлээ хэвлүүлсэн. том үүрэгматематикийн дараагийн түүхэнд. Энэ бол дулаан дамжуулах математикийн онол юм. Аргын нийтлэг байдлаас шалтгаалан энэ ном бүхний эх сурвалж болсон орчин үеийн аргуудматематик физик. Энэ ажилд Фурье олсон дифференциал тэгшитгэлдулаан дамжилтын чанар болон боловсруулсан санаанууд, хамгийн ерөнхий утгаарааӨмнө нь Д.Бернулли тодорхойлсон бөгөөд тодорхой өгөгдсөн хилийн нөхцлийн дулааны тэгшитгэлийг шийдвэрлэхийн тулд хувьсагчдыг салгах аргыг (Фурьегийн арга) боловсруулж, хэд хэдэн онцгой тохиолдлуудад (шоо, цилиндр гэх мэт) хэрэглэжээ. Энэ арга нь функцуудыг тригонометрийн Фурье цувралаар дүрслэн харуулахад суурилдаг.

Фурье цуваа нь одоо хэсэгчилсэн дифференциал тэгшитгэлийн онолд хилийн бодлогын асуудлыг шийдвэрлэх сайн хөгжсөн хэрэгсэл болжээ.

1. Фурье цувралын тухай ойлголт.(х. 94, Уваренков)

Фурье цувралууд нь математик физик, уян хатан байдлын онол, цахилгаан инженерчлэл, ялангуяа тэдгээрийн шинжлэх ухаанд чухал үүрэг гүйцэтгэдэг. онцгой тохиолдолЭдгээр нь тригонометрийн Фурье цувралууд юм.

Тригонометрийн цуваа нь хэлбэрийн цуваа юм

эсвэл бэлгэдлийн хувьд:

(1)

Энд ω, a 0 , a 1 , …, a n , …, b 0 , b 1 , …, b n , … нь тогтмол тоонууд (ω>0) .

Физикийн зарим асуудлууд түүхэндээ ийм цувралуудыг судлахад хүргэсэн, жишээлбэл, утаснуудын чичиргээний асуудал (18-р зуун), дулаан дамжилтын үзэгдлийн зүй тогтолын асуудал гэх мэт. Хэрэглээнд тригонометрийн цувааг авч үзэх. , нь үндсэндээ y = ƒ(χ) тэгшитгэлээр тодорхойлсон өгөгдсөн хөдөлгөөнийг илэрхийлэх асуудалтай холбоотой.

ихэвчлэн хязгааргүй байдлаар авдаг хамгийн энгийн гармоник хэлбэлзлийн нийлбэр хэлбэрээр их тоо, өөрөөр хэлбэл (1) хэлбэрийн цувааны нийлбэр байдлаар.

Тиймээс бид дараах асуудалд хүрнэ: өгөгдсөн интервал дээрх ƒ(x) функцийн хувьд энэ интервал дээр энэ функцэд нийлэх цуваа (1) байгаа эсэхийг олж мэдэх. Хэрэв ингэх боломжтой бол ƒ(x) функц нь энэ интервал дээр тригонометрийн цуваа болж тэлнэ гэж хэлнэ.

Цуврал (1) нь функцүүдийн үечилсэн байдлаас шалтгаалан x 0 цэгт нийлдэг

(n=1,2,..), энэ нь мөн хэлбэрийн бүх цэгүүдэд нийлэх болно (m нь дурын бүхэл тоо), улмаар түүний S(x) нийлбэр нь (цувралын нийлэх мужид) үе үе байх болно. функц: хэрэв S n ( x) - n-р хэсэгЭнэ цувралын нийлбэр, тэгвэл бид байна

Тиймээс

, өөрөөр хэлбэл S(x 0 +T)=S(x 0). Иймд ƒ(x) функцийг (1) хэлбэрийн цуваа болгон өргөтгөх тухай ярихдаа ƒ(x)-ийг үечилсэн функц гэж үзнэ.

2. Цувралын коэффициентийг Фурье томъёогоор тодорхойлох.

2π хугацаатай ƒ(x) үечилсэн функцийг (-π, π) интервал дахь өгөгдсөн функцэд ойртож буй тригонометрийн цуваагаар дүрслэгдэхээр, өөрөөр хэлбэл энэ цувааны нийлбэр болно.

. (2)

Энэ тэгшитгэлийн зүүн талын функцийн интеграл нь энэ цувралын гишүүн орнуудын интегралуудын нийлбэртэй тэнцүү гэж бодъё. Хэрэв бид өгөгдсөн тригонометрийн цувралын коэффициентуудаас бүрдэх тооны цуваа туйлын нийлдэг, өөрөөр хэлбэл эерэг тооны цуваа нийлдэг гэж үзвэл энэ нь үнэн болно.

(3)

Цуврал (1) нь үндсэн шинж чанартай бөгөөд (-π, π) интервалд гишүүнээр нь нэгтгэж болно. Бид тэгш байдлын хоёр хэсгийг нэгтгэдэг (2):

.

Бид баруун талд байгаа интеграл бүрийг тусад нь тооцдог.

, , .

Энэ замаар,

, хаана . (4)

Фурье коэффициентийн тооцоо.(Бугров)

Теорем 1. 2π үеийн ƒ(x) функцийг тасралтгүй дериватив ƒ ( s) (x) дараалал Бүх бодит тэнхлэг дээрх тэгш бус байдлыг хангах:

│ ƒ (s) (x)│≤ M s ; (тав)

дараа нь функцийн Фурье коэффициентүүд ƒ тэгш бус байдлыг хангана

(6)

Баталгаа. Хэсэг хэсгээр нэгтгэж, үүнийг харгалзан үзэх

ƒ(-π) = ƒ(π), бидэнд байна

ƒ ΄ , …, ƒ (s-1) деривативууд тасралтгүй бөгөөд (s-1) гэж үзээд (7)-ын баруун талыг дараалан интегралцвал ижил утгууд t = -π ба t = π цэгүүд, түүнчлэн тооцоолол (5) дээр бид эхний тооцоог (6) авна.

Хоёр дахь тооцоог (6) ижил төстэй аргаар олж авна.

Теорем 2. Фурье коэффициент ƒ(x) нь тэгш бус байдлыг хангана

(8)

Баталгаа. Бидэнд байгаа

Байгаль, технологид тохиолддог олон үйл явц нь тодорхой давтамжтайгаар давтагдах шинж чанартай байдаг. Ийм процессыг үе үе гэж нэрлэдэг бөгөөд математикийн хувьд үечилсэн функцээр тодорхойлогддог. Эдгээр шинж чанарууд орно нүгэл(х) , cos(х) , нүгэл(wx), cos(wx) . Хоёр үечилсэн функцийн нийлбэр, жишээлбэл, хэлбэрийн функц , ерөнхийдөө үе үе байхаа больсон. Гэхдээ харьцаж байгаа бол үүнийг харуулж болно w 1 / w 2 нь рационал тоо бол энэ нийлбэр нь үечилсэн функц болно.

Хамгийн энгийн үечилсэн процессууд - гармоник хэлбэлзэл нь үечилсэн функцээр тодорхойлогддог нүгэл(wx) Тэгээд cos(wx). Илүү нарийн төвөгтэй үечилсэн процессуудыг хэлбэрийн төгсгөлтэй эсвэл хязгааргүй тооны гишүүнчлэлийн аль нэгээс бүрдэх функцээр дүрсэлдэг. нүгэл(wx) Тэгээд cos(wx).

3.2. тригонометрийн цуврал. Фурье коэффициентүүд

Маягтын функциональ цувралыг авч үзье.

Энэ мөрийг нэрлэдэг тригонометр; тоо гэхдээ 0 , б 0 , а 1 , б 1 , гэхдээ 2 , б 2 …, а n , б n ,… дуудсан коэффициентүүдтригонометрийн цуврал. Цуврал (1) нь ихэвчлэн дараах байдлаар бичигддэг.

. (2)

Тригонометрийн цувралын гишүүд (2) нийтлэг үетэй байдаг
, тэгвэл цувааны нийлбэр нь нийлбэл мөн үетэй үетэй функц болно
.

функц гэж үзье е(х) Энэ цувралын нийлбэр нь:

. (3)

Энэ тохиолдолд функцийг гэж хэлнэ е(х) тригонометрийн цуваа болж өргөжиж байна. Энэ цуваа интервалд жигд нийлдэг гэж үзвэл
, та түүний коэффициентийг томъёогоор тодорхойлж болно:

,
,
. (4)

Эдгээр томьёогоор тодорхойлогддог цувралын коэффициентүүдийг нэрлэнэ Фурье коэффициентүүд.

Коэффициент нь Фурье (4) томъёогоор тодорхойлогддог тригонометрийн цуваа (2) гэж нэрлэгддэг. Фурьегийн ойролцоофункцтэй тохирч байна е(х).

Тиймээс, хэрэв үечилсэн функц е(х) нь нийлсэн тригонометрийн цувааны нийлбэр бол энэ цуврал нь түүний Фурьегийн цуваа болно.

3.3. Фурье цувралын нэгдэл

Формула (4) нь Фурье коэффициентийг ямар ч интервалын интегралд тооцож болно гэдгийг харуулж байна

- үечилсэн функц, өөрөөр хэлбэл. Ийм функцийн хувьд Фурье цувралыг үргэлж үүсгэж болно. Гэхдээ энэ цуврал функцэд нийлэх үү е(х) мөн ямар нөхцөлд?

Функц гэдгийг санаарай е(х), сегмент дээр тодорхойлсон [ а; б] , хэрэв энэ болон түүний дериватив нь хамгийн ихдээ хязгаарлагдмал тооны нэгдүгээр төрлийн тасалдлын цэгтэй бол түүнийг хэсэгчилсэн гөлгөр гэж нэрлэдэг.

Дараах теорем нь функцийг Фурьегийн цуваа болгон тэлэх хангалттай нөхцөлийг өгдөг.

Дирихлетийн теорем. Байцгаая
- үечилсэн функц е(х) хэсэгчлэн жигд байна
. Дараа нь түүний Фурье цуврал нийлдэг е(х) түүний тасралтгүй байдлын цэг бүр дээр болон үнэ цэнэ 0,5(е(х+0)+ е(х-0)) таслах цэг дээр.

Жишээ 1.

Фурье цуврал дахь функцийг өргөжүүлэх е(х)= х, интервал дээр өгөгдсөн
.

Шийдэл.Энэ функц нь Дирихлегийн нөхцлийг хангадаг тул Фурье цуврал болгон өргөжүүлж болно. Томьёог хэрэглэх (4) ба хэсгүүдээр нэгтгэх арга
, бид Фурье коэффициентийг олно:

Тиймээс функцийн Фурье цуврал е(х) харцтай.