Allgemeine Fourier-Reihe. Fourier-Reihe: Geschichte und Einfluss des mathematischen Mechanismus auf die Entwicklung der Wissenschaft

Die sind schon ziemlich satt. Und ich fühle, dass der Moment gekommen ist, in dem es an der Zeit ist, neue Konserven aus den strategischen Reserven der Theorie zu extrahieren. Ist es möglich, die Funktion auf andere Weise zu einer Reihe zu erweitern? Zum Beispiel ein gerades Liniensegment durch Sinus und Cosinus ausdrücken? Es scheint unglaublich, aber solche scheinbar entfernten Funktionen bieten sich an
"Wiedervereinigung". Neben den bekannten Abschlüssen in Theorie und Praxis gibt es weitere Ansätze, eine Funktion zu einer Reihe zu erweitern.

In dieser Lektion werden wir uns mit der trigonometrischen Fourier-Reihe vertraut machen, das Thema ihrer Konvergenz und Summe ansprechen und natürlich zahlreiche Beispiele für die Erweiterung von Funktionen zu einer Fourier-Reihe analysieren. Ich wollte den Artikel aufrichtig „Fourierreihe für Dummies“ nennen, aber das wäre schlau, da das Lösen von Problemen Kenntnisse in anderen Bereichen der mathematischen Analyse und einige praktische Erfahrungen erfordert. Daher wird die Präambel dem Training von Astronauten ähneln =)

Erstens sollte das Studium der Seitenmaterialien in ausgezeichneter Form angegangen werden. Schläfrig, ausgeruht und nüchtern. Ohne starke Emotionen über ein gebrochenes Hamsterbein und obsessive Gedanken über die Strapazen des Lebens Aquarienfische. Die Fourier-Reihe ist vom Verständnis her nicht schwierig, praktische Aufgaben erfordern jedoch einfach eine erhöhte Konzentration der Aufmerksamkeit – idealerweise sollte man auf äußere Reize komplett verzichten. Die Situation wird durch die Tatsache verschlimmert, dass es keine einfache Möglichkeit gibt, die Lösung und die Antwort zu überprüfen. Wenn Ihre Gesundheit also unterdurchschnittlich ist, dann ist es besser, etwas Einfacheres zu tun. Wahrheit.

Zweitens müssen Sie das Armaturenbrett studieren, bevor Sie in den Weltraum fliegen Raumschiff. Beginnen wir mit den Werten der Funktionen, die auf der Maschine angeklickt werden sollen:

Für jeden natürlichen Wert:

eines) . Und tatsächlich "blitzt" die Sinuskurve die x-Achse durch jedes "pi":
. Bei negativen Werten des Arguments ist das Ergebnis natürlich dasselbe: .

2). Aber das wussten nicht alle. Der Kosinus „pi en“ entspricht einem „Blinklicht“:

Ein negatives Argument ändert nichts am Fall: .

Vielleicht genug.

Und drittens, liebes Kosmonautenkorps, müssen Sie in der Lage sein ... integrieren.
Insbesondere sicher Bringen Sie eine Funktion unter ein Differentialzeichen, partiell integrieren und sich gut verstehen Newton-Leibniz-Formel. Beginnen wir mit den wichtigen Übungen vor dem Flug. Ich empfehle dringend, es nicht zu überspringen, damit Sie später nicht in der Schwerelosigkeit platt machen:

Beispiel 1

Bestimmte Integrale berechnen

wo nimmt natürliche Werte.

Lösung: Die Integration wird über die Variable "x" ausgeführt und in diesem Stadium wird die diskrete Variable "en" als Konstante betrachtet. In allen Integralen Bringen Sie die Funktion unter das Vorzeichen des Differentials:

Eine kurze Version der Lösung, die gut zum Schießen wäre, sieht so aus:

Sich an etwas gewöhnen:

Die vier verbleibenden Punkte sind für sich alleine. Versuchen Sie, die Aufgabe gewissenhaft zu bearbeiten und die Integrale kurz zu ordnen. Beispiellösungen am Ende der Lektion.

Nach einer QUALITÄTSübung ziehen wir Raumanzüge an
und startklar machen!

Erweiterung einer Funktion in einer Fourier-Reihe auf das Intervall

Betrachten wir eine Funktion, die definiert zumindest auf dem Intervall (und möglicherweise auf einem größeren Intervall). Wenn diese Funktion auf dem Segment integrierbar ist, kann sie in eine trigonometrische erweitert werden die Fourierreihe:
, wo sind die sog Fourier-Koeffizienten.

In diesem Fall wird die Nummer angerufen Zersetzungszeit, und die Zahl ist Halbwertszeitzerlegung.

Offensichtlich besteht die Fourier-Reihe im allgemeinen Fall aus Sinus und Cosinus:

Schreiben wir es in der Tat im Detail:

Der Nullterm der Reihe wird normalerweise als geschrieben.

Fourier-Koeffizienten werden mit den folgenden Formeln berechnet:

Ich verstehe sehr gut, dass neue Begriffe für Anfänger immer noch undurchsichtig sind, um das Thema zu studieren: Zersetzungszeit, Halbzyklus, Fourier-Koeffizienten usw. Keine Panik, das ist nicht vergleichbar mit der Aufregung vor dem Gehen Weltraum. Lassen Sie uns alles im nächsten Beispiel herausfinden, bevor Sie es ausführen, was logisch ist, dringende praktische Fragen zu stellen:

Was müssen Sie bei den folgenden Aufgaben tun?

Erweitern Sie die Funktion zu einer Fourier-Reihe. Außerdem ist es oft erforderlich, einen Funktionsgraphen, einen Reihensummengraphen, eine Partialsumme zu zeichnen und bei ausgefeilten Professorenphantasien noch etwas anderes zu tun.

Wie erweitert man eine Funktion in eine Fourier-Reihe?

Im Wesentlichen müssen Sie finden Fourier-Koeffizienten, das heißt, komponiere und berechne drei bestimmte Integrale.

Bitte übertrage die allgemeine Form der Fourier-Reihe und die drei Arbeitsformeln in dein Heft. Ich freue mich sehr, dass bei einigen Besuchern der Website ein Kindheitstraum, Astronaut zu werden, vor meinen Augen wahr wird =)

Beispiel 2

Erweitern Sie die Funktion in eine Fourier-Reihe auf dem Intervall . Erstellen Sie einen Graphen, einen Graphen der Summe einer Reihe und einer Teilsumme.

Lösung: Der erste Teil der Aufgabe besteht darin, die Funktion zu einer Fourier-Reihe zu erweitern.

Der Anfang ist Standard, notieren Sie sich Folgendes:

In diesem Problem ist die Expansionsperiode , Halbperiode .

Wir erweitern die Funktion in einer Fourier-Reihe auf das Intervall:

Unter Verwendung der entsprechenden Formeln finden wir Fourier-Koeffizienten. Jetzt müssen wir drei zusammensetzen und berechnen bestimmte Integrale. Der Einfachheit halber nummeriere ich die Punkte:

1) Das erste Integral ist das einfachste, erfordert aber schon Auge und Auge:

2) Wir verwenden die zweite Formel:

Dieses Integral ist bekannt und er nimmt es Stück für Stück:

Wenn gebraucht gefunden Methode, eine Funktion unter ein Differentialzeichen zu bringen.

Bei der betrachteten Aufgabe ist es bequemer, sie sofort zu verwenden Formel für die partielle Integration in ein bestimmtes Integral :

Ein paar technische Anmerkungen. Zuerst nach Anwendung der Formel der gesamte Ausdruck muss in große Klammern eingeschlossen werden, da vor dem ursprünglichen Integral eine Konstante steht. Lass es uns nicht verlieren! Klammern können bei jedem weiteren Schritt geöffnet werden, ich habe es in der allerletzten Runde gemacht. Im ersten "Stück" Wir zeigen extreme Genauigkeit bei der Substitution, wie Sie sehen können, ist die Konstante aus dem Geschäft und die Integrationsgrenzen werden in das Produkt eingesetzt. Diese Aktion ist mit eckigen Klammern gekennzeichnet. Nun, das Integral des zweiten "Stücks" der Formel ist Ihnen aus der Trainingsaufgabe bekannt ;-)

Und vor allem - die ultimative Aufmerksamkeitskonzentration!

3) Wir suchen den dritten Fourier-Koeffizienten:

Ein Relativer des vorherigen Integrals wird erhalten, was auch ist stückweise integriert:

Diese Instanz ist etwas komplizierter, ich werde die weiteren Schritte Schritt für Schritt auskommentieren:

(1) Der gesamte Ausdruck wird in große Klammern eingeschlossen.. Ich wollte nicht wie ein Langweiler wirken, sie verlieren zu oft die Konstante.

(2) In diesem Fall habe ich diese großen Klammern sofort erweitert. Besondere Aufmerksamkeit widmen wir uns dem ersten „Stück“: das raucht ständig am Rande und beteiligt sich nicht an der Substitution der Integrationsgrenzen ( und ) in das Produkt . Angesichts der Unordnung des Protokolls empfiehlt es sich wiederum, diese Aktion in eckigen Klammern hervorzuheben. Mit dem zweiten "Stück" alles ist einfacher: Hier erschien der Bruch nach dem Öffnen großer Klammern und die Konstante - als Ergebnis der Integration des bekannten Integrals ;-)

(3) In eckigen Klammern führen wir Transformationen durch und im rechten Integral setzen wir die Integrationsgrenzen ein.

(4) Wir entfernen den „Flasher“ aus den eckigen Klammern: , danach öffnen wir die inneren Klammern: .

(5) Wir streichen 1 und -1 in Klammern, wir machen letzte Vereinfachungen.

Endlich alle drei Fourier-Koeffizienten gefunden:

Setze sie in die Formel ein :

Vergessen Sie nicht, in zwei Hälften zu teilen. Im letzten Schritt wird die Konstante ("minus zwei"), die nicht von "en" abhängt, aus der Summe entfernt.

Damit haben wir die Entwicklung der Funktion in einer Fourier-Reihe auf das Intervall erhalten:

Betrachten wir die Frage der Konvergenz der Fourier-Reihe. Ich werde insbesondere die Theorie erläutern Satz von Dirichlet, wörtlich "an den Fingern", wenn Sie also strenge Formulierungen benötigen, schlagen Sie bitte in einem Lehrbuch über Analysis nach (zum Beispiel der 2. Band von Bohan; oder der 3. Band von Fichtenholtz, aber darin ist es schwieriger).

Im zweiten Teil der Aufgabe gilt es, einen Graphen, einen Reihensummengraphen und einen Teilsummengraphen zu zeichnen.

Der Graph der Funktion ist der übliche Gerade im Flugzeug, die mit einer schwarzen gepunkteten Linie gezeichnet ist:

Wir beschäftigen uns mit der Summe der Reihen. Wie Sie wissen, konvergieren Funktionsreihen zu Funktionen. In unserem Fall die konstruierte Fourier-Reihe für jeden Wert von "x" konvergiert gegen die rot dargestellte Funktion. Diese Funktion unterliegt Pausen der 1. Art in Punkten , sondern auch darin definiert (rote Punkte in der Zeichnung)

Auf diese Weise: . Es ist leicht zu erkennen, dass es sich deutlich von der ursprünglichen Funktion unterscheidet, weshalb in der Notation Anstelle eines Gleichheitszeichens wird eine Tilde verwendet.

Untersuchen wir einen Algorithmus, mit dem es bequem ist, die Summe einer Reihe zu bilden.

Auf dem zentralen Intervall konvergiert die Fourier-Reihe zur Funktion selbst (das zentrale rote Segment fällt mit der schwarz gepunkteten Linie der linearen Funktion zusammen).

Lassen Sie uns nun ein wenig über die Natur der betrachteten trigonometrischen Erweiterung sprechen. die Fourierreihe enthält nur periodische Funktionen (Konstante, Sinus und Cosinus), also die Summe der Reihen ist ebenfalls eine periodische Funktion.

Was bedeutet das in unserem konkretes Beispiel? Und das bedeutet, dass die Summe der Reihe –unbedingt periodisch und das rote Segment des Intervalls muss links und rechts unendlich wiederholt werden.

Ich denke, dass jetzt endlich die Bedeutung des Ausdrucks "Zeit der Zersetzung" klar geworden ist. Einfach gesagt, jedes Mal wiederholt sich die Situation immer wieder.

In der Praxis reicht es meist aus, wie in der Zeichnung drei Zersetzungsperioden darzustellen. Nun, und weitere "Stümpfe" benachbarter Perioden - um deutlich zu machen, dass das Diagramm fortgesetzt wird.

Von besonderem Interesse sind Unstetigkeitsstellen 1. Art. An solchen Stellen konvergiert die Fourier-Reihe zu isolierten Werten, die sich genau in der Mitte des Unstetigkeits-"Sprungs" befinden (rote Punkte in der Zeichnung). Wie findet man die Ordinate dieser Punkte? Suchen wir zunächst die Ordinate der „oberen Etage“: Dazu berechnen wir den Wert der Funktion am äußersten rechten Punkt der mittleren Expansionsperiode: . Um die Ordinate der „unteren Etage“ zu berechnen, nehmen Sie am einfachsten den Wert ganz links im gleichen Zeitraum: . Die Ordinate des Mittelwertes ist das arithmetische Mittel der Summe aus „oben und unten“: . Schön ist, dass man beim Erstellen einer Zeichnung sofort sieht, ob die Mitte richtig oder falsch berechnet ist.

Bilden wir eine Partialsumme der Reihe und wiederholen wir gleichzeitig die Bedeutung des Begriffs "Konvergenz". Das Motiv ist aus der Lektion über bekannt die Summe der Zahlenreihe. Lassen Sie uns unser Vermögen im Detail beschreiben:

Um eine Teilsumme zu bilden, musst du null + zwei weitere Terme der Reihe aufschreiben. Also,

In der Zeichnung ist der Graph der Funktion dargestellt in grün, und wie Sie sehen können, „wickelt“ es die gesamte Summe ziemlich eng ein. Wenn wir eine Teilsumme von fünf Termen der Reihe betrachten, wird der Graph dieser Funktion die roten Linien noch genauer annähern, wenn es hundert Terme gibt, dann verschmilzt die „grüne Schlange“ tatsächlich vollständig mit den roten Segmenten, usw. Somit konvergiert die Fourier-Reihe gegen ihre Summe.

Es ist interessant festzustellen, dass jede Teilsumme ist kontinuierliche Funktion, aber die Gesamtsumme der Reihe ist immer noch unstetig.

In der Praxis ist es nicht ungewöhnlich, einen Partialsummengraphen zu erstellen. Wie kann man das machen? In unserem Fall ist es notwendig, die Funktion auf dem Segment zu berücksichtigen und ihre Werte an den Enden des Segments und an Zwischenpunkten zu berechnen (je mehr Punkte Sie berücksichtigen, desto genauer wird das Diagramm). Dann sollten Sie diese Punkte auf der Zeichnung markieren und sorgfältig ein Diagramm über die Periode zeichnen und es dann in benachbarte Intervalle „replizieren“. Wie sonst? Approximation ist schließlich auch eine periodische Funktion ... ... deren Graph erinnert mich irgendwie an einen gleichmäßigen Herzrhythmus auf dem Display eines Medizingerätes.

Natürlich ist es nicht sehr bequem, die Konstruktion durchzuführen, da Sie äußerst vorsichtig sein müssen und eine Genauigkeit von nicht weniger als einem halben Millimeter einhalten müssen. Ich werde jedoch Leser erfreuen, die mit dem Zeichnen uneins sind - bei einer "echten" Aufgabe ist es bei weitem nicht immer notwendig, eine Zeichnung durchzuführen, irgendwo in 50% der Fälle ist es erforderlich, die Funktion zu einer Fourier-Reihe zu erweitern und das ist es.

Nach Abschluss der Zeichnung erledigen wir die Aufgabe:

Antworten:

Bei vielen Aufgaben leidet die Funktion Ruptur 1. Art direkt am Zersetzungszeitraum:

Beispiel 3

Erweitern Sie in einer Fourier-Reihe die auf dem Intervall gegebene Funktion. Zeichnen Sie einen Graphen der Funktion und der Gesamtsumme der Reihe.

Die vorgeschlagene Funktion ist stückweise gegeben (und wohlgemerkt nur auf dem Segment) und aushalten Ruptur 1. Art am Punkt . Kann man die Fourier-Koeffizienten berechnen? Kein Problem. Sowohl der linke als auch der rechte Teil der Funktion sind in ihren Intervallen integrierbar, daher sollten die Integrale in jeder der drei Formeln als Summe von zwei Integralen dargestellt werden. Sehen wir uns zum Beispiel an, wie dies für einen Koeffizienten von Null gemacht wird:

Das zweite Integral stellte sich als gleich Null heraus, was die Arbeit reduzierte, aber das ist nicht immer der Fall.

Zwei andere Fourier-Koeffizienten werden ähnlich geschrieben.

Wie zeigt man die Summe einer Reihe an? Auf dem linken Intervall zeichnen wir ein gerades Liniensegment und auf dem Intervall - ein gerades Liniensegment (markieren Sie den Achsenabschnitt fett-fett). Das heißt, im Expansionsintervall stimmt die Summe der Reihe überall mit der Funktion überein, mit Ausnahme von drei "schlechten" Punkten. An der Unstetigkeitsstelle der Funktion konvergiert die Fourier-Reihe gegen einen isolierten Wert, der genau in der Mitte des „Sprungs“ der Unstetigkeit liegt. Es ist nicht schwer, es mündlich zu sehen: linke Grenze:, rechte Grenze: und offensichtlich ist die Ordinate des Mittelpunkts 0,5.

Aufgrund der Periodizität der Summe muss das Bild in benachbarte Perioden „multipliziert“ werden, insbesondere auf den Intervallen und dasselbe darstellen. In diesem Fall konvergiert die Fourier-Reihe an den Punkten gegen die Medianwerte.

Eigentlich gibt es hier nichts Neues.

Versuchen Sie, dieses Problem selbst zu lösen. Ein ungefähres Beispiel für feines Design und Zeichnen am Ende der Lektion.

Entwicklung einer Funktion in einer Fourier-Reihe auf eine beliebige Periode

Für eine beliebige Expansionsperiode, bei der "el" eine beliebige positive Zahl ist, unterscheiden sich die Formeln für die Fourier-Reihe und die Fourier-Koeffizienten in einem etwas komplizierteren Sinus- und Cosinus-Argument:

Wenn , dann erhalten wir die Formeln für das Intervall, mit dem wir begonnen haben.

Der Algorithmus und die Prinzipien zur Lösung des Problems bleiben vollständig erhalten, aber die technische Komplexität der Berechnungen nimmt zu:

Beispiel 4

Erweitern Sie die Funktion zu einer Fourier-Reihe und zeichnen Sie die Summe.

Lösung: in der Tat ein Analogon von Beispiel Nr. 3 mit Ruptur 1. Art am Punkt . In diesem Problem ist die Expansionsperiode , Halbperiode . Die Funktion ist nur auf dem Halbintervall definiert, aber das ändert nichts - es ist wichtig, dass beide Teile der Funktion integrierbar sind.

Erweitern wir die Funktion zu einer Fourier-Reihe:

Da die Funktion am Ursprung unstetig ist, sollte jeder Fourier-Koeffizient offensichtlich als Summe zweier Integrale geschrieben werden:

1) Ich schreibe das erste Integral so detailliert wie möglich:

2) Schauen Sie vorsichtig in die Oberfläche des Mondes:

Zweites Integral Teile aufnehmen:

Worauf sollten Sie genau achten, nachdem wir die Fortsetzung der Lösung mit einem Sternchen geöffnet haben?

Erstens verlieren wir das erste Integral nicht , wo wir sofort ausführen unter das Vorzeichen des Differentials bringen. Zweitens, vergessen Sie nicht die unglückselige Konstante vor den großen Klammern und Lassen Sie sich nicht von Zeichen verwirren bei Verwendung der Formel . Große Klammern ist es schließlich bequemer, sie gleich im nächsten Schritt zu öffnen.

Der Rest ist eine Frage der Technik, nur unzureichende Erfahrung beim Lösen von Integralen kann zu Schwierigkeiten führen.

Ja, es war nicht umsonst, dass die bedeutenden Kollegen des französischen Mathematikers Fourier empört waren - wie konnte er es wagen, Funktionen in trigonometrische Reihen zu zerlegen?! =) Wahrscheinlich interessiert sich übrigens jeder für die praktische Bedeutung der jeweiligen Aufgabe. Fourier selbst arbeitete an einem mathematischen Modell der Wärmeleitung, und in der Folge begann man mit der nach ihm benannten Reihe viele periodische Prozesse zu untersuchen, die in der Außenwelt scheinbar unsichtbar sind. Jetzt habe ich mich übrigens dabei ertappt, dass ich den Graphen des zweiten Beispiels nicht zufällig mit einem periodischen Herzrhythmus verglichen habe. Wer möchte, kann sich damit vertraut machen praktische Anwendung Fourier-Transformationen aus Drittquellen. ... Obwohl es besser ist, es nicht zu tun - es wird als First Love in Erinnerung bleiben =)

3) Angesichts der immer wieder erwähnten Schwachstellen behandeln wir den dritten Koeffizienten:

Teilweise integrieren:

Wir setzen die gefundenen Fourier-Koeffizienten in die Formel ein , ohne zu vergessen, den Nullkoeffizienten zu halbieren:

Lassen Sie uns die Summe der Reihe zeichnen. Lassen Sie uns den Vorgang kurz wiederholen: Auf dem Intervall bauen wir eine Linie und auf dem Intervall - eine Linie. Bei einem Nullwert von "x" setzen wir einen Punkt in die Mitte des "Sprungs" der Lücke und "replizieren" das Diagramm für benachbarte Perioden:


An den "Verbindungspunkten" der Perioden ist die Summe auch gleich den Mittelpunkten des "Sprungs" der Lücke.

Bereit. Ich erinnere Sie daran, dass die Funktion selbst nur im Halbintervall bedingt definiert ist und offensichtlich mit der Summe der Reihen in den Intervallen übereinstimmt

Antworten:

Manchmal ist eine stückweise gegebene Funktion auch auf der Expansionsperiode stetig. Das einfachste Beispiel: . Lösung (Siehe Bohan Band 2) ist dasselbe wie in den beiden vorherigen Beispielen: trotz Funktionskontinuität am Punkt wird jeder Fourier-Koeffizient als Summe zweier Integrale ausgedrückt.

In der Trennungspause Unstetigkeitsstellen 1. Art und/oder "Knoten"-Punkte des Graphen können mehr sein (zwei, drei und im Allgemeinen beliebige Finale Menge). Wenn eine Funktion auf jedem Teil integrierbar ist, dann ist sie auch in einer Fourier-Reihe erweiterbar. Aber aus praktischer Erfahrung erinnere ich mich nicht an eine solche Dose. Trotzdem gibt es schwierigere Aufgaben als gerade betrachtet, und am Ende des Artikels gibt es für alle Links zu Fourier-Reihen mit erhöhter Komplexität.

In der Zwischenzeit entspannen wir uns, lehnen uns in unseren Stühlen zurück und betrachten die endlosen Weiten der Sterne:

Beispiel 5

Erweitern Sie die Funktion in eine Fourier-Reihe auf dem Intervall und zeichnen Sie die Summe der Reihen.

In dieser Aufgabe ist die Funktion kontinuierlich auf dem Zersetzungshalbintervall, was die Lösung vereinfacht. Alles ist Beispiel #2 sehr ähnlich. Aus dem Raumschiff kommst du nicht weg - du musst dich entscheiden =) Musterdesign am Ende der Stunde, der Stundenplan ist beigefügt.

Fourier-Reihenentwicklung von geraden und ungeraden Funktionen

Bei geraden und ungeraden Funktionen wird die Problemlösung spürbar vereinfacht. Und deshalb. Kehren wir zur Erweiterung der Funktion in einer Fourier-Reihe auf eine Periode von "zwei Pi" zurück und beliebiger Zeitraum "zwei Ales" .

Nehmen wir an, unsere Funktion ist gerade. Wie Sie sehen können, enthält der allgemeine Begriff der Reihe gerade Kosinusse und ungerade Sinusse. Und wenn wir eine GERADE-Funktion zerlegen, warum brauchen wir dann ungerade Sinus?! Lassen Sie uns den unnötigen Koeffizienten zurücksetzen: .

Auf diese Weise, Eine gerade Funktion wird nur in Kosinus zu einer Fourier-Reihe erweitert:

Weil die Integrale gerader Funktionenüber ein zu Null symmetrisches Integrationssegment verdoppelt werden, dann werden auch die übrigen Fourier-Koeffizienten vereinfacht.

Für Spanne:

Für ein beliebiges Intervall:

Lehrbuchbeispiele, die in fast jedem Lehrbuch für Analysis zu finden sind, beinhalten Erweiterungen von geraden Funktionen . Darüber hinaus haben sie sich in meiner persönlichen Praxis immer wieder getroffen:

Beispiel 6

Gegeben eine Funktion. Erforderlich:

1) Erweitern Sie die Funktion in eine Fourier-Reihe mit Punkt , wobei eine beliebige positive Zahl ist;

2) Schreiben Sie die Erweiterung des Intervalls auf, bauen Sie eine Funktion auf und stellen Sie die Gesamtsumme der Reihe graphisch dar.

Lösung: Im ersten Absatz wird vorgeschlagen, das Problem allgemein zu lösen, und das ist sehr praktisch! Es wird einen Bedarf geben - ersetzen Sie einfach Ihren Wert.

1) In diesem Problem ist die Expansionsperiode , Halbperiode . Im weiteren Verlauf, insbesondere beim Integrieren, wird "el" als Konstante betrachtet

Die Funktion ist gerade, was bedeutet, dass sie nur in Kosinus zu einer Fourier-Reihe expandiert: .

Fourier-Koeffizienten werden durch die Formeln gesucht . Achten Sie auf sie unbedingte Vorteile. Zunächst wird die Integration über das positive Segment der Erweiterung durchgeführt, was bedeutet, dass wir das Modul sicher loswerden , wobei nur "x" von zwei Stücken berücksichtigt wird. Und zweitens wird die Integration spürbar vereinfacht.

Zwei:

Teilweise integrieren:

Auf diese Weise:
, während die Konstante , die nicht von "en" abhängt, aus der Summe entfernt wird.

Antworten:

2) Wir schreiben die Erweiterung auf das Intervall, dazu setzen wir den gewünschten Wert der Halbperiode in die allgemeine Formel ein:

Die Fourier-Reihe ist eine Darstellung einer willkürlich genommenen Funktion mit einer bestimmten Periode als Reihe. Im Algemeinen diese Entscheidung heißt die Zerlegung eines Elements in eine orthogonale Basis. Die Erweiterung von Funktionen in einer Fourier-Reihe ist aufgrund der Eigenschaften dieser Transformation beim Integrieren, Differenzieren sowie beim Verschieben eines Ausdrucks in einem Argument und einer Faltung ein ziemlich leistungsfähiges Werkzeug zum Lösen verschiedener Probleme.

Eine Person, die nicht vertraut ist höhere Mathematik, sowie mit den Werken des französischen Wissenschaftlers Fourier, werden höchstwahrscheinlich nicht verstehen, was diese „Serien“ sind und wozu sie dienen. Mittlerweile ist diese Transformation ziemlich dicht in unserem Leben geworden. Es wird nicht nur von Mathematikern verwendet, sondern auch von Physikern, Chemikern, Medizinern, Astronomen, Seismologen, Ozeanographen und vielen anderen. Werfen wir auch einen genaueren Blick auf die Werke des großen französischen Wissenschaftlers, der seiner Zeit voraus eine Entdeckung gemacht hat.

Der Mensch und die Fourier-Transformation

Die Fourier-Reihe ist eine der Methoden (zusammen mit der Analyse und anderen). Dieser Prozess tritt jedes Mal auf, wenn eine Person einen Ton hört. Unser Ohr wandelt Elementarteilchen automatisch in ein elastisches Medium um, sie werden in Reihen (entlang des Spektrums) aufeinanderfolgender Werte des Lautstärkepegels für Töne unterschiedlicher Höhe zerlegt. Als nächstes verwandelt das Gehirn diese Daten in uns vertraute Geräusche. All dies geschieht zusätzlich zu unserem Wunsch oder Bewusstsein, von selbst, aber um diese Prozesse zu verstehen, wird es mehrere Jahre dauern, höhere Mathematik zu studieren.

Mehr zur Fourier-Transformation

Die Fourier-Transformation kann durch analytische, numerische und andere Verfahren durchgeführt werden. Fourier-Reihen beziehen sich auf die numerische Methode zur Zerlegung aller oszillierenden Prozesse – von Meeresgezeiten und Lichtwellen bis hin zu Zyklen der Sonnenaktivität (und anderer astronomischer Objekte). Mit diesen mathematischen Techniken ist es möglich, Funktionen zu analysieren, die beliebige oszillatorische Prozesse als eine Reihe von sinusförmigen Komponenten darstellen, die vom Minimum zum Maximum und umgekehrt verlaufen. Die Fourier-Transformation ist eine Funktion, die die Phase und Amplitude von Sinuskurven beschreibt, die einer bestimmten Frequenz entsprechen. Mit diesem Verfahren lassen sich sehr komplexe Gleichungen lösen, die dynamische Prozesse beschreiben, die unter dem Einfluss von thermischer, Licht- oder elektrischer Energie ablaufen. Außerdem ermöglichen Fourier-Reihen, die konstanten Komponenten in komplexen Schwingungssignalen zu isolieren, was es ermöglichte, die erhaltenen experimentellen Beobachtungen in Medizin, Chemie und Astronomie richtig zu interpretieren.

Geschichtlicher Bezug

Begründer dieser Theorie ist der französische Mathematiker Jean Baptiste Joseph Fourier. Diese Transformation wurde später nach ihm benannt. Zunächst wandte der Wissenschaftler seine Methode an, um die Mechanismen der Wärmeleitung – die Ausbreitung von Wärme in Festkörpern – zu untersuchen und zu erklären. Fourier schlug vor, dass die ursprüngliche unregelmäßige Verteilung in die einfachsten Sinuskurven zerlegt werden kann, von denen jede ihr eigenes Temperaturminimum und -maximum sowie ihre eigene Phase hat. In diesem Fall wird jede dieser Komponenten vom Minimum zum Maximum und umgekehrt gemessen. Die mathematische Funktion, die die oberen und unteren Spitzen der Kurve sowie die Phase jeder der Harmonischen beschreibt, wird als Fourier-Transformation des Temperaturverteilungsausdrucks bezeichnet. Der Autor der Theorie allgemeine Funktion Verteilung, die mathematisch schwer zu beschreiben ist, in eine sehr bequeme Reihe von Cosinus und Sinus, die sich summieren, um die ursprüngliche Verteilung zu ergeben.

Das Prinzip der Verwandlung und die Ansichten der Zeitgenossen

Die Zeitgenossen des Wissenschaftlers – die führenden Mathematiker des frühen 19. Jahrhunderts – akzeptierten diese Theorie nicht. Der Haupteinwand war Fouriers Behauptung, dass eine diskontinuierliche Funktion, die eine gerade Linie oder eine diskontinuierliche Kurve beschreibt, als Summe von sinusförmigen Ausdrücken dargestellt werden kann, die kontinuierlich sind. Betrachten Sie als Beispiel den "Schritt" von Heaviside: Sein Wert ist null links von der Lücke und eins rechts von der Lücke. Diese Funktion beschreibt die Abhängigkeit elektrischer Strom von der temporären Variablen, wenn der Stromkreis geschlossen ist. Die damaligen Zeitgenossen der Theorie hatten noch nie eine solche Situation erlebt, in der ein diskontinuierlicher Ausdruck durch eine Kombination kontinuierlicher, gewöhnlicher Funktionen wie Exponential-, Sinus-, Linear- oder Quadratfunktionen beschrieben wurde.

Was verwirrte französische Mathematiker in der Fourier-Theorie?

Denn wenn der Mathematiker mit seinen Aussagen recht hatte, dann kann man durch Aufsummieren der unendlichen trigonometrischen Fourier-Reihe eine exakte Darstellung des schrittweisen Ausdrucks erhalten, selbst wenn er viele ähnliche Schritte hat. Zu Beginn des 19. Jahrhunderts erschien eine solche Aussage absurd. Aber trotz aller Zweifel haben viele Mathematiker den Umfang der Untersuchung dieses Phänomens erweitert und ihn über die Untersuchung der Wärmeleitfähigkeit hinausgeführt. Die meisten Wissenschaftler quälten sich jedoch weiterhin mit der Frage: „Kann die Summe einer Sinusreihe gegen konvergieren genauer Wert diskontinuierliche Funktion?"

Konvergenz der Fourier-Reihe: Ein Beispiel

Die Frage der Konvergenz stellt sich immer dann, wenn es darum geht, unendliche Zahlenreihen zu summieren. Betrachten Sie ein klassisches Beispiel, um dieses Phänomen zu verstehen. Können Sie jemals die Wand erreichen, wenn jeder aufeinanderfolgende Schritt halb so groß ist wie der vorherige? Angenommen, Sie sind zwei Meter vom Ziel entfernt, der erste Schritt bringt Sie näher an die Halbzeit, der nächste an die Dreiviertelmarke, und nach dem fünften werden Sie fast 97 Prozent des Weges überwinden. Aber egal, wie viele Schritte Sie gehen, Sie werden das beabsichtigte Ziel im streng mathematischen Sinne nicht erreichen. Mittels numerischer Berechnungen lässt sich zeigen, dass es letztlich möglich ist, sich einer beliebig kleinen gegebenen Distanz anzunähern. Dieser Beweis ist gleichbedeutend mit dem Nachweis, dass der Gesamtwert von einem halben, einem Viertel usw. gegen eins tendieren wird.

Eine Frage der Konvergenz: Das zweite Kommen oder Lord Kelvins Gerät

Diese Frage wurde Ende des 19. Jahrhunderts erneut gestellt, als versucht wurde, mithilfe von Fourier-Reihen die Intensität von Ebbe und Flut vorherzusagen. Zu dieser Zeit erfand Lord Kelvin ein Gerät, bei dem es sich um ein analoges Rechengerät handelte, das es Seeleuten der Militär- und Handelsflotte ermöglichte, dies zu verfolgen ein natürliches Phänomen. Dieser Mechanismus bestimmte die Sätze von Phasen und Amplituden aus einer Tabelle mit Gezeitenhöhen und ihren entsprechenden Zeitpunkten, die während des Jahres in einem bestimmten Hafen sorgfältig gemessen wurden. Jeder Parameter war eine sinusförmige Komponente des Gezeitenhöhenausdrucks und war eine der regulären Komponenten. Die Ergebnisse der Messungen wurden in den Rechner von Lord Kelvin eingegeben, der eine Kurve synthetisierte, die die Höhe des Wassers als Funktion der Zeit vorhersagte nächstes Jahr. Sehr bald wurden ähnliche Kurven für alle Häfen der Welt erstellt.

Und wenn der Prozess durch eine unstetige Funktion unterbrochen wird?

Damals schien es naheliegend, dass ein Flutwellen-Prädiktor mit große Menge Elemente des Kontos berechnen können große Menge Phasen und Amplituden und liefern so genauere Vorhersagen. Es stellte sich jedoch heraus, dass diese Regelmäßigkeit in den Fällen nicht beobachtet wird, in denen der zu synthetisierende Gezeitenausdruck einen scharfen Sprung enthielt, dh diskontinuierlich war. Falls Daten aus der Tabelle der Zeitmomente in das Gerät eingegeben werden, berechnet es mehrere Fourier-Koeffizienten. Die ursprüngliche Funktion wird dank der sinusförmigen Komponenten (gemäß den gefundenen Koeffizienten) wiederhergestellt. Die Diskrepanz zwischen dem ursprünglichen und dem wiederhergestellten Ausdruck kann an jedem Punkt gemessen werden. Bei wiederholten Berechnungen und Vergleichen ist zu erkennen, dass der Wert des größten Fehlers nicht abnimmt. Sie sind jedoch in dem Bereich lokalisiert, der dem Diskontinuitätspunkt entspricht, und gehen an jedem anderen Punkt gegen Null. 1899 wurde dieses Ergebnis von Joshua Willard Gibbs von der Yale University theoretisch bestätigt.

Konvergenz von Fourier-Reihen und die Entwicklung der Mathematik im Allgemeinen

Die Fourier-Analyse ist nicht auf Ausdrücke anwendbar, die eine unendliche Anzahl von Bursts in einem bestimmten Intervall enthalten. Im Allgemeinen Fourier-Reihen, wenn die ursprüngliche Funktion durch das Ergebnis einer reellen Zahl dargestellt wird physikalische Dimension, konvergieren immer. Fragen der Konvergenz dieses Prozesses für bestimmte Klassen von Funktionen haben zur Entstehung neuer Bereiche in der Mathematik geführt, beispielsweise der Theorie der verallgemeinerten Funktionen. Es ist mit Namen wie L. Schwartz, J. Mikusinsky und J. Temple verbunden. Im Rahmen dieser Theorie eine klare und präzise theoretischer Hintergrund unter solchen Ausdrücken wie der Dirac-Delta-Funktion (sie beschreibt eine Region eines einzelnen Bereichs, der in einer infinitesimalen Nachbarschaft eines Punktes konzentriert ist) und Heavisides "Schritt". Dank dieser Arbeit wurden Fourier-Reihen anwendbar, um Gleichungen und Probleme zu lösen, in denen intuitive Konzepte auftauchen: eine Punktladung, eine Punktmasse, magnetische Dipole und auch eine konzentrierte Last auf einem Balken.

Fourier-Methode

Fourier-Reihen beginnen gemäß den Prinzipien der Interferenz mit der Entwicklung komplexe Formen zu einfacheren. Beispielsweise wird eine Änderung des Wärmeflusses durch den Durchgang durch verschiedene Hindernisse aus einem wärmeisolierenden Material erklärt. unregelmäßige Form oder eine Veränderung der Erdoberfläche - ein Erdbeben, eine Veränderung der Umlaufbahn Himmelskörper- der Einfluss der Planeten. In der Regel werden ähnliche Gleichungen, die einfache klassische Systeme beschreiben, für jede einzelne Welle elementar gelöst. Fourier hat das gezeigt einfache Lösungen kann auch summiert werden, um eine Lösung von mehr zu erhalten herausfordernde Aufgaben. In der Sprache der Mathematik ausgedrückt, ist die Fourier-Reihe eine Technik zur Darstellung eines Ausdrucks als Summe von Harmonischen – Cosinus und Sinuskurven. Daher wird diese Analyse auch als „Harmonische Analyse“ bezeichnet.

Fourierreihen - die ideale Technik vor dem "Computerzeitalter"

Vor der Entwicklung der Computertechnologie war die Fourier-Technik die beste Waffe im Arsenal der Wissenschaftler bei der Arbeit mit der Wellennatur unserer Welt. Die Fourier-Reihe in komplexer Form ermöglicht die Lösung nicht nur einfacher Probleme, die direkt auf die Gesetze der Newtonschen Mechanik angewendet werden können, sondern auch Grundgleichungen. Die meisten Entdeckungen der Newtonschen Wissenschaft im 19. Jahrhundert wurden nur durch Fouriers Technik ermöglicht.

Fourierreihen heute

Mit der Entwicklung von Computern sind Fourier-Transformationen auf ein qualitativ neues Niveau gestiegen. Diese Technik ist in fast allen Bereichen der Wissenschaft und Technik fest verankert. Ein Beispiel ist ein digitales Audio- und Videosignal. Seine Verwirklichung wurde nur dank der von entwickelten Theorie möglich Französischer Mathematiker zu Beginn des neunzehnten Jahrhunderts. So ermöglichte die Fourier-Reihe in komplexer Form einen Durchbruch in der Erforschung des Weltraums. Darüber hinaus beeinflusste dies das Studium der Physik von Halbleitermaterialien und Plasma, Mikrowellenakustik, Ozeanographie, Radar und Seismologie.

Trigonometrische Fourier-Reihe

In der Mathematik ist eine Fourier-Reihe eine Möglichkeit, beliebige Zahlen darzustellen komplexe Funktionen die Summe der einfacheren. BEI häufige Fälle die Anzahl solcher Ausdrücke kann unendlich sein. Darüber hinaus ist das Endergebnis umso genauer, je mehr ihre Anzahl in der Berechnung berücksichtigt wird. Am häufigsten als das einfachste verwendet trigonometrische Funktionen Kosinus oder Sinus. In diesem Fall werden die Fourier-Reihen als trigonometrisch bezeichnet, und die Lösung solcher Ausdrücke wird als Erweiterung der Harmonischen bezeichnet. Diese Methode spielt wichtige Rolle in Mathematik. Zunächst einmal bietet die trigonometrische Reihe ein Mittel für das Bild sowie für das Studium der Funktionen, sie ist der Hauptapparat der Theorie. Darüber hinaus ermöglicht es die Lösung einer Reihe von Problemen der mathematischen Physik. Schließlich trug diese Theorie zur Entwicklung bei und brachte eine Reihe sehr wichtiger Bereiche der mathematischen Wissenschaft zum Leben (die Theorie der Integrale, die Theorie der periodischen Funktionen). Darüber hinaus diente es als Ausgangspunkt für die Entwicklung der folgenden Funktionen einer reellen Variablen und markierte auch den Beginn der harmonischen Analyse.

Fourier-Reihe periodischer Funktionen mit Periode 2π.

Mit der Fourier-Reihe können Sie periodische Funktionen untersuchen, indem Sie sie in Komponenten zerlegen. Wechselströme und Spannungen, Verschiebungen, Geschwindigkeit und Beschleunigung von Kurbelmechanismen und Schallwellen sind typisch praktische Beispiele Anwendung periodischer Funktionen in technischen Berechnungen.

Die Fourier-Reihenentwicklung basiert auf der Annahme, dass alle praktischer Wert Funktionen im Intervall -π ≤ x≤ π können als konvergente trigonometrische Reihe ausgedrückt werden (eine Reihe wird als konvergent betrachtet, wenn eine aus ihren Mitgliedern zusammengesetzte Folge von Partialsummen konvergiert):

Standard (=übliche) Notation durch die Summe von sinx und cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

wobei a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. reelle Konstanten sind, d.h.

Wobei für den Bereich von -π bis π die Koeffizienten der Fourier-Reihe nach den Formeln berechnet werden:

Die Koeffizienten a o , a n und b n werden aufgerufen Fourier-Koeffizienten, und wenn sie gefunden werden können, wird Reihe (1) aufgerufen in der Nähe von Fourier, entsprechend der Funktion f(x). Für die Reihe (1) wird der Term (a 1 cosx+b 1 sinx) das erste Oder genannt Hauptharmonika,

Eine andere Möglichkeit, eine Reihe zu schreiben, ist die Verwendung der Beziehung acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Wo a o eine Konstante ist, sind c 1 \u003d (a 1 2 + b 1 2) 1/2, c n \u003d (a n 2 + b n 2) 1/2 die Amplituden der verschiedenen Komponenten und gleich a n \ u003d arctg ein n /b n.

Für die Reihe (1) wird der Term (a 1 cosx + b 1 sinx) oder c 1 sin (x + α 1) das erste Oder genannt Hauptharmonika,(a 2 cos2x+b 2 sin2x) oder c 2 sin(2x+α 2) heißt zweite Harmonische usw.

Um ein komplexes Signal genau darzustellen, ist normalerweise eine unendliche Anzahl von Termen erforderlich. Bei vielen praktischen Problemen reicht es jedoch aus, nur die ersten Terme zu betrachten.

Fourier-Reihe nichtperiodischer Funktionen mit Periode 2π.

Zerlegung nichtperiodischer Funktionen.

Wenn die Funktion f(x) nicht periodisch ist, dann kann sie nicht für alle Werte von x in eine Fourier-Reihe entwickelt werden. Es ist jedoch möglich, eine Fourier-Reihe zu definieren, die eine Funktion über einen beliebigen Bereich der Breite 2π darstellt.

Bei einer nichtperiodischen Funktion kann man eine neue Funktion zusammensetzen, indem man f(x)-Werte innerhalb eines bestimmten Bereichs wählt und sie außerhalb dieses Bereichs in 2π-Intervallen wiederholt. Da die neue Funktion periodisch mit einer Periode von 2π ist, kann sie für alle Werte von x in eine Fourier-Reihe entwickelt werden. Beispielsweise ist die Funktion f(x)=x nicht periodisch. Wenn es jedoch notwendig ist, es zu einer Fourier-Reihe auf dem Intervall von 0 bis 2π zu entwickeln, dann wird eine periodische Funktion mit einer Periode von 2π außerhalb dieses Intervalls konstruiert (wie in der folgenden Abbildung gezeigt).

Bei nichtperiodischen Funktionen wie f(x)=x ist die Summe der Fourier-Reihe an allen Punkten im gegebenen Bereich gleich dem Wert von f(x), aber für Punkte ist sie nicht gleich f(x). außerhalb der Reichweite. Um die Fourier-Reihe einer nichtperiodischen Funktion im Bereich 2π zu finden, wird die gleiche Formel der Fourier-Koeffizienten verwendet.

Gerade und ungerade Funktionen.

Sie sagen die Funktion y=f(x) eben wenn f(-x)=f(x) für alle Werte von x. Graphen gerader Funktionen sind immer symmetrisch zur y-Achse (also gespiegelt). Zwei Beispiele für gerade Funktionen: y=x 2 und y=cosx.

Sie sagen, dass die Funktion y=f(x) seltsam, wenn f(-x)=-f(x) für alle Werte von x. Graphen ungerader Funktionen sind immer symmetrisch zum Ursprung.

Viele Funktionen sind weder gerade noch ungerade.

Fourier-Reihenentwicklung in Cosinus.

Die Fourier-Reihe einer geradzahligen periodischen Funktion f(x) mit der Periode 2π enthält nur Cosinus-Terme (d. h. enthält keine Sinus-Terme) und kann einen konstanten Term enthalten. Folglich,

wo sind die Koeffizienten der Fourier-Reihe,

Die Fourier-Reihe einer ungeradzahligen periodischen Funktion f(x) mit Periode 2π enthält nur Terme mit Sinus (d. h. enthält keine Terme mit Cosinus).

Folglich,

wo sind die Koeffizienten der Fourier-Reihe,

Fourier-Reihe auf einem Halbzyklus.

Wenn eine Funktion über einen Bereich definiert ist, sagen wir 0 bis π und nicht nur 0 bis 2π, kann sie nur in Bezug auf Sinus oder nur in Bezug auf Kosinus in eine Reihe erweitert werden. Die resultierende Fourier-Reihe wird aufgerufen in der Nähe von Fourier auf einem Halbzyklus.

Wenn Sie eine Zerlegung erhalten möchten Fourier auf einem Halbzyklus in Cosinus Funktionen f(x) im Bereich von 0 bis π, dann ist es notwendig, eine gerade periodische Funktion zu bilden. Auf Abb. unten ist die Funktion f(x)=x, die auf dem Intervall von x=0 bis x=π aufgebaut ist. Da die gerade Funktion symmetrisch zur f(x)-Achse ist, zeichnen wir die Linie AB, wie in Abb. unter. Wenn wir davon ausgehen, dass außerhalb des betrachteten Intervalls die resultierende Dreiecksform periodisch mit einer Periode von 2π ist, dann hat der endgültige Graph die Form display. in Abb. unter. Da es erforderlich ist, die Fourier-Entwicklung nach wie vor in Cosinus zu erhalten, berechnen wir die Fourier-Koeffizienten a o und a n

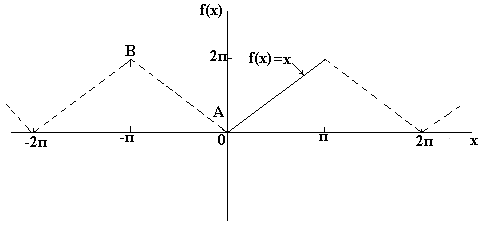
Wenn Sie bekommen müssen Sinus-Halbzyklus-Fourier-Entwicklung Funktion f(x) im Bereich von 0 bis π, dann ist es notwendig, eine ungerade periodische Funktion zu bilden. Auf Abb. unten ist die Funktion f(x)=x, die auf dem Intervall von x=0 bis x=π aufgebaut ist. Da die ungerade Funktion symmetrisch zum Ursprung ist, konstruieren wir die Gerade CD, wie in Abb. Wenn wir davon ausgehen, dass das empfangene Sägezahnsignal außerhalb des betrachteten Intervalls periodisch mit einer Periode von 2π ist, dann hat der endgültige Graph die in Abb. Da es erforderlich ist, die Fourier-Entwicklung auf einem Halbzyklus in Form von Sinus zu erhalten, berechnen wir wie zuvor den Fourier-Koeffizienten. b

Fourier-Reihe für ein beliebiges Intervall.

Erweiterung einer periodischen Funktion mit der Periode L.

Die periodische Funktion f(x) wiederholt sich, wenn x um L zunimmt, d.h. f(x+L)=f(x). Der Übergang von den bisher betrachteten Funktionen mit Periode 2π zu Funktionen mit Periode L ist recht einfach, da er über einen Variablenwechsel erfolgen kann.

Um die Fourier-Reihe der Funktion f(x) im Bereich –L/2≤x≤L/2 zu finden, führen wir eine neue Variable u ein, sodass die Funktion f(x) eine Periode von 2π bezüglich u hat. Wenn u=2πx/L, dann x=-L/2 für u=-π und x=L/2 für u=π. Sei auch f(x)=f(Lu/2π)=F(u). Die Fourier-Reihe F(u) hat die Form

(Integrationsgrenzen können durch beliebige Intervalle der Länge L ersetzt werden, z. B. von 0 bis L)

Fourierreihen auf einer Halbperiode für Funktionen, die im Intervall L≠2π gegeben sind.

Für die Substitution u=πx/L entspricht das Intervall von x=0 bis x=L dem Intervall von u=0 bis u=π. Daher kann die Funktion nur nach Kosinus oder nur nach Sinus in eine Reihe entwickelt werden, d.h. in Fourier-Reihe auf einem Halbzyklus.

Die Kosinusentwicklung im Bereich von 0 bis L hat die Form

Ministerium für allgemeine und berufliche Bildung

Sotschi Staatliche Universität Tourismus

und Resortgeschäft

Pädagogisches Institut

Fakultät für Mathematik

Institut für Allgemeine Mathematik

DIPLOMARBEIT

Fourierreihen und ihre Anwendungen

in der mathematischen Physik.

Abgeschlossen von: Student im 5. Jahr

Tagessignatur

Spezialität 010100

"Mathe"

Kasperova N.S.

Studentenausweis Nr. 95471

Wissenschaftlicher Berater: außerordentlicher Professor, Ph.D.

technische Signatur. Wissenschaften

Posin P.A.

Sotschi, 2000

1. Einleitung.

2. Das Konzept einer Fourier-Reihe.

2.1. Bestimmung der Koeffizienten der Fourier-Reihe.

2.2. Integrale periodischer Funktionen.

3. Kriterien für die Konvergenz von Fourierreihen.

3.1. Beispiele für die Erweiterung von Funktionen in Fourier-Reihen.

4. Eine Anmerkung zur Entwicklung einer periodischen Funktion in einer Fourier-Reihe

5. Fourierreihen für gerade und ungerade Funktionen.

6. Fourierreihe für Funktionen mit Periode 2 l .

7. Fourierentwicklung einer nichtperiodischen Funktion.

Einführung.

Jean Baptiste Joseph Fourier - französischer Mathematiker, Mitglied der Pariser Akademie der Wissenschaften (1817).

Die ersten Arbeiten von Fourier beziehen sich auf Algebra. Bereits in den Vorlesungen von 1796 stellte er den Satz über die Zahl der reellen Wurzeln auf algebraische Gleichung zwischen diesen Grenzen liegend (publiziert 1820), nach ihm benannt; Eine vollständige Lösung für die Anzahl der reellen Wurzeln einer algebraischen Gleichung wurde 1829 von J.Sh.F. Sturm. 1818 untersuchte Fourier die Frage nach den Bedingungen für die Anwendbarkeit der von Newton entwickelten Methode zur numerischen Lösung von Gleichungen, ohne Kenntnis von ähnlichen Ergebnissen, die der französische Mathematiker J.R. Murail. Das Ergebnis von Fouriers Arbeit an numerischen Methoden zum Lösen von Gleichungen ist die Analyse bestimmter Gleichungen, die 1831 posthum veröffentlicht wurde.

Fouriers Hauptstudiengebiet war die mathematische Physik. 1807 und 1811 legte er der Pariser Akademie der Wissenschaften seine ersten Entdeckungen zur Theorie der Wärmeausbreitung in Festkörpern vor, und 1822 veröffentlichte er das bekannte Werk Analytical Theory of Heat, das spielte große Rolle in der späteren Geschichte der Mathematik. Das ist die mathematische Theorie der Wärmeleitung. Aufgrund der Allgemeingültigkeit der Methode ist dieses Buch zur Quelle von allem geworden moderne Methoden Mathematische Physik. In dieser Arbeit leitete Fourier ab Differentialgleichung Wärmeleitfähigkeit und entwickelte Ideen, in den meisten Fällen allgemein gesagt zuvor von D. Bernoulli skizziert, entwickelte eine Methode zur Trennung von Variablen (Fourier-Methode), um die Wärmegleichung für bestimmte gegebene Randbedingungen zu lösen, die er auf eine Reihe von Spezialfällen (Würfel, Zylinder usw.) anwendete. Dieses Verfahren basiert auf der Darstellung von Funktionen durch trigonometrische Fourierreihen.

Fourierreihen sind mittlerweile ein gut entwickeltes Werkzeug in der Theorie partieller Differentialgleichungen zur Lösung von Randwertproblemen.

1. Das Konzept einer Fourier-Reihe.(S. 94, Uwarenkow)

Fourier-Reihen spielen eine wichtige Rolle in der mathematischen Physik, der Elastizitätstheorie, der Elektrotechnik und insbesondere ihrer besonderer Fall sind trigonometrische Fourierreihen.

Eine trigonometrische Reihe ist eine Reihe der Form

oder symbolisch:

(1)

wobei ω, a 0 , a 1 , …, a n , …, b 0 , b 1 , …, b n , … konstante Zahlen sind (ω>0) .

Einige Probleme der Physik führten historisch zum Studium solcher Reihen, zB das Problem der Saitenschwingungen (18. Jh.), das Problem der Gesetzmäßigkeiten bei den Phänomenen der Wärmeleitung etc. In der Anwendung Berücksichtigung trigonometrischer Reihen , bezieht sich hauptsächlich auf das Problem der Darstellung einer gegebenen Bewegung, beschrieben durch die Gleichung y = ƒ(χ), in

in Form der Summe der einfachsten harmonischen Schwingungen, oft ins Unendliche genommen große Zahlen, also als Summe einer Reihe der Form (1).

Damit kommen wir zu folgendem Problem: herauszufinden, ob es für eine gegebene Funktion ƒ(x) auf einem gegebenen Intervall eine Reihe (1) gibt, die auf diesem Intervall gegen diese Funktion konvergieren würde. Wenn dies möglich ist, dann soll die Funktion ƒ(x) auf diesem Intervall zu einer trigonometrischen Reihe expandieren.

Die Reihe (1) konvergiert wegen der Periodizität der Funktionen an einem Punkt x 0

(n=1,2,..), wird sie auch an allen Punkten der Form konvergieren (m ist eine beliebige ganze Zahl), und somit wird ihre Summe S(x) (im Konvergenzbereich der Reihe) eine Periodische sein Funktion: wenn S n ( x) - nter Teil die Summe dieser Reihe, dann haben wir

und deshalb

, d.h. S(x 0 + T)=S(x 0). Wenn wir also über die Erweiterung einer Funktion ƒ(x) in eine Reihe der Form (1) sprechen, nehmen wir an, dass ƒ(x) eine periodische Funktion ist.

2. Bestimmung der Koeffizienten der Reihe durch die Fourier-Formeln.

Eine periodische Funktion ƒ(x) mit einer Periode von 2π sei so beschaffen, dass sie durch eine trigonometrische Reihe dargestellt wird, die im Intervall (-π, π) gegen eine gegebene Funktion konvergiert, d. h. die Summe dieser Reihe ist:

. (2)

Angenommen, das Integral der Funktion auf der linken Seite dieser Gleichheit ist gleich der Summe der Integrale der Terme dieser Reihe. Dies gilt, wenn wir annehmen, dass die aus den Koeffizienten der gegebenen trigonometrischen Reihen zusammengesetzte Zahlenreihe absolut konvergiert, d. h. die positive Zahlenreihe konvergiert

(3)

Reihe (1) ist majorisiert und kann Term für Term im Intervall (-π, π) integriert werden. Wir integrieren beide Teile der Gleichheit (2):

.

Wir berechnen jedes auf der rechten Seite auftretende Integral separat:

, , .

Auf diese Weise,

, wo . (4)

Schätzung der Fourier-Koeffizienten.(Bugrow)

Satz 1. Eine Funktion ƒ(x) der Periode 2π habe eine stetige Ableitung ƒ ( s) (x) Ordnung s Erfüllen der Ungleichung auf der gesamten reellen Achse:

│ ƒ (s) (x)│≤ M s ; (5)

dann die Fourier-Koeffizienten der Funktion ƒ die Ungleichheit befriedigen

(6)

Nachweisen. Teileweise integrieren und das berücksichtigen

ƒ(-π) = ƒ(π), haben wir

Integrieren der rechten Seite von (7) sequentiell unter Berücksichtigung, dass die Ableitungen ƒ ΄ , …, ƒ (s-1) stetig sind und nehmen gleiche Werte an den Punkten t = -π und t = π sowie der Abschätzung (5) erhalten wir die erste Abschätzung (6).

Die zweite Schätzung (6) wird auf ähnliche Weise erhalten.

Satz 2. Die Fourier-Koeffizienten ƒ(x) erfüllen die Ungleichung

(8)

Nachweisen. Wir haben

Viele Prozesse in Natur und Technik haben die Eigenschaft, sich in regelmäßigen Abständen zu wiederholen. Solche Prozesse heißen periodisch und werden mathematisch durch periodische Funktionen beschrieben. Zu diesen Funktionen gehören Sünde(x) , cos(x) , Sünde(wx), cos(wx) . Die Summe zweier periodischer Funktionen, zum Beispiel eine Funktion der Form , ist im Allgemeinen nicht mehr periodisch. Aber es kann gezeigt werden, dass, wenn die Beziehung w 1 / w 2 eine rationale Zahl ist, dann ist diese Summe eine periodische Funktion.

Die einfachsten periodischen Prozesse - harmonische Schwingungen - werden durch periodische Funktionen beschrieben Sünde(wx) und cos(wx). Komplexere periodische Prozesse werden durch Funktionen beschrieben, die entweder aus endlichen oder unendlich vielen Termen der Form zusammengesetzt sind Sünde(wx) und cos(wx).

3.2. trigonometrische Reihe. Fourier-Koeffizienten

Betrachten Sie eine Funktionsreihe der Form:

Diese Reihe heißt trigonometrisch; Zahlen a 0 , b 0 , a 1 , b 1 ,a 2 , b 2 …, a n , b n ,… genannt Koeffizienten trigonometrische Reihe. Reihe (1) wird oft wie folgt geschrieben:

. (2)

Da die Mitglieder der trigonometrischen Reihe (2) eine gemeinsame Periode haben
, dann ist die Summe der Reihe, falls sie konvergiert, auch eine periodische Funktion mit Periode
.

Nehmen wir an, die Funktion f(x) ist die Summe dieser Reihe:

. (3)

In diesem Fall heißt die Funktion f(x) erweitert sich zu einer trigonometrischen Reihe. Angenommen, diese Reihe konvergiert gleichmäßig über das Intervall
, können Sie seine Koeffizienten durch die Formeln bestimmen:

,
,
. (4)

Die durch diese Formeln bestimmten Koeffizienten der Reihe werden aufgerufen Fourier-Koeffizienten.

Die trigonometrische Reihe (2), deren Koeffizienten durch die Fourier-Formeln (4) bestimmt werden, werden aufgerufen in der Nähe von Fourier entsprechend der Funktion f(x).

Wenn also die periodische Funktion f(x) die Summe einer konvergenten trigonometrischen Reihe ist, dann ist diese Reihe ihre Fourier-Reihe.

3.3. Konvergenz der Fourier-Reihe

Die Formeln (4) zeigen, dass die Fourier-Koeffizienten für jedes integrierbare Intervall berechnet werden können

-periodische Funktion, d.h. für eine solche Funktion kann man immer eine Fourier-Reihe bilden. Aber wird diese Reihe zur Funktion konvergieren f(x) und unter welchen bedingungen?

Denken Sie daran, dass die Funktion f(x), auf dem Segment definiert [ a; b] , heißt stückweise glatt, wenn sie und ihre Ableitung höchstens endlich viele Unstetigkeitsstellen erster Art haben.

Der folgende Satz liefert hinreichende Bedingungen für die Entwicklung einer Funktion in eine Fourier-Reihe.

Satz von Dirichlet. Lassen
-periodische Funktion f(x) ist stückweise glatt auf
. Dann konvergiert seine Fourier-Reihe zu f(x) an jedem ihrer Kontinuitätspunkte und zum Wert 0,5(f(x+0)+ f(x-0)) an der Sollbruchstelle.

Beispiel 1.

Erweitern Sie die Funktion in einer Fourier-Reihe f(x)= x, im Intervall gegeben
.

Lösung. Diese Funktion erfüllt die Dirichlet-Bedingungen und kann daher zu einer Fourier-Reihe erweitert werden. Anwendung der Formeln (4) und der Methode der partiellen Integration
, finden wir die Fourier-Koeffizienten:

Also die Fourier-Reihe für die Funktion f(x) hat einen blick.