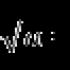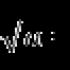Oder kurz - die Ableitung einer impliziten Funktion. Was ist eine implizite Funktion? Da mein Unterricht praktisch ist, versuche ich Definitionen, Formulierungen von Theoremen zu vermeiden, aber hier wäre es angebracht, dies zu tun. Was ist überhaupt eine Funktion?

Eine Funktion einer Variablen ist die Regel, dass jeder Wert der unabhängigen Variablen genau einem Wert der Funktion entspricht.

Die Variable wird aufgerufen unabhängige Variable oder Streit.
Die Variable wird aufgerufen abhängige Variable oder Funktion.

Grob gesagt ist der Buchstabe "y" in diesem Fall die Funktion.

Bisher haben wir Funktionen betrachtet, die in definiert sind explizit bilden. Was bedeutet das? Lassen Sie uns eine Nachbesprechung zu konkreten Beispielen vereinbaren.

Betrachten Sie die Funktion

Wir sehen, dass wir links ein einzelnes "y" (Funktion) haben und rechts - nur x. Nämlich die Funktion ausdrücklich ausgedrückt in Bezug auf die unabhängige Variable .

Betrachten wir eine andere Funktion:

Hier liegen die Variablen und "gemischt". Und irgendwie unmöglich drücken Sie "Y" nur durch "X" aus. Was sind diese Methoden? Übertragen von Termen von Teil zu Teil mit Vorzeichenwechsel, Klammern, Werfen von Faktoren nach der Proportionsregel etc. Schreibe die Gleichheit um und versuche „y“ explizit auszudrücken:. Sie können die Gleichung stundenlang drehen und wenden, aber Sie werden keinen Erfolg haben.

Gestatten Sie mir, Folgendes vorzustellen: - ein Beispiel implizite Funktion.

Im Laufe der mathematischen Analyse wurde bewiesen, dass die implizite Funktion existiert(aber nicht immer), es hat einen Graphen (genau wie eine "normale" Funktion). Dasselbe gilt für eine implizite Funktion. existiert erste Ableitung, zweite Ableitung usw. Wie sie sagen, werden alle Rechte sexueller Minderheiten respektiert.

Und in dieser Lektion werden wir lernen, wie man die Ableitung einer implizit gegebenen Funktion findet. Es ist nicht so schwer! Alle Ableitungsregeln, Ableitungstabelle elementare Funktionen in Kraft bleiben. Der Unterschied liegt in einem besonderen Punkt, den wir gleich betrachten werden.

Ja, und ich sage Ihnen die gute Nachricht - die unten besprochenen Aufgaben werden nach einem ziemlich starren und klaren Algorithmus ohne einen Stein vor drei Spuren ausgeführt.

Beispiel 1

1) In der ersten Phase hängen wir Striche an beide Teile:

2) Wir verwenden die Regeln der Linearität der Ableitung (die ersten beiden Regeln der Lektion Wie finde ich die Ableitung? Lösungsbeispiele):

3) Direkte Differenzierung.
Wie zu differenzieren und völlig verständlich. Was tun, wenn unter den Strichen „Spiele“ stehen?

Nur zur Schande Die Ableitung einer Funktion ist gleich ihrer Ableitung: .

Wie man unterscheidet

Hier haben wir komplexe Funktion. Wieso den? Es scheint, dass es unter dem Sinus nur einen Buchstaben "Y" gibt. Aber Tatsache ist, dass es nur einen Buchstaben "y" gibt - IST EINE FUNKTION FÜR SICH(siehe die Definition am Anfang der Lektion). Der Sinus ist also eine externe Funktion, - interne Funktion. Wir verwenden die Ableitungsregel einer komplexen Funktion :

Das Produkt ist nach der üblichen Regel differenzierbar :

Bitte beachten Sie, dass - auch eine komplexe Funktion ist, Jedes "Spiel mit Schnickschnack" ist eine komplexe Funktion:

Das Design der Lösung selbst sollte in etwa so aussehen:

Wenn Klammern vorhanden sind, öffnen Sie sie:

4) Auf der linken Seite sammeln wir die Begriffe, in denen ein „y“ mit Strich steht. Auf der rechten Seite - wir übertragen alles andere:

5) Auf der linken Seite nehmen wir die Ableitung aus Klammern heraus:

6) Und gemäß der Proportionsregel lassen wir diese Klammern in den Nenner der rechten Seite fallen:

Das Derivat wurde gefunden. Bereit.

Es ist interessant festzustellen, dass jede Funktion implizit umgeschrieben werden kann. Zum Beispiel die Funktion kann so umgeschrieben werden: . Und nach dem eben betrachteten Algorithmus differenzieren. Tatsächlich unterscheiden sich die Ausdrücke „implizite Funktion“ und „implizite Funktion“ in einer semantischen Nuance. Der Ausdruck "implizit definierte Funktion" ist allgemeiner und richtiger, - diese Funktion ist implizit gegeben, aber hier können Sie "y" ausdrücken und die Funktion explizit darstellen. Der Ausdruck "implizite Funktion" bedeutet eine "klassische" implizite Funktion, wenn "y" nicht ausgedrückt werden kann.

Der zweite Lösungsweg

Aufmerksamkeit! Mit der zweiten Methode können Sie sich nur vertraut machen, wenn Sie sicher wissen, wie man partielle Ableitungen findet. Anfänger zum Studieren von Analysis und Dummies, lesen und überspringen Sie diesen Absatz bitte nicht, sonst ist Ihr Kopf ein komplettes Chaos.

Finden Sie die Ableitung der impliziten Funktion auf dem zweiten Weg.

Wir verschieben alle Terme auf die linke Seite:

Und betrachten Sie eine Funktion von zwei Variablen:

Dann kann unsere Ableitung durch die Formel gefunden werden

Lassen Sie uns partielle Ableitungen finden:

Auf diese Weise:

Mit der zweiten Lösung können Sie eine Überprüfung durchführen. Es ist jedoch nicht wünschenswert, eine endgültige Version der Aufgabe für ihn zu erstellen, da partielle Ableitungen später gemeistert werden und ein Student, der sich mit dem Thema „Ableitung einer Funktion einer Variablen“ befasst, partielle Ableitungen nicht kennen sollte.

Sehen wir uns noch ein paar weitere Beispiele an.

Beispiel 2

Finde die Ableitung einer implizit gegebenen Funktion

Wir hängen Striche an beide Teile:

Wir verwenden die Linearitätsregeln:

Derivate finden:

Erweitern aller Klammern:

Wir übertragen alle Terme mit auf die linke Seite, den Rest - auf die rechte Seite:

Auf der linken Seite setzen wir es aus Klammern:

Endgültige Antwort:

Beispiel 3

Finde die Ableitung einer implizit gegebenen Funktion

Vollständige Lösung und Designbeispiel am Ende der Lektion.

Nicht selten treten nach der Differenzierung Brüche auf. In solchen Fällen müssen Fraktionen verworfen werden. Schauen wir uns zwei weitere Beispiele an.

Sehr oft treten bei der Lösung praktischer Probleme (z. B. in der höheren Geodäsie oder der analytischen Photogrammetrie) komplexe Funktionen mehrerer Variablen auf, dh Argumente x, y, z eine Funktion f(x,y,z) ) sind selbst Funktionen der neuen Variablen U, V, W ).

So passiert es beispielsweise beim Bewegen aus einem festen Koordinatensystem Oxyz zum mobilen System Ö 0 UVW und zurück. In diesem Fall ist es wichtig, alle partiellen Ableitungen bezüglich der „festen“ – „alten“ und „bewegten“ – „neuen“ Variablen zu kennen, da diese partiellen Ableitungen in der Regel die Lage eines Objekts in diesen Koordinatensystemen charakterisieren, und insbesondere die Zuordnung von Luftbildern zu einem realen Objekt betreffen . In solchen Fällen gelten die folgenden Formeln:

Das heißt, eine komplexe Funktion gegeben T drei "neue" Variablen U, V, W durch drei "alte" Variablen x, y, z dann:

Kommentar. Variationen in der Anzahl der Variablen sind möglich. Zum Beispiel: Wenn

Insbesondere wenn z = f(xy), y = y(x) , dann erhalten wir die sogenannte "totale Ableitungsformel":

Dieselbe Formel für die "Gesamtableitung" im Fall von:

wird die Form annehmen:

Andere Variationen der Formeln (1.27) - (1.32) sind ebenfalls möglich.

Hinweis: Die „Gesamtableitungsformel“ wird im Physikunterricht, Abschnitt „Hydrodynamik“ bei der Ableitung des fundamentalen Gleichungssystems der Flüssigkeitsbewegung verwendet.

Beispiel 1.10. Gegeben:

Nach (1.31):

§7 Partielle Ableitungen einer implizit gegebenen Funktion mehrerer Variablen

Wie Sie wissen, ist eine implizit definierte Funktion einer Variablen wie folgt definiert: die Funktion der unabhängigen Variablen x heißt implizit, wenn sie durch eine nach nicht aufgelöste Gleichung gegeben ist j :

Beispiel 1.11.

Die gleichung

definiert implizit zwei Funktionen:

Und die Gleichung

definiert keine Funktion.

Satz 1.2 (Existenz einer impliziten Funktion).

Lassen Sie die Funktion z \u003d f (x, y) und seine partiellen Ableitungen F" x und F" j definiert und kontinuierlich in einer Nachbarschaft U M0 Punkte m 0 (x 0 j 0 ) . Außerdem, f(x 0 , ja 0 )=0 und f"(x 0 , ja 0 )≠0 , dann bestimmt Gleichung (1.33) in der Nachbarschaft U M0 implizite Funktion y= y(x) , stetig und in einem Intervall differenzierbar D auf einen Punkt zentriert x 0 , und y(x 0 )=y 0 .

Ohne Beweis.

Aus Satz 1.2 folgt auf diesem Intervall D :

das heißt, es gibt eine Identität in

wobei die "gesamte" Ableitung nach (1.31) gefunden wird

Das heißt, (1.35) gibt implizit eine Formel zum Finden der Ableitung an gegebene Funktion eine Variable x .

Eine implizite Funktion von zwei oder mehr Variablen wird ähnlich definiert.

Zum Beispiel, wenn in einem Bereich v Platz Oxyz die Gleichung ist erfüllt:

dann unter bestimmten Bedingungen auf die Funktion F es definiert implizit eine Funktion

Außerdem werden in Analogie zu (1.35) seine partiellen Ableitungen wie folgt gefunden.

Definition. Die Funktion \(y = f(x) \) sei in einem Intervall definiert, das den Punkt \(x_0 \) enthält. Lassen Sie uns \(\Delta x \) zum Argument erhöhen, um dieses Intervall nicht zu verlassen. Finde das entsprechende Inkrement der Funktion \(\Delta y \) (beim Übergang vom Punkt \(x_0 \) zum Punkt \(x_0 + \Delta x \)) und bilde die Beziehung \(\frac(\Delta y )(\Delta x) \). Gibt es einen Grenzwert dieser Relation bei \(\Delta x \rightarrow 0 \), so wird der angegebene Grenzwert aufgerufen Ableitungsfunktion\(y=f(x) \) am Punkt \(x_0 \) und bezeichnen \(f"(x_0) \).

$$ \lim_(\Delta x \to 0) \frac(\Delta y)(\Delta x) = f"(x_0) $$

Das Symbol y wird oft verwendet, um die Ableitung zu bezeichnen. Beachten Sie, dass y" = f(x) eine neue Funktion ist, aber natürlich mit der Funktion y = f(x) verbunden ist, die an allen Punkten x definiert ist, an denen die obige Grenze existiert. Diese Funktion wird wie folgt aufgerufen: Ableitung der Funktion y \u003d f (x).

Die geometrische Bedeutung der Ableitung besteht aus folgendem. Wenn eine Tangente, die nicht parallel zur y-Achse ist, an einem Punkt mit der Abszisse x \u003d a in den Graphen der Funktion y \u003d f (x) gezeichnet werden kann, dann drückt f (a) die Steigung der Tangente aus:
\(k = f"(a)\)

Da \(k = tg(a) \), ist die Gleichheit \(f"(a) = tg(a) \) wahr.

Und jetzt interpretieren wir die Definition der Ableitung in Bezug auf ungefähre Gleichheiten. Die Funktion \(y = f(x) \) habe an einem bestimmten Punkt \(x \) eine Ableitung:
$$ \lim_(\Delta x \to 0) \frac(\Delta y)(\Delta x) = f"(x) $$
Das bedeutet, dass in der Nähe des Punktes x die ungefähre Gleichheit \(\frac(\Delta y)(\Delta x) \approx f"(x) \), also \(\Delta y \approx f"(x) \cdot \Delta\). Die sinnvolle Bedeutung der erhaltenen ungefähren Gleichheit ist wie folgt: Das Inkrement der Funktion ist „fast proportional“ zum Inkrement des Arguments, und der Proportionalitätskoeffizient ist der Wert der Ableitung in gegebener Punkt X. Beispielsweise gilt für die Funktion \(y = x^2 \) die ungefähre Gleichheit \(\Delta y \approx 2x \cdot \Delta x \). Wenn wir die Definition der Ableitung sorgfältig analysieren, werden wir feststellen, dass sie einen Algorithmus enthält, um sie zu finden.

Formulieren wir es.

Wie finde ich die Ableitung der Funktion y \u003d f (x) ?

1. Wert \(x \) fixieren, \(f(x) \) finden
2. Erhöhe \(x \) Argument \(\Delta x \), gehe zu einem neuen Punkt \(x+ \Delta x \), finde \(f(x+ \Delta x) \)
3. Finden Sie das Funktionsinkrement: \(\Delta y = f(x + \Delta x) - f(x) \)
4. Bilden Sie die Beziehung \(\frac(\Delta y)(\Delta x) \)
5. Berechne $$ \lim_(\Delta x \to 0) \frac(\Delta y)(\Delta x) $$
Diese Grenze ist die Ableitung der Funktion bei x.

Wenn die Funktion y = f(x) an der Stelle x eine Ableitung hat, dann heißt sie an der Stelle x differenzierbar. Das Verfahren zum Ermitteln der Ableitung der Funktion y \u003d f (x) wird aufgerufen Unterscheidung Funktionen y = f(x).

Diskutieren wir folgende Frage: Wie hängen Stetigkeit und Differenzierbarkeit einer Funktion an einem Punkt zusammen?

Die Funktion y = f(x) sei an der Stelle x differenzierbar. Dann kann eine Tangente an den Graphen der Funktion am Punkt M (x; f (x)) gezogen werden, und, erinnern Sie sich, die Steigung der Tangente ist gleich f "(x). Ein solcher Graph kann nicht "brechen". Punkt M, dh die Funktion muss bei x stetig sein.

Es war Argumentation "an den Fingern". Lassen Sie uns ein strengeres Argument präsentieren. Wenn die Funktion y = f(x) im Punkt x differenzierbar ist, dann gilt die ungefähre Gleichheit \(\Delta y \approx f"(x) \cdot \Delta x \). Null, dann ist \(\Delta y \ ) wird ebenfalls gegen Null gehen, und dies ist die Bedingung für die Stetigkeit der Funktion in einem Punkt.

So, Wenn eine Funktion an einem Punkt x differenzierbar ist, dann ist sie dort auch stetig.

Die Umkehrung ist nicht wahr. Zum Beispiel: Funktion y = |x| ist überall stetig, insbesondere im Punkt x = 0, aber die Tangente an den Graphen der Funktion im „Gelenkpunkt“ (0; 0) existiert nicht. Wenn es an einer Stelle unmöglich ist, eine Tangente an den Funktionsgraphen zu ziehen, dann gibt es an dieser Stelle keine Ableitung.

Noch ein Beispiel. Die Funktion \(y=\sqrt(x) \) ist stetig auf dem gesamten Zahlenstrahl, auch am Punkt x = 0. Und die Tangente an den Graphen der Funktion existiert an jedem Punkt, auch am Punkt x = 0 .. An diesem Punkt fällt die Tangente jedoch mit der y-Achse zusammen, dh sie steht senkrecht auf der Abszissenachse, ihre Gleichung hat die Form x \u003d 0. Neigung es gibt keine solche Zeile, was bedeutet, dass \(f"(0) \) auch nicht existiert

Wir haben also eine neue Eigenschaft einer Funktion kennengelernt - die Differenzierbarkeit. Wie können Sie feststellen, ob eine Funktion vom Graphen einer Funktion differenzierbar ist?

Die Antwort ist eigentlich oben gegeben. Lässt sich an irgendeiner Stelle eine Tangente an den Graphen einer Funktion ziehen, die nicht senkrecht zur x-Achse steht, dann ist die Funktion an dieser Stelle differenzierbar. Wenn an einer Stelle die Tangente an den Graphen der Funktion nicht existiert oder senkrecht auf der x-Achse steht, dann ist die Funktion an dieser Stelle nicht differenzierbar.

Abgrenzungsregeln

Die Operation zum Finden der Ableitung wird aufgerufen Unterscheidung. Bei dieser Operation müssen Sie häufig mit Quotienten, Summen, Produkten von Funktionen sowie mit „Funktionen von Funktionen“, also komplexen Funktionen, arbeiten. Aus der Definition der Ableitung lassen sich Ableitungsregeln ableiten, die diese Arbeit erleichtern. Wenn C eine konstante Zahl ist und f=f(x), g=g(x) einige differenzierbare Funktionen sind, dann gilt Folgendes Unterscheidungsregeln:

$$ C"=0 $$ $$ x"=1 $$ $$ (f+g)"=f"+g" $$ $$ (fg)"=f"g + fg" $$ $$ ( Cf)"=Cf" $$ $$ \left(\frac(f)(g) \right) " = \frac(f"g-fg")(g^2) $$ $$ \left(\frac (C)(g) \right) " = -\frac(Cg")(g^2) $$ Ableitung zusammengesetzter Funktionen:
$$ f"_x(g(x)) = f"_g \cdot g"_x $$

Tabelle der Ableitungen einiger Funktionen

$$ \left(\frac(1)(x) \right) " = -\frac(1)(x^2) $$ $$ (\sqrt(x)) " = \frac(1)(2\ sqrt(x)) $$ $$ \left(x^a \right) " = ax^(a-1) $$ $$ \left(a^x \right) " = a^x \cdot \ln a $$ $$ \left(e^x \right) " = e^x $$ $$ (\ln x)" = \frac(1)(x) $$ $$ (\log_a x)" = \frac (1)(x\ln a) $$ $$ (\sin x)" = \cos x $$ $$ (\cos x)" = -\sin x $$ $$ (\text(tg) x) " = \frac(1)(\cos^2 x) $$ $$ (\text(ctg) x)" = -\frac(1)(\sin^2 x) $$ $$ (\arcsin x) " = \frac(1)(\sqrt(1-x^2)) $$ $$ (\arccos x)" = \frac(-1)(\sqrt(1-x^2)) $$ $$ (\text(arctg) x)" = \frac(1)(1+x^2) $$ $$ (\text(arctg) x)" = \frac(-1)(1+x^2) $ $

Wir werden lernen, Ableitungen von Funktionen zu finden, die implizit gegeben sind, das heißt, gegeben durch einige Gleichungen, die Variablen miteinander in Beziehung setzen x und j. Beispiele für implizit definierte Funktionen:

,

,

Ableitungen von impliziten Funktionen oder Ableitungen von impliziten Funktionen sind ziemlich einfach zu finden. Lass es uns jetzt herausfinden entsprechende Regel und ein Beispiel, und finden Sie dann heraus, warum wir es überhaupt brauchen.

Um die Ableitung einer implizit gegebenen Funktion zu finden, müssen beide Seiten der Gleichung nach x differenziert werden. Diejenigen Terme, in denen nur x vorhanden ist, werden zur üblichen Ableitung einer Funktion von x. Und die Terme mit y müssen nach der Ableitungsregel einer komplexen Funktion differenziert werden, da y eine Funktion von x ist. Wenn es ganz einfach ist, dann sollte sich in der resultierenden Ableitung des Terms mit x herausstellen: die Ableitung der Funktion von y, multipliziert mit der Ableitung von y. Zum Beispiel wird die Ableitung des Begriffs als geschrieben, die Ableitung des Begriffs wird als geschrieben. Außerdem ist es aus all dem notwendig, diesen "y-Strich" auszudrücken, und die gewünschte Ableitung der implizit gegebenen Funktion wird erhalten. Schauen wir uns das an einem Beispiel an.

Beispiel 1

Lösung. Wir differenzieren beide Seiten der Gleichung nach x, wobei wir davon ausgehen, dass y eine Funktion von x ist:

Von hier erhalten wir die Ableitung, die in der Aufgabe benötigt wird:

Nun etwas über die mehrdeutige Eigenschaft implizit definierter Funktionen und warum spezielle Regeln für ihre Differenzierung benötigt werden. In manchen Fällen kann man dafür sorgen, dass die Substitution in einer gegebenen Gleichung (siehe Beispiele oben) statt des y ihres Ausdrucks durch x dazu führt, dass diese Gleichung zu einer Identität wird. So. Die obige Gleichung definiert implizit die folgenden Funktionen:

Nachdem wir den Ausdruck y im Quadrat durch x in die ursprüngliche Gleichung eingesetzt haben, erhalten wir die Identität:

.

Die Ausdrücke, die wir ersetzt haben, wurden durch Lösen der Gleichung für das y erhalten.

Wenn wir die entsprechende explizite Funktion differenzieren würden

dann würden wir eine Antwort wie in Beispiel 1 erhalten - von einer implizit angegebenen Funktion:

Aber nicht jede implizit gegebene Funktion kann in der Form dargestellt werden j = F(x) . Also zum Beispiel die implizit definierten Funktionen

werden nicht in elementaren Funktionen ausgedrückt, das heißt, diese Gleichungen können nicht in Bezug auf den Spieler gelöst werden. Daher gibt es eine Regel zum Ableiten einer implizit gegebenen Funktion, die wir bereits untersucht haben und die wir in anderen Beispielen konsequent anwenden werden.

Beispiel 2 Finden Sie die Ableitung einer implizit gegebenen Funktion:

.

Wir drücken die Primzahl y und - am Ausgang - die Ableitung der implizit gegebenen Funktion aus:

Beispiel 3 Finden Sie die Ableitung einer implizit gegebenen Funktion:

.

Lösung. Differenziere beide Seiten der Gleichung nach x:

.

Beispiel 4 Finden Sie die Ableitung einer implizit gegebenen Funktion:

.

Lösung. Differenziere beide Seiten der Gleichung nach x:

.

Wir drücken aus und erhalten die Ableitung:

.

Beispiel 5 Finden Sie die Ableitung einer implizit gegebenen Funktion:

Lösung. Wir übertragen die Terme auf der rechten Seite der Gleichung auf die linke Seite und lassen rechts die Null stehen. Differenziere beide Seiten der Gleichung nach x.

Die Ableitung einer implizit gegebenen Funktion.
Ableitung einer parametrisch definierten Funktion

In diesem Artikel betrachten wir zwei weitere typische Aufgaben, die häufig in Kontrollarbeit an höhere Mathematik. Um den Stoff erfolgreich zu meistern, ist es notwendig, Derivate zumindest auf durchschnittlichem Niveau finden zu können. Wie Sie Derivate praktisch von Grund auf finden, lernen Sie in zwei grundlegenden Lektionen und Ableitung einer komplexen Funktion. Wenn mit Differenzierungsfähigkeit alles in Ordnung ist, dann los.

Ableitung einer implizit definierten Funktion

Oder kurz gesagt die Ableitung einer impliziten Funktion. Was ist eine implizite Funktion? Erinnern wir uns zunächst an die eigentliche Definition einer Funktion einer Variablen:

Funktion einer Variablen gilt die Regel, dass jeder Wert der unabhängigen Variablen genau einem Wert der Funktion entspricht.

Die Variable wird aufgerufen unabhängige Variable oder Streit.
Die Variable wird aufgerufen abhängige Variable oder Funktion .

Bisher haben wir Funktionen betrachtet, die in definiert sind explizit bilden. Was bedeutet das? Lassen Sie uns eine Nachbesprechung zu konkreten Beispielen vereinbaren.

Betrachten Sie die Funktion

Wir sehen, dass wir links ein einsames „y“ haben und rechts - nur x. Nämlich die Funktion ausdrücklich ausgedrückt in Bezug auf die unabhängige Variable .

Betrachten wir eine andere Funktion:

Hier liegen die Variablen und "gemischt". Und irgendwie unmöglich drücken Sie "Y" nur durch "X" aus. Was sind diese Methoden? Übertragen von Termen von Teil zu Teil mit Vorzeichenwechsel, Klammern, Werfen von Faktoren nach der Proportionsregel etc. Schreibe die Gleichheit um und versuche „y“ explizit auszudrücken:. Sie können die Gleichung stundenlang drehen und wenden, aber Sie werden keinen Erfolg haben.

Gestatten Sie mir, Folgendes vorzustellen: - ein Beispiel implizite Funktion.

Im Laufe der mathematischen Analyse wurde bewiesen, dass die implizite Funktion existiert(aber nicht immer), es hat einen Graphen (genau wie eine "normale" Funktion). Dasselbe gilt für eine implizite Funktion. existiert erste Ableitung, zweite Ableitung usw. Wie sie sagen, werden alle Rechte sexueller Minderheiten respektiert.

Und in dieser Lektion werden wir lernen, wie man die Ableitung einer implizit gegebenen Funktion findet. Es ist nicht so schwer! Alle Ableitungsregeln, die Tabelle der Ableitungen elementarer Funktionen bleiben in Kraft. Der Unterschied liegt in einem besonderen Punkt, den wir gleich betrachten werden.

Ja, und ich sage Ihnen die gute Nachricht - die unten besprochenen Aufgaben werden nach einem ziemlich starren und klaren Algorithmus ohne einen Stein vor drei Spuren ausgeführt.

Beispiel 1

1) In der ersten Phase hängen wir Striche an beide Teile:

2) Wir verwenden die Regeln der Linearität der Ableitung (die ersten beiden Regeln der Lektion Wie finde ich die Ableitung? Lösungsbeispiele):

3) Direkte Differenzierung.
Wie zu differenzieren und völlig verständlich. Was tun, wenn unter den Strichen „Spiele“ stehen?

- nur zur Schande, Die Ableitung einer Funktion ist gleich ihrer Ableitung: .

Wie man unterscheidet
Hier haben wir komplexe Funktion. Wieso den? Es scheint, dass es unter dem Sinus nur einen Buchstaben "Y" gibt. Aber Tatsache ist, dass nur ein Buchstabe "y" - IST EINE FUNKTION FÜR SICH(siehe die Definition am Anfang der Lektion). Somit ist der Sinus eine externe Funktion, ist eine interne Funktion. Wir verwenden die Ableitungsregel einer komplexen Funktion :

Das Produkt ist nach der üblichen Regel differenzierbar :

Beachten Sie, dass dies auch eine komplexe Funktion ist, Jedes „Drehspielzeug“ ist eine komplexe Funktion:

Das Design der Lösung selbst sollte in etwa so aussehen:


Wenn Klammern vorhanden sind, öffnen Sie sie:

4) Auf der linken Seite sammeln wir die Begriffe, in denen ein „y“ mit Strich steht. Auf der rechten Seite - wir übertragen alles andere:

5) Auf der linken Seite nehmen wir die Ableitung aus Klammern heraus:

6) Und gemäß der Proportionsregel lassen wir diese Klammern in den Nenner der rechten Seite fallen:

Das Derivat wurde gefunden. Bereit.

Es ist interessant festzustellen, dass jede Funktion implizit umgeschrieben werden kann. Zum Beispiel die Funktion kann so umgeschrieben werden: . Und nach dem eben betrachteten Algorithmus differenzieren. Tatsächlich unterscheiden sich die Ausdrücke „implizite Funktion“ und „implizite Funktion“ in einer semantischen Nuance. Der Ausdruck "implizit definierte Funktion" ist allgemeiner und richtiger, - diese Funktion ist implizit gegeben, aber hier können Sie "y" ausdrücken und die Funktion explizit darstellen. Der Ausdruck "implizite Funktion" bedeutet eine "klassische" implizite Funktion, wenn "y" nicht ausgedrückt werden kann.

Der zweite Lösungsweg

Aufmerksamkeit! Sie können sich nur mit der zweiten Methode vertraut machen, wenn Sie wissen, wie man sicher findet partielle Ableitungen. Rechnen-Anfänger und Dummies bitte lesen und überspringen Sie diesen Absatz nicht, sonst ist der Kopf ein komplettes Durcheinander.

Finden Sie die Ableitung der impliziten Funktion auf dem zweiten Weg.

Wir verschieben alle Terme auf die linke Seite:

Und betrachten Sie eine Funktion von zwei Variablen:

Dann kann unsere Ableitung durch die Formel gefunden werden
Lassen Sie uns partielle Ableitungen finden:

Auf diese Weise:

Mit der zweiten Lösung können Sie eine Überprüfung durchführen. Es ist jedoch nicht wünschenswert, eine endgültige Version der Aufgabe für ihn zu erstellen, da partielle Ableitungen später gemeistert werden und ein Student, der sich mit dem Thema „Ableitung einer Funktion einer Variablen“ befasst, partielle Ableitungen nicht kennen sollte.

Sehen wir uns noch ein paar weitere Beispiele an.

Beispiel 2

Finde die Ableitung einer implizit gegebenen Funktion

Wir hängen Striche an beide Teile:

Wir verwenden die Linearitätsregeln:

Derivate finden:

Erweitern aller Klammern:

Wir übertragen alle Terme mit auf die linke Seite, den Rest - auf die rechte Seite:

Endgültige Antwort:

Beispiel 3

Finde die Ableitung einer implizit gegebenen Funktion

Vollständige Lösung und Designbeispiel am Ende der Lektion.

Nicht selten treten nach der Differenzierung Brüche auf. In solchen Fällen müssen Fraktionen verworfen werden. Schauen wir uns zwei weitere Beispiele an.

Beispiel 4

Finde die Ableitung einer implizit gegebenen Funktion

Wir schließen beide Teile unter Strichen ab und wenden die Linearitätsregel an:

Wir differenzieren nach der Ableitungsregel einer komplexen Funktion und die Ableitungsregel des Quotienten :

Erweitern der Klammern:

Jetzt müssen wir den Bruch loswerden. Dies kann später erfolgen, aber es ist vernünftiger, es sofort zu tun. Der Nenner des Bruchs ist . Multiplizieren auf der . Im Detail wird es so aussehen:

Manchmal erscheinen nach der Differenzierung 2-3 Fraktionen. Wenn wir zum Beispiel noch einen Bruch hätten, müsste die Operation wiederholt werden - multiplizieren jeder Begriff von jedem Teil auf der

Auf der linken Seite setzen wir es aus Klammern:

Endgültige Antwort:

Beispiel 5

Finde die Ableitung einer implizit gegebenen Funktion

Dies ist ein Do-it-yourself-Beispiel. Das einzige, was darin ist, bevor Sie die Fraktion loswerden, müssen Sie zuerst die dreistöckige Struktur der Fraktion selbst loswerden. Vollständige Lösung und Antwort am Ende der Lektion.

Ableitung einer parametrisch definierten Funktion

Überanstrengen Sie sich nicht, auch in diesem Absatz ist alles ganz einfach. Sie können die allgemeine Formel einer parametrisch gegebenen Funktion aufschreiben, aber um es klarzustellen, werde ich es sofort aufschreiben konkretes Beispiel. In parametrischer Form wird die Funktion durch zwei Gleichungen angegeben: . Oft werden Gleichungen nicht unter geschweiften Klammern geschrieben, sondern nacheinander:,.

Die Variable wird als Parameter bezeichnet und kann Werte von "minus unendlich" bis "plus unendlich" annehmen. Betrachten Sie zum Beispiel den Wert und setzen Sie ihn in beide Gleichungen ein: . Oder menschlich: „Wenn x gleich vier ist, dann ist y gleich eins.“ Sie können einen Punkt auf der Koordinatenebene markieren, und dieser Punkt entspricht dem Wert des Parameters. Ebenso können Sie einen Punkt für jeden Wert des Parameters "te" finden. Was die "normale" Funktion betrifft, werden auch für die Indianer einer parametrisch gegebenen Funktion alle Rechte respektiert: Sie können einen Graphen zeichnen, Ableitungen finden und so weiter. Übrigens, wenn es notwendig ist, einen Graphen einer parametrisch gegebenen Funktion zu erstellen, können Sie mein Programm verwenden.

Im einfachsten Fall ist es möglich, die Funktion explizit darzustellen. Wir drücken den Parameter aus der ersten Gleichung aus: und in die zweite Gleichung einsetzen: . Das Ergebnis ist eine gewöhnliche kubische Funktion.

In "schwereren" Fällen funktioniert ein solcher Trick nicht. Aber das spielt keine Rolle, denn es gibt eine Formel, um die Ableitung einer parametrischen Funktion zu finden:

Wir finden die Ableitung von "the player in Bezug auf die Variable te":

Für den Buchstaben gelten natürlich alle Ableitungsregeln und die Ableitungstabelle, also Der Prozess der Suche nach Derivaten ist nicht neu. Ersetzen Sie einfach alle "x" in der Tabelle durch den Buchstaben "te".

Wir finden die Ableitung von "x nach der Variablen te":

Jetzt müssen wir nur noch die gefundenen Ableitungen in unsere Formel einsetzen:

Bereit. Die Ableitung hängt wie die Funktion selbst auch vom Parameter ab.

Was die Notation betrifft, so könnte man sie, anstatt in die Formel zu schreiben, einfach ohne Index schreiben, da dies die „normale“ Ableitung „nach x“ ist. Aber es gibt immer eine Variante in der Literatur, daher werde ich nicht vom Standard abweichen.

Beispiel 6

Wir verwenden die Formel

In diesem Fall:

Auf diese Weise:

Ein Merkmal beim Finden der Ableitung einer parametrischen Funktion ist die Tatsache, dass Bei jedem Schritt ist es vorteilhaft, das Ergebnis so weit wie möglich zu vereinfachen. In dem betrachteten Beispiel habe ich also beim Finden die Klammern unter der Wurzel geöffnet (obwohl ich dies möglicherweise nicht getan habe). Es besteht eine große Chance, dass beim Ersetzen und in der Formel viele Dinge gut reduziert werden. Obwohl es natürlich Beispiele mit ungeschickten Antworten gibt.

Beispiel 7

Finde die Ableitung einer parametrisch gegebenen Funktion

Dies ist ein Do-it-yourself-Beispiel.

Im Artikel Die einfachsten typischen Probleme mit einem Derivat Wir haben Beispiele betrachtet, in denen es erforderlich war, die zweite Ableitung einer Funktion zu finden. Für eine parametrisch gegebene Funktion können Sie auch die zweite Ableitung finden, und zwar mit der folgenden Formel: . Es ist ziemlich offensichtlich, dass man zuerst die erste Ableitung finden muss, um die zweite Ableitung zu finden.

Beispiel 8

Finden Sie die erste und zweite Ableitung einer parametrisch gegebenen Funktion

Lassen Sie uns zuerst die erste Ableitung finden.
Wir verwenden die Formel

In diesem Fall:

Wir setzen die gefundenen Ableitungen in die Formel ein. Der Einfachheit halber verwenden wir die trigonometrische Formel: