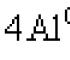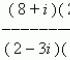Lösung von Matrixsystemen. Matrixverfahren zum Lösen eines Systems linearer algebraischer Gleichungen

Der Online-Rechner löst ein lineares Gleichungssystem nach der Matrixmethode. Sehr gegeben ausführliche Lösung. Um ein lineares Gleichungssystem zu lösen, wählen Sie die Anzahl der Variablen aus. Wählen Sie eine Methode zur Berechnung der inversen Matrix. Geben Sie dann die Daten in die Zellen ein und klicken Sie auf die Schaltfläche "Berechnen".

Warnung

Alle Zellen löschen?

Klar schließen

Anweisung zur Dateneingabe. Zahlen werden als ganze Zahlen (Beispiele: 487, 5, -7623 etc.), Dezimalzahlen (zB 67, 102,54 etc.) oder Bruchzahlen eingegeben. Der Bruch muss in der Form a/b eingegeben werden, wobei a und b ganze Zahlen oder sind Dezimal Zahlen. Beispiele 45/5, 6,6/76,4, -7/6,7 usw.

Matrixverfahren zum Lösen von linearen Gleichungssystemen

Erwägen nächstes System lineare Gleichungen:

Unter Berücksichtigung der Definition der inversen Matrix haben wir EIN −1 EIN=E, wo E ist die Identitätsmatrix. Daher kann (4) wie folgt geschrieben werden:

Um das lineare Gleichungssystem (1) (oder (2)) zu lösen, genügt es also, die Inverse mit zu multiplizieren EIN Matrix pro Beschränkungsvektor B.

Beispiele für die Lösung eines linearen Gleichungssystems mit der Matrixmethode

Beispiel 1. Lösen Sie das folgende lineare Gleichungssystem mit der Matrixmethode:

Finden wir die Inverse der Matrix A mit der Jordan-Gauß-Methode. Auf der rechten Seite der Matrix EIN Schreiben Sie die Identitätsmatrix:

Lassen Sie uns die Elemente der 1. Spalte der Matrix unterhalb der Hauptdiagonalen ausschließen. Addieren Sie dazu die Zeilen 2,3 mit Zeile 1, multipliziert mit -1/3 bzw. -1/3:

Lassen Sie uns die Elemente der 2. Spalte der Matrix unterhalb der Hauptdiagonalen ausschließen. Dazu addieren Sie Zeile 3 mit Zeile 2 multipliziert mit -24/51:

Lassen Sie uns die Elemente der 2. Spalte der Matrix über der Hauptdiagonalen ausschließen. Dazu addierst du Zeile 1 mit Zeile 2, multipliziert mit -3/17:

Trennen Sie die rechte Seite der Matrix. Die resultierende Matrix ist die Umkehrung von EIN :

Matrixform zum Schreiben eines Systems linearer Gleichungen: ax=b, wo

Berechnen Sie alle algebraischen Komplemente der Matrix EIN:

Die inverse Matrix wird aus dem folgenden Ausdruck berechnet.

(manchmal wird diese Methode auch als Matrixmethode oder inverse Matrixmethode bezeichnet) erfordert eine vorherige Vertrautheit mit einem solchen Konzept wie der Matrixform des Schreibens von SLAE. Das Verfahren der inversen Matrix ist zum Lösen solcher Systeme linearer algebraischer Gleichungen gedacht, für die die Determinante der Systemmatrix ungleich Null ist. Dies impliziert natürlich, dass die Matrix des Systems quadratisch ist (das Konzept einer Determinante existiert nur für quadratische Matrizen). Das Wesen der inversen Matrixmethode kann in drei Punkten ausgedrückt werden:

Schreiben Sie drei Matrizen auf: die Systemmatrix $A$, die Matrix der Unbekannten $X$, die Matrix der freien Terme $B$.
Finden Sie die inverse Matrix $A^(-1)$.
Mit der Gleichheit $X=A^(-1)\cdot B$ erhält man die Lösung der gegebenen SLAE.

Jede SLAE kann in Matrixform als $A\cdot X=B$ geschrieben werden, wobei $A$ die Matrix des Systems ist, $B$ die Matrix der freien Terme ist, $X$ die Matrix der Unbekannten ist. Lassen Sie die Matrix $A^(-1)$ existieren. Multipliziere beide Seiten der Gleichheit $A\cdot X=B$ mit der Matrix $A^(-1)$ links:

$$A^(-1)\cdot A\cdot X=A^(-1)\cdot B.$$

Da $A^(-1)\cdot A=E$ ($E$ ist die Identitätsmatrix) wird die oben geschriebene Gleichheit zu:

$$E\cdot X=A^(-1)\cdot B.$$

Da $E\cdot X=X$, dann:

$$X=A^(-1)\cdot B.$$

Beispiel 1

Lösen Sie die SLAE $ \left \( \begin(aligned) & -5x_1+7x_2=29;\\ & 9x_1+8x_2=-11. \end(aligned) \right.$ mit der inversen Matrix.

$$ A=\left(\begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right);\; B=\left(\begin(array) (c) 29\\ -11 \end(array)\right);\; X=\left(\begin(array) (c) x_1\\ x_2 \end(array)\right). $$

Finden wir die inverse Matrix zur Matrix des Systems, d.h. Berechnen Sie $A^(-1)$. In Beispiel #2

$$ A^(-1)=-\frac(1)(103)\cdot\left(\begin(array)(cc) 8 & -7\\ -9 & -5\end(array)\right) . $$

Lassen Sie uns nun alle drei Matrizen ($X$, $A^(-1)$, $B$) in die Gleichung $X=A^(-1)\cdot B$ einsetzen. Dann führen wir eine Matrixmultiplikation durch

$$ \left(\begin(array) (c) x_1\\ x_2 \end(array)\right)= -\frac(1)(103)\cdot\left(\begin(array)(cc) 8 & -7\\ -9 & -5\end(array)\right)\cdot \left(\begin(array) (c) 29\\ -11 \end(array)\right)=\\ =-\frac (1)(103)\cdot \left(\begin(array) (c) 8\cdot 29+(-7)\cdot (-11)\\ -9\cdot 29+(-5)\cdot (- 11) \end(array)\right)= -\frac(1)(103)\cdot \left(\begin(array) (c) 309\\ -206 \end(array)\right)=\left( \begin(array) (c) -3\\ 2\end(array)\right). $$

Also haben wir $\left(\begin(array) (c) x_1\\ x_2 \end(array)\right)=\left(\begin(array) (c) -3\\ 2\end(array )\ rechts)$. Aus dieser Gleichheit haben wir: $x_1=-3$, $x_2=2$.

Antworten: $x_1=-3$, $x_2=2$.

Beispiel #2

Löse SLAE $ \left\(\begin(aligned) & x_1+7x_2+3x_3=-1;\\ & -4x_1+9x_2+4x_3=0;\\ & 3x_2+2x_3=6. \end(aligned)\right .$ nach der Methode der inversen Matrix.

Schreiben wir die Matrix des Systems $A$, die Matrix der freien Terme $B$ und die Matrix der Unbekannten $X$ auf.

$$ A=\left(\begin(array) (ccc) 1 & 7 & 3\\ -4 & 9 & 4 \\0 & 3 & 2\end(array)\right);\; B=\left(\begin(array) (c) -1\\0\\6\end(array)\right);\; X=\left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right). $$

Jetzt ist es an der Zeit, die inverse Matrix der Systemmatrix zu finden, d.h. Finde $A^(-1)$. In Beispiel 3 auf der Seite zum Finden inverser Matrizen wurde die inverse Matrix bereits gefunden. Lassen Sie uns das fertige Ergebnis verwenden und $A^(-1)$ schreiben:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array)\right). $$

Jetzt setzen wir alle drei Matrizen ($X$, $A^(-1)$, $B$) in die Gleichheit $X=A^(-1)\cdot B$ ein, danach führen wir rechts eine Matrixmultiplikation durch Seite dieser Gleichheit.

$$ \left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right)= \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \end(array) \right)\cdot \left(\begin(array) (c) -1\\0\ \6\end(array)\right)=\\ =\frac(1)(26)\cdot \left(\begin(array) (c) 6\cdot(-1)+(-5)\cdot 0 +1\cdot 6 \\ 8\cdot (-1)+2\cdot 0+(-16)\cdot 6 \\ -12\cdot (-1)+(-3)\cdot 0+37\cdot 6 \end(array)\right)=\frac(1)(26)\cdot \left(\begin(array) (c) 0\\-104\\234\end(array)\right)=\left( \begin(array) (c) 0\\-4\\9\end(array)\right) $$

Also haben wir $\left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right)=\left(\begin(array) (c) 0\\-4\ \9 \end(array)\right)$. Aus dieser Gleichheit haben wir: $x_1=0$, $x_2=-4$, $x_3=9$.

Thema 2. SYSTEME LINEARER ALGEBRAISCHER GLEICHUNGEN.

Grundlegendes Konzept.

Bestimmung 1. System m lineare Gleichungen mit n unbekannt ist ein System der Form:

wo und Zahlen sind.

Bestimmung 2. Die Lösung des Systems (I) ist eine solche Menge von Unbekannten, in der jede Gleichung dieses Systems zu einer Identität wird.

Bestimmung 3. System (I) wird aufgerufen gemeinsam wenn es mindestens eine Lösung hat und unvereinbar wenn es keine Lösungen hat. Das gemeinsame System heißt sicher wenn es eine eindeutige Lösung hat, und unsicher sonst.

Bestimmung 4. Gleichung eingeben

namens Null, und eine Gleichung der Form

namens unvereinbar. Offensichtlich ist ein Gleichungssystem, das eine inkonsistente Gleichung enthält, inkonsistent.

Bestimmung 5. Die beiden linearen Gleichungssysteme werden aufgerufen gleichwertig wenn jede Lösung eines Systems eine Lösung eines anderen und umgekehrt jede Lösung des zweiten Systems eine Lösung des ersten ist.

Matrixschreibweise für ein System linearer Gleichungen.

Betrachten Sie System (I) (siehe §1).

Bezeichnen:

Koeffizientenmatrix für Unbekannte

Matrix - Spalte der freien Mitglieder

Matrix - Spalte von Unbekannten

Bestimmung 1. Die Matrix wird aufgerufen die Hauptmatrix des Systems(I), und die Matrix ist die erweiterte Matrix des Systems (I).

Durch die Definition der Matrixgleichheit entspricht System (I) der Matrixgleichheit:

Die rechte Seite dieser Gleichheit durch die Definition des Produkts von Matrizen ( siehe Definition 3 § 5 Kapitel 1) kann faktorisiert werden:

, d.h.

Gleichstellung (2) namens Matrixschreibweise des Systems (I).

Lösen eines linearen Gleichungssystems nach Cramers Methode.

Einlasssystem (I) (siehe §1) m=n, d.h. die Anzahl der Gleichungen ist gleich der Anzahl der Unbekannten, und die Hauptmatrix des Systems ist nicht entartet, d.h. . Dann hat System (I) aus §1 eine eindeutige Lösung

wo ∆ = det A Haupt genannt Systemdeterminante(I), ∆ ich erhält man aus der Determinante Δ durch Ersetzen ich-te Spalte zur Spalte der freien Mitglieder des Systems (I).

Beispiel: Lösen Sie das System nach Cramers Methode:

Durch Formeln (3) .

Wir berechnen die Determinanten des Systems:

Um die Determinante zu erhalten, haben wir die erste Spalte in der Determinante durch eine Spalte mit freien Termen ersetzt; indem wir die 2. Spalte in der Determinante durch eine Spalte mit freien Elementen ersetzen, erhalten wir ; In ähnlicher Weise erhalten wir, wenn wir die dritte Spalte in der Determinante durch eine Spalte mit freien Elementen ersetzen, . Systemlösung:

Lösen von linearen Gleichungssystemen mit einer inversen Matrix.

Einlasssystem (I) (siehe §1) m=n und die Hauptmatrix des Systems ist nicht entartet. Wir schreiben System (I) in Matrixform ( siehe §2):

weil Matrix EIN nicht ausgeartet ist, dann hat sie eine inverse Matrix ( siehe Theorem 1 §6 von Kapitel 1). Multiplizieren Sie beide Seiten der Gleichung (2) dann zur Matrix

Per Definition der inversen Matrix . Von der Gleichberechtigung (3) wir haben

Lösen Sie das System mit der inversen Matrix

Bezeichnen

Im Beispiel (§ 3) haben wir die Determinante berechnet, also die Matrix EIN hat eine inverse Matrix. Dann in Kraft (4) , d.h.

. (5)

Finden Sie die Matrix ( siehe §6 Kapitel 1)

, , ,

Gauss-Methode.

Gegeben sei das lineare Gleichungssystem:

. (ICH)

Es ist erforderlich, alle Lösungen des Systems (I) zu finden oder sicherzustellen, dass das System inkonsistent ist.

Bestimmung 1.Nennen wir die elementare Transformation des Systems(I) eine der drei Aktionen:

1) Streichung der Nullgleichung;

2) Hinzufügen der entsprechenden Teile der anderen Gleichung zu beiden Teilen der Gleichung, multipliziert mit der Zahl l;

3) Vertauschen von Termen in den Gleichungen des Systems, so dass Unbekannte mit denselben Zahlen in allen Gleichungen dieselben Stellen einnehmen, d.h. Wenn wir zum Beispiel in der 1. Gleichung den 2. und 3. Term geändert haben, dann muss das gleiche in allen Gleichungen des Systems gemacht werden.

Das Gauß-Verfahren besteht darin, dass das System (I) mit Hilfe elementarer Transformationen auf ein äquivalentes System reduziert wird, dessen Lösung direkt gefunden oder dessen Unlösbarkeit festgestellt wird.

Wie in §2 beschrieben, ist System (I) durch seine erweiterte Matrix und alle eindeutig bestimmt elementare Verwandlung System (I) entspricht der elementaren Transformation der erweiterten Matrix:

Transformation 1) entspricht dem Löschen der Nullzeile in der Matrix , Transformation 2) ist äquivalent dem Hinzufügen der anderen Zeile der Matrix zu der entsprechenden Zeile der Matrix, multipliziert mit der Zahl l, Transformation 3) ist äquivalent dem Neuanordnen der Spalten in der Matrix .

Es ist leicht einzusehen, dass im Gegenteil jeder elementaren Transformation der Matrix eine elementare Transformation des Systems (I) entspricht. Im Hinblick auf das Gesagte werden wir anstelle von Operationen mit dem System (I) mit der erweiterten Matrix dieses Systems arbeiten.

In der Matrix besteht die 1. Spalte aus Koeffizienten bei x 1, 2. Spalte - von den Koeffizienten bei x 2 usw. Bei der Umordnung von Spalten ist zu berücksichtigen, dass diese Bedingung verletzt wird. Wenn wir zum Beispiel die 1. und 2. Spalte vertauschen, dann gibt es jetzt in der 1. Spalte Koeffizienten bei x 2, und in der 2. Spalte - Koeffizienten bei x 1.

Wir werden das System (I) nach der Gauß-Methode lösen.

1. Streiche alle Nullzeilen in der Matrix, falls vorhanden (d. h. streiche alle Nullgleichungen im System (I).

2. Prüfen Sie, ob es unter den Zeilen der Matrix eine Zeile gibt, in der alle Elemente außer dem letzten gleich Null sind (nennen wir eine solche Zeile inkonsistent). Offensichtlich entspricht eine solche Linie einer inkonsistenten Gleichung in System (I), daher hat System (I) keine Lösungen, und hier endet der Prozess.

3. Die Matrix möge keine inkonsistenten Zeilen enthalten (System (I) enthält nicht widersprüchliche Gleichungen). Wenn a 11 = 0, dann finden wir in der 1. Zeile ein Element (außer dem letzten), das von Null verschieden ist, und ordnen die Spalten so an, dass in der 1. Zeile keine Null an erster Stelle steht. Das nehmen wir jetzt an (d.h. wir vertauschen die entsprechenden Terme in den Gleichungen des Systems (I)).

4. Multiplizieren Sie die 1. Reihe mit und addieren Sie das Ergebnis zur 2. Reihe, dann multiplizieren Sie die 1. Reihe mit und addieren Sie das Ergebnis zur 3. Reihe usw. Offensichtlich ist dieser Prozess gleichbedeutend mit der Eliminierung des Unbekannten x 1 aus allen Gleichungen des Systems (I), außer der 1. In der neuen Matrix erhalten wir Nullen in der 1. Spalte unter dem Element eine 11:

5. Streichen Sie alle Nullzeilen in der Matrix, falls vorhanden, prüfen Sie, ob es eine inkonsistente Zeile gibt (wenn es eine gibt, dann ist das System inkonsistent und die Lösung ist abgeschlossen). Lassen Sie uns prüfen, ob a 22 / =0, wenn ja, dann finden wir in der 2. Zeile ein von Null verschiedenes Element und ordnen die Spalten so um, dass . Als nächstes multiplizieren wir die Elemente der 2. Reihe mit und addiere mit den entsprechenden Elementen der 3. Reihe, dann - die Elemente der 2. Reihe an und addiere mit den entsprechenden Elementen der 4. Reihe, usw., bis wir Nullen darunter bekommen a 22 /

Die durchgeführten Handlungen sind gleichbedeutend mit der Beseitigung des Unbekannten x 2 aus allen Gleichungen des Systems (I), außer der 1. und 2. Da die Anzahl der Zeilen endlich ist, werden wir also nach einer endlichen Anzahl von Schritten erhalten, dass entweder das System inkonsistent ist, oder wir werden zu einer Schrittmatrix ( siehe Definition 2 §7 Kapitel 1) :

Schreiben wir das der Matrix entsprechende Gleichungssystem auf. Dieses System entspricht dem System (I)

Aus der letzten Gleichung drücken wir aus; wir setzen in die vorherige Gleichung ein, finden usw., bis wir erhalten.

Bemerkung 1. Wenn wir also das System (I) nach dem Gauß-Verfahren lösen, gelangen wir zu einem der folgenden Fälle.

1. System (I) ist inkonsistent.

2. System (I) hat eine eindeutige Lösung, wenn die Anzahl der Zeilen in der Matrix gleich der Anzahl der Unbekannten ist ().

3. System (I) hat unendlich viele Lösungen, wenn die Anzahl der Zeilen in der Matrix kleiner ist als die Anzahl der Unbekannten ().

Daher gilt der folgende Satz.

Satz. Das lineare Gleichungssystem ist entweder inkonsistent oder hat eine eindeutige Lösung, oder es gibt eine unendliche Menge von Lösungen.

Beispiele. Lösen Sie das Gleichungssystem nach dem Gauß-Verfahren oder beweisen Sie seine Widersprüchlichkeit:

B) ;

a) Schreiben wir das gegebene System um in die Form:

Wir haben die 1. und 2. Gleichung des ursprünglichen Systems vertauscht, um die Berechnungen zu vereinfachen (statt mit Brüchen werden wir mit einer solchen Permutation nur mit ganzen Zahlen operieren).

Wir erstellen eine erweiterte Matrix:

Es gibt keine Nullzeilen; keine inkompatiblen Zeilen, ; wir schließen die 1. Unbekannte aus allen Gleichungen des Systems außer der 1. aus. Dazu multiplizieren wir die Elemente der 1. Reihe der Matrix mit „-2“ und addieren sie zu den entsprechenden Elementen der 2. Reihe, was gleichbedeutend damit ist, die 1. Gleichung mit „-2“ zu multiplizieren und zu addieren 2. Gleichung. Dann multiplizieren wir die Elemente der 1. Reihe mit „-3“ und addieren sie zu den entsprechenden Elementen der dritten Reihe, also multipliziere die 2. Gleichung des gegebenen Systems mit "-3" und addiere es zur 3. Gleichung. Werden

Die Matrix entspricht einem Gleichungssystem). - (siehe Definition 3 § 7 von Kapitel 1).

Gleichungen im Allgemeinen, lineare algebraische Gleichungen und ihre Systeme sowie Methoden zu ihrer Lösung nehmen sowohl in der theoretischen als auch in der angewandten Mathematik einen besonderen Platz ein.

Dies liegt an der Tatsache, dass die überwiegende Mehrheit der physischen, wirtschaftlichen, technischen und sogar pädagogische Aufgaben können mit verschiedenen Gleichungen und deren Systemen beschrieben und gelöst werden. v In letzter Zeit Die mathematische Modellierung hat bei Forschern, Wissenschaftlern und Praktikern in fast allen Fachgebieten besondere Popularität erlangt, was sich durch ihre offensichtlichen Vorteile gegenüber anderen bekannten und bewährten Methoden zum Studium von Objekten verschiedener Art erklärt, insbesondere gegenüber den sogenannten komplexe Systeme. Es gibt eine große Vielfalt verschiedene Definitionen mathematisches Modell von Wissenschaftlern in andere Zeiten, aber unserer Meinung nach am erfolgreichsten ist die folgende Aussage. Ein mathematisches Modell ist eine Idee, die durch eine Gleichung ausgedrückt wird. Daher ist die Fähigkeit, Gleichungen und ihre Systeme aufzustellen und zu lösen, ein wesentliches Merkmal eines modernen Spezialisten.

Um lineare algebraische Gleichungssysteme zu lösen, sind die am häufigsten verwendeten Methoden: Cramer, Jordan-Gauß und die Matrixmethode.

Matrix-Methode Lösungen - eine Methode zum Lösen von Systemen linearer algebraischer Gleichungen mit einer Determinante ungleich Null unter Verwendung einer inversen Matrix.

Wenn wir die Koeffizienten für die unbekannten Werte xi in die Matrix A schreiben, die unbekannten Werte in den Vektor der Spalte X und die freien Terme in den Vektor der Spalte B sammeln, dann kann das System der linearen algebraischen Gleichungen geschrieben werden als folgende Matrixgleichung AX = B, die nur dann eine eindeutige Lösung hat, wenn die Determinante der Matrix A ungleich Null ist. In diesem Fall kann die Lösung des Gleichungssystems auf folgende Weise gefunden werden x = EIN-eins · B, wo EIN-1 - inverse Matrix.

Das Matrixlösungsverfahren ist wie folgt.

Gegeben sei ein lineares Gleichungssystem mit n Unbekannt:

Es kann in Matrixform umgeschrieben werden: AXT = B, wo EIN- die Hauptmatrix des Systems, B und x- Spalten mit freien Mitgliedern bzw. Lösungen des Systems:

Lass es uns multiplizieren Matrixgleichung links zu EIN-1 - Matrix invers zur Matrix EIN: EIN -1 (AXT) = EIN -1 B

Als EIN -1 EIN = E, wir bekommen x= A -1 B. Die rechte Seite dieser Gleichung ergibt eine Spalte mit Lösungen für das ursprüngliche System. Die Anwendbarkeitsbedingung für dieses Verfahren (wie auch für das Vorhandensein einer Lösung im Allgemeinen) ist es nicht homogenes System lineare Gleichungen mit Anzahl von Gleichungen, gleich der Zahl Unbekannte) ist die Nichtsingularität der Matrix EIN. Eine notwendige und hinreichende Bedingung dafür ist, dass die Determinante der Matrix EIN: det EIN≠ 0.

Für ein homogenes System linearer Gleichungen, dh wenn der Vektor B = 0 , Ja wirklich umgekehrte Regel: System AXT = 0 hat nur dann eine nicht-triviale (d. h. von Null verschiedene) Lösung, wenn det EIN= 0. Eine solche Verbindung zwischen den Lösungen homogener und inhomogener linearer Gleichungssysteme wird als Fredholm-Alternative bezeichnet.

Beispiel Lösungen eines inhomogenen Systems linearer algebraischer Gleichungen.

Stellen wir sicher, dass die Determinante der Matrix, die sich aus den Koeffizienten der Unbekannten des linearen algebraischen Gleichungssystems zusammensetzt, nicht gleich Null ist.

Der nächste Schritt ist die Berechnung algebraische Additionen für die Elemente der Matrix, die aus den Koeffizienten der Unbekannten besteht. Sie werden benötigt, um die inverse Matrix zu finden.

Die Verwendung von Gleichungen ist in unserem Leben weit verbreitet. Sie werden in vielen Berechnungen, Konstruktionen und sogar im Sport verwendet. Gleichungen werden seit der Antike vom Menschen verwendet, und seitdem hat ihre Verwendung nur zugenommen. Die Matrixmethode ermöglicht es, Lösungen für SLAE (System linearer algebraischer Gleichungen) beliebiger Komplexität zu finden. Der gesamte Prozess zur Lösung von SLAE besteht aus zwei Hauptschritten:

Bestimmung der inversen Matrix ausgehend von der Hauptmatrix:

Multiplikation der resultierenden inversen Matrix mit dem Spaltenvektor der Lösungen.

Angenommen, wir erhalten eine SLAE der folgenden Form:

\[\left\(\begin(matrix) 5x_1 + 2x_2 & = & 7 \\ 2x_1 + x_2 & = & 9 \end(matrix)\right.\]

Beginnen wir mit der Lösung gegebene Gleichung aus dem Ausschreiben der Matrix des Systems:

Rechte Matrix:

Lassen Sie uns eine inverse Matrix definieren. Sie können eine Matrix der 2. Ordnung wie folgt finden: 1 - die Matrix selbst muss nichtsingulär sein; 2 - seine Elemente, die sich auf der Hauptdiagonale befinden, werden vertauscht, und für die Elemente der Nebendiagonale führen wir einen Vorzeichenwechsel in das Gegenteil durch, wonach wir die Division der erhaltenen Elemente durch die Determinante der Matrix durchführen. Wir bekommen:

\[\begin(pmatrix) 7 \\ 9 \end(pmatrix)=\begin(pmatrix) -11 \\ 31 \end(pmatrix)\Rightarrow \begin(pmatrix) x_1 \\ x_2 \end(pmatrix) =\ begin(pmatrix) -11 \\ 31 \end(pmatrix) \]

2 Matrizen werden als gleich angesehen, wenn ihre entsprechenden Elemente gleich sind. Als Ergebnis haben wir die folgende Antwort der SLAE-Lösung:

Wo kann ich ein Gleichungssystem mit der Matrixmethode online lösen?

Sie können das Gleichungssystem auf unserer Website lösen. Mit dem kostenlosen Online-Solver können Sie eine Online-Gleichung beliebiger Komplexität in Sekundenschnelle lösen. Sie müssen lediglich Ihre Daten in den Solver eingeben. Auf unserer Website können Sie auch lernen, wie Sie die Gleichung lösen. Und wenn Sie Fragen haben, können Sie sie in unserer Vkontakte-Gruppe stellen.