Methoden zum Finden einer Matrix. Inverse Matrix. Lösen von Matrixgleichungen

Ähnlich der Umkehrung in vielen Eigenschaften.

College-YouTube

1 / 5

✪ So finden Sie die Inverse einer Matrix - bezbotvy

✪ Inverse Matrix (2 Wege zum Finden)

✪ Inverse Matrix # 1

2015-01-28. Inverse 3x3-Matrix

2015-01-27. Inverse 2x2-Matrix

Untertitel

Eigenschaften der inversen Matrix

det A - 1 = 1 det A (\ displaystyle \ det A ^ (- 1) = (\ frac (1) (\ det A))), wo det (\ displaystyle \ \ det) bezeichnet eine Determinante.
(A B) - 1 = B - 1 A - 1 (\ displaystyle \ (AB) ^ (- 1) = B ^ (- 1) A ^ (- 1)) für zwei quadratische invertierbare Matrizen A (\ Anzeigestil A) und B (\ Anzeigestil B).
(A T) - 1 = (A - 1) T (\ Displaystyle \ (A ^ (T)) ^ (- 1) = (A ^ (- 1)) ^ (T)), wo (...) T (\ Anzeigestil (...) ^ (T)) bezeichnet eine transponierte Matrix.
(k A) - 1 = k - 1 A - 1 (\ displaystyle \ (kA) ^ (- 1) = k ^ (- 1) A ^ (- 1)) für jeden Koeffizienten k ≠ 0 (\ displaystyle k \ not = 0).
E - 1 = E (\ displaystyle \ E ^ (- 1) = E).
Wenn es notwendig ist, ein lineares Gleichungssystem zu lösen, (b ist ein Vektor ungleich Null) wobei x (\ Anzeigestil x) ist der erforderliche Vektor, und wenn A - 1 (\ Anzeigestil A ^ (- 1)) existiert dann x = A - 1 b (\ Displaystil x = A ^ (- 1) b)... Andernfalls ist entweder die Dimension des Lösungsraums größer als Null oder es gibt keine.

Methoden zum Finden der inversen Matrix

Wenn die Matrix invertierbar ist, können Sie eine der folgenden Methoden verwenden, um die Inverse der Matrix zu finden:

Exakte (direkte) Methoden

Gauß-Jordan-Methode

Nehmen wir zwei Matrizen: sich selbst EIN und eine einzelne E... Geben wir eine Matrix EIN auf die Identitätsmatrix durch die Gauß-Jordan-Methode, indem Transformationen nach Zeilen angewendet werden (Sie können auch Transformationen nach Spalten anwenden, aber nicht mischen). Nachdem Sie jede Operation auf die erste Matrix angewendet haben, wenden Sie dieselbe Operation auf die zweite an. Wenn die Reduktion der ersten Matrix auf die Einheitsform abgeschlossen ist, ist die zweite Matrix gleich A -1.

Bei der Gaußschen Methode wird die erste Matrix von links mit einer der Elementarmatrizen multipliziert Λ i (\ displaystyle \ Lambda _ (i))(Transvektions- oder Diagonalmatrix mit Einsen auf der Hauptdiagonalen bis auf eine Position):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A - 1 (\ displaystyle \ Lambda _ (1) \ cdot \ dots \ cdot \ Lambda _ (n) \ cdot A = \ Lambda A = E \ Pfeil nach rechts \ Lambda = A ^ (- 1)). Λ m = [1… 0 - a 1 m / amm 0… 0… 0… 1 - am - 1 m / amm 0… 0 0… 0 1 / amm 0… 0 0… 0 - am + 1 m / amm 1 … 0… 0… 0 - anm / amm 0… 1] (\ displaystyle \ Lambda _ (m) = (\ begin (bmatrix) 1 & \ dots & 0 & -a_ (1m) / a_ (mm) & 0 & \ Punkte & 0 \\ &&& \ Punkte &&& \\ 0 & \ Punkte & 1 & -a_ (m-1m) / a_ (mm) & 0 & \ Punkte & 0 \\ 0 & \ Punkte & 0 & 1 / a_ (mm) & 0 & \ Punkte & 0 \\ 0 & \ Punkte & 0 & -a_ ( m + 1m) / a_ (mm) & 1 & \ Punkte & 0 \\ &&& \ Punkte &&& \\ 0 & \ Punkte & 0 & -a_ (nm) / a_ (mm) & 0 & \ Punkte & 1 \ Ende (bmatrix))).

Die zweite Matrix nach Anwendung aller Operationen ist gleich Λ (\ displaystyle \ Lambda), das heißt, es wird das gewünschte sein. Komplexität des Algorithmus - O (n 3) (\ Anzeigestil O (n ^ (3))).

Verwenden der Matrix der algebraischen Komplemente

Matrix invers zu Matrix A (\ Anzeigestil A), kann dargestellt werden als

A - 1 = adj (A) det (A) (\ displaystyle (A) ^ (- 1) = (((\ mbox (adj)) (A)) \ over (\ det (A))))

wo adj (A) (\ displaystyle (\ mbox (adj)) (A))- beigefügte Matrix;

Die Komplexität des Algorithmus hängt von der Komplexität des Algorithmus zur Berechnung der Determinante O det ab und ist gleich O (n²) · O det.

Verwenden der LU / LUP-Zerlegung

Matrixgleichung A X = I n (\ Anzeigestil AX = I_ (n)) für die inverse Matrix X (\ Anzeigestil X) kann als Sammlung angesehen werden n (\ Anzeigestil n) Systeme der Form A x = b (\ displaystyle Ax = b)... Wir bezeichnen i (\ displaystyle i) Spalte der Matrix X (\ Anzeigestil X)über X i (\ Anzeigestil X_ (i)); dann A X i = e i (\ displaystyle AX_ (i) = e_ (i)), i = 1,…, n (\ displaystyle i = 1, \ ldots, n),soweit i (\ displaystyle i) Spalte der Matrix I n (\ Anzeigestil I_ (n)) ist der Einheitsvektor e i (\ displaystyle e_ (i))... mit anderen Worten, das Finden der inversen Matrix reduziert sich auf das Lösen von n Gleichungen mit einer Matrix und verschiedenen rechten Seiten. Nachdem die LUP-Zerlegung (Zeit O (n³)) durchgeführt wurde, benötigt das Lösen jeder der n Gleichungen Zeit O (n²), so dass dieser Teil der Arbeit auch Zeit O (n³) benötigt.

Wenn die Matrix A nicht entartet ist, kann die LUP-Zerlegung für sie berechnet werden P A = L U (\ Anzeigestil PA = LU)... Lassen P A = B (\ Anzeigestil PA = B), B - 1 = D (\ Anzeigestil B ^ (- 1) = D)... Aus den Eigenschaften der inversen Matrix können wir dann schreiben: D = U - 1 L - 1 (\ Displaystil D = U ^ (- 1) L ^ (- 1))... Wenn wir diese Gleichheit mit U und L multiplizieren, erhalten wir zwei Gleichheiten der Form U D = L - 1 (\ Anzeigestil UD = L ^ (- 1)) und D L = U - 1 (\ Anzeigestil DL = U ^ (- 1))... Die erste dieser Gleichungen ist ein System von n² linearen Gleichungen für n (n + 1) 2 (\ displaystyle (\ frac (n (n + 1)) (2))) von denen die rechten Seiten bekannt sind (aus den Eigenschaften von Dreiecksmatrizen). Die zweite repräsentiert ebenfalls ein System von n² linearen Gleichungen für n (n - 1) 2 (\ displaystyle (\ frac (n (n-1)) (2))) von denen die rechten Seiten bekannt sind (auch aus den Eigenschaften von Dreiecksmatrizen). Zusammen bilden sie ein System von n² Gleichheiten. Mit diesen Gleichungen können wir alle n² Elemente der Matrix D rekursiv bestimmen. Dann erhalten wir aus der Gleichheit (PA) −1 = A −1 P −1 = B −1 = D. die Gleichheit A - 1 = D P (\ Anzeigestil A ^ (- 1) = DP).

Bei Verwendung der LU-Zerlegung ist keine Permutation der Spalten der Matrix D erforderlich, aber die Lösung kann divergieren, selbst wenn die Matrix A nicht entartet ist.

Die Komplexität des Algorithmus ist O (n³).

Iterative Methoden

Schultz-Methoden

(Ψ k = E - AU k, U k + 1 = U k ∑ i = 0 n Ψ ki (\ displaystyle (\ begin (Fälle) \ Psi _ (k) = E-AU_ (k), \\ U_ ( k + 1) = U_ (k) \ sum_ (i = 0) ^ (n) \ Psi _ (k) ^ (i) \ end (Fälle))

Fehlerabschätzung

Eine erste Vermutung wählen

Das Problem der Wahl einer anfänglichen Näherung bei den hier betrachteten Prozessen der iterativen Matrixinversion erlaubt es nicht, sie als unabhängige universelle Methoden zu behandeln, die mit direkten Methoden der Inversion konkurrieren, die beispielsweise auf der LU-Zerlegung von Matrizen basieren. Es gibt einige Empfehlungen zur Auswahl U 0 (\ Anzeigestil U_ (0)) Sicherstellung der Erfüllung der Bedingung ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (der Spektralradius der Matrix ist kleiner als eins), was für die Konvergenz des Prozesses notwendig und ausreichend ist. In diesem Fall ist es jedoch zunächst erforderlich, die obere Schranke für das Spektrum der invertierten Matrix A oder der Matrix . zu kennen A A T (\ Anzeigestil AA ^ (T))(nämlich wenn A eine symmetrische positiv-definite Matrix ist und ρ (A) ≤ β (\ displaystyle \ rho (A) \ leq \ beta), dann kannst du nehmen U 0 = α E (\ Anzeigestil U_ (0) = (\ Alpha) E), wo ; wenn A eine beliebige nicht entartete Matrix ist und ρ (A A T) ≤ β (\ displaystyle \ rho (AA ^ (T)) \ leq \ beta) dann wird geglaubt U 0 = α A T (\ Anzeigestil U_ (0) = (\ Alpha) A ^ (T)) wo auch α ∈ (0, 2 β) (\ displaystyle \ alpha \ in \ left (0, (\ frac (2) (\ beta)) \ right)); Sie können die Situation natürlich vereinfachen und die Tatsache ausnutzen, dass ρ (A A T) ≤ k A A T k (\ displaystyle \ rho (AA ^ (T)) \ leq (\ mathcal (k)) AA ^ (T) (\ mathcal (k))), stellen U 0 = A T ‖ A A T ‖ (\ displaystyle U_ (0) = (\ frac (A ^ (T)) (\ | AA ^ (T) \ |)))). Zweitens gibt es mit einer solchen Definition der Anfangsmatrix keine Garantie dafür, dass ‖ Ψ 0 ‖ (\ displaystyle \ | \ Psi _ (0) \ |) wird klein sein (es kann sogar sein ‖ Ψ 0 ‖> 1 (\ displaystyle \ | \ Psi _ (0) \ |> 1)) und eine Konvergenzrate hoher Ordnung wird nicht sofort aufgedeckt.

Beispiele von

Matrix 2x2

A – 1 = [a b c d] – 1 = 1 det (A) [d – b – c a] = 1 a d – b c [d – b – c a]. (\ displaystyle \ mathbf (A) ^ (- 1) = (\ begin (bmatrix) a & b \\ c & d \\\ end (bmatrix)) ^ (- 1) = (\ frac (1) (\ det (\ mathbf (A)))) (\ begin (bmatrix) \, \, \, d & \! \! - b \\ - c & \, a \\\ end (bmatrix)) = (\ frac (1) (ad- bc)) (\ begin (bmatrix) \, \, \, d & \! \! - b \\ - c & \, a \\\ end (bmatrix)).)

Die Inversion einer 2x2-Matrix ist nur möglich, wenn a d - b c = det A ≠ 0 (\ displaystyle ad-bc = \ det A \ neq 0).

Finden der inversen Matrix- eine Aufgabe, die oft mit zwei Methoden gelöst wird:

die Methode der algebraischen Komplemente, bei der es erforderlich ist, Determinanten zu finden und Matrizen zu transponieren;
durch das Verfahren der Eliminierung von Unbekannten nach Gauss, bei dem es erforderlich ist, elementare Matrixtransformationen durchzuführen (Zeilen hinzufügen, Zeilen mit derselben Zahl multiplizieren usw.).

Für besonders Neugierige gibt es andere Methoden, zum Beispiel die Methode der linearen Transformationen. In dieser Lektion werden wir die drei genannten Methoden und Algorithmen analysieren, um mit diesen Methoden die inverse Matrix zu finden.

Inverse Matrix EIN, eine solche Matrix heißt

EIN
. (1)

Inverse Matrix , die für eine gegebene quadratische Matrix benötigt wird EIN, eine solche Matrix heißt

Produkt, bei dem Matrizen EIN rechts ist die Identitätsmatrix, d. h.
. (1)

Die Identitätsmatrix ist eine Diagonalmatrix, bei der alle Diagonalelemente gleich eins sind.

Satz.Für jede nicht singuläre (nicht entartete, nicht singuläre) quadratische Matrix gibt es die inverse Matrix, und außerdem nur eine. Für eine spezielle (entartete, singuläre) quadratische Matrix existiert die Inverse nicht.

Die quadratische Matrix heißt nicht speziell(oder nicht entartet, Nicht-Einzahl) wenn seine Determinante nicht Null ist, und Besondere(oder degenerieren, Singular), wenn seine Determinante null ist.

Die inverse Matrix kann nur für eine quadratische Matrix gefunden werden. Natürlich ist auch die inverse Matrix quadratisch und hat die gleiche Ordnung wie die gegebene Matrix. Eine Matrix, für die eine inverse Matrix gefunden werden kann, heißt invertierbare Matrix.

Zum inverse Matrix es gibt eine treffende Analogie zum Reziproken. Für jede Zahl ein, ungleich Null, gibt es eine solche Zahl B dass die Arbeit ein und B gleich eins: ab= 1. Nummer B heißt die Umkehrung der Zahl B... Für die Zahl 7 ist die Umkehrung beispielsweise 1/7, da 7 * 1/7 = 1 ist.

Finden der inversen Matrix nach der Methode der algebraischen Komplemente (Unionsmatrix)

Für eine nicht singuläre quadratische Matrix EIN die Umkehrung ist die Matrix

wo ist die Determinante der Matrix EIN, a ist die zur Matrix adjungierte Matrix EIN.

Vereinigung mit quadratischer Matrix EIN heißt Matrix gleicher Ordnung, deren Elemente die algebraischen Komplemente der entsprechenden Elemente der Determinante der Matrix sind, die bezüglich der Matrix A transponiert sind

dann

und

Algorithmus zum Finden der inversen Matrix nach der Methode der algebraischen Komplemente

1. Finden Sie die Determinante einer gegebenen Matrix EIN... Wenn die Determinante Null ist, endet die Suche nach der inversen Matrix, da die Matrix entartet ist und ihre Inverse nicht existiert.

2. Finden Sie die bezüglich transponierte Matrix EIN.

3. Berechnen Sie die Elemente der adjungierten Matrix als die algebraischen Komplemente der in Schritt 2 gefundenen Maritsa.

4. Wende Formel (2) an: Multipliziere den Kehrwert der Determinante der Matrix EIN, zu der in Schritt 4 gefundenen adjungierten Matrix.

5. Überprüfen Sie das in Schritt 4 erhaltene Ergebnis, indem Sie diese Matrix multiplizieren EIN zur inversen Matrix. Wenn das Produkt dieser Matrizen gleich der Identitätsmatrix ist, wurde die inverse Matrix korrekt gefunden. Starten Sie andernfalls den Lösungsprozess erneut.

Beispiel 1. Für Matrix

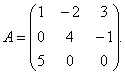
finde die Inverse der Matrix.

Lösung. Um die inverse Matrix zu finden, ist es notwendig, die Determinante der Matrix zu finden EIN... Wir finden nach der Dreiecksregel:

Daher die Matrix EIN- nicht singulär (nicht entartet, nicht singulär) und dafür gibt es eine Umkehrung.

Finden Sie die Matrix, die an die gegebene Matrix angrenzt EIN.

Finden Sie die bezüglich der Matrix transponierte Matrix EIN:

Berechnen Sie die Elemente der adjungierten Matrix als die algebraischen Komplemente der bezüglich der Matrix transponierten Matrix EIN:

Daher ist die an die Matrix angrenzende Matrix EIN, hat die Form

Kommentar. Die Reihenfolge der Berechnung der Elemente und der Transposition der Matrix kann unterschiedlich sein. Man kann zunächst die algebraischen Komplemente der Matrix berechnen EIN und dann die Komplementmatrix transponieren. Das Ergebnis sollten die gleichen Elemente der Unionsmatrix sein.

Unter Anwendung von Formel (2) finden wir die Matrix invers zur Matrix EIN:

Finden der inversen Matrix durch Gaußsche Elimination

Der erste Schritt zum Auffinden der inversen Matrix durch das Gaußsche Eliminationsverfahren besteht darin, der Matrix EIN die Identitätsmatrix derselben Ordnung und trennt sie durch einen vertikalen Balken. Wir erhalten eine verdoppelte Matrix. Wir multiplizieren beide Seiten dieser Matrix mit, dann erhalten wir

Algorithmus zum Auffinden der inversen Matrix durch Gaußsche Elimination von Unbekannten

1. Zur Matrix EIN ordnen Sie die Identitätsmatrix derselben Ordnung zu.

2. Transformieren Sie die resultierende Doppelmatrix so, dass die Identitätsmatrix auf der linken Seite erhalten wird, dann wird automatisch die inverse Matrix anstelle der Identitätsmatrix auf der rechten Seite. Matrix EIN auf der linken Seite wird durch elementare Matrixtransformationen in die Identitätsmatrix transformiert.

2. Wenn bei der Transformation der Matrix EIN in die Identitätsmatrix in jeder Zeile oder in jeder Spalte gibt es nur Nullen, dann ist die Determinante der Matrix gleich Null und daher die Matrix EIN wird entartet und hat keine inverse Matrix. In diesem Fall ist das weitere Finden der inversen Matrix beendet.

Beispiel 2. Für Matrix

finde die Inverse der Matrix.

und wir transformieren es so, dass wir auf der linken Seite die Identitätsmatrix erhalten. Wir beginnen mit Transformationen.

Multiplizieren Sie die erste Zeile der linken und rechten Matrix mit (-3) und fügen Sie sie der zweiten Zeile hinzu, und dann multiplizieren Sie die erste Zeile mit (-4) und fügen Sie sie der dritten Zeile hinzu, dann erhalten wir

Damit es bei nachfolgenden Transformationen möglichst keine Bruchzahlen gibt, erstellen wir zunächst eine Einheit in der zweiten Zeile auf der linken Seite der verdoppelten Matrix. Multiplizieren Sie dazu die zweite Zeile mit 2 und subtrahieren Sie die dritte Zeile davon, dann erhalten wir

Fügen Sie die erste Reihe zur zweiten hinzu, multiplizieren Sie dann die zweite Reihe mit (-9) und fügen Sie sie der dritten Reihe hinzu. Dann bekommen wir

Teilen Sie die dritte Zeile durch 8, dann

Lassen Sie uns die dritte Zeile mit 2 multiplizieren und zur zweiten Zeile hinzufügen. Es stellt sich heraus:

Vertauschen wir die zweite und dritte Zeile, dann erhalten wir endlich:

Wir sehen, dass die Einheitsmatrix auf der linken Seite erhalten wird, daher wird die inverse Matrix auf der rechten Seite erhalten. Auf diese Weise:

Sie können die Richtigkeit der Berechnungen überprüfen, indem Sie die ursprüngliche Matrix mit der gefundenen inversen Matrix multiplizieren:

Das Ergebnis sollte eine inverse Matrix sein.

Beispiel 3. Für Matrix

finde die Inverse der Matrix.

Lösung. Zusammensetzen einer Doppelmatrix

und wir werden es verwandeln.

Wir multiplizieren die erste Reihe mit 3 und die zweite mit 2 und subtrahieren von der zweiten, und dann multiplizieren wir die erste Reihe mit 5 und die dritte mit 2 und subtrahieren von der dritten Reihe, dann erhalten wir

Wir multiplizieren die erste Zeile mit 2 und addieren sie zur zweiten und subtrahieren dann die zweite von der dritten Zeile, dann erhalten wir

Wir sehen, dass in der dritten Zeile von links alle Elemente gleich Null sind. Folglich ist die Matrix entartet und hat keine inverse Matrix. Wir hören auf, die umgekehrte Maritza weiter zu finden.

Die Matrix $ A ^ (- 1) $ heißt invers zur quadratischen Matrix $ A $, wenn die Bedingung $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ erfüllt ist , wobei $ E $ die Identitätsmatrix ist, deren Ordnung gleich der Ordnung der Matrix $ A $ ist.

Nicht entartete Matrix - eine Matrix, deren Determinante ungleich Null ist. Dementsprechend ist eine entartete Matrix eine Matrix, bei der die Determinante gleich Null ist.

Die inverse Matrix $ A ^ (- 1) $ existiert genau dann, wenn die Matrix $ A $ nicht entartet ist. Wenn die inverse Matrix $ A ^ (- 1) $ existiert, dann ist sie eindeutig.

Es gibt mehrere Möglichkeiten, die Inverse einer Matrix zu finden, und wir werden uns zwei davon ansehen. Auf dieser Seite wird die adjungierte Matrixmethode diskutiert, die in den meisten höheren Mathematikkursen als Standard gilt. Die zweite Methode zum Auffinden der inversen Matrix (die Methode der elementaren Transformationen), bei der die Gauß-Methode oder die Gauß-Jordan-Methode verwendet wird, wird im zweiten Teil diskutiert.

Die adjungierte (adjungierte) Matrixmethode

Gegeben sei die Matrix $ A_ (n \ mal n) $. Um das Inverse von $ A ^ (- 1) $ zu finden, sind drei Schritte erforderlich:

Bestimmen Sie die Determinante der Matrix $ A $ und stellen Sie sicher, dass $ \ Delta A \ neq 0 $, d.h. dass die Matrix A nicht entartet ist.
Bilden Sie die algebraischen Komplemente $ A_ (ij) $ jedes Elements der Matrix $ A $ und schreiben Sie die Matrix $ A_ (n \ mal n) ^ (*) = \ left (A_ (ij) \ right) $ aus dem algebraische Komplemente gefunden.
Schreiben Sie die inverse Matrix unter Berücksichtigung der Formel $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $.

Die Matrix $ (A ^ (*)) ^ T $ wird oft als adjungiert (reziprok, adjungiert) zur Matrix $ A $ bezeichnet.

Wenn die Lösung manuell durchgeführt wird, ist die erste Methode nur für Matrizen relativ kleiner Ordnung geeignet: zweite (), dritte (), vierte (). Andere Methoden werden verwendet, um die Inverse einer Matrix höherer Ordnung zu finden. Zum Beispiel die Gauss-Methode, die im zweiten Teil diskutiert wird.

Beispiel 1

Finden Sie die Umkehrung von $ A = \ left (\ begin (array) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & - 1 & -9 & 0 \ Ende (Array) \ Rechts) $.

Da alle Elemente der vierten Spalte gleich Null sind, ist $ \ Delta A = 0 $ (dh die Matrix $ A $ ist entartet). Da $ \ Delta A = 0 $ ist, existiert die zur Matrix $ A $ inverse Matrix nicht.

Beispiel Nr. 2

Finden Sie die Inverse der Matrix $ A = \ left (\ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) $.

Wir verwenden das adjungierte Matrixverfahren. Zuerst finden wir die Determinante der gegebenen Matrix $ A $:

$$ \ Delta A = \ links | \ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

Da $ \ Delta A \ neq 0 $ dann die inverse Matrix existiert, werden wir die Lösung fortsetzen. Algebraische Komplemente finden

\ begin (ausgerichtet) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9;\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ end (ausgerichtet)

Wir setzen eine Matrix aus algebraischen Komplementen zusammen: $ A ^ (*) = \ left (\ begin (array) (cc) 8 & -9 \\ -7 & -5 \ end (array) \ right) $.

Transponiere die resultierende Matrix: $ (A ^ (*)) ^ T = \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) $ (das resultierende Matrix wird oft als adjungierte oder adjungierte Matrix zur $ A $ -Matrix bezeichnet). Mit der Formel $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ erhalten wir:

$$ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $$

Die Umkehrung ergibt sich also: $ A ^ (- 1) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $. Um die Wahrheit des Ergebnisses zu überprüfen, genügt es, die Wahrheit einer der Gleichungen zu überprüfen: $ A ^ (- 1) \ cdot A = E $ oder $ A \ cdot A ^ (- 1) = E $. Prüfen wir die Gleichheit $ A ^ (- 1) \ cdot A = E $. Um weniger mit Brüchen zu arbeiten, ersetzen wir die Matrix $ A ^ (- 1) $ nicht in der Form $ \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $, und als $ - \ frac (1) (103) \ cdot \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array ) \ right) $:

Antworten: $ A ^ (- 1) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $.

Beispiel Nr. 3

Finden Sie die Inverse der Matrix $ A = \ left (\ begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right) $.

Beginnen wir mit der Berechnung der Determinante der Matrix $ A $. Die Determinante der Matrix $ A $ lautet also:

$$ \ Delta A = \ links | \ begin (array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ right | = 18-36 + 56-12 = 26. $$

Da $ \ Delta A \ neq 0 $ dann die inverse Matrix existiert, werden wir die Lösung fortsetzen. Wir finden die algebraischen Komplemente jedes Elements einer gegebenen Matrix:

Wir stellen eine Matrix aus algebraischen Komplementen zusammen und transponieren sie:

$$ A ^ * = \ left (\ begin (array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ end (array) \ right); \; (A ^ *) ^ T = \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) $$

Mit der Formel $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ erhalten wir:

$$ A ^ (- 1) = \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37 \ end (array) \ right) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ Ende (Array) \ rechts) $$

Also $ A ^ (- 1) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \ end (Array) \ right) $. Um die Wahrheit des Ergebnisses zu überprüfen, genügt es, die Wahrheit einer der Gleichungen zu überprüfen: $ A ^ (- 1) \ cdot A = E $ oder $ A \ cdot A ^ (- 1) = E $. Prüfen wir die Gleichheit $ A \ cdot A ^ (- 1) = E $. Um weniger mit Brüchen zu arbeiten, ersetzen wir die Matrix $ A ^ (- 1) $ nicht in der Form $ \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ end (array) \ right) $, und als $ \ frac (1) (26) \ cdot \ left ( \ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (array) \ right) $:

Die Prüfung war erfolgreich, das Inverse $ A ^ (- 1) $ wurde korrekt gefunden.

Antworten: $ A ^ (- 1) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 / 13 & -3/26 & 37/26 \ end (Array) \ right) $.

Beispiel Nr. 4

Finden Sie die Umkehrung von $ A = \ left (\ begin (array) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8 & -8 & -3 \ Ende (Array) \ rechts) $.

Für eine Matrix vierter Ordnung ist es etwas schwierig, die inverse Matrix unter Verwendung von algebraischen Komplementen zu finden. Solche Beispiele finden sich jedoch in Testpapieren.

Um die Inverse einer Matrix zu finden, müssen Sie zunächst die Determinante der Matrix $ A $ berechnen. In dieser Situation können Sie dies am besten tun, indem Sie die Determinante zeilenweise (Spalte) erweitern. Wir wählen eine beliebige Zeile oder Spalte aus und finden die algebraischen Komplemente jedes Elements der ausgewählten Zeile oder Spalte.

Matrix Algebra - Inverse Matrix

inverse Matrix

Inverse Matrix heißt Matrix, die sowohl rechts als auch links mit einer gegebenen Matrix multipliziert die Identitätsmatrix ergibt.
Bezeichnen wir die Matrix invers zur Matrix EIN durch, dann erhalten wir gemäß der Definition:

wo E Ist die Identitätsmatrix.
Quadratische Matrix namens nicht speziell (nicht entartet), wenn seine Determinante nicht null ist. Ansonsten heißt es Besondere (degenerieren) oder Singular.

Es gilt folgender Satz: jede nichtsinguläre Matrix hat eine Inverse.

Die Operation zum Finden der inversen Matrix heißt appellieren Matrizen. Betrachten Sie den Matrixinversionsalgorithmus. Gegeben sei eine nichtsinguläre Matrix n-te Bestellung:

wobei Δ = det EIN ≠ 0.

Algebraisches Komplement eines Elements Matrizen n-te Ordnung EIN die Determinante der Matrix ( n–1) te Ordnung, die durch Löschen erhalten wird ich-te Zeile und J Spalte der Matrix EIN:

Lassen Sie uns die sogenannte befestigt Matrix:

wo sind die algebraischen Komplemente der entsprechenden Elemente der Matrix EIN.
Beachten Sie, dass die algebraischen Komplemente der Elemente der Zeilen der Matrix EIN werden in die entsprechenden Spalten der Matrix gesetzt Ã , das heißt, die Matrix wird gleichzeitig transponiert.
Durch Teilen aller Elemente der Matrix Ã durch Δ - der Wert der Determinante der Matrix EIN, erhalten wir als Ergebnis die inverse Matrix:

Wir beachten eine Reihe besonderer Eigenschaften der inversen Matrix:
1) für eine gegebene Matrix EIN seine inverse Matrix ist der einzige;
2) wenn es eine inverse Matrix gibt, dann rechts rückwärts und links rückwärts Matrizen fallen damit zusammen;
3) eine spezielle (entartete) quadratische Matrix hat keine inverse Matrix.

Die wichtigsten Eigenschaften der inversen Matrix:
1) die Determinante der inversen Matrix und die Determinante der ursprünglichen Matrix sind reziproke Werte;
2) die inverse Matrix des Produkts der quadratischen Matrizen ist gleich dem Produkt der inversen Matrizen von Faktoren, genommen in umgekehrter Reihenfolge:

3) die transponierte Inverse der Matrix ist gleich der Inversen der gegebenen transponierten Matrix:

BEISPIEL Berechnen Sie die Inverse der gegebenen Matrix.

Es gebe eine quadratische Matrix n-ter Ordnung

Die Matrix A -1 heißt inverse Matrix bezüglich der Matrix A, falls A * A -1 = E, wobei E die Einheitsmatrix n-ter Ordnung ist.

Einheitenmatrix- eine solche quadratische Matrix, in der alle Elemente entlang der Hauptdiagonale von der oberen linken Ecke zur unteren rechten Ecke Einsen und der Rest Nullen sind, zum Beispiel:

inverse Matrix kann existieren nur für quadratische Matrizen jene. für die Matrizen mit der gleichen Anzahl von Zeilen und Spalten.

Der Satz über die Bedingung für die Existenz einer inversen Matrix

Damit eine Matrix eine inverse Matrix hat, ist es notwendig und ausreichend, dass sie nicht entartet ist.

Die Matrix A = (A1, A2, ... A n) heißt nicht entartet wenn die Spaltenvektoren linear unabhängig sind. Die Anzahl der linear unabhängigen Spaltenvektoren einer Matrix wird als Rang der Matrix bezeichnet. Daher können wir sagen, dass es für die Existenz einer inversen Matrix notwendig und ausreichend ist, dass der Rang der Matrix gleich ihrer Dimension ist, d.h. r = n.

Algorithmus zum Finden der inversen Matrix

Schreiben Sie Matrix A in die Tabelle zur Lösung von Gleichungssystemen nach der Gauß-Methode und ordnen Sie rechts (anstelle der rechten Seite der Gleichungen) Matrix E zu.
Reduzieren Sie mit der Jordan-Transformation die Matrix A auf eine Matrix, die aus Einheitsspalten besteht; in diesem Fall ist es notwendig, gleichzeitig die Matrix E zu transformieren.
Ordnen Sie gegebenenfalls die Zeilen (Gleichungen) der letzten Tabelle so um, dass wir unter der Matrix A der ursprünglichen Tabelle die Einheitsmatrix E erhalten.
Schreiben Sie die inverse Matrix A -1 auf, die in der letzten Tabelle unter der Matrix E der ursprünglichen Tabelle steht.

Beispiel 1

Finden Sie für Matrix A die inverse Matrix A -1

Lösung: Wir schreiben die Matrix A auf und ordnen rechts die Identitätsmatrix E zu. Mit den Jordan-Transformationen reduzieren wir die Matrix A auf die Identitätsmatrix E. Die Berechnungen sind in Tabelle 31.1 dargestellt.

Lassen Sie uns die Richtigkeit der Berechnungen überprüfen, indem wir die ursprüngliche Matrix A und die inverse Matrix A -1 multiplizieren.

Als Ergebnis der Matrixmultiplikation wird die Einheitsmatrix erhalten. Daher sind die Berechnungen korrekt.

Antworten:

Lösen von Matrixgleichungen

Matrixgleichungen können die Form haben:

AX = B, XA = B, AXB = C,

wobei A, B, C die angegebenen Matrizen sind, X die erforderliche Matrix.

Matrixgleichungen werden gelöst, indem die Gleichung mit ihren inversen Matrizen multipliziert wird.

Um beispielsweise eine Matrix aus einer Gleichung zu finden, multiplizieren Sie diese Gleichung mit der linken.

Um eine Lösung der Gleichung zu finden, müssen Sie daher die inverse Matrix finden und mit der Matrix auf der rechten Seite der Gleichung multiplizieren.

Andere Gleichungen werden ähnlich gelöst.

Beispiel 2

Löse die Gleichung AX = B falls

Lösung: Da die Inverse der Matrix ist (siehe Beispiel 1)

Matrixmethode in der Wirtschaftsanalyse

Neben anderen finden sie auch Anwendung in Matrixmethoden... Diese Methoden basieren auf Linear- und Vektor-Matrix-Algebra. Solche Methoden werden verwendet, um komplexe und mehrdimensionale ökonomische Phänomene zu analysieren. Am häufigsten werden diese Methoden verwendet, wenn eine vergleichende Bewertung der Funktionsweise von Organisationen und ihrer Struktureinheiten erforderlich ist.

Bei der Anwendung von Matrixanalysemethoden können mehrere Stufen unterschieden werden.

In der ersten Phase ein System von Wirtschaftsindikatoren wird gebildet und auf seiner Grundlage eine Matrix von Ausgangsdaten erstellt, die eine Tabelle ist, in der die Systemnummern in separaten Zeilen aufgeführt sind (i = 1,2, ...., n), und entlang der vertikalen Spalten - die Anzahl der Indikatoren (j = 1,2, ...., m).

In der zweiten Stufe für jede vertikale Spalte wird der größte der verfügbaren Werte von Indikatoren angezeigt, der als Einheit verwendet wird.

Danach werden alle in dieser Spalte angegebenen Beträge durch den größten Wert geteilt und eine Matrix standardisierter Koeffizienten gebildet.

In der dritten Stufe alle Bestandteile der Matrix werden quadriert. Wenn sie unterschiedliche Bedeutung haben, wird jedem Indikator der Matrix ein bestimmter Gewichtungsfaktor zugewiesen k... Der Wert der letzteren wird durch Expertenurteil bestimmt.

Beim letzten, vierte Stufe gefundene Werte von Bewertungen R j werden nach steigender oder fallender Reihenfolge gruppiert.

Die skizzierten Matrixmethoden sollten beispielsweise bei der vergleichenden Analyse verschiedener Investitionsprojekte sowie bei der Bewertung anderer wirtschaftlicher Indikatoren der Aktivitäten von Organisationen verwendet werden.