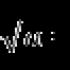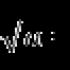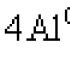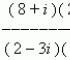Schreiben Sie eine Gleichung für eine Tangente an einen gegebenen Punkt. Lektion "die Gleichung der Tangente an den Graphen der Funktion"
Tangente ist eine Gerade , die den Funktionsgraphen in einem Punkt berührt und deren alle Punkte den geringsten Abstand zum Funktionsgraphen haben. Daher geht die Tangente in einem bestimmten Winkel tangential an den Funktionsgraphen und mehrere Tangenten können nicht durch den Tangentenpunkt darunter gehen verschiedene Winkel. Die Tangentengleichungen und die Gleichungen der Normalen zum Graphen der Funktion werden unter Verwendung der Ableitung erstellt.
Die Tangentengleichung wird aus der Geradengleichung abgeleitet .
Wir leiten die Gleichung der Tangente und dann die Gleichung der Normalen zum Graphen der Funktion her.
j = kx + B .
In ihm k- Winkelkoeffizient.
Von hier erhalten wir folgenden Eintrag:
j - j 0 = k(x - x 0 ) .
Abgeleiteter Wert F "(x 0 ) Funktionen j = F(x) am Punkt x0 gleich der Steigung k=tg φ Tangente an den Graphen einer durch einen Punkt gezeichneten Funktion m0 (x 0 , j 0 ) , wo j0 = F(x 0 ) . Das ist was geometrische Bedeutung der Ableitung .
Somit können wir ersetzen k auf der F "(x 0 ) und bekomme folgendes die Gleichung der Tangente an den Graphen der Funktion :
j - j 0 = F "(x 0 )(x - x 0 ) .
Bei Aufgaben zum Erstellen der Gleichung einer Tangente an den Graphen einer Funktion (und wir werden bald zu ihnen übergehen) ist es erforderlich, die aus der obigen Formel erhaltene Gleichung zu bringen allgemeine Geradengleichung. Dazu müssen Sie alle Buchstaben und Zahlen auf die linke Seite der Gleichung übertragen und auf der rechten Seite Null lassen.
Nun zur Normalgleichung. Normal ist eine Gerade, die durch den Tangentenpunkt zum Graphen der Funktion senkrecht zur Tangente verläuft. Normale Gleichung :
(x - x 0 ) + F "(x 0 )(j - j 0 ) = 0
Um das erste Beispiel aufzuwärmen, werden Sie gebeten, es selbst zu lösen und sich dann die Lösung anzusehen. Es gibt allen Grund zu hoffen, dass diese Aufgabe für unsere Leser keine „kalte Dusche“ sein wird.
Beispiel 0. Stellen Sie die Gleichung der Tangente und die Gleichung der Normalen zum Graphen der Funktion an einem Punkt zusammen m (1, 1) .
Beispiel 1 Stellen Sie die Gleichung der Tangente und die Gleichung der Normalen zum Graphen der Funktion zusammen ![]() wenn die Abszisse des Berührungspunkts ist.
wenn die Abszisse des Berührungspunkts ist.
Finden wir die Ableitung der Funktion:
Jetzt haben wir alles, was in den Eintrag in der theoretischen Referenz eingesetzt werden muss, um die Tangentengleichung zu erhalten. Wir bekommen
![]()
In diesem Beispiel hatten wir Glück: Die Steigung stellte sich als gleich Null heraus, also bringen Sie die Gleichung separat auf Gesamtansicht musste nicht. Jetzt können wir die Normalgleichung schreiben:
![]()
In der Abbildung unten: Graph der Funktion Burgund, Tangente Grüne Farbe, die normale ist orange.

Das nächste Beispiel ist ebenfalls nicht kompliziert: Die Funktion ist wie im vorherigen auch ein Polynom, aber der Steigungskoeffizient wird nicht gleich Null sein, also wird ein weiterer Schritt hinzugefügt - wodurch die Gleichung auf eine allgemeine Form gebracht wird.
Beispiel 2
Lösung. Finden wir die Ordinate des Berührungspunkts:
Finden wir die Ableitung der Funktion:
![]() .
.
Lassen Sie uns den Wert der Ableitung am Kontaktpunkt ermitteln, dh die Steigung der Tangente:
Wir setzen alle erhaltenen Daten in die "leere Formel" ein und erhalten die Tangentengleichung:
![]()
Wir bringen die Gleichung auf eine allgemeine Form (wir sammeln alle Buchstaben und Zahlen außer Null auf der linken Seite und lassen Null auf der rechten Seite):
Wir bilden die Gleichung der Normalen:

Beispiel 3 Stellen Sie die Gleichung der Tangente und die Gleichung der Normalen auf den Graphen der Funktion auf, wenn die Abszisse des Kontaktpunktes ist.
Lösung. Finden wir die Ordinate des Berührungspunkts:
Finden wir die Ableitung der Funktion:
![]() .
.
Lassen Sie uns den Wert der Ableitung am Kontaktpunkt ermitteln, dh die Steigung der Tangente:
![]() .
.
Wir finden die Tangentengleichung:

Bevor Sie die Gleichung auf eine allgemeine Form bringen, müssen Sie sie ein wenig „kombinieren“: Multiplizieren Sie Term für Term mit 4. Wir tun dies und bringen die Gleichung auf eine allgemeine Form:
Wir bilden die Gleichung der Normalen:

Beispiel 4 Stellen Sie die Gleichung der Tangente und die Gleichung der Normalen auf den Graphen der Funktion auf, wenn die Abszisse des Kontaktpunktes ist.
Lösung. Finden wir die Ordinate des Berührungspunkts:
![]() .
.
Finden wir die Ableitung der Funktion:
Lassen Sie uns den Wert der Ableitung am Kontaktpunkt ermitteln, dh die Steigung der Tangente:
![]() .
.
Wir erhalten die Tangentengleichung:
Wir bringen die Gleichung auf eine allgemeine Form:
Wir bilden die Gleichung der Normalen:
![]()
Ein häufiger Fehler beim Schreiben von Tangenten- und Normalgleichungen besteht darin, nicht zu bemerken, dass die im Beispiel angegebene Funktion komplex ist, und ihre Ableitung als Ableitung einer einfachen Funktion zu berechnen. Die folgenden Beispiele sind bereits komplexe Funktionen(die entsprechende Lektion öffnet sich in einem neuen Fenster).
Beispiel 5 Stellen Sie die Gleichung der Tangente und die Gleichung der Normalen auf den Graphen der Funktion auf, wenn die Abszisse des Kontaktpunktes ist.
Lösung. Finden wir die Ordinate des Berührungspunkts:
Aufmerksamkeit! Diese Funktion ist komplex, da das Argument des Tangens (2 x) ist selbst eine Funktion. Daher finden wir die Ableitung einer Funktion als Ableitung einer komplexen Funktion.
Der Artikel gibt eine detaillierte Erklärung der Definitionen, der geometrischen Bedeutung der Ableitung mit grafischer Notation. Die Gleichung der Tangente wird an Beispielen betrachtet, die Gleichungen der Tangente an Kurven 2. Ordnung werden gefunden.
Yandex.RTB R-A-339285-1 Definition 1
Der Neigungswinkel der Geraden y \u003d k x + b wird als Winkel α bezeichnet, der von der positiven Richtung der x-Achse zur Geraden y \u003d k x + b in positiver Richtung gemessen wird.
In der Abbildung ist die Richtungsachse durch einen grünen Pfeil und einen grünen Bogen und der Neigungswinkel durch einen roten Bogen gekennzeichnet. Die blaue Linie bezieht sich auf eine gerade Linie.
Bestimmung 2
Die Steigung der Geraden y \u003d k x + b wird als numerischer Koeffizient k bezeichnet.
Die Steigung ist gleich der Steigung der Geraden, also k = t g α .
- Die Steigung der Geraden ist nur dann 0, wenn o x parallel ist und die Steigung gleich null ist, weil die Tangente von null 0 ist. Die Form der Gleichung ist also y = b.
- Ist der Neigungswinkel der Geraden y = k x + b spitz, so sind die Bedingungen 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 , und es gibt eine Zunahme im Diagramm.
- Wenn α \u003d π 2, dann ist die Position der Linie senkrecht zu x. Gleichheit wird durch die Gleichheit x = c angegeben, wobei der Wert c eine reelle Zahl ist.
- Ist der Neigungswinkel der Geraden y = k x + b stumpf, so entspricht er den Bedingungen π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Eine Sekante ist eine Gerade, die durch 2 Punkte der Funktion f (x) geht. Mit anderen Worten, eine Sekante ist eine gerade Linie, die durch zwei beliebige Punkte in der Grafik verläuft. gegebene Funktion.

Die Abbildung zeigt, dass A B eine Sekante ist und f (x) eine schwarze Kurve ist, α ein roter Bogen ist, der den Neigungswinkel der Sekante anzeigt.
Wenn die Steigung einer Geraden gleich der Tangente des Neigungswinkels ist, ist es klar, dass die Tangente eines rechtwinkligen Dreiecks A B C in Bezug auf das gegenüberliegende Bein des benachbarten gefunden werden kann.
Bestimmung 4
Wir erhalten die Formel zur Bestimmung der Sekante der Form:
k = tg α = BCAC = f (x B) - fx A x B - x A , wobei die Abszissen der Punkte A und B die Werte x A , x B und f (x A) , f (x B) sind die Wertefunktionen an diesen Punkten.
Offensichtlich wird die Steigung der Sekante durch die Gleichheit k \u003d f (x B) - f (x A) x B - x A oder k \u003d f (x A) - f (x B) x A - x definiert B, und die Gleichung muss geschrieben werden als y = f (x B) - f (x A) x B - x A x - x A + f (x A) oder
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .
Die Sekante teilt den Graphen visuell in 3 Teile: links von Punkt A, von A nach B, rechts von B. Die folgende Abbildung zeigt, dass es drei Sekanten gibt, die als gleich angesehen werden, das heißt, sie sind es mit einer ähnlichen Gleichung setzen.

Per Definition ist klar, dass in diesem Fall die Gerade und ihre Sekante zusammenfallen.
Eine Sekante kann den Graphen einer bestimmten Funktion mehrmals schneiden. Wenn es für die Sekante eine Gleichung der Form y \u003d 0 gibt, ist die Anzahl der Schnittpunkte mit der Sinuskurve unendlich.
Bestimmung 5
Tangente an den Graphen der Funktion f (x) im Punkt x 0 ; f (x 0) heißt Gerade, die durch einen gegebenen Punkt x 0 geht; f (x 0) , mit Vorhandensein eines Segments, das viele x-Werte in der Nähe von x 0 hat.
Beispiel 1
Schauen wir uns das folgende Beispiel genauer an. Dann ist ersichtlich, dass die durch die Funktion y = x + 1 gegebene Linie an dem Punkt mit den Koordinaten (1 ; 2) als tangential zu y = 2 x angesehen wird. Zur Verdeutlichung müssen Diagramme mit Werten in der Nähe von (1; 2) betrachtet werden. Die Funktion y = 2 x ist schwarz markiert, die blaue Linie ist die Tangente, der rote Punkt ist der Schnittpunkt.

Offensichtlich verschmilzt y \u003d 2 x mit der Linie y \u003d x + 1.
Um die Tangente zu bestimmen, sollte man das Verhalten der Tangente A B betrachten, wenn Punkt B sich Punkt A unendlich nähert.Der Übersichtlichkeit halber zeigen wir eine Abbildung.

Die Sekante A B, angezeigt durch die blaue Linie, tendiert zur Position der Tangente selbst, und der Neigungswinkel der Sekante α wird beginnen, sich dem Neigungswinkel der Tangente selbst α x anzunähern.
Bestimmung 6
Die Tangente an den Graphen der Funktion y \u003d f (x) am Punkt A ist die Grenzposition der Sekante A B bei B, die zu A tendiert, dh B → A.
Nun wenden wir uns der Betrachtung der geometrischen Bedeutung der Ableitung einer Funktion an einem Punkt zu.
Kommen wir zur Betrachtung der Sekante AB für die Funktion f (x), wobei A und B die Koordinaten x 0, f (x 0) und x 0 + ∆ x, f (x 0 + ∆ x) und ∆ haben x wird als Inkrement des Arguments bezeichnet. Nun nimmt die Funktion die Form ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) an. Nehmen wir zur Verdeutlichung ein Bild als Beispiel.

Betrachten Sie das resultierende rechtwinklige Dreieck A B C. Wir verwenden die Definition der Tangente für die Lösung, dh wir erhalten das Verhältnis ∆ y ∆ x = t g α . Aus der Definition einer Tangente folgt, dass lim ∆ x → 0 ∆ y ∆ x = t g α x . Gemäß der Ableitungsregel an einem Punkt haben wir, dass die Ableitung f (x) am Punkt x 0 die Grenze des Verhältnisses des Inkrements der Funktion zum Inkrement des Arguments heißt, wobei ∆ x → 0, dann bezeichnet als f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Daraus folgt, dass f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, wobei k x als Steigung der Tangente bezeichnet wird.
Das heißt, wir erhalten, dass f ' (x) am Punkt x 0 existieren kann und sowie die Tangente an den gegebenen Graphen der Funktion am Kontaktpunkt gleich x 0 , f 0 (x 0) , wobei der Wert der Steigung der Tangente am Punkt ist gleich der Ableitung am Punkt x 0 . Dann erhalten wir, dass k x = f "(x 0) .
Die geometrische Bedeutung der Ableitung einer Funktion an einem Punkt ist, dass das Konzept der Existenz einer Tangente an den Graphen an demselben Punkt gegeben ist.
Um die Gleichung einer geraden Linie in der Ebene zu schreiben, muss der Punkt, durch den sie verläuft, eine Steigung haben. Seine Bezeichnung wird als x 0 am Schnittpunkt genommen.
Die Gleichung der Tangente an den Graphen der Funktion y \u003d f (x) am Punkt x 0, f 0 (x 0) hat die Form y \u003d f "(x 0) x - x 0 + f (x 0) .
Dies bedeutet, dass der Endwert der Ableitung f "(x 0) die Position der Tangente bestimmen kann, dh vertikal unter der Bedingung lim x → x 0 + 0 f" (x) = ∞ und lim x → x 0 - 0 f "(x ) = ∞ oder gar keine Abwesenheit unter der Bedingung lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f "(x) .
Die Position der Tangente hängt vom Wert ihrer Steigung ab kx \u003d f "(x 0). Wenn parallel zur x-Achse, erhalten wir, dass kk \u003d 0, wenn parallel zu etwa y - kx \u003d ∞, und die Form der Tangentengleichung x \u003d x 0 steigt mit kx > 0 , nimmt mit kx ab< 0 .
Beispiel 2
Stellen Sie die Gleichung der Tangente an den Graphen der Funktion y \u003d ex + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 an einem Punkt mit den Koordinaten (1; 3) mit der Definition des Winkels von zusammen Neigung.
Lösung
Nach Annahme haben wir, dass die Funktion für alle reellen Zahlen definiert ist. Wir erhalten, dass der Punkt mit den durch die Bedingung (1 ; 3) angegebenen Koordinaten der Kontaktpunkt ist, dann ist x 0 = - 1 , f (x 0) = - 3 .
Es ist notwendig, die Ableitung am Punkt mit dem Wert -1 zu finden. Das verstehen wir
y "= ex + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" == ex + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = ex + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Der Wert von f ’ (x) am Kontaktpunkt ist Neigungsfaktor Tangente, die gleich der Tangente der Steigung ist.
Dann ist k x = t g α x = y "(x 0) = 3 3
Daraus folgt, dass α x = a r c t g 3 3 = π 6
Antworten: die Tangentengleichung nimmt die Form an
y \u003d f "(x 0) x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3
Zur Verdeutlichung geben wir ein Beispiel in einer grafischen Darstellung.
Schwarze Farbe wird für das Diagramm der ursprünglichen Funktion verwendet, blaue Farbe- das Bild der Tangente, der rote Punkt - der Kontaktpunkt. Die Abbildung rechts zeigt eine vergrößerte Ansicht.

Beispiel 3
Finden Sie die Existenz einer Tangente an den Graphen einer gegebenen Funktion heraus
y = 3 x - 1 5 + 1 am Punkt mit den Koordinaten (1 ; 1) . Stelle eine Gleichung auf und bestimme den Neigungswinkel.
Lösung
Nach Annahme haben wir, dass der Definitionsbereich der gegebenen Funktion die Menge aller reellen Zahlen ist.
Kommen wir zur Ermittlung der Ableitung
y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
Wenn x 0 = 1 , dann ist f ' (x) nicht definiert, aber die Grenzen werden geschrieben als lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 1 + 0 = + ∞ und lim x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ , was Existenz vertikale Tangente an bedeutet Punkt (1 ; 1) .
Antworten: Die Gleichung hat die Form x \u003d 1, wobei der Neigungswinkel gleich π 2 ist.
Lassen Sie es uns zur Verdeutlichung grafisch darstellen.

Beispiel 4
Finden Sie die Punkte des Funktionsgraphen y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 , wobei
- Die Tangente existiert nicht;
- Die Tangente ist parallel zu x;
- Die Tangente ist parallel zur Linie y = 8 5 x + 4 .
Lösung
Dabei ist auf den Definitionsbereich zu achten. Nach Annahme haben wir, dass die Funktion auf der Menge aller reellen Zahlen definiert ist. Erweitern Sie den Modul und lösen Sie das System mit Intervallen x ∈ - ∞ ; 2 und [-2; +∞) . Das verstehen wir
y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)
Die Funktion muss differenziert werden. Wir haben das
y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 " , x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)
Wenn x = - 2, dann existiert die Ableitung nicht, weil die einseitigen Grenzen an dieser Stelle nicht gleich sind:
lim x → - 2 - 0 y "(x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Wir berechnen den Wert der Funktion am Punkt x \u003d - 2, wo wir das bekommen
- y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, dh die Tangente an der Punkt (- 2; - 2) wird nicht existieren.
- Die Tangente ist parallel zu x, wenn die Steigung Null ist. Dann kx \u003d tg α x \u003d f "(x 0). Das heißt, es ist notwendig, die Werte eines solchen x zu finden, wenn die Ableitung der Funktion es auf Null bringt. Das heißt, die Werte von f ' (x) und werden Berührungspunkte sein, an denen die Tangente parallel zu x ist.
Wenn x ∈ - ∞ ; - 2 , dann - 1 5 (x 2 + 12 x + 35) = 0 , und für x ∈ (- 2 ; + ∞) erhalten wir 1 5 (x 2 - 4 x + 3) = 0 .
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞
Wir berechnen die entsprechenden Werte der Funktion
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
Daher - 5; 8 5 , - 4 ; 4 3 , 1 ; 85, 3; 4 3 werden als die gewünschten Punkte des Graphen der Funktion angesehen.
Erwägen grafisches Bild Lösungen.

Die schwarze Linie ist der Graph der Funktion, die roten Punkte sind die Berührungspunkte.
- Wenn die Linien parallel sind, sind die Steigungen gleich. Dann müssen die Punkte des Funktionsgraphen gesucht werden, an denen die Steigung gleich dem Wert 8 5 ist. Dazu müssen Sie eine Gleichung der Form y "(x) = 8 5 lösen. Wenn dann x ∈ - ∞; - 2, erhalten wir - 1 5 (x 2 + 12 x + 35) = 8 5, und wenn x ∈ ( - 2 ; + ∞) , dann 1 5 (x 2 - 4 x + 3) = 8 5 .
Die erste Gleichung hat keine Wurzeln, weil die Diskriminante weniger als Null. Schreiben wir das auf
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
Eine andere Gleichung hat dann zwei reelle Wurzeln
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞
Fahren wir fort, um die Werte der Funktion zu finden. Das verstehen wir
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
Punkte mit Werten - 1 ; 4 15 , 5 ; 8 3 sind die Punkte, an denen die Tangenten parallel zur Linie y = 8 5 x + 4 sind.
Antworten: schwarze Linie - Diagramm der Funktion, rote Linie - Diagramm y \u003d 8 5 x + 4, blaue Linie - Tangenten an Punkten - 1; 4 15 , 5 ; 8 3 .

Die Existenz unendlich vieler Tangenten für gegebene Funktionen ist möglich.
Beispiel 5
Schreiben Sie die Gleichungen aller verfügbaren Tangenten der Funktion y = 3 cos 3 2 x - π 4 - 1 3 , die senkrecht auf der Linie y = - 2 x + 1 2 stehen.
Lösung
Um die Tangentengleichung aufzustellen, müssen der Koeffizient und die Koordinaten des Kontaktpunkts basierend auf der Bedingung der Rechtwinkligkeit der Linien ermittelt werden. Die Definition klingt so: Das Produkt der Steigungen, die senkrecht zu den Geraden stehen, ist gleich - 1, d. h. es wird geschrieben als k x · k ⊥ = - 1. Aus der Bedingung, dass die Steigung senkrecht zur Geraden steht und gleich k ⊥ = - 2 ist, ist k x = - 1 k ⊥ = - 1 - 2 = 1 2 .
Jetzt müssen wir die Koordinaten der Berührungspunkte finden. Sie müssen x finden, danach seinen Wert für eine bestimmte Funktion. Beachten Sie das aus der geometrischen Bedeutung der Ableitung an dem Punkt
x 0 erhalten wir das k x \u003d y "(x 0) . Aus dieser Gleichheit finden wir die x-Werte für die Berührungspunkte.
Das verstehen wir
y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3" = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 \u003d - 9 2 Sünde 3 2 x 0 - π 4 ⇒ kx \u003d y "(x 0) ⇔ - 9 2 Sünde 3 2 x 0 - π 4 \u003d 1 2 ⇒ Sünde 3 2 x 0 - π 4 = - 1 9
Das trigonometrische Gleichung wird verwendet, um die Ordinaten der Berührungspunkte zu berechnen.
3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk oder 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk
3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk oder 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk oder x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z ist die Menge der ganzen Zahlen.
x Anlaufstellen gefunden. Jetzt müssen Sie zur Suche nach y-Werten gehen:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - Sünde 2 3 2 x 0 - π 4 - 1 3 oder y 0 = 3 - 1 - Sünde 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 oder y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 oder y 0 = - 4 5 + 1 3
Von hier erhalten wir, dass 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 sind Berührungspunkte.
Antworten: die notwendigen Gleichungen werden als geschrieben
y = 1 2 x - 2 3 π 4 - arc sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + arc sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
Betrachten Sie für eine visuelle Darstellung die Funktion und die Tangente an der Koordinatenlinie.
Die Abbildung zeigt, dass die Position der Funktion im Intervall [-10; 10 ] , wobei die schwarze Linie der Graph der Funktion ist, die blauen Linien Tangenten sind, die senkrecht zu der gegebenen Linie der Form y = - 2 x + 1 2 stehen. Rote Punkte sind Berührungspunkte.

Die kanonischen Kurvengleichungen 2. Ordnung sind keine einwertigen Funktionen. Tangentengleichungen für sie werden nach bekannten Schemata erstellt.
Tangente zum Kreis
Um einen Kreis zu setzen, der an einem Punkt x c e n t e r zentriert ist; y c e n t e r und Radius R, wird die Formel x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 verwendet.
Diese Gleichheit kann als Vereinigung zweier Funktionen geschrieben werden:
y = R 2 - x - x Mitte 2 + y Mitte r y = - R 2 - x - x Mitte 2 + y Mitte
Die erste Funktion befindet sich oben und die zweite unten, wie in der Abbildung gezeigt.

Um eine Kreisgleichung an einem Punkt x 0 aufzustellen; y 0 , das sich im oberen oder unteren Halbkreis befindet, sollten Sie die Gleichung des Funktionsgraphen der Form y \u003d R 2 - x - xcenter 2 + ycenter oder y \u003d - R 2 - x - xcenter finden 2 + ycenter am angegebenen Punkt.
Wenn an den Punkten x c e n t e r ; y c e n t e r + R und x c e n t e r ; y c e n t e r - R Tangenten können durch die Gleichungen y = y c e n t e r + R und y = y c e n t e r - R und an den Punkten x c e n t e r + R gegeben werden; y c e n t e r und
x c e n t e r - R ; y c e n t e r parallel zu y, dann erhalten wir Gleichungen der Form x = x c e n t e r + R und x = x c e n t e r - R .

Tangente an Ellipse
Wenn die Ellipse bei x c e n t e r zentriert ist; y c e n t e r mit den Halbachsen a und b , dann kann es durch die Gleichung x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 gegeben werden .
Eine Ellipse und ein Kreis können bezeichnet werden, indem zwei Funktionen kombiniert werden, nämlich die obere und die untere Halbellipse. Dann bekommen wir das
y = b a a 2 - (x - x Mitte) 2 + y Mitte y = - b a a 2 - (x - x Mitte) 2 + y Mitte

Liegen die Tangenten an den Scheitelpunkten der Ellipse, dann sind sie parallel zu x oder zu y. Betrachten Sie zur Verdeutlichung die folgende Abbildung.

Beispiel 6
Schreiben Sie die Gleichung der Tangente an die Ellipse x - 3 2 4 + y - 5 2 25 = 1 an Punkten mit x-Werten gleich x = 2 .
Lösung
Es gilt Berührungspunkte zu finden, die dem Wert x = 2 entsprechen. Wir nehmen eine Substitution in die bestehende Gleichung der Ellipse vor und erhalten diese
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
Dann 2 ; 5 3 2 + 5 und 2 ; - 5 3 2 + 5 sind die Tangentenpunkte, die zur oberen und unteren Halbellipse gehören.
Lassen Sie uns weitergehen, um die Gleichung einer Ellipse in Bezug auf y zu finden und aufzulösen. Das verstehen wir
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
Es ist offensichtlich, dass die obere Halbellipse durch eine Funktion der Form y = 5 + 5 2 4 - x - 3 2 und die untere y = 5 - 5 2 4 - x - 3 2 angegeben wird.
Wir wenden den Standardalgorithmus an, um die Gleichung der Tangente an den Graphen einer Funktion in einem Punkt zu formulieren. Wir schreiben, dass die Gleichung für die erste Tangente im Punkt 2 ; 5 3 2 + 5 aussehen wird
y "= 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
Damit erhalten wir die Gleichung der zweiten Tangente mit dem Wert am Punkt
2; - 5 3 2 + 5 wird
y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
Grafisch werden Tangenten wie folgt bezeichnet:

Tangente an Übertreibung
Wenn die Hyperbel einen Mittelpunkt im Punkt x c e n t e r hat; y c e n t e r und Eckpunkte x c e n t e r + α ; y c e n t e r und x c e n t e r - α ; y c e n t e r , die Ungleichung x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 ist gegeben, wenn mit Knoten x c e n t e r ; y c e n t e r + b und x c e n t e r ; y c e n t e r - b ist dann gegeben durch die Ungleichung x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = -1 .

Eine Hyperbel kann als zwei kombinierte Funktionen der Form dargestellt werden
y = ba (x - xcenter) 2 - a 2 + ycentery = - ba (x - xcenter) 2 - a 2 + ycenter oder y = ba (x - xcenter) 2 + a 2 + ycentery = - ba (x - xcenter ) 2 + a 2 + yzentrum

Im ersten Fall sind die Tangenten parallel zu y und im zweiten Fall parallel zu x.
Daraus folgt, dass man, um die Gleichung einer Tangente an eine Hyperbel zu finden, herausfinden muss, zu welcher Funktion der Tangentenpunkt gehört. Um dies zu bestimmen, ist es notwendig, eine Substitution in den Gleichungen vorzunehmen und sie auf Identität zu überprüfen.
Beispiel 7
Schreiben Sie die Gleichung der Tangente an die Hyperbel x - 3 2 4 - y + 3 2 9 = 1 an Punkt 7; - 3 3 - 3 .
Lösung
Es ist notwendig, den Datensatz der Lösung zum Finden der Hyperbel mit 2 Funktionen zu transformieren. Das verstehen wir
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 oder y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
Es ist notwendig herauszufinden, zu welcher Funktion der gegebene Punkt mit den Koordinaten 7 gehört; - 3 3 - 3 .
Offensichtlich braucht man zur Überprüfung der ersten Funktion y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 , dann gehört der Punkt nicht zum Graphen, da die Gleichheit ist nicht erfüllt.
Für die zweite Funktion gilt y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , was bedeutet, dass der Punkt zu dem gegebenen Graphen gehört. Von hier aus sollten Sie den Steigungskoeffizienten finden.
Das verstehen wir
y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ kx = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
Antworten: Die Tangentengleichung kann dargestellt werden als
y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
Es wird wie folgt visualisiert:

Tangente an die Parabel
Um die Gleichung der Tangente an die Parabel y \u003d ax 2 + bx + c am Punkt x 0, y (x 0) zu erstellen, müssen Sie den Standardalgorithmus verwenden, dann hat die Gleichung die Form y \u003d y " (x 0) x - x 0 + y ( x 0) Eine solche Tangente am Scheitelpunkt ist parallel zu x.
Die Parabel x = a y 2 + b y + c sollte als Vereinigung zweier Funktionen definiert werden. Daher müssen wir die Gleichung nach y lösen. Das verstehen wir
x = ay 2 + by + c ⇔ ay 2 + by + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 ay = - b - b 2 - 4 a (c - x) 2 a
Lassen Sie es uns grafisch darstellen als:

Um herauszufinden, ob ein Punkt x 0 , y (x 0) zu einer Funktion gehört, folgen Sie vorsichtig dem Standardalgorithmus. Eine solche Tangente wird in Bezug auf die Parabel parallel zu y sein.
Beispiel 8
Schreiben Sie die Gleichung der Tangente an den Graphen x - 2 y 2 - 5 y + 3, wenn wir eine Tangentensteigung von 150 ° haben.
Lösung
Wir beginnen die Lösung, indem wir die Parabel als zwei Funktionen darstellen. Das verstehen wir
2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 xy = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4
Der Wert der Steigung ist gleich dem Wert der Ableitung am Punkt x 0 dieser Funktion und gleich der Tangente der Steigung.
Wir bekommen:
k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3
Von hier aus bestimmen wir den Wert von x für die Berührungspunkte.
Die erste Funktion wird geschrieben als
y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Offensichtlich gibt es keine wirklichen Wurzeln, da wir einen negativen Wert erhalten haben. Wir schließen daraus, dass es für eine solche Funktion keine Tangente mit einem Winkel von 150 ° gibt.
Die zweite Funktion wird geschrieben als
y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
Wir haben, dass die Berührungspunkte - 23 4 ; - 5 + 3 4 .
Antworten: die Tangentengleichung nimmt die Form an
y = - 1 3 x - 23 4 + - 5 + 3 4
Lassen Sie es uns so grafisch darstellen:

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Enter
Anweisung
Wir bestimmen die Steigung der Tangente an die Kurve im Punkt M.
Die Kurve, die den Graphen der Funktion y = f(x) darstellt, ist in einer gewissen Umgebung des Punktes M (einschließlich des Punktes M selbst) stetig.
Existiert der Wert f‘(x0) nicht, dann gibt es entweder keine Tangente oder sie verläuft senkrecht. In Anbetracht dessen ist das Vorhandensein der Ableitung der Funktion am Punkt x0 auf das Vorhandensein einer nicht vertikalen Tangente zurückzuführen, die den Graphen der Funktion am Punkt (x0, f(x0)) berührt. In diesem Fall ist die Steigung der Tangente gleich f "(x0). Dadurch wird die geometrische Bedeutung der Ableitung klar - die Berechnung der Steigung der Tangente.
Finden Sie den Wert der Abszisse des Kontaktpunkts, der mit dem Buchstaben "a" bezeichnet wird. Wenn es mit dem gegebenen Tangentenpunkt zusammenfällt, dann ist "a" seine x-Koordinate. Bestimmen Sie den Wert Funktionen f(a), Einsetzen in die Gleichung Funktionen die Größe der Abszisse.
Bestimme die erste Ableitung der Gleichung Funktionen f'(x) und ersetzen Sie den Wert des Punktes "a" darin.
Nehmen allgemeine Gleichung Tangente, die als y \u003d f (a) \u003d f (a) (x - a) definiert ist, und ersetzen Sie die gefundenen Werte von a, f (a), f "(a) darin Als Ergebnis wird die Lösung des Graphen und der Tangente gefunden.
Lösen Sie das Problem auf andere Weise, wenn der gegebene Tangentenpunkt nicht mit dem Tangentenpunkt übereinstimmt. In diesem Fall ist es notwendig, "a" anstelle von Zahlen in der Tangentengleichung einzusetzen. Ersetzen Sie danach anstelle der Buchstaben "x" und "y" den Wert der Koordinaten des angegebenen Punktes. Lösen Sie die resultierende Gleichung, in der "a" die Unbekannte ist. Setzen Sie den resultierenden Wert in die Tangentengleichung ein.
Schreiben Sie eine Gleichung für eine Tangente mit dem Buchstaben "a", wenn die Gleichung in der Bedingung der Aufgabe gegeben ist Funktionen und Gleichung Parallele bezüglich der gesuchten Tangente. Danach benötigen Sie ein Derivat Funktionen zur Koordinate am Punkt "a". Setzen Sie den entsprechenden Wert in die Tangentengleichung ein und lösen Sie die Funktion.
Ihre Privatsphäre ist uns wichtig. Aus diesem Grund haben wir eine Datenschutzrichtlinie entwickelt, die beschreibt, wie wir Ihre Informationen verwenden und speichern. Bitte lesen Sie unsere Datenschutzerklärung und lassen Sie uns wissen, wenn Sie Fragen haben.
Erhebung und Verwendung personenbezogener Daten
Personenbezogene Daten sind Daten, mit denen eine bestimmte Person identifiziert oder kontaktiert werden kann.
Sie können jederzeit um die Angabe Ihrer persönlichen Daten gebeten werden, wenn Sie uns kontaktieren.
Im Folgenden finden Sie einige Beispiele für die Arten von personenbezogenen Daten, die wir möglicherweise erfassen, und wie wir diese Daten möglicherweise verwenden.
Welche personenbezogenen Daten wir erheben:
- Wenn Sie eine Bewerbung auf der Website einreichen, erfassen wir möglicherweise verschiedene Informationen, einschließlich Ihres Namens, Ihrer Telefonnummer und Ihrer Adresse Email usw.
Wie wir Ihre personenbezogenen Daten verwenden:
- Die von uns gesammelten personenbezogenen Daten ermöglichen es uns, Sie zu kontaktieren und Sie über einzigartige Angebote, Werbeaktionen und andere Veranstaltungen und bevorstehende Veranstaltungen zu informieren.
- Von Zeit zu Zeit können wir Ihre personenbezogenen Daten verwenden, um Ihnen wichtige Mitteilungen und Nachrichten zu senden.
- Wir können personenbezogene Daten auch für interne Zwecke wie Audits, Datenanalysen und verschiedene Studien um die von uns angebotenen Dienstleistungen zu verbessern und Ihnen Empfehlungen zu unseren Dienstleistungen zu geben.
- Wenn Sie an einer Verlosung, einem Wettbewerb oder einem ähnlichen Anreiz teilnehmen, können wir die von Ihnen bereitgestellten Informationen verwenden, um solche Programme zu verwalten.
Weitergabe an Dritte
Wir geben die von Ihnen erhaltenen Informationen nicht an Dritte weiter.
Ausnahmen:
- Für den Fall, dass es erforderlich ist - gemäß dem Gesetz, der gerichtlichen Anordnung, in Gerichtsverfahren und / oder aufgrund öffentlicher Anfragen oder Anfragen staatlicher Stellen im Hoheitsgebiet der Russischen Föderation - Ihre personenbezogenen Daten offenzulegen. Wir können auch Informationen über Sie offenlegen, wenn wir feststellen, dass eine solche Offenlegung für Sicherheits-, Strafverfolgungs- oder andere Zwecke von öffentlichem Interesse notwendig oder angemessen ist.
- Im Falle einer Umstrukturierung, Fusion oder eines Verkaufs können wir die von uns erfassten personenbezogenen Daten an den entsprechenden Drittnachfolger übertragen.
Schutz personenbezogener Daten
Wir treffen Vorkehrungen – einschließlich administrativer, technischer und physischer – zum Schutz Ihrer personenbezogenen Daten vor Verlust, Diebstahl und Missbrauch sowie vor unbefugtem Zugriff, Offenlegung, Änderung und Zerstörung.
Wahrung Ihrer Privatsphäre auf Unternehmensebene
Um sicherzustellen, dass Ihre persönlichen Daten sicher sind, kommunizieren wir Datenschutz- und Sicherheitspraktiken an unsere Mitarbeiter und setzen Datenschutzpraktiken strikt durch.
Dieses mathematische Programm findet die Gleichung der Tangente an den Graphen der Funktion \(f(x) \) an einem benutzerdefinierten Punkt \(a \).
Das Programm zeigt nicht nur die Tangentengleichung an, sondern auch den Lösungsprozess des Problems.
Dieser Online-Rechner kann für Gymnasiasten nützlich sein allgemeinbildende Schulen in Vorbereitung für Kontrollarbeit und Prüfungen, beim Testen von Wissen vor der Prüfung, Eltern, um die Lösung vieler Probleme in Mathematik und Algebra zu kontrollieren. Oder ist es Ihnen vielleicht zu teuer, einen Nachhilfelehrer einzustellen oder neue Lehrbücher zu kaufen? Oder willst du einfach nur deine Mathe- oder Algebra-Hausaufgaben so schnell wie möglich erledigen? Auch in diesem Fall können Sie unsere Programme mit einer Detaillösung nutzen.
Auf diese Weise können Sie Ihr eigenes Training und/oder das Training Ihrer jüngeren Geschwister durchführen, während das Bildungsniveau im Bereich der zu lösenden Aufgaben erhöht wird.
Wenn Sie die Ableitung einer Funktion finden müssen, dann haben wir dafür die Aufgabe Ableitung finden.
Wenn Sie mit den Regeln zur Einführung von Funktionen nicht vertraut sind, empfehlen wir Ihnen, sich damit vertraut zu machen.
Geben Sie den Funktionsausdruck \(f(x)\) und die Zahl \(a\) ein Finden Sie die Tangentengleichung Es wurde festgestellt, dass einige Skripte, die zur Lösung dieser Aufgabe erforderlich sind, nicht geladen wurden und das Programm möglicherweise nicht funktioniert.
Möglicherweise haben Sie AdBlock aktiviert.
Deaktivieren Sie es in diesem Fall und aktualisieren Sie die Seite.
JavaScript muss aktiviert sein, damit die Lösung angezeigt wird.
Hier finden Sie Anweisungen zum Aktivieren von JavaScript in Ihrem Browser.
Denn Es gibt viele Leute, die das Problem lösen möchten, Ihre Anfrage ist in der Warteschlange.
Nach einigen Sekunden erscheint die Lösung unten.
Bitte warten Sie Sek...
Wenn Sie einen Fehler in der Lösung bemerkt, dann kannst du im Feedback - Formular darüber schreiben .
Vergessen Sie nicht angeben, welche Aufgabe du entscheidest was in die Felder eintragen.
Unsere Spiele, Puzzles, Emulatoren:
Ein bisschen Theorie.
Steigung einer Geraden
Erinnere dich daran, dass der Graph der linearen Funktion \(y=kx+b\) eine gerade Linie ist. Die Zahl \(k=tg \alpha \) wird aufgerufen Steigung einer Geraden, und der Winkel \(\alpha \) ist der Winkel zwischen dieser Linie und der Ox-Achse
Wenn \(k>0\), dann \(0 Wenn \(kDie Gleichung der Tangente an den Graphen der Funktion
Wenn der Punkt M (a; f (a)) zum Graphen der Funktion gehört y \u003d f (x) und wenn es an diesem Punkt möglich ist, eine Tangente an den Graphen der Funktion zu ziehen, die nicht senkrecht zu dem steht x-Achse, dann folgt aus der geometrischen Bedeutung der Ableitung, dass die Steigung der Tangente gleich f "(a) ist. Als nächstes entwickeln wir einen Algorithmus zum Erstellen der Gleichung der Tangente an den Graphen einer beliebigen Funktion.
Gegeben sei die Funktion y \u003d f (x) und der Punkt M (a; f (a)) im Graphen dieser Funktion; lassen Sie wissen, dass f "(a) existiert. Lassen Sie uns die Gleichung der Tangente an den Graphen der gegebenen Funktion in zusammensetzen gegebener Punkt. Diese Gleichung hat wie die Gleichung jeder geraden Linie, die nicht parallel zur y-Achse ist, die Form y = kx + b, also besteht das Problem darin, die Werte der Koeffizienten k und b zu finden.
Mit der Steigung k ist alles klar: Es ist bekannt, dass k \u003d f "(a). Um den Wert von b zu berechnen, verwenden wir die Tatsache, dass die gewünschte Gerade durch den Punkt M verläuft (a; f (a)) Das bedeutet, wenn wir die Koordinaten des Punktes M in die Gleichung einer geraden Linie einsetzen, erhalten wir die richtige Gleichheit: \ (f (a) \u003d ka + b \), dh \ (b \u003d f (a ) - ka \).
Es bleibt übrig, die gefundenen Werte der Koeffizienten k und b in die Gleichung einer geraden Linie einzusetzen:
Wir bekamen die Gleichung der Tangente an den Graphen der Funktion\(y = f(x) \) an der Stelle \(x=a \).
Algorithmus zum Finden der Gleichung der Tangente an den Graphen der Funktion \(y=f(x)\)
1. Bezeichnen Sie die Abszisse des Kontaktpunkts mit dem Buchstaben \ (a \)
2. Berechnen Sie \(f(a) \)
3. Finde \(f"(x) \) und berechne \(f"(a) \)
4. Ersetzen Sie die gefundenen Zahlen \ (a, f (a), f "(a) \) in die Formel \ (y \u003d f (a) + f "(a) (x-a) \)