Apibrėžimas 9.3. Vektorius X paskambino nuosavas vektorius matricos A jei yra toks skaičius λ, kad lygybė galioja: A X= λ X, tai yra kreipimosi rezultatas X tiesinė transformacija, pateikta matricos A, yra šio vektoriaus padauginimas iš skaičiaus λ . Pats skaičius λ paskambino savo numerį matricos A.

Keitimas į formules (9.3) x` j = λx j , gauname lygčių sistemą savojo vektoriaus koordinatėms nustatyti:

. (9.5)

Ši tiesinė vienalytė sistema turės netrivialų sprendimą tik tuo atveju, jei jos pagrindinis determinantas yra 0 (Cramerio taisyklė). Įrašę šią sąlygą formoje:

gauname savųjų reikšmių nustatymo lygtį λ paskambino charakteristikos lygtis. Trumpai tariant, jis gali būti pavaizduotas taip:

| A-λE | = 0, (9.6)

kadangi jo kairioji pusė yra matricos determinantas A-λE. Polinomas atžvilgiu λ | A-λE| paskambino būdingas daugianario matricos a.

Būdingojo daugianario savybės:

1) Tiesinės transformacijos charakteringas daugianomas nepriklauso nuo pagrindo pasirinkimo. Įrodymas. (žr. (9.4)), bet vadinasi,. Taigi tai nepriklauso nuo pagrindo pasirinkimo. Vadinasi, ir | A-λE| nesikeičia pereinant prie naujo pagrindo.

2) Jei matrica A tiesinė transformacija yra simetriškas(tie. a ij = a ji), tada visos šaknys charakteristikos lygtis(9.6) yra realieji skaičiai.

Savųjų reikšmių ir savųjų vektorių savybės:

1) Jei pagrindą pasirinksime iš savųjų vektorių x 1, x 2, x 3 atitinkančias savąsias reikšmes λ 1 , λ 2 , λ 3 matricos A, tada tiesinė transformacija A turi įstrižainę matricą:

(9.7) Šios savybės įrodymas išplaukia iš savųjų vektorių apibrėžimo.

2) Jei savąsias reikšmes transformacijos A yra skirtingi, tada juos atitinkantys savieji vektoriai yra tiesiškai nepriklausomi.

3) Jei matricos charakteringasis daugianario A turi tris skirtingas šaknis, tada tam tikru pagrindu matrica A turi įstrižainę formą.

Raskime matricos savitąsias reikšmes ir savuosius vektorius Padarykime charakteristikų lygtį: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Raskite kiekvieną rastą reikšmę atitinkančių savųjų vektorių koordinates λ. Iš (9.5) išplaukia, kad jeigu X (1) ={x 1, x 2, x 3) yra savasis vektorius, atitinkantis λ 1 = -2, tada

yra bendradarbiaujanti, bet neapibrėžta sistema. Jo sprendimas gali būti parašytas kaip X (1) ={a,0,-a), kur a yra bet koks skaičius. Visų pirma, jei jums to reikia | x (1) |=1, X (1) =

Pakeitimas į sistemą (9.5) λ 2 =3, gauname antrojo savojo vektoriaus koordinačių nustatymo sistemą - x (2) ={y1, y2, y3}:

, kur X (2) ={b,-b,b) arba, jei | x (2) |=1, x (2) =

Dėl λ 3 = 6 raskite savąjį vektorių x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) arba normalizuotoje versijoje

x (3) = Galima matyti, kad X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = pr. Kr- 2bc + bc= 0. Taigi šios matricos savieji vektoriai yra poriniai stačiakampiai.

10 paskaita

Kvadratinės formos ir jų ryšys su simetrinėmis matricomis. Simetrinės matricos savųjų vektorių ir savųjų reikšmių savybės. Kvadratinės formos redukcija į kanoninę formą.

Apibrėžimas 10.1.kvadratine forma realūs kintamieji x 1, x 2,…, x nšių kintamųjų atžvilgiu vadinamas antrojo laipsnio daugianario, kuriame nėra laisvojo laipsnio ir pirmojo laipsnio terminų.

Kvadratinių formų pavyzdžiai:

(n = 2),

(n = 3). (10.1)

Prisiminkite simetrinės matricos apibrėžimą, pateiktą paskutinėje paskaitoje:

Apibrėžimas 10.2. Kvadratinė matrica vadinama simetriškas, jei , tai yra, jei pagrindinės įstrižainės atžvilgiu simetriški matricos elementai yra lygūs.

Simetrinės matricos savųjų reikšmių ir savųjų vektorių savybės:

1) Visos simetrinės matricos savosios reikšmės yra tikros.

Įrodymas (dėl n = 2).

Tegul matrica A atrodo kaip: . Padarykime charakteristikų lygtį:

(10.2) Raskite diskriminantą:

Todėl lygtis turi tik realias šaknis.

2) Simetrinės matricos savieji vektoriai yra stačiakampiai.

Įrodymas (dėl n= 2).

Savųjų vektorių koordinatės ir turi tenkinti lygtis.

Savosios reikšmės (skaičiai) ir savieji vektoriai.
Sprendimo pavyzdžiai

Būk savimi

Iš abiejų lygčių matyti, kad .

Tada įdėkime: .

Kaip rezultatas: yra antrasis savasis vektorius.

Pakartokime svarbius punktus sprendimai:

– sukurta sistema tikrai turi bendras sprendimas(lygtys yra tiesiškai priklausomos);

- "Y" parenkamas taip, kad jis būtų sveikasis skaičius, o pirmoji "x" koordinatė būtų sveikoji, teigiama ir kiek įmanoma mažesnė.

– patikriname, ar konkretus sprendimas tenkina kiekvieną sistemos lygtį.

Atsakymas .

Tarpinių „kontrolinių taškų“ visiškai pakako, todėl lygybių tikrinimas iš principo yra perteklinis.

Įvairiuose informacijos šaltiniuose savųjų vektorių koordinatės dažnai rašomos ne stulpeliais, o eilutėmis, pvz.: (ir, tiesą pasakius, aš pats jas rašydavau eilėmis). Ši parinktis yra priimtina, tačiau atsižvelgiant į temą tiesinės transformacijos techniškai patogiau naudoti stulpelių vektoriai.

Galbūt sprendimas jums atrodė labai ilgas, bet taip yra tik todėl, kad labai išsamiai pakomentavau pirmąjį pavyzdį.

2 pavyzdys

matricos

Treniruojamės savarankiškai! Apytikslis galutinio užduoties dizaino pavyzdys pamokos pabaigoje.

Kartais reikia padaryti papildoma užduotis, būtent:

parašykite matricos kanoninį skaidymą

Kas tai yra?

Jei matricos savieji vektoriai susidaro pagrindu, tada jis gali būti pavaizduotas taip:

Kur yra matrica, sudaryta iš savųjų vektorių koordinačių, - įstrižainės matrica su atitinkamomis savosiomis reikšmėmis.

Šis matricos skaidymas vadinamas kanoninis arba įstrižainės.

Apsvarstykite pirmojo pavyzdžio matricą. Jos pačios vektoriai tiesiškai nepriklausomas(nekolinearinis) ir sudaro pagrindą. Iš jų koordinačių sudarykime matricą:

Ant pagrindinė įstrižainė matricos tinkama tvarka yra savosios reikšmės, o likę elementai yra lygūs nuliui:
- dar kartą pabrėžiu eilės svarbą: "du" atitinka 1 vektorių, todėl yra 1 stulpelyje, "trys" - 2 vektorių.

Pagal įprastą paieškos algoritmą atvirkštinė matrica arba Gauss-Jordan metodas rasti . Ne, tai nėra rašybos klaida! - prieš tave yra reta, kaip saulės užtemimasįvykis, kai atvirkštinė vertė atitiko pradinę matricą.

Belieka parašyti kanoninį matricos skaidymą:

Sistema gali būti išspręsta naudojant elementarios transformacijos o toliau pateiktuose pavyzdžiuose pasitelksime šį metodą. Tačiau čia „mokyklos“ metodas veikia daug greičiau. Iš 3 lygties išreiškiame: - pakeiskite į antrąją lygtį:

Kadangi pirmoji koordinatė lygi nuliui, gauname sistemą , Iš kiekvienos lygties išplaukia, kad .

Ir vėl atkreipkite dėmesį į privalomą linijinio ryšio buvimą. Jei gaunamas tik trivialus sprendimas , tada arba savoji reikšmė buvo rasta neteisingai, arba sistema buvo sudaryta / išspręsta su klaida.

Kompaktiškos koordinatės suteikia vertę

Savasvektorius:

Ir dar kartą patikriname, ar rastas sprendimas tenkina kiekvieną sistemos lygtį. Tolesnėse pastraipose ir tolesnėse užduotyse rekomenduoju šį norą priimti kaip privalomą taisyklę.

2) Dėl savosios reikšmės, vadovaudamiesi tuo pačiu principu, gauname kita sistema:

Iš 2-osios sistemos lygties išreiškiame: - pakeiskite į trečiąją lygtį:

Kadangi "Z" koordinatė lygi nuliui, gauname sistemą, iš kurios kiekvienos lygties atsiranda tiesinė priklausomybė.

Leisti

Mes patikriname, ar sprendimas tenkina kiekvieną sistemos lygtį.

Taigi savasis vektorius: .

3) Ir, galiausiai, sistema atitinka savo vertę:

Antroji lygtis atrodo paprasčiausia, todėl ją išreiškiame ir pakeičiame į 1 ir 3 lygtis:

Viskas gerai – atsiskleidė linijinė priklausomybė, kurią pakeičiame išraiška:

Dėl to "X" ir "Y" buvo išreikšti per "Z": . Praktiškai nebūtina siekti tik tokių santykių, kai kuriais atvejais patogiau išreikšti tiek per arba ir per . Ar net „traukinys“ – pavyzdžiui, nuo „X“ iki „Y“ ir „Y“ iki „Z“

Tada įdėkime:

Mes patikriname, ar rastas sprendimas tenkina kiekvieną sistemos lygtį ir parašo trečiąjį savąjį vektorių

Atsakymas: savieji vektoriai:

Geometriškai šie vektoriai apibrėžia tris skirtingas erdvines kryptis ("Ten ir vėl atgal"), pagal kurią tiesinė transformacija nulinius vektorius (saviškuosius vektorius) paverčia jiems kolineariais vektoriais.

Jei pagal sąlygą reikėjo rasti kanoninį išplėtimą, tai čia įmanoma, nes skirtingos savosios reikšmės atitinka skirtingus tiesiškai nepriklausomus savuosius vektorius. Sudarome matricą iš jų koordinačių – įstrižainės matricos iš Aktualus savąsias reikšmes ir rasti atvirkštinė matrica .

Jeigu pagal sąlygą reikia rašyti tiesinės transformacijos matrica savųjų vektorių pagrindu, tada pateikiame atsakymą formoje . Yra skirtumas ir reikšmingas skirtumas!Šiai matricai yra matrica „de“.

Užduotis su paprastesniais savarankiško sprendimo skaičiavimais:

5 pavyzdys

Raskite tiesinės transformacijos savuosius vektorius, pateiktus matrica

Surasdami savo skaičius stenkitės, kad atvejis nebūtų įtrauktas į 3 laipsnio daugianarį. Be to, jūsų sistemos sprendimai gali skirtis nuo mano sprendimų – čia nėra vienareikšmiškumo; ir rasti vektoriai gali skirtis nuo pavyzdinių vektorių iki proporcingumo jų atitinkamoms koordinatėms. Pavyzdžiui, ir. Estetiškiau pateikti atsakymą forma , bet gerai, jei sustosite ties antruoju variantu. Tačiau viskam yra pagrįstos ribos, versija nebeatrodo labai gerai.

Apytikslis galutinis užduoties pavyzdys pamokos pabaigoje.

Kaip išspręsti problemą, kai yra daug savųjų reikšmių?

Bendras algoritmas išlieka toks pat, tačiau turi savų ypatumų, todėl kai kurias sprendimo dalis patartina išlaikyti griežtesniu akademiniu stiliumi:

6 pavyzdys

Raskite savąsias reikšmes ir savuosius vektorius

Sprendimas

Žinoma, didžiosiomis raidėmis pasakykime pirmąjį stulpelį:

Ir, įvertinus kvadratinį trinarį:

Dėl to gaunamos savosios reikšmės, iš kurių dvi yra kartotinės.

Raskime savuosius vektorius:

1) Su vienišu kariu susitvarkysime pagal „supaprastintą“ schemą:

Iš paskutinių dviejų lygčių aiškiai matoma lygybė, kurią, be abejo, reikėtų pakeisti 1-ąja sistemos lygtimi:

Nėra geresnio derinio:
Savasvektorius:

2-3) Dabar pašaliname porą sargybinių. Šiuo atveju gali būti arba du arba vienas savasis vektorius. Neatsižvelgiant į šaknų daugumą, determinanto reikšmę pakeičiame , kuri mums pateikia šiuos dalykus vienalytė tiesinių lygčių sistema:

Savotieji vektoriai yra būtent tie vektoriai
pagrindinė sprendimų sistema

Tiesą sakant, per visą pamoką mes užsiėmėme tik pagrindinės sistemos vektorių paieška. Tik kol kas Šis terminas nebuvo ypač reikalaujama. Beje, tie vikrūs mokiniai, kurie maskuodamiesi vienarūšės lygtys, dabar bus priverstas jį parūkyti.

Vienintelis veiksmas buvo pašalinti papildomas eilutes. Rezultatas yra „vienas po trijų“ matrica su formaliu „žingsniu“ viduryje.
– pagrindinis kintamasis, – laisvieji kintamieji. Yra du laisvi kintamieji, todėl taip pat yra du pagrindinės sistemos vektoriai.

Išreikškime pagrindinį kintamąjį laisvaisiais kintamaisiais: . Nulinis koeficientas priešais „x“ leidžia jam įgyti absoliučiai bet kokias reikšmes (tai taip pat aiškiai matoma iš lygčių sistemos).

Šios problemos kontekste bendrąjį sprendimą patogiau rašyti ne eilute, o stulpelyje:

Pora atitinka savąjį vektorių:
Pora atitinka savąjį vektorių:

Pastaba : sudėtingi skaitytojai gali pasiimti šiuos vektorius žodžiu – tiesiog analizuodami sistemą , bet čia reikia tam tikrų žinių: yra trys kintamieji, sistemos matricos rangas- vienetas reiškia pagrindinė sprendimų sistema susideda iš 3 – 1 = 2 vektorių. Tačiau rasti vektoriai yra puikiai matomi net ir be šių žinių, grynai intuityviu lygmeniu. Šiuo atveju trečiasis vektorius bus parašytas dar „gražiau“: . Tačiau perspėju, kitame pavyzdyje gali nebūti paprastos atrankos, todėl rezervacija skirta patyrusiems žmonėms. Be to, kodėl gi ne kaip trečiąjį vektorių, tarkime, ? Juk jos koordinatės taip pat tenkina kiekvieną sistemos lygtį ir vektorius yra tiesiškai nepriklausomi. Ši parinktis iš esmės yra tinkama, bet „kreiva“, nes „kitas“ vektorius yra linijinis pagrindinės sistemos vektorių derinys.

Atsakymas: savosios reikšmės: , savieji vektoriai:

Panašus „pasidaryk pats“ sprendimo pavyzdys:

7 pavyzdys

Raskite savąsias reikšmes ir savuosius vektorius

Apytikslis užbaigimo pavyzdys pamokos pabaigoje.

Pažymėtina, kad tiek 6, tiek 7 pavyzdžiuose gaunamas tiesiškai nepriklausomų savųjų vektorių trigubas, todėl pradinė matrica gali būti pavaizduota kanoninėje plėtinyje . Tačiau tokios avietės pasitaiko ne visais atvejais:

8 pavyzdys

Sprendimas: sudaryti ir išspręsti charakteristikos lygtį:

Determinantą išplečiame pirmuoju stulpeliu:

Tolesnius supaprastinimus atliekame pagal nagrinėjamą metodą, išvengdami 3-ojo laipsnio daugianario:

yra savosios reikšmės.

Raskime savuosius vektorius:

1) Su šaknimis nėra jokių sunkumų:

Nenustebkite, be komplekto, taip pat naudojami kintamieji - čia nėra skirtumo.

Iš 3 lygties išreiškiame - pakeičiame į 1 ir 2 lygtis:

Iš abiejų lygčių seka:

Leisk tada:

2-3) Jei yra kelios reikšmės, gauname sistemą .

Užrašykime sistemos matricą ir naudodami elementariąsias transformacijas perkelkime ją į laiptuotą formą:

". Pirmoje dalyje išdėstomos nuostatos, kurios minimaliai reikalingos chemometrijai suprasti, o antroje dalyje pateikiami faktai, kuriuos reikia žinoti norint giliau suprasti daugiamatės analizės metodus. Pristatymas iliustruotas Excel darbaknygėje padarytais pavyzdžiais Matrica.xls kuris pridedamas prie šio dokumento.

Nuorodos į pavyzdžius pateikiamos tekste kaip Excel objektai. Šie pavyzdžiai yra abstraktaus pobūdžio, jie niekaip nesusiję su analitinės chemijos problemomis. Tikri pavyzdžiai matricinės algebros naudojimas chemometrikoje yra aptariamas kituose tekstuose, skirtuose įvairiems chemometrijos taikymams.

Dauguma analitinės chemijos matavimų yra ne tiesioginiai, o netiesioginis. Tai reiškia, kad eksperimente vietoj norimos analitės C reikšmės (koncentracijos) gaunama kita reikšmė x(signalas), susijęs su C, bet jam nelygus, t.y. x(C) ≠ C. Paprastai priklausomybės tipas x(C) nėra žinomas, bet, laimei, analitinėje chemijoje dauguma matavimų yra proporcingi. Tai reiškia, kad esant C koncentracijai a kartų, signalas X padidės tiek pat., t.y. x(a C) = a x(C). Be to, signalai taip pat yra adityvūs, todėl signalas iš mėginio, kuriame yra dvi medžiagos, kurių koncentracija C 1 ir C 2, bus yra lygi sumai signalai iš kiekvieno komponento, t.y. x(C1 + C2) = x(C1)+ x(C2). Proporcingumas ir adityvumas kartu duoda tiesiškumas. Tiesiškumo principui iliustruoti galima pateikti daug pavyzdžių, tačiau pakanka paminėti du ryškiausius pavyzdžius – chromatografiją ir spektroskopiją. Antrasis analitinės chemijos eksperimentui būdingas bruožas yra daugiakanalis. Šiuolaikinė analitinė įranga vienu metu matuoja daugelio kanalų signalus. Pavyzdžiui, šviesos pralaidumo intensyvumas matuojamas iš karto keliems bangos ilgiams, t.y. diapazonas. Todėl eksperimente susiduriame su įvairiais signalais x 1 , x 2 ,...., x n, apibūdinantis tiriamoje sistemoje esančių medžiagų koncentracijų C 1 ,C 2 , ..., C m aibę.

Ryžiai. 1 spektras

Taigi, analitiniam eksperimentui būdingas tiesiškumas ir daugiamatiškumas. Todėl eksperimentinius duomenis patogu laikyti vektoriais ir matricomis ir jais manipuliuoti matricinės algebros aparatu. Šio metodo vaisingumą iliustruoja pavyzdys, parodytas , kuriame rodomi trys spektrai, paimti 200 bangų ilgių nuo 4000 iki 4796 cm–1. Pirmas ( x 1) ir antrasis ( x 2) spektrai gauti standartiniams mėginiams, kuriuose žinomos dviejų medžiagų A ir B koncentracijos: pirmame mėginyje [A] = 0,5, [B] = 0,1, o antrajame mėginyje [A] = 0,2, [ B] = 0,6. Ką galima pasakyti apie naują nežinomą pavyzdį, kurio spektras nurodytas x 3 ?

Apsvarstykite tris eksperimentinius spektrus x 1 , x 2 ir x 3 kaip trys 200 matmenų vektoriai. Naudojant tiesinę algebrą, galima nesunkiai tai parodyti x 3 = 0.1 x 1 +0.3 x 2 , todėl trečiajame mėginyje akivaizdžiai yra tik medžiagos A ir B, kurių koncentracija [A] = 0,5×0,1 + 0,2×0,3 = 0,11 ir [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Pagrindinė informacija

1.1 Matricos

Matrica vadinama, pavyzdžiui, stačiakampe skaičių lentele

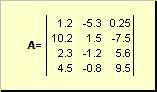
Ryžiai. 2 Matrica

Matricos žymimos didžiosiomis paryškintomis raidėmis ( A), o jų elementai – atitinkami mažosios raidės su indeksais, t.y. a ij . Pirmasis indeksas numeruoja eilutes, o antrasis - stulpelius. Chemometrikoje įprasta didžiausią indekso reikšmę žymėti ta pačia raide kaip ir pats indeksas, bet didžiosiomis raidėmis. Todėl matrica A taip pat gali būti parašytas kaip ( a ij , i = 1,..., aš; j = 1,..., J). Pavyzdinei matricai aš = 4, J= 3 ir a 23 = −7.5.

Skaičių pora aš ir J vadinamas matricos dimensija ir žymimas kaip aš× J. Chemometrijos matricos pavyzdys yra spektrų rinkinys, gautas už aš pavyzdžiai ant J bangos ilgiai.

1.2. Paprasčiausios operacijos su matricomis

Matricos gali padauginti iš skaičių. Šiuo atveju kiekvienas elementas padauginamas iš šio skaičiaus. Pavyzdžiui -

Ryžiai. 3 Matricos padauginimas iš skaičiaus

Dvi to paties matmens matricos gali būti elementinės sulankstyti ir atimti. Pavyzdžiui,

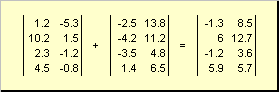
Ryžiai. 4 Matricos pridėjimas

Padauginus iš skaičiaus ir sudėjus, gaunama to paties matmens matrica.

Nulinė matrica yra matrica, susidedanti iš nulių. Jis yra paskirtas O. Tai akivaizdu A+O = A, A−A = O ir 0 A = O.

Matrica gali perkelti. Šios operacijos metu matrica apverčiama, t.y. eilutės ir stulpeliai yra sukeisti. Perkėlimas žymimas brūkšneliu, A“ arba rodyklė A t . Taigi, jei A = {a ij , i = 1,..., aš; j = 1,...,J), tada A t = ( a ji , j = 1,...,J; i = 1,..., aš). pavyzdžiui

Ryžiai. 5 Matricos perkėlimas

Akivaizdu, kad ( A t) t = A, (A+B) t = A t+ B t .

1.3. Matricos daugyba

Matricos gali padauginti, bet tik jei jie turi atitinkamus matmenis. Kodėl taip yra, paaiškės iš apibrėžimo. Matricos gaminys A, matmuo aš× K, ir matricos B, matmuo K× J, vadinamas matrica C, matmuo aš× J, kurio elementai yra skaičiai

Taigi dėl produkto AB būtina, kad stulpelių skaičius kairėje matricoje A buvo lygus eilučių skaičiui dešinėje matricoje B. Matricos gaminio pavyzdys -

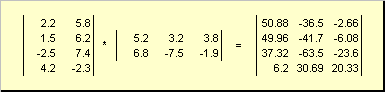
6 pav. Matricų sandauga

Matricos daugybos taisyklę galima suformuluoti taip. Norėdami rasti matricos elementą C stovintis sankryžoje i-toji eilutė ir j- stulpelis ( c ij) turi būti padaugintas iš elemento i- pirmosios matricos eilutė A ant j-antrosios matricos stulpelis B ir sudėkite visus rezultatus. Taigi parodytame pavyzdyje elementas iš trečios eilutės ir antrojo stulpelio gaunamas kaip trečios eilutės elementų sandaugų suma A ir antrasis stulpelis B

7 pav. Matricų sandaugos elementas

Matricų sandauga priklauso nuo eilės, t.y. AB ≠ BA, bent jau dėl matmenų priežasčių. Sakoma, kad jis nekeičiamas. Tačiau matricų sandauga yra asociatyvi. Tai reiškia kad ABC = (AB)C = A(pr. Kr). Be to, jis yra ir paskirstomasis, t.y. A(B+C) = AB+AC. Tai akivaizdu AO = O.

1.4. Kvadratinės matricos

Jei matricos stulpelių skaičius yra lygus jos eilučių skaičiui ( aš = J = N), tada tokia matrica vadinama kvadratine. Šiame skyriuje nagrinėsime tik tokias matricas. Tarp šių matricų galima išskirti ypatingų savybių turinčias matricas.

vienišas matrica (žymima aš ir kartais E) – tai matrica, kurioje visi elementai lygūs nuliui, išskyrus įstrižinius, kurie lygūs 1, t.y.

Akivaizdu AI = IA = A.

Matrica vadinama įstrižainės, jei visi jo elementai, išskyrus įstrižinius ( a ii) yra lygūs nuliui. pavyzdžiui

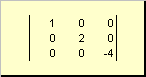
Ryžiai. 8 Įstrižainė matrica

Matrica A vadinama viršūne trikampis, jei visi jo elementai, esantys žemiau įstrižainės, yra lygūs nuliui, t.y. a ij= 0, at i>j. pavyzdžiui

Ryžiai. 9 Viršutinė trikampė matrica

Apatinė trikampė matrica apibrėžiama panašiai.

Matrica A paskambino simetriškas, jei A t = A. Kitaip tariant a ij = a ji. pavyzdžiui

Ryžiai. 10 Simetrinė matrica

Matrica A paskambino stačiakampis, jei

A t A = AA t = aš.

Matrica vadinama normalus jeigu

1.5. Pėdsakas ir determinantas

Sekant kvadratinė matrica A(žymima Tr( A) arba Sp( A)) yra jo įstrižainių elementų suma,

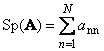
Pavyzdžiui,

Ryžiai. 11 Matricos pėdsakas

Tai akivaizdu

Sp(α A) = α Sp( A) ir

Sp( A+B) = Sp( A)+ Sp( B).

Galima parodyti, kad

Sp( A) = Sp( A t), Sp( aš) = N,

ir taip pat tai

Sp( AB) = Sp( BA).

Kita svarbi kvadratinės matricos savybė yra jos determinantas(žymima det( A)). Determinanto apibrėžimas bendras atvejis gana sudėtinga, todėl pradėsime nuo paprasčiausio varianto – matricos A matmuo (2×2). Tada

(3 × 3) matricos determinantas bus lygus

Matricos atveju ( N× N) determinantas apskaičiuojamas kaip suma 1 2 3 ... N= N! terminai, kurių kiekvienas yra lygus

Indeksai k 1 , k 2 ,..., k N apibrėžiami kaip visos galimos sutvarkytos permutacijos r skaičiai rinkinyje (1, 2, ... , N). Matricos determinanto apskaičiavimas yra sudėtinga procedūra, kuri praktiškai atliekama naudojant specialias programas. Pavyzdžiui,

Ryžiai. 12 Matricos determinantas

Atkreipiame dėmesį tik į akivaizdžias savybes:

det( aš) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Vektoriai

Jei matrica turi tik vieną stulpelį ( J= 1), tada toks objektas vadinamas vektorius. Tiksliau, stulpelio vektorius. pavyzdžiui

Pavyzdžiui, taip pat gali būti svarstomos matricos, susidedančios iš vienos eilutės

Šis objektas taip pat yra vektorius, bet eilutės vektorius. Analizuojant duomenis svarbu suprasti, su kokiais vektoriais turime reikalą – stulpeliais ar eilutėmis. Taigi spektras, paimtas vienam mėginiui, gali būti laikomas eilutės vektoriumi. Tada spektrinio intensyvumo rinkinys tam tikru bangos ilgiu visiems mėginiams turėtų būti traktuojamas kaip stulpelio vektorius.

Vektoriaus matmuo yra jo elementų skaičius.

Aišku, kad bet kuris stulpelio vektorius gali būti transformuojamas į eilučių vektorių transpozicijos būdu, t.y.

Tais atvejais, kai vektoriaus forma nėra konkrečiai nurodyta, o tiesiog sakomas vektorius, tada jie reiškia stulpelio vektorių. Mes taip pat laikysimės šios taisyklės. Vektorius žymimas mažąja tiesiogine paryškinta raide. Nulinis vektorius yra vektorius, kurio visi elementai yra lygūs nuliui. Jis žymimas 0 .

1.7. Paprasčiausios operacijos su vektoriais

Vektorius galima sudėti ir padauginti iš skaičių taip pat, kaip ir matricas. Pavyzdžiui,

Ryžiai. 13 Veiksmai su vektoriais

Du vektoriai x ir y paskambino kolinearinis, jei yra toks skaičius α, kad

1.8. Vektorių sandaugos

Du vienodo matmens vektoriai N galima padauginti. Tegul yra du vektoriai x = (x 1 , x 2 ,...,x N) t ir y = (y 1 , y 2 ,...,y N) t. Vadovaudamiesi daugybos taisykle „eilutė po stulpelio“, iš jų galime pagaminti du produktus: x t y ir xy t . Pirmas darbas

paskambino skaliarinis arba vidinis. Jo rezultatas yra skaičius. Taip pat naudojamas žymėjimas ( x,y)= x t y. Pavyzdžiui,

Ryžiai. 14 Vidinis (skaliarinis) sandauga

Antras darbas

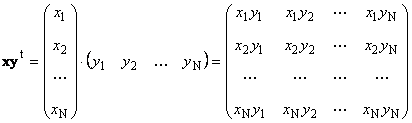
paskambino išorės. Jo rezultatas yra matmenų matrica ( N× N). Pavyzdžiui,

Ryžiai. 15 Išorinis gaminys

Vadinami vektoriai, kurių skaliarinė sandauga lygi nuliui stačiakampis.

1.9. Vektorinė norma

Vektoriaus su savimi skaliarinė sandauga vadinama skaliariniu kvadratu. Ši vertė

apibrėžia kvadratą ilgio vektorius x. Pažymėti ilgį (taip pat vadinamas norma vektorius) naudojamas žymėjimas

Pavyzdžiui,

Ryžiai. 16 Vektorinė norma

Vieneto ilgio vektorius (|| x|| = 1) vadinamas normalizuotu. Nenulinis vektorius ( x ≠ 0 ) galima normalizuoti padalijus iš ilgio, t.y. x = ||x|| (x/||x||) = ||x|| e. čia e = x/||x|| yra normalizuotas vektorius.

Vektoriai vadinami ortonormaliais, jei jie visi normalizuoti ir poromis stačiakampiai.

1.10. Kampas tarp vektorių

Skaliarinis sandauga apibrėžia ir injekcijaφ tarp dviejų vektorių x ir y

Jei vektoriai yra stačiakampiai, tai cosφ = 0 ir φ = π/2, o jei yra kolinearūs, tai cosφ = 1 ir φ = 0.

1.11. Matricos vektorinis vaizdavimas

Kiekviena matrica A dydis aš× J gali būti pavaizduotas kaip vektorių rinkinys

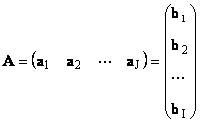
Čia kiekvienas vektorius a j yra j- stulpelio ir eilutės vektorius b i yra i- matricos eilutė A

1.12. Tiesiškai priklausomi vektoriai

To paties matmens vektoriai ( N) galima sudėti ir padauginti iš skaičiaus, kaip ir matricas. Rezultatas yra to paties dydžio vektorius. Tegul yra keli tos pačios dimensijos vektoriai x 1 , x 2 ,...,x K ir tiek pat skaičių α α 1 , α 2 ,..., α K. Vektorius

y= α 1 x 1 + α 2 x 2 +...+α K x K

paskambino linijinis derinys vektoriai x k .

Jei yra tokių nulinių skaičių α k ≠ 0, k = 1,..., K, ką y = 0 , tada tokia vektorių rinkinys x k paskambino tiesiškai priklausomas. Priešingu atveju vektoriai vadinami tiesiškai nepriklausomais. Pavyzdžiui, vektoriai x 1 = (2, 2) t ir x 2 = (−1, −1) t yra tiesiškai priklausomi, nes x 1 +2x 2 = 0

1.13. Matricos rangas

Apsvarstykite rinkinį K vektoriai x 1 , x 2 ,...,x K matmenys N. Šios vektorių sistemos rangas yra maksimalus tiesiškai nepriklausomų vektorių skaičius. Pavyzdžiui, rinkinyje

Pavyzdžiui, yra tik du tiesiškai nepriklausomi vektoriai x 1 ir x 2, taigi jo rangas yra 2.

Akivaizdu, kad jei aibėje yra daugiau vektorių nei jų matmuo ( K>N), tada jie būtinai yra tiesiškai priklausomi.

Matricos rangas(žymima rangu ( A)) yra vektorių sistemos, iš kurios ji susideda, rangas. Nors bet kurią matricą galima pavaizduoti dviem būdais (stulpelių vektoriais arba eilučių vektoriais), tai neturi įtakos rango reikšmei, nes

1.14. atvirkštinė matrica

kvadratinė matrica A vadinamas neišsigimusiu, jei turi unikalų atvirkščiai matrica A-1 , nustatoma pagal sąlygas

AA −1 = A −1 A = aš.

Atvirkštinė matrica neegzistuoja visoms matricoms. Būtina ir pakankama neišsigimimo sąlyga yra

det( A) ≠ 0 arba rangas ( A) = N.

Matricos inversija yra sudėtinga procedūra, kuriai yra specialios programos. Pavyzdžiui,

Ryžiai. 17 Matricos inversija

Pateikiame paprasčiausio atvejo formules - matricas 2 × 2

Jei matricos A ir B tada jie nėra išsigimę

(AB) −1 = B −1 A −1 .

1.15. Pseudo atvirkštinė matrica

Jei matrica A yra išsigimęs ir atvirkštinė matrica neegzistuoja, kai kuriais atvejais galite naudoti pseudo atvirkštinis matrica, kuri apibrėžiama kaip tokia matrica A+ tai

AA + A = A.

Pseudo atvirkštinė matrica nėra vienintelė ir jos forma priklauso nuo konstravimo metodo. Pavyzdžiui, stačiakampei matricai galite naudoti Moore-Penrose metodą.

Jei stulpelių skaičius yra mažesnis už eilučių skaičių, tada

A + =(A t A) −1 A t

Pavyzdžiui,

Ryžiai. 17a Pseudo matricos inversija

Jei stulpelių skaičius daugiau numerio tada eilutės

A + =A t ( AA t) −1

1.16. Vektoriaus padauginimas iš matricos

Vektorius x galima padauginti iš matricos A tinkamas matmuo. Šiuo atveju stulpelio vektorius padauginamas dešinėje Ax, o vektoriaus eilutė yra kairėje x t A. Jei vektoriaus matmuo J, ir matricos matmuo aš× J tada rezultatas yra dimensijos vektorius aš. Pavyzdžiui,

Ryžiai. 18 Vektorinės matricos daugyba

Jei matrica A- kvadratas ( aš× aš), tada vektorius y = Ax turi tokį patį matmenį kaip x. Tai akivaizdu

A(α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Taigi matricas galima žiūrėti kaip tiesinės transformacijos vektoriai. Ypač x = x, Jautis = 0 .

2. Papildoma informacija

2.1. Tiesinių lygčių sistemos

Leisti A- matricos dydis aš× J, a b- matmenų vektorius J. Apsvarstykite lygtį

Ax = b

vektoriaus atžvilgiu x, matmenys aš. Iš esmės tai yra sistema aš tiesines lygtis Su J nežinomas x 1 ,...,x J. Sprendimas egzistuoja tada ir tik tada

rangas ( A) = rangas ( B) = R,

kur B yra padidintų matmenų matrica aš×( J+1) sudarytas iš matricos A, paminkštintas stulpeliu b, B = (A b). Priešingu atveju lygtys yra nenuoseklios.

Jeigu R = aš = J, tada sprendimas yra unikalus

x = A −1 b.

Jeigu R < aš, tada yra daug skirtingų sprendinių, kuriuos galima išreikšti tiesine kombinacija J−R vektoriai. Sistema vienarūšės lygtys Ax = 0 su kvadratine matrica A (N× N) turi nebanalų sprendimą ( x ≠ 0 ) tada ir tik jei det( A) = 0. Jei R= rangas ( A)<N, tada yra N−R tiesiškai nepriklausomi sprendimai.

2.2. Dvilinijinės ir kvadratinės formos

Jeigu A- tai kvadratinė matrica, a x ir y- atitinkamo matmens vektoriai, tada formos skaliarinė sandauga x t Ai paskambino dvilinijinis matricos apibrėžta forma A. At x = y išraiška x t Ax paskambino kvadratinis forma.

2.3. Teigiamos apibrėžtosios matricos

kvadratinė matrica A paskambino teigiamas apibrėžtas, jei bet kuriam nuliui skirtingam vektoriui x ≠ 0 ,

x t Ax > 0.

The neigiamas (x t Ax < 0), neneigiamas (x t Ax≥ 0) ir ne teigiamas (x t Ax≤ 0) tam tikros matricos.

2.4. Cholesky skilimas

Jei simetrinė matrica A yra teigiamas apibrėžtas, tada yra unikali trikampė matrica U su teigiamais elementais, kuriems

A = U t U.

Pavyzdžiui,

Ryžiai. 19 Cholesky skilimas

2.5. polinis skilimas

Leisti A yra neišsigimusi matmenų kvadratinė matrica N× N. Tada yra unikalus poliarinis atstovavimas

A = SR,

kur S yra neneigiama simetrinė matrica, ir R yra ortogonali matrica. matricos S ir R galima aiškiai apibrėžti:

S 2 = AA t arba S = (AA t) ½ ir R = S −1 A = (AA t) −½ A.

Pavyzdžiui,

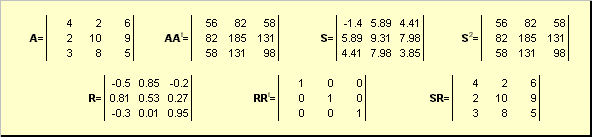
Ryžiai. 20 Poliarinis skilimas

Jei matrica A yra išsigimęs, tada skilimas nėra unikalus – būtent: S vis dar vienas, bet R gali būti daug. Polinis skilimas reiškia matricą A kaip suspaudimo/tempimo derinys S ir pasukimas R.

2.6. Savotieji vektoriai ir savosios reikšmės

Leisti A yra kvadratinė matrica. Vektorius v paskambino nuosavas vektorius matricos A, jei

Av = λ v,

kur vadinamas skaičius λ savoji vertė matricos A. Taigi, transformacija, kurią atlieka matrica A virš vektoriaus v, sumažinamas iki paprasto tempimo arba suspaudimo su koeficientu λ. Savasis vektorius nustatomas iki daugybos iš konstantos α ≠ 0, t.y. jeigu v yra savasis vektorius, tada α v taip pat yra savasis vektorius.

2.7. Savosios vertybės

Prie matricos A, matmuo ( N× N) negali būti didesnis nei N savąsias reikšmes. Jie tenkina charakteristikos lygtis

det( A − λ aš) = 0,

esamas algebrinė lygtis N– įsakymas. Visų pirma, 2 × 2 matricai būdinga lygtis turi tokią formą

Pavyzdžiui,

Ryžiai. 21 savosios vertės

Savųjų reikšmių rinkinys λ 1 ,..., λ N matricos A paskambino spektras A.

Spektras turi įvairių savybių. Ypač

det( A) = λ 1×...×λ N, Sp( A) = λ 1 +...+λ N.

Savavališkos matricos savosios reikšmės gali būti kompleksiniai skaičiai, bet jei matrica yra simetriška ( A t = A), tada jo savosios reikšmės yra tikros.

2.8. Savieji vektoriai

Prie matricos A, matmuo ( N× N) negali būti didesnis nei N savieji vektoriai, kurių kiekvienas atitinka savo vertę. Norėdami nustatyti savąjį vektorių v n reikia išspręsti vienarūšių lygčių sistemą

(A − λ n aš)v n = 0 .

Jis turi nebanalų sprendimą, nes det( A-λ n aš) = 0.

Pavyzdžiui,

Ryžiai. 22 savieji vektoriai

Simetrinės matricos savieji vektoriai yra stačiakampiai.

HOMOGENINIŲ TIESINIŲ LYGČIŲ SISTEMA

Vienalyčių tiesinių lygčių sistema yra formos sistema

Akivaizdu, kad šiuo atveju , nes visi vieno iš šių determinantų stulpelių elementai yra lygūs nuliui.

Kadangi nežinomieji randami pagal formules , tada tuo atveju, kai Δ ≠ 0, sistema turi unikalų nulinį sprendimą x = y = z= 0. Tačiau daugelyje uždavinių įdomus klausimas, ar vienalytė sistema turi kitų sprendimų nei nulis.

Teorema. Kad tiesinių vienalyčių lygčių sistema turėtų nulinį sprendimą, būtina ir pakanka, kad Δ ≠ 0.

Taigi, jei determinantas yra Δ ≠ 0, tada sistema turi unikalų sprendimą. Jei Δ ≠ 0, tai tiesinių vienarūšių lygčių sistema turi begalinį sprendinių skaičių.

Pavyzdžiai.

Savotieji vektoriai ir matricos savosios reikšmės

Tegu duota kvadratinė matrica , X yra tam tikra matrica-stulpelis, kurio aukštis sutampa su matricos tvarka A. .

Daugelyje problemų reikia atsižvelgti į lygtį X

kur λ yra koks nors skaičius. Akivaizdu, kad bet kuriai λ ši lygtis turi nulinį sprendimą.

Vadinamas skaičius λ, kuriam ši lygtis turi nulinius sprendinius savoji vertė matricos A, a X nes toks λ vadinamas nuosavas vektorius matricos A.

Raskime matricos savąjį vektorių A. Tiek, kiek E∙X = X, tada matricos lygtį galima perrašyti kaip arba . Išplėstoje formoje šią lygtį galima perrašyti kaip tiesinių lygčių sistemą. Tikrai .

Ir todėl

Taigi, gavome vienalyčių tiesinių lygčių sistemą koordinatėms nustatyti x 1, x2, x 3 vektorius X. Kad sistema turėtų nulinius sprendinius, būtina ir pakanka, kad sistemos determinantas būtų lygus nuliui, t.y.

Tai yra 3 laipsnio lygtis λ atžvilgiu. Tai vadinama charakteristikos lygtis matricos A ir padeda nustatyti savąsias reikšmes λ.

Kiekviena savoji reikšmė λ atitinka savąjį vektorių X, kurios koordinatės nustatomos pagal atitinkamą λ reikšmę iš sistemos.

Pavyzdžiai.

VEKTORIUS ALGEBRA. VEKTORINĖ SAMPRATA

Studijuojant įvairias fizikos šakas, yra dydžių, kurie visiškai nustatomi nustatant jų skaitines reikšmes, pavyzdžiui, ilgis, plotas, masė, temperatūra ir kt. Tokios vertės vadinamos skaliarinėmis. Tačiau be jų yra ir dydžių, kuriems nustatyti, be skaitinės reikšmės, reikia žinoti ir jų kryptį erdvėje, pavyzdžiui, kūną veikiančią jėgą, greitį ir pagreitį. kūno, kai jis juda erdvėje, įtampa magnetinis laukas tam tikrame erdvės taške ir kt. Tokie dydžiai vadinami vektoriniais dydžiais.

Pateiksime griežtą apibrėžimą.

Kryptinis segmentas Pavadinkime segmentą, kurio galų atžvilgiu žinoma, kuris iš jų yra pirmasis, o kuris antras.

Vektorius vadinama nukreipta atkarpa, turinti tam tikrą ilgį, t.y. Tai tam tikro ilgio atkarpa, kurioje vienas iš jį ribojančių taškų laikomas pradžia, o antrasis – pabaiga. Jeigu A yra vektoriaus pradžia, B yra jo pabaiga, tada vektorius žymimas simboliu, be to, vektorius dažnai žymimas viena raide . Paveiksle vektorius pažymėtas atkarpa, o jo kryptis – rodykle.

modulis arba ilgio vektorius vadinamas jį apibrėžiančio nukreipto atkarpos ilgiu. Žymima || arba ||.

Taip vadinamas nulinis vektorius, kurio pradžia ir pabaiga sutampa, taip pat bus vadinamas vektoriais. Jis yra pažymėtas. Nulinis vektorius neturi apibrėžtos krypties ir jo modulis lygus nuliui ||=0.

Vektoriai ir vadinami kolinearinis jei jie yra toje pačioje linijoje arba lygiagrečiose tiesėse. Šiuo atveju, jei vektoriai ir yra vienodai nukreipti, rašysime , priešingai.

Vadinami vektoriai, esantys tiesėse, lygiagrečiose tai pačiai plokštumai koplanarinis.

Du vektoriai ir vadinami lygus jei jie yra kolineriški, turi tą pačią kryptį ir yra vienodo ilgio. Tokiu atveju parašykite.

Iš vektorių lygybės apibrėžimo išplaukia, kad vektorius gali būti perkeltas lygiagrečiai sau, pastatant jo pradžią bet kuriame erdvės taške.

pavyzdžiui.

LINIJAS VEKTORIAUS OPERACIJOS

1. Vektoriaus padauginimas iš skaičiaus.

   Vektoriaus sandauga iš skaičiaus λ yra naujas vektorius, kuris:

   Vektoriaus ir skaičiaus λ sandauga žymima .

   

   Pavyzdžiui, yra vektorius, nukreiptas ta pačia kryptimi kaip ir vektorius ir kurio ilgis yra perpus mažesnis nei vektoriaus .

   Įvesta operacija turi šiuos dalykus savybių:

2. Vektorių pridėjimas.

   Tegul ir yra du savavališki vektoriai. Paimkite savavališką tašką O ir sukurti vektorių . Po to iš taško A atidėti vektorių . Vadinamas vektorius, jungiantis pirmojo vektoriaus pradžią su antrojo pabaiga sumašių vektorių ir yra žymimas .

   

   Suformuluotas vektorių pridėjimo apibrėžimas vadinamas lygiagretainio taisyklė, nes tą pačią vektorių sumą galima gauti taip. Atidėkite nuo taško O vektoriai ir . Sukurkite lygiagretainį ant šių vektorių OABC. Kadangi vektoriai , tada vektorius , kuris yra lygiagretainio, nubrėžto iš viršūnės, įstrižainė O, akivaizdu, kad bus vektorių suma.

   

   Nesunku patikrinti toliau nurodytus dalykus vektoriaus sudėjimo savybės.

3. Vektorių skirtumas.

   Vadinamas vektorius, kolinearinis tam tikram vektoriui , vienodo ilgio ir priešingos krypties priešingas vektoriaus vektorius ir žymimas . Priešingą vektorių galima laikyti vektoriaus dauginimo iš skaičiaus λ = –1 rezultatu: .

Įstrižainės matricos yra paprasčiausiai išdėstytos. Kyla klausimas, ar įmanoma rasti pagrindą, kuriame tiesinio operatoriaus matrica turėtų įstrižainę. Toks pagrindas yra.
Tegu duota tiesinė erdvė R n ir joje veikiantis tiesinis operatorius A; šiuo atveju operatorius A paima R n į save, tai yra A:R n → R n .

Apibrėžimas. Nenulinis vektorius vadinamas savuoju operatoriaus A vektoriumi, jei operatorius A virsta jam kolineariniu vektoriumi, ty . Skaičius λ vadinamas savąja reikšme arba savąja operatoriaus A reikšme, atitinkančia savąjį vektorių .
Atkreipiame dėmesį į kai kurias savųjų reikšmių ir savųjų vektorių savybes.
1. Bet koks tiesinis savųjų vektorių derinys operatoriaus A, atitinkančio tą pačią savąją reikšmę, λ yra savasis vektorius, turintis tą pačią savąją reikšmę.
2. Savotieji vektoriai operatorius A su poromis skirtingomis savosiomis reikšmėmis λ 1 , λ 2 , …, λ m yra tiesiškai nepriklausomas.
3. Jei savosios reikšmės λ 1 =λ 2 = λ m = λ, tai savoji reikšmė λ atitinka ne daugiau kaip m tiesiškai nepriklausomų savųjų vektorių.

Taigi, jei yra n tiesiškai nepriklausomų savųjų vektorių atitinkančias skirtingas savąsias reikšmes λ 1 , λ 2 , …, λ n , tada jos yra tiesiškai nepriklausomos, todėl jas galima laikyti erdvės R n pagrindu. Raskime tiesinio operatoriaus A matricos formą jos savųjų vektorių pagrindu, kuriai veikiame su operatoriumi A baziniais vektoriais: tada .
Taigi, tiesinio operatoriaus A matrica savo savųjų vektorių pagrindu turi įstrižainę, o operatoriaus A savosios reikšmės yra įstrižainėje.
Ar yra dar vienas pagrindas, kuriame matrica turi įstrižinę formą? Atsakymą į šį klausimą duoda tokia teorema.

Teorema. Tiesinio operatoriaus A matrica bazėje (i = 1..n) turi įstrižainę tada ir tik tada, kai visi pagrindo vektoriai yra operatoriaus A savieji vektoriai.

Taisyklė, kaip rasti savąsias reikšmes ir savuosius vektorius

Tegul vektorius , kur x 1 , x 2 , …, x n - vektoriaus koordinatės pagrindo atžvilgiu ir yra tiesinio operatoriaus A savasis vektorius, atitinkantis savąją reikšmę λ, t.y. Šis ryšys gali būti parašytas matricos forma

. (*)

Lygtį (*) galima laikyti lygtimi ieškant , ir , tai yra, mus domina netrivialūs sprendiniai, nes savasis vektorius negali būti lygus nuliui. Yra žinoma, kad netrivialūs vienalytės tiesinių lygčių sistemos sprendiniai egzistuoja tada ir tik tada, kai det(A - λE) = 0. Taigi, kad λ būtų operatoriaus A savoji reikšmė, būtina ir pakanka, kad det(A - λE) ) = 0.
Jei lygtis (*) parašyta išsamiai koordinačių forma, tada gauname tiesinių vienalyčių lygčių sistemą:

(1)
kur yra tiesinio operatoriaus matrica.

Sistema (1) turi nulinį sprendinį, jei jos determinantas D yra lygus nuliui

Gavome lygtį savųjų reikšmių paieškai.
Ši lygtis vadinama charakteringąja lygtimi, o kairioji jos pusė – matricos (operatoriaus) A charakteringuoju polinomu. Jei charakteringasis daugianomas neturi realių šaknų, tai matrica A neturi savųjų vektorių ir negali būti redukuojama į įstrižainę.
Tegul λ 1 , λ 2 , …, λ n yra tikrosios charakteristikos lygties šaknys ir tarp jų gali būti kartotiniai. Pakeitę šias reikšmes į sistemą (1), randame savuosius vektorius.

12 pavyzdys. Tiesinis operatorius A veikia R 3 pagal dėsnį , kur x 1 , x 2 , .., x n yra pagrindo vektoriaus koordinatės , , . Raskite šio operatoriaus savąsias reikšmes ir savuosius vektorius.
Sprendimas. Sudarome šio operatoriaus matricą:
.
Sudarome savųjų vektorių koordinačių nustatymo sistemą:

Sudarome charakteristikų lygtį ir ją išsprendžiame:

.
λ 1,2 = -1, λ 3 = 3.
Sistemoje pakeitę λ = -1, gauname:
arba
Nes , tada yra du priklausomi kintamieji ir vienas laisvas kintamasis.
Tada tegul x 1 yra laisvas nežinomasis Mes sprendžiame šią sistemą bet kokiu būdu ir randame bendrą šios sistemos sprendimą: Fundamentali sistema sprendinius sudaro vienas sprendinys, nes n - r = 3 - 2 = 1.
Savųjų vektorių aibė, atitinkanti savąją reikšmę λ = -1, turi formą: , kur x 1 yra bet koks skaičius, išskyrus nulį. Pažymime vieną vektorių iš šios aibės, pavyzdžiui, nustatydami x 1 = 1: .
Panašiai argumentuodami randame savąjį vektorių, atitinkantį savąją reikšmę λ = 3: .
Erdvėje R 3 pagrindas susideda iš trijų tiesiškai nepriklausomų vektorių, tačiau gavome tik du tiesiškai nepriklausomus savuosius vektorius, iš kurių negalima sudaryti pagrindo R 3. Vadinasi, tiesinio operatoriaus matrica A negali būti redukuota į įstrižainę.

13 pavyzdys Duota matrica .
1. Įrodykite, kad vektorius yra matricos A savasis vektorius. Raskite šį savąjį vektorių atitinkančią savąją reikšmę.
2. Raskite pagrindą, kuriame matrica A turi įstrižainę.
Sprendimas.
1. Jei , tai yra savivektorius

.
Vektorius (1, 8, -1) yra savasis vektorius. Savoji reikšmė λ = -1.
Matrica turi įstrižainę formą, kurią sudaro savieji vektoriai. Vienas iš jų yra žinomas. Suraskime likusius.
Ieškome savųjų vektorių iš sistemos:

Charakteristinė lygtis: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Raskite savąjį vektorių, atitinkantį savąją reikšmę λ = -3:

Šios sistemos matricos rangas yra lygus dviem ir yra lygus nežinomųjų skaičiui, todėl ši sistema turi tik nulinį sprendinį x 1 = x 3 = 0. x 2 čia gali būti bet kas kitas nei nulis, pvz. x 2 = 1. Taigi vektorius (0 ,1,0) yra savasis vektorius, atitinkantis λ = -3. Patikrinkime:
.
Jei λ = 1, tada gauname sistemą
Matricos rangas yra du. Nubraukite paskutinę lygtį.
Tegul x 3 yra laisvas nežinomasis. Tada x 1 \u003d -3x 3, 4x 2 = 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 = 9x 3.
Darant prielaidą, kad x 3 = 1, turime (-3,-9,1) - savąjį vektorių, atitinkantį savąją reikšmę λ = 1. Patikrinkite:

.
Kadangi savosios reikšmės yra realios ir skirtingos, jas atitinkantys vektoriai yra tiesiškai nepriklausomi, todėl juos galima paimti kaip pagrindą R 3 . Taigi, pagrinde , , A matrica turi tokią formą:
.
Ne kiekviena tiesinio operatoriaus A:R n → R n matrica gali būti redukuojama į įstrižainę, nes kai kuriems tiesiniams operatoriams gali būti mažiau nei n tiesiškai nepriklausomų savųjų vektorių. Tačiau, jei matrica yra simetriška, tada lygiai m tiesiškai nepriklausomų vektorių atitinka būdingos daugumos m lygties šaknį.

Apibrėžimas. Simetrinė matrica yra kvadratinė matrica, kurioje elementai, kurie yra simetriški pagrindinės įstrižainės atžvilgiu, yra lygūs, tai yra, kurioje .
Pastabos. 1. Visos simetrinės matricos savosios reikšmės yra tikros.
2. Simetrinės matricos savieji vektoriai, atitinkantys poromis skirtingas savąsias reikšmes, yra ortogonalūs.
Kaip vieną iš daugelio tiriamo aparato pritaikymo būdų, mes laikome antros eilės kreivės formos nustatymo problemą.