Kvadratinės matricos savasis vektorius yra tas, kurį padauginus iš nurodytos matricos, gaunamas kolinearinis vektorius. Paprastais žodžiais tariant, kai matrica padauginama iš savojo vektoriaus, pastarasis lieka toks pat, bet padauginamas iš tam tikro skaičiaus.

Apibrėžimas

Savasis vektorius yra nulinis vektorius V, kurį padauginus iš kvadratinės matricos M, jis virsta savimi, padidintu tam tikru skaičiumi λ. Algebriniu žymėjimu tai atrodo taip:

M × V = λ × V,

kur λ yra matricos M savoji reikšmė.

Pažvelkime į skaitmeninį pavyzdį. Kad būtų patogiau, skaičiai matricoje bus atskirti kabliataškiu. Turėkime matricą:

• M = 0; 4;
• 6; 10.

Padauginkime jį iš stulpelio vektoriaus:

• V = -2;

Padauginus matricą iš stulpelio vektoriaus, gauname ir stulpelio vektorių. Griežtai matematiškai formulė 2 × 2 matricos padauginimui iš stulpelio vektoriaus atrodys taip:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 reiškia matricos M elementą, esantį pirmoje eilutėje ir pirmame stulpelyje, o M22 - elementą, esantį antroje eilutėje ir antrame stulpelyje. Mūsų matricoje šie elementai yra lygūs M11 = 0, M12 = 4, M21 = 6, M22 10. Stulpelio vektoriui šios reikšmės yra V11 = –2, V21 = 1. Pagal šią formulę gauname toks kvadratinės matricos sandaugos iš vektoriaus rezultatas:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Kad būtų patogiau, parašykime stulpelio vektorių į eilutę. Taigi, kvadratinę matricą padauginome iš vektoriaus (-2; 1), gaudami vektorių (4; -2). Akivaizdu, kad tai yra tas pats vektorius, padaugintas iš λ = -2. Lambda šiuo atveju reiškia matricos savąją reikšmę.

Matricos savasis vektorius yra kolinearinis vektorius, tai yra objektas, kuris nekeičia savo padėties erdvėje, padauginus iš matricos. Vektorinės algebros kolineariškumas yra panašus į geometrijos lygiagretumą. Geometrinėje interpretacijoje kolineariniai vektoriai yra lygiagrečios skirtingo ilgio kryptinės linijos atkarpos. Nuo Euklido laikų žinome, kad viena tiesė turi begalinį lygiagrečių tiesių skaičių, todėl logiška manyti, kad kiekviena matrica turi begalinį skaičių savųjų vektorių.

Iš ankstesnio pavyzdžio matote, kad savieji vektoriai gali būti (-8; 4) ir (16; -8) ir (32, -16). Visi tai yra kolineariniai vektoriai, atitinkantys savąją reikšmę λ = -2. Pradinę matricą padauginus iš šių vektorių, vis tiek gausime vektorių, kuris skiriasi nuo originalo 2 kartus. Štai kodėl, sprendžiant savojo vektoriaus radimo uždavinius, reikia rasti tik tiesiškai nepriklausomus vektorinius objektus. Dažniausiai n × n matricoje yra n-asis savųjų vektorių skaičius. Mūsų skaičiuotuvas yra pritaikytas antros eilės kvadratinių matricų analizei, todėl beveik visada bus rasti du savieji vektoriai, išskyrus atvejus, kai jie sutampa.

Aukščiau pateiktame pavyzdyje mes iš anksto žinojome pradinės matricos savąjį vektorių ir aiškiai nustatėme lambda skaičių. Tačiau praktikoje viskas vyksta atvirkščiai: pradžioje randamos savosios reikšmės, o tik tada atsiranda savieji vektoriai.

Sprendimo algoritmas

Peržiūrėkime pradinę matricą M ir pabandykime rasti abu jos savuosius vektorius. Taigi matrica atrodo taip:

• M = 0; 4;
• 6; 10.

Pirmiausia turime nustatyti savąją reikšmę λ, kuriai turime apskaičiuoti šios matricos determinantą:

• (0 - λ); 4;
• 6; (10 - λ).

Ši matrica gaunama iš pagrindinės įstrižainės elementų atėmus nežinomą λ. Determinantas nustatomas naudojant standartinę formulę:

• detA = M11 × M21 - M12 × M22
• detA = (0 – λ) × (10 – λ) – 24

Kadangi mūsų vektorius neturi būti lygus nuliui, gautą lygtį laikome tiesiškai priklausoma ir savo determinantą detA prilyginame nuliui.

(0 – λ) × (10 – λ) – 24 = 0

Atidarykime skliaustus ir gaukime būdingą matricos lygtį:

λ 2 - 10 λ - 24 = 0

Tai yra standartinė kvadratinė lygtis, kurią reikia išspręsti naudojant diskriminantą.

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

Diskriminanto šaknis yra sqrt (D) = 14, todėl λ1 = -2, λ2 = 12. Dabar kiekvienai lambda reikšmei reikia rasti savąjį vektorių. Išreikškime sistemos koeficientus, kai λ = -2.

• M - λ × E = 2; 4;
• 6; 12.

Šioje formulėje E yra tapatybės matrica. Remdamiesi gauta matrica, sudarome tiesinių lygčių sistemą:

2x + 4m = 6x + 12m,

kur x ir y yra savojo vektoriaus elementai.

Surinkite visus X kairėje ir visus žaidėjus dešinėje. Akivaizdu – 4x = 8m. Padalinkite išraišką iš - 4 ir gaukite x = -2y. Dabar galime nustatyti pirmąjį matricos savąjį vektorių, paimdami bet kokias nežinomųjų reikšmes (prisiminkime tiesiškai priklausomų savųjų vektorių begalybę). Paimkime y = 1, tada x = –2. Todėl pirmasis savasis vektorius atrodo kaip V1 = (–2; 1). Grįžkite į straipsnio pradžią. Šiame vektoriaus objekte mes padauginome matricą, kad parodytume savojo vektoriaus sąvoką.

Dabar rasime savąjį vektorių, kai λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Sudarykime tą pačią tiesinių lygčių sistemą;

• -12x + 4m = 6x - 2m
• -18x = -6m
• 3x = y.

Dabar imkime x = 1, taigi y = 3. Taigi antrasis savasis vektorius atrodo kaip V2 = (1; 3). Kai pradinė matrica padauginama iš šio vektoriaus, rezultatas visada bus tas pats vektorius, padaugintas iš 12. Taip baigiamas sprendimo algoritmas. Dabar jūs žinote, kaip rankiniu būdu apibrėžti matricos savąjį vektorių.

• determinantas;
• pėdsakas, tai yra pagrindinės įstrižainės elementų suma;
• rangas, tai yra maksimalus tiesiškai nepriklausomų eilučių / stulpelių skaičius.

Programa veikia pagal aukščiau pateiktą algoritmą, sumažindama sprendimo procesą. Svarbu pažymėti, kad lambda programoje žymima raide „c“. Paimkime skaitinį pavyzdį.

Programos pavyzdys

Pabandykime apibrėžti šios matricos savuosius vektorius:

• M = 5; 13;
• 4; 14.

Įveskime šias reikšmes į skaičiuoklės langelius ir gaukime atsakymą tokia forma:

• Matricos reitingas: 2
• Matricos determinantas: 18;
• Matricos pėdsakas: 19;
• Savojo vektoriaus apskaičiavimas: c 2 - 19.00c + 18.00 (charakteristinė lygtis);
• Savojo vektoriaus skaičiavimas: 18 (pirmoji lambda reikšmė);
• Savojo vektoriaus skaičiavimas: 1 (antra lambda reikšmė);
• 1 vektoriaus lygčių sistema: -13x1 + 13y1 = 4x1 - 4y1;
• 2 vektoriaus lygčių sistema: 4x1 + 13y1 = 4x1 + 13y1;
• 1 savasis vektorius: (1; 1);
• 2 savasis vektorius: (-3,25; 1).

Taigi mes gavome du tiesiškai nepriklausomus savuosius vektorius.

Išvada

Tiesinė algebra ir analitinė geometrija yra standartiniai dalykai kiekvienam pirmakursiui inžinerijoje. Didelis vektorių ir matricų skaičius kelia siaubą, o atliekant tokius sudėtingus skaičiavimus lengva suklysti. Mūsų programa leis studentams patikrinti savo skaičiavimus arba automatiškai išspręs savo vektoriaus radimo problemą. Mūsų kataloge yra ir kitų tiesinės algebros skaičiuotuvų, naudokite juos studijose ar darbe.

". Pirmoje dalyje pateikiamos minimalios chemometrijos supratimo nuostatos, o antroje dalyje pateikiami faktai, kuriuos reikia žinoti norint giliau suprasti daugiamatės analizės metodus. Pristatymas iliustruojamas Excel darbaknygėje atliktais pavyzdžiais Matrica.xls kuris pridedamas prie šio dokumento.

Nuorodos į pavyzdžius tekste pateikiamos kaip Excel objektai. Šie pavyzdžiai yra abstraktaus pobūdžio, jie niekaip nesusiję su analitinės chemijos problemomis. Realūs matricinės algebros panaudojimo chemometrikoje pavyzdžiai nagrinėjami kituose tekstuose, skirtuose įvairioms chemometrinėms programoms.

Dauguma analitinės chemijos matavimų yra ne tiesioginiai, o netiesioginis... Tai reiškia, kad eksperimente vietoj norimos analitės C reikšmės (koncentracijos) gaunama kita reikšmė x(signalas) susijęs, bet nelygus C, t.y. x(C) ≠ C. Paprastai priklausomybės tipas x(C) nežinoma, tačiau, laimei, analitinėje chemijoje dauguma matavimų yra proporcingi. Tai reiškia, kad padidėjus C koncentracijai in a kartų, signalas X padidės tiek pat. x(a C) = a x(C). Be to, signalai taip pat yra adityvūs, todėl signalas iš mėginio, kuriame yra dvi C 1 ir C 2 koncentracijos medžiagos, bus lygus kiekvieno komponento signalų sumai, t.y. x(C 1 + C 2) = x(C 1) + x(C 2). Proporcingumas ir adityvumas kartu duoda tiesiškumas... Tiesiškumo principui iliustruoti yra daug pavyzdžių, tačiau pakanka paminėti du ryškiausius pavyzdžius – chromatografiją ir spektroskopiją. Antroji analitinės chemijos eksperimento charakteristika yra daugiakanalis... Šiuolaikinė analitinė įranga vienu metu matuoja daugelio kanalų signalus. Pavyzdžiui, šviesos pralaidumo intensyvumas matuojamas iš karto keliems bangos ilgiams, t.y. spektras. Todėl eksperimente susiduriame su daugybe signalų x 1 , x 2 ,...., x n, apibūdinanti tiriamoje sistemoje esančių medžiagų koncentracijų C 1, C 2, ..., C m aibę.

Ryžiai. 1 spektras

Taigi, analitiniam eksperimentui būdingas tiesiškumas ir daugiamatiškumas. Todėl eksperimentinius duomenis patogu laikyti vektoriais ir matricomis ir jais manipuliuoti matricinės algebros aparatu. Šio metodo vaisingumą iliustruoja pavyzdyje parodytas pavyzdys, kuriame rodomi trys spektrai, užfiksuoti 200 bangų ilgių nuo 4000 iki 4796 cm – 1. Pirmas ( x 1) ir antrasis ( x 2) gauti spektrai standartiniams mėginiams, kuriuose žinoma dviejų medžiagų A ir B koncentracija: pirmame mėginyje [A] = 0,5, [B] = 0,1, o antrajame mėginyje [A] = 0,2, [B ] = 0,6. Ką galima pasakyti apie naują, nežinomą pavyzdį, kurio spektras yra nurodytas x 3 ?

Apsvarstykite tris eksperimentinius spektrus x 1 , x 2 ir x 3 kaip trys vektoriai, kurių matmuo 200. Naudojant tiesinę algebrą galima lengvai parodyti, kad x 3 = 0.1 x 1 +0.3 x 2; todėl trečiajame mėginyje akivaizdžiai yra tik medžiagos A ir B, kurių koncentracija [A] = 0,5 × 0,1 + 0,2 × 0,3 = 0,11 ir [B] = 0,1 × 0,1 + 0,6 × 0,3 = 0,19.

1. Pagrindinė informacija

1.1 Matricos

Matrica vadinama, pavyzdžiui, stačiakampe skaičių lentele

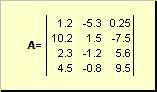
Ryžiai. 2 Matrica

Matricos žymimos paryškintomis didžiosiomis raidėmis ( A), o jų elementai – atitinkamos mažosios raidės su indeksais, t.y. a ij. Pirmoji rodyklė sunumeruoja eilutes, o antroji – stulpelius. Chemometrikoje įprasta didžiausią indekso reikšmę žymėti ta pačia raide kaip ir pats indeksas, bet didžiosiomis raidėmis. Todėl matrica A taip pat gali būti parašytas kaip ( a ij , i = 1,..., aš; j = 1,..., J). Pavyzdyje parodytai matricai aš = 4, J= 3 ir a 23 = −7.5.

Skaičių pora aš ir J vadinamas matricos dimensija ir žymimas kaip aš× J... Chemometrijos matricos pavyzdys yra spektrų rinkinys, gautas už aš pavyzdžiai ant J bangos ilgiai.

1.2. Paprastos matricos operacijos

Matricos gali padauginti iš skaičių... Šiuo atveju kiekvienas elementas padauginamas iš šio skaičiaus. Pavyzdžiui -

Ryžiai. 3 Matricos daugyba iš skaičiaus

Dvi to paties matmens matricos gali būti elementinės sulankstyti ir atimti... Pavyzdžiui,

Ryžiai. 4 Matricos pridėjimas

Padauginus iš skaičiaus ir sudėjus, gaunama to paties matmens matrica.

Nulinė matrica yra matrica, susidedanti iš nulių. Jis žymimas O... Tai akivaizdu A+O = A, A−A = O ir 0 A = O.

Matrica gali būti perkelti... Šios operacijos metu matrica apverčiama, t.y. eilutės ir stulpeliai yra sukeisti. Perkėlimas rodomas potėpiu, A“ arba indeksas A t. Taigi, jei A = {a ij , i = 1,..., aš; j = 1,...,J), tada A t = ( a ji , j = 1,...,J; i = 1, ..., aš). Pavyzdžiui

Ryžiai. 5 Transponuoti matricą

Akivaizdu, kad ( A t) t = A, (A+B) t = A t + B t.

1.3. Matricos daugyba

Matricos gali padauginti, bet tik jei jie turi atitinkamus matmenis. Kodėl taip yra, paaiškės iš apibrėžimo. Matricos sandauga A, matmuo aš× K, ir matricos B, matmuo K× J vadinama matrica C, matmuo aš× J kurio elementai yra skaičiai

Taigi, gaminti AB būtina, kad stulpelių skaičius kairėje matricoje A buvo lygus eilučių skaičiui dešinėje matricoje B... Matricinio produkto pavyzdys -

6 pav. Matricos gaminys

Matricos daugybos taisyklę galima suformuluoti taip. Norėdami rasti matricos elementą C stovintis sankryžoje i-toji eilutė ir j- stulpelis ( c ij) turi būti padaugintas iš elemento i pirmosios matricos eilutė Aįjungta j antrosios matricos stulpelis B ir sudėkite visus rezultatus. Taigi parodytame pavyzdyje elementas iš trečios eilutės ir antrojo stulpelio gaunamas kaip trečios eilutės elementų sandaugų suma A ir antrasis stulpelis B

7 pav. Matricos gaminio elementas

Matricų sandauga priklauso nuo eilės, t.y. AB ≠ BA, jei tik dėl matmenų. Sakoma, kad jis nekeičiamas. Tačiau matriciniai produktai yra asociatyvūs. Tai reiškia kad ABC = (AB)C = A(pr. Kr). Be to, jis yra ir paskirstomasis, t.y. A(B+C) = AB+AC... Tai akivaizdu AO = O.

1.4. Kvadratinės matricos

Jei matricos stulpelių skaičius yra lygus jos eilučių skaičiui ( aš = J = N), tada tokia matrica vadinama kvadratine. Šiame skyriuje nagrinėsime tik tokias matricas. Tarp šių matricų galima išskirti ypatingų savybių turinčias matricas.

Vienišas matrica (žymima aš, ir kartais E) – tai matrica, kurioje visi elementai lygūs nuliui, išskyrus įstrižinius, kurie lygūs 1, t.y.

Akivaizdu Ai = IA = A.

Matrica vadinama įstrižainės jei visi jo elementai, išskyrus įstrižinius ( a ii) yra lygūs nuliui. Pavyzdžiui

Ryžiai. 8 Įstrižainė matrica

Matrica A vadinama viršūne trikampis jeigu visi jo elementai žemiau įstrižainės yra lygūs nuliui, t.y. a ij= 0, už i>j... Pavyzdžiui

Ryžiai. 9 Viršutinė trikampė matrica

Apatinė trikampė matrica apibrėžiama panašiai.

Matrica A paskambino simetriškas, jei A t = A... Kitaip tariant a ij = a ji... Pavyzdžiui

Ryžiai. 10 Simetrinė matrica

Matrica A paskambino stačiakampis, jei

A t A = AA t = aš.

Matrica vadinama normalus jeigu

1.5. Pėdsakas ir determinantas

Sekant kvadratinė matrica A(žymimas Tr ( A) arba Sp ( A)) yra jo įstrižainių elementų suma,

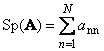
Pavyzdžiui,

Ryžiai. 11 Matricos pėdsakas

Tai akivaizdu

Sp (α A) = α Sp ( A) ir

Sp ( A+B) = Sp ( A) + Sp ( B).

Galima parodyti, kad

Sp ( A) = Sp ( A t), Sp ( aš) = N,

ir taip pat tai

Sp ( AB) = Sp ( BA).

Kita svarbi kvadratinės matricos savybė yra jos determinantas(žymima det ( A)). Nustatyti determinantą bendruoju atveju yra gana sunku, todėl pradėsime nuo paprasčiausios versijos - matricos A matmuo (2 × 2). Tada

(3 × 3) matricos determinantas bus

Matricos atveju ( N× N) determinantas apskaičiuojamas kaip 1 2 3 ... suma N= N! terminai, kurių kiekvienas yra lygus

Indeksai k 1 , k 2 ,..., k N apibrėžiami kaip visos galimos sutvarkytos permutacijos r skaičiai rinkinyje (1, 2, ..., N). Matricos determinanto apskaičiavimas yra sudėtinga procedūra, kuri praktiškai atliekama naudojant specialias programas. Pavyzdžiui,

Ryžiai. 12 Matricos determinantas

Atkreipiame dėmesį tik į akivaizdžias savybes:

det ( aš) = 1, det ( A) = det ( A t),

det ( AB) = det ( A) det ( B).

1.6. Vektoriai

Jei matricą sudaro tik vienas stulpelis ( J= 1), tada toks objektas vadinamas vektorius... Tiksliau, stulpelio vektorius. Pavyzdžiui

Taip pat galima apsvarstyti, pavyzdžiui, matricas, sudarytas iš vienos eilutės

Šis objektas taip pat yra vektorius, bet eilutės vektorius... Analizuojant duomenis svarbu suprasti, su kokiais vektoriais turime reikalą – stulpeliais ar eilutėmis. Taigi spektras, paimtas vienam mėginiui, gali būti laikomas eilutės vektoriumi. Tada spektrinio intensyvumo rinkinys tam tikram bangos ilgiui visiems mėginiams turi būti traktuojamas kaip stulpelio vektorius.

Vektoriaus matmuo yra jo elementų skaičius.

Aišku, kad bet kuris stulpelio vektorius gali būti transformuojamas į eilučių vektorių transpozicijos būdu, t.y.

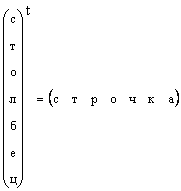
Tais atvejais, kai vektoriaus forma nėra konkrečiai nurodyta, o tiesiog sakomas vektorius, tada jie reiškia stulpelio vektorių. Mes taip pat laikysimės šios taisyklės. Vektorius žymimas mažąja tiesiai paryškinta raide. Nulinis vektorius yra vektorius, kurio visi elementai yra lygūs nuliui. Jis yra paskirtas 0 .

1.7. Pagrindinės operacijos su vektoriais

Vektorius galima sudėti ir padauginti iš skaičių taip pat, kaip ir matricas. Pavyzdžiui,

Ryžiai. 13 Vektorinės operacijos

Du vektoriai x ir y yra vadinami tiesinė jei yra skaičius α toks

1.8. Vektorių sandaugos

Du vienodo matmens vektoriai N galima padauginti. Tegul yra du vektoriai x = (x 1 , x 2 ,...,x N) t ir y = (y 1 , y 2 ,...,y N) t. Vadovaudamiesi daugybos taisykle „eilutė po stulpelio“, iš jų galime sudaryti du produktus: x t y ir xy t. Pirmas gabalas

paskambino skaliarinis arba vidinis... Jo rezultatas yra skaičius. Taip pat naudojamas žymėjimas ( x,y)= x t y... Pavyzdžiui,

Ryžiai. 14 Vidinis gaminys (taškinis gaminys)

Antras gabalas

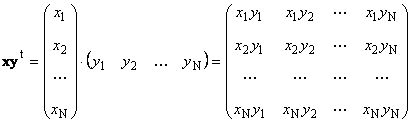
paskambino išorės... Jo rezultatas yra matmenų matrica ( N× N). Pavyzdžiui,

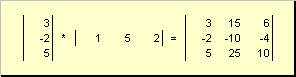
Ryžiai. 15 Išorės darbai

Vadinami vektoriai, kurių skaliarinė sandauga lygi nuliui stačiakampis.

1.9. Vektorinė norma

Pati vektoriaus skaliarinė sandauga vadinama skaliariniu kvadratu. Ši vertė

apibrėžia kvadratą ilgio vektorius x... Pažymėti ilgį (taip pat vadinamas norma vektorius), naudojamas žymėjimas

Pavyzdžiui,

Ryžiai. 16 Vektorinė norma

Vienetinio ilgio vektorius (|| x|| = 1) vadinamas normalizuotu. Nenulinis vektorius ( x ≠ 0 ) galima normalizuoti padalijus iš ilgio, t.y. x = ||x|| (x /||x||) = ||x|| e... čia e = x /||x|| yra normalizuotas vektorius.

Vektoriai vadinami ortonormaliais, jei jie visi normalizuoti ir poromis stačiakampiai.

1.10. Kampas tarp vektorių

Taškinis produktas apibrėžia ir injekcijaφ tarp dviejų vektorių x ir y

Jei vektoriai yra stačiakampiai, tada cosφ = 0 ir φ = π / 2, o jei jie yra kolinearūs, tada cosφ = 1 ir φ = 0.

1.11. Matricos vektorinis vaizdavimas

Kiekviena matrica A dydis aš× J gali būti pavaizduotas kaip vektorių rinkinys

Čia kiekvienas vektorius a j yra j stulpelis ir eilutės vektorius b i yra i- matricos eilutė A

1.12. Tiesiškai priklausomi vektoriai

To paties matmens vektoriai ( N) galima sudėti ir padauginti iš skaičiaus, kaip ir matricas. Rezultatas bus to paties dydžio vektorius. Tegul yra keli tos pačios dimensijos vektoriai x 1 , x 2 ,...,x K ir tiek pat skaičių α α 1, α 2, ..., α K... Vektorius

y= α 1 x 1 + α 2 x 2 + ... + α K x K

paskambino linijinis derinys vektoriai x k .

Jei yra nulinių skaičių α k ≠ 0, k = 1,..., K, ką y = 0 , tada tokia vektorių rinkinys x k paskambino tiesiškai priklausomas... Priešingu atveju vektoriai vadinami tiesiškai nepriklausomais. Pavyzdžiui, vektoriai x 1 = (2, 2) t ir x 2 = (−1, −1) t yra tiesiškai priklausomi, nes x 1 +2x 2 = 0

1.13. Matricos rangas

Apsvarstykite rinkinį K vektoriai x 1 , x 2 ,...,x K matmenys N... Šios vektorių sistemos rangas yra maksimalus tiesiškai nepriklausomų vektorių skaičius. Pavyzdžiui, rinkinyje

Pavyzdžiui, yra tik du tiesiškai nepriklausomi vektoriai x 1 ir x 2, taigi jo rangas yra 2.

Akivaizdu, kad jei aibėje yra daugiau vektorių nei jų matmuo ( K>N), tada jie būtinai yra tiesiškai priklausomi.

Pagal matricos rangą(žymima rangu ( A)) yra vektorių sistemos, iš kurios ji susideda, rangas. Nors bet kurią matricą galima pavaizduoti dviem būdais (stulpelių vektoriais arba eilutėmis), tai neturi įtakos rango reikšmei, nes

1.14. atvirkštinė matrica

Kvadratinė matrica A vadinamas neišsigimusiu, jei turi unikalų atvirkščiai matrica A-1 nustatoma pagal sąlygas

AA −1 = A −1 A = aš.

Atvirkštinė matrica neegzistuoja visoms matricoms. Būtina ir pakankama neišsigimimo sąlyga yra

det ( A) ≠ 0 arba rangas ( A) = N.

Matricos inversija yra sudėtinga procedūra, kuriai yra specialios programos. Pavyzdžiui,

Ryžiai. 17 Matricos inversija

Pateikiame paprasčiausio atvejo formules – 2 × 2 matricas

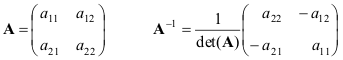
Jei matricos A ir B tada neišsigimęs

(AB) −1 = B −1 A −1 .

1.15. Pseudoinversinė matrica

Jei matrica A yra išsigimęs, o atvirkštinė matrica neegzistuoja, kai kuriais atvejais galite naudoti pseudo atvirkštinis matrica, kuri apibrėžiama kaip tokia matrica A+ tai

AA + A = A.

Pseudo atvirkštinė matrica nėra vienintelė ir jos tipas priklauso nuo konstravimo metodo. Pavyzdžiui, stačiakampei matricai galite naudoti Moore-Penrose metodą.

Jei stulpelių skaičius yra mažesnis už eilučių skaičių, tada

A + =(A t A) −1 A t

Pavyzdžiui,

Ryžiai. 17a Matricos pseudoinversija

Jei stulpelių skaičius yra didesnis už eilučių skaičių, tada

A + =A t ( AA t) −1

1.16. Vektoriaus padauginimas iš matricos

Vektorius x galima padauginti iš matricos A tinkamas matmuo. Šiuo atveju stulpelio vektorius padauginamas dešinėje Ax o eilutės vektorius yra kairėje x t A... Jei vektoriaus matmuo J, ir matricos matmuo aš× J tada rezultatas yra dimensijos vektorius aš... Pavyzdžiui,

Ryžiai. 18 Matricos daugybos vektorius

Jei matrica A- kvadratas ( aš× aš), tada vektorius y = Ax turi tokį patį matmenį kaip x... Tai akivaizdu

A(α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Todėl į matricas galima žiūrėti kaip į tiesines vektorių transformacijas. Ypač Ix = x, Jautis = 0 .

2. Papildoma informacija

2.1. Tiesinių lygčių sistemos

Leisti būti A- matricos dydis aš× J, a b- matmenų vektorius J... Apsvarstykite lygtį

Ax = b

vektoriaus atžvilgiu x, matmenys aš... Tiesą sakant, tai yra sistema aš tiesines lygtis su J nežinomas x 1 ,...,x J... Sprendimas egzistuoja tada ir tik tada

rangas ( A) = rangas ( B) = R,

kur B yra išplėstinių matmenų matrica aš×( J + 1) susidedanti iš matricos A paminkštintas stulpeliu b, B = (A b). Priešingu atveju lygtys yra nenuoseklios.

Jeigu R = aš = J, tada sprendimas yra unikalus

x = A −1 b.

Jeigu R < aš, tada yra daug skirtingų sprendimų, kuriuos galima išreikšti tiesiniu deriniu J−R vektoriai. Vienalyčių lygčių sistema Ax = 0 kvadratinė matrica A (N× N) turi netrivialų sprendimą ( x ≠ 0 ) tada ir tik jei det ( A) = 0. Jei R= rangas ( A)<N tada egzistuoti N−R tiesiškai nepriklausomi sprendimai.

2.2. Dvilinijinės ir kvadratinės formos

Jeigu A yra kvadratinė matrica ir x ir y yra atitinkamo matmens vektoriai, tada formos skaliarinė sandauga x t Ai paskambino dvilinijinis matricos apibrėžta forma A... At x = y išraiška x t Ax paskambino kvadratinis forma.

2.3. Teigiamos apibrėžtosios matricos

Kvadratinė matrica A paskambino teigiamai apibrėžtas jei kokiam nuliui nuliniam vektoriui x ≠ 0 ,

x t Ax > 0.

Panašiai, neigiamai (x t Ax < 0), neneigiamas (x t Ax≥ 0) ir ne teigiamas (x t Ax≤ 0) tam tikros matricos.

2.4. Cholesky skilimas

Jei simetrinė matrica A yra teigiamas apibrėžtas, tada yra unikali trikampė matrica U su teigiamais elementais, kuriems

A = U t U.

Pavyzdžiui,

Ryžiai. 19 Cholesky skilimas

2.5. Poliarinis skilimas

Leisti būti A yra neišsigimusi matmenų kvadratinė matrica N× N... Tada yra vienas su vienu poliarinis spektaklis

A = SR,

kur S yra neneigiama simetrinė matrica, ir R yra ortogonali matrica. Matricos S ir R galima aiškiai apibrėžti:

S 2 = AA t arba S = (AA t) ½ ir R = S −1 A = (AA t) −1 A.

Pavyzdžiui,

Ryžiai. 20 Poliarinis skilimas

Jei matrica A yra išsigimęs, tada plėtra nėra unikali – būtent: S vis dar vienas, bet R gal daug. Polinis skilimas reiškia matricą A kaip suspaudimo / tempimo derinys S ir pasukimas R.

2.6. Savotieji vektoriai ir savosios reikšmės

Leisti būti A yra kvadratinė matrica. Vektorius v paskambino nuosavas vektorius matricos A, jei

Av = λ v,

kur vadinamas skaičius λ savo prasmę matricos A... Taigi, transformacija, kurią atlieka matrica A virš vektoriaus v, sumažinamas iki paprasto tempimo arba suspaudimo su koeficientu λ. Savasis vektorius nustatomas iki daugybos iš konstantos α ≠ 0, t.y. jeigu v yra savasis vektorius, tada α v taip pat yra savasis vektorius.

2.7. Savosios vertybės

Matrica A, matmuo ( N× N) negali būti daugiau nei N savąsias reikšmes. Jie tenkina charakteristikos lygtis

det ( A − λ aš) = 0,

kuri yra algebrinė lygtis Nįsakymas. Visų pirma, 2 × 2 matricai būdinga lygtis turi tokią formą

Pavyzdžiui,

Ryžiai. 21 savosios vertės

Savųjų reikšmių rinkinys λ 1, ..., λ N matricos A paskambino spektras A.

Spektras turi įvairių savybių. Ypač

det ( A) = λ 1 × ... × λ N, Sp ( A) = λ 1 + ... + λ N.

Savavališkos matricos savosios reikšmės gali būti kompleksiniai skaičiai, bet jei matrica yra simetriška ( A t = A), tada jo savosios reikšmės yra tikros.

2.8. Nuosavi vektoriai

Matrica A, matmuo ( N× N) negali būti daugiau nei N savieji vektoriai, kurių kiekvienas atitinka savo vertę. Norėdami nustatyti savąjį vektorių v n reikia išspręsti vienarūšių lygčių sistemą

(A − λ n aš)v n = 0 .

Jis turi netrivialų sprendimą, nes det ( A -λ n aš) = 0.

Pavyzdžiui,

Ryžiai. 22 savieji vektoriai

Simetrinės matricos savieji vektoriai yra stačiakampiai.

Apibrėžimas 9.3. Vektorius NS paskambino nuosavas vektorius matricos A jei yra toks skaičius λ, kad lygybė galioja: A NS= λ NS, tai yra kreipimosi rezultatas NS tiesinė transformacija, pateikta matricos A, yra šio vektoriaus padauginimas iš skaičiaus λ ... Pats skaičius λ paskambino savo numerį matricos A.

Keitimas į formules (9.3) x` j = λx j, gauname lygčių sistemą savojo vektoriaus koordinatėms nustatyti:

. (9.5)

Ši tiesinė vienalytė sistema turės netrivialų sprendimą tik tuo atveju, jei jos pagrindinis determinantas yra 0 (Cramerio taisyklė). Rašydami šią sąlygą tokia forma:

gauname savųjų reikšmių nustatymo lygtį λ paskambino charakteristikos lygtis... Ją galima trumpai pristatyti taip:

| A - λE | = 0, (9.6)

nes jo kairėje pusėje yra matricos determinantas A-λE... Polinomas atžvilgiu λ | A - λE| paskambino būdingas daugianario matricos A.

Būdingos daugianario savybės:

1) Tiesinės transformacijos charakteringas daugianomas nepriklauso nuo pagrindo pasirinkimo. Įrodymas. (žr. (9.4)), bet vadinasi,. Taigi tai nepriklauso nuo pagrindo pasirinkimo. Vadinasi, ir | A-λE| pereinant prie naujo pagrindo nesikeičia.

2) Jei matrica A tiesinė transformacija yra simetriškas(tie. ir ij = a ji), tada visos charakteristikų lygties (9.6) šaknys yra realieji skaičiai.

Savųjų reikšmių ir savųjų vektorių savybės:

1) Jei pasirinksime savųjų vektorių pagrindą x 1, x 2, x 3 atitinkančias savąsias reikšmes λ 1, λ 2, λ 3 matricos A, tada tiesinė transformacija A turi įstrižainės formos matricą:

(9.7) Šios savybės įrodymas išplaukia iš savųjų vektorių apibrėžimo.

2) Jei transformacijos savosios reikšmės A yra skirtingi, tada atitinkami savieji vektoriai yra tiesiškai nepriklausomi.

3) Jei matricos charakteringasis daugianario A turi tris skirtingas šaknis, tada tam tikru pagrindu matrica A turi įstrižainę formą.

Raskime matricos savąsias reikšmes ir savuosius vektorius. Sudarykime charakteristikos lygtį: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Raskime kiekvieną rastą reikšmę atitinkančių savųjų vektorių koordinates λ. Iš (9.5) išplaukia, kad jeigu NS (1) ={x 1, x 2, x 3) Ar atitinka savąjį vektorių λ 1 = -2, tada

- bendradarbiaujanti, bet neapibrėžta sistema. Jo sprendimas gali būti parašytas kaip NS (1) ={a,0,-a), kur a yra bet koks skaičius. Visų pirma, jei to reikalaujame | x (1) |=1, NS (1) =

Pakeitimas į sistemą (9.5) λ 2 = 3, gauname antrojo savojo vektoriaus koordinačių nustatymo sistemą - x (2) ={y 1, y 2, y 3}:

, kur NS (2) ={b, -b, b) arba, atsižvelgiant į | x (2) |=1, x (2) =

Dėl λ 3 = 6 raskite savąjį vektorių x (3) ={z 1, z 2, z 3}:

, x (3) ={c,2c, c) arba normalizuotoje versijoje

x (3) = Jūs galite tai pamatyti NS (1) NS (2) = ab - ab= 0, x (1) x (3) = ac - ac= 0, x (2) x (3) = pr. Kr- 2bc + bc= 0. Taigi šios matricos savieji vektoriai yra poriniai stačiakampiai.

10 paskaita.

Kvadratinės formos ir jų ryšys su simetrinėmis matricomis. Simetrinės matricos savųjų vektorių ir savųjų reikšmių savybės. Kvadratinės formos redukcija į kanoninę formą.

Apibrėžimas 10.1.Kvadratinė forma realūs kintamieji x 1, x 2, ..., x n yra antrojo laipsnio daugianario šių kintamųjų atžvilgiu, kuriame nėra pirmojo laipsnio laisvojo termino ir terminų.

Kvadratinių formų pavyzdžiai:

(n = 2),

(n = 3). (10.1)

Prisiminkime simetrinės matricos apibrėžimą, pateiktą paskutinėje paskaitoje:

Apibrėžimas 10.2. Kvadratinė matrica vadinama simetriškas, jei, tai yra, jei pagrindinei įstrižainei simetriški matricos elementai yra lygūs.

Simetrinės matricos savųjų reikšmių ir savųjų vektorių savybės:

1) Visos simetrinės matricos savosios reikšmės yra tikros.

Įrodymas (dėl n = 2).

Tegul matrica A atrodo kaip: ... Sudarykime charakteristikų lygtį:

(10.2) Raskite diskriminantą:

Todėl lygtis turi tik realias šaknis.

2) Simetrinės matricos savieji vektoriai yra stačiakampiai.

Įrodymas (dėl n= 2).

Savųjų vektorių koordinatės ir turi tenkinti lygtis.

Su matrica A, jei yra toks skaičius l, kad AX = lX.

Be to, vadinamas skaičius l savo prasmę operatorius (matrica A), atitinkantis vektorių X.

Kitaip tariant, savasis vektorius yra vektorius, kuris, veikiant tiesiniam operatoriui, virsta kolineariniu vektoriumi, t.y. tiesiog padauginta iš kažkokio skaičiaus. Priešingai, netinkamus vektorius yra sunkiau transformuoti.

Parašykime savojo vektoriaus apibrėžimą lygčių sistemos forma:

Perkelkite visus terminus į kairę pusę:

Pastaroji sistema gali būti parašyta matricos forma taip:

(A – lE) X = O

Gautoje sistemoje visada yra nulinis sprendimas X = O. Tokios sistemos, kuriose visi laisvieji nariai lygūs nuliui, vadinamos vienalytis... Jei tokios sistemos matrica yra kvadratinė, o jos determinantas nėra lygus nuliui, tai naudojant Cramerio formules visada gauname unikalų sprendimą – nulį. Galima įrodyti, kad sistema turi nulinius sprendinius tada ir tik tada, kai šios matricos determinantas yra lygus nuliui, t.y.

| A – LE | = = 0

Ši lygtis su nežinomu l vadinama charakteristikos lygtis (būdingas daugianario) matricos A (tiesinis operatorius).

Galima parodyti, kad tiesinio operatoriaus charakteringasis polinomas nepriklauso nuo pagrindo pasirinkimo.

Pavyzdžiui, suraskime tiesinio operatoriaus savąsias reikšmes ir savuosius vektorius, pateiktus matrica A =.

Tam sudarome charakteristikų lygtį | A - lЕ | = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; savosios reikšmės l 1 = (2 - 12) / 2 = -5; l 2 = (2 + 12) / 2 = 7.

Norėdami rasti savuosius vektorius, išsprendžiame dvi lygčių sistemas

(A + 5E) X = O

(A – 7E) X = O

Pirmajam iš jų išsiplėtusi matrica įgauna formą

,

iš kur x 2 = c, x 1 + (2/3) c = 0; x 1 = - (2/3) s, t.y. X (1) = (- (2/3) s; s).

Antrajam iš jų išsiplėtusi matrica įgauna formą

,

iš kur x 2 = c 1, x 1 - (2/3) c 1 = 0; x 1 = (2/3) s 1, t.y. X (2) = ((2/3) s 1; s 1).

Taigi šio tiesinio operatoriaus savieji vektoriai yra visi formos (- (2/3) с; с) vektoriai, kurių savoji reikšmė (-5), ir visi formos vektoriai ((2/3) с 1; с 1) su savąja reikšme 7...

Galima įrodyti, kad operatoriaus A matrica bazėje, kurią sudaro jo savieji vektoriai, yra įstrižainė ir turi tokią formą:

,

kur l i yra šios matricos savosios reikšmės.

Taip pat yra atvirkščiai: jei matrica A kokiame nors pagrinde yra įstrižainė, tai visi šio pagrindo vektoriai bus šios matricos savieji vektoriai.

Taip pat galima įrodyti, kad jei tiesinis operatorius turi n porų skirtingų savųjų reikšmių, tai atitinkami savieji vektoriai yra tiesiškai nepriklausomi, o šio operatoriaus matrica atitinkamame pagrinde turi įstrižainę.

Paaiškinkime tai ankstesniu pavyzdžiu. Imame savavališkas nulines reikšmes с ir с 1, bet tokias, kad vektoriai X (1) ir X (2) būtų tiesiškai nepriklausomi, t.y. sudarytų pagrindą. Pavyzdžiui, tegul c = c 1 = 3, tada X (1) = (-2; 3), X (2) = (2; 3).

Patikrinkime šių vektorių tiesinę nepriklausomybę:

12 ≠ 0. Šiame naujame pagrinde matrica A įgis A * = formą.

Norėdami tai patikrinti, naudojame formulę A * = C -1 AC. Pirmiausia randame C -1.

С -1 = ;

Kvadratinės formos

Kvadratinė forma n kintamųjų f (x 1, x 2, xn) vadinama suma, kurios kiekvienas narys yra arba vieno iš kintamųjų kvadratas, arba dviejų skirtingų kintamųjų sandauga, paimta su tam tikru koeficientu: f (x 1) , x 2, xn) = (a ij = a ji).

Iš šių koeficientų sudaryta matrica A vadinama matrica kvadratine forma. Tai visada simetriškas matrica (t. y. matrica, simetriška pagrindinei įstrižainei, a ij = a ji).

Matricos žymėjime kvadratinė forma yra f (X) = X T AX, kur

Iš tikrųjų

Pavyzdžiui, kvadratinę formą parašykime matricos forma.

Norėdami tai padaryti, randame kvadratinės formos matricą. Jo įstrižainės elementai lygūs kintamųjų kvadratų koeficientams, o likę elementai lygūs pusei atitinkamų kvadratinės formos koeficientų. Štai kodėl

Tegu kintamųjų X matrica-stulpelis gaunamas nedegeneruota tiesine matricos-stulpelio Y transformacija, t.y. X = CY, kur С yra neišsigimusi n eilės matrica. Tada kvadratinė forma f (X) = X T AX = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y.

Taigi su neišsigimusia tiesine transformacija C kvadratinės formos matrica įgauna tokią formą: A * = C T AC.

Pavyzdžiui, suraskime kvadratinę formą f (y 1, y 2), gautą iš kvadratinės formos f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 tiesine transformacija.

Kvadratinė forma vadinama kanoninis(Tai turi kanoninis požiūris), jei visi jo koeficientai a ij = 0, kai i ≠ j, tai yra,
f (x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Jo matrica yra įstrižainė.

Teorema(čia nepateikta jokių įrodymų). Bet kuri kvadratinė forma gali būti sumažinta iki kanoninės formos, naudojant neišsigimusią tiesinę transformaciją.

Pavyzdžiui, į kanoninę formą įtraukiame kvadratinę formą
f (x 1, x 2, x 3) = 2 x 1 2 + 4 x 1 x 2 - 3 x 2 2 - x 2 x 3.

Norėdami tai padaryti, pirmiausia pasirinkite visą kvadratą su kintamuoju x 1:

f (x 1, x 2, x 3) = 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2 (x 1 + x 2) 2 - 5 x 2 2 - x 2 x 3.

Dabar pasirenkame visą kvadratą su kintamuoju x 2:

f (x 1, x 2, x 3) = 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 =
= 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Tada neišsigimusi tiesinė transformacija y 1 = x 1 + x 2, y 2 = x 2 + (1/10) x 3 ir y 3 = x 3 sumažina šią kvadratinę formą iki kanoninės formos f (y 1, y 2 , y 3) = 2y 1 2 - 5y 2 2 + (1/20) y 3 2.

Atkreipkite dėmesį, kad kvadratinės formos kanoninė forma nustatoma dviprasmiškai (viena ir ta pati kvadratinė forma gali būti įvairiai redukuojama į kanoninę formą). Tačiau įvairiais būdais gautos kanoninės formos turi nemažai bendrų savybių. Visų pirma, terminų, turinčių teigiamus (neigiamus) kvadratinės formos koeficientus, skaičius nepriklauso nuo formos sumažinimo iki šios formos metodo (pavyzdžiui, nagrinėjamame pavyzdyje visada bus du neigiami ir vienas teigiamas koeficientas). . Ši savybė vadinama kvadratinių formų inercijos dėsniu.

Patikriname tai redukuodami tą pačią kvadratinę formą į kanoninę formą kitu būdu. Pradėkime transformaciją nuo kintamojo x 2:

f (x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3 (x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 – (2/3) x 1) 2 + 2x 1 2 =
= -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 = f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, kur y 1 = - (2/3) x 1 + x 2 + (1/6) x 3, y 2 = (2/3) x 1 + (1/6) x 3 ir y 3 = x 1. Čia neigiamas koeficientas -3 y 1 ir du teigiami koeficientai 3 ir 2 y 2 ir y 3 (ir naudojant kitą metodą, gavome neigiamą koeficientą (-5) y 2 ir du teigiamus: 2, kai y 1 ir 1/20 už 3 m.).

Taip pat pažymėtina, kad kvadratinės formos matricos rangas, vadinamas kvadratinės formos rangas, yra lygus kanoninės formos nulinių koeficientų skaičiui ir nesikeičia atliekant tiesines transformacijas.

Vadinama kvadratinė forma f (X). teigiamai (neigiamai) tam tikras jei visoms kintamųjų reikšmėms, kurios vienu metu nėra lygios nuliui, jis yra teigiamas, t.y. f (X)> 0 (neigiamas, t.y.
f (X)< 0).

Pavyzdžiui, kvadratinė forma f 1 (X) = x 1 2 + x 2 2 yra teigiama apibrėžtoji, nes yra kvadratų suma, o kvadratinė forma f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 yra neigiama apibrėžtoji, nes reiškia, kad jis gali būti pavaizduotas kaip f 2 (X) = - (x 1 - x 2) 2.

Daugumoje praktinių situacijų kvadratinės formos apibrėžtumą nustatyti yra kiek sunkiau, todėl tam naudojama viena iš šių teoremų (jas formuluosime be įrodymų).

Teorema... Kvadratinė forma yra teigiama (neigiama) apibrėžta tada ir tik tada, kai visos jos matricos savosios reikšmės yra teigiamos (neigiamos).

Teorema(Sylvesterio kriterijus). Kvadratinė forma yra teigiama apibrėžta tada ir tik tada, kai visos pagrindinės šios formos matricos minorinės yra teigiamos.

Didysis (kampinis) minoras N-osios eilės matricos A k-oji eilė vadinama matricos determinantu, sudaryta iš pirmųjų k matricos A () eilučių ir stulpelių.

Atkreipkite dėmesį, kad neigiamose apibrėžtinėse kvadratinėse formose didžiųjų minorų ženklai kaitaliojasi, o pirmosios eilės minorinis turi būti neigiamas.

Pavyzdžiui, panagrinėkime kvadratinę formą f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 ženklų apibrėžtumui.

= (2 - l) *
* (3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
... Todėl kvadratinė forma yra teigiama apibrėžta.

2 metodas. Matricos pirmosios eilės pagrindinis minoras А D 1 = a 11 = 2> 0. Antrosios eilės pagrindinis minoras D 2 = = 6 - 4 = 2> 0. Todėl pagal Sylvesterio kriterijų, 2010 m. kvadratinė forma yra teigiama apibrėžtoji.

Išnagrinėkime kitą kvadratinę ženklo apibrėžtumo formą, f (x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

1 būdas. Sukurkime kvadratinės formos A = matricą. Būdingoji lygtis turės formą = (-2 - l) *
* (- 3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
... Todėl kvadratinė forma yra neigiama apibrėžta.

2 metodas. Matricos pirmosios eilės pagrindinis minoras A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Todėl pagal Sylvesterio kriterijų kvadratinė forma yra neigiama apibrėžtoji (didžiųjų minorų ženklai kaitaliojasi, pradedant minusu).

Ir kaip kitą pavyzdį panagrinėkime kvadratinę formą f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 ženklų apibrėžtumui.

1 būdas. Sukurkime kvadratinės formos A = matricą. Būdingoji lygtis turės formą = (2 - l) *
* (- 3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Vienas iš šių skaičių yra neigiamas, o kitas – teigiamas. Savųjų reikšmių ženklai yra skirtingi. Vadinasi, kvadratinė forma negali būti nei neigiama, nei teigiama apibrėžtoji, t.y. ši kvadratinė forma nėra apibrėžta (ji gali turėti bet kurio ženklo reikšmes).

2 metodas. Matricos pirmos eilės pagrindinė mažoji A D 1 = a 11 = 2> 0. Antrosios eilės mažoji D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

Įstrižainės matricos yra pačios paprasčiausios. Kyla klausimas, ar įmanoma rasti pagrindą, kuriame tiesinio operatoriaus matrica turėtų įstrižainę. Toks pagrindas yra.
Tegu duota tiesinė erdvė R n ir joje veikiantis tiesinis operatorius A; šiuo atveju operatorius A paima R n į save, tai yra A: R n → R n.

Apibrėžimas. Nenulinis vektorius vadinamas savuoju operatoriaus A vektoriumi, jei operatorius A transformuojasi į vektorių, kuris yra jam kolineariai, ty. Skaičius λ vadinamas operatoriaus A savąja reikšme arba savąja reikšme, atitinkančia savąjį vektorių.
Atkreipkime dėmesį į kai kurias savųjų reikšmių ir savųjų vektorių savybes.
1. Bet koks tiesinis savųjų vektorių derinys operatoriaus A, atitinkančio tą pačią savąją reikšmę, λ yra savasis vektorius, turintis tą pačią savąją reikšmę.
2. Savotieji vektoriai operatoriaus A su poromis skirtingomis savybėmis λ 1, λ 2,…, λ m yra tiesiškai nepriklausomos.
3. Jei savosios reikšmės λ 1 = λ 2 = λ m = λ, tai savoji reikšmė λ atitinka daugiausia m tiesiškai nepriklausomų savųjų vektorių.

Taigi, jei yra n tiesiškai nepriklausomų savųjų vektorių atitinkančias skirtingas savąsias reikšmes λ 1, λ 2,…, λ n, tada jos yra tiesiškai nepriklausomos, todėl jas galima laikyti erdvės R n pagrindu. Raskime tiesinio operatoriaus A matricos formą jo savųjų vektorių pagrindu, kuriai operatoriaus A veikiame baziniais vektoriais: tada .
Taigi tiesinio operatoriaus A matrica, pagrįsta jos savaisiais vektoriais, turi įstrižainę, o operatoriaus A savosios reikšmės yra įstrižainėje.
Ar yra kitas pagrindas, kuriame matrica yra įstriža? Atsakymą į šį klausimą duoda tokia teorema.

Teorema. Tiesinio operatoriaus A matrica bazėje (i = 1..n) turi įstrižainę tada ir tik tada, kai visi pagrindo vektoriai yra operatoriaus A savieji vektoriai.

Taisyklė, kaip rasti savąsias reikšmes ir savuosius vektorius

Tegu pateikiamas vektorius , kur x 1, x 2, ..., x n yra vektoriaus koordinatės pagrindo atžvilgiu ir yra tiesinio operatoriaus A savasis vektorius, atitinkantis savąją reikšmę λ, tai yra. Šis ryšys gali būti parašytas matricos forma

. (*)

Lygtį (*) galima laikyti lygtimi ieškant, be to, tai yra, mus domina netrivialūs sprendiniai, nes savasis vektorius negali būti lygus nuliui. Yra žinoma, kad netrivialūs vienalytės tiesinių lygčių sistemos sprendiniai egzistuoja tada ir tik tada, kai det (A - λE) = 0. Taigi, kad λ būtų operatoriaus A savoji reikšmė, būtina ir pakanka, kad det (A - λE) = 0.
Jei lygtis (*) parašyta išsamiai koordinačių forma, tada gauname tiesinių vienalyčių lygčių sistemą:

(1)
kur yra tiesinio operatoriaus matrica.

Sistema (1) turi nulinį sprendinį, jei jos determinantas D yra lygus nuliui

Gauta lygtis savųjų reikšmių paieškai.
Ši lygtis vadinama charakteringąja lygtimi, o kairioji jos pusė vadinama charakteringuoju matricos (operatoriaus) polinomu. Jei charakteringasis daugianomas neturi realių šaknų, tai matrica A neturi savųjų vektorių ir negali būti redukuojama į įstrižainę formą. .
Tegul λ 1, λ 2,…, λ n yra tikrosios charakteristikos lygties šaknys, tarp jų gali būti kelios šaknys. Pakeitę šias reikšmes į sistemą (1), randame savuosius vektorius.

12 pavyzdys. Tiesinis operatorius A veikia R 3 pagal dėsnį, kur x 1, x 2, .., x n yra pagrindo vektoriaus koordinatės , , ... Raskite šio operatoriaus savąsias reikšmes ir savuosius vektorius.
Sprendimas. Sukuriame šio operatoriaus matricą:
.
Sudarome savųjų vektorių koordinačių nustatymo sistemą:

Sudarome charakteringą lygtį ir ją išsprendžiame:

.
λ 1,2 = -1, λ 3 = 3.
Sistemoje pakeitę λ = -1, gauname:
arba
Nes , tada yra du priklausomi kintamieji ir vienas laisvasis kintamasis.
Tada tegul x 1 yra laisvas nežinomasis Šią sistemą išsprendžiame bet kokiu būdu ir randame bendrą šios sistemos sprendimą: Pagrindinė sprendinių sistema susideda iš vieno sprendinio, nes n - r = 3 - 2 = 1.
Savųjų vektorių aibė, atitinkanti savąją reikšmę λ = -1, turi formą:, kur x 1 yra bet koks skaičius, kuris nėra nulis. Pasirinkime vieną vektorių iš šios aibės, pavyzdžiui, įvesdami x 1 = 1: .
Panašiai argumentuodami randame savąjį vektorių, atitinkantį savąją reikšmę λ = 3: .
Erdvėje R 3 pagrindas susideda iš trijų tiesiškai nepriklausomų vektorių, bet mes gavome tik du tiesiškai nepriklausomus savuosius vektorius, iš kurių negalima sudaryti pagrindo R 3. Vadinasi, tiesinio operatoriaus matrica A negali būti redukuota į įstrižainę.

13 pavyzdys. Duota matrica .
1. Įrodykite, kad vektorius yra matricos A savasis vektorius. Raskite šį savąjį vektorių atitinkančią savąją reikšmę.
2. Raskite pagrindą, kuriame matrica A turi įstrižainę.
Sprendimas.
1. Jei, tada - savasis vektorius

.
Vektorius (1, 8, -1) yra savasis vektorius. Savoji reikšmė λ = -1.
Matrica turi įstrižainę formą, kurią sudaro savieji vektoriai. Vienas iš jų yra žinomas. Suraskime likusius.
Mes ieškome savųjų vektorių iš sistemos:

Charakteristinė lygtis: ;
(3 + λ) [- 2 (2-λ) (2 + λ) +3] = 0; (3 + λ) (λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Raskime savąjį vektorių, atitinkantį savąją reikšmę λ = -3:

Šios sistemos matricos rangas yra lygus dviem ir yra lygus nežinomųjų skaičiui, todėl ši sistema turi tik nulinį sprendinį x 1 = x 3 = 0. x 2 čia gali būti bet koks nulis, pavyzdžiui, x 2 = 1. Taigi vektorius (0 , 1,0) yra savasis vektorius, atitinkantis λ = -3. Patikrinkime:
.
Jei λ = 1, tada gauname sistemą
Matricos rangas yra du. Išbraukiame paskutinę lygtį.
Tegul x 3 yra laisvas nežinomasis. Tada x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Nustačius x 3 = 1, gauname (-3, -9,1) - savąjį vektorių, atitinkantį savąją reikšmę λ = 1. Patikrinimas:

.
Kadangi savosios reikšmės yra tikrosios ir skirtingos, jas atitinkantys vektoriai yra tiesiškai nepriklausomi, todėl juos galima paimti kaip pagrindą R 3. Taigi, pagrinde , , A matrica turi tokią formą:
.
Ne kiekviena tiesinio operatoriaus A matrica: R n → R n gali būti redukuojama į įstrižainę, nes kai kuriems tiesiniams operatoriams tiesiškai nepriklausomi savieji vektoriai gali būti mažesni už n. Tačiau, jei matrica yra simetriška, tada lygiai m tiesiškai nepriklausomų vektorių atitinka būdingos daugumos m lygties šaknį.

Apibrėžimas. Simetrinė matrica yra kvadratinė matrica, kurioje pagrindinės įstrižainės atžvilgiu simetriški elementai yra lygūs, tai yra, kurioje.
Pastabos. 1. Visos simetrinės matricos savosios reikšmės yra tikros.
2. Simetrinės matricos savieji vektoriai, atitinkantys poromis skirtingas savąsias reikšmes, yra ortogonalūs.
Kaip vieną iš daugelio tiriamo aparato pritaikymo būdų, panagrinėkime antros eilės kreivės formos nustatymo problemą.