اندازه گیری واریانس کل واریانس و انحراف معیار

پراکندگی یک متغیر تصادفی معیاری برای اندازه گیری پراکندگی مقادیر این متغیر است. واریانس کوچک به این معنی است که مقادیر نزدیک به یکدیگر دسته بندی شده اند. واریانس بزرگ نشان دهنده پراکندگی شدید مقادیر است. مفهوم پراکندگی یک متغیر تصادفی در آمار استفاده می شود. به عنوان مثال، اگر واریانس مقادیر دو کمیت (مانند نتایج مشاهدات بیماران زن و مرد) را با هم مقایسه کنید، می توانید اهمیت برخی از متغیرها را آزمایش کنید. واریانس هنگام ساخت مدل‌های آماری نیز استفاده می‌شود، زیرا واریانس کوچک می‌تواند نشانه‌ای از تطبیق بیش از حد مقادیر باشد.

مراحل

محاسبه واریانس نمونه

1. مقادیر نمونه را ثبت کنید.در بیشتر موارد، فقط نمونه هایی از جمعیت های خاص در دسترس آماردانان است. به عنوان مثال، به عنوان یک قاعده، آماردانان هزینه نگهداری جمعیت همه خودروها در روسیه را تجزیه و تحلیل نمی کنند - آنها نمونه تصادفی چند هزار خودرو را تجزیه و تحلیل می کنند. چنین نمونه ای به تعیین میانگین هزینه برای هر خودرو کمک می کند، اما به احتمال زیاد، مقدار حاصل از مقدار واقعی بسیار دور خواهد بود.

   • به عنوان مثال، بیایید تعداد نان های فروخته شده در یک کافه در 6 روز را به ترتیب تصادفی تجزیه و تحلیل کنیم. نمونه به شکل زیر است: 17، 15، 23، 7، 9، 13. این یک نمونه است، نه یک جمعیت، زیرا ما اطلاعاتی در مورد نان های فروخته شده برای هر روز باز بودن کافه نداریم.
   • اگر به شما یک جامعه داده می شود و نه نمونه ای از مقادیر، به بخش بعدی بروید.

2. فرمول محاسبه واریانس نمونه را بنویسید.پراکندگی معیاری برای گسترش مقادیر یک مقدار است. هر چه مقدار پراکندگی به صفر نزدیک‌تر باشد، مقادیر نزدیک‌تر به هم گروه‌بندی می‌شوند. هنگام کار با نمونه ای از مقادیر، از فرمول زیر برای محاسبه واریانس استفاده کنید:

   • s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))-ایکس) 2 (\displaystyle ^(2))] / (n - 1)
   • s 2 (\displaystyle s^(2))پراکندگی است. پراکندگی در اندازه گیری می شود واحدهای مربعیاندازه گیری ها
   • x i (\displaystyle x_(i))- هر مقدار در نمونه
   • x i (\displaystyle x_(i))باید x را کم کنید، مربع آن را بگیرید و سپس نتایج را اضافه کنید.
   • x̅ – میانگین نمونه (میانگین نمونه).
   • n تعداد مقادیر موجود در نمونه است.

3. میانگین نمونه را محاسبه کنید.به صورت x نشان داده می شود. میانگین نمونه مانند یک میانگین حسابی معمولی محاسبه می شود: تمام مقادیر موجود در نمونه را جمع کنید و سپس نتیجه را بر تعداد مقادیر موجود در نمونه تقسیم کنید.

   • در مثال ما، مقادیر موجود در نمونه را اضافه کنید: 15 + 17 + 23 + 7 + 9 + 13 = 84
     اکنون نتیجه را بر تعداد مقادیر موجود در نمونه تقسیم کنید (در مثال ما 6 عدد وجود دارد): 84 ÷ 6 = 14.
     میانگین نمونه x = 14.
   • میانگین نمونه مقدار مرکزی است که مقادیر موجود در نمونه حول آن توزیع می شود. اگر مقادیر در خوشه نمونه در اطراف نمونه میانگین باشد، واریانس کوچک است. در غیر این صورت، پراکندگی بزرگ است.

4. میانگین نمونه را از هر مقدار در نمونه کم کنید.حالا تفاوت را محاسبه کنید x i (\displaystyle x_(i))- x̅، کجا x i (\displaystyle x_(i))- هر مقدار در نمونه هر نتیجه به دست آمده نشان دهنده میزان انحراف یک مقدار خاص از میانگین نمونه است، یعنی اینکه این مقدار چقدر از میانگین نمونه فاصله دارد.

   • در مثال ما:
     x 1 (\displaystyle x_(1))- x = 17 - 14 = 3
     x 2 (\displaystyle x_(2))- x = 15 - 14 = 1
     x 3 (\displaystyle x_(3))- x = 23 - 14 = 9
     x 4 (\displaystyle x_(4))- x = 7 - 14 = -7
     x 5 (\displaystyle x_(5))- x = 9 - 14 = -5
     x 6 (\displaystyle x_(6))- x = 13 - 14 = -1
   • صحت نتایج به دست آمده به راحتی قابل بررسی است، زیرا مجموع آنها باید برابر با صفر باشد. این به تعیین مقدار متوسط ​​مربوط می شود، زیرا مقادیر منفی (فاصله از مقدار متوسط ​​تا مقادیر کوچکتر) کاملاً با مقادیر مثبت (فاصله از مقدار متوسط ​​تا مقادیر بزرگتر) جبران می شود.

5. همانطور که در بالا ذکر شد، مجموع تفاوت ها x i (\displaystyle x_(i))- x̅ باید برابر با صفر باشد. این به آن معنا است واریانس متوسطهمیشه برابر با صفر است، که هیچ ایده ای در مورد گسترش مقادیر یک مقدار مشخص نمی دهد. برای حل این مشکل، هر تفاوت را مربع کنید x i (\displaystyle x_(i))- ایکس. این باعث می شود که شما فقط اعداد مثبتی دریافت کنید که وقتی با هم جمع شوند، هرگز به 0 نمی رسند.

   • در مثال ما:
     (x 1 (\displaystyle x_(1))-ایکس) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
     (x 2 (\displaystyle (x_(2))-ایکس) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
     9 2 = 81
     (-7) 2 = 49
     (-5) 2 = 25
     (-1) 2 = 1
   • شما مربع تفاوت را پیدا کرده اید - x̅) 2 (\displaystyle ^(2))برای هر مقدار در نمونه

6. مجموع مجذور تفاوت ها را محاسبه کنید.یعنی بخشی از فرمول را که به این صورت نوشته شده است پیدا کنید: ∑[( x i (\displaystyle x_(i))-ایکس) 2 (\displaystyle ^(2))]. در اینجا علامت Σ به معنای مجموع مجذور اختلافات برای هر مقدار است x i (\displaystyle x_(i))در نمونه شما قبلاً تفاوت های مربعی را پیدا کرده اید (x i (\displaystyle (x_(i))-ایکس) 2 (\displaystyle ^(2))برای هر مقدار x i (\displaystyle x_(i))در نمونه؛ حالا فقط این مربع ها را اضافه کنید.

   • در مثال ما: 9 + 1 + 81 + 49 + 25 + 1 = 166 .

7. نتیجه را بر n - 1 تقسیم کنید، جایی که n تعداد مقادیر موجود در نمونه است.مدتی پیش، برای محاسبه واریانس نمونه، آماردانان به سادگی نتیجه را بر n تقسیم کردند. در این حالت، میانگین واریانس مجذور را دریافت خواهید کرد که برای توصیف واریانس یک نمونه معین ایده آل است. اما به یاد داشته باشید که هر نمونه تنها بخش کوچکی از جمعیت عمومی مقادیر است. اگر نمونه متفاوتی بگیرید و محاسبات مشابهی را انجام دهید، نتیجه متفاوتی خواهید گرفت. همانطور که مشخص است، تقسیم بر n - 1 (به جای فقط n) تخمین بهتری از واریانس جمعیت می دهد، که همان چیزی است که شما دنبال آن هستید. تقسیم بر n - 1 امری عادی شده است، بنابراین در فرمول محاسبه واریانس نمونه گنجانده شده است.

   • در مثال ما، نمونه شامل 6 مقدار است، یعنی n = 6.
     واریانس نمونه = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2

8. تفاوت بین واریانس و انحراف معیار.توجه داشته باشید که فرمول حاوی یک توان است، بنابراین واریانس برحسب واحد مربع مقدار تحلیل شده اندازه گیری می شود. گاهی اوقات عملکرد چنین مقداری بسیار دشوار است. در چنین مواردی از انحراف معیار استفاده می شود که برابر با جذر واریانس است. به همین دلیل است که واریانس نمونه به صورت مشخص شده است s 2 (\displaystyle s^(2))، ولی انحراف معیارنمونه ها - چگونه s (\displaystyle s).

   • در مثال ما، انحراف استاندارد نمونه این است: s = √33.2 = 5.76.

   محاسبه واریانس جمعیت

   1. مجموعه ای از ارزش ها را تجزیه و تحلیل کنید.مجموعه شامل تمام مقادیر مقدار مورد نظر است. مثلاً اگر سن ساکنین را مطالعه کنید منطقه لنینگراد، سپس جمعیت شامل سن همه ساکنان این منطقه می شود. در مورد کار با یک دانه، توصیه می شود یک جدول ایجاد کنید و مقادیر کل را در آن وارد کنید. به مثال زیر توجه کنید:

      • در یک اتاق خاص 6 آکواریوم وجود دارد. هر آکواریوم حاوی تعداد ماهی زیر است:
        x 1 = 5 (\displaystyle x_(1)=5)
        x 2 = 5 (\displaystyle x_(2)=5)
        x 3 = 8 (\displaystyle x_(3)=8)
        x 4 = 12 (\displaystyle x_(4)=12)
        x 5 = 15 (\displaystyle x_(5)=15)
        x 6 = 18 (\displaystyle x_(6)=18)

   2. فرمول محاسبه واریانس جمعیت را بنویسید.از آنجایی که مجموعه شامل تمام مقادیر یک مقدار مشخص است، فرمول زیر به شما اجازه می دهد تا دریافت کنید ارزش دقیقواریانس جمعیت برای تشخیص واریانس جامعه از واریانس نمونه (که فقط یک تخمین است)، آماردانان از متغیرهای مختلفی استفاده می کنند:

      • σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n
      • σ 2 (\displaystyle ^(2))- واریانس جمعیت (خوانده شده به عنوان "سیگما مربع"). پراکندگی بر حسب واحد مربع اندازه گیری می شود.
      • x i (\displaystyle x_(i))- هر مقدار در مجموع.
      • Σ علامت جمع است. یعنی برای هر مقدار x i (\displaystyle x_(i))μ را تفریق کرده، آن را مربع کنید و سپس نتایج را اضافه کنید.
      • μ میانگین جمعیت است.
      • n تعداد مقادیر در جمعیت عمومی است.

   3. میانگین جمعیت را محاسبه کنید.هنگام کار با جمعیت عمومی، مقدار متوسط ​​آن به عنوان μ (mu) نشان داده می شود. میانگین جمعیت به عنوان میانگین حسابی معمول محاسبه می شود: تمام مقادیر موجود در جامعه را جمع کنید و سپس نتیجه را بر تعداد مقادیر موجود در جامعه تقسیم کنید.

      • به خاطر داشته باشید که میانگین ها همیشه به عنوان میانگین حسابی محاسبه نمی شوند.
      • در مثال ما، میانگین جمعیت: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5

   4. میانگین جمعیت را از هر مقدار در جامعه کم کنید.هر چه مقدار تفاوت به صفر نزدیکتر باشد، مقدار خاص به میانگین جمعیت نزدیکتر است. تفاوت بین هر مقدار در جامعه و میانگین آن را پیدا کنید، و اولین نگاهی به توزیع مقادیر خواهید داشت.

      • در مثال ما:
        x 1 (\displaystyle x_(1))- μ = 5 - 10.5 = -5.5
        x 2 (\displaystyle x_(2))- μ = 5 - 10.5 = -5.5
        x 3 (\displaystyle x_(3))- μ = 8 - 10.5 = -2.5
        x 4 (\displaystyle x_(4))- μ = 12 - 10.5 = 1.5
        x 5 (\displaystyle x_(5))- μ = 15 - 10.5 = 4.5
        x 6 (\displaystyle x_(6))- μ = 18 - 10.5 = 7.5

   5. هر نتیجه ای را که می گیرید مربع کنید.مقادیر تفاوت هم مثبت و هم منفی خواهد بود. اگر این مقادیر را روی یک خط عددی قرار دهید، در سمت راست و چپ میانگین جمعیت قرار می گیرند. این برای محاسبه واریانس خوب نیست، زیرا اعداد مثبت و منفی یکدیگر را خنثی می کنند. بنابراین، هر اختلاف را مربع کنید تا اعداد منحصراً مثبت به دست آورید.

      • در مثال ما:
        (x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))برای هر مقدار جمعیت (از i = 1 تا i = 6):
        (-5,5)2 (\displaystyle ^(2)) = 30,25
        (-5,5)2 (\displaystyle ^(2))، جایی که x n (\displaystyle x_(n))آخرین مقدار در جمعیت است.
      • برای محاسبه میانگین مقدار نتایج به دست آمده، باید مجموع آنها را پیدا کنید و آن را بر n تقسیم کنید: (( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2))) / n
      • حالا بیایید توضیح بالا را با استفاده از متغیرها بنویسیم: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n و فرمولی برای محاسبه واریانس جمعیت بدست آورید.

پراکندگی در آمار به عنوان انحراف استاندارد مقادیر فردی یک صفت مجذور میانگین حسابی تعریف می شود. یک روش معمول برای محاسبه مجذور انحراف گزینه ها از میانگین و سپس میانگین آنها.

در تجزیه و تحلیل اقتصادی و آماری، مرسوم است که تغییرات یک ویژگی را اغلب با استفاده از انحراف معیار، که جذر واریانس است، ارزیابی می‌کنند.

(3)

این نوسان مطلق مقادیر ویژگی متغیر را مشخص می کند و در واحدهای مشابه با انواع بیان می شود. در آمار، اغلب لازم است که تنوع ویژگی های مختلف را با هم مقایسه کنیم. برای چنین مقایسه‌هایی، از یک شاخص نسبی تغییرات، یعنی ضریب تغییرات استفاده می‌شود.

خواص پراکندگی:

1) اگر هر عددی را از همه گزینه ها کم کنید، واریانس تغییر نخواهد کرد.

2) اگر همه مقادیر متغیر بر عدد b تقسیم شوند، واریانس به میزان b^2 برابر کاهش می یابد، یعنی.

3) اگر مجذور میانگین انحرافات از هر عددی را با میانگین حسابی نامساوی محاسبه کنید، از واریانس بیشتر خواهد بود. در این مورد، با یک مقدار خوب تعریف شده در هر مربع از تفاوت بین مقدار متوسط ​​pos.

واریانس را می توان به عنوان تفاوت بین میانگین مربع و میانگین مربع تعریف کرد.

17. تغییرات گروهی و بین گروهی. قانون جمع واریانس

اگر جامعه آماری با توجه به ویژگی مورد مطالعه به گروه ها یا قسمت هایی تقسیم شود، برای چنین جامعه ای می توان انواع پراکندگی زیر را محاسبه کرد: گروهی (خصوصی)، میانگین گروهی (خصوصی) و بین گروهی.

واریانس کل- منعکس کننده تنوع یک صفت به دلیل همه شرایط و علل موجود در یک جامعه آماری معین است.

واریانس گروهی- برابر است با مجذور میانگین انحراف مقادیر فردی صفت درون گروه از میانگین حسابی این گروه که میانگین گروه نامیده می شود. در این حالت میانگین گروه با میانگین کل کل جمعیت منطبق نیست.

واریانس گروهی منعکس کننده تنوع یک صفت تنها به دلیل شرایط و علل فعال در گروه است.

میانگین واریانس های گروهی- به عنوان میانگین حسابی وزنی پراکندگی گروه ها تعریف می شود که وزن ها حجم گروه ها هستند.

واریانس بین گروهی- برابر است با مجذور میانگین انحراف میانگین های گروه از میانگین کل.

واریانس بین گروهی تغییر ویژگی حاصل را به دلیل ویژگی گروه بندی مشخص می کند.

رابطه معینی بین انواع واریانس های در نظر گرفته شده وجود دارد: واریانس کل برابر است با مجموع میانگین گروه و واریانس بین گروهی.

این رابطه قانون جمع واریانس نامیده می شود.

18. سری پویا و عناصر تشکیل دهنده آن. انواع سری های پویا

سری در آمار- اینها داده های دیجیتالی هستند که نشان می دهند آیا یک پدیده در زمان یا مکان تغییر می کند و امکان مقایسه آماری پدیده ها را هم در روند توسعه آنها در زمان و هم در زمان ممکن می کند. اشکال گوناگونو انواع فرآیندها به لطف این، می توان وابستگی متقابل پدیده ها را تشخیص داد.

روند توسعه حرکت پدیده های اجتماعی در زمان را معمولاً پویایی می نامند. برای نمایش پویایی، مجموعه‌ای از دینامیک (زمان‌شناسی، زمانی) ساخته می‌شود که مجموعه‌ای از مقادیر متغیر با زمان یک شاخص آماری (به عنوان مثال، تعداد محکومان بالای 10 سال) هستند که به ترتیب زمانی مرتب شده‌اند. عناصر تشکیل دهنده آنها مقادیر عددی یک شاخص معین و دوره ها یا نقاط زمانی است که آنها به آنها اشاره می کنند.

مهمترین ویژگی سری های زمانی- اندازه آنها (حجم، ارزش) این یا آن پدیده، در یک دوره خاص یا در یک لحظه خاص به دست آمده است. بر این اساس، بزرگی اصطلاحات سری دینامیک سطح آن است. تمیز دادنسطوح اولیه، میانی و نهایی سری پویا. سطح اولارزش اولین، نهایی - ارزش آخرین عضو سری را نشان می دهد. سطح متوسطمیانگین دامنه تغییرات زمانی را نشان می دهد و بسته به اینکه سری زمانی بازه ای یا لحظه ای باشد محاسبه می شود.

یکی دیگر از ویژگی های مهم سری پویا- زمان سپری شده از مشاهده اولیه تا نهایی یا تعداد این مشاهدات.

سری های زمانی انواع مختلفی دارند که می توان آنها را بر اساس معیارهای زیر طبقه بندی کرد.

1) بسته به نحوه بیان سطوح، سری های دینامیک به سری شاخص های مطلق و مشتق (مقادیر نسبی و متوسط) تقسیم می شوند.

2) بسته به نحوه بیان سطوح سریال وضعیت پدیده را در مقاطع زمانی معین (در ابتدای ماه، سه ماهه، سال و غیره) یا مقدار آن برای بازه های زمانی معین (مثلاً در روز، ماه، سال و غیره) و غیره)، به ترتیب لحظه و سری بازه ایپویایی شناسی. سریال های لحظه ای در کار تحلیلی سازمان های مجری قانون نسبتاً به ندرت استفاده می شود.

در تئوری آمار، دینامیک با توجه به تعدادی از ویژگی های طبقه بندی دیگر نیز متمایز می شود: بسته به فاصله بین سطوح - با سطوح مساوی و سطوح نابرابر در زمان. بسته به وجود روند اصلی فرآیند مورد مطالعه - ثابت و غیر ثابت. هنگام تجزیه و تحلیل سری های پویا، سطوح زیر از سری به عنوان مولفه ارائه می شود:

Y t \u003d TP + E (t)

که در آن TR یک جزء قطعی است که روند کلی تغییر در طول زمان یا یک روند را تعیین می کند.

E (t) یک جزء تصادفی است که باعث نوسانات سطح می شود.

پراکندگیمتغیر تصادفی- اندازه گیری پراکندگی یک داده متغیر تصادفی، یعنی او انحرافاتاز انتظارات ریاضی در آمار، نماد (سیگما مربع) اغلب برای نشان دادن واریانس استفاده می شود. جذر واریانس نامیده می شود انحراف معیاریا پخش استاندارد انحراف استاندارد با واحدهای مشابه اندازه گیری می شود مقدار تصادفی، و واریانس در مربع های آن واحد اندازه گیری می شود.

اگرچه استفاده از تنها یک مقدار (مانند میانگین یا حالت و میانه) برای تخمین کل نمونه بسیار راحت است، اما این رویکرد به راحتی می تواند به نتایج اشتباه منجر شود. دلیل این وضعیت در خود مقدار نیست، بلکه در این واقعیت است که یک مقدار به هیچ وجه منعکس کننده گسترش مقادیر داده نیست.

به عنوان مثال، در نمونه:

میانگین 5 است.

با این حال، هیچ عنصری در خود نمونه با مقدار 5 وجود ندارد. ممکن است لازم باشد بدانید که هر عنصر از نمونه چقدر به مقدار میانگین خود نزدیک است. یا به عبارت دیگر، باید واریانس مقادیر را بدانید. با دانستن میزان تغییر داده ها، می توانید بهتر تفسیر کنید منظور داشتن, میانهو روش. درجه تغییر در مقادیر نمونه با محاسبه واریانس و انحراف معیار آنها تعیین می شود.

پراکندگی و ریشه دوماز واریانس، که انحراف معیار نامیده می شود، میانگین انحراف از میانگین نمونه را مشخص می کند. در میان این دو مقدار بالاترین ارزشاین دارد انحراف معیار. این مقدار را می توان به عنوان فاصله متوسطی که عناصر از عنصر میانی نمونه قرار دارند نشان داد.

تفسیر معنادار پراکندگی دشوار است. با این حال، جذر این مقدار انحراف معیار است و به خوبی به تفسیر کمک می کند.

انحراف معیار ابتدا با تعیین واریانس و سپس محاسبه جذر واریانس محاسبه می شود.

به عنوان مثال، برای آرایه داده نشان داده شده در شکل، مقادیر زیر به دست می آید:

تصویر 1

در اینجا، میانگین اختلاف مجذور 717.43 است. برای به دست آوردن انحراف معیار، فقط باید جذر این عدد را بگیرید.

نتیجه تقریباً 26.78 خواهد بود.

باید به خاطر داشت که انحراف استاندارد به عنوان فاصله متوسطی که عناصر از میانگین نمونه قرار دارند تفسیر می شود.

انحراف معیار نشان می دهد که میانگین چقدر کل نمونه را توصیف می کند.

فرض کنید شما مدیر هستید بخش تولیدمونتاژ کامپیوتر. گزارش سه ماهه می گوید که خروجی در سه ماهه گذشته 2500 رایانه شخصی بوده است. بد است یا خوب؟ شما خواسته اید (یا قبلاً این ستون در گزارش وجود دارد) انحراف استاندارد برای این داده ها در گزارش نمایش داده شود. به عنوان مثال، عدد انحراف استاندارد 2000 است. برای شما به عنوان رئیس بخش مشخص می شود که خط تولید به کنترل بهتری نیاز دارد (انحرافات بسیار زیاد در تعداد رایانه های شخصی در حال مونتاژ).

یادمان باشد: چه زمانی سایز بزرگاگر انحراف معیار خیلی کم باشد، داده ها به طور گسترده در اطراف میانگین پراکنده می شوند و اگر انحراف استاندارد کم باشد، آنها نزدیک به میانگین خوشه بندی می شوند.

چهار تابع آماری VAR()، VAR()، STDEV() و STDEV() برای محاسبه واریانس و انحراف استاندارد اعداد در محدوده ای از سلول ها طراحی شده اند. قبل از اینکه بتوانید واریانس و انحراف معیار یک مجموعه داده را محاسبه کنید، باید تعیین کنید که آیا داده ها نشان دهنده جامعه هستند یا نمونه ای از جامعه. در مورد نمونه ای از جمعیت عمومی، باید از توابع VARP() و STDEV() و در مورد جمعیت عمومی، از توابع VARP() و STDEV() استفاده شود:

جمعیت	تابع
	VARP()
	STDLONG()
نمونه
	VARI()
	STDEV()

پراکندگی (و همچنین انحراف استاندارد)، همانطور که اشاره کردیم، نشان دهنده میزان پراکندگی مقادیر موجود در مجموعه داده ها در اطراف میانگین حسابی است.

مقدار کمی از واریانس یا انحراف معیار نشان می دهد که تمام داده ها حول میانگین حسابی متمرکز شده اند و مقدار زیاد این مقادیر نشان می دهد که داده ها در محدوده وسیعی از مقادیر پراکنده شده اند.

تفسیر معنادار واریانس نسبتاً دشوار است (معنی یک مقدار کوچک، یک مقدار بزرگ چیست؟). کارایی وظایف 3به شما این امکان را می دهد که به صورت بصری، در یک نمودار، معنای واریانس یک مجموعه داده را نشان دهید.

وظایف

· تمرین 1.

· 2.1. مفاهیم: واریانس و انحراف معیار را بیان کنید. نام نمادین آنها در پردازش داده های آماری.

· 2.2. مطابق شکل 1 یک کاربرگ تهیه کنید و محاسبات لازم را انجام دهید.

· 2.3. فرمول های اصلی مورد استفاده در محاسبات را بیان کنید

· 2.4. تمام نمادهای ( , , ) را توضیح دهید

· 2.5. توضیح ارزش عملیمفاهیم واریانس و انحراف معیار

وظیفه 2.

1.1. مفاهیم: جمعیت عمومی و نمونه را بیان کنید. ارزش مورد انتظارو میانگین حسابی آنها در هنگام پردازش داده های آماری تعیین می شود.

1.2. مطابق شکل 2، یک کاربرگ تهیه کنید و محاسبات را انجام دهید.

1.3. فرمول های اساسی مورد استفاده در محاسبات (برای جمعیت عمومی و نمونه) را بیان کنید.

شکل 2

1.4. توضیح دهید که چرا می توان مقادیر میانگین های حسابی را در نمونه هایی مانند 46.43 و 48.78 به دست آورد (به فایل پیوست مراجعه کنید). نتیجه گیری.

وظیفه 3.

دو نمونه با مجموعه متفاوتداده ها، اما میانگین آنها یکسان خواهد بود:

شکل 3

3.1. مطابق شکل 3 یک کاربرگ تهیه کرده و محاسبات لازم را انجام دهید.

3.2. فرمول های اصلی محاسبات را ارائه دهید.

3.3. نمودارها را مطابق شکل های 4 و 5 بسازید.

3.4. وابستگی های حاصل را توضیح دهید.

3.5. محاسبات مشابهی را برای این دو نمونه انجام دهید.

نمونه اولیه 11119999

مقادیر نمونه دوم را طوری انتخاب کنید که میانگین حسابی نمونه دوم یکسان باشد، به عنوان مثال:

مقادیر نمونه دوم را خودتان انتخاب کنید. محاسبات را مرتب کنید و مانند شکل های 3، 4، 5 ترسیم کنید. فرمول های اصلی را که در محاسبات استفاده شده است نشان دهید.

نتیجه گیری مناسب را انجام دهید.

کلیه وظایف باید در قالب یک گزارش همراه با تمام شکل ها، نمودارها، فرمول ها و توضیحات مختصر ارائه شود.

نکته: ساخت نمودارها باید با شکل و توضیحات مختصر توضیح داده شود.

برای داده های گروه بندی شده پراکندگی باقی مانده- میانگین پراکندگی درون گروهی:

جایی که σ 2 j واریانس درون گروهی گروه j -ام است.

برای داده های گروه بندی نشده پراکندگی باقی ماندهاندازه گیری دقت تقریبی است، یعنی. تقریب خط رگرسیون به داده های اصلی:
که در آن y(t) پیش بینی مطابق با معادله روند است. y t - سری اولیه دینامیک. n تعداد نقاط است. p تعداد ضرایب معادله رگرسیون (تعداد متغیرهای توضیحی) است.
در این مثال نامیده می شود تخمین بی طرفانه واریانس.

مثال شماره 1. توزیع کارگران سه شرکت از یک انجمن بر اساس دسته های تعرفه با داده های زیر مشخص می شود:

دسته دستمزد کارگر	تعداد کارگران شرکت
	شرکت 1	شرکت 2	شرکت 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

تعريف كردن:
1. پراکندگی برای هر شرکت (پراکندگی درون گروهی).
2. میانگین پراکندگی درون گروهی.
3. پراکندگی بین گروهی.
4. واریانس کل.

راه حل.
قبل از اقدام برای حل مشکل، باید دریابید که کدام ویژگی موثر و کدام فاکتوریل است. در مثال مورد بررسی، ویژگی مؤثر «دسته تعرفه» و ویژگی عامل «تعداد (نام) شرکت» است.
سپس سه گروه (شرکت) داریم که برای آنها باید میانگین گروه و واریانس درون گروهی محاسبه شود:

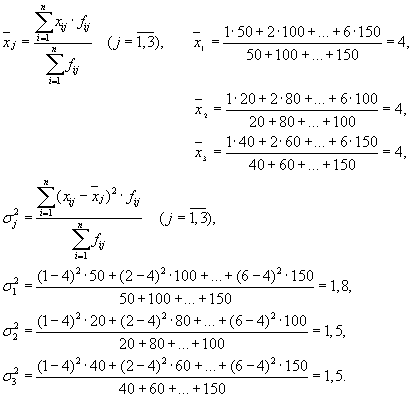
شرکت	میانگین گروهی،	واریانس درون گروهی،
1	4	1,8

میانگین واریانس های درون گروهی ( پراکندگی باقی مانده) با فرمول محاسبه می شود:

جایی که می توانید محاسبه کنید:
یا:

سپس:
پراکندگی کل برابر خواهد بود: s 2 \u003d 1.6 + 0 \u003d 1.6.
واریانس کل را می توان با استفاده از یکی از دو فرمول زیر محاسبه کرد:

هنگام حل مسائل عملی، اغلب باید با علامتی برخورد کرد که فقط دو مقدار جایگزین را می گیرد. در این مورد، آنها در مورد وزن ارزش خاصی از یک ویژگی صحبت نمی کنند، بلکه در مورد سهم آن در کل صحبت می کنند. اگر نسبت واحدهای جمعیتی که دارای صفت مورد مطالعه هستند با " نشان داده شود. آر"، و نه داشتن - از طریق" q"، سپس پراکندگی را می توان با فرمول محاسبه کرد:
s 2 = p×q

مثال شماره 2. با توجه به داده های مربوط به توسعه شش کارگر تیپ، واریانس بین گروهی را تعیین کنید و در صورتی که واریانس کل 12.2 باشد، تأثیر شیفت کاری بر بهره وری کار آنها را ارزیابی کنید.

شماره تیپ کار	خروجی کار، عدد
	در شیفت اول	در شیفت دوم
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

راه حل. اطلاعات اولیه

ایکس	f1	f2	f 3	f4	f5	f6	جمع
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
جمع	31	33	37	37	40	38

سپس 6 گروه داریم که باید میانگین گروهی و واریانس درون گروهی را محاسبه کرد.
1. مقادیر میانگین هر گروه را بیابید.







2. میانگین مربع هر گروه را بیابید.







ما نتایج محاسبات را در یک جدول خلاصه می کنیم:

شماره گروه	میانگین گروه	واریانس درون گروهی
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. واریانس درون گروهیتغییر (تغییر) صفت مورد مطالعه (نتیجه) را در گروه تحت تأثیر همه عوامل به جز عامل زیربنایی گروه بندی مشخص می کند:
میانگین پراکندگی درون گروهی را با استفاده از فرمول محاسبه می کنیم:


4. واریانس بین گروهیتغییر (تغییر) صفت مورد مطالعه (نتیجه) تحت تأثیر یک عامل (ویژگی عاملی) زیربنای گروه بندی را مشخص می کند.
پراکندگی بین گروهی به صورت زیر تعریف می شود:

جایی که


سپس

واریانس کلتغییر (تغییر) صفت مورد مطالعه (نتیجه) را تحت تأثیر همه عوامل (ویژگی های فاکتوری) بدون استثنا مشخص می کند. با شرط مشکل برابر با 12.2 است.
رابطه همبستگی تجربیاندازه گیری می کند که چه مقدار از کل نوسانات صفت حاصل توسط عامل مورد مطالعه ایجاد می شود. این نسبت واریانس فاکتوریل به کل واریانس است:

ما رابطه همبستگی تجربی را تعیین می کنیم:

روابط بین ویژگی ها می تواند ضعیف یا قوی (نزدیک) باشد. معیارهای آنها در مقیاس چادوک ارزیابی می شود:
0.1 0.3 0.5 0.7 0.9 در مثال ما، رابطه بین ویژگی Y عامل X ضعیف است
ضریب تعیین.

بیایید ضریب تعیین را تعریف کنیم:

بنابراین 0.67 درصد از تغییرات به دلیل تفاوت بین صفات و 99.37 درصد به دلیل سایر عوامل است.
خروجی: در این مورد، خروجی کارگران به کار در یک شیفت خاص بستگی ندارد، یعنی. تأثیر شیفت کاری بر بهره وری نیروی کار آنها قابل توجه نبوده و ناشی از عوامل دیگر است.

مثال شماره 3. بر اساس میانگین دستمزدو مجذور انحراف از مقدار آن برای دو گروه از کارگران، واریانس کل را با اعمال قانون برای جمع واریانس ها بیابید:

راه حل:
میانگین واریانس های درون گروهی

پراکندگی بین گروهی به صورت زیر تعریف می شود:


واریانس کل خواهد بود: 480 + 13824 = 14304

اگر جمعیت بر اساس صفت مورد مطالعه به گروه‌هایی تقسیم شود، می‌توان انواع پراکندگی زیر را برای این جمعیت محاسبه کرد: کل، گروه (درون گروه)، میانگین گروه (میانگین درون گروهی)، بین گروهی.

در ابتدا، ضریب تعیین را محاسبه می کند، که نشان می دهد چه بخشی از تغییرات کل صفت مورد مطالعه، تغییرات بین گروهی است، یعنی. به دلیل گروه بندی:

نسبت همبستگی تجربی، تنگی ارتباط بین گروه بندی (عاملی) و نشانه های مؤثر را مشخص می کند.

نسبت همبستگی تجربی می تواند مقادیری از 0 تا 1 داشته باشد.

برای ارزیابی نزدیکی رابطه بر اساس نسبت همبستگی تجربی، می توانید از روابط Chaddock استفاده کنید:

مثال 4داده های زیر در مورد عملکرد کار توسط سازمان های طراحی و بررسی وجود دارد اشکال مختلفویژگی:

تعريف كردن:

1) واریانس کل؛

2) پراکندگی گروهی؛

3) میانگین پراکندگی گروه.

4) پراکندگی بین گروهی؛

5) واریانس کل بر اساس قانون اضافه کردن واریانس ها.

6) ضریب تعیین و همبستگی تجربی.

نتیجه گیری خود را انجام دهید.

راه حل:

1. تعریف کنید حجم متوسطانجام کارهای شرکت های دارای دو شکل مالکیت:

واریانس کل را محاسبه کنید:

2. میانگین گروه را تعریف کنید:

میلیون روبل؛

میلیون روبل

واریانس های گروهی:

;

3. میانگین واریانس گروه را محاسبه کنید:

4. واریانس بین گروهی را تعیین کنید:

5. واریانس کل را بر اساس قانون اضافه کردن واریانس ها محاسبه کنید:

6. ضریب تعیین را تعیین کنید:

.

بنابراین، میزان کار انجام شده توسط سازمان های طراحی و بررسی تا 22 درصد به شکل مالکیت بنگاه ها بستگی دارد.

نسبت همبستگی تجربی با فرمول محاسبه می شود

.

مقدار شاخص محاسبه شده نشان می دهد که وابستگی مقدار کار به شکل مالکیت شرکت کوچک است.

مثال 5در نتیجه بررسی رشته فنی سایت های تولید، داده های زیر به دست آمد:

ضریب تعیین را تعیین کنید