واریانس در مثال های آمار ریاضی. پراکندگی یک متغیر تصادفی گسسته. انحراف معیار
با این حال، این ویژگی به تنهایی برای مطالعه کافی نیست متغیر تصادفی. دو تیرانداز را تصور کنید که به یک هدف شلیک می کنند. یکی با دقت شلیک می کند و نزدیک به مرکز ضربه می زند و دیگری ... فقط سرگرم می شود و حتی هدف نمی گیرد. اما آنچه خنده دار است این است وسطنتیجه دقیقاً مشابه تیرانداز اول خواهد بود! این وضعیت به صورت مشروط با متغیرهای تصادفی زیر نشان داده می شود:
"تک تیرانداز" ارزش مورد انتظاربا این حال، برای "فرد جالب" برابر است: - همچنین صفر است!
بنابراین، نیاز به تعیین کمیت تا کجا وجود دارد پراکندهگلوله ها (مقادیر یک متغیر تصادفی) نسبت به مرکز هدف (انتظار). خوب و پراکندگیاز لاتین فقط به عنوان ترجمه شده است پراکندگی .
بیایید ببینیم چگونه این تعریف شده است. مشخصه عددیدر یکی از نمونه های قسمت اول درس: 
در آنجا ما یک انتظار ریاضی ناامیدکننده از این بازی پیدا کردیم و اکنون باید واریانس آن را محاسبه کنیم که نشان داده شده استدر سراسر .
بیایید دریابیم که بردها/باخت ها تا چه اندازه نسبت به مقدار متوسط "پراکنده" هستند. بدیهی است که برای این باید محاسبه کنیم تفاوتبین مقادیر یک متغیر تصادفیو او انتظارات ریاضی:
–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5
اکنون به نظر می رسد لازم است نتایج را جمع بندی کنیم، اما این راه خوب نیست - به این دلیل که نوسانات به سمت چپ با نوسانات سمت راست یکدیگر را خنثی می کنند. بنابراین، برای مثال، تیرانداز "آماتور". (مثال بالا)تفاوت ها خواهد بود 
، و وقتی اضافه شوند صفر می دهند، بنابراین هیچ تخمینی از پراکندگی تیراندازی او نخواهیم گرفت.
برای دور زدن این ناراحتی، در نظر بگیرید ماژول هاتفاوت ها، اما دلایل فنیاین رویکرد زمانی ریشه می گیرد که آنها مربع شوند. راحت تر است که راه حل را در یک جدول مرتب کنید: 
و در اینجا التماس برای محاسبه است میانگین وزنیمقدار انحرافات مجذور چیست؟ مال آن هاست ارزش مورد انتظار، که معیار پراکندگی است:
– تعریفپراکندگی بلافاصله از تعریف مشخص می شود که واریانس نمی تواند منفی باشد- برای تمرین توجه داشته باشید!
بیایید به یاد بیاوریم که چگونه انتظارات را پیدا کنیم. مجذور اختلافات را در احتمالات مربوطه ضرب کنید (ادامه جدول):
- به طور مجازی، این "نیروی کشش" است،
و نتایج را خلاصه کنید:
آیا فکر نمی کنید که در پس زمینه بردها، نتیجه خیلی بزرگ بود؟ درست است - ما مربع می کردیم و برای بازگشت به بعد بازی خود باید استخراج کنیم ریشه دوم. این مقدار نامیده می شود انحراف معیار
و با حرف یونانی "سیگما" نشان داده می شود:
گاهی به این معنا گفته می شود انحراف معیار .
معنی آن چیست؟ اگر با میانگین از انتظار ریاضی به چپ و راست منحرف شویم انحراف معیار:
- سپس محتمل ترین مقادیر متغیر تصادفی در این بازه "متمرکز" خواهد بود. آنچه ما در واقع می بینیم:
با این حال، این اتفاق افتاد که در تجزیه و تحلیل پراکندگی تقریباً همیشه با مفهوم پراکندگی عمل می شود. بیایید ببینیم در رابطه با بازی ها چه معنایی دارد. اگر در مورد تیراندازان ما در مورد "دقت" ضربه ها نسبت به مرکز هدف صحبت می کنیم، در اینجا پراکندگی دو چیز را مشخص می کند:
اولاً بدیهی است که با افزایش نرخ ها، واریانس نیز افزایش می یابد. به عنوان مثال، اگر 10 برابر افزایش دهیم، انتظار ریاضی 10 برابر و واریانس 100 برابر افزایش می یابد. (به محض اینکه یک مقدار درجه دوم باشد). اما توجه داشته باشید که قوانین بازی تغییر نکرده است! فقط نرخ ها تغییر کرده اند، به طور کلی، ما قبلاً 10 روبل شرط می کردیم، اکنون 100.
دومین نکته جالب تر این است که واریانس سبک بازی را مشخص می کند. به طور ذهنی نرخ بازی را اصلاح کنید در یک سطح معینو ببینید اینجا چیست:
یک بازی با واریانس کم یک بازی محتاطانه است. بازیکن تمایل دارد که قابل اعتمادترین طرح ها را انتخاب کند، جایی که در یک زمان زیاد نمی بازد/برد. به عنوان مثال، سیستم قرمز/سیاه در رولت (به مثال 4 مقاله مراجعه کنید متغیرهای تصادفی) .
بازی با واریانس بالا او اغلب نامیده می شود پراکندگیبازی این یک سبک بازی ماجراجویانه یا تهاجمی است که در آن بازیکن طرح های "آدرنالین" را انتخاب می کند. حداقل یادمون باشه "مارتینگل"، که در آن مبالغ مورد نظر مرتبه های بزرگتر از بازی "آرام" پاراگراف قبلی است.
وضعیت در پوکر نشان دهنده است: به اصطلاح وجود دارد تنگبازیکنانی که تمایل دارند محتاط باشند و روی آنها "لرزند". بازی یعنی (بانک). جای تعجب نیست که سرمایه آنها نوسان زیادی ندارد (واریانس کم). برعکس، اگر بازیکنی واریانس بالایی داشته باشد، مهاجم است. او اغلب ریسک می‌کند، شرط‌بندی بزرگ می‌کند و هم می‌تواند یک بانک بزرگ را بشکند و هم تکه تکه شود.
همین اتفاق در فارکس و غیره رخ می دهد - نمونه های زیادی وجود دارد.
علاوه بر این، در همه موارد مهم نیست که بازی برای یک پنی باشد یا برای هزاران دلار. هر سطح بازیکنان واریانس کم و زیاد خود را دارد. خوب، برای برد متوسط، همانطور که به یاد داریم، "مسئول" ارزش مورد انتظار.
احتمالا متوجه شده اید که یافتن واریانس فرآیندی طولانی و پر دردسر است. اما ریاضیات سخاوتمندانه است:
فرمول یافتن واریانس
این فرمولمستقیماً از تعریف واریانس گرفته شده است و ما بلافاصله آن را در گردش قرار می دهیم. پلاک را با بازی خودمان از بالا کپی می کنم: 
و انتظار پیدا شده .
واریانس را به روش دوم محاسبه می کنیم. ابتدا، بیایید انتظار ریاضی را پیدا کنیم - مربع متغیر تصادفی. توسط تعریف انتظارات ریاضی:
در این مورد:
بنابراین، طبق فرمول:
همانطور که می گویند، تفاوت را احساس کنید. و البته در عمل بهتر است از فرمول استفاده شود (مگر اینکه شرط اقتضا کند).
ما به تکنیک حل و طراحی مسلط هستیم:
مثال 6
انتظارات ریاضی، واریانس و انحراف معیار آن را بیابید.
این وظیفه در همه جا یافت می شود، و، به عنوان یک قاعده، بدون معنای معنی دار است.
شما می توانید چندین لامپ با اعداد را تصور کنید که در یک دیوانه با احتمالات خاص روشن می شوند :)
راه حل: خلاصه کردن محاسبات اصلی در یک جدول راحت است. ابتدا داده های اولیه را در دو خط بالا می نویسیم. سپس محصولات را محاسبه می کنیم، سپس و در نهایت مجموع ستون سمت راست را محاسبه می کنیم: 
در واقع، تقریبا همه چیز آماده است. در خط سوم، یک انتظار ریاضی آماده ترسیم شد: 
.
پراکندگی با فرمول محاسبه می شود:
و در نهایت انحراف معیار:
- شخصاً من معمولاً 2 رقم اعشار گرد می کنم.
تمام محاسبات را می توان در یک ماشین حساب و حتی بهتر از آن - در اکسل انجام داد:
اینجا اشتباه کردن سخته :)
پاسخ:
آنهایی که آرزو دارند می توانند زندگی خود را بیشتر ساده کنند و از من استفاده کنند ماشین حساب (نسخه ی نمایشی)، که نه تنها فوراً حل می شود این وظیفه، بلکه ساختن گرافیک موضوعی (زود بیا). برنامه می تواند دانلود در کتابخانه- اگر حداقل یکی را دانلود کرده اید مطالب آموزشییا دریافت کنید یک راه دیگر. با تشکر برای حمایت از پروژه!
چند کار برای راه حل مستقل:
مثال 7
واریانس متغیر تصادفی مثال قبلی را بر اساس تعریف محاسبه کنید.
و یک مثال مشابه:
مثال 8
یک متغیر تصادفی گسسته توسط قانون توزیع خودش داده می شود:
بله، مقادیر متغیر تصادفی می تواند بسیار بزرگ باشد (نمونه ای از کار واقعی)و در اینجا در صورت امکان از Excel استفاده کنید. همانطور که، به هر حال، در مثال 7 - سریعتر، قابل اعتمادتر و دلپذیرتر است.
راه حل ها و پاسخ ها در پایین صفحه.
در پایان بخش دوم درس، ما یک کار معمولی دیگر را تجزیه و تحلیل خواهیم کرد، حتی می توان گفت یک ریبوس کوچک:
مثال 9
یک متغیر تصادفی گسسته می تواند تنها دو مقدار بگیرد: و، و. احتمال، انتظارات ریاضی و واریانس مشخص است.
راه حل: بیایید با یک احتمال مجهول شروع کنیم. از آنجایی که یک متغیر تصادفی می تواند تنها دو مقدار بگیرد، مجموع احتمالات رویدادهای مربوطه برابر است با:
و از آن پس .
باقی می ماند برای پیدا کردن ...، گفتن آسان :) اما اوه خوب، شروع شد. با تعریف انتظارات ریاضی: 
- مقادیر شناخته شده را جایگزین کنید:
- و هیچ چیز دیگری نمی توان از این معادله خارج کرد، به جز اینکه می توانید آن را در جهت معمول بازنویسی کنید: 
یا: 
در مورد اقدامات بعدی، فکر می کنم می توانید حدس بزنید. بیایید سیستم را ایجاد و حل کنیم: 
اعداد اعشاری- البته این مایه شرمساری کامل است. هر دو معادله را در 10 ضرب کنید: 
و تقسیم بر 2: 
این بهتر است. از معادله 1 بیان می کنیم: 
(این راه ساده تر است)- جایگزین در معادله 2:
ما در حال ساختن هستیم مربعو ساده سازی کنید: 
ضرب می کنیم در: 
در نتیجه، معادله درجه دوم، متمایز آن را پیدا کنید:
- کامل!
و دو راه حل می گیریم:
1) اگر 
، سپس 
;
2) اگر 
، سپس .
اولین جفت مقادیر شرط را برآورده می کند. از جانب احتمال زیادهمه چیز درست است، اما، با این وجود، بیایید قانون توزیع را بنویسیم: 
و یک بررسی انجام دهید، یعنی انتظار را پیدا کنید:
اغلب در آمار، هنگام تجزیه و تحلیل یک پدیده یا فرآیند، لازم است نه تنها اطلاعات مربوط به میانگین سطوح شاخص های مورد مطالعه را نیز در نظر گرفت. پراکندگی یا تغییر در مقادیر واحدهای مجزا که از ویژگی های مهم جامعه مورد مطالعه می باشد.
قیمت سهام، حجم عرضه و تقاضا در معرض بیشترین تغییرات است. نرخ بهرهکه در دوره های مختلفزمان و در مکان های مختلف
شاخص های اصلی که تنوع را مشخص می کند ، دامنه، واریانس، انحراف معیار و ضریب تغییرات هستند.
تنوع دهانه تفاوت بین حداکثر و حداقل مقادیرامضاء کردن: R = Xmax - Xmin. نقطه ضعف این شاخص این است که فقط مرزهای تنوع صفت را ارزیابی می کند و نوسان آن را در این مرزها منعکس نمی کند.
پراکندگی عاری از این کاستی به عنوان مجذور میانگین انحراف مقادیر مشخصه از مقدار میانگین آنها محاسبه می شود:
روش ساده برای محاسبه واریانس با استفاده از فرمول های زیر (ساده و وزنی) انجام می شود:
نمونه هایی از کاربرد این فرمول ها در وظایف 1 و 2 ارائه شده است.
یک شاخص پرکاربرد در عمل است انحراف معیار :
انحراف معیار به عنوان جذر واریانس تعریف می شود و ابعادی مشابه با صفت مورد مطالعه دارد.
شاخص های در نظر گرفته شده امکان به دست آوردن مقدار مطلق تغییرات را فراهم می کند، یعنی. آن را در واحدهای اندازه گیری صفت مورد مطالعه ارزیابی کنید. بر خلاف آنها، ضریب تغییرات نوسانات را در شرایط نسبی اندازه گیری می کند - نسبت به سطح متوسط، که در بسیاری از موارد ارجح است.
فرمول محاسبه ضریب تغییرات.
نمونه هایی از حل مسائل با موضوع "شاخص های تنوع در آمار"
وظیفه 1 . هنگام مطالعه تأثیر تبلیغات بر اندازه میانگین سپرده ماهانه در بانک های منطقه، 2 بانک مورد بررسی قرار گرفتند. نتایج زیر بدست می آید:
تعريف كردن:
1) برای هر بانک: الف) میانگین سپرده ماهانه. ب) پراکندگی سهم؛
2) میانگین سپرده ماهیانه برای دو بانک با هم.
3) پراکندگی سپرده برای 2 بانک، بسته به تبلیغات.
4) پراکندگی سپرده برای 2 بانک بسته به همه عوامل به جز تبلیغات.
5) واریانس کل با استفاده از قانون جمع.
6) ضریب تعیین;
7) رابطه همبستگی.
راه حل
1) بیایید یک جدول محاسباتی برای یک بانک با تبلیغات درست کنیم . برای تعیین میانگین سپرده ماهانه، نقاط میانی فواصل را پیدا می کنیم. در عین حال، ارزش بازه باز(اولی) مشروط به اندازه فاصله مجاور آن (دوم) برابر است.
ما اندازه متوسط سهم را با استفاده از فرمول میانگین حسابی وزنی پیدا می کنیم:
29000/50 = 580 روبل
پراکندگی سهم با فرمول بدست می آید:
23 400/50 = 468
اقدامات مشابهی را انجام خواهیم داد برای یک بانک بدون تبلیغات :
2) میانگین سپرده دو بانک را با هم بیابید. Xav \u003d (580 × 50 + 542.8 × 50) / 100 \u003d 561.4 روبل.
3) واریانس سپرده، برای دو بانک، بسته به تبلیغات، با فرمول: σ 2 = pq (فرمول واریانس یک ویژگی جایگزین) خواهیم یافت. در اینجا p=0.5 نسبت عواملی است که به تبلیغات بستگی دارد. q=1-0.5، سپس σ 2 =0.5*0.5=0.25.
4) از آنجایی که سهم سایر عوامل 0.5 است پس واریانس سپرده برای دو بانک که به همه عوامل به جز تبلیغات بستگی دارد نیز 0.25 است.
5) تعریف کنید واریانس کلبا استفاده از قانون جمع
= (468*50+636,16*50)/100=552,08
= [(580-561,4)250+(542,8-561,4)250] / 100= 34 596/ 100=345,96
σ 2 \u003d σ 2 واقعیت + σ 2 استراحت \u003d 552.08 + 345.96 \u003d 898.04
6) ضریب تعیین η 2 = σ 2 واقعیت / σ 2 = 345.96/898.04 = 0.39 = 39٪ - اندازه سهم به تبلیغات 39٪ بستگی دارد.
7) نسبت همبستگی تجربی η = √η 2 = √0.39 = 0.62 - رابطه کاملاً نزدیک است.
وظیفه 2 . گروه بندی شرکت ها بر اساس ارزش محصولات قابل فروش وجود دارد:
تعیین: 1) پراکندگی ارزش محصولات قابل فروش؛ 2) انحراف معیار؛ 3) ضریب تغییرات.
راه حل
1) با شرط ارائه شده است سری بازه ایتوزیع باید به صورت گسسته بیان شود، یعنی وسط بازه (x") را پیدا کنید. در گروه های بازه های بسته، وسط را با میانگین حسابی ساده می یابیم. در گروه هایی که حد بالایی دارند، به عنوان تفاوت بین این حد بالا. و نصف اندازه فاصله بعد از آن (200-(400 -200):2=100).
در گروه هایی با حد پایین تر - مجموع این حد پایین و نصف اندازه فاصله قبلی (800+(800-600):2=900).
محاسبه میانگین ارزش محصولات قابل بازار بر اساس فرمول زیر انجام می شود:
Хср = k×((Σ((x"-a):k)×f):Σf)+a. در اینجا a=500 اندازه متغیر در بالاترین فرکانس است، k=600-400=200 برابر است اندازه بازه در بالاترین فرکانس نتیجه را در یک جدول قرار می دهیم:
بنابراین، مقدار متوسطمحصولات قابل فروش برای دوره مورد مطالعه به طور کلی Xav = (-5:37) × 200 + 500 = 472.97 هزار روبل است.
2) با استفاده از فرمول زیر پراکندگی را پیدا می کنیم:
σ 2 \u003d (33/37) * 2002-(472.97-500) 2 \u003d 35675.67-730.62 \u003d 34945.05
3) انحراف استاندارد: σ = ±√σ 2 = ±√34 945.05 ≈ ± 186.94 هزار روبل.
4) ضریب تغییرات: V \u003d (σ / Xav) * 100 \u003d (186.94 / 472.97) * 100 \u003d 39.52٪
برای داده های گروه بندی شده پراکندگی باقی مانده- میانگین پراکندگی درون گروهی:جایی که σ 2 j واریانس درون گروهی گروه j -ام است.
برای داده های گروه بندی نشده پراکندگی باقی ماندهاندازه گیری دقت تقریبی است، یعنی. تقریب خط رگرسیون به داده های اصلی: 
که در آن y(t) پیش بینی مطابق با معادله روند است. y t - سری اولیه دینامیک. n تعداد نقاط است. p تعداد ضرایب معادله رگرسیون (تعداد متغیرهای توضیحی) است.
در این مثال نامیده می شود تخمین بی طرفانه واریانس.
مثال شماره 1. توزیع کارگران سه شرکت از یک انجمن بر اساس دسته های تعرفه با داده های زیر مشخص می شود:
| دسته دستمزد کارگر | تعداد کارگران شرکت | ||
| شرکت 1 | شرکت 2 | شرکت 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
تعريف كردن:
1. پراکندگی برای هر شرکت (پراکندگی درون گروهی).
2. میانگین پراکندگی درون گروهی.
3. پراکندگی بین گروهی.
4. واریانس کل.
راه حل.
قبل از اقدام برای حل مشکل، باید دریابید که کدام ویژگی موثر و کدام فاکتوریل است. در مثال مورد بررسی، ویژگی مؤثر «دسته تعرفه» و ویژگی عامل «تعداد (نام) شرکت» است.
سپس سه گروه (شرکت) داریم که برای آنها باید میانگین گروه و واریانس درون گروهی محاسبه شود:
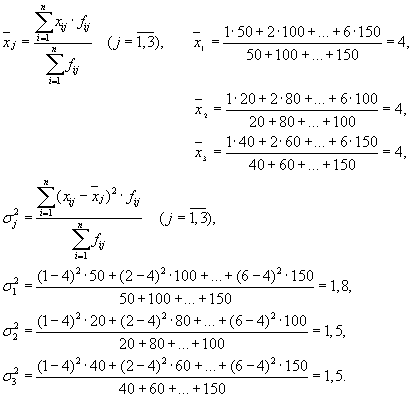
| شرکت | میانگین گروهی، | واریانس درون گروهی، |
| 1 | 4 | 1,8 |
میانگین واریانس های درون گروهی ( پراکندگی باقی مانده) با فرمول محاسبه می شود:
جایی که می توانید محاسبه کنید:
یا:
سپس:
پراکندگی کل برابر خواهد بود: s 2 \u003d 1.6 + 0 \u003d 1.6.
واریانس کل را می توان با استفاده از یکی از دو فرمول زیر محاسبه کرد:
هنگام حل مسائل عملی، اغلب باید با علامتی برخورد کرد که فقط دو مقدار جایگزین را می گیرد. در این مورد، آنها در مورد وزن ارزش خاصی از یک ویژگی صحبت نمی کنند، بلکه در مورد سهم آن در کل صحبت می کنند. اگر نسبت واحدهای جمعیتی که دارای صفت مورد مطالعه هستند با " نشان داده شود. آر"، و نه داشتن - از طریق" q"، سپس پراکندگی را می توان با فرمول محاسبه کرد:
s 2 = p×q
مثال شماره 2. بر اساس داده های مربوط به خروجی شش کارگر تیپ، واریانس بین گروهی را تعیین کنید و در صورتی که واریانس کل 12.2 باشد، تأثیر شیفت کاری بر بهره وری نیروی کار آنها را ارزیابی کنید.
| شماره تیپ کار | خروجی کار، عدد | |
| در شیفت اول | در شیفت دوم | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
راه حل. اطلاعات اولیه
| ایکس | f1 | f2 | f 3 | f4 | f5 | f6 | جمع |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| جمع | 31 | 33 | 37 | 37 | 40 | 38 |
سپس 6 گروه داریم که باید میانگین گروهی و واریانس درون گروهی را محاسبه کرد.
1. مقادیر میانگین هر گروه را بیابید.
2. میانگین مربع هر گروه را بیابید.
ما نتایج محاسبات را در یک جدول خلاصه می کنیم:
| شماره گروه | میانگین گروه | واریانس درون گروهی |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. واریانس درون گروهیتغییر (تغییر) صفت مورد مطالعه (نتیجه) را در گروه تحت تأثیر همه عوامل به جز عامل زیربنایی گروه بندی مشخص می کند:
میانگین پراکندگی درون گروهی را با استفاده از فرمول محاسبه می کنیم:
4. واریانس بین گروهیتغییر (تغییر) صفت مورد مطالعه (نتیجه) را تحت تأثیر یک عامل (ویژگی فاکتوری) زیربنای گروه بندی مشخص می کند.
پراکندگی بین گروهی به صورت زیر تعریف می شود:
جایی که
سپس
واریانس کلتغییر (تغییر) صفت مورد مطالعه (نتیجه) را تحت تأثیر همه عوامل (ویژگی های فاکتوری) بدون استثنا مشخص می کند. با شرط مشکل برابر با 12.2 است.
رابطه همبستگی تجربیاندازه گیری می کند که چه مقدار از کل نوسانات صفت حاصل توسط عامل مورد مطالعه ایجاد می شود. این نسبت واریانس فاکتوریل به کل واریانس است:
ما رابطه همبستگی تجربی را تعیین می کنیم:
روابط بین ویژگی ها می تواند ضعیف یا قوی (نزدیک) باشد. معیارهای آنها در مقیاس چادوک ارزیابی می شود:
0.1 0.3 0.5 0.7 0.9 در مثال ما، رابطه بین ویژگی Y عامل X ضعیف است
ضریب تعیین.
بیایید ضریب تعیین را تعریف کنیم:
بنابراین 0.67 درصد از تغییرات به دلیل تفاوت بین صفات و 99.37 درصد به دلیل سایر عوامل است.
خروجی: در این مورد، خروجی کارگران به کار در یک شیفت خاص بستگی ندارد، یعنی. تأثیر شیفت کاری بر بهره وری نیروی کار آنها قابل توجه نبوده و ناشی از عوامل دیگر است.
مثال شماره 3. بر اساس میانگین دستمزدو مجذور انحراف از مقدار آن برای دو گروه از کارگران، واریانس کل را با اعمال قانون برای جمع واریانس ها بیابید:
راه حل:میانگین واریانس های درون گروهی
پراکندگی بین گروهی به صورت زیر تعریف می شود:
واریانس کل خواهد بود: 480 + 13824 = 14304
انتظار ریاضی (مقدار متوسط) یک متغیر تصادفی X که در یک فضای احتمال گسسته داده می شود، عدد m =M[X]=∑x i p i است، اگر سری کاملاً همگرا شود.
واگذاری خدمات. با کمک سرویس حالت آنلاین انتظارات ریاضی، واریانس و انحراف معیار محاسبه می شود(نمونه را ببینید). علاوه بر این، نمودار تابع توزیع F(X) رسم شده است.
ویژگی های انتظار ریاضی از یک متغیر تصادفی
- انتظار ریاضی یک مقدار ثابت با خودش برابر است: M[C]=C، C یک ثابت است.
- M=C M[X]
- انتظارات ریاضی از مجموع متغیرهای تصادفی برابر است با مجموع انتظارات ریاضی آنها: M=M[X]+M[Y]
- انتظار ریاضی حاصلضرب متغیرهای تصادفی مستقل با حاصلضرب انتظارات ریاضی آنها برابر است: اگر X و Y مستقل باشند M=M[X] M[Y].
خواص پراکندگی
- پراکندگی یک مقدار ثابت برابر با صفر است: D(c)=0.
- ضریب ثابت را می توان با مربع کردن آن از زیر علامت پراکندگی خارج کرد: D(k*X)= k 2 D(X).
- اگر متغیرهای تصادفی X و Y مستقل باشند، واریانس مجموع برابر است با مجموع واریانس‌ها: D(X+Y)=D(X)+D(Y).
- اگر متغیرهای تصادفی X و Y وابسته باشند: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- برای واریانس، فرمول محاسباتی معتبر است:
D(X)=M(X 2)-(M(X)) 2
مثال. انتظارات ریاضی و واریانس دو متغیر تصادفی مستقل X و Y مشخص است: M(x)=8، M(Y)=7، D(X)=9، D(Y)=6. انتظارات ریاضی و واریانس متغیر تصادفی Z=9X-8Y+7 را پیدا کنید.
راه حل. بر اساس ویژگی های انتظار ریاضی: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23.
بر اساس خواص پراکندگی: D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345
الگوریتم محاسبه انتظارات ریاضی
ویژگی های متغیرهای تصادفی گسسته: همه مقادیر آنها را می توان با اعداد طبیعی شماره گذاری کرد. به هر مقدار یک احتمال غیر صفر نسبت دهید.- جفت ها را یکی در یک ضرب کنید: x i در p i .
- حاصلضرب هر جفت x i p i را اضافه می کنیم.
به عنوان مثال، برای n = 4: m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
مثال شماره 1.
| x i | 1 | 3 | 4 | 7 | 9 |
| پی | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
انتظارات ریاضی با فرمول m = ∑x i p i بدست می آید.
انتظارات ریاضی M[X].
M[x] = 1*0.1 + 3*0.2 + 4*0.1 + 7*0.3 + 9*0.3 = 5.9
پراکندگی با فرمول d = ∑x 2 i p i - M[x] 2 پیدا می شود.
پراکندگی D[X].
D[X] = 1 2 * 0.1 + 3 2 * 0.2 + 4 2 * 0.1 + 7 2 * 0.3 + 9 2 * 0.3 - 5.9 2 = 7.69
انحراف معیار σ(x).
σ = sqrt(D[X]) = sqrt(7.69) = 2.78
مثال شماره 2. یک متغیر تصادفی گسسته دارای سری توزیع زیر است:
| ایکس | -10 | -5 | 0 | 5 | 10 |
| آر | ولی | 0,32 | 2آ | 0,41 | 0,03 |
راه حل. مقدار a از رابطه به دست می آید: Σp i = 1
Σp i = a + 0.32 + 2 a + 0.41 + 0.03 = 0.76 + 3 a = 1
0.76 + 3 a = 1 یا 0.24 = 3 a، از این رو a = 0.08
مثال شماره 3. قانون توزیع یک متغیر تصادفی گسسته را در صورتی که واریانس آن مشخص باشد، تعیین کنید و x 1
p 1 = 0.3; p2=0.3; p3=0.1; p 4 \u003d 0.3
d(x)=12.96
راه حل.
در اینجا باید فرمولی برای یافتن واریانس d (x) بسازید:
d(x) = x 1 2 p 1 + x 2 2 p 2 + x 3 2 p 3 + x 4 2 p 4 -m(x) 2
جایی که انتظار m(x)=x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
برای داده های ما
m(x)=6*0.3+9*0.3+x 3 *0.1+15*0.3=9+0.1x 3
12.96 = 6 2 0.3+9 2 0.3+x 3 2 0.1+15 2 0.3-(9+0.1x 3) 2
یا -9/100 (x 2 -20x+96)=0
بر این اساس، باید ریشه های معادله را پیدا کرد و دو تا از آنها وجود خواهد داشت.
x 3 \u003d 8، x 3 \u003d 12
ما یکی را انتخاب می کنیم که شرط x 1 را برآورده کند
قانون توزیع یک متغیر تصادفی گسسته
x 1 = 6; x2=9; x 3 \u003d 12; x4=15
p 1 = 0.3; p2=0.3; p3=0.1; p 4 \u003d 0.3
