Suminės dispersijos matai. Dispersija ir standartinis nuokrypis

Atsitiktinio dydžio dispersija yra šio kintamojo reikšmių sklaidos matas. Mažas dispersija reiškia, kad reikšmės yra sugrupuotos arti viena kitos. Didelė dispersija rodo stiprią reikšmių sklaidą. Statistikoje vartojama atsitiktinio dydžio sklaidos sąvoka. Pavyzdžiui, jei lyginate dviejų dydžių verčių dispersiją (pvz., pacientų vyrų ir moterų stebėjimų rezultatus), galite patikrinti kai kurių kintamųjų reikšmę. Nuokrypis taip pat naudojamas kuriant statistinius modelius, nes maža dispersija gali būti ženklas, kad pervertinate vertes.

Žingsniai

Imties dispersijos apskaičiavimas

Užrašykite pavyzdines vertes. Daugeliu atvejų statistikams prieinami tik tam tikrų populiacijų pavyzdžiai. Pavyzdžiui, statistikai paprastai neanalizuoja visų Rusijos automobilių populiacijos išlaikymo išlaidų – jie analizuoja atsitiktinę kelių tūkstančių automobilių imtį. Toks pavyzdys padės nustatyti vidutines automobilio išlaidas, tačiau greičiausiai gauta vertė bus toli nuo tikrosios.
- Pavyzdžiui, paanalizuokime per 6 dienas kavinėje parduotų bandelių skaičių atsitiktine tvarka. Imtis yra tokios formos: 17, 15, 23, 7, 9, 13. Tai yra imtis, o ne visuma, nes neturime duomenų apie parduotas bandeles kiekvienai kavinės darbo dienai.
- Jei jums pateikiama populiacija, o ne reikšmių pavyzdys, pereikite prie kito skyriaus.
Užrašykite imties dispersijos apskaičiavimo formulę. Sklaida yra tam tikro dydžio verčių sklaidos matas. Kuo dispersijos reikšmė arčiau nulio, tuo arčiau reikšmės sugrupuojamos. Dirbdami su reikšmių pavyzdžiu, dispersijai apskaičiuoti naudokite šią formulę:
- s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))-x̅) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2)) yra dispersija. Sklaida matuojama kvadratinių vienetų matavimai.
- x i (\displaystyle x_(i))- kiekviena imties reikšmė.
- x i (\displaystyle x_(i)) reikia atimti x̅, kvadratą ir pridėti rezultatus.
- x̅ – imties vidurkis (imties vidurkis).
- n yra imties verčių skaičius.
Apskaičiuokite imties vidurkį. Jis žymimas x̅. Imties vidurkis apskaičiuojamas kaip įprastas aritmetinis vidurkis: sudėkite visas imties reikšmes ir padalykite rezultatą iš imtyje esančių reikšmių skaičiaus.
- Mūsų pavyzdyje pridėkite vertes pavyzdyje: 15 + 17 + 23 + 7 + 9 + 13 = 84
  Dabar padalykite rezultatą iš imties verčių skaičiaus (mūsų pavyzdyje yra 6): 84 ÷ 6 = 14.
  Imties vidurkis x̅ = 14.
- Imties vidurkis yra centrinė vertė, aplink kurią pasiskirsto imties reikšmės. Jei imties klasterio reikšmės aplink imtį yra vidutinės, tada dispersija yra maža; kitu atveju dispersija yra didelė.
Iš kiekvienos imties vertės atimkite imties vidurkį. Dabar apskaičiuokite skirtumą x i (\displaystyle x_(i))- x̅, kur x i (\displaystyle x_(i))- kiekviena imties reikšmė. Kiekvienas rezultatas nurodo tam tikros reikšmės nuokrypio nuo imties vidurkio laipsnį, tai yra, kiek ši vertė yra nuo imties vidurkio.
- Mūsų pavyzdyje:
  x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
  x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
  x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
  x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
  x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
  x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
- Gautų rezultatų teisingumą patikrinti nesunku, nes jų suma turi būti lygi nuliui. Tai susiję su vidutinės vertės nustatymu, nes neigiamos reikšmės (atstumai nuo vidutinės vertės iki mažesnių verčių) yra visiškai kompensuojamos teigiamomis reikšmėmis (atstumai nuo vidutinės vertės iki didesnių verčių).
Kaip minėta aukščiau, skirtumų suma x i (\displaystyle x_(i))- x̅ turi būti lygus nuliui. Tai reiškia kad vidutinė dispersija visada yra lygus nuliui, o tai nesuteikia jokio supratimo apie tam tikro dydžio verčių sklaidą. Norėdami išspręsti šią problemą, kiekvieną skirtumą padalykite kvadratu x i (\displaystyle x_(i))- x̅. Taip gausite tik teigiamus skaičius, kuriuos sudėjus niekada nebus iki 0.
- Mūsų pavyzdyje:
  (x 1 (\displaystyle x_(1))-x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
  (x 2 (\displaystyle (x_(2)))-x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
  9 2 = 81
  (-7) 2 = 49
  (-5) 2 = 25
  (-1) 2 = 1
- Jūs radote skirtumo kvadratą - x̅) 2 (\displaystyle ^(2)) kiekvienai imties vertei.
Apskaičiuokite skirtumų kvadratu sumą. Tai yra, suraskite formulės dalį, kuri parašyta taip: ∑[( x i (\displaystyle x_(i))-x̅) 2 (\displaystyle ^(2))]. Čia ženklas Σ reiškia kiekvienos reikšmės skirtumų kvadratu sumą x i (\displaystyle x_(i)) pavyzdyje. Jau radote skirtumus kvadratu (x i (\displaystyle (x_(i))-x̅) 2 (\displaystyle ^(2)) kiekvienai vertei x i (\displaystyle x_(i)) mėginyje; dabar tiesiog pridėkite šiuos kvadratus.
- Mūsų pavyzdyje: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
Padalinkite rezultatą iš n - 1, kur n yra imties verčių skaičius. Prieš kurį laiką, norėdami apskaičiuoti imties dispersiją, statistikai tiesiog padalijo rezultatą iš n; šiuo atveju gausite kvadratinės dispersijos vidurkį, kuris idealiai tinka tam tikros imties dispersijai apibūdinti. Tačiau atminkite, kad bet kuri imtis yra tik nedidelė bendrosios vertybių visumos dalis. Jei paimsite kitą pavyzdį ir atliksite tuos pačius skaičiavimus, gausite kitokį rezultatą. Kaip paaiškėjo, padalijus iš n – 1 (o ne tik iš n), gaunamas geresnis populiacijos dispersijos įvertis, ko ir siekiate. Dalijimas iš n - 1 tapo įprastas, todėl įtrauktas į imties dispersijos skaičiavimo formulę.
- Mūsų pavyzdyje pavyzdyje yra 6 reikšmės, ty n = 6.
  Imties dispersija = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
Skirtumas tarp dispersijos ir standartinio nuokrypio. Atkreipkite dėmesį, kad formulėje yra eksponentas, todėl dispersija matuojama analizuojamos reikšmės kvadratiniais vienetais. Kartais tokią vertę gana sunku valdyti; tokiais atvejais naudojamas standartinis nuokrypis, kuris yra lygus dispersijos kvadratinei šaknei. Štai kodėl imties dispersija žymima kaip s 2 (\displaystyle s^(2)), a standartinis nuokrypis pavyzdžiai – kaip s (\displaystyle s).
- Mūsų pavyzdyje imties standartinis nuokrypis yra: s = √33,2 = 5,76.
Populiacijos dispersijos skaičiavimas
1. Išanalizuokite kai kurias vertybes. Rinkinyje yra visos nagrinėjamo kiekio reikšmės. Pavyzdžiui, jei tirsi gyventojų amžių Leningrado sritis, tada į gyventojų skaičių įtraukiamas visų šios vietovės gyventojų amžius. Dirbant su agregatu, rekomenduojama sukurti lentelę ir į ją įvesti agregato reikšmes. Apsvarstykite šį pavyzdį:
  - Tam tikroje patalpoje yra 6 akvariumai. Kiekviename akvariume yra toks žuvų skaičius:
    x 1 = 5 (\displaystyle x_(1) = 5)
    x 2 = 5 (\displaystyle x_(2) = 5)
    x 3 = 8 (\displaystyle x_(3) = 8)
    x 4 = 12 (\displaystyle x_(4) = 12)
    x 5 = 15 (\displaystyle x_(5) = 15)
    x 6 = 18 (\displaystyle x_(6) = 18)
2. Užsirašykite populiacijos dispersijos apskaičiavimo formulę. Kadangi rinkinyje yra visos tam tikro kiekio reikšmės, toliau pateikta formulė leidžia gauti tiksli vertė populiacijos dispersija. Norėdami atskirti populiacijos dispersiją nuo imties dispersijos (tai tik apytikslis), statistikai naudoja įvairius kintamuosius:
  - σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n
  - σ 2 (\displaystyle ^(2))– populiacijos dispersija (skaitoma kaip „sigmos kvadratas“). Sklaida matuojama kvadratiniais vienetais.
  - x i (\displaystyle x_(i))– kiekviena bendra reikšmė.
  - Σ yra sumos ženklas. Tai yra, kiekvienai vertei x i (\displaystyle x_(i)) atimkite μ, kvadratą ir pridėkite rezultatus.
  - μ yra gyventojų vidurkis.
  - n yra reikšmių skaičius bendroje populiacijoje.
3. Apskaičiuokite gyventojų vidurkį. Dirbant su bendrąja populiacija, jos vidutinė reikšmė žymima μ (mu). Visuomenės vidurkis apskaičiuojamas kaip įprastas aritmetinis vidurkis: sudėkite visas populiacijos reikšmes ir padalykite rezultatą iš populiacijos reikšmių skaičiaus.
  - Atminkite, kad vidurkiai ne visada skaičiuojami kaip aritmetinis vidurkis.
  - Mūsų pavyzdyje populiacijos reikšmė: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
4. Iš kiekvienos populiacijos vertės atimkite populiacijos vidurkį. Kuo skirtumo reikšmė arčiau nulio, tuo konkreti reikšmė artimesnė populiacijos vidurkiui. Raskite skirtumą tarp kiekvienos populiacijos reikšmės ir jos vidurkio, ir pirmą kartą pamatysite reikšmių pasiskirstymą.
  - Mūsų pavyzdyje:
    x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
    x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
    x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
    x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
    x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
    x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5
5. Kiekvieno gauto rezultato kvadratas. Skirtumo reikšmės bus teigiamos ir neigiamos; jei šias reikšmes įtrauksite į skaičių eilutę, tada jos bus dešinėje ir kairėje nuo populiacijos vidurkio. Tai nėra gerai skaičiuojant dispersiją, nes teigiami ir neigiami skaičiai panaikina vienas kitą. Todėl kiekvieną skirtumą padalykite kvadratu, kad gautumėte tik teigiamus skaičius.
  - Mūsų pavyzdyje:
    (x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) kiekvienai populiacijos vertei (nuo i = 1 iki i = 6):
    (-5,5)2 (\displaystyle ^(2)) = 30,25
    (-5,5)2 (\displaystyle ^(2)), kur x n (\displaystyle x_(n)) yra paskutinė populiacijos reikšmė.
  - Norėdami apskaičiuoti gautų rezultatų vidutinę reikšmę, turite rasti jų sumą ir padalyti iš n: (( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2))) / n
  - Dabar parašykime aukščiau pateiktą paaiškinimą naudodami kintamuosius: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n ir gaukite populiacijos dispersijos apskaičiavimo formulę.

Sklaida statistikoje apibrėžiama kaip atskirų požymio verčių standartinis nuokrypis nuo aritmetinio vidurkio kvadratu. Įprastas būdas apskaičiuoti pasirinkimų kvadratinius nuokrypius nuo vidurkio ir tada juos suvesti.

Atliekant ekonominę ir statistinę analizę, požymio kitimą įprasta vertinti dažniausiai naudojant standartinį nuokrypį, kuris yra kvadratinė šaknis nuo dispersijos.

(3)

Jis apibūdina absoliutų kintamojo atributo verčių svyravimą ir išreiškiamas tais pačiais vienetais kaip ir variantai. Statistikoje dažnai tenka lyginti įvairių ypatybių variaciją. Tokiems palyginimams naudojamas santykinis variacijos rodiklis – variacijos koeficientas.

Dispersijos savybės:

1) jei iš visų parinkčių atimsite bet kurį skaičių, tada dispersija nepasikeis;

2) jei visas varianto reikšmes padalinsime iš kažkokio skaičiaus b, tai dispersija sumažės b^2 kartus, t.y.

3) jei apskaičiuosite vidutinį nuokrypių kvadratą nuo bet kurio skaičiaus su nelygiu aritmetiniu vidurkiu, tai jis bus didesnis už dispersiją. Šiuo atveju, tiksliai apibrėžta skirtumo tarp vidutinės pozicijos vertės kvadratui verte.

Dispersiją galima apibrėžti kaip skirtumą tarp vidurkio kvadrato ir vidutinio kvadrato.

17. Grupinės ir tarpgrupinės variacijos. Nuokrypių pridėjimo taisyklė

Jei statistinė populiacija skirstoma į grupes arba dalis pagal tiriamą požymį, tai tokiai populiacijai galima skaičiuoti tokius sklaidos tipus: grupinė (privati), grupės vidutinė (privati) ir tarpgrupinė.

Bendra dispersija- atspindi bruožo kitimą dėl visų sąlygų ir priežasčių, veikiančių tam tikroje statistinėje populiacijoje.

Grupės dispersija- yra lygus atskirų atributo reikšmių nuokrypių nuo šios grupės aritmetinio vidurkio kvadrato vidurkiui, vadinamam grupės vidurkiu. Šiuo atveju grupės vidurkis nesutampa su bendru visos populiacijos vidurkiu.

Grupės dispersija atspindi bruožo kitimą tik dėl sąlygų ir priežasčių, veikiančių grupėje.

Vidutinės grupės dispersijos- apibrėžiamas kaip svertinis aritmetinis grupių dispersijų vidurkis, o svoriai yra grupių tūriai.

Tarpgrupinė dispersija- yra lygus grupės vidurkių nuokrypių nuo bendrojo vidurkio vidutiniam kvadratui.

Tarpgrupinė dispersija apibūdina gauto požymio kitimą dėl grupavimo požymio.

Tarp nagrinėjamų dispersijų tipų yra tam tikras ryšys: bendra dispersija yra lygi vidutinės grupės ir tarpgrupinės dispersijos sumai.

Šis ryšys vadinamas dispersijos pridėjimo taisykle.

18. Dinaminė eilutė ir ją sudarantys elementai. Dinaminių serijų tipai.

Serija statistikoje- tai skaitmeniniai duomenys, rodantys, ar reiškinys kinta laike ar erdvėje ir leidžia atlikti statistinį reiškinių palyginimą tiek jų raidos procese, tiek laike. įvairių formų ir procesų tipai. Dėl to galima aptikti reiškinių tarpusavio priklausomybę.

Socialinių reiškinių judėjimo laike raidos procesas statistikoje paprastai vadinamas dinamika. Dinamikai parodyti sudaromos dinamikos (chronologinės, laiko) eilutės, kurios yra laiko atžvilgiu kintančių statistinio rodiklio (pavyzdžiui, nuteistųjų per 10 metų skaičius) reikšmių serijos, išdėstytos chronologine tvarka. Jų sudedamosios dalys yra tam tikro rodiklio skaitinės reikšmės ir laikotarpiai arba laiko momentai, su kuriais jie susiję.

Svarbiausia laiko eilučių charakteristika- jų dydis (apimtis, vertė) to ar kito reiškinio, pasiekto tam tikru laikotarpiu ar tam tikru momentu. Atitinkamai, dinamikos serijos terminų dydis yra jos lygis. Išskirti pradinis, vidurinis ir galutinis dinaminės serijos lygiai. Pirmas lygis rodo pirmojo, galutinio – paskutinio serijos nario reikšmę. Vidurinis lygis reiškia vidutinį chronologinį kitimo diapazoną ir apskaičiuojamas atsižvelgiant į tai, ar laiko eilutė yra intervalinė, ar momentinė.

Kita svarbi dinaminės serijos savybė- laikas, praėjęs nuo pradinio iki galutinio stebėjimo, arba tokių stebėjimų skaičius.

Laiko eilučių yra įvairių tipų, jas galima klasifikuoti pagal šiuos kriterijus.

1) Priklausomai nuo lygių išreiškimo būdo, dinamikos eilutės skirstomos į absoliučių ir išvestinių rodiklių eilutes (santykinės ir vidutinės reikšmės).

2) Priklausomai nuo to, kaip eilučių lygiai išreiškia reiškinio būseną tam tikrais laiko momentais (mėnesio, ketvirčio, metų pradžioje ir pan.) arba jo reikšmę tam tikrais laiko intervalais (pavyzdžiui, per dieną, mėnuo, metai ir pan.) ir tt), atitinkamai atskirkite momentą ir intervalų serijos dinamika. Momentų serijos teisėsaugos institucijų analitiniame darbe naudojamos palyginti retai.

Statistikos teorijoje dinamika išskiriama ir pagal eilę kitų klasifikavimo požymių: priklausomai nuo atstumo tarp lygių – su vienodais atstumais ir nevienodais laike lygiais; priklausomai nuo pagrindinės tiriamo proceso tendencijos buvimo – stacionarus ir nestacionarus. Analizuojant dinamines eilutes, kaip komponentai pateikiami šie serijų lygiai:

Y t \u003d TP + E (t)

kur TR yra deterministinis komponentas, kuris lemia bendrą pokyčio tendenciją laikui bėgant arba tendenciją.

E (t) yra atsitiktinis komponentas, sukeliantis lygio svyravimus.

Sklaidaatsitiktinis kintamasis- duotosios sklaidos matas atsitiktinis kintamasis, tai yra, ji nukrypimai iš matematinio lūkesčio. Statistikoje žymėjimas (sigma kvadratas) dažnai naudojamas dispersijai žymėti. Dispersijos kvadratinė šaknis vadinama standartinis nuokrypis arba standartinis užtepimas. Standartinis nuokrypis matuojamas tais pačiais vienetais kaip ir atsitiktinė vertė, o dispersija matuojama to vieneto kvadratais.

Nors labai patogu naudoti tik vieną reikšmę (pvz., vidurkį arba režimą ir medianą), norint įvertinti visą imtį, šis metodas gali lengvai padaryti neteisingas išvadas. Tokios situacijos priežastis slypi ne pačioje vertėje, o tame, kad viena reikšmė niekaip neatspindi duomenų reikšmių sklaidos.

Pavyzdžiui, pavyzdyje:

vidurkis yra 5.

Tačiau pačiame imtyje nėra elemento, kurio vertė būtų 5. Gali reikėti žinoti, kiek kiekvienas imties elementas yra arti jo vidutinės vertės. Arba, kitaip tariant, reikia žinoti reikšmių dispersiją. Žinodami, kiek pasikeitė duomenys, galite geriau interpretuoti reiškia, mediana ir mada. Mėginių verčių kitimo laipsnis nustatomas apskaičiuojant jų dispersiją ir standartinį nuokrypį.

dispersija ir Kvadratinė šaknis dispersijos, vadinamos standartiniu nuokrypiu, apibūdina vidutinį nuokrypį nuo imties vidurkio. Tarp šių dviejų kiekių didžiausia vertė Tai turi standartinis nuokrypis. Šią reikšmę galima pavaizduoti kaip vidutinį atstumą, kuriuo elementai yra nuo vidurinio imties elemento.

Sklaidą sunku prasmingai interpretuoti. Tačiau šios vertės kvadratinė šaknis yra standartinis nuokrypis ir puikiai tinka interpretacijai.

Standartinis nuokrypis apskaičiuojamas pirmiausia nustatant dispersiją, o po to apskaičiuojant dispersijos kvadratinę šaknį.

Pavyzdžiui, paveikslėlyje parodytam duomenų masyvui bus gautos šios reikšmės:

1 paveikslas

Čia skirtumų kvadratu vidurkis yra 717,43. Norint gauti standartinį nuokrypį, belieka paimti šio skaičiaus kvadratinę šaknį.

Rezultatas bus maždaug 26,78.

Reikia atsiminti, kad standartinis nuokrypis interpretuojamas kaip vidutinis atstumas, kuriuo elementai yra nuo imties vidurkio.

Standartinis nuokrypis parodo, kaip gerai vidurkis apibūdina visą imtį.

Tarkime, kad esate vadovas gamybos skyrius PC surinkimas. Ketvirčio ataskaitoje teigiama, kad praėjusį ketvirtį buvo pagaminta 2500 kompiuterių. Ar tai blogai ar gerai? Prašėte (arba ataskaitoje jau yra šis stulpelis), kad ataskaitoje būtų rodomas standartinis šių duomenų nuokrypis. Standartinio nuokrypio skaičius, pavyzdžiui, yra 2000. Jums, kaip skyriaus vedėjui, tampa aišku, kad gamybos liniją reikia geriau kontroliuoti (per dideli surenkamų kompiuterių skaičiaus nuokrypiai).

Prisiminkime: kada didelis dydis Jei standartinis nuokrypis yra per mažas, duomenys yra plačiai išsibarstę aplink vidurkį, o jei standartinis nuokrypis mažas, jie sugrupuojami arti vidurkio.

Keturios statistinės funkcijos VARP(), VARP(), STDEV() ir STDEV() skirtos skaičių dispersijai ir standartiniam nuokrypiui apskaičiuoti langelių diapazone. Prieš apskaičiuodami duomenų rinkinio dispersiją ir standartinį nuokrypį, turite nustatyti, ar duomenys atspindi populiaciją, ar jos imtį. Jei imtis yra iš bendrosios visumos, reikia naudoti VARP() ir STDEV() funkcijas, o bendrosios visumos atveju – VARP() ir STDEV() funkcijas:

Gyventojų skaičius	Funkcija
	VARP()
	STDLONG ()
Pavyzdys
	VARI()
	STDEV()

Dispersija (taip pat ir standartinis nuokrypis), kaip pažymėjome, rodo, kokiu mastu į duomenų rinkinį įtrauktos reikšmės yra išsklaidytos aplink aritmetinį vidurkį.

Maža dispersijos arba standartinio nuokrypio reikšmė rodo, kad visi duomenys yra sutelkti aplink aritmetinį vidurkį, o didelė šių reikšmių reikšmė rodo, kad duomenys yra išsibarstę po platų verčių diapazoną.

Dispersiją gana sunku prasmingai interpretuoti (ką reiškia maža reikšmė, didelė reikšmė?). Spektaklis 3 užduotys leis vizualiai, grafike, parodyti duomenų rinkinio dispersijos reikšmę.

Užduotys

· 1 pratimas.

· 2.1. Pateikite sąvokas: dispersija ir standartinis nuokrypis; simbolinis jų žymėjimas apdorojant statistinius duomenis.

· 2.2. Sudarykite darbalapį pagal 1 paveikslą ir atlikite reikiamus skaičiavimus.

· 2.3. Pateikite pagrindines skaičiavimuose naudojamas formules

· 2.4. Paaiškinkite visas žymes ( , , )

· 2.5. paaiškinti praktinė vertė dispersijos ir standartinio nuokrypio sąvokas.

2 užduotis.

1.1. Pateikite sąvokas: bendroji visuma ir imtis; tikėtina vertė ir jų aritmetinis vidurkis simbolinis žymėjimas statistinių duomenų apdorojimo metu.

1.2. Pagal 2 paveikslą sudarykite darbalapį ir atlikite skaičiavimus.

1.3. Pateikite pagrindines skaičiavimuose naudotas formules (bendrai visumai ir imčiai).

2 pav

1.4. Paaiškinkite, kodėl pavyzdžiuose kaip 46,43 ir 48,78 galima gauti tokias aritmetinių vidurkių reikšmes (žr. failo priedą). Daryti išvadas.

3 užduotis.

Yra du pavyzdžiai su skirtingas rinkinys duomenis, tačiau jų vidurkis bus toks pat:

3 pav

3.1. Sudarykite darbalapį pagal 3 paveikslą ir atlikite reikiamus skaičiavimus.

3.2. Pateikite pagrindines skaičiavimo formules.

3.3. Sudarykite grafikus pagal 4, 5 paveikslus.

3.4. Paaiškinkite susidariusias priklausomybes.

3.5. Atlikite panašius šių dviejų pavyzdžių skaičiavimus.

Pradinis pavyzdys 11119999

Pasirinkite antrojo imties reikšmes taip, kad antrojo imties aritmetinis vidurkis būtų toks pat, pavyzdžiui:

Antrojo pavyzdžio vertes pasirinkite patys. Išdėstykite skaičiavimus ir braižykite kaip 3, 4, 5 paveikslus. Parodykite pagrindines skaičiavimuose naudotas formules.

Padarykite atitinkamas išvadas.

Visos užduotys turi būti pateiktos ataskaitos forma su visais reikalingais skaičiais, grafikais, formulėmis ir trumpais paaiškinimais.

Pastaba: grafikų konstrukcija turi būti paaiškinta skaičiais ir trumpais paaiškinimais.

Sugrupuotiems duomenims likutinė dispersija- grupės vidaus dispersijų vidurkis:

Kur σ 2 j yra j-osios grupės dispersija grupės viduje.

Nesugrupuotiems duomenims likutinė dispersija yra aproksimacijos tikslumo matas, t.y. regresijos tiesės aproksimacija pirminiams duomenims:
čia y(t) yra prognozė pagal tendencijos lygtį; y t – pradinė dinamikos eilė; n yra taškų skaičius; p – regresijos lygties koeficientų skaičius (aiškinamųjų kintamųjų skaičius).
Šiame pavyzdyje jis vadinamas nešališkas dispersijos įvertinimas.

1 pavyzdys. Trijų vienos asociacijos įmonių darbuotojų pasiskirstymas pagal tarifų kategorijas apibūdinamas šiais duomenimis:

Darbuotojo darbo užmokesčio kategorija	Darbuotojų skaičius įmonėje
Darbuotojo darbo užmokesčio kategorija	įmonė 1	įmonė 2	įmonė 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Apibrėžkite:
1. sklaida kiekvienai įmonei (vidinė dispersija);
2. vidinės grupės dispersijų vidurkis;
3. tarpgrupinė sklaida;
4. bendroji dispersija.

Sprendimas.
Prieš pradedant spręsti problemą, būtina išsiaiškinti, kuri funkcija yra efektyvi, o kuri faktorinė. Nagrinėjamame pavyzdyje galiojantis požymis yra „Tarifo kategorija“, o faktoriaus atributas – „Įmonės numeris (pavadinimas).
Tada turime tris grupes (įmones), kurioms reikia apskaičiuoti grupės vidurkį ir grupės vidaus dispersijas:

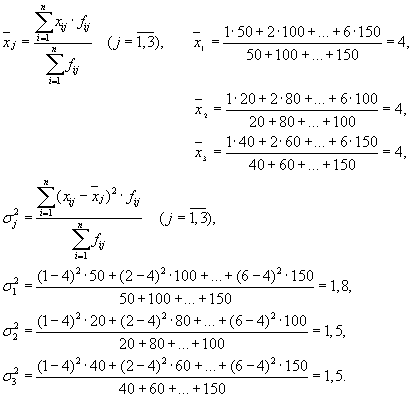
Įmonė	grupės vidurkis,	dispersija grupės viduje,
1	4	1,8

Vidutinės grupės dispersijų vidurkis ( likutinė dispersija) apskaičiuojamas pagal formulę:

kur galima paskaičiuoti:

arba:

tada:
Bendra dispersija bus lygi: s 2 \u003d 1,6 + 0 \u003d 1,6.
Bendrą dispersiją taip pat galima apskaičiuoti naudojant vieną iš šių dviejų formulių:

Sprendžiant praktines problemas, dažnai tenka susidurti su ženklu, kuris ima tik dvi alternatyvias vertybes. Šiuo atveju kalbama ne apie konkrečios ypatybės reikšmės svorį, o apie jos dalį visumoje. Jei populiacijos vienetų, turinčių tiriamą požymį, dalis yra pažymėta " R", o neturintis - per" q“, tada dispersiją galima apskaičiuoti pagal formulę:
s2 = p×q

2 pavyzdys. Remdamiesi šešių brigados darbuotojų produkcijos duomenimis, nustatykite tarpgrupinę dispersiją ir įvertinkite darbo pamainos įtaką jų darbo našumui, jei bendra dispersija yra 12,2.

Darbo brigados Nr	Darbinė produkcija, vnt.
Darbo brigados Nr	pirmoje pamainoje	2-oje pamainoje
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Sprendimas. Pradiniai duomenys

X	f1	f2	f 3	f4	f5	f6	Iš viso
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Iš viso	31	33	37	37	40	38

Tada turime 6 grupes, kurioms reikia apskaičiuoti grupės vidurkį ir grupės vidaus dispersijas.
1. Raskite kiekvienos grupės vidutines vertes.

2. Raskite kiekvienos grupės vidutinį kvadratą.

Skaičiavimo rezultatus apibendriname lentelėje:

Grupės numeris	Grupės vidurkis	Vidinė grupės dispersija
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Vidinė grupės dispersija apibūdina tiriamo (rezultato) bruožo kitimą (variaciją) grupėje, veikiant visiems veiksniams, išskyrus veiksnį, kuriuo grindžiamas grupavimas:
Apskaičiuojame vidinės grupės dispersijų vidurkį pagal formulę:

4. Tarpgrupinė dispersija apibūdina tiriamo (rezultato) požymio kitimą (variaciją) veikiant veiksniui (faktoriniam požymiui), kuriuo grindžiamas grupavimas.
Tarpgrupinė dispersija apibrėžiama taip:

kur

Tada

Bendra dispersija charakterizuoja tiriamo (rezultato) požymio kitimą (variaciją) veikiant visiems be išimties veiksniams (faktoriniams požymiams). Pagal uždavinio sąlygą jis lygus 12,2.
Empirinis koreliacinis ryšys matuoja, kiek viso gauto požymio svyravimo sukelia tiriamas veiksnys. Tai faktorinės dispersijos ir bendros dispersijos santykis:

Mes nustatome empirinį koreliacijos ryšį:

Ryšiai tarp požymių gali būti silpni arba stiprūs (glaudūs). Jų kriterijai vertinami Chaddock skalėje:
0,1 0,3 0,5 0,7 0,9 Mūsų pavyzdyje ryšys tarp Y veiksnio X yra silpnas
Determinacijos koeficientas.

Apibrėžkime determinacijos koeficientą:

Taigi 0,67 % svyravimo atsiranda dėl bruožų skirtumų, o 99,37 % – dėl kitų veiksnių.
Išvada: šiuo atveju darbuotojų išeiga nepriklauso nuo darbo konkrečioje pamainoje, t.y. darbo pamainos įtaka jų darbo našumui nėra reikšminga ir yra nulemta kitų veiksnių.

3 pavyzdys. Remiantis vidurkiu darbo užmokesčio ir nukrypimus nuo jo vertės kvadratu dviem darbuotojų grupėms, raskite bendrą dispersiją taikydami nuokrypių pridėjimo taisyklę:

Sprendimas:
Vidurkis skirtumų grupės viduje

Tarpgrupinė dispersija apibrėžiama taip:

Bendra dispersija bus: 480 + 13824 = 14304

Jeigu populiacija skirstoma į grupes pagal tiriamą požymį, tai šiai populiacijai galima skaičiuoti tokius sklaidos tipus: suminė, grupė (intragrupė), grupės vidurkis (vidutinis grupės vidaus), tarpgrupinis.

Iš pradžių apskaičiuojamas determinacijos koeficientas, kuris parodo, kokia visos tiriamo požymio kitimo dalis yra tarpgrupinė variacija, t.y. dėl grupavimo:

Empirinis koreliacijos santykis apibūdina grupavimo (faktorinio) ir efektinių ženklų ryšio glaudumą.

Empirinis koreliacijos santykis gali būti nuo 0 iki 1.

Norėdami įvertinti santykių glaudumą pagal empirinį koreliacijos santykį, galite naudoti Chaddock ryšius:

4 pavyzdys Pateikiami šie projektavimo ir tyrimo organizacijų darbų atlikimo duomenys skirtingos formos nuosavybė:

Apibrėžkite:

1) visuminė dispersija;

2) grupinės dispersijos;

3) grupių dispersijų vidurkis;

4) tarpgrupinė sklaida;

5) bendroji dispersija, pagrįsta dispersijų sudėjimo taisykle;

6) determinacijos koeficientas ir empirinė koreliacija.

Padarykite išvadas patys.

Sprendimas:

1. Apibrėžkite vidutinis tūris dviejų nuosavybės formų įmonių darbų atlikimas:

Apskaičiuokite bendrą dispersiją:

2. Apibrėžkite grupės vidurkius:

milijonas rublių;

mln rub.

Grupės skirtumai:

;

3. Apskaičiuokite grupių dispersijų vidurkį:

4. Nustatykite tarpgrupinę dispersiją:

5. Apskaičiuokite bendrą dispersiją pagal dispersijų pridėjimo taisyklę:

6. Nustatykite determinacijos koeficientą:

Taigi projektavimo ir tyrimo organizacijų atliekamų darbų kiekis 22% priklauso nuo įmonių nuosavybės formos.

Empirinis koreliacijos santykis apskaičiuojamas pagal formulę

Apskaičiuoto rodiklio reikšmė rodo, kad darbo kiekio priklausomybė nuo įmonės nuosavybės formos yra nedidelė.

5 pavyzdys Atlikus gamybos vietų technologinės disciplinos tyrimą buvo gauti šie duomenys:

Nustatykite determinacijos koeficientą

Suminės dispersijos matai. Dispersija ir standartinis nuokrypis

Žingsniai

Imties dispersijos apskaičiavimas

Populiacijos dispersijos skaičiavimas

17. Grupinės ir tarpgrupinės variacijos. Nuokrypių pridėjimo taisyklė

18. Dinaminė eilutė ir ją sudarantys elementai. Dinaminių serijų tipai.