Matematinės statistikos pavyzdžių dispersija. Diskretinio atsitiktinio dydžio sklaida. Standartinis nuokrypis

Tačiau vien šios charakteristikos vis dar nepakanka atsitiktiniam dydžiui ištirti. Įsivaizduokite, kad du šauliai šaudo į taikinį. Vienas šaudo taikliai ir pataiko arti centro, o kitas... tiesiog linksminasi ir net nesitaiko. Bet juokinga yra jo vidutinis rezultatas bus lygiai toks pat kaip ir pirmojo šaulio! Šią situaciją paprastai iliustruoja šie atsitiktiniai dydžiai:

„Snaiperio“ matematinis lūkestis yra lygus, tačiau „įdomiai asmenybei“: – irgi lygus nuliui!

Taigi reikia kiekybiškai įvertinti, kiek išsibarstę kulkos (atsitiktinio dydžio reikšmės), palyginti su taikinio centru (matematinis lūkestis). gerai ir išsibarstymas iš lotynų kalbos verčiama tik kaip dispersija .

Pažiūrėkime, kaip ši skaitinė charakteristika nustatoma viename iš 1-osios pamokos dalies pavyzdžių:

Ten radome nuviliančius matematinius šio žaidimo lūkesčius, o dabar turime apskaičiuoti jo dispersiją, kuri yra žymimas skersai .

Išsiaiškinkime, kiek pergalės/pralaimėjimai yra „išsibarstę“ vidurkio atžvilgiu. Akivaizdu, kad tam reikia apskaičiuoti skirtumai tarp atsitiktinio dydžio reikšmės ir ji matematinis lūkestis:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Dabar, regis, reikia apibendrinti rezultatus, bet šis kelias netinka – dėl to, kad svyravimai į kairę, svyravimai į dešinę, panaikinami. Taigi, pavyzdžiui, „mėgėjiškas“ šaulys (pavyzdys aukščiau) skirtumas yra , o pridėjus duos nulį, todėl negausime jokio jo šaudymo sklaidos įvertinimo.

Norėdami išvengti šio nepatogumo, galite apsvarstyti moduliai skirtumai, tačiau dėl techninių priežasčių požiūris įsitvirtino, kai jie yra kvadratiniai. Patogiau sprendimą sudaryti lentele:

Ir čia reikia skaičiuoti svertinis vidurkis nuokrypių kvadratų reikšmė. Kas tai? Tai jų tikėtina vertė, kuris yra sklaidos matas:

– apibrėžimas dispersija. Iš apibrėžimo iš karto aišku, kad dispersija negali būti neigiama- atkreipkite dėmesį į praktiką!

Prisiminkime, kaip rasti lūkesčius. Skirtumų kvadratus padauginame iš atitinkamų tikimybių (Lentelės tęsinys):
- vaizdžiai tariant, tai yra „traukianti jėga“,
ir apibendrinkite rezultatus:

Ar nemanote, kad laimėjimų fone rezultatas pasirodė per didelis? Teisingai – mes kvadratavome, o norėdami grįžti į savo žaidimo dimensiją, turime išgauti kvadratinę šaknį. Šis kiekis vadinamas standartinis nuokrypis ir žymimas graikiška raide „sigma“:

Ši vertė kartais vadinama standartinis nuokrypis .

Kokia jo prasmė? Jei nuo matematinio lūkesčio nukrypstame į kairę ir į dešinę standartiniu nuokrypiu:

- tada labiausiai tikėtinos atsitiktinio dydžio reikšmės bus „koncentruotos“ šiame intervale. Ką mes iš tikrųjų stebime:

Tačiau atsitiko taip, kad analizuojant sklaidą beveik visada operuojama su dispersijos sąvoka. Pažiūrėkime, ką tai reiškia žaidimų atžvilgiu. Jei rodyklių atveju kalbame apie smūgių „tikslumą“ taikinio centro atžvilgiu, tai čia dispersija apibūdina du dalykus:

Pirma, akivaizdu, kad didėjant rodikliams didėja ir dispersija. Taigi, pavyzdžiui, jei padidinsime 10 kartų, tada matematinis lūkestis padidės 10 kartų, o dispersija - 100 kartų (jei tai yra kvadratinis dydis)... Tačiau atkreipkite dėmesį, kad pačios žaidimo taisyklės nepasikeitė! Pasikeitė tik įkainiai, grubiai tariant, statydavome 10 rublių, dabar 100.

Antras, įdomesnis dalykas, yra tas, kad žaidimo stiliui būdinga dispersija. Protiškai sureguliuokime žaidimo įkainius tam tikrame lygyje, ir pažiūrėkite, kas čia:

Mažos dispersijos žaidimas yra atsargus žaidimas. Žaidėjas yra linkęs rinktis patikimiausias schemas, kuriose vienu metu nepraranda/laimi per daug. Pavyzdžiui, raudona / juoda sistema ruletėje (žr. 4 straipsnio pavyzdį Atsitiktiniai kintamieji) .

Didelės dispersijos žaidimas. Ji dažnai vadinama dispersinisžaidimas. Tai nuotykių kupinas arba agresyvus žaidimo stilius, kai žaidėjas pasirenka adrenalino siurbimo schemas. Prisiminkime bent Martingale, kuriame rizikuojamos sumos, kurios yra daug didesnės nei ankstesnėje pastraipoje nurodytas „tylus“ žaidimas.

Situacija pokeryje yra orientacinė: yra vadinamųjų ankštusžaidėjai, kurie linkę būti atsargūs ir „nerimti“ dėl savo žaidimų turto (pagal bankrotą)... Nenuostabu, kad jų bankrotas mažai svyruoja (maža dispersija). Priešingai, jei žaidėjas turi didelę dispersiją, tai yra agresorius. Jis dažnai rizikuoja, daro didelius statymus ir gali sugriauti didžiulį banką ir sugriauti.

Tas pats vyksta Forex ir panašiai – pavyzdžių yra daug.

Be to, visais atvejais nesvarbu – ar žaidimas kainuoja centą, ar tūkstančius dolerių. Kiekvienas lygis turi savo mažos ir didelės dispersijos žaidėjus. Na, o vidutinis atlyginimas, kaip prisimename, yra „atsakingas“ tikėtina vertė.

Tikriausiai pastebėjote, kad dispersijos nustatymas yra ilgas ir kruopštus procesas. Tačiau matematika yra dosni:

Sklaidos nustatymo formulė

Ši formulė yra tiesiogiai išvesta iš dispersijos apibrėžimo, ir mes iš karto pateikiame ją į apyvartą. Nukopijuosiu lėkštės viršų su mūsų žaidimu:

ir rastą lūkestį.

Apskaičiuokime dispersiją antruoju būdu. Pirmiausia randame matematinį lūkestį – atsitiktinio dydžio kvadratą. Autorius lūkesčių apibrėžimas:

Tokiu atveju:

Taigi, pagal formulę:

Pajuskite skirtumą, kaip sakoma. Ir praktiškai, žinoma, geriau taikyti formulę (nebent sąlyga reikalauja kitaip).

Įvaldome sprendimo ir dizaino techniką:

6 pavyzdys

Raskite jo matematinį lūkestį, dispersiją ir standartinį nuokrypį.

Ši užduotis randama visur ir, kaip taisyklė, neturi prasmės.
Galite įsivaizduoti kelias lemputes su skaičiais, kurios su tam tikra tikimybe užsidega beprotnamyje :)

Sprendimas: Pagrindiniai skaičiavimai patogiai apibendrinti lentelėje. Pirma, pirminius duomenis įrašome į dvi viršutines eilutes. Tada apskaičiuojame produktus, tada ir galiausiai sumas dešiniajame stulpelyje:

Tiesą sakant, beveik viskas yra paruošta. Trečioje eilutėje yra paruoštas matematinis lūkestis: .

Dispersiją apskaičiuojame pagal formulę:

Ir galiausiai standartinis nuokrypis:
– asmeniškai aš dažniausiai apvalinu iki 2 skaitmenų po kablelio.

Visus skaičiavimus galima atlikti skaičiuotuvu, o dar geriau - Excel:

čia sunku suklysti :)

Atsakymas:

Norintys gali dar labiau supaprastinti savo gyvenimą ir pasinaudoti mano skaičiuotuvas (demo versija), kuris ne tik akimirksniu išspręs šią problemą, bet ir pastatys teminės diagramos (greitai atvyksime)... Programa gali parsisiųsti bibliotekoje- jei įkėlėte bent vieną mokomąją medžiagą arba gaukite Kitas būdas... Ačiū už paramą projektui!

Keletas užduočių savarankiškam sprendimui:

7 pavyzdys

Apskaičiuokite atsitiktinio dydžio dispersiją iš ankstesnio pavyzdžio pagal apibrėžimą.

Ir panašus pavyzdys:

8 pavyzdys

Diskretus atsitiktinis kintamasis nurodomas jo paskirstymo dėsniu:

Taip, atsitiktinio dydžio reikšmės gali būti gana didelės (pavyzdys iš tikro darbo), o čia, jei įmanoma, naudokite Excel. Kaip, beje, 7 pavyzdyje - greičiau, patikimiau ir maloniau.

Sprendimai ir atsakymai puslapio apačioje.

2-osios pamokos dalies pabaigoje panagrinėsime dar vieną tipišką problemą, galima sakyti, net nedidelį rebusą:

9 pavyzdys

Diskretus atsitiktinis dydis gali turėti tik dvi reikšmes: ir, be to. Yra žinomos tikimybės, matematinės lūkesčiai ir dispersija.

Sprendimas: Pradėkime nuo nežinomos tikimybės. Kadangi atsitiktinis dydis gali turėti tik dvi reikšmes, atitinkamų įvykių tikimybių suma:

ir nuo tada.

Belieka rasti... lengva pasakyti :) Bet va, važiuojam. Pagal matematinio lūkesčio apibrėžimą:
- pakeičiame žinomas reikšmes:

- ir nieko daugiau iš šios lygties negalima išspausti, išskyrus tai, kad galite ją perrašyti įprasta kryptimi:

arba:

Manau, galite spėti apie tolesnius veiksmus. Sudarykime ir išspręskime sistemą:

Dešimtainės trupmenos, žinoma, yra visiška gėda; padauginkite abi lygtis iš 10:

ir padalinti iš 2:

Taip geriau. Iš 1 lygties išreiškiame:
(tai paprastesnis būdas)- 2-oje lygtyje pakeičiame:

Mes statome kvadratu ir padaryti supaprastinimus:

Padauginti iš:

Rezultatas yra kvadratinė lygtis, randame jo diskriminaciją:
- puikus!

ir gauname du sprendimus:

1) jei , tada ;

2) jei , tada.

Pirmoji verčių pora atitinka sąlygą. Su didele tikimybe viskas teisinga, bet vis dėlto rašome paskirstymo dėsnį:

ir mes patikrinsime, o būtent, rasime lūkesčius:

Dažnai statistikoje, analizuojant reiškinį ar procesą, reikia atsižvelgti ne tik į informaciją apie vidutinius tiriamų rodiklių lygius, bet ir atskirų vienetų verčių sklaida arba kitimas , kuri yra svarbi tikslinės populiacijos savybė.

Akcijų kainos, pasiūlos ir paklausos apimtys, palūkanų normos skirtingu laiku ir skirtingose ​​vietose yra didžiausios.

Pagrindiniai kitimą apibūdinantys rodikliai , yra diapazonas, dispersija, standartinis nuokrypis ir variacijos koeficientas.

Perbraukimo variantas yra skirtumas tarp didžiausių ir mažiausių atributo verčių: R = Xmax – Xmin... Šio rodiklio trūkumas yra tas, kad jis įvertina tik požymio kitimo ribas ir neatspindi jo svyravimų šiose ribose.

Sklaida neturi šio trūkumo. Jis apskaičiuojamas kaip būdingų verčių nuokrypių nuo jų vidutinės vertės vidutinis kvadratas:

Supaprastintas dispersijos skaičiavimo būdas atliekama naudojant šias formules (paprastas ir svertines):

Šių formulių naudojimo pavyzdžiai pateikti 1 ir 2 užduotyse.

Praktikoje plačiai naudojamas rodiklis yra standartinis nuokrypis :

Standartinis nuokrypis apibrėžiamas kaip dispersijos kvadratinė šaknis ir turi tokį patį matmenį kaip ir tiriamas požymis.

Nagrinėjami rodikliai leidžia gauti absoliučią variacijos reikšmę, t.y. įvertinti jį tiriamo požymio vienetais. Skirtingai nei jie, variacijos koeficientas matuoja svyravimus santykiniais dydžiais – palyginti su vidutiniu lygiu, kuris daugeliu atvejų yra pageidautinas.

Variacijos koeficiento apskaičiavimo formulė.

Problemų sprendimo pavyzdžiai tema „Statistikos kitimo rodikliai“

1 problema ... Tiriant reklamos įtaką vidutinio mėnesinio indėlio dydžiui regiono bankuose, buvo ištirti 2 bankai. Buvo gauti šie rezultatai:

Apibrėžkite:
1) kiekvienam bankui: a) vidutinis mėnesio indėlio dydis; b) įnašo dispersija;
2) vidutinis mėnesinis indėlis dviem bankams kartu;
3) Užstato paskirstymas 2 bankams, priklausomai nuo reklamos;
4) Indėlio paskirstymas 2 bankams, priklausomai nuo visų faktorių, išskyrus reklamą;
5) Bendra dispersija naudojant sudėjimo taisyklę;
6) Determinacijos koeficientas;
7) Koreliacijos koeficientas.

Sprendimas

1) Sudarykime skaičiavimo lentelę bankui su reklama ... Norėdami nustatyti vidutinį mėnesio indėlio dydį, rasime intervalų vidurio taškus. Šiuo atveju atvirojo intervalo reikšmė (pirmasis) sąlyginai prilyginama šalia esančio intervalo reikšmei (antrasis).

Vidutinį įnašo dydį randame pagal aritmetinio svertinio vidurkio formulę:

29 000/50 = 580 rublių.

Įnašo dispersiją randame pagal formulę:

23 400/50 = 468

Mes atliksime panašius veiksmus bankui be reklamos :

2) Raskime vidutinį indėlio dydį dviem bankams kartu. Xav = (580 × 50 + 542,8 × 50) / 100 = 561,4 rubliai.

3) Dviejų bankų įnašo dispersiją, priklausomai nuo reklamos, randame pagal formulę: σ 2 = pq (alternatyvaus požymio dispersijos formulė). Čia p = 0,5 yra veiksnių, kurie priklauso nuo reklamos, dalis; q = 1-0,5, tada σ 2 = 0,5 * 0,5 = 0,25.

4) Kadangi kitų veiksnių dalis yra 0,5, dviejų bankų įnašo dispersija, kuri priklauso nuo visų veiksnių, išskyrus reklamą, taip pat yra 0,25.

5) Naudodami sudėjimo taisyklę, nustatykite bendrą dispersiją.

= (468*50+636,16*50)/100=552,08

= [(580-561,4)250+(542,8-561,4)250] / 100= 34 596/ 100=345,96

σ 2 = σ 2 faktas + σ 2 poilsis = 552,08 + 345,96 = 898,04

6) Determinacijos koeficientas η 2 = σ 2 faktas / σ 2 = 345,96 / 898,04 = 0,39 = 39% - įnašo dydis priklauso nuo reklamos 39%.

7) Empirinis koreliacijos koeficientas η = √η 2 = √0,39 = 0,62 – ryšys gana glaudus.

2 užduotis ... Yra įmonių grupavimas pagal parduodamų produktų dydį:

Nustatyti: 1) prekinių gaminių vertės dispersiją; 2) standartinis nuokrypis; 3) variacijos koeficientas.

Sprendimas

1) Pagal sąlygą pateikiama intervalų pasiskirstymo eilutė. Jis turi būti išreikštas diskretiškai, tai yra rasti intervalo vidurį (x "). Uždarųjų intervalų grupėse vidurį rasime paprastu aritmetiniu vidurkiu. Grupėse su viršutine riba kaip skirtumas tarp šios viršutinės ribą ir pusę po jos einančio intervalo dydžio (200- (400 -200): 2 = 100).

Grupėse su apatine kraštine - šios apatinės kraštinės ir pusės ankstesnio intervalo dydžio suma (800+ (800-600): 2 = 900).

Vidutinę parduodamų produktų vertę apskaičiuojame pagal formulę:

Xav = k × ((Σ ((x "-a): k) × f): Σf) + a. Čia a = 500 yra didžiausio dažnio varianto dydis, k = 600-400 = 200 yra intervalo dydis didžiausiu dažniu . Įdėkite rezultatą į lentelę:

Taigi vidutinė parduodamos produkcijos vertė tiriamuoju laikotarpiu paprastai yra lygi Xav = (-5: 37) × 200 + 500 = 472,97 tūkst.

2) Dispersiją randame pagal šią formulę:

σ 2 = (33/37) * 2002- (472,97-500) 2 = 35 675,67-730,62 = 34 945,05

3) standartinis nuokrypis: σ = ± √σ 2 = ± √34 945,05 ≈ ± 186,94 tūkst.

4) variacijos koeficientas: V = (σ / Xav) * 100 = (186,94 / 472,97) * 100 = 39,52 %

Sugrupuotiems duomenims liekamoji dispersija- grupės vidaus dispersijų vidurkis:

Kur σ 2 j yra j -osios grupės vidinė dispersija.

Nesugrupuotiems duomenims liekamoji dispersija Ar aproksimacijos tikslumo matas, t.y. regresijos tiesės aproksimacija pirminiams duomenims:
čia y (t) yra prognozė pagal tendencijos lygtį; y t yra pradinė dinamikos eilutė; n yra taškų skaičius; p – regresijos lygties koeficientų skaičius (aiškinamųjų kintamųjų skaičius).
Šiame pavyzdyje jis vadinamas nešališkas dispersijos įvertinimas.

1 pavyzdys. Vienos asociacijos trijų įmonių darbuotojų pasiskirstymas pagal tarifų kategorijas apibūdinamas šiais duomenimis:

Darbuotojo darbo užmokesčio norma	Darbuotojų skaičius įmonėje
	įmonė 1	įmonė 2	įmonė 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Apibrėžkite:
1. dispersija kiekvienai įmonei (intragroup dispersija);
2. grupės vidaus dispersijų vidurkis;
3. tarpgrupinė dispersija;
4. bendroji dispersija.

Sprendimas.
Prieš pradedant spręsti problemą, būtina išsiaiškinti, kuri funkcija yra efektyvi, o kuri faktorinė. Nagrinėjamame pavyzdyje galiojantis požymis yra „Tarifo kategorija“, o faktoriaus atributas – „Įmonės numeris (pavadinimas).
Tada turime tris grupes (įmones), kurioms reikia apskaičiuoti grupės vidurkį ir grupės vidaus dispersijas:

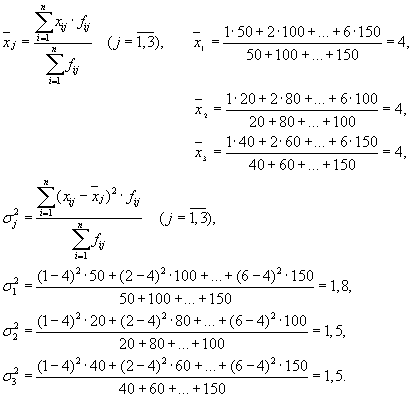
Bendrovė	Grupės vidurkis,	dispersija tarp grupės,
1	4	1,8

Vidutinės grupės dispersijų vidurkis ( liekamoji dispersija) bus apskaičiuojamas pagal formulę:

kur galima paskaičiuoti:
arba:

tada:
Bendra dispersija bus lygi: s 2 = 1,6 + 0 = 1,6.
Bendrą dispersiją taip pat galima apskaičiuoti naudojant vieną iš šių dviejų formulių:

Sprendžiant praktines problemas, dažnai tenka susidurti su savybe, kuri turi tik dvi alternatyvias reikšmes. Šiuo atveju kalbama ne apie konkrečios atributo reikšmės svorį, o apie jos dalį visumoje. Jei tiriamą požymį turinčių vienetų dalis populiacijoje žymima „ R", O neturėti - per" q“, Tada dispersiją galima apskaičiuoti pagal formulę:
s 2 = p × q

2 pavyzdys. Remdamiesi šešių komandoje dirbančių darbuotojų produkcijos duomenimis, nustatykite tarpgrupinę dispersiją ir įvertinkite darbo pamainos įtaką jų darbo našumui, jei bendra dispersija yra 12,2.

Darbo brigados numeris	Darbininkų produkcija, vnt.
	1-oje pamainoje	antros pamainos metu
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Sprendimas... Pradiniai duomenys

X	f 1	f 2	f 3	f 4	f 5	f 6	Iš viso
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Iš viso	31	33	37	37	40	38

Tada turime 6 grupes, kurioms reikia apskaičiuoti grupės vidurkį ir grupės vidaus dispersijas.
1. Raskite kiekvienos grupės vidutines vertes.







2. Raskite kiekvienos grupės vidutinį kvadratą.







Skaičiavimo rezultatai apibendrinti lentelėje:

Grupės numeris	Grupės vidurkis	Grupės dispersija
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Grupės dispersija apibūdina tiriamo (veiksmingo) bruožo kitimą (variaciją) grupėje, veikiant visiems jai veiksniams, išskyrus veiksnį, kuriuo grindžiamas grupavimas:
Vidutinės grupės dispersijų vidurkis apskaičiuojamas pagal formulę:


4. Tarpgrupinė dispersija charakterizuoja tiriamo (efektyvaus) požymio kitimą (variaciją) veikiant jam veiksniui (veiksnio požymiui), kuris yra grupavimo pagrindas.
Tarpgrupinė dispersija apibrėžiama taip:

kur


Tada

Bendra dispersija charakterizuoja tiriamo (efektyvaus) požymio kitimą (variaciją) veikiant visiems be išimties veiksniams (veiksnių atributams). Pagal uždavinio sąlygą jis lygus 12,2.
Empirinis koreliacinis ryšys matuoja, kiek bendro efektyvaus požymio kintamumo lemia tiriamas veiksnys. Tai faktoriaus dispersijos ir bendros dispersijos santykis:

Nustatykite empirinį koreliacijos santykį:

Ryšiai tarp ženklų gali būti silpni ir stiprūs (glaudūs). Jų kriterijai vertinami Chaddock skalėje:
0,1 0,3 0,5 0,7 0,9 Mūsų pavyzdyje ryšys tarp Y bruožo ir faktoriaus X yra silpnas
Determinacijos koeficientas.

Apibrėžkime determinacijos koeficientą:

Taigi 0,67 % svyravimo atsiranda dėl bruožų skirtumų, o 99,37 % – kitų veiksnių.
Išvada: šiuo atveju darbuotojų gamyba nepriklauso nuo darbo konkrečioje pamainoje, t.y. darbo pamainos įtaka jų darbo našumui nėra reikšminga ir atsiranda dėl kitų veiksnių.

3 pavyzdys. Remdamiesi dviejų darbuotojų grupių vidutinio darbo užmokesčio duomenimis ir nuokrypių nuo jo reikšmės kvadratais, raskite bendrą dispersiją taikydami dispersijų pridėjimo taisyklę:

Sprendimas:
Vidurkis skirtumų grupės viduje

Tarpgrupinė dispersija apibrėžiama taip:


Bendra dispersija bus: 480 + 13824 = 14304

Atsitiktinio dydžio X matematinė prognozė (vidutinė reikšmė), pateikta diskrečioje tikimybių erdvėje, yra skaičius m = M [X] = ∑x i p i, jei eilutė absoliučiai konverguoja.

Paslaugos tikslas... Paslaugos naudojimas internetu apskaičiuojama matematinė prognozė, dispersija ir standartinis nuokrypis(žr. pavyzdį). Be to, nubraižytas skirstinio funkcijos F (X) grafikas.

Atsitiktinio dydžio matematinio lūkesčio savybės

1. Matematinis pastovios reikšmės lūkestis yra lygus jai pačiai: M [C] = C, C yra konstanta;
2. M = C M [X]
3. Atsitiktinių dydžių sumos matematinis lūkestis yra lygus jų matematinių lūkesčių sumai: M = M [X] + M [Y]
4. Nepriklausomų atsitiktinių dydžių sandaugos matematinis lūkestis yra lygus jų matematinių lūkesčių sandaugai: M = M [X] M [Y], jei X ir Y yra nepriklausomi.

Dispersijos savybės

1. Konstantos dispersija lygi nuliui: D (c) = 0.
2. Pastovųjį koeficientą galima išimti iš dispersijos ženklo, padalijus jį kvadratu: D (k * X) = k 2 D (X).
3. Jeigu atsitiktiniai dydžiai X ir Y yra nepriklausomi, tai sumos dispersija lygi dispersijų sumai: D (X + Y) = D (X) + D (Y).
4. Jei atsitiktiniai dydžiai X ir Y yra priklausomi: D (X + Y) = DX + DY + 2 (X-M [X]) (Y-M [Y])
5. Skaičiavimo formulė galioja dispersijai:
   D (X) = M (X 2) – (M (X)) 2

Pavyzdys. Žinomi dviejų nepriklausomų atsitiktinių dydžių X ir Y matematiniai lūkesčiai ir dispersijos: M (x) = 8, M (Y) = 7, D (X) = 9, D (Y) = 6. Raskite atsitiktinio dydžio Z = 9X-8Y + 7 matematinę lūkesčius ir dispersiją.
Sprendimas. Remiantis matematinio lūkesčio savybėmis: M (Z) = M (9X-8Y + 7) = 9 * M (X) - 8 * M (Y) + M (7) = 9 * 8 - 8 * 7 + 7 = 23 ...
Remiantis dispersijos savybėmis: D (Z) = D (9X-8Y + 7) = D (9X) - D (8Y) + D (7) = 9 ^ 2D (X) - 8 ^ 2D (Y) + 0 = 81 * 9 - 64 * 6 = 345

Tikėtinos vertės apskaičiavimo algoritmas

Diskrečiųjų atsitiktinių dydžių savybės: visas jų reikšmes galima pernumeruoti natūraliaisiais skaičiais; kiekvienai reikšmei priskirkite nulinę tikimybę.

1. Poras: x i padauginame iš p i savo ruožtu.
2. Sudėkite kiekvienos poros sandaugą x i p i.
   Pavyzdžiui, jei n = 4: m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4

Diskretinio atsitiktinio dydžio pasiskirstymo funkcija laipsniškai jis staigiai didėja tuose taškuose, kurių tikimybė yra teigiama.

1 pavyzdys.

x i	1	3	4	7	9
p i	0.1	0.2	0.1	0.3	0.3

Matematinį lūkestį randame pagal formulę m = ∑x i p i.
Matematinis lūkestis M [X].
M [x] = 1 * 0,1 + 3 * 0,2 + 4 * 0,1 + 7 * 0,3 + 9 * 0,3 = 5,9
Dispersiją randame pagal formulę d = ∑x 2 i p i - M [x] 2.
Dispersija D [X].
D [X] = 1 2 * 0,1 + 3 2 * 0,2 + 4 2 * 0,1 + 7 2 * 0,3 + 9 2 * 0,3 - 5,9 2 = 7,69
Standartinis nuokrypis σ (x).
σ = kvadratas (D [X]) = kvadratas (7,69) = 2,78

2 pavyzdys. Diskretus atsitiktinis kintamasis turi tokią pasiskirstymo eilutę:

X	-10	-5	0	5	10
R	a	0,32	2a	0,41	0,03

Raskite šio atsitiktinio dydžio reikšmę a, matematinį lūkestį ir standartinį nuokrypį.

Sprendimas. Reikšmę a randame iš santykio: Σp i = 1
Σp i = a + 0,32 + 2 a + 0,41 + 0,03 = 0,76 + 3 a = 1
0,76 + 3 a = 1 arba 0,24 = 3 a, iš kur a = 0,08

3 pavyzdys. Nustatykite diskrečiojo atsitiktinio dydžio pasiskirstymo dėsnį, jei žinoma jo dispersija, ir x 1 x 1 = 6; x 2 = 9; x 3 = x; x 4 = 15
p 1 = 0,3; p 2 = 0,3; p 3 = 0,1; p 4 = 0,3
d (x) = 12,96

Sprendimas.
Čia reikia sudaryti formulę, kaip rasti dispersiją d (x):
d (x) = x 1 2 p 1 + x 2 2 p 2 + x 3 2 p 3 + x 4 2 p 4 -m (x) 2
kur lūkestis m (x) = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
Mūsų duomenims
m (x) = 6 * 0,3 + 9 * 0,3 + x 3 * 0,1 + 15 * 0,3 = 9 + 0,1 x 3
12,96 = 6 2 0,3 + 9 2 0,3 + x 3 2 0,1 + 15 2 0,3 (9 + 0,1 x 3) 2
arba -9/100 (x 2 -20x + 96) = 0
Atitinkamai, reikia rasti lygties šaknis, ir jų bus dvi.
x 3 = 8, x 3 = 12
Mes pasirenkame tą, kuris tenkina sąlygą x 1 x 3 = 12

Diskretinio atsitiktinio dydžio pasiskirstymo dėsnis
x 1 = 6; x 2 = 9; x 3 = 12; x 4 = 15
p 1 = 0,3; p 2 = 0,3; p 3 = 0,1; p 4 = 0,3