Gesamtvarianzmaße. Varianz und Standardabweichung

Die Streuung einer Zufallsvariablen ist ein Maß für die Streuung der Werte dieser Variablen. Kleine Varianz bedeutet, dass die Werte nahe beieinander liegen. Eine große Varianz weist auf eine starke Streuung der Werte hin. Der Begriff der Streuung einer Zufallsvariablen wird in der Statistik verwendet. Wenn Sie beispielsweise die Varianz der Werte zweier Größen vergleichen (z. B. die Ergebnisse von Beobachtungen männlicher und weiblicher Patienten), können Sie die Signifikanz einiger Variablen testen. Die Varianz wird auch beim Erstellen statistischer Modelle verwendet, da eine kleine Varianz ein Zeichen dafür sein kann, dass Sie Werte überanpassen.

Schritte

Stichprobenabweichungsberechnung

1. Notieren Sie die Probenwerte. In den meisten Fällen stehen den Statistikern nur Stichproben bestimmter Grundgesamtheiten zur Verfügung. Beispielsweise analysieren Statistiker in der Regel nicht die Kosten für die Aufrechterhaltung der Population aller Autos in Russland - sie analysieren eine Zufallsstichprobe von mehreren tausend Autos. Eine solche Stichprobe hilft bei der Bestimmung der durchschnittlichen Kosten pro Auto, aber höchstwahrscheinlich wird der resultierende Wert weit vom tatsächlichen Wert entfernt sein.

   • Analysieren wir zum Beispiel die Anzahl der Brötchen, die in einem Café in 6 Tagen in zufälliger Reihenfolge verkauft wurden. Die Stichprobe hat die folgende Form: 17, 15, 23, 7, 9, 13. Dies ist eine Stichprobe, keine Grundgesamtheit, da wir keine Daten über die verkauften Brötchen für jeden Tag haben, an dem das Café geöffnet ist.
   • Wenn Sie eine Grundgesamtheit und keine Stichprobe von Werten erhalten, fahren Sie mit dem nächsten Abschnitt fort.

2. Schreiben Sie die Formel zur Berechnung der Stichprobenvarianz auf. Streuung ist ein Maß für die Streuung von Werten einer bestimmten Menge. Je näher der Dispersionswert an Null liegt, desto enger werden die Werte gruppiert. Wenn Sie mit einer Stichprobe von Werten arbeiten, verwenden Sie die folgende Formel, um die Varianz zu berechnen:

   • s 2 (\displaystyle s^(2)) = ∑[(x ich (\ displaystyle x_ (i))-x) 2 (\displaystyle^(2))] / (n - 1)
   • s 2 (\displaystyle s^(2)) ist die Streuung. Die Streuung wird gemessen quadratische Einheiten Messungen.
   • x ich (\ displaystyle x_ (i))- jeder Wert in der Probe.
   • x ich (\ displaystyle x_ (i)) Sie müssen x̅ subtrahieren, quadrieren und dann die Ergebnisse addieren.
   • x̅ – Stichprobenmittelwert (Stichprobenmittelwert).
   • n ist die Anzahl der Werte in der Stichprobe.

3. Berechnen Sie den Stichprobenmittelwert. Es wird mit x̅ bezeichnet. Der Stichprobenmittelwert wird wie ein normaler arithmetischer Mittelwert berechnet: Addieren Sie alle Werte in der Stichprobe und dividieren Sie dann das Ergebnis durch die Anzahl der Werte in der Stichprobe.

   • Addieren Sie in unserem Beispiel die Werte in der Stichprobe: 15 + 17 + 23 + 7 + 9 + 13 = 84
     Teilen Sie nun das Ergebnis durch die Anzahl der Werte in der Stichprobe (in unserem Beispiel sind es 6): 84 ÷ 6 = 14.
     Stichprobenmittelwert x̅ = 14.
   • Der Stichprobenmittelwert ist der zentrale Wert, um den die Werte in der Stichprobe verteilt sind. Clustern sich die Werte in der Stichprobe um den Stichprobenmittelwert, dann ist die Varianz gering; andernfalls ist die Streuung groß.

4. Subtrahieren Sie den Stichprobenmittelwert von jedem Wert in der Stichprobe. Berechnen Sie nun die Differenz x ich (\ displaystyle x_ (i))- x̅, wo x ich (\ displaystyle x_ (i))- jeder Wert in der Probe. Jedes Ergebnis gibt den Grad der Abweichung eines bestimmten Werts vom Stichprobenmittelwert an, dh wie weit dieser Wert vom Stichprobenmittelwert entfernt ist.

   • In unserem Beispiel:
     x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
     x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
     x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
     x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
     x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
     x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
   • Die Richtigkeit der erhaltenen Ergebnisse ist leicht zu überprüfen, da ihre Summe gleich Null sein muss. Dies hängt mit der Ermittlung des Mittelwerts zusammen, da negative Werte (Abstände vom Mittelwert zu kleineren Werten) durch positive Werte (Abstände vom Mittelwert zu größeren Werten) vollständig ausgeglichen werden.

5. Wie oben erwähnt, die Summe der Differenzen x ich (\ displaystyle x_ (i))- x̅ muss gleich Null sein. Das bedeutet es durchschnittliche Abweichung immer gleich Null ist, was keine Aussage über die Streuung der Werte einer bestimmten Größe gibt. Um dieses Problem zu lösen, quadriere jede Differenz x ich (\ displaystyle x_ (i))- x. Dies führt dazu, dass Sie nur positive Zahlen erhalten, die zusammengenommen niemals 0 ergeben.

   • In unserem Beispiel:
     (x 1 (\displaystyle x_(1))-x) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
     (x 2 (\displaystyle (x_(2))-x) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
     9 2 = 81
     (-7) 2 = 49
     (-5) 2 = 25
     (-1) 2 = 1
   • Du hast das Quadrat der Differenz gefunden - x̅) 2 (\displaystyle^(2)) für jeden Wert in der Stichprobe.

6. Berechnen Sie die Summe der quadrierten Differenzen. Das heißt, finden Sie den Teil der Formel, der so geschrieben ist: ∑[( x ich (\ displaystyle x_ (i))-x) 2 (\displaystyle^(2))]. Hier bedeutet das Zeichen Σ die Summe der quadrierten Differenzen für jeden Wert x ich (\ displaystyle x_ (i)) in der Probe. Sie haben bereits die quadrierten Differenzen gefunden (x ich (\displaystyle (x_(i))-x) 2 (\displaystyle^(2)) für jeden Wert x ich (\ displaystyle x_ (i)) in der Probe; Fügen Sie jetzt einfach diese Quadrate hinzu.

   • In unserem Beispiel: 9 + 1 + 81 + 49 + 25 + 1 = 166 .

7. Teilen Sie das Ergebnis durch n - 1, wobei n die Anzahl der Werte in der Stichprobe ist. Vor einiger Zeit dividierten Statistiker zur Berechnung der Stichprobenvarianz einfach das Ergebnis durch n; In diesem Fall erhalten Sie den Mittelwert der quadrierten Varianz, was ideal ist, um die Varianz einer bestimmten Stichprobe zu beschreiben. Denken Sie jedoch daran, dass jede Stichprobe nur einen kleinen Teil der allgemeinen Wertepopulation darstellt. Wenn Sie eine andere Probe nehmen und die gleichen Berechnungen durchführen, erhalten Sie ein anderes Ergebnis. Wie sich herausstellt, ergibt eine Division durch n - 1 (anstatt nur durch n) eine bessere Schätzung der Populationsvarianz, worauf Sie hinaus wollen. Die Division durch n - 1 ist alltäglich geworden, daher ist sie in der Formel zur Berechnung der Stichprobenvarianz enthalten.

   • In unserem Beispiel enthält die Stichprobe 6 Werte, also n = 6.
     Probenvarianz = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2

8. Die Differenz zwischen der Varianz und der Standardabweichung. Beachten Sie, dass die Formel einen Exponenten enthält, sodass die Varianz in Quadrateinheiten des analysierten Werts gemessen wird. Manchmal ist ein solcher Wert ziemlich schwierig zu handhaben; in solchen Fällen wird die Standardabweichung verwendet, die gleich der Quadratwurzel der Varianz ist. Deshalb wird die Stichprobenvarianz als bezeichnet s 2 (\displaystyle s^(2)), a Standardabweichung Proben - wie s (\displaystyle s).

   • In unserem Beispiel beträgt die Standardabweichung der Stichprobe: s = √33,2 = 5,76.

   Populationsvarianzberechnung

   1. Analysieren Sie einige Werte. Das Set enthält alle Werte der betrachteten Menge. Zum Beispiel, wenn man das Alter der Einwohner untersucht Gebiet Leningrad, dann umfasst die Einwohnerzahl das Alter aller Einwohner dieses Gebiets. Bei der Arbeit mit einem Aggregat empfiehlt es sich, eine Tabelle zu erstellen und dort die Werte des Aggregats einzutragen. Betrachten Sie das folgende Beispiel:

      • Es gibt 6 Aquarien in einem bestimmten Raum. Jedes Aquarium enthält die folgende Anzahl an Fischen:
        x 1 = 5 (\displaystyle x_(1)=5)
        x 2 = 5 (\displaystyle x_(2)=5)
        x 3 = 8 (\displaystyle x_(3)=8)
        x 4 = 12 (\displaystyle x_(4)=12)
        x 5 = 15 (\displaystyle x_(5)=15)
        x 6 = 18 (\displaystyle x_(6)=18)

   2. Schreiben Sie die Formel zur Berechnung der Populationsvarianz auf. Da das Set alle Werte einer bestimmten Menge enthält, können Sie die folgende Formel erhalten genauer Wert Bevölkerungsvarianz. Um die Populationsvarianz von der Stichprobenvarianz (die nur eine Schätzung ist) zu unterscheiden, verwenden Statistiker verschiedene Variablen:

      • σ 2 (\displaystyle^(2)) = (∑(x ich (\ displaystyle x_ (i)) - μ) 2 (\displaystyle^(2))) / n
      • σ 2 (\displaystyle^(2))- Populationsvarianz (gelesen als "Sigma im Quadrat"). Die Streuung wird in Quadrateinheiten gemessen.
      • x ich (\ displaystyle x_ (i))- jeder Wert insgesamt.
      • Σ ist das Vorzeichen der Summe. Das heißt, für jeden Wert x ich (\ displaystyle x_ (i)) subtrahieren Sie μ, quadrieren Sie es und addieren Sie dann die Ergebnisse.
      • μ ist der Populationsmittelwert.
      • n ist die Anzahl der Werte in der Allgemeinbevölkerung.

   3. Berechnen Sie den Populationsmittelwert. Bei der Arbeit mit der allgemeinen Bevölkerung wird sein Durchschnittswert als μ (mu) bezeichnet. Der Populationsmittelwert wird als übliches arithmetisches Mittel berechnet: Addieren Sie alle Werte in der Population und dividieren Sie dann das Ergebnis durch die Anzahl der Werte in der Population.

      • Beachten Sie, dass Durchschnittswerte nicht immer als arithmetisches Mittel berechnet werden.
      • In unserem Beispiel bedeutet die Population: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5

   4. Subtrahieren Sie den Mittelwert der Grundgesamtheit von jedem Wert in der Grundgesamtheit. Je näher der Differenzwert bei Null liegt, desto näher liegt der jeweilige Wert am Grundgesamtheitsmittelwert. Finden Sie die Differenz zwischen jedem Wert in der Grundgesamtheit und ihrem Mittelwert, und Sie erhalten einen ersten Blick auf die Verteilung der Werte.

      • In unserem Beispiel:
        x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
        x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
        x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
        x 4 (\displaystyle x_(4))- µ = 12 - 10,5 = 1,5
        x 5 (\displaystyle x_(5))- µ = 15 - 10,5 = 4,5
        x 6 (\displaystyle x_(6))- µ = 18 - 10,5 = 7,5

   5. Quadriere jedes Ergebnis, das du erhältst. Die Differenzwerte sind sowohl positiv als auch negativ; wenn Sie diese Werte auf einen Zahlenstrahl setzen, dann liegen sie rechts und links vom Mittelwert der Grundgesamtheit. Dies ist nicht gut für die Berechnung der Varianz, da sich positive und negative Zahlen gegenseitig aufheben. Quadrieren Sie daher jede Differenz, um ausschließlich positive Zahlen zu erhalten.

      • In unserem Beispiel:
        (x ich (\ displaystyle x_ (i)) - μ) 2 (\displaystyle^(2)) für jeden Populationswert (von i = 1 bis i = 6):
        (-5,5)2 (\displaystyle^(2)) = 30,25
        (-5,5)2 (\displaystyle^(2)), wo xn (\displaystyle x_(n)) ist der letzte Wert in der Grundgesamtheit.
      • Um den Durchschnittswert der erhaltenen Ergebnisse zu berechnen, müssen Sie ihre Summe finden und durch n dividieren: (( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle^(2)) + ... + (xn (\displaystyle x_(n)) - μ) 2 (\displaystyle^(2))) / n
      • Lassen Sie uns nun die obige Erklärung unter Verwendung von Variablen schreiben: (∑( x ich (\ displaystyle x_ (i)) - μ) 2 (\displaystyle^(2))) / n und erhalten eine Formel zur Berechnung der Populationsvarianz.

Streuung wird in der Statistik definiert als die Standardabweichung der Einzelwerte eines Merkmals zum Quadrat vom arithmetischen Mittel. Eine gängige Methode, um die quadratischen Abweichungen von Optionen vom Mittelwert zu berechnen und dann zu mitteln.

In der wirtschaftlichen und statistischen Analyse ist es üblich, die Variation eines Merkmals meistens anhand der Standardabweichung zu bewerten, die die Quadratwurzel der Varianz ist.

(3)

Sie charakterisiert die absolute Schwankung der Werte des Variablenattributs und wird in den gleichen Einheiten wie die Varianten ausgedrückt. In der Statistik ist es oft notwendig, die Streuung verschiedener Merkmale zu vergleichen. Für solche Vergleiche wird ein relativer Variationsindikator, der Variationskoeffizient, verwendet.

Dispersionseigenschaften:

1) Wenn Sie eine beliebige Zahl von allen Optionen abziehen, ändert sich die Varianz nicht;

2) Wenn alle Werte der Variante durch eine Zahl b geteilt werden, verringert sich die Varianz um b^2 mal, d.h.

3) Wenn Sie das durchschnittliche Quadrat der Abweichungen von einer beliebigen Zahl mit einem ungleichen arithmetischen Mittel berechnen, ist es größer als die Varianz. In diesem Fall um einen genau definierten Wert pro Quadrat der Differenz zwischen dem Mittelwert von pos.

Die Varianz kann als Differenz zwischen dem Mittelwert im Quadrat und dem Mittelwert im Quadrat definiert werden.

17. Gruppen- und Intergruppenvariationen. Varianzadditionsregel

Wenn die statistische Grundgesamtheit gemäß dem untersuchten Merkmal in Gruppen oder Teile unterteilt wird, können für eine solche Grundgesamtheit die folgenden Arten der Streuung berechnet werden: Gruppe (privat), Gruppendurchschnitt (privat) und Intergruppe.

Totale Varianz- spiegelt die Variation eines Merkmals aufgrund aller Bedingungen und Ursachen wider, die in einer bestimmten statistischen Population wirken.

Gruppenvarianz- ist gleich dem mittleren Quadrat der Abweichungen der Einzelwerte des Attributs innerhalb der Gruppe vom arithmetischen Mittel dieser Gruppe, dem sogenannten Gruppenmittel. In diesem Fall stimmt der Gruppendurchschnitt nicht mit dem Gesamtdurchschnitt der Gesamtbevölkerung überein.

Die Gruppenvarianz spiegelt die Variation eines Merkmals nur aufgrund der Bedingungen und Ursachen wider, die innerhalb der Gruppe wirken.

Durchschnittliche Gruppenabweichungen- ist definiert als das gewichtete arithmetische Mittel der Gruppenstreuungen, wobei die Gewichte die Volumina der Gruppen sind.

Intergruppenvarianz- ist gleich dem mittleren Quadrat der Abweichungen der Gruppenmittel vom Gesamtmittel.

Die Intergruppenvarianz charakterisiert die Variation des resultierenden Attributs aufgrund des Gruppierungsattributs.

Zwischen den betrachteten Arten von Streuungen besteht eine gewisse Beziehung: Die Gesamtstreuung ist gleich der Summe der durchschnittlichen Gruppen- und Intergruppenstreuung.

Diese Beziehung wird Varianzadditionsregel genannt.

18. Dynamische Reihen und ihre Bestandteile. Arten dynamischer Reihen.

Reihe in der Statistik- dies sind digitale Daten, die zeigen, ob sich ein Phänomen zeitlich oder räumlich verändert und die einen statistischen Vergleich von Phänomenen sowohl im Verlauf ihrer zeitlichen als auch in ihrer Entwicklung ermöglichen verschiedene Formen und Arten von Prozessen. Dadurch ist es möglich, die gegenseitige Abhängigkeit von Phänomenen zu erkennen.

Der Entwicklungsprozess der zeitlichen Bewegung sozialer Phänomene in der Statistik wird üblicherweise als Dynamik bezeichnet. Um die Dynamik darzustellen, werden Reihen von Dynamiken (chronologisch, zeitlich) aufgebaut, die Reihen von zeitlich veränderlichen Werten eines statistischen Indikators (z. B. die Anzahl der Sträflinge über 10 Jahre) sind, die in chronologischer Reihenfolge angeordnet sind. Ihre Bestandteile sind die Zahlenwerte eines bestimmten Indikators und die Zeiträume oder Zeitpunkte, auf die sie sich beziehen.

Das wichtigste Merkmal von Zeitreihen- ihre Größe (Volumen, Wert) dieses oder jenes Phänomens, das in einem bestimmten Zeitraum oder zu einem bestimmten Zeitpunkt erreicht wurde. Dementsprechend ist die Größe der Terme der Dynamikreihe ihre Ebene. Unterscheiden Anfangs-, Mittel- und Endstufe der dynamischen Reihe. Erste Ebene zeigt den Wert des ersten, letzten - den Wert des letzten Mitglieds der Reihe. Durchschnittsniveau stellt den durchschnittlichen zeitlichen Schwankungsbereich dar und wird in Abhängigkeit davon berechnet, ob es sich bei der Zeitreihe um ein Intervall oder einen Augenblick handelt.

Ein weiteres wichtiges Merkmal der dynamischen Serie- die verstrichene Zeit von der ersten bis zur letzten Beobachtung oder die Anzahl solcher Beobachtungen.

Es gibt verschiedene Arten von Zeitreihen, die nach folgenden Kriterien klassifiziert werden können.

1) Abhängig von der Art, die Niveaus auszudrücken, werden die Reihen der Dynamik in Reihen von absoluten und abgeleiteten Indikatoren (relative und durchschnittliche Werte) unterteilt.

2) Je nachdem, wie die Stufen der Reihe den Zustand des Phänomens zu bestimmten Zeitpunkten (Monats-, Quartals-, Jahresanfang usw.) oder seinen Wert für bestimmte Zeitintervalle (z. B. pro Tag, Monat, Jahr usw.) usw.), jeweils Moment und unterscheiden Intervallserie Dynamik. Momentenreihen in der analytischen Arbeit von Strafverfolgungsbehörden werden relativ selten verwendet.

In der Theorie der Statistik wird die Dynamik auch nach einer Reihe weiterer Gliederungsmerkmale unterschieden: je nach Abstand zwischen den Ebenen - mit äquidistanten Ebenen und zeitlich ungleichen Ebenen; abhängig vom Vorhandensein des Haupttrends des untersuchten Prozesses - stationär und nicht stationär. Bei der Analyse dynamischer Reihen werden die folgenden Ebenen der Reihe als Komponenten dargestellt:

Y t \u003d TP + E (t)

wobei TR eine deterministische Komponente ist, die den allgemeinen Änderungstrend im Laufe der Zeit oder einen Trend bestimmt.

E (t) ist eine Zufallskomponente, die Pegelschwankungen verursacht.

Streuungzufällige Variable- ein Maß für die Streuung einer gegebenen zufällige Variable, das ist sie Abweichungen aus mathematischer Erwartung. In der Statistik wird häufig die Notation (Sigma zum Quadrat) verwendet, um die Varianz zu bezeichnen. Die Quadratwurzel der Varianz wird aufgerufen Standardabweichung oder Standardaufstrich. Die Standardabweichung wird in denselben Einheiten gemessen wie die Zufallswert, und die Varianz wird in den Quadraten dieser Einheit gemessen.

Obwohl es sehr praktisch ist, nur einen Wert (z. B. Mittelwert oder Modus und Median) zu verwenden, um die gesamte Stichprobe zu schätzen, kann dieser Ansatz leicht zu falschen Schlussfolgerungen führen. Der Grund für diese Situation liegt nicht im Wert selbst, sondern darin, dass ein Wert in keiner Weise die Streuung von Datenwerten widerspiegelt.

Zum Beispiel im Beispiel:

der Durchschnitt liegt bei 5.

Es gibt jedoch kein Element in der Stichprobe selbst mit einem Wert von 5. Möglicherweise müssen Sie wissen, wie nahe jedes Element der Stichprobe an seinem Mittelwert liegt. Oder mit anderen Worten, Sie müssen die Varianz der Werte kennen. Wenn Sie wissen, inwieweit sich die Daten geändert haben, können Sie sie besser interpretieren mittlere Bedeutung, Median und Mode. Der Grad der Änderung der Stichprobenwerte wird durch Berechnung ihrer Varianz und Standardabweichung bestimmt.

Streuung u Quadratwurzel der Varianz, genannt Standardabweichung, charakterisieren die mittlere Abweichung vom Mittelwert der Stichprobe. Unter diesen beiden Größen Höchster Wert Es hat Standardabweichung. Dieser Wert kann als durchschnittlicher Abstand dargestellt werden, in dem sich die Elemente vom mittleren Element der Probe befinden.

Streuung ist schwer sinnvoll zu interpretieren. Die Quadratwurzel dieses Werts ist jedoch die Standardabweichung und eignet sich gut zur Interpretation.

Die Standardabweichung wird berechnet, indem zuerst die Varianz bestimmt und dann die Quadratwurzel der Varianz berechnet wird.

Für das in der Abbildung gezeigte Datenarray werden beispielsweise die folgenden Werte erhalten:

Bild 1

Hier beträgt der Mittelwert der quadrierten Differenzen 717,43. Um die Standardabweichung zu erhalten, muss nur noch die Quadratwurzel dieser Zahl gezogen werden.

Das Ergebnis wird etwa 26,78 sein.

Es sollte daran erinnert werden, dass die Standardabweichung als der durchschnittliche Abstand interpretiert wird, in dem die Elemente vom Stichprobenmittelwert entfernt sind.

Die Standardabweichung zeigt, wie gut der Mittelwert die gesamte Stichprobe beschreibt.

Angenommen, Sie sind der Manager Produktionsabteilung PC-Montage. Der Quartalsbericht sagt, dass der Output für das letzte Quartal 2500 PCs betrug. Ist es schlecht oder gut? Sie haben darum gebeten (oder es gibt diese Spalte bereits im Bericht), die Standardabweichung für diese Daten im Bericht anzuzeigen. Die Standardabweichungszahl ist beispielsweise 2000. Als Abteilungsleiter wird Ihnen klar, dass die Produktionslinie besser kontrolliert werden muss (zu große Abweichungen in der Anzahl der zu montierenden PCs).

Erinnern wir uns: wann große Größe Wenn die Standardabweichung zu niedrig ist, liegen die Daten weit um den Mittelwert herum gestreut, und wenn die Standardabweichung niedrig ist, werden sie in der Nähe des Mittelwerts geclustert.

Die vier statistischen Funktionen VAR(), VAR(), STDEV() und STDEV() wurden entwickelt, um die Varianz und Standardabweichung von Zahlen in einem Bereich von Zellen zu berechnen. Bevor Sie die Varianz und Standardabweichung eines Datensatzes berechnen können, müssen Sie bestimmen, ob die Daten die Grundgesamtheit oder eine Stichprobe der Grundgesamtheit darstellen. Im Falle einer Stichprobe aus der Allgemeinbevölkerung sollten die Funktionen VARP() und STABW() verwendet werden, und im Falle der Allgemeinbevölkerung sollten die Funktionen VARP() und STABW() verwendet werden:

Bevölkerung	Funktion
	VARP()
	STDLONG()
Probe
	VARI()
	STABW()

Die Streuung (wie auch die Standardabweichung) gibt, wie wir angemerkt haben, an, inwieweit die im Datensatz enthaltenen Werte um das arithmetische Mittel gestreut sind.

Ein kleiner Wert der Varianz oder Standardabweichung zeigt an, dass sich alle Daten um das arithmetische Mittel konzentrieren, und ein großer Wert dieser Werte zeigt an, dass die Daten über einen weiten Wertebereich verstreut sind.

Die Varianz ist eher schwer sinnvoll zu interpretieren (was bedeutet ein kleiner Wert, ein großer Wert?). Leistung Aufgaben 3 ermöglicht es Ihnen, die Bedeutung der Varianz für einen Datensatz visuell in einem Diagramm darzustellen.

Aufgaben

· Übung 1.

· 2.1. Nennen Sie die Begriffe: Varianz und Standardabweichung; ihre symbolische Bezeichnung in der statistischen Datenverarbeitung.

· 2.2. Erstellen Sie ein Arbeitsblatt gemäß Abbildung 1 und führen Sie die erforderlichen Berechnungen durch.

· 2.3. Geben Sie die Grundformeln an, die in den Berechnungen verwendet werden

· 2.4. Erklären Sie alle Schreibweisen ( , , )

· 2.5. erklären praktischer Wert die Begriffe Varianz und Standardabweichung.

Aufgabe 2.

1.1. Nennen Sie die Begriffe: Allgemeinbevölkerung und Stichprobe; erwarteter Wert und ihr arithmetisches Mittel symbolische Bezeichnung während der statistischen Datenverarbeitung.

1.2. Erstellen Sie gemäß Abbildung 2 ein Arbeitsblatt und führen Sie Berechnungen durch.

1.3. Geben Sie die grundlegenden Formeln an, die in den Berechnungen verwendet wurden (für die allgemeine Bevölkerung und die Stichprobe).

Figur 2

1.4. Erklären Sie, warum es möglich ist, solche arithmetischen Mittelwerte in Beispielen wie 46,43 und 48,78 zu erhalten (siehe Dateianhang). Schlussfolgern.

Aufgabe 3.

Es gibt zwei Proben mit anderer Satz Daten, aber der Durchschnitt für sie wird derselbe sein:

Figur 3

3.1. Erstellen Sie ein Arbeitsblatt gemäß Abbildung 3 und führen Sie die erforderlichen Berechnungen durch.

3.2. Geben Sie die grundlegenden Berechnungsformeln an.

3.3. Erstellen Sie Diagramme gemäß den Abbildungen 4, 5.

3.4. Erklären Sie die daraus resultierenden Abhängigkeiten.

3.5. Führen Sie ähnliche Berechnungen für diese beiden Proben durch.

Erstmuster 11119999

Wählen Sie die Werte der zweiten Stichprobe so, dass das arithmetische Mittel für die zweite Stichprobe gleich ist, zum Beispiel:

Wählen Sie die Werte für die zweite Probe selbst aus. Ordnen Sie Berechnungen und Plots wie in den Abbildungen 3, 4, 5 an. Zeigen Sie die wichtigsten Formeln, die bei den Berechnungen verwendet wurden.

Ziehen Sie die entsprechenden Schlüsse.

Alle Aufgaben sollten in Form eines Berichts mit allen erforderlichen Zahlen, Grafiken, Formeln und kurzen Erläuterungen präsentiert werden.

Hinweis: Die Konstruktion von Graphen muss mit Abbildungen und kurzen Erläuterungen erläutert werden.

Für gruppierte Daten Restdispersion- Durchschnitt der Streuungen innerhalb der Gruppe:

Wobei σ 2 j die gruppeninterne Varianz der j-ten Gruppe ist.

Für nicht gruppierte Daten Restdispersion ist ein Maß für die Näherungsgenauigkeit, d.h. Annäherung der Regressionsgerade an die Originaldaten:
wobei y(t) die Prognose gemäß der Trendgleichung ist; y t – Anfangsserie der Dynamik; n ist die Anzahl der Punkte; p ist die Anzahl der Koeffizienten der Regressionsgleichung (die Anzahl der erklärenden Variablen).
In diesem Beispiel heißt es unvoreingenommene Schätzung der Varianz.

Beispiel 1. Die Verteilung der Arbeitnehmer von drei Unternehmen eines Verbandes nach Tarifkategorien ist durch folgende Daten gekennzeichnet:

Lohnklasse des Arbeiters	Anzahl der Arbeitnehmer im Unternehmen
	Unternehmen 1	Unternehmen 2	Unternehmen 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Definieren:
1. Streuung je Unternehmen (konzerninterne Streuung);
2. Durchschnitt der gruppeninternen Streuungen;
3. Streuung zwischen den Gruppen;
4. Gesamtvarianz.

Lösung.
Bevor Sie mit der Lösung des Problems fortfahren, müssen Sie herausfinden, welches Merkmal effektiv und welches faktoriell ist. Im betrachteten Beispiel ist das Wirkmerkmal „Tarifgruppe“ und das Faktormerkmal „Nummer (Name) des Unternehmens“.
Dann haben wir drei Gruppen (Unternehmen), für die es notwendig ist, den Gruppendurchschnitt und die gruppeninternen Varianzen zu berechnen:

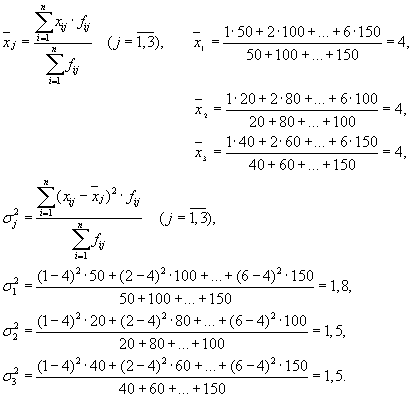
Gesellschaft	Gruppendurchschnitt,	Varianz innerhalb der Gruppe,
1	4	1,8

Der Durchschnitt der gruppeninternen Varianzen ( Restdispersion) berechnet nach der Formel:

wo kann man rechnen:
oder:

dann:
Die Gesamtdispersion ist gleich: s 2 \u003d 1,6 + 0 \u003d 1,6.
Die Gesamtabweichung kann auch mit einer der beiden folgenden Formeln berechnet werden:

Bei der Lösung praktischer Probleme hat man es oft mit einem Zeichen zu tun, das nur zwei alternative Werte annimmt. In diesem Fall sprechen sie nicht über das Gewicht eines bestimmten Werts eines Merkmals, sondern über seinen Anteil am Aggregat. Wenn der Anteil der Bevölkerungseinheiten, die das untersuchte Merkmal aufweisen, mit " R", und nicht besitzen - durch" q“, dann kann die Streuung nach folgender Formel berechnet werden:
s 2 = p × q

Beispiel #2. Bestimmen Sie auf der Grundlage der Daten zur Leistung von sechs Arbeitern der Brigade die Varianz zwischen den Gruppen und bewerten Sie die Auswirkungen der Arbeitsschicht auf ihre Arbeitsproduktivität, wenn die Gesamtvarianz 12,2 beträgt.

Nr. der Arbeitsbrigade	Arbeitsleistung, Stk.
	in der ersten Schicht	in 2 Schicht
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Lösung. Ausgangsdaten

X	f1	f2	f 3	f4	f5	f6	Gesamt
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Gesamt	31	33	37	37	40	38

Dann haben wir 6 Gruppen, für die es notwendig ist, den Gruppenmittelwert und die gruppeninternen Varianzen zu berechnen.
1. Finden Sie die Durchschnittswerte jeder Gruppe.







2. Ermitteln Sie das mittlere Quadrat jeder Gruppe.







Wir fassen die Ergebnisse der Berechnung in einer Tabelle zusammen:

Gruppennummer	Gruppendurchschnitt	Varianz innerhalb der Gruppe
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Varianz innerhalb der Gruppe charakterisiert die Veränderung (Variation) des untersuchten (resultierenden) Merkmals innerhalb der Gruppe unter dem Einfluss aller Faktoren, mit Ausnahme des der Gruppierung zugrunde liegenden Faktors:
Den Durchschnitt der gruppeninternen Streuungen berechnen wir nach folgender Formel:


4. Intergruppenvarianz charakterisiert die Veränderung (Variation) des untersuchten (resultierenden) Merkmals unter dem Einfluss eines der Gruppierung zugrunde liegenden Faktors (faktorielles Merkmal).
Streuung zwischen Gruppen ist definiert als:

wo


Dann

Totale Varianz charakterisiert die Veränderung (Variation) des untersuchten (resultierenden) Merkmals unter dem Einfluss aller Faktoren (faktorielle Merkmale) ausnahmslos. Durch den Zustand des Problems ist es gleich 12.2.
Empirische Korrelationsbeziehung misst, wie viel der Gesamtschwankung des resultierenden Attributs durch den untersuchten Faktor verursacht wird. Dies ist das Verhältnis der faktoriellen Varianz zur Gesamtvarianz:

Wir bestimmen die empirische Korrelationsbeziehung:

Beziehungen zwischen Merkmalen können schwach oder stark (eng) sein. Ihre Kriterien werden auf der Chaddock-Skala bewertet:
0,1 0,3 0,5 0,7 0,9 In unserem Beispiel ist die Beziehung zwischen Merkmal Y Faktor X schwach
Bestimmtheitsmaß.

Lassen Sie uns das Bestimmtheitsmaß definieren:

Somit sind 0,67 % der Variation auf Unterschiede zwischen den Merkmalen und 99,37 % auf andere Faktoren zurückzuführen.
Fazit: In diesem Fall hängt die Leistung der Arbeiter nicht von der Arbeit in einer bestimmten Schicht ab, d.h. der Einfluss der Arbeitsschicht auf ihre Arbeitsproduktivität ist nicht signifikant und auf andere Faktoren zurückzuführen.

Beispiel #3. Basierend auf dem Durchschnitt Löhne und quadrierte Abweichungen von seinem Wert für zwei Gruppen von Arbeitern, finden Sie die Gesamtvarianz, indem Sie die Regel zum Addieren von Varianzen anwenden:

Lösung:
Durchschnitt der Varianzen innerhalb der Gruppe

Streuung zwischen Gruppen ist definiert als:


Die Gesamtvarianz beträgt: 480 + 13824 = 14304

Wenn die Population gemäß dem untersuchten Merkmal in Gruppen eingeteilt wird, können für diese Population die folgenden Arten der Streuung berechnet werden: Gesamt, Gruppe (Intragruppen), Gruppendurchschnitt (Durchschnitt der Intragruppen), Intergruppen.

Zunächst berechnet es das Bestimmtheitsmaß, das zeigt, welcher Teil der Gesamtvariation des untersuchten Merkmals die Intergruppenvariation ist, d.h. wegen Gruppierung:

Das empirische Korrelationsverhältnis charakterisiert die Enge des Zusammenhangs zwischen der Gruppierung (faktoriell) und den effektiven Vorzeichen.

Das empirische Korrelationsverhältnis kann Werte von 0 bis 1 annehmen.

Um die Nähe der Beziehung basierend auf dem empirischen Korrelationsverhältnis zu beurteilen, können Sie die Chaddock-Beziehungen verwenden:

Beispiel 4 Es gibt die folgenden Daten zur Arbeitsleistung von Design- und Umfrageorganisationen verschiedene Formen Eigentum:

Definieren:

1) Gesamtvarianz;

2) Gruppendispersionen;

3) der Durchschnitt der Gruppenstreuungen;

4) Streuung zwischen den Gruppen;

5) Gesamtvarianz basierend auf der Regel der Addition von Varianzen;

6) Bestimmtheitsmaß und empirische Korrelation.

Ziehen Sie Ihre eigenen Schlüsse.

Lösung:

1. Definieren durchschnittliches Volumen Ausführung von Arbeiten von Unternehmen mit zwei Eigentumsformen:

Berechnen Sie die Gesamtvarianz:

2. Gruppendurchschnitte definieren:

Millionen Rubel;

mln reiben.

Gruppenabweichungen:

;

3. Berechnen Sie den Durchschnitt der Gruppenvarianzen:

4. Bestimmen Sie die Intergruppenvarianz:

5. Berechnen Sie die Gesamtabweichung anhand der Regel zum Addieren von Abweichungen:

6. Bestimmtheitsmaß bestimmen:

.

So hängt der Arbeitsaufwand von Design- und Umfrageorganisationen zu 22% von der Eigentumsform der Unternehmen ab.

Das empirische Korrelationsverhältnis wird durch die Formel berechnet

.

Der Wert des berechneten Indikators zeigt, dass die Abhängigkeit des Arbeitsaufwands von der Eigentumsform des Unternehmens gering ist.

Beispiel 5 Als Ergebnis einer Erhebung der technologischen Disziplin der Produktionsstätten wurden folgende Daten erhalten:

Bestimme das Bestimmtheitsmaß