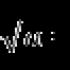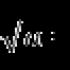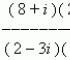Formel zur Berechnung der Varianz einer Zufallsvariablen x. Mathematische Erwartung einer diskreten Zufallsvariablen

Für gruppierte Daten Restdispersion- Durchschnitt der Streuungen innerhalb der Gruppe:

Wobei σ 2 j die gruppeninterne Varianz der j-ten Gruppe ist.

Für nicht gruppierte Daten Restdispersion ist ein Maß für die Näherungsgenauigkeit, d.h. Annäherung der Regressionsgerade an die Originaldaten:
wobei y(t) die Prognose gemäß der Trendgleichung ist; y t – Anfangsserie der Dynamik; n ist die Anzahl der Punkte; p ist die Anzahl der Koeffizienten der Regressionsgleichung (die Anzahl der erklärenden Variablen).
In diesem Beispiel heißt es unvoreingenommene Schätzung der Varianz.

Beispiel 1. Die Verteilung der Arbeitnehmer von drei Unternehmen eines Verbandes nach Tarifkategorien ist durch folgende Daten gekennzeichnet:

Lohnklasse des Arbeiters	Anzahl der Arbeitnehmer im Unternehmen
	Unternehmen 1	Unternehmen 2	Unternehmen 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Definieren:
1. Streuung je Unternehmen (konzerninterne Streuung);
2. Durchschnitt der gruppeninternen Streuungen;
3. Streuung zwischen den Gruppen;
4. Gesamtvarianz.

Lösung.
Bevor Sie mit der Lösung des Problems fortfahren, müssen Sie herausfinden, welches Merkmal effektiv und welches faktoriell ist. Im betrachteten Beispiel ist das Wirkmerkmal „Tarifgruppe“ und das Faktormerkmal „Nummer (Name) des Unternehmens“.
Dann haben wir drei Gruppen (Unternehmen), für die es notwendig ist, den Gruppendurchschnitt und die gruppeninternen Varianzen zu berechnen:

Begleitung	Gruppendurchschnitt,	Varianz innerhalb der Gruppe,
1	4	1,8

Der Durchschnitt der gruppeninternen Varianzen ( Restdispersion) berechnet nach der Formel:

wo kann man rechnen:
oder:

dann:
Die Gesamtdispersion ist gleich: s 2 \u003d 1,6 + 0 \u003d 1,6.
Die Gesamtabweichung kann auch mit einer der beiden folgenden Formeln berechnet werden:

Bei der Lösung praktischer Probleme hat man es oft mit einem Zeichen zu tun, das nur zwei alternative Werte annimmt. In diesem Fall sprechen sie nicht über das Gewicht eines bestimmten Werts eines Merkmals, sondern über seinen Anteil am Aggregat. Wenn der Anteil der Bevölkerungseinheiten, die das untersuchte Merkmal aufweisen, mit " R", und nicht besitzen - durch" Q“, dann kann die Streuung nach folgender Formel berechnet werden:
s 2 = p × q

Beispiel #2. Bestimmen Sie auf der Grundlage der Daten zur Leistung von sechs Arbeitern der Brigade die Varianz zwischen den Gruppen und bewerten Sie die Auswirkungen der Arbeitsschicht auf ihre Arbeitsproduktivität, wenn die Gesamtvarianz 12,2 beträgt.

Nr. der Arbeitsbrigade	Arbeitsleistung, Stk.
	in der ersten Schicht	in 2 Schicht
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Lösung. Ausgangsdaten

x	f1	f2	f 3	f4	f5	f6	Gesamt
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Gesamt	31	33	37	37	40	38

Dann haben wir 6 Gruppen, für die es notwendig ist, den Gruppenmittelwert und die gruppeninternen Varianzen zu berechnen.
1. Finden Sie die Durchschnittswerte jeder Gruppe.







2. Ermitteln Sie das mittlere Quadrat jeder Gruppe.







Wir fassen die Ergebnisse der Berechnung in einer Tabelle zusammen:

Gruppennummer	Gruppendurchschnitt	Varianz innerhalb der Gruppe
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Varianz innerhalb der Gruppe charakterisiert die Veränderung (Variation) des untersuchten (resultierenden) Merkmals innerhalb der Gruppe unter dem Einfluss aller Faktoren, mit Ausnahme des der Gruppierung zugrunde liegenden Faktors:
Den Durchschnitt der gruppeninternen Streuungen berechnen wir nach folgender Formel:


4. Intergruppenvarianz charakterisiert die Veränderung (Variation) des untersuchten (resultierenden) Merkmals unter dem Einfluss eines der Gruppierung zugrunde liegenden Faktors (faktorielles Merkmal).
Streuung zwischen Gruppen ist definiert als:

wo


Dann

Totale Varianz charakterisiert die Veränderung (Variation) des untersuchten (resultierenden) Merkmals unter dem Einfluss aller Faktoren (faktorielle Merkmale) ausnahmslos. Durch den Zustand des Problems ist es gleich 12.2.
Empirische Korrelationsbeziehung misst, wie viel der Gesamtschwankung des resultierenden Attributs durch den untersuchten Faktor verursacht wird. Dies ist das Verhältnis der faktoriellen Varianz zu Gesamtvarianz:

Wir bestimmen die empirische Korrelationsbeziehung:

Beziehungen zwischen Merkmalen können schwach oder stark (eng) sein. Ihre Kriterien werden auf der Chaddock-Skala bewertet:
0,1 0,3 0,5 0,7 0,9 In unserem Beispiel ist die Beziehung zwischen Merkmal Y Faktor X schwach
Bestimmtheitsmaß.

Lassen Sie uns das Bestimmtheitsmaß definieren:

Somit sind 0,67 % der Variation auf Unterschiede zwischen Merkmalen und 99,37 % auf andere Faktoren zurückzuführen.
Fazit: In diesem Fall hängt die Leistung der Arbeiter nicht von der Arbeit in einer bestimmten Schicht ab, d.h. der Einfluss der Arbeitsschicht auf ihre Arbeitsproduktivität ist nicht signifikant und auf andere Faktoren zurückzuführen.

Beispiel #3. Basierend auf dem Durchschnitt Löhne und quadrierte Abweichungen von seinem Wert für zwei Gruppen von Arbeitern, finden Sie die Gesamtvarianz, indem Sie die Regel zum Addieren von Varianzen anwenden:

Lösung:
Durchschnitt der Varianzen innerhalb der Gruppe

Streuung zwischen Gruppen ist definiert als:


Die Gesamtvarianz beträgt: 480 + 13824 = 14304

Die wichtigsten verallgemeinernden Indikatoren für Variationen in Statistiken sind Varianzen und Mittelwerte Standardabweichung.

Streuung es arithmetisches Mittel quadrierte Abweichungen jedes Merkmalswerts vom Gesamtmittelwert. Die Varianz wird üblicherweise als mittleres Quadrat der Abweichungen bezeichnet und mit  2 bezeichnet. Je nach Ausgangsdaten kann die Varianz aus dem arithmetischen Mittel einfach oder gewichtet berechnet werden:

 ungewichtete (einfache) Streuung;

 gewichtete Varianz.

Standardabweichung ist ein verallgemeinerndes Merkmal absoluter Dimensionen Variationen Eigenschaft in der Summe. Es wird in denselben Einheiten wie das Vorzeichen ausgedrückt (in Metern, Tonnen, Prozent, Hektar usw.).

Die Standardabweichung ist die Quadratwurzel der Varianz und wird mit  bezeichnet:

 ungewichtete Standardabweichung;

 gewichtete Standardabweichung.

Die Standardabweichung ist ein Maß für die Zuverlässigkeit des Mittelwerts. Je kleiner die Standardabweichung, desto besser spiegelt das arithmetische Mittel die gesamte dargestellte Grundgesamtheit wider.

Der Berechnung der Standardabweichung geht die Berechnung der Varianz voraus.

Das Verfahren zur Berechnung der gewichteten Varianz ist wie folgt:

1) Bestimmen Sie den arithmetisch gewichteten Durchschnitt:

2) Berechnen Sie die Abweichungen der Optionen vom Durchschnitt:

3) Quadriere die Abweichung jeder Option vom Mittelwert:

4) Quadratische Abweichungen mit Gewichten (Frequenzen) multiplizieren:

5) fassen die erhaltenen Arbeiten zusammen:

6) Der resultierende Betrag wird durch die Summe der Gewichte dividiert:

Beispiel 2.1

Berechnen Sie den arithmetisch gewichteten Durchschnitt:

Die Werte der Abweichungen vom Mittelwert und ihre Quadrate sind in der Tabelle dargestellt. Lassen Sie uns die Varianz definieren:

Die Standardabweichung ist gleich:

Wenn die Quelldaten als Intervall dargestellt werden Verteilungsserie , dann müssen Sie zuerst den diskreten Wert des Merkmals bestimmen und dann die beschriebene Methode anwenden.

Beispiel 2.2

Lassen Sie uns die Berechnung der Varianz für die Intervallreihe anhand der Daten zur Verteilung der Aussaatfläche der Kolchose nach Weizenertrag zeigen.

Das arithmetische Mittel ist:

Lassen Sie uns die Varianz berechnen:

6.3. Berechnung der Streuung nach der Formel für individuelle Daten

Berechnungstechnik Streuung komplex und kann bei großen Werten von Optionen und Frequenzen umständlich sein. Berechnungen können mit Hilfe der Dispersionseigenschaften vereinfacht werden.

Die Dispersion hat die folgenden Eigenschaften.

1. Eine Verringerung oder Erhöhung der Gewichte (Frequenzen) eines variablen Merkmals um eine bestimmte Anzahl von Malen ändert die Streuung nicht.

2. Verringern oder Erhöhen jedes Merkmalswerts um denselben konstanten Wert EIN Die Streuung ändert sich nicht.

3. Verringern oder Erhöhen jedes Merkmalswerts um eine bestimmte Anzahl von Malen k verringert bzw. erhöht die Varianz in k 2 mal Standardabweichung  ein k Einmal.

4. Die Varianz eines Merkmals relativ zu einem willkürlichen Wert ist immer um das Quadrat der Differenz zwischen dem Mittelwert und dem willkürlichen Wert größer als die Varianz relativ zum arithmetischen Mittel:

Wenn EIN 0, dann erhalten wir folgende Gleichheit:

d.h. die Varianz eines Merkmals ist gleich der Differenz zwischen dem mittleren Quadrat der Merkmalswerte und dem Quadrat des Mittelwerts.

Jede Eigenschaft kann allein oder in Kombination mit anderen bei der Berechnung der Varianz verwendet werden.

Das Verfahren zur Berechnung der Varianz ist einfach:

1) bestimmen arithmetisches Mittel :

2) quadriere das arithmetische Mittel:

3) Quadrieren Sie die Abweichung jeder Variante der Reihe:

x ich 2 .

4) Finden Sie die Summe der Quadrate der Optionen:

5) Teilen Sie die Summe der Quadrate der Optionen durch ihre Anzahl, d. H. Bestimmen Sie das durchschnittliche Quadrat:

6) Bestimmen Sie die Differenz zwischen dem mittleren Quadrat des Merkmals und dem Quadrat des Mittelwerts:

Beispiel 3.1 Wir haben die folgenden Daten über die Produktivität der Arbeitnehmer:

Machen wir folgende Berechnungen:

Streuung in der Statistik findet man als Einzelwerte des Merkmals im Quadrat von . Abhängig von den Ausgangsdaten wird sie durch die einfachen und gewichteten Varianzformeln bestimmt:

1. (für nicht gruppierte Daten) wird nach folgender Formel berechnet:

2. Gewichtete Varianz (für eine Variationsreihe):

wobei n die Frequenz ist (Wiederholbarkeitsfaktor X)

Ein Beispiel zum Finden der Varianz

Diese Seite beschreibt ein Standardbeispiel zum Finden der Abweichung, Sie können sich auch andere Aufgaben ansehen, um sie zu finden

Beispiel 1. Wir haben die folgenden Daten für eine Gruppe von 20 Studenten Korrespondenzabteilung. Bauen müssen Intervallserie Verteilung des Merkmals, berechnen Sie den Mittelwert des Merkmals und untersuchen Sie seine Varianz

Lassen Sie uns eine Intervallgruppierung erstellen. Lassen Sie uns den Bereich des Intervalls durch die Formel bestimmen:

wobei X max der Maximalwert des Gruppierungsmerkmals ist;
X min ist der Mindestwert des Gruppierungsmerkmals;
n ist die Anzahl der Intervalle:

Wir akzeptieren n=5. Der Schritt ist: h \u003d (192 - 159) / 5 \u003d 6,6

Machen wir eine Intervallgruppierung

Für weitere Berechnungen bauen wir eine Hilfstabelle auf:

X'i ist die Mitte des Intervalls. (zum Beispiel die Mitte des Intervalls 159 - 165,6 = 162,3)

Das durchschnittliche Wachstum der Schüler wird durch die Formel des arithmetisch gewichteten Durchschnitts bestimmt:

Wir bestimmen die Dispersion nach der Formel:

Die Varianzformel lässt sich wie folgt umrechnen:

Aus dieser Formel folgt das die Abweichung ist die Differenz zwischen dem Mittelwert der Quadrate der Optionen und dem Quadrat und dem Mittelwert.

Streuung ein Variationsreihe mit gleichen Intervallen nach der Momentenmethode kann auf folgende Weise unter Verwendung der zweiten Streuungseigenschaft (Teilung aller Optionen durch den Wert des Intervalls) berechnet werden. Definition von Varianz, berechnet nach der Momentenmethode, nach folgender Formel ist weniger zeitaufwändig:

wobei i der Wert des Intervalls ist;
A - bedingte Null, die praktisch ist, um die Mitte des Intervalls mit der höchsten Frequenz zu verwenden;
m1 ist das Momentenquadrat erster Ordnung;
m2 - Moment zweiter Ordnung

(Wenn sich in der statistischen Grundgesamtheit das Attribut so ändert, dass es nur zwei sich gegenseitig ausschließende Optionen gibt, dann wird diese Variabilität als Alternative bezeichnet) kann durch die Formel berechnet werden:

Setzen wir in diese Dispersionsformel q = 1- p ein, erhalten wir:

Arten der Dispersion

Totale Varianz misst die Variation eines Merkmals über die gesamte Population als Ganzes unter dem Einfluss aller Faktoren, die diese Variation verursachen. Sie ist gleich dem mittleren Quadrat der Abweichungen der Einzelwerte des Attributs x vom Gesamtmittelwert x und kann als einfache Varianz oder gewichtete Varianz definiert werden.

charakterisiert zufällige Variation, d.h. Teil der Variation, der auf den Einfluss nicht berücksichtigter Faktoren zurückzuführen ist und nicht von dem der Gruppierung zugrunde liegenden Vorzeichenfaktor abhängt. Diese Varianz ist gleich dem mittleren Quadrat der Abweichungen der Einzelwerte des Attributs innerhalb der X-Gruppe vom arithmetischen Mittel der Gruppe und kann als einfache Varianz oder als gewichtete Varianz berechnet werden.

Auf diese Weise, Varianzmaße innerhalb der Gruppe Variation eines Merkmals innerhalb einer Gruppe und wird durch die Formel bestimmt:

wo xi - Gruppendurchschnitt;
ni ist die Anzahl der Einheiten in der Gruppe.

Beispielsweise zeigen gruppeninterne Varianzen, die bei der Aufgabe bestimmt werden müssen, den Einfluss der Qualifikationen der Arbeiter auf das Niveau der Arbeitsproduktivität im Betrieb zu untersuchen, Variationen im Output in jeder Gruppe, die von allen verursacht werden mögliche Faktoren (technischer Zustand Ausrüstung, Verfügbarkeit von Werkzeugen und Materialien, Alter der Arbeiter, Arbeitsintensität usw.), außer bei Unterschieden in der Qualifikationskategorie (innerhalb der Gruppe haben alle Arbeiter die gleiche Qualifikation).

Der Durchschnitt der gruppeninternen Varianzen spiegelt den Zufall wider, d. h. den Teil der Variation, der unter dem Einfluss aller anderen Faktoren mit Ausnahme des Gruppierungsfaktors aufgetreten ist. Es wird nach der Formel berechnet:

Es charakterisiert die systematische Variation des resultierenden Merkmals, die auf den Einfluss des der Gruppierung zugrunde liegenden Merkmalsfaktors zurückzuführen ist. Er ist gleich dem mittleren Quadrat der Abweichungen der Gruppenmittelwerte vom Gesamtmittelwert. Die Varianz zwischen den Gruppen wird nach folgender Formel berechnet:

Varianzadditionsregel in der Statistik

Gemäß Varianzadditionsregel die Gesamtvarianz ist gleich der Summe des Durchschnitts der Intragruppen- und Intergruppenvarianzen:

Die Bedeutung dieser Regel ist, dass die Gesamtvarianz, die sich unter dem Einfluss aller Faktoren ergibt, gleich der Summe der Varianzen ist, die sich unter dem Einfluss aller anderen Faktoren ergibt, und der Varianz, die sich aufgrund des Gruppierungsfaktors ergibt.

Mit der Formel zur Addition von Varianzen ist es möglich, aus zwei bekannten Varianzen die dritte Unbekannte zu ermitteln und auch die Stärke des Einflusses des Gruppierungsmerkmals zu beurteilen.

Dispersionseigenschaften

1. Wenn alle Werte des Attributs um denselben konstanten Wert verringert (erhöht) werden, ändert sich die Abweichung davon nicht.
2. Wenn alle Werte des Attributs um die gleiche Anzahl von n-mal verringert (erhöht) werden, dann wird die Varianz entsprechend um n^2-mal verringert (erhöht).

Neben der Untersuchung der Variation eines Merkmals in der gesamten Population als Ganzes ist es oft notwendig, die quantitativen Änderungen des Merkmals in Gruppen, in die die Population unterteilt ist, sowie zwischen Gruppen zu verfolgen. Diese Variationsstudie wird durch die Berechnung und Analyse erreicht verschiedene Sorten Streuung.
Unterscheiden Sie zwischen Gesamt-, Intergruppen- und Intragruppenstreuung.
Gesamtvarianz σ 2 misst die Variation eines Merkmals über die gesamte Population unter dem Einfluss aller Faktoren, die diese Variation verursacht haben, .

Die Intergruppenvarianz (δ) charakterisiert die systematische Variation, d.h. Unterschiede in der Größe des untersuchten Merkmals, die unter dem Einfluss des Merkmalsfaktors entstehen, der der Gruppierung zugrunde liegt. Es wird nach der Formel berechnet:
.

Varianz innerhalb der Gruppe (σ) spiegelt zufällige Schwankungen wider, d.h. Teil der Variation, der unter dem Einfluss nicht berücksichtigter Faktoren auftritt und nicht von dem Merkmalsfaktor abhängt, der der Gruppierung zugrunde liegt. Es wird nach der Formel berechnet:
.

Durchschnitt der Varianzen innerhalb der Gruppe: .

Es gibt ein Gesetz, das 3 Arten von Dispersion miteinander verbindet. Die Gesamtvarianz ist gleich der Summe des Durchschnitts der Intragruppen- und Intergruppenvarianzen: .
Dieses Verhältnis heißt Varianzadditionsregel.

In der Analyse wird häufig ein Maß verwendet, nämlich der Anteil der Varianz zwischen den Gruppen an der Gesamtvarianz. Es trägt den Namen Empirisches Bestimmtheitsmaß (η 2): .
Die Quadratwurzel des empirischen Bestimmtheitsmaßes wird genannt Empirisches Korrelationsverhältnis (η):
.
Sie charakterisiert den Einfluss des der Gruppierung zugrunde liegenden Attributs auf die Variation des resultierenden Attributs. Das empirische Korrelationsverhältnis variiert von 0 bis 1.
Die praktische Anwendung zeigen wir im folgenden Beispiel (Tabelle 1).

Beispiel 1. Tabelle 1 - Arbeitsproduktivität von zwei Gruppen von Arbeitern einer der Werkstätten der NPO "Cyclone"

Berechnen Sie die Gesamt- und Gruppendurchschnitte und Varianzen:

Die Ausgangsdaten zur Berechnung des Durchschnitts der Streuung innerhalb und zwischen den Gruppen sind in der Tabelle dargestellt. 2.
Tabelle 2
Berechnung und δ 2 für zwei Arbeitergruppen.

Arbeitergruppen	Anzahl der Arbeiter, Pers.	Durchschnitt, Det./Schicht.	Streuung
Technische Ausbildung bestanden	5	95	42,0
Nicht technisch ausgebildet	5	81	231,2
Alle Arbeiter	10	88	185,6

Lassen Sie uns die Punkte berechnen. Durchschnitt der Varianzen innerhalb der Gruppe:
.
Intergruppenvarianz

Gesamtabweichung:
Damit ergibt sich das empirische Korrelationsverhältnis: .

Neben der Variation quantitativer Merkmale ist auch eine Variation qualitativer Merkmale zu beobachten. Diese Variationsstudie wird durch die Berechnung der folgenden Arten von Varianzen erreicht:

Die konzerninterne Varianz des Anteils wird durch die Formel ermittelt

wo n ich– die Anzahl der Einheiten in separaten Gruppen.
Der Anteil des untersuchten Merkmals an der Gesamtpopulation, der durch die Formel bestimmt wird:
Die drei Arten der Streuung stehen wie folgt miteinander in Beziehung:
.

Dieses Varianzverhältnis wird als Feature-Share-Varianz-Additionstheorem bezeichnet.

Diese Eigenschaft allein reicht jedoch nicht aus, um sie zu studieren zufällige Variable. Stellen Sie sich zwei Schützen vor, die auf eine Scheibe schießen. Der eine schießt genau und trifft nah am Zentrum, der andere ... einfach nur Spaß haben und nicht einmal zielen. Aber was lustig ist, ist das Durchschnitt das Ergebnis wird genau das gleiche sein wie beim ersten Schützen! Diese Situation wird durch folgende Zufallsvariablen bedingt veranschaulicht:

Die mathematische Erwartung des "Scharfschützen" ist jedoch für die "interessante Person" gleich: - sie ist ebenfalls Null!

Es muss also quantifiziert werden, wie weit verstreut Kugeln (Werte einer Zufallsvariablen) relativ zum Zentrum des Ziels (Erwartung). gut und Streuungübersetzt aus dem Lateinischen nur als Streuung .

Mal sehen, wie das definiert ist. numerisches Merkmal an einem der Beispiele aus dem 1. Teil der Lektion:

Dort fanden wir eine enttäuschende mathematische Erwartung dieses Spiels, und jetzt müssen wir seine Varianz berechnen, die bezeichnetüber .

Lassen Sie uns herausfinden, wie weit die Gewinne/Verluste relativ zum Durchschnittswert „gestreut“ sind. Dazu müssen wir natürlich rechnen Unterschiede zwischen Werte einer Zufallsvariablen und sie mathematische Erwartung:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Nun scheint es notwendig, die Ergebnisse zusammenzufassen, aber dieser Weg ist nicht gut - weil sich die Schwingungen nach links mit den Schwingungen nach rechts gegenseitig aufheben. Also zum Beispiel der "Amateur"-Shooter (Beispiel oben) die unterschiede werden , und wenn sie hinzugefügt werden, ergeben sie Null, sodass wir keine Schätzung der Streuung seines Schießens erhalten.

Um diesen Ärger zu umgehen, sollten Sie überlegen Module Unterschiede, aber technische Gründe Der Ansatz hat Wurzeln geschlagen, wenn sie quadriert sind. Bequemer ist es, die Lösung in einer Tabelle anzuordnen:

Und hier heißt es rechnen gewichteter Durchschnitt der Wert der quadrierten Abweichungen. Was ist es? Es gehört ihnen erwarteter Wert, das ist das Maß der Streuung:

– Definition Streuung. Das geht aus der Definition sofort hervor Varianz kann nicht negativ sein- zur Übung beachten!

Erinnern wir uns, wie man die Erwartung findet. Multiplizieren Sie die quadrierten Differenzen mit den entsprechenden Wahrscheinlichkeiten (Fortsetzung der Tabelle):
- bildlich gesprochen ist dies "Zugkraft",
und fasse die Ergebnisse zusammen:

Glauben Sie nicht, dass das Ergebnis vor dem Hintergrund der Gewinne zu groß ausgefallen ist? Das ist richtig - wir haben quadriert, und um zur Dimension unseres Spiels zurückzukehren, müssen wir extrahieren Quadratwurzel. Dieser Wert wird aufgerufen Standardabweichung und wird mit dem griechischen Buchstaben „sigma“ bezeichnet:

Manchmal wird diese Bedeutung genannt Standardabweichung .

Was ist seine Bedeutung? Wenn wir von der mathematischen Erwartung nach links und rechts um die Standardabweichung abweichen:

– dann werden die wahrscheinlichsten Werte der Zufallsvariablen auf dieses Intervall „konzentriert“. Was wir tatsächlich sehen:

Allerdings kommt es vor, dass man bei der Analyse der Streuung fast immer mit dem Begriff der Dispersion arbeitet. Mal sehen, was es in Bezug auf Spiele bedeutet. Wenn wir bei Schützen von der "Genauigkeit" von Treffern relativ zur Scheibenmitte sprechen, dann charakterisiert die Streuung hier zwei Dinge:

Erstens ist es offensichtlich, dass mit steigenden Raten auch die Varianz zunimmt. Wenn wir also beispielsweise um das 10-fache erhöhen, erhöht sich die mathematische Erwartung um das 10-fache und die Varianz um das 100-fache (sobald es sich um einen quadratischen Wert handelt). Beachten Sie jedoch, dass sich die Spielregeln nicht geändert haben! Nur die Kurse haben sich geändert, grob gesagt haben wir früher 10 Rubel gesetzt, jetzt 100.

Der zweite, interessantere Punkt ist, dass die Varianz den Spielstil charakterisiert. Fixieren Sie die Spielraten mental auf einem bestimmten Niveau, und sehen Sie hier, was was ist:

Ein Spiel mit geringer Varianz ist ein vorsichtiges Spiel. Der Spieler neigt dazu, die zuverlässigsten Schemata zu wählen, bei denen er nicht zu viel auf einmal verliert/gewinnt. Zum Beispiel das Rot/Schwarz-System beim Roulette (siehe Beispiel 4 des Artikels zufällige Variablen) .

Spiel mit hoher Varianz. Sie wird oft angerufen Streuung Spiel. Dies ist ein abenteuerlicher oder aggressiver Spielstil, bei dem der Spieler "Adrenalin"-Schemata wählt. Erinnern wir uns wenigstens "Martingal", bei dem die Summen, um die es geht, um Größenordnungen höher sind als bei dem „stillen“ Spiel des vorherigen Absatzes.

Die Situation beim Poker ist bezeichnend: Es gibt sogenannte fest Spieler, die dazu neigen, vorsichtig zu sein und an ihren eigenen „zu zittern“. Spiel bedeutet (Guthaben). Es überrascht nicht, dass ihre Bankroll nicht stark schwankt (geringe Varianz). Umgekehrt, wenn ein Spieler eine hohe Varianz hat, dann ist es der Angreifer. Er geht oft Risiken ein, macht große Wetten und kann sowohl eine riesige Bank sprengen als auch in Stücke gehen.

Dasselbe passiert bei Forex und so weiter – es gibt viele Beispiele.

Darüber hinaus spielt es in allen Fällen keine Rolle, ob das Spiel für einen Penny oder für Tausende von Dollar ist. Jedes Level hat seine Spieler mit niedriger und hoher Varianz. Nun, für den durchschnittlichen Gewinn, wie wir uns erinnern, "verantwortlich" erwarteter Wert.

Sie haben wahrscheinlich bemerkt, dass das Finden der Varianz ein langer und mühsamer Prozess ist. Aber Mathematik ist großzügig:

Formel zum Finden der Varianz

Diese Formel direkt aus der Definition der Varianz abgeleitet, und wir haben es sofort in Umlauf gebracht. Ich werde die Platte mit unserem Spiel von oben kopieren:

und die gefundene Erwartung .

Wir berechnen die Varianz auf die zweite Weise. Lassen Sie uns zuerst die mathematische Erwartung ermitteln – das Quadrat der Zufallsvariablen . Durch Definition der mathematischen Erwartung:

In diesem Fall:

Also nach der Formel:

Spüren Sie den Unterschied, wie sie sagen. Und in der Praxis ist es natürlich besser, die Formel anzuwenden (es sei denn, die Bedingung erfordert etwas anderes).

Wir beherrschen die Technik des Lösens und Entwerfens:

Beispiel 6

Finden Sie den mathematischen Erwartungswert, die Varianz und die Standardabweichung.

Diese Aufgabe findet sich überall und entbehrt in der Regel einer sinnvollen Bedeutung.
Man kann sich mehrere Glühbirnen mit Zahlen vorstellen, die mit bestimmten Wahrscheinlichkeiten in einem Irrenhaus leuchten :)

Lösung: Es ist praktisch, die wichtigsten Berechnungen in einer Tabelle zusammenzufassen. Zuerst schreiben wir die Anfangsdaten in die oberen beiden Zeilen. Dann berechnen wir die Produkte, dann und schließlich die Summen in der rechten Spalte:

Eigentlich ist fast alles fertig. In der dritten Zeile wurde eine fertige mathematische Erwartung gezeichnet: .

Die Streuung wird nach folgender Formel berechnet:

Und schließlich die Standardabweichung:
- Ich persönlich runde normalerweise auf 2 Dezimalstellen.

Alle Berechnungen können auf einem Taschenrechner durchgeführt werden, und noch besser - in Excel:

Hier kann man nichts falsch machen :)

Antworten:

Wer möchte, kann sein Leben noch weiter vereinfachen und von my profitieren Taschenrechner (Demo), die nicht nur sofort gelöst werden diese Aufgabe, sondern auch bauen thematische Grafiken (komme bald). Das Programm kann in der Bibliothek herunterladen– wenn Sie mindestens eine heruntergeladen haben Unterrichtsmaterial oder bekommen ein anderer Weg. Danke für die Unterstützung des Projekts!

Ein paar Aufgaben zur unabhängigen Lösung:

Beispiel 7

Berechnen Sie per Definition die Varianz der Zufallsvariablen des vorherigen Beispiels.

Und ein ähnliches Beispiel:

Beispiel 8

Eine diskrete Zufallsvariable ist durch ihr eigenes Verteilungsgesetz gegeben:

Ja, die Werte der Zufallsvariablen können recht groß werden (Beispiel aus der realen Arbeit), und verwenden Sie hier, wenn möglich, Excel. Wie übrigens in Beispiel 7 - es ist schneller, zuverlässiger und angenehmer.

Lösungen und Antworten unten auf der Seite.

Zum Abschluss des 2. Teils der Lektion analysieren wir noch eine typische Aufgabe, man könnte sogar sagen einen kleinen Rebus:

Beispiel 9

Eine diskrete Zufallsvariable kann nur zwei Werte annehmen: und , und . Die Wahrscheinlichkeit, der mathematische Erwartungswert und die Varianz sind bekannt.

Lösung: Beginnen wir mit einer unbekannten Wahrscheinlichkeit. Da eine Zufallsvariable nur zwei Werte annehmen kann, ist die Summe der Wahrscheinlichkeiten der entsprechenden Ereignisse:

und seitdem .

Es bleibt zu finden ..., leicht gesagt :) Aber na ja, es fing an. Per Definition der mathematischen Erwartung:
- ersetzen Sie die bekannten Werte:

- und aus dieser Gleichung lässt sich nichts mehr herausquetschen, außer dass man sie in die übliche Richtung umschreiben kann:

oder:

Über weitere Aktionen, denke ich, kann man raten. Lassen Sie uns das System erstellen und lösen:

Dezimalstellen- das ist natürlich eine völlige Schande; beide Gleichungen mit 10 multiplizieren:

und durch 2 teilen:

Das ist besser. Aus der 1. Gleichung drücken wir aus:
(das ist der einfachere weg)- Ersatz in der 2. Gleichung:

Wir bauen kariert und vereinfachen:

Wir multiplizieren mit:

Infolge, quadratische Gleichung, finde seine Diskriminante:
- perfekt!

und wir erhalten zwei Lösungen:

1) wenn , dann ;

2) wenn , dann .

Das erste Wertepaar erfüllt die Bedingung. MIT hohe Wahrscheinlichkeit alles ist richtig, aber schreiben wir trotzdem das Verteilungsgesetz auf:

und eine Überprüfung durchführen, nämlich die Erwartung finden: