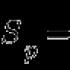Die einfachsten trigonometrischen Lösungsgleichungen. Lösung trigonometrischer Gleichungen. So lösen Sie eine trigonometrische Gleichung

Methoden zum Lösen trigonometrischer Gleichungen

Einführung 2

Methoden zum Lösen trigonometrischer Gleichungen 5

Algebraisch 5

Lösen von Gleichungen unter Verwendung der Gleichheitsbedingung gleichnamiger trigonometrischer Funktionen 7

Factoring 8

Reduktion auf eine homogene Gleichung 10

Einführung des Hilfswinkels 11

Wandeln Sie das Produkt in die Summe 14 um

Universelle Substitution 14

Fazit 17

Einführung

Bis zur zehnten Klasse ist die Handlungsreihenfolge vieler zum Ziel führender Übungen in der Regel eindeutig festgelegt. Zum Beispiel linear und quadratische Gleichungen und Ungleichungen, gebrochene und quadratische Gleichungen usw. Ohne das Prinzip der Lösung jedes der genannten Beispiele im Detail zu analysieren, bemerken wir die allgemeine Sache, die für ihre erfolgreiche Lösung notwendig ist.

In den meisten Fällen müssen Sie bestimmen, um welche Art von Aufgabe es sich handelt, sich an die Abfolge der Aktionen erinnern, die zum Ziel führen, und diese Aktionen ausführen. Es ist offensichtlich, dass der Erfolg oder Misserfolg des Schülers bei der Beherrschung der Methoden zur Lösung von Gleichungen hauptsächlich davon abhängt, wie sehr er in der Lage sein wird, die Art der Gleichung richtig zu bestimmen und sich an die Abfolge aller Phasen ihrer Lösung zu erinnern. Dies setzt natürlich voraus, dass der Student über die Fähigkeiten verfügt, dies zu leisten identische Transformationen und Rechnen.

Eine völlig andere Situation tritt auf, wenn ein Schüler auf trigonometrische Gleichungen trifft. Gleichzeitig ist es nicht schwierig festzustellen, dass die Gleichung trigonometrisch ist. Schwierigkeiten treten auf, wenn eine Vorgehensweise gefunden wird, die dazu führen würde positives Ergebnis. Und hier steht der Student vor zwei Problemen. Durch das Auftreten Gleichungen sind schwierig, den Typ zu bestimmen. Und ohne die Art zu kennen, ist es fast unmöglich, die gewünschte Formel aus den mehreren Dutzend verfügbaren auszuwählen.

Um den Schülern den Weg durch das komplexe Labyrinth der trigonometrischen Gleichungen zu erleichtern, werden sie zunächst in die Gleichungen eingeführt, die nach Einführung einer neuen Variablen auf quadratische Gleichungen reduziert werden. Dann homogene Gleichungen lösen und auf sie reduzieren. Alles endet in der Regel mit Gleichungen, für deren Lösung es notwendig ist, die linke Seite zu faktorisieren und dann jeden der Faktoren mit Null gleichzusetzen.

Der Lehrer versteht, dass die eineinhalb Dutzend Gleichungen, die im Unterricht analysiert werden, eindeutig nicht ausreichen, um den Schüler selbstständig auf dem trigonometrischen "Meer" segeln zu lassen, und fügt dem Lehrer einige weitere Empfehlungen von sich selbst hinzu.

Um die trigonometrische Gleichung zu lösen, müssen wir versuchen:

Bringen Sie alle in der Gleichung enthaltenen Funktionen auf "die gleichen Winkel";

Bringen Sie die Gleichung auf "die gleichen Funktionen";

Faktorisiere die linke Seite der Gleichung usw.

Aber trotz der Kenntnis der Haupttypen trigonometrischer Gleichungen und mehrerer Prinzipien zum Finden ihrer Lösung finden sich viele Schüler immer noch in einer Sackgasse vor jeder Gleichung wieder, die sich geringfügig von den zuvor gelösten unterscheidet. Es bleibt unklar, was man anstreben soll, wenn man die eine oder andere Gleichung hat, warum man in einem Fall die Doppelwinkelformeln anwenden muss, im anderen - den Halbwinkel und im dritten - die Additionsformeln usw.

Bestimmung 1. Eine trigonometrische Gleichung ist eine Gleichung, in der die Unbekannte unter dem Vorzeichen trigonometrischer Funktionen enthalten ist.

Bestimmung 2. Eine trigonometrische Gleichung hat dieselben Winkel, wenn alle darin enthaltenen trigonometrischen Funktionen gleiche Argumente haben. Eine trigonometrische Gleichung heißt funktionsgleich, wenn sie nur eine der trigonometrischen Funktionen enthält.

Bestimmung 3. Der Grad eines Monoms, das trigonometrische Funktionen enthält, ist die Summe der Exponenten der Potenzen der darin enthaltenen trigonometrischen Funktionen.

Bestimmung 4. Eine Gleichung heißt homogen, wenn alle darin enthaltenen Monome den gleichen Grad haben. Dieser Grad wird als Ordnung der Gleichung bezeichnet.

Bestimmung 5. Trigonometrische Gleichung, die nur Funktionen enthält Sünde und cos, heißt homogen, wenn alle Monome bezüglich trigonometrischer Funktionen haben den gleichen Grad, und die trigonometrischen Funktionen selbst haben gleiche Winkel und die Anzahl der Monome ist um 1 größer als die Ordnung der Gleichung.

Methoden zum Lösen trigonometrischer Gleichungen.

Die Lösung trigonometrischer Gleichungen besteht aus zwei Schritten: der Transformation der Gleichung, um ihre einfachste Form zu erhalten, und der Lösung der resultierenden einfachsten trigonometrischen Gleichung. Es gibt sieben grundlegende Methoden zum Lösen trigonometrischer Gleichungen.

ich. algebraische Methode. Dieses Verfahren ist aus der Algebra bekannt. (Methode der Ersetzung von Variablen und Substitution).

Gleichungen lösen.

Führen wir die Notation ein x=2 Sünde3 T, wir bekommen

Lösen wir diese Gleichung, erhalten wir:
oder

jene. kann geschrieben werden

Beim Schreiben der Lösung aufgrund des Vorhandenseins von Zeichen erhalten Grad
es hat keinen sinn zu schreiben.

Antworten:

Bezeichnen

Wir erhalten eine quadratische Gleichung
. Seine Wurzeln sind Zahlen
und
. So gegebene Gleichung reduziert sich auf die einfachsten trigonometrischen Gleichungen
und
. Wenn wir sie lösen, finden wir das
oder
.

Antworten:
;
.

Bezeichnen

erfüllt die Bedingung nicht

Bedeutet

Antworten:

Transformieren wir die linke Seite der Gleichung:

Somit kann diese Anfangsgleichung geschrieben werden als:

, d.h.

Bezeichnung
, wir bekommen
Wenn wir diese quadratische Gleichung lösen, haben wir:

erfüllt die Bedingung nicht

Wir schreiben die Lösung der ursprünglichen Gleichung auf:

Antworten:

Auswechslung
reduziert diese Gleichung auf eine quadratische Gleichung
. Seine Wurzeln sind Zahlen
und
. Als
, dann hat die gegebene Gleichung keine Wurzeln.

Antwort: keine Wurzeln.

II. Lösung von Gleichungen unter Verwendung der Gleichheitsbedingung der gleichnamigen trigonometrischen Funktionen.

ein)
, wenn

B)
, wenn

v)
, wenn

Betrachten Sie unter Verwendung dieser Bedingungen die Lösung der folgenden Gleichungen:

Mit dem, was in Punkt a) gesagt wurde, finden wir, dass die Gleichung genau dann eine Lösung hat, wenn
.

Lösen wir diese Gleichung, finden wir
.

Wir haben zwei Gruppen von Lösungen:

.

7) Lösen Sie die Gleichung:
.

Unter Verwendung der Bedingung von Teil b) leiten wir das ab
.

Lösen wir diese quadratischen Gleichungen, erhalten wir:

8) Lösen Sie die Gleichung
.

Aus dieser Gleichung leiten wir das ab. Wenn wir diese quadratische Gleichung lösen, finden wir das

.

III. Faktorisierung.

Wir betrachten diese Methode anhand von Beispielen.

9) Lösen Sie die Gleichung
.

Lösung. Verschieben wir alle Terme der Gleichung nach links: .

Wir transformieren und faktorisieren den Ausdruck auf der linken Seite der Gleichung:
.

1)
2)

Denn
und
nehmen Sie nicht den Wert null

gleichzeitig, dann trennen wir beide Teile

Gleichungen für
,

Antworten:

10) Lösen Sie die Gleichung:

Lösung.

oder

Antworten:

11) Lösen Sie die Gleichung

Lösung:

1)
2)
3)

Antworten:

IV. Reduktion auf eine homogene Gleichung.

Lösen homogene Gleichung notwendig:

Verschieben Sie alle seine Mitglieder auf die linke Seite;

Setzen Sie alle gemeinsamen Faktoren aus Klammern;

Alle Faktoren und Klammern gleich Null setzen;

Mit Null gleichgesetzte Klammern ergeben eine homogene Gleichung geringeren Grades, die durch dividiert werden sollte
(oder
) im höheren Studiengang;

Lösung erhalten algebraische Gleichung verhältnismäßig
.

Betrachten Sie Beispiele:

12) Lösen Sie die Gleichung:

Lösung.

Teilen Sie beide Seiten der Gleichung durch
,

Einführung in die Notation
, Name

Die Wurzeln dieser Gleichung sind:

ab hier 1)
2)

Antworten:

13) Löse die Gleichung:

Lösung. Unter Verwendung der Doppelwinkelformeln und der grundlegenden trigonometrischen Identität reduzieren wir diese Gleichung auf ein halbes Argument:

Nach Reduzierung gleicher Terme haben wir:

Dividieren der homogenen letzten Gleichung durch
, wir bekommen

Ich werde benennen
, erhalten wir die quadratische Gleichung
, deren Wurzeln Zahlen sind

Auf diese Weise

Ausdruck
verschwindet bei
, d.h. beim
,
.

Unsere Lösung der Gleichung enthält diese Zahlen nicht.

Antworten:
, .

v. Einführung eines Hilfswinkels.

Betrachten Sie eine Gleichung der Form

Wo a, b, c- Koeffizienten, x- Unbekannt.

Teilen Sie beide Seiten dieser Gleichung durch

Jetzt haben die Koeffizienten der Gleichung die Eigenschaften von Sinus und Cosinus, nämlich: Der Modul von jedem von ihnen überschreitet nicht Eins, und die Summe ihrer Quadrate ist gleich 1.

Dann können wir sie entsprechend beschriften
(Hier - Hilfswinkel) und unsere Gleichung hat die Form: .

Dann

Und seine Entscheidung

Beachten Sie, dass die eingeführte Notation austauschbar ist.

14) Löse die Gleichung:

Lösung. Hier
, also teilen wir beide Seiten der Gleichung durch

Antworten:

15) Lösen Sie die Gleichung

Lösung. Als
, dann ist diese Gleichung äquivalent zur Gleichung

Als
, dann gibt es einen solchen Winkel
,
(jene.
).

Wir haben

Als
, dann erhalten wir endlich:

Beachten Sie, dass eine Gleichung der Form genau dann eine Lösung hat, wenn

16) Löse die Gleichung:

Um diese Gleichung zu lösen, gruppieren wir trigonometrische Funktionen mit denselben Argumenten

Teilen Sie beide Seiten der Gleichung durch zwei

Wir transformieren die Summe trigonometrischer Funktionen in ein Produkt:

Antworten:

VI. Produkt in Summe umwandeln.

Hier werden die entsprechenden Formeln verwendet.

17) Löse die Gleichung:

Lösung. Wandeln wir die linke Seite in eine Summe um:

VII.Universelle Substitution.

Diese Formeln gelten für alle

Auswechslung
universell genannt.

18) Löse die Gleichung:

Lösung: Ersetzen Sie und
zu ihrem Ausdruck durch
und bezeichnen
.

Wir erhalten eine rationale Gleichung
, die in ein Quadrat umgewandelt wird
.

Die Wurzeln dieser Gleichung sind die Zahlen
.

Daher wurde das Problem auf die Lösung von zwei Gleichungen reduziert
.

Wir glauben, dass
.

Wert anzeigen
erfüllt nicht die ursprüngliche Gleichung, was durch Überprüfung verifiziert wird - Ersetzen des gegebenen Werts T zur ursprünglichen Gleichung.

Antworten:
.

Kommentar. Gleichung 18 könnte auf andere Weise gelöst werden.

Teilen Sie beide Seiten dieser Gleichung durch 5 (d.h. durch
):
.

Als
, dann gibt es eine Zahl
, was
und
. Die Gleichung wird also:
oder
. Ab hier finden wir das
wo
.

19) Lösen Sie die Gleichung
.

Lösung. Da die Funktionen
und
den größten Wert gleich 1 haben, dann ist ihre Summe gleich 2, wenn
und
, gleichzeitig, das ist
.

Antworten:
.

Beim Lösen dieser Gleichung wurde die Beschränktheit der Funktionen und verwendet.

Fazit.

Bei der Arbeit am Thema „Lösungen trigonometrischer Gleichungen“ ist es für jeden Lehrer sinnvoll, die folgenden Empfehlungen zu beachten:

Methoden zur Lösung trigonometrischer Gleichungen systematisieren.

Wählen Sie selbst die Schritte zur Durchführung der Analyse der Gleichung und die Anzeichen für die Zweckmäßigkeit der Verwendung der einen oder anderen Lösungsmethode.

Über Möglichkeiten der Selbstkontrolle der Tätigkeit nach der Durchführung der Methode nachzudenken.

Lernen Sie, "Ihre" Gleichungen für jede der untersuchten Methoden zu erstellen.

Antrag Nr. 1

Lösen Sie homogene oder reduzierbare Gleichungen.

1.	Rep.
	Rep.

	Rep.
5.	Rep.
	Rep.
7.	Rep.
	Rep.

Ihre Privatsphäre ist uns wichtig. Aus diesem Grund haben wir eine Datenschutzrichtlinie entwickelt, die beschreibt, wie wir Ihre Informationen verwenden und speichern. Bitte lesen Sie unsere Datenschutzerklärung und lassen Sie uns wissen, wenn Sie Fragen haben.

Erhebung und Verwendung personenbezogener Daten

Personenbezogene Daten sind Daten, mit denen eine bestimmte Person identifiziert oder kontaktiert werden kann.

Sie können jederzeit um die Angabe Ihrer persönlichen Daten gebeten werden, wenn Sie uns kontaktieren.

Im Folgenden finden Sie einige Beispiele für die Arten von personenbezogenen Daten, die wir möglicherweise erfassen, und wie wir diese Daten möglicherweise verwenden.

Welche personenbezogenen Daten wir erheben:

Wenn Sie eine Bewerbung auf der Website einreichen, erfassen wir möglicherweise verschiedene Informationen, einschließlich Ihres Namens, Ihrer Telefonnummer und Ihrer Adresse Email usw.

Wie wir Ihre personenbezogenen Daten verwenden:

Die von uns gesammelten personenbezogenen Daten ermöglichen es uns, Sie zu kontaktieren und Sie über einzigartige Angebote, Werbeaktionen und andere Veranstaltungen und bevorstehende Veranstaltungen zu informieren.
Von Zeit zu Zeit können wir Ihre personenbezogenen Daten verwenden, um Ihnen wichtige Mitteilungen und Nachrichten zu senden.
Wir können personenbezogene Daten auch für interne Zwecke wie Audits, Datenanalysen und verschiedene Studien um die von uns angebotenen Dienstleistungen zu verbessern und Ihnen Empfehlungen zu unseren Dienstleistungen zu geben.
Wenn Sie an einer Verlosung, einem Wettbewerb oder einem ähnlichen Anreiz teilnehmen, können wir die von Ihnen bereitgestellten Informationen verwenden, um solche Programme zu verwalten.

Weitergabe an Dritte

Wir geben die von Ihnen erhaltenen Informationen nicht an Dritte weiter.

Ausnahmen:

Für den Fall, dass es erforderlich ist - in Übereinstimmung mit dem Gesetz, der gerichtlichen Anordnung, in Gerichtsverfahren und / oder aufgrund öffentlicher Anfragen oder Anfragen staatlicher Stellen im Hoheitsgebiet der Russischen Föderation - Ihre personenbezogenen Daten offenzulegen. Wir können auch Informationen über Sie offenlegen, wenn wir feststellen, dass eine solche Offenlegung für Sicherheits-, Strafverfolgungs- oder andere Zwecke von öffentlichem Interesse notwendig oder angemessen ist.
Im Falle einer Umstrukturierung, Fusion oder eines Verkaufs können wir die von uns erfassten personenbezogenen Daten an den entsprechenden Drittnachfolger übertragen.

Schutz personenbezogener Daten

Wir treffen Vorkehrungen – einschließlich administrativer, technischer und physischer – zum Schutz Ihrer personenbezogenen Daten vor Verlust, Diebstahl und Missbrauch sowie vor unbefugtem Zugriff, Offenlegung, Änderung und Zerstörung.

Wahrung Ihrer Privatsphäre auf Unternehmensebene

Um sicherzustellen, dass Ihre persönlichen Daten sicher sind, kommunizieren wir Datenschutz- und Sicherheitspraktiken an unsere Mitarbeiter und setzen Datenschutzpraktiken strikt durch.

Lektion der komplexen Anwendung von Wissen.

Unterrichtsziele.

Erwägen verschiedene Methoden Lösungen trigonometrischer Gleichungen.
Entwicklung der kreativen Fähigkeiten der Schüler durch das Lösen von Gleichungen.
Ermutigung der Schüler zur Selbstkontrolle, gegenseitigen Kontrolle und Selbstanalyse ihrer Bildungsaktivitäten.

Ausstattung: Leinwand, Beamer, Referenzmaterial.

Während des Unterrichts

Einführungsgespräch.

Die Hauptmethode zum Lösen trigonometrischer Gleichungen ist ihre einfachste Reduktion. Bewerben Sie sich dabei herkömmliche Weisen, beispielsweise Faktorisierungen, sowie Techniken, die nur zum Lösen trigonometrischer Gleichungen verwendet werden. Es gibt ziemlich viele dieser Tricks, zum Beispiel verschiedene trigonometrische Substitutionen, Winkeltransformationen, Transformationen trigonometrischer Funktionen. Die unterschiedslose Anwendung irgendwelcher trigonometrischer Transformationen vereinfacht die Gleichung normalerweise nicht, sondern verkompliziert sie katastrophal. Zum Trainieren allgemein gesagt Um die Gleichung zu lösen, einen Weg zu skizzieren, um die Gleichung auf das einfachste zu reduzieren, müssen Sie zuerst die Winkel analysieren - die Argumente der in der Gleichung enthaltenen trigonometrischen Funktionen.

Heute werden wir über Methoden zum Lösen trigonometrischer Gleichungen sprechen. Eine richtig gewählte Methode ermöglicht es oft, die Lösung erheblich zu vereinfachen, daher sollten alle von uns untersuchten Methoden immer im Bereich unserer Aufmerksamkeit bleiben, um Probleme zu lösen. trigonometrische Gleichungen die geeignetste Methode.

II. (Mit einem Projektor wiederholen wir die Methoden zum Lösen von Gleichungen.)

1. Ein Verfahren zum Reduzieren einer trigonometrischen Gleichung auf eine algebraische.

Es ist notwendig, alle trigonometrischen Funktionen mit demselben Argument durch eine auszudrücken. Dies kann unter Verwendung der grundlegenden trigonometrischen Identität und ihrer Folgerungen erfolgen. Wir erhalten eine Gleichung mit einer trigonometrischen Funktion. Wenn wir es als neue Unbekannte nehmen, erhalten wir eine algebraische Gleichung. Wir finden seine Wurzeln und kehren zum alten Unbekannten zurück, indem wir die einfachsten trigonometrischen Gleichungen lösen.

2. Methode der Faktorisierung.

Um Winkel zu ändern, sind häufig Reduktionsformeln, Summen und Differenzen von Argumenten sowie Formeln zum Umwandeln der Summe (Differenz) trigonometrischer Funktionen in ein Produkt und umgekehrt nützlich.

sinx + sin3x = sin2x + sin4x

3. Verfahren zum Einbringen eines zusätzlichen Winkels.

4. Methode zur Verwendung der universellen Substitution.

Gleichungen der Form F(sinx, cosx, tgx) = 0 werden durch die universelle trigonometrische Substitution auf algebraische Gleichungen reduziert

Ausdrücken von Sinus, Cosinus und Tangens durch die Tangente eines halben Winkels. Dieser Trick kann zu einer Gleichung höherer Ordnung führen. Die Entscheidung darüber ist schwierig.

Trigonometrische Gleichungen sind nicht das einfachste Thema. Leider sind sie vielfältig.) Zum Beispiel diese:

sin2x + cos3x = ctg5x

sin(5x+π /4) = ctg(2x-π /3)

sinx + cos2x + tg3x = ctg4x

Und dergleichen...

Aber diese (und alle anderen) trigonometrischen Monster haben zwei gemeinsame und obligatorische Merkmale. Erstens – Sie werden es nicht glauben – es gibt trigonometrische Funktionen in den Gleichungen.) Zweitens: Alle Ausdrücke mit x sind innerhalb dieser gleichen Funktionen. Und nur dort! Wenn x irgendwo vorkommt außen, Beispielsweise, sin2x + 3x = 3, Dies wird die Gleichung sein gemischter Typ. Solche Gleichungen erfordern einen individuellen Ansatz. Hier werden wir sie nicht berücksichtigen.

Wir werden auch in dieser Lektion keine bösen Gleichungen lösen.) Hier werden wir uns damit befassen die einfachsten trigonometrischen Gleichungen. Wieso den? Ja, weil die Entscheidung beliebig trigonometrische Gleichungen bestehen aus zwei Stufen. In der ersten Stufe wird die böse Gleichung durch verschiedene Transformationen auf eine einfache reduziert. Auf der zweiten - diese einfachste Gleichung wird gelöst. Kein anderer Weg.

Wenn Sie also Probleme in der zweiten Stufe haben, macht die erste Stufe nicht viel Sinn.)

Wie sehen elementare trigonometrische Gleichungen aus?

sinx = a

cos = a

tgx = a

ctgx = a

Hier ein steht für eine beliebige Zahl. Beliebig.

Übrigens kann es innerhalb der Funktion kein reines x geben, sondern eine Art Ausdruck, wie zum Beispiel:

cos(3x+π /3) = 1/2

und dergleichen. Dies macht das Leben komplizierter, beeinflusst jedoch nicht die Methode zur Lösung der trigonometrischen Gleichung.

Wie löst man trigonometrische Gleichungen?

Trigonometrische Gleichungen können auf zwei Arten gelöst werden. Der erste Weg: mit Logik und einem trigonometrischen Kreis. Wir werden diesen Weg hier erkunden. Der zweite Weg - mit Gedächtnis und Formeln - wird in der nächsten Lektion betrachtet.

Der erste Weg ist klar, zuverlässig und schwer zu vergessen.) Er eignet sich gut zum Lösen von trigonometrischen Gleichungen, Ungleichungen und allerlei kniffligen, nicht standardmäßigen Beispielen. Logik ist stärker als das Gedächtnis!

Wir lösen Gleichungen mit einem trigonometrischen Kreis.

Wir beinhalten elementare Logik und die Fähigkeit, einen trigonometrischen Kreis zu verwenden. Kannst du nicht!? Allerdings ... In Trigonometrie wird es schwierig für Sie ...) Aber es spielt keine Rolle. Schauen Sie sich die Lektionen "Trigonometrischer Kreis ...... Was ist das?" und "Winkel auf einem trigonometrischen Kreis zählen." Da ist alles einfach. Im Gegensatz zu Lehrbüchern ...)

Ach, weißt du!? Und sogar „Praktische Arbeit mit einem trigonometrischen Kreis“ gemeistert!? Glückwünsche annehmen. Dieses Thema wird Ihnen nah und verständlich sein.) Besonders erfreulich ist, dass es dem trigonometrischen Kreis egal ist, welche Gleichung Sie lösen. Sinus, Kosinus, Tangens, Kotangens – für ihn ist alles gleich. Das Lösungsprinzip ist das gleiche.

Wir nehmen also eine beliebige elementare trigonometrische Gleichung. Zumindest das:

cos = 0,5

Ich muss X finden. In menschlicher Sprache sprechen, müssen Sie Finde den Winkel (x), dessen Kosinus 0,5 ist.

Wie haben wir den Kreis vorher benutzt? Wir haben eine Ecke darauf gezeichnet. In Grad oder Bogenmaß. Und sofort gesehen trigonometrische Funktionen dieses Winkels. Machen wir jetzt das Gegenteil. Zeichnen Sie einen Kosinus gleich 0,5 auf den Kreis und sofort wir werden sehen Injektion. Es bleibt nur die Antwort aufzuschreiben.) Ja, ja!

Wir zeichnen einen Kreis und markieren den Kosinus gleich 0,5. Auf der Kosinusachse natürlich. So:

Lassen Sie uns nun den Winkel zeichnen, den uns dieser Kosinus gibt. Bewegen Sie die Maus über das Bild (oder berühren Sie das Bild auf einem Tablet) und sehen diese selbe Ecke X.

Welcher Winkel hat einen Kosinus von 0,5?

x \u003d π / 3

cos 60°= cos( π /3) = 0,5

Manche werden skeptisch grunzen, ja... Sie sagen, hat es sich gelohnt, den Kreis einzuzäunen, wenn sowieso alles klar ist... Da kann man natürlich grunzen...) Fakt ist aber, dass das ein Irrtum ist Antworten. Oder besser gesagt, unzureichend. Kreiskenner wissen, dass es noch eine ganze Reihe von Winkeln gibt, die ebenfalls einen Kosinus von 0,5 ergeben.

Wenn Sie die bewegliche Seite OA drehen für eine volle Umdrehung, Punkt A kehrt in seine ursprüngliche Position zurück. Mit dem gleichen Kosinus gleich 0,5. Jene. der winkel ändert sich 360° oder 2π Radiant und Kosinus ist es nicht. Der neue Winkel 60° + 360° = 420° wird auch eine Lösung unserer Gleichung sein, denn

Es gibt unendlich viele solcher vollen Drehungen ... Und all diese neuen Winkel werden Lösungen unserer trigonometrischen Gleichung sein. Und sie müssen alle irgendwie aufgeschrieben werden. Alles. Andernfalls wird die Entscheidung nicht berücksichtigt, ja ...)

Die Mathematik kann das einfach und elegant. Schreiben Sie in einer kurzen Antwort auf unendlicher Satz Lösungen. So sieht es für unsere Gleichung aus:

x = π /3 + 2π n, n ∈ Z

Ich werde entziffern. Schreib trotzdem sinnvoll schöner, als dumm ein paar mysteriöse Buchstaben zu zeichnen, oder?)

π /3 ist der gleiche Winkel, dass wir gesehen auf dem Kreis u bestimmt nach der Kosinustafel.

2π ist eine volle Umdrehung im Bogenmaß.

n - dies ist die Anzahl der vollständigen, d.h. ganz Revolutionen. Es ist klar, dass n kann 0, ±1, ±2, ±3 ... und so weiter sein. Was ist angegeben kurze Anmerkung:

n ∈ Z

n gehört ( ∈ ) auf die Menge der ganzen Zahlen ( Z ). Übrigens, anstelle des Briefes n Buchstaben können verwendet werden k, m, t usw.

Diese Notation bedeutet, dass Sie jede ganze Zahl nehmen können n . Mindestens -3, mindestens 0, mindestens +55. Was willst du. Wenn Sie diese Zahl in Ihre Antwort einsetzen, erhalten Sie einen bestimmten Blickwinkel, der mit Sicherheit die Lösung unserer harten Gleichung ist.)

Oder mit anderen Worten, x \u003d π / 3 ist die einzige Wurzel einer unendlichen Menge. Um alle anderen Nullstellen zu erhalten, genügt es, π / 3 ( n ) im Bogenmaß. Jene. 2πn Bogenmaß.

Alles? Nein. Ich dehne gezielt das Vergnügen aus. Um sich besser zu erinnern.) Wir haben nur einen Teil der Antworten auf unsere Gleichung erhalten. Ich werde diesen ersten Teil der Lösung wie folgt schreiben:

x 1 = π /3 + 2π n, n ∈ Z

x 1 - nicht eine Wurzel, es ist eine ganze Reihe von Wurzeln, in Kurzform geschrieben.

Aber es gibt auch andere Winkel, die ebenfalls einen Kosinus von 0,5 ergeben!

Kehren wir zu unserem Bild zurück, nach dem wir die Antwort aufgeschrieben haben. Da ist sie:

Bewegen Sie die Maus über das Bild und sehen eine andere Ecke, die ergibt auch einen Kosinus von 0,5. Was denkst du, ist es gleich? Die Dreiecke sind gleich... Ja! Es ist gleich dem Winkel x , nur in negativer Richtung aufgetragen. Das ist die Ecke -X. Aber wir haben x schon berechnet. π /3 bzw 60°. Daher können wir sicher schreiben:

x 2 \u003d - π / 3

Und natürlich addieren wir alle Winkel, die sich durch volle Umdrehungen ergeben:

x 2 = - π /3 + 2π n, n ∈ Z

Das ist jetzt alles.) In einem trigonometrischen Kreis, wir gesehen(wer versteht natürlich)) alle Winkel, die einen Kosinus von 0,5 ergeben. Und sie haben diese Winkel in einer kurzen mathematischen Form aufgeschrieben. Die Antwort sind zwei unendliche Reihen von Wurzeln:

x 1 = π /3 + 2π n, n ∈ Z

x 2 = - π /3 + 2π n, n ∈ Z

Dies ist die richtige Antwort.

Hoffen, allgemeines Prinzip zur Lösung trigonometrischer Gleichungen mit Hilfe eines Kreises ist verständlich. Wir markieren den Kosinus (Sinus, Tangens, Kotangens) aus der gegebenen Gleichung auf dem Kreis, zeichnen die entsprechenden Winkel und schreiben das Ergebnis auf. Natürlich müssen Sie herausfinden, was für Ecken wir sind gesehen auf dem Kreis. Manchmal ist es nicht so offensichtlich. Nun, wie gesagt, hier ist Logik gefragt.)

Lassen Sie uns zum Beispiel eine andere trigonometrische Gleichung analysieren:

Bitte beachten Sie, dass die Zahl 0,5 nicht die einzig mögliche Zahl in den Gleichungen ist!) Es ist einfach bequemer für mich, sie zu schreiben als Wurzeln und Brüche.

Wir arbeiten nach dem allgemeinen Prinzip. Wir zeichnen einen Kreis, markieren (natürlich auf der Sinusachse!) 0,5. Wir zeichnen sofort alle diesem Sinus entsprechenden Winkel. Wir erhalten dieses Bild:

Beschäftigen wir uns zuerst mit dem Winkel. x im ersten Quartal. Wir erinnern uns an die Sinustabelle und bestimmen den Wert dieses Winkels. Die Sache ist einfach:

x \u003d π / 6

Wir erinnern uns an volle Umdrehungen und schreiben mit gutem Gewissen die erste Reihe von Antworten auf:

x 1 = π /6 + 2π n, n ∈ Z

Die Hälfte der Arbeit ist erledigt. Jetzt müssen wir definieren zweite ecke... Das ist kniffliger als Kosinus, ja ... Aber die Logik wird uns retten! So bestimmen Sie den zweiten Winkel durch x? Ja einfach! Die Dreiecke im Bild sind gleich, und die rote Ecke x gleich dem Winkel x . Es wird nur ab dem Winkel π in negativer Richtung gezählt. Deshalb ist es rot.) Und für die Antwort brauchen wir einen korrekt gemessenen Winkel von der positiven Halbachse OX, also aus einem Winkel von 0 Grad.

Bewegen Sie den Mauszeiger über das Bild und sehen Sie alles. Ich habe die erste Ecke entfernt, um das Bild nicht zu verkomplizieren. Der für uns interessante Winkel (grün gezeichnet) ist gleich:

π - x

x wir wissen es π /6 . Der zweite Winkel wird also sein:

π - π/6 = 5π/6

Wir erinnern uns wieder an die Addition von vollen Umdrehungen und schreiben die zweite Reihe von Antworten auf:

x 2 = 5π /6 + 2π n, n ∈ Z

Das ist alles. Eine vollständige Antwort besteht aus zwei Reihen von Wurzeln:

x 1 = π /6 + 2π n, n ∈ Z

x 2 = 5π /6 + 2π n, n ∈ Z

Gleichungen mit Tangens und Kotangens können leicht gelöst werden, indem das gleiche allgemeine Prinzip zum Lösen trigonometrischer Gleichungen verwendet wird. Es sei denn natürlich, Sie wissen, wie man Tangens und Kotangens auf einem trigonometrischen Kreis zeichnet.

In den obigen Beispielen habe ich den Tabellenwert von Sinus und Cosinus verwendet: 0,5. Jene. eine dieser Bedeutungen, die der Student kennt muss. Lassen Sie uns nun unsere Fähigkeiten erweitern alle anderen Werte. Entscheide dich, also entscheide dich!)

Nehmen wir also an, wir müssen die folgende trigonometrische Gleichung lösen:

In den kurzen Tabellen gibt es keinen solchen Wert des Kosinus. Wir ignorieren diese schreckliche Tatsache kühl. Wir zeichnen einen Kreis, markieren 2/3 auf der Kosinusachse und zeichnen die entsprechenden Winkel. Wir bekommen dieses Bild.

Wir verstehen, für den Anfang, mit einem Winkel im ersten Viertel. Um zu wissen, was x gleich ist, würden sie sofort die Antwort aufschreiben! Wir wissen es nicht ... Scheitern!? Ruhig! Die Mathematik lässt sich in Schwierigkeiten nicht zurück! Für diesen Fall erfand sie Arkuskosinus. Weiß nicht? Vergeblich. Finden Sie es heraus, es ist viel einfacher als Sie denken. Laut diesem Link gibt es keinen einzigen kniffligen Zauberspruch über "umgekehrte trigonometrische Funktionen" ... Es ist in diesem Thema überflüssig.

Wenn Sie es wissen, sagen Sie sich einfach: "X ist ein Winkel, dessen Kosinus 2/3 ist." Und sofort, rein per Definition des Arkuskosinus, können wir schreiben:

Wir erinnern uns an zusätzliche Wendungen und schreiben ruhig die erste Reihe von Wurzeln unserer trigonometrischen Gleichung auf:

x 1 = arccos 2/3 + 2π n, n ∈ Z

Die zweite Reihe von Wurzeln wird auch fast automatisch für den zweiten Winkel geschrieben. Alles ist gleich, nur x (arccos 2/3) wird mit einem Minus sein:

x 2 = - arccos 2/3 + 2π n, n ∈ Z

Und alles! Dies ist die richtige Antwort. Noch einfacher als mit Tabellenwerten. Sie müssen sich nichts merken.) Übrigens werden die Aufmerksamsten bemerken, dass dieses Bild mit der Lösung durch den Arkuskosinus ist unterscheidet sich im Wesentlichen nicht von dem Bild für die Gleichung cosx = 0,5.

Genau so! Allgemeines Prinzip deshalb ist es üblich! Ich habe speziell zwei fast identische Bilder gezeichnet. Der Kreis zeigt uns den Winkel x durch seinen Kosinus. Es ist ein tabellarischer Kosinus, oder nicht - der Kreis weiß es nicht. Was das für ein Winkel ist, π / 3, oder was für ein Arkuskosinus ist unsere Entscheidung.

Mit einem Sinus das gleiche Lied. Zum Beispiel:

Wieder zeichnen wir einen Kreis, markieren den Sinus gleich 1/3, zeichnen die Ecken. Es stellt sich dieses Bild heraus:

Und wieder ist das Bild fast dasselbe wie bei der Gleichung sin x = 0,5. Auch hier starten wir im ersten Viertel aus der Ecke. Was ist x gleich, wenn sein Sinus 1/3 ist? Kein Problem!

Die erste Packung Wurzeln ist also fertig:

x 1 = arcsin 1/3 + 2π n, n ∈ Z

Schauen wir uns den zweiten Winkel an. Im Beispiel mit einem Tabellenwert von 0,5 war es gleich:

π - x

Also hier wird es genau so sein! Nur x ist anders, arcsin 1/3. Na und!? Sie können das zweite Wurzelpaket sicher schreiben:

x 2 = π - arcsin 1/3 + 2π n, n ∈ Z

Dies ist eine völlig richtige Antwort. Obwohl es nicht sehr vertraut aussieht. Aber es ist verständlich, hoffe ich.)

So werden trigonometrische Gleichungen mit einem Kreis gelöst. Dieser Weg ist klar und nachvollziehbar. Er spart in trigonometrischen Gleichungen mit der Auswahl von Wurzeln in einem bestimmten Intervall, in trigonometrischen Ungleichungen - sie werden im Allgemeinen fast immer im Kreis gelöst. Kurz gesagt, bei allen Aufgaben, die etwas komplizierter sind als die Standardaufgaben.

Wissen in die Praxis umsetzen?

Lösen Sie trigonometrische Gleichungen:

Am Anfang ist es einfacher, direkt in dieser Lektion.

Jetzt ist es schwieriger.

Hinweis: Hier muss man an den Kreis denken. Persönlich.)

Und jetzt äußerlich unprätentiös ... Sie werden auch Sonderfälle genannt.

Sünde = 0

Sünde = 1

cos = 0

cos = -1

Hinweis: Hier müssen Sie in einem Kreis herausfinden, wo es zwei Antwortreihen gibt und wo es eine gibt ... Und wie Sie eine statt zwei Antwortreihen aufschreiben. Ja, damit keine einzige Wurzel aus unendlich vielen verloren geht!)

Naja, ganz einfach):

Sünde = 0,3

cos = π

tgx = 1,2

ctgx = 3,7

Hinweis: Hier müssen Sie wissen, was Arkussinus, Arkuskosinus ist? Was ist arc tangens, arc tangens? Die meisten einfache Definitionen. Sie müssen sich aber keine Tabellenwerte merken!)

Die Antworten sind natürlich durcheinander:

x 1= arcsin0,3 + 2πn, n ∈ Z
x 2= π - arcsin0,3 + 2

Nicht alles klappt? Es passiert. Lesen Sie die Lektion noch einmal. Nur nachdenklich(sowas gibt es veraltetes Wort...) Und folgen Sie den Links. Die Hauptlinks beziehen sich auf den Kreis. Ohne es in der Trigonometrie - wie man die Straße mit verbundenen Augen überquert. Manchmal funktioniert es.)

Wenn Ihnen diese Seite gefällt...

Übrigens habe ich noch ein paar interessantere Seiten für Sie.)

Sie können das Lösen von Beispielen üben und Ihr Niveau herausfinden. Testen mit sofortiger Verifizierung. Lernen - mit Interesse!)

Sie können sich mit Funktionen und Ableitungen vertraut machen.

Beim Lösen vieler Mathe Probleme, insbesondere vor der 10. Klasse, ist die Reihenfolge der durchgeführten Aktionen, die zum Ziel führen, klar definiert. Solche Probleme umfassen beispielsweise lineare und quadratische Gleichungen, lineare und quadratische Ungleichungen, Bruchgleichungen und Gleichungen, die sich auf quadratische reduzieren. Das Prinzip der erfolgreichen Lösung jeder der genannten Aufgaben lautet wie folgt: Es muss festgestellt werden, welche Art von Aufgabe gelöst wird, und sich an die erforderliche Abfolge von Aktionen erinnern, die zum gewünschten Ergebnis führen, d. H. beantworten und diesen Schritten folgen.

Offensichtlich hängt der Erfolg oder Misserfolg bei der Lösung eines bestimmten Problems hauptsächlich davon ab, wie richtig die Art der zu lösenden Gleichung bestimmt wird, wie richtig die Reihenfolge aller Schritte ihrer Lösung wiedergegeben wird. Natürlich ist es in diesem Fall notwendig, die Fähigkeiten zu haben, identische Transformationen und Berechnungen durchzuführen.

Eine andere Situation tritt auf mit trigonometrische Gleichungen. Es ist nicht schwer festzustellen, dass die Gleichung trigonometrisch ist. Schwierigkeiten ergeben sich bei der Bestimmung der Handlungsabfolge, die zur richtigen Antwort führen würde.

Es ist manchmal schwierig, seinen Typ durch das Auftreten einer Gleichung zu bestimmen. Und ohne die Art der Gleichung zu kennen, ist es fast unmöglich, aus mehreren Dutzend trigonometrischen Formeln die richtige auszuwählen.

Um die trigonometrische Gleichung zu lösen, müssen wir versuchen:

1. Bringe alle in der Gleichung enthaltenen Funktionen auf "die gleichen Winkel";
2. Bringe die Gleichung auf "die gleichen Funktionen";
3. faktorisiere die linke Seite der Gleichung usw.

Erwägen grundlegende Methoden zum Lösen trigonometrischer Gleichungen.

I. Reduktion auf die einfachsten trigonometrischen Gleichungen

Lösungsschema

Schritt 1.äußern Trigonometrische Funktion durch bekannte Komponenten.

Schritt 2 Funktionsargument mithilfe von Formeln finden:

cos x = a; x = ±arccos a + 2πn, n ´Z.

Sünde x = a; x \u003d (-1) n arcsin a + πn, n Є Z.

tan x = a; x \u003d arctg a + πn, n Є Z.

ctg x = a; x \u003d arcctg a + πn, n Є Z.

Schritt 3 Finden Sie eine unbekannte Variable.

Beispiel.

2 cos(3x – π/4) = -√2.

Lösung.

1) cos(3x - π/4) = -√2/2.

2) 3x – π/4 = ±(π – π/4) + 2πn, n ä Z;

3x – π/4 = ±3π/4 + 2πn, n Є Z.

3) 3x = ±3π/4 + π/4 + 2πn, n ´ Z;

x = ±3π/12 + π/12 + 2πn/3, n ´ Z;

x = ±π/4 + π/12 + 2πn/3, n ´ Z.

Antwort: ±π/4 + π/12 + 2πn/3, n ´ Z.

II. Variable Substitution

Lösungsschema

Schritt 1. Bringen Sie die Gleichung bezüglich einer der trigonometrischen Funktionen in eine algebraische Form.

Schritt 2 Bezeichnen Sie die resultierende Funktion mit der Variablen t (führen Sie gegebenenfalls Einschränkungen für t ein).

Schritt 3 Schreiben Sie die resultierende algebraische Gleichung auf und lösen Sie sie.

Schritt 4 Führen Sie eine umgekehrte Substitution durch.

Schritt 5 Lösen Sie die einfachste trigonometrische Gleichung.

Beispiel.

2cos 2 (x/2) - 5sin (x/2) - 5 = 0.

Lösung.

1) 2(1 - Sünde 2 (x/2)) - 5 Sünde (x/2) - 5 = 0;

2sin 2(x/2) + 5sin(x/2) + 3 = 0.

2) Sei sin (x/2) = t, wobei |t| ≤ 1.

3) 2t 2 + 5t + 3 = 0;

t = 1 oder e = -3/2 erfüllt die Bedingung |t| nicht ≤ 1.

4) Sünde (x/2) = 1.

5) x/2 = π/2 + 2πn, n ´ Z;

x = π + 4πn, n ´ Z.

Antwort: x = π + 4πn, n ´ Z.

III. Methode zur Reduktion der Gleichungsreihenfolge

Lösungsschema

Schritt 1. Ersetzen Sie diese Gleichung durch eine lineare, indem Sie die Formeln zur Leistungsreduzierung verwenden:

sin 2 x \u003d 1/2 (1 - cos 2x);

cos 2 x = 1/2 (1 + cos 2x);

tan 2 x = (1 - cos 2x) / (1 + cos 2x).

Schritt 2 Lösen Sie die resultierende Gleichung mit den Methoden I und II.

Beispiel.

cos2x + cos2x = 5/4.

Lösung.

1) cos 2x + 1/2 (1 + cos 2x) = 5/4.

2) cos 2x + 1/2 + 1/2 cos 2x = 5/4;

3/2 cos 2x = 3/4;

2x = ±π/3 + 2πn, n ´ Z;

x = ±π/6 + πn, n ´ Z.

Antwort: x = ±π/6 + πn, n ´ Z.

IV. Homogene Gleichungen

Lösungsschema

Schritt 1. Bringen Sie diese Gleichung in die Form

a) a sin x + b cos x = 0 (homogene Gleichung ersten Grades)

oder zur Aussicht

b) a sin 2 x + b sin x cos x + c cos 2 x = 0 (homogene Gleichung zweiten Grades).

Schritt 2 Teilen Sie beide Seiten der Gleichung durch

a) cos x ≠ 0;

b) cos 2 x ≠ 0;

und erhalte die Gleichung für tg x:

a) a tg x + b = 0;

b) a tg 2 x + b arctg x + c = 0.

Schritt 3 Lösen Sie die Gleichung mit bekannten Methoden.

Beispiel.

5sin 2 x + 3sin x cos x - 4 = 0.

Lösung.

1) 5sin 2 x + 3sin x cos x – 4(sin 2 x + cos 2 x) = 0;

5sin 2 x + 3sin x cos x – 4sin² x – 4cos 2 x = 0;

sin 2 x + 3sin x cos x - 4cos 2 x \u003d 0 / cos 2 x ≠ 0.

2) tg 2 x + 3tg x - 4 = 0.

3) Sei also tg x = t

t2 + 3t – 4 = 0;

t = 1 oder t = -4, also

tg x = 1 oder tg x = -4.

Aus der ersten Gleichung x = π/4 + πn, n ´ Z; aus der zweiten Gleichung x = -arctg 4 + πk, k ´ Z.

Antwort: x = π/4 + πn, n ´ Z; x \u003d -arctg 4 + πk, k Є Z.

V. Verfahren zum Transformieren einer Gleichung unter Verwendung trigonometrischer Formeln

Lösungsschema

Schritt 1. Mit allen möglichen trigonometrische Formeln, bringen Sie diese Gleichung in die Gleichung, die mit den Methoden I, II, III, IV gelöst wurde.

Schritt 2 Lösen Sie die resultierende Gleichung mit bekannten Methoden.

Beispiel.

sinx + sin2x + sin3x = 0.

Lösung.

1) (Sünde x + Sünde 3x) + Sünde 2x = 0;

2sin 2x cos x + sin 2x = 0.

2) Sünde 2x (2cos x + 1) = 0;

sin 2x = 0 oder 2cos x + 1 = 0;

Aus der ersten Gleichung 2x = π/2 + πn, n ´ Z; aus der zweiten Gleichung cos x = -1/2.

Es gilt x = π/4 + πn/2, n ´ Z; aus der zweiten Gleichung x = ±(π – π/3) + 2πk, k Є Z.

Als Ergebnis x \u003d π / 4 + πn / 2, n Є Z; x = ±2π/3 + 2πk, k ´ Z.

Antwort: x \u003d π / 4 + πn / 2, n Є Z; x = ±2π/3 + 2πk, k ´ Z.

Die Fähigkeit und Fähigkeiten, trigonometrische Gleichungen zu lösen, sind sehr gut wichtig, ihre Entwicklung erfordert erhebliche Anstrengungen, sowohl auf Seiten des Schülers als auch des Lehrers.

Mit der Lösung trigonometrischer Gleichungen sind viele Probleme der Stereometrie, Physik usw. verbunden.Der Prozess der Lösung solcher Probleme enthält sozusagen viele der Kenntnisse und Fähigkeiten, die beim Studium der Elemente der Trigonometrie erworben werden.

Trigonometrische Gleichungen nehmen einen wichtigen Platz im Prozess des Mathematikunterrichts und der Persönlichkeitsentwicklung im Allgemeinen ein.

Haben Sie irgendwelche Fragen? Sie wissen nicht, wie man trigonometrische Gleichungen löst?
Um die Hilfe eines Tutors zu erhalten, registrieren Sie sich.
Die erste Lektion ist kostenlos!

Site, mit vollständigem oder teilweisem Kopieren des Materials, ist ein Link zur Quelle erforderlich.