Мерки за обща дисперсия. Дисперсия и стандартно отклонение
стъпки
Примерно изчисляване на дисперсията
-
Запишете пробните стойности.В повечето случаи само извадки от определени популации са достъпни за статистиците. Например, като правило, статистиците не анализират разходите за поддържане на популацията на всички автомобили в Русия - те анализират произволна извадка от няколко хиляди коли. Такава извадка ще помогне да се определи средната цена на автомобил, но най-вероятно получената стойност ще бъде далеч от реалната.
- Например, нека анализираме броя на кифлите, продадени в кафене за 6 дни, взети в произволен ред. Извадката има следния вид: 17, 15, 23, 7, 9, 13. Това е извадка, а не съвкупност, тъй като нямаме данни за продадени кифли за всеки ден, в който работи кафенето.
- Ако ви е дадена популация, а не извадка от стойности, преминете към следващия раздел.
-
Запишете формулата за изчисляване на дисперсията на извадката.Дисперсията е мярка за разпространението на стойностите на някакво количество. Колкото по-близо е стойността на дисперсията до нула, толкова по-близо са групирани стойностите. Когато работите с извадка от стойности, използвайте следната формула, за да изчислите дисперсията:
- s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))-х) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2))е дисперсията. Дисперсията се измерва в квадратни единициизмервания.
- x i (\displaystyle x_(i))- всяка стойност в извадката.
- x i (\displaystyle x_(i))трябва да извадите x̅, да го повдигнете на квадрат и след това да добавите резултатите.
- x̅ – извадкова средна (извадкова средна).
- n е броят на стойностите в извадката.
-
Изчислете средната стойност на извадката.Означава се като x̅. Средната стойност на извадката се изчислява като нормална средна аритметична стойност: добавете всички стойности в извадката и след това разделете резултата на броя на стойностите в извадката.
- В нашия пример добавете стойностите в извадката: 15 + 17 + 23 + 7 + 9 + 13 = 84
Сега разделете резултата на броя на стойностите в извадката (в нашия пример има 6): 84 ÷ 6 = 14.
Примерна средна x̅ = 14. - Средната стойност на извадката е централната стойност, около която се разпределят стойностите в извадката. Ако стойностите в клъстера на извадката около извадката са средни, тогава дисперсията е малка; в противен случай дисперсията е голяма.
- В нашия пример добавете стойностите в извадката: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
Извадете средната стойност на извадката от всяка стойност в извадката.Сега изчислете разликата x i (\displaystyle x_(i))- x̅, където x i (\displaystyle x_(i))- всяка стойност в извадката. Всеки получен резултат показва степента, до която определена стойност се отклонява от средната стойност на извадката, тоест колко далеч е тази стойност от средната стойност на извадката.
- В нашия пример:
x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1 - Правилността на получените резултати е лесна за проверка, тъй като тяхната сума трябва да е равна на нула. Това е свързано с определянето на средната стойност, тъй като отрицателните стойности (разстояния от средната стойност до по-малки стойности) са напълно компенсирани от положителни стойности (разстояния от средната стойност до по-големи стойности).
- В нашия пример:
-
Както беше отбелязано по-горе, сумата от разликите x i (\displaystyle x_(i))- x̅ трябва да е равно на нула. Означава, че средна дисперсиявинаги е равно на нула, което не дава никаква представа за разпространението на стойностите на определена величина. За да разрешите тази задача, повдигнете на квадрат всяка разлика x i (\displaystyle x_(i))- х. Това ще доведе до получаване само на положителни числа, които, когато се съберат, никога няма да дадат 0.
- В нашия пример:
(x 1 (\displaystyle x_(1))-х) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
(x 2 (\displaystyle (x_(2))-х) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
9 2 = 81
(-7) 2 = 49
(-5) 2 = 25
(-1) 2 = 1 - Намерихте квадрата на разликата - x̅) 2 (\displaystyle ^(2))за всяка стойност в извадката.
- В нашия пример:
-
Изчислете сумата на квадратите на разликите.Тоест намерете частта от формулата, която е написана така: ∑[( x i (\displaystyle x_(i))-х) 2 (\displaystyle ^(2))]. Тук знакът Σ означава сумата от квадратните разлики за всяка стойност x i (\displaystyle x_(i))в пробата. Вече намерихте разликите на квадрат (x i (\displaystyle (x_(i))-х) 2 (\displaystyle ^(2))за всяка стойност x i (\displaystyle x_(i))в пробата; сега просто добавете тези квадратчета.
- В нашия пример: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
-
Разделете резултата на n - 1, където n е броят на стойностите в извадката.Преди време, за да изчислят дисперсията на извадката, статистиците просто разделиха резултата на n; в този случай ще получите средната стойност на квадратната дисперсия, която е идеална за описание на дисперсията на дадена проба. Но не забравяйте, че всяка извадка е само малка част от общата съвкупност от стойности. Ако вземете различна проба и направите същите изчисления, ще получите различен резултат. Както се оказва, разделянето на n - 1 (вместо само на n) дава по-добра оценка на дисперсията на съвкупността, което е това, което търсите. Деленето на n - 1 е станало обичайно, така че е включено във формулата за изчисляване на дисперсията на извадката.
- В нашия пример извадката включва 6 стойности, тоест n = 6.
Дисперсия на извадката = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
- В нашия пример извадката включва 6 стойности, тоест n = 6.
-
Разликата между дисперсията и стандартното отклонение.Имайте предвид, че формулата съдържа експонента, така че дисперсията се измерва в квадратни единици на анализираната стойност. Понякога такава стойност е доста трудна за работа; в такива случаи се използва стандартното отклонение, което е равно на корен квадратен от дисперсията. Ето защо дисперсията на извадката се означава като s 2 (\displaystyle s^(2)), а стандартно отклонениепроби - как s (\displaystyle s).
- В нашия пример примерното стандартно отклонение е: s = √33,2 = 5,76.
Изчисляване на дисперсията на популацията
-
Анализирайте някакъв набор от стойности.Комплектът включва всички стойности на разглежданото количество. Например, ако изследвате възрастта на жителите Ленинградска област, тогава населението включва възрастта на всички жители на тази област. В случай на работа с агрегат се препоръчва да създадете таблица и да въведете стойностите на агрегата в нея. Разгледайте следния пример:
- В дадена стая има 6 аквариума. Всеки аквариум съдържа следния брой риби:
x 1 = 5 (\displaystyle x_(1)=5)
x 2 = 5 (\displaystyle x_(2)=5)
x 3 = 8 (\displaystyle x_(3)=8)
x 4 = 12 (\displaystyle x_(4)=12)
x 5 = 15 (\displaystyle x_(5)=15)
x 6 = 18 (\displaystyle x_(6)=18)
- В дадена стая има 6 аквариума. Всеки аквариум съдържа следния брой риби:
-
Запишете формулата за изчисляване на дисперсията на съвкупността.Тъй като наборът включва всички стойности на определено количество, формулата по-долу ви позволява да получите точна стойноствариация на населението. За да разграничат вариацията на популацията от вариацията на извадката (която е само приблизителна), статистиците използват различни променливи:
- σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / н
- σ 2 (\displaystyle ^(2))- дисперсия на популацията (разчетена като "сигма на квадрат"). Дисперсията се измерва в квадратни единици.
- x i (\displaystyle x_(i))- всяка стойност в съвкупността.
- Σ е знакът на сумата. Тоест за всяка стойност x i (\displaystyle x_(i))извадете μ, повдигнете го на квадрат и след това добавете резултатите.
- μ е средната популация.
- n е броят на стойностите в общата съвкупност.
-
Изчислете средната стойност на населението.Когато се работи с генералната съвкупност, нейната средна стойност се означава като μ (mu). Средната популация се изчислява като обичайната средна аритметична стойност: добавете всички стойности в популацията и след това разделете резултата на броя на стойностите в популацията.
- Имайте предвид, че средните стойности не винаги се изчисляват като средно аритметично.
- В нашия пример населението означава: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
-
Извадете средната популация от всяка стойност в популацията.Колкото по-близо е стойността на разликата до нула, толкова по-близо е конкретната стойност до средната за съвкупността. Намерете разликата между всяка стойност в популацията и нейната средна стойност и ще получите първи поглед върху разпределението на стойностите.
- В нашия пример:
x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5
- В нашия пример:
-
Квадратирайте всеки получен резултат.Стойностите на разликата ще бъдат както положителни, така и отрицателни; ако поставите тези стойности на числова ос, тогава те ще лежат отдясно и отляво на средната стойност на съвкупността. Това не е добре за изчисляване на дисперсията, тъй като положителните и отрицателните числа взаимно се компенсират. Затова повдигнете на квадрат всяка разлика, за да получите изключително положителни числа.
- В нашия пример:
(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))за всяка стойност на популацията (от i = 1 до i = 6):
(-5,5)2 (\displaystyle ^(2)) = 30,25
(-5,5)2 (\displaystyle ^(2)), където x n (\displaystyle x_(n))е последната стойност в популацията. - За да изчислите средната стойност на получените резултати, трябва да намерите тяхната сума и да я разделите на n: (( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2))) / н
- Сега нека напишем горното обяснение с помощта на променливи: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n и получете формула за изчисляване на дисперсията на съвкупността.
- В нашия пример:
Дисперсията в статистиката се определя като стандартното отклонение на индивидуалните стойности на характеристика на квадрат от средното аритметично. Често срещан начин за изчисляване на квадратните отклонения на опциите от средната стойност и след това осредняването им.
![]()
В икономическия и статистически анализ е обичайно да се оценява вариацията на характеристика, като се използва най-често стандартното отклонение, което е корен квадратен от дисперсията.
 (3)
(3)
Той характеризира абсолютната флуктуация на стойностите на атрибута на променливата и се изразява в същите единици като вариантите. В статистиката често става необходимо да се сравняват вариациите на различни характеристики. За такива сравнения се използва относителен показател за вариация, коефициентът на вариация.
Дисперсионни свойства:
1) ако извадите произволно число от всички опции, тогава дисперсията няма да се промени;
2) ако всички стойности на варианта се разделят на някакво число b, тогава дисперсията ще намалее с b^2 пъти, т.е.
3) ако изчислите средния квадрат на отклоненията от произволно число с неравно аритметично средно, тогава той ще бъде по-голям от дисперсията. В този случай, чрез точно определена стойност на квадрат от разликата между средната стойност на поз.
![]()
Дисперсията може да се определи като разликата между средната стойност на квадрат и средната стойност на квадрат.
17. Групови и междугрупови вариации. Правило за добавяне на дисперсии
Ако статистическата популация е разделена на групи или части според изследваната характеристика, тогава за такава популация могат да се изчислят следните видове дисперсии: групова (частна), средна за групата (частна) и междугрупова.
Обща дисперсия- отразява вариацията на даден признак поради всички условия и причини, действащи в дадена статистическа съвкупност. ![]()
Групова дисперсия- е равна на средния квадрат на отклоненията на отделните стойности на атрибута в рамките на групата от средната аритметична стойност на тази група, наречена групова средна стойност. В този случай средното за групата не съвпада с общото средно за цялата популация.
![]()
Груповата вариация отразява вариацията на черта само поради условията и причините, действащи в групата.
Средни групови дисперсии- се определя като средноаритметично претеглено на груповите дисперсии, като теглата са обемите на групите.
Междугрупова дисперсия- е равно на средния квадрат на отклоненията на груповите средни от общата средна стойност.
Междугруповата вариация характеризира вариацията на резултатния атрибут, дължаща се на групиращия атрибут.
Между разглежданите типове дисперсии съществува определена връзка: общата дисперсия е равна на сумата от средната групова и междугрупова дисперсия.
Тази връзка се нарича правило за добавяне на дисперсии.
18. Динамичен ред и съставните му елементи. Видове динамични редове.
Серии в статистиката- това са цифрови данни, показващи дали дадено явление се променя във времето или пространството и дават възможност за статистическо съпоставяне на явленията както в процеса на тяхното развитие във времето, така и в различни формии видове процеси. Благодарение на това е възможно да се открие взаимната зависимост на явленията.
Процесът на развитие на движението на обществените явления във времето в статистиката обикновено се нарича динамика. За да се покаже динамиката, се изграждат серии от динамики (хронологични, времеви), които са серии от променящи се във времето стойности на статистически показател (например брой осъдени над 10 години), подредени в хронологичен ред. Техните съставни елементи са числените стойности на даден показател и периодите или моментите от времето, за които се отнасят.
Най-важната характеристика на времевия ред- техният размер (обем, стойност) на това или онова явление, постигнато в определен период или в определен момент. Съответно, величината на членовете на серията от динамика е нейното ниво. Разграничетеначално, средно и крайно ниво на динамичния ред. Първо нивопоказва стойността на първия, крайният - стойността на последния член на серията. Средно нивопредставлява средния хронологичен вариационен диапазон и се изчислява в зависимост от това дали времевият ред е интервален или мигновен.
Друга важна характеристика на динамичните серии- времето, изминало от първоначалното до последното наблюдение, или броя на тези наблюдения.
Има различни видове времеви редове, те могат да бъдат класифицирани според следните критерии.
1) В зависимост от начина на изразяване на нивата, сериите от динамика се разделят на серии от абсолютни и производни показатели (относителни и средни стойности).
2) В зависимост от това как нивата на реда изразяват състоянието на явлението в определени моменти от време (в началото на месеца, тримесечието, годината и т.н.) или неговата стойност за определени интервали от време (например за ден, месец, година и т.н.) и т.н.), разграничават съответно момент и интервални сериидинамика. Моментните серии в аналитичната работа на правоприлагащите органи се използват сравнително рядко.
В теорията на статистиката динамиката се разграничава и по редица други класификационни признаци: в зависимост от разстоянието между нивата - с равноотдалечени нива и неравномерни във времето нива; в зависимост от наличието на основната тенденция на изследвания процес – стационарни и нестационарни. При анализ на динамични серии, следните нива на серията са представени като компоненти:
Y t \u003d TP + E (t)
където TR е детерминистичен компонент, който определя общата тенденция на промяна във времето или тенденция.
E (t) е случаен компонент, причиняващ колебания на нивото.
дисперсияслучайна величина- мярка за дисперсията на дадено случайна величина, тоест нея отклоненияот математическото очакване. В статистиката нотацията (сигма на квадрат) често се използва за обозначаване на дисперсия. Корен квадратен от дисперсията се нарича стандартно отклонениеили стандартен спред. Стандартното отклонение се измерва в същите единици като произволна стойност, а дисперсията се измерва в квадратите на тази единица.
Въпреки че е много удобно да се използва само една стойност (като средна стойност или режим и медиана) за оценка на цялата извадка, този подход може лесно да доведе до неправилни заключения. Причината за тази ситуация не се крие в самата стойност, а във факта, че една стойност по никакъв начин не отразява разпространението на стойностите на данните.
Например в извадката:
средното е 5.
В самата извадка обаче няма елемент със стойност 5. Може да се наложи да знаете колко близо е всеки елемент от извадката до средната си стойност. Или, с други думи, трябва да знаете дисперсията на стойностите. Знаейки степента, до която данните са се променили, можете да интерпретирате по-добре означава, Медианаи мода. Степента на промяна в стойностите на извадката се определя чрез изчисляване на тяхната дисперсия и стандартно отклонение.
дисперсия и Корен квадратенна дисперсията, наречена стандартно отклонение, характеризира средното отклонение от средната стойност на извадката. Сред тези две количества най-висока стойностТо има стандартно отклонение. Тази стойност може да бъде представена като средното разстояние, на което елементите са от средния елемент на пробата.
Дисперсията е трудна за смислено тълкуване. Въпреки това квадратният корен от тази стойност е стандартното отклонение и се поддава добре на тълкуване.
Стандартното отклонение се изчислява, като първо се определи дисперсията и след това се изчисли квадратният корен от дисперсията.
Например, за масива от данни, показан на фигурата, ще бъдат получени следните стойности:

Снимка 1
Тук средната стойност на квадратните разлики е 717,43. За да получите стандартното отклонение, остава само да вземете корен квадратен от това число.
Резултатът ще бъде приблизително 26,78.
Трябва да се помни, че стандартното отклонение се интерпретира като средното разстояние, на което са елементите от средната стойност на извадката.
Стандартното отклонение показва колко добре средната стойност описва цялата извадка.
Да кажем, че вие сте управителят производствен отделСглобяване на компютър. Тримесечният отчет казва, че продукцията за последното тримесечие е била 2500 компютъра. Лошо ли е или добро? Вие поискахте (или вече има тази колона в отчета) да се покаже стандартното отклонение за тези данни в отчета. Стандартното отклонение например е 2000. За вас като ръководител на отдел става ясно, че производствената линия се нуждае от по-добър контрол (твърде големи отклонения в броя на компютрите, които се сглобяват).
Да припомним: кога голям размерАко стандартното отклонение е твърде ниско, данните са широко разпръснати около средната стойност, а ако стандартното отклонение е ниско, те са групирани близо до средната стойност.
Четири статистически функции VARP(), VARP(), STDEV() и STDEV() са предназначени за изчисляване на дисперсията и стандартното отклонение на числа в диапазон от клетки. Преди да можете да изчислите дисперсията и стандартното отклонение на набор от данни, трябва да определите дали данните представляват популацията или извадка от популацията. В случай на извадка от генералната съвкупност трябва да се използват функциите VARP() и STDEV(), а в случай на генерална съвкупност трябва да се използват функциите VARP() и STDEV():
| Население | функция |
 | VARP() |
 | STDLONG() |
| проба | |
 | ВАРИ() |
 | STDEV() |
Дисперсията (както и стандартното отклонение), както отбелязахме, показва степента, в която стойностите, включени в набора от данни, са разпръснати около средното аритметично.
Малка стойност на дисперсията или стандартното отклонение показва, че всички данни са центрирани около средната аритметична стойност, а голяма стойност на тези стойности показва, че данните са разпръснати в широк диапазон от стойности.
Дисперсията е доста трудна за смислено тълкуване (какво означава малка стойност, голяма стойност?). производителност Задачи 3ще ви позволи визуално, върху графика, да покажете значението на дисперсията за набор от данни.
Задачи
· Упражнение 1.
· 2.1. Дайте понятията: дисперсия и стандартно отклонение; тяхното символно обозначение при статистическа обработка на данни.
· 2.2. Направете работен лист в съответствие с фигура 1 и направете необходимите изчисления.
· 2.3. Дайте основните формули, използвани при изчисленията
· 2.4. Обяснете всички обозначения ( , , )
· 2.5. обясни практическа стойностпонятията дисперсия и стандартно отклонение.
Задача 2.
1.1. Дайте понятията: генерална съвкупност и извадка; очаквана стойности средноаритметичното им символно обозначение по време на статистическата обработка на данните.
1.2. В съответствие с фигура 2 направете работен лист и направете изчисления.
1.3. Дайте основните формули, използвани при изчисленията (за генералната съвкупност и извадката).

Фигура 2
1.4. Обяснете защо е възможно да се получат такива стойности на средните аритметични стойности в проби като 46.43 и 48.78 (вижте Приложението на файла). За заключение.
Задача 3.
Има две проби с различен комплектданни, но средната стойност за тях ще бъде същата:

Фигура 3
3.1. Направете работен лист в съответствие с фигура 3 и направете необходимите изчисления.
3.2. Дайте основните формули за изчисление.
3.3. Изградете графики в съответствие с фигури 4, 5.
3.4. Обяснете получените зависимости.
3.5. Извършете подобни изчисления за тези две проби.
Първоначална проба 11119999
Изберете стойностите на втората проба, така че средноаритметичната стойност за втората проба да е същата, например:

Изберете сами стойностите за втората проба. Подредете изчисленията и графиките като фигури 3, 4, 5. Покажете основните формули, използвани при изчисленията.
Направете съответните заключения.
Всички задачи трябва да бъдат представени под формата на доклад с всички необходими цифри, графики, формули и кратки обяснения.
Забележка: изграждането на графиките трябва да бъде обяснено с фигури и кратки обяснения.
За групирани данни остатъчна дисперсия- средна стойност на вътрешногруповите дисперсии:Където σ 2 j е вътрешногруповата дисперсия на j -тата група.
За негрупирани данни остатъчна дисперсияе мярка за точността на приближението, т.е. приближаване на регресионната линия към оригиналните данни: 
където y(t) е прогнозата според уравнението на тенденцията; y t – начална серия от динамика; n е броят на точките; p е броят на коефициентите на регресионното уравнение (броят на обяснителните променливи).
В този пример се нарича безпристрастна оценка на дисперсията.
Пример #1. Разпределението на работниците от три предприятия от една асоциация по тарифни категории се характеризира със следните данни:
| Категория на заплатата на работника | Броят на работниците в предприятието | ||
| предприятие 1 | предприятие 2 | предприятие 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
Определете:
1. дисперсия за всяко предприятие (вътрешногрупова дисперсия);
2. средна стойност на вътрешногруповите дисперсии;
3. междугрупова дисперсия;
4. обща дисперсия.
Решение.
Преди да се пристъпи към решаване на проблема, е необходимо да се установи коя характеристика е ефективна и коя факторна. В разглеждания пример действащият признак е "Тарифна категория", а факторният признак е "Номер (име) на предприятието".
След това имаме три групи (предприятия), за които е необходимо да се изчисли средната групова и вътрешногруповата дисперсия:
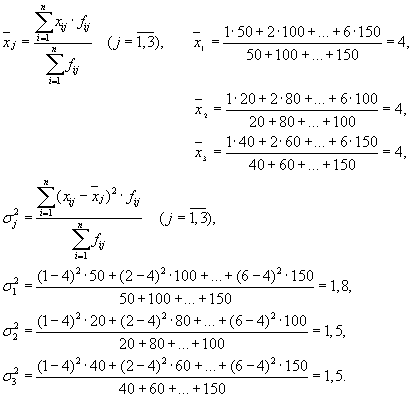
| Търговско дружество | средна група, | дисперсия в рамките на групата, |
| 1 | 4 | 1,8 |
Средната стойност на вътрешногруповите дисперсии ( остатъчна дисперсия), изчислено по формулата:

където можете да изчислите:

или:

тогава:
Общата дисперсия ще бъде равна на: s 2 \u003d 1,6 + 0 \u003d 1,6.
Общата дисперсия може също да се изчисли с помощта на една от следните две формули:

Когато решавате практически проблеми, често трябва да се справяте със знак, който приема само две алтернативни стойности. В този случай те не говорят за тежестта на определена стойност на характеристика, а за нейния дял в съвкупността. Ако съотношението единици на популацията, които притежават изследваната характеристика, се означи с " Р", а не притежаване - чрез" р”, тогава дисперсията може да се изчисли по формулата:
s 2 = p×q
Пример #2. Според данните за развитието на шестима работници от бригадата, определете междугруповата вариация и оценете влиянието на работната смяна върху тяхната производителност на труда, ако общата вариация е 12,2.
| No на работната бригада | Работна мощност, бр. | |
| в първа смяна | на 2-ра смяна | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Решение. Изходни данни
| х | f1 | f2 | е 3 | f4 | f5 | f6 | Обща сума |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Обща сума | 31 | 33 | 37 | 37 | 40 | 38 |
След това имаме 6 групи, за които е необходимо да се изчисли груповата средна и вътрешногруповата дисперсия.
1. Намерете средните стойности на всяка група.
2. Намерете средния квадрат на всяка група.
Обобщаваме резултатите от изчислението в таблица:
| Номер на групата | Групово средно | Вътрешногрупова дисперсия |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Вътрешногрупова дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) черта в рамките на групата под влияние на всички фактори, с изключение на фактора, който е в основата на групирането:
Изчисляваме средната стойност на вътрешногруповите дисперсии по формулата:
4. Междугрупова дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) черта под влиянието на фактор (факторна черта), лежащ в основата на групирането.
Междугруповата дисперсия се определя като:
където
Тогава
Обща дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) черта под въздействието на всички фактори (факторни черти) без изключение. По условието на задачата то е равно на 12,2.
Емпирична корелационна връзкаизмерва каква част от общата флуктуация на резултантния атрибут е причинена от изследвания фактор. Това е съотношението на факторната дисперсия към общата дисперсия:
Определяме емпиричната корелационна връзка:
Връзките между характеристиките могат да бъдат слаби или силни (близки). Техните критерии се оценяват по скалата на Chaddock:
0,1 0,3 0,5 0,7 0,9 В нашия пример връзката между функция Y фактор X е слаба
Коефициент на определяне.
Нека да определим коефициента на детерминация:
По този начин 0,67% от вариацията се дължи на разлики между признаците, а 99,37% се дължи на други фактори.
Заключение: в този случай продукцията на работниците не зависи от работата в определена смяна, т.е. влиянието на работната смяна върху тяхната производителност на труда не е значително и се дължи на други фактори.
Пример #3. Въз основа на средната стойност заплатии квадратни отклонения от неговата стойност за две групи работници, намерете общата дисперсия, като приложите правилото за добавяне на дисперсии:
Решение:Средна стойност на дисперсиите в рамките на групата
Междугруповата дисперсия се определя като:
Общата дисперсия ще бъде: 480 + 13824 = 14304
Ако популацията е разделена на групи според изследваната характеристика, тогава за тази популация могат да се изчислят следните видове дисперсия: обща, групова (вътрешногрупова), групова средна (средна за вътрешногрупова), междугрупова.
Първоначално изчислява коефициента на детерминация, който показва каква част от общата вариация на изследвания признак е междугруповата вариация, т.е. поради групиране:
Емпиричното съотношение на корелация характеризира плътността на връзката между груповите (факторни) и ефективните признаци.
Емпиричното съотношение на корелация може да приема стойности от 0 до 1.
За да оцените близостта на връзката въз основа на емпиричното съотношение на корелация, можете да използвате отношенията на Chaddock:
Пример 4Има следните данни за изпълнението на работата от проектантски и проучвателни организации различни формиИмот:
Определете:
1) обща дисперсия;
2) групови дисперсии;
3) средната стойност на груповите дисперсии;
4) междугрупова дисперсия;
5) обща дисперсия въз основа на правилото за добавяне на дисперсии;
6) коефициент на детерминация и емпирична корелация.
Направете си изводите.
Решение:
1. Дефинирайте среден обемизвършване на работи на предприятия от две форми на собственост:
Изчислете общата дисперсия:
![]()
2. Определете груповите средни стойности:
![]() милиона рубли;
милиона рубли;
![]() милиони рубли.
милиони рубли.
Групови отклонения:
![]() ;
;
3. Изчислете средната стойност на груповите дисперсии:
4. Определете междугруповата дисперсия:
5. Изчислете общата дисперсия въз основа на правилото за добавяне на дисперсии:
6. Определете коефициента на детерминация:
![]() .
.
Така обемът на работата, извършена от проектантските и проучвателните организации с 22% зависи от формата на собственост на предприятията.
Емпиричното съотношение на корелация се изчислява по формулата
![]() .
.
Стойността на изчисления показател показва, че зависимостта на обема на работата от формата на собственост на предприятието е малка.
Пример 5В резултат на проучване на технологичната дисциплина на производствените обекти са получени следните данни:
Определете коефициента на детерминация