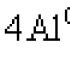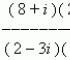Решете системата от уравнения онлайн, като използвате метода на обратната матрица. Правилото на Крамер. Метод на обратна матрица
В първата част разгледахме някои теоретични материали, метода на заместване, както и метода на почленно събиране на системни уравнения. На всички, които са попаднали в сайта чрез тази страница, препоръчвам да прочетете първата част. Може би някои посетители ще намерят материала за твърде прост, но в хода на решаването на системи линейни уравнениянаправих много важни бележкии изводи относно решаването на математически задачи като цяло.
И сега ще анализираме правилото на Крамер, както и решението на система от линейни уравнения с помощта на обратната матрица (матричен метод). Всички материали са представени просто, подробно и ясно, почти всички читатели ще могат да научат как да решават системи, използвайки горните методи.
Първо разглеждаме подробно правилото на Крамер за система от две линейни уравнения с две неизвестни. За какво? - След всичко най-простата системаможе да се реши по училищния метод, чрез срочно събиране!
Факт е, че дори и понякога, но има такава задача - да се реши система от две линейни уравнения с две неизвестни с помощта на формулите на Крамер. Второ, по-прост пример ще ви помогне да разберете как да използвате правилото на Крамер за повече труден случай– системи от три уравнения с три неизвестни.
Освен това има системи от линейни уравнения с две променливи, които е препоръчително да се решават точно според правилото на Крамер!
Помислете за системата от уравнения
На първата стъпка изчисляваме детерминанта , той се нарича основният детерминант на системата.
Метод на Гаус.
Ако , тогава системата има уникално решение и за да намерим корените, трябва да изчислим още два детерминанта:
и
На практика горните квалификатори могат да бъдат обозначени и с латинската буква.
Корените на уравнението се намират по формулите:
,
Пример 7
Решаване на система от линейни уравнения 
Решение: Виждаме, че коефициентите на уравнението са доста големи, от дясната страна има десетични знацисъс запетая. Запетаята е доста рядък гост в практически задачи по математика; аз взех тази система от иконометричен проблем.
Как да се реши такава система? Можете да опитате да изразите една променлива по отношение на друга, но в този случай със сигурност ще получите ужасни фантастични фракции, които са изключително неудобни за работа, а дизайнът на решението ще изглежда просто ужасен. Можете да умножите второто уравнение по 6 и да извадите член по член, но тук ще се появят същите дроби.
Какво да правя? В такива случаи на помощ идват формулите на Крамер.
;
;
Отговор: ,
И двата корена имат безкрайни опашки и се намират приблизително, което е доста приемливо (и дори обичайно) за иконометрични проблеми.
Тук не са необходими коментари, тъй като задачата се решава по готови формули, но има едно предупреждение. Когато използвате този метод, задължителенФрагментът от заданието е следният фрагмент: "така че системата има уникално решение". В противен случай рецензентът може да ви накаже за незачитане на теоремата на Крамър.
Няма да е излишно да проверите, което е удобно да се извърши на калкулатор: заместваме приблизителните стойности в лявата страна на всяко уравнение на системата. В резултат на това с малка грешка трябва да се получат числа, които са от дясната страна.
Пример 8
Изразете отговора си в обикновени неправилни дроби. Направете проверка.
Това е пример за самостоятелно решение (пример за фин дизайн и отговор в края на урока).
Преминаваме към разглеждането на правилото на Крамер за система от три уравнения с три неизвестни: 
Намираме главния детерминант на системата: 
Ако , тогава системата има безкрайно много решения или е непоследователна (няма решения). В този случай правилото на Крамер няма да помогне, трябва да използвате метода на Гаус.
Ако , тогава системата има уникално решение и за да намерим корените, трябва да изчислим още три детерминанта: 
, 
, 
И накрая, отговорът се изчислява по формулите: 
Както можете да видите, случаят „три по три“ не се различава по същество от случая „две по две“, колоната със свободни термини последователно „върви“ отляво надясно по колоните на главния детерминант.
Пример 9
Решете системата с помощта на формулите на Крамер. 
Решение: Нека решим системата с помощта на формулите на Крамер. 
, така че системата има уникално решение.
Отговор: 
.
Всъщност тук отново няма какво особено да се коментира, предвид факта, че решението се взема по готови формули. Но има няколко бележки.
Случва се в резултат на изчисления да се получат „лоши“ неприводими дроби, например: .
Препоръчвам следния алгоритъм за "лечение". Ако няма компютър под ръка, правим това:
1) Възможно е да има грешка в изчисленията. Веднага след като срещнете „лош“ изстрел, трябва незабавно да проверите дали дали условието е пренаписано правилно. Ако условието е пренаписано без грешки, тогава трябва да преизчислите детерминантите, като използвате разширението в друг ред (колона).
2) Ако в резултат на проверката не са открити грешки, най-вероятно е допусната печатна грешка в състоянието на заданието. В този случай спокойно и ВНИМАТЕЛНО решете задачата до края, а след това не забравяйте да проверитеи го изготви на чисто копие след решението. Разбира се, проверката на частичен отговор е неприятна задача, но това ще бъде обезоръжаващ аргумент за учителя, който наистина обича да поставя минус за всяко лошо нещо като. Как да работим с дроби е подробно описано в отговора за пример 8.
Ако имате компютър под ръка, използвайте автоматизирана програма, за да го проверите, която може да бъде изтеглена безплатно в самото начало на урока. Между другото, най-изгодно е да използвате програмата веднага (дори преди да започнете решението), веднага ще видите междинната стъпка, при която сте направили грешка! Същият калкулатор автоматично изчислява решението на системата матричен метод.
Втора забележка. От време на време има системи, в чиито уравнения липсват някои променливи, например: 
Тук в първото уравнение няма променлива, във второто няма променлива. В такива случаи е много важно правилно и ВНИМАТЕЛНО да запишете главния детерминант: 
– нули се поставят на мястото на липсващите променливи.
Между другото, рационално е да се отварят детерминанти с нули в реда (колона), в който се намира нулата, тъй като има забележимо по-малко изчисления.
Пример 10
Решете системата с помощта на формулите на Крамер. 
Това е пример за самостоятелно решаване (завършване на проба и отговор в края на урока).
За случая на система от 4 уравнения с 4 неизвестни, формулите на Крамер се записват по подобни принципи. Можете да видите пример на живо в урока Свойства на детерминантите. Намаляване на реда на детерминантата - пет детерминанта от 4-ти ред са доста разрешими. Въпреки че задачата вече много напомня на професорска обувка на гърдите на щастлив студент.
Решение на системата с помощта на обратната матрица
Методът на обратната матрица е по същество специален случай матрично уравнение(Вижте Пример № 3 от посочения урок).
За да изучавате този раздел, трябва да можете да разширите детерминантите, да намерите обратната матрица и да извършите умножение на матрицата. Съответните връзки ще бъдат дадени в хода на обяснението.
Пример 11
Решете системата с матричния метод 
Решение: Записваме системата в матричен вид:
, където 
Моля, вижте системата от уравнения и матриците. По какъв принцип записваме елементи в матрици, мисля, че всеки разбира. Единственият коментар: ако някои променливи липсват в уравненията, тогава ще трябва да се поставят нули на съответните места в матрицата.
Намираме обратната матрица по формулата:
, където е транспонираната матрица алгебрични допълнениясъответни елементи на матрицата.
Първо, нека се занимаваме с детерминанта:
Тук детерминантата се разширява с първия ред.
Внимание! Ако , тогава обратната матрица не съществува и е невъзможно да се реши системата по матричния метод. В този случай системата се решава чрез елиминиране на неизвестните (метод на Гаус).
Сега трябва да изчислите 9 малки и да ги запишете в матрицата на минорите 
справка:Полезно е да се знае значението на двойните индекси в линейната алгебра. Първата цифра е номерът на реда, на който е даден елемент. Втората цифра е номерът на колоната, в която се намира елементът: 
Тоест двоен индекс показва, че елементът е в първия ред, третата колона, докато, например, елементът е в 3-ти ред, 2-ра колона
Обмисли система от линейни алгебрични уравнения(БАВНО) относно ннеизвестен х 1 , х 2 , ..., х н :
Тази система в "сгънат" вид може да бъде написана, както следва:
С н i=1 а ij х j = b и , i=1,2, ..., n.
В съответствие с правилото за умножение на матрицата, разглежданата система от линейни уравнения може да бъде записана в матрична форма ax=b, където
,
,.
Матрица А, чиито колони са коефициентите за съответните неизвестни, а редовете са коефициентите за неизвестните в съответното уравнение се нарича системна матрица. колонна матрица б, чиито елементи са правилните части от уравненията на системата, се нарича матрица на дясната част или просто дясната страна на системата. колонна матрица х , чиито елементи са неизвестни неизвестни, се нарича системно решение.
Системата от линейни алгебрични уравнения, записана като ax=b, е матрично уравнение.
Ако матрицата на системата неизродени, тогава има обратна матрицаи след това решението на системата ax=bсе дава по формулата:
x=A -1 б.
ПримерРешете системата 
матричен метод.
Решениенамерете обратната матрица за коефициентната матрица на системата
Изчислете детерминанта чрез разширяване на първия ред:
Дотолкова доколкото Δ ≠ 0 , тогава А -1 съществува.
Обратната матрица е намерена правилно.
Нека намерим решение на системата 
следователно, х 1 = 1, х 2 = 2, х 3 = 3 .
Преглед: 
7. Теоремата на Кронекер-Капели за съвместимостта на система от линейни алгебрични уравнения.
Система от линейни уравненияизглежда като:
a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2 , (5.1)
a m1 x 1 + a m1 x 2 +... + a mn x n = b m .
Тук са дадени a i j и b i (i = ; j = ), а x j са неизвестни реални числа. Използвайки концепцията за произведение на матрици, можем да пренапишем системата (5.1) във вида:
където A = (a i j) е матрицата, състояща се от коефициентите на неизвестните на системата (5.1), която се нарича системна матрица, X = (x 1 , x 2 ,..., x n) T , B = (b 1 , b 2 ,..., b m) T - вектори колони, съставени съответно от неизвестни x j и свободни членове b i .
Поръчана колекция нреални числа (c 1 , c 2 ,..., c n) се наричат системно решение(5.1) ако в резултат на заместване на тези числа вместо съответните променливи x 1 , x 2 ,..., x n всяко уравнение на системата се превръща в аритметично тъждество; с други думи, ако съществува вектор C= (c 1 , c 2 ,..., c n) T такъв, че AC B.
Извиква се система (5.1). става,или разрешимоако има поне едно решение. Системата се нарича несъвместими,или неразтворимако няма решения.
,
образувано чрез присвояване на колона от свободни термини на матрицата A отдясно, се нарича разширена матрична система.
Въпросът за съвместимостта на система (5.1) се решава със следната теорема.
Теорема на Кронекер-Капели . Системата от линейни уравнения е последователна, ако и само ако ранговете на матриците A и A съвпадат, т.е. r(A) = r(A) = r.
За множеството M от решения на система (5.1) има три възможности:
1) M = (в този случай системата е непоследователна);
2) M се състои от един елемент, т.е. системата има уникално решение (в този случай системата се нарича сигурен);
3) M се състои от повече от един елемент (тогава системата се нарича несигурен). В третия случай системата (5.1) има безкраен брой решения.
Системата има уникално решение само ако r(A) = n. В този случай броят на уравненията е не по-малък от броя на неизвестните (mn); ако m>n, тогава m-n уравненияса последствия от другите. Ако 0 За да се реши произволна система от линейни уравнения, човек трябва да може да решава системи, в които броят на уравненията е равен на броя на неизвестните, т.нар. Системи тип Крамер: a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 , a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2 , (5.3) ...
... ... ...
... ... a n1 x 1 + a n1 x 2 +... + a nn x n = b n . Системите (5.3) се решават по един от следните начини: 1) по метода на Гаус или по метода за елиминиране на неизвестни; 2) по формулите на Крамер; 3) по матричния метод. Пример 2.12. Изследвайте системата от уравнения и я решете, ако е съвместима: 5x 1 - x 2 + 2x 3 + x 4 = 7, 2x1 + x2 + 4x3 - 2x4 = 1, x 1 - 3x 2 - 6x 3 + 5x 4 = 0. Решение.Изписваме разширената матрица на системата:
Нека изчислим ранга на основната матрица на системата. Очевидно е, че например минорът от втори ред в горния ляв ъгъл = 7 0; минорите от трети ред, които го съдържат, са равни на нула: Следователно рангът на основната матрица на системата е 2, т.е. r(A) = 2. За да изчислите ранга на разширената матрица A, вземете предвид граничния минор следователно, рангът на разширената матрица е r(A) = 3. Тъй като r(A) r(A), системата е непоследователна. Нека има квадратна матрица от n-ти ред Матрицата A -1 се нарича обратна матрицапо отношение на матрицата A, ако A * A -1 = E, където E е идентичната матрица от n-ти ред. Матрица за идентичност- такава квадратна матрица, в която всички елементи по главния диагонал, преминаващи от горния ляв ъгъл към долния десен ъгъл, са единици, а останалите са нули, например: обратна матрицаможе да съществува само за квадратни матрицитези. за тези матрици, които имат еднакъв брой редове и колони. За да има една матрица обратна матрица, е необходимо и достатъчно тя да е неизродена. Матрицата A = (A1, A2,...A n) се нарича неизродениако векторите на колоните са линейно независими. Броят на линейно независими вектори на колона на матрица се нарича ранг на матрицата. Следователно можем да кажем, че за да съществува обратна матрица, е необходимо и достатъчно рангът на матрицата да е равен на нейната размерност, т.е. r = n. За матрица A намерете обратната матрица A -1 Решение: Записваме матрицата A и отдясно присвояваме матрицата на идентичност E. Използвайки трансформациите на Йордан, намаляваме матрицата A до матрицата на идентичността E. Изчисленията са показани в Таблица 31.1. Нека проверим правилността на изчисленията, като умножим оригиналната матрица A и обратната матрица A -1. В резултат на умножението на матрицата се получава матрицата за идентичност. Следователно изчисленията са правилни. Отговор: Матричните уравнения могат да изглеждат така: AX = B, XA = B, AXB = C, където A, B, C са дадени матрици, X е желаната матрица. Матричните уравнения се решават чрез умножаване на уравнението по обратни матрици.
Например, за да намерите матрицата от уравнение, трябва да умножите това уравнение по отляво. Следователно, за да намерите решение на уравнението, трябва да намерите обратната матрица и да я умножите по матрицата от дясната страна на уравнението. Други уравнения се решават по подобен начин. Решете уравнението AX = B, ако Решение: Тъй като обратното на матрицата е равно (виж пример 1) Заедно с други те също намират приложение матрични методи. Тези методи се основават на линейна и векторно-матрична алгебра. Такива методи се използват за целите на анализа на сложни и многоизмерни икономически явления. Най-често тези методи се използват, когато е необходимо да се сравни функционирането на организациите и техните структурни подразделения. В процеса на прилагане на матричните методи за анализ могат да се разграничат няколко етапа. На първия етапсе извършва формирането на система от икономически показатели и въз основа на нея се съставя матрица от изходни данни, която представлява таблица, в която номерата на системата са показани в отделните й редове (i = 1,2,....,n), а по вертикалните графики - номера на индикаторите (j = 1,2,....,m). На втория етапза всяка вертикална колона се разкрива най-голямата от наличните стойности на индикаторите, която се приема като единица. След това всички суми, отразени в тази колона, се разделят на най-голямата стойност и се формира матрица от стандартизирани коефициенти. На третия етапвсички компоненти на матрицата са на квадрат. Ако те имат различно значение, тогава на всеки индикатор на матрицата се присвоява определен коефициент на тежест к. Стойността на последния се определя от експерт. На последния четвърти етапнамерени стойности на оценките Rjгрупирани в ред на нарастване или намаляване. Горните матрични методи трябва да се използват, например, при сравнителен анализ на различни инвестиционни проекти, както и при оценка на други показатели за икономическа ефективност на организациите. Тема 2. СИСТЕМИ ОТ ЛИНЕЙНИ АЛГЕБРАИЧНИ УРАВНЕНИЯ. Основни понятия. Определение 1. система млинейни уравнения с ннеизвестно е система от вида: където и са числата. Определение 2. Решението на системата (I) е такъв набор от неизвестни, в който всяко уравнение на тази система се превръща в тъждество. Определение 3. Системата (I) се нарича ставаако има поне едно решение и несъвместимиако няма решения. Ставната система се нарича сигуренако има уникално решение и несигуренв противен случай. Определение 4. Тип уравнение Наречен нула, и уравнение на формата Наречен несъвместими. Очевидно една система от уравнения, съдържаща непоследователно уравнение, е непоследователна. Определение 5. Двете системи от линейни уравнения се наричат еквивалентенако всяко решение на една система е решение на друга и, обратно, всяко решение на втората система е решение на първата. Матрична нотация за система от линейни уравнения. Помислете за система (I) (вижте §1). Означете: Коефициентна матрица за неизвестни Матрица - колона със свободни членове Матрица - колона от неизвестни Определение 1.Матрицата се нарича основната матрица на системата(I), а матрицата е разширената матрица на системата (I). По дефиницията на матричното равенство, система (I) съответства на матричното равенство: Дясната страна на това равенство по дефиницията на произведението на матриците ( виж дефиниция 3 § 5, глава 1) може да се разложи на множители: Равенство (2)
Наречен матрична нотация на системата (I). Решаване на система от линейни уравнения по метода на Крамер. Нека в система (I) (виж §1) m=n, т.е. броят на уравненията е равен на броя на неизвестните, а основната матрица на системата е неизродена, т.е. . Тогава система (I) от §1 има единствено решение където ∆ = детайл Анаречена основна системен детерминант(I), ∆ исе получава от детерминантата Δ чрез заместване и-та колона към колоната на свободните членове на системата (I). Пример. Решете системата по метода на Крамер: По формули (3)
Изчисляваме детерминантите на системата: За да получим детерминанта, заменихме първата колона в детерминанта с колона със свободни термини; замествайки 2-ра колона в детерминантата с колона от свободни членове, получаваме ; по подобен начин, заменяйки 3-та колона в детерминантата с колона от свободни членове, получаваме . Системно решение: Решаване на системи от линейни уравнения с помощта на обратна матрица. Нека в система (I) (виж §1) m=nи основната матрица на системата е неизродена. Записваме система (I) в матрична форма ( виж §2): защото матрица Ае неизродена, то има обратна матрица ( виж теорема 1 §6 от глава 1). Умножете двете страни на уравнението (2)
към матрицата, тогава По дефиниция на обратната матрица. От равенство (3)
ние имаме Решете системата с помощта на обратната матрица Означете В примера (§ 3) изчислихме детерминанта , следователно, матрицата Аима обратна матрица. След това в сила (4)
, т.е. Намерете матрицата ( виж §6, глава 1) Метод на Гаус. Нека е дадена системата от линейни уравнения: Необходимо е да се намерят всички решения на система (I) или да се уверите, че системата е непоследователна. Определение 1.Нека наречем елементарна трансформация на системата(I) всяко от трите действия: 1) изтриване на нулевото уравнение; 2) добавяне към двете части на уравнението на съответните части от другото уравнение, умножено по числото l; 3) размяна на членове в уравненията на системата, така че неизвестните с еднакви числа във всички уравнения да заемат едни и същи места, т.е. ако например в 1-во уравнение сме променили 2-ри и 3-ти член, тогава същото трябва да се направи и във всички уравнения на системата. Методът на Гаус се състои в това, че системата (I) с помощта на елементарни трансформации се свежда до еквивалентна система, чието решение се намира директно или се установява нейната неразрешимост. Както е описано в §2, система (I) се определя уникално от нейната разширена матрица и всяка елементарна трансформация на система (I) съответства на елементарна трансформация на разширената матрица: Трансформация 1) съответства на изтриване на нулевия ред в матрицата, трансформация 2) е еквивалентна на добавяне към съответния ред на матрицата на другия й ред, умножен по числото l, трансформация 3) е еквивалентна на пренареждане на колоните в матрицата. Лесно е да се види, че, напротив, всяка елементарна трансформация на матрицата съответства на елементарна трансформация на системата (I). С оглед на казаното, вместо операции със системата (I), ще работим с разширената матрица на тази система. В матрицата 1-ва колона се състои от коефициенти при х 1, 2-ра колона - от коефициентите при х 2и т.н. В случай на пренареждане на колоните трябва да се има предвид, че това условие е нарушено. Например, ако разменим 1-ва и 2-ра колони, сега в 1-ва колона ще има коефициенти при х 2, а във 2-ра колона - коефициенти при х 1. Ще решим система (I) по метода на Гаус. 1. Зачеркнете всички нулеви редове в матрицата, ако има такива (т.е. зачеркнете всички нулеви уравнения в система (I). 2. Проверете дали между редовете на матрицата има ред, в който всички елементи с изключение на последния са равни на нула (нека наречем такъв ред непоследователен). Очевидно такава линия съответства на непоследователно уравнение в система (I), следователно, система (I) няма решения и тук процесът завършва. 3. Нека матрицата не съдържа несъвместими редове (система (I) не съдържа несъвместими уравнения). Ако а 11 =0, тогава намираме в 1-ви ред някакъв елемент (освен последния), който е различен от нула и пренареждаме колоните, така че да няма нула в 1-ви ред на 1-во място. Сега приемаме, че (т.е. разменяме съответните членове в уравненията на системата (I)). 4. Умножете 1-вия ред по и добавете резултата към 2-рия ред, след това умножете 1-вия ред по и добавете резултата към 3-ия ред и т.н. Очевидно този процес е еквивалентен на елиминиране на неизвестното х 1от всички уравнения на системата (I), с изключение на 1-во. В новата матрица получаваме нули в 1-ва колона под елемента а 11: 5. Зачеркнете всички нулеви редове в матрицата, ако има такива, проверете дали има непоследователен ред (ако има такъв, значи системата е непоследователна и това завършва решението). Нека проверим дали а 22 / =0, ако е така, тогава намираме елемент във 2-рия ред, който е различен от нула и пренареждаме колоните, така че . След това умножаваме елементите на 2-рия ред по Извършените действия са еквивалентни на премахване на неизвестното х 2от всички уравнения на системата (I), с изключение на 1-во и 2-ро. Тъй като броят на редовете е краен, така че след краен брой стъпки получаваме, че или системата е непоследователна, или в крайна сметка получаваме матрица на стъпки ( виж дефиниция 2 §7, глава 1) : Нека запишем системата от уравнения, съответстваща на матрицата. Тази система е еквивалентна на системата (I) От последното уравнение изразяваме ; заместваме в предишното уравнение, намираме и т.н., докато получим . Забележка 1.Така при решаване на система (I) по метода на Гаус стигаме до един от следните случаи. 1. Системата (I) е непоследователна. 2. Система (I) има уникално решение, ако броят на редовете в матрицата е равен на броя на неизвестните (). 3. Система (I) има безкраен брой решения, ако броят на редовете в матрицата е по-малък от броя на неизвестните (). Следователно е валидна следната теорема. Теорема.Системата от линейни уравнения или е непоследователна, или има уникално решение, или има безкраен набор от решения. Примери. Решете системата от уравнения по метода на Гаус или докажете нейното несъответствие: б) а) Нека пренапишем дадената система във вида: Разменихме 1-во и 2-ро уравнения на оригиналната система, за да опростим изчисленията (вместо дроби, ще оперираме само с цели числа, използвайки такава пермутация). Ние съставяме разширена матрица: Няма нулеви редове; няма несъвместими линии, ; изключваме 1-то неизвестно от всички уравнения на системата, с изключение на 1-то. За да направите това, умножаваме елементите от 1-ви ред на матрицата по "-2" и ги добавяме към съответните елементи на 2-ри ред, което е еквивалентно на умножаване на 1-во уравнение по "-2" и добавянето му към 2-ро уравнение. След това умножаваме елементите от 1-ви ред по "-3" и ги добавяме към съответните елементи от третия ред, т.е. умножете 2-рото уравнение на дадената система по "-3" и го добавете към 3-тото уравнение. Вземи Матрицата съответства на система от уравнения). - (виж дефиниция 3 § 7 от глава 1). Методът на обратната матрица е специален случай матрично уравнение Решете системата с матричния метод Решение: Записваме системата в матричен вид.Намираме решението на системата по формулата (вижте последната формула) Намираме обратната матрица по формулата: Първо, нека се занимаваме с детерминанта: Тук детерминантата се разширява с първия ред. Внимание! Ако, тогава обратната матрица не съществува и е невъзможно да се реши системата по матричния метод. В този случай системата се решава чрез метода на елиминиране на неизвестните (метод на Гаус). Сега трябва да изчислите 9 малки и да ги запишете в матрицата на минорите справка:Полезно е да се знае значението на двойните индекси в линейната алгебра. Първата цифра е номерът на реда, в който се намира елементът. Втората цифра е номерът на колоната, в която се намира елементът: В хода на решаването е по-добре да се опише подробно изчислението на непълнолетните, въпреки че с определен опит те могат да бъдат коригирани, за да се броят с грешки устно. Редът на изчисляване на непълнолетните абсолютно не е важен, тук ги изчислих от ляво на дясно ред по ред. Беше възможно да се изчисляват непълнолетните по колони (това е още по-удобно). По този начин: е матрицата на алгебричните събирания. е транспонираната матрица на алгебричните събирания. Повтарям, стъпките, които изпълнихме, бяха подробно анализирани в урока. Как да намеря обратната матрица? Сега пишем обратната матрица: В никакъв случай не влизаме в матрицата, това сериозно ще усложни по-нататъшните изчисления. Делението би трябвало да се извърши, ако всички числа в матрицата се делят на 60 без остатък. Но добавянето на минус към матрицата в този случай е много необходимо, напротив, това ще опрости по-нататъшните изчисления. Остава да се извърши матрично умножение. Можете да научите как да умножавате матрици в урока Действия с матрици. Между другото, има абсолютно същия пример. Имайте предвид, че делението на 60 е направено последно. Отговор: Пример 12 Решете системата с помощта на обратната матрица. Това е пример за самостоятелно решаване (завършване на проба и отговор в края на урока). Най-универсалният начин за решаване на системата е метод за елиминиране на неизвестни (метод на Гаус). Не е толкова лесно да обясня алгоритъма по достъпен начин, но се опитах!. Пожелавам ти успех! Отговори: Пример 3:
Пример 6:
Пример 8:
,
. Можете да видите или изтеглите примерно решение за този пример (връзка по-долу). Примери 10, 12: Продължаваме да разглеждаме системи от линейни уравнения. Този урок е трети по темата. Ако имате неясна представа какво представлява системата от линейни уравнения като цяло, чувствате се като чайник, тогава препоръчвам да започнете с основите на страницата След това, полезно е да изучите урока. Методът на Гаус е лесен!Защо? Известният немски математик Йохан Карл Фридрих Гаус приживе получава признание за най-великия математик на всички времена, гений и дори прозвището "Крал на математиката". И всичко гениално, както знаете, е просто!Между другото, в парите влизат не само гадове, но и гении – портретът на Гаус се фука на банкнота от 10 германски марки (преди въвеждането на еврото), а Гаус все още мистериозно се усмихва на германците от обикновени пощенски марки. Методът на Гаус е прост с това, че СА ДОСТАТЪЧНИ ЗНАНИЯТА НА ПЕТОКЛАСНИК, за да го овладеят. Трябва да може да събира и умножава!Неслучайно методът за последователно елиминиране на неизвестните често се разглежда от учителите в училищните факултети по математика. Парадоксално е, но методът на Гаус създава най-големи затруднения за учениците. Нищо изненадващо - всичко е за методологията и ще се опитам да разкажа в достъпна форма за алгоритъма на метода. Първо, систематизираме малко знанията за системите от линейни уравнения. Система от линейни уравнения може: 1) Имате уникално решение. Методът на Гаус е най-мощният и универсален инструмент за намиране на решение всякаквисистеми от линейни уравнения. Както си спомняме Правило на Крамер и матричен методса неподходящи в случаите, когато системата има безкрайно много решения или е непоследователна. Метод за последователно елиминиране на неизвестни така или иначедоведе ни до отговора! В този урок отново ще разгледаме метода на Гаус за случай № 1 (единственото решение на системата), като статия е запазена за ситуациите на точки № 2-3. Отбелязвам, че самият алгоритъм на метода работи по същия начин и в трите случая. Нека се върнем към най-простата система от урока Как да решим система от линейни уравнения? Първата стъпка е да напишете разширена матрична система: справка:
Препоръчвам да запомнитетермини
линейна алгебра.Системна матрица
е матрица, съставена само от коефициенти за неизвестни, в този пример матрицата на системата:
.
Разширена системна матрица
е същата матрица на системата плюс колона от свободни членове, в този случай:
. Всяка от матриците може да се нарече просто матрица за краткост. След като разширената матрична система е написана, е необходимо да се извършат някои действия с нея, които също се наричат елементарни трансформации. Има следните елементарни трансформации: 1) Струниматрици могат да бъдат пренаредениместа. Например, в разглежданата матрица можете безопасно да пренаредите първия и втория ред: 2) Ако има (или се появиха) пропорционални (като специален случай - идентични) редове в матрицата, тогава следва Изтрийот матрицата, всички тези редове с изключение на един. Помислете например за матрицата 3) Ако по време на трансформациите в матрицата се появи нулев ред, той също следва Изтрий. Няма да чертая, разбира се, нулевата линия е линията, в която само нули. 4) Редът на матрицата може да бъде умножавам (делим)за произволно число различен от нула. Да разгледаме, например, матрицата. Тук е препоръчително да разделите първия ред на -3 и да умножите втория ред по 2: 5) Тази трансформация създава най-много трудности, но всъщност няма нищо сложно. До реда на матрицата, можете добавете друг низ, умножен по число, различен от нула. Разгледайте нашата матрица от практически пример: . Първо, ще опиша много подробно трансформацията. Умножете първия ред по -2: На практика, разбира се, те не рисуват толкова подробно, а пишат по-кратко: "Пренаписвам матрицата и пренаписвам първия ред:" Първо първата колона. По-долу трябва да получа нула. Следователно умножавам горната единица по -2: и добавям първата към втория ред: 2 + (-2) = 0. Записвам резултата във втория ред: „Сега втората колона. Над -1 пъти -2: . Добавям първия към втория ред: 1 + 2 = 3. Пиша резултата във втория ред: " „И третата колона. Над -5 пъти -2: . Добавям първия ред към втория ред: -7 + 10 = 3. Пиша резултата във втория ред: Моля, помислете внимателно за този пример и разберете алгоритъма за последователно изчисление, ако разбирате това, тогава методът на Гаус е практически "в джоба ви". Но, разбира се, ние все още работим върху тази трансформация. Елементарните трансформации не променят решението на системата от уравнения ! ВНИМАНИЕ:считани за манипулации не може да използва, ако ви бъде предложена задача, при която матриците са дадени "от само себе си". Например с "класически" матрицив никакъв случай не трябва да пренареждате нещо вътре в матриците! Да се върнем към нашата система. Тя е почти готова. Нека напишем увеличената матрица на системата и, използвайки елементарни трансформации, да я намалим до стъпаловиден изглед: (1) Първият ред беше добавен към втория ред, умножен по -2. Между другото, защо умножаваме първия ред по -2? За да получите нула на дъното, което означава да се отървете от една променлива във втория ред. (2) Разделете втория ред на 3. Целта на елементарните трансформации–
преобразуване на матрицата в стъпка форма: В резултат на елементарни трансформации получихме еквивалентеноригинална система от уравнения: Сега системата трябва да бъде "развита" в обратна посока - отдолу нагоре този процес се нарича обратен метод на Гаус. В долното уравнение вече имаме готовия резултат: . Помислете за първото уравнение на системата и заменете вече известната стойност на "y" в него: Нека разгледаме най-често срещаната ситуация, когато методът на Гаус е необходим за решаване на система от три линейни уравнения с три неизвестни. Пример 1 Решете системата от уравнения по метода на Гаус: Нека напишем разширената матрица на системата: Сега веднага ще начертая резултата, до който ще стигнем в хода на решението: Първо погледнете горния ляв номер: Сега първият ред ще остане непроменен до края на решението. Сега добре. Звеното в горния ляв ъгъл е организирано. Сега трябва да получите нули на тези места: Нулите се получават само с помощта на "трудна" трансформация. Първо, ние се занимаваме с втория ред (2, -1, 3, 13). Какво трябва да се направи, за да се получи нула на първа позиция? Трябва да към втория ред добавете първия ред, умножен по -2. Мислено или на чернова, умножаваме първия ред по -2: (-2, -4, 2, -18). И ние последователно извършваме (отново мислено или на чернова) добавяне, към втория ред добавяме първия ред, вече умножен по -2: Резултатът се записва на втория ред: По същия начин се справяме с третия ред (3, 2, -5, -1). За да получите нула на първа позиция, трябва към третия ред добавете първия ред, умножен по -3. Мислено или на чернова, умножаваме първия ред по -3: (-3, -6, 3, -27). И към третия ред добавяме първия ред, умножен по -3: Резултатът е написан на третия ред: На практика тези действия обикновено се извършват устно и се записват в една стъпка: Няма нужда да броите всичко наведнъж и по едно и също време. Редът на изчисленията и "вмъкването" на резултатите последователени обикновено така: първо пренаписваме първия ред и се надуваме тихо - ПОСЛЕДОВАТЕЛНО и ВНИМАТЕЛНО: В този пример това е лесно да се направи, разделяме втория ред на -5 (тъй като всички числа там се делят на 5 без остатък). В същото време разделяме третия ред на -2, защото колкото по-малко е числото, толкова по-просто е решението: На последния етап на елементарните трансформации тук трябва да се получи още една нула: За това към третия ред добавяме втория ред, умножен по -2: Последното извършено действие е прическата на резултата, разделете третия ред на 3. В резултат на елементарни трансформации се получава еквивалентна начална система от линейни уравнения: Сега влиза в действие обратният ход на метода на Гаус. Уравненията се „развиват“ отдолу нагоре. В третото уравнение вече имаме готовия резултат: Нека разгледаме второто уравнение: . Значението на "z" вече е известно, така: И накрая, първото уравнение: . "Y" и "Z" са известни, въпросът е малък: Отговор: Както многократно беше отбелязано, за всяка система от уравнения е възможно и необходимо да се провери намереното решение, за щастие, това не е трудно и бързо. Пример 2 Това е пример за самостоятелно решаване, пример за довършване и отговор в края на урока. Трябва да се отбележи, че вашият начин на действиеможе да не съвпада с моя начин на действие, и това е особеност на метода на Гаус. Но отговорите трябва да са едни и същи! Пример 3 Решете система от линейни уравнения по метода на Гаус Пишем разширената матрица на системата и, използвайки елементарни трансформации, я привеждаме в стъпаловидна форма: Разглеждаме горната лява "стъпка". Там трябва да имаме единица. Проблемът е, че в първата колона изобщо няма такива, така че нищо не може да се реши с пренареждане на редовете. В такива случаи единицата трябва да бъде организирана с помощта на елементарна трансформация. Обикновено това може да стане по няколко начина. Направих това: (1) Към първия ред добавяме втория ред, умножен по -1. Тоест, мислено умножихме втория ред по -1 и извършихме добавянето на първия и втория ред, докато вторият ред не се промени. Сега горе вляво -1, което ни устройва напълно. Който иска да получи +1, може да извърши допълнителен жест: умножете първия ред по -1 (променете знака му). (2) Първият ред, умножен по 5, се добавя към втория ред. Първият ред, умножен по 3, се добавя към третия ред. (3) Първият ред беше умножен по -1, по принцип това е за красота. Знакът на третия ред също беше променен и преместен на второ място, така че на втората „стъпка“ имахме желаната единица. (4) Вторият ред, умножен по 2, се добавя към третия ред. (5) Третият ред беше разделен на 3. Лош знак, който показва грешка в изчислението (по-рядко печатна грешка), е „лошият“ край. Тоест, ако получим нещо като по-долу и, съответно, Ние зареждаме обратния ход, при проектирането на примери самата система често не се пренаписва и уравненията са „взети директно от дадената матрица“. Обратното движение, напомням, работи отдолу нагоре: Отговор: Пример 4 Решете система от линейни уравнения по метода на Гаус Това е пример за независимо решение, малко по-сложно е. Няма проблем, ако някой се обърка. Пълно решение и примерен дизайн в края на урока. Вашето решение може да се различава от моето. В последната част ще разгледаме някои характеристики на алгоритъма на Гаус. Втората особеност е тази. Във всички разгледани примери поставихме или –1, или +1 на „стъпките“. Може ли да има други числа? В някои случаи могат. Помислете за системата: Тук на горната лява "стъпка" имаме двойка. Но забелязваме факта, че всички числа в първата колона се делят на 2 без остатък - и още две и шест. И двойката горе вляво ще ни подхожда! На първата стъпка трябва да извършите следните трансформации: добавете първия ред, умножен по -1, към втория ред; към третия ред добавете първия ред, умножен по -3. Така ще получим желаните нули в първата колона. Или друг хипотетичен пример: Методът на Гаус е универсален, но има една особеност. Можете уверено да се научите как да решавате системи по други методи (метод на Крамер, матричен метод) буквално от първия път - има много твърд алгоритъм. Но за да се чувствате уверени в метода на Гаус, трябва да „напълните ръката си“ и да решите поне 5-10 десет системи. Следователно в началото може да има объркване, грешки в изчисленията и в това няма нищо необичайно или трагично. Дъждовно есенно време извън прозореца .... Следователно, за всеки, по-сложен пример за независимо решение: Пример 5 Решете система от 4 линейни уравнения с четири неизвестни по метода на Гаус. Подобна задача на практика не е толкова рядка. Мисля, че дори чайник, който е проучил тази страница подробно, разбира алгоритъма за решаване на такава система интуитивно. По принцип същото - само повече действие. В урока се разглеждат случаите, когато системата няма решения (непоследователни) или има безкрайно много решения. Несъвместими системи и системи с общо решение. Там можете да коригирате разглеждания алгоритъм на метода на Гаус. Пожелавам ти успех! Решения и отговори: Пример 2: Нека запишем увеличената матрица на системата и с помощта на елементарни трансформации я приведем в стъпаловидна форма. Обратно движение:
Пример 4: Пишем разширената матрица на системата и, използвайки елементарни трансформации, я привеждаме в стъпаловидна форма: Извършени реализации: С втората "стъпка" всичко е по-лошо
, "кандидатите" за него са числата 17 и 23, като ни трябва или едно, или -1. Трансформациите (3) и (4) ще бъдат насочени към получаване на желаната единица (3) Вторият ред беше добавен към третия ред, умножен по -1.
.
Теорема за условието за съществуване на обратна матрица
Алгоритъм за намиране на обратната матрица
Пример 1 
Решение на матрични уравнения
Матричен метод в икономическия анализ
.
.
, т.е.
.
.
,
,
. .
. (5)
, 
, 
,
, 
, 
,
,
.
. (аз) .
.
и добавете със съответните елементи от 3-ти ред, след това - елементите от 2-ри ред и добавете със съответните елементи от 4-ти ред и т.н., докато получим нули под а 22 /
.
,
.
;
.
.
.
, където е транспонираната матрица на алгебричните допълнения на съответните елементи на матрицата .
Тоест двоен индекс показва, че елементът е в първия ред, третата колона, докато, например, елементът е в 3-ти ред, 2-ра колона
е матрицата на минорите на съответните елементи на матрицата .
Понякога може да не е напълно разделено, т.е. може да получи "лоши" дроби. Какво да правим в такива случаи, вече казах, когато анализирахме правилото на Крамер.
2) Имат безкрайно много решения.
3) Нямат решения (бъде несъвместими).
и го реши по метода на Гаус.
. По какъв принцип се записват коефициентите, мисля, че всеки може да види. Вертикалната линия вътре в матрицата не носи никакво математическо значение - това е просто зачертаване за улесняване на дизайна.
. В тази матрица последните три реда са пропорционални, така че е достатъчно да оставите само един от тях: 
.
. Това действие е много полезно, тъй като опростява по-нататъшните трансформации на матрицата.
, и към втория ред добавяме първия ред, умножен по -2: . Сега първият ред може да бъде разделен "назад" с -2: . Както можете да видите, линията, която е ДОБАВЕНА LI – не се е променило. Е винагиреда е променен, КЪМ КОЯТО ДОБАВЕНО UT.
Още веднъж: към втория ред добави първия ред, умножен по -2. Редът обикновено се умножава устно или на чернова, докато умственият ход на изчисленията е нещо подобно:
» »
. При проектирането на задачата те директно изтеглят „стълбата“ с обикновен молив, а също така ограждат числата, които се намират на „стъпките“. Самият термин "стъпаловиден изглед" не е изцяло теоретичен; в научната и образователната литература често се нарича трапецовиден изгледили триъгълен изглед.
И повтарям, нашата цел е да приведем матрицата в стъпаловидна форма, използвайки елементарни трансформации. Откъде да започнете да предприемате действия?
Почти винаги трябва да е тук мерна единица. Най-общо казано, -1 (а понякога и други числа) също са подходящи, но някак си традиционно се случва, че там обикновено се поставя единица. Как да организираме единица? Гледаме първата колона - имаме готова единица! Трансформация първа: разменете първия и третия ред: 
И вече разгледах мисловния ход на самите изчисления по-горе.
Опитайте сами да анализирате това действие - мислено умножете втория ред по -2 и извършете събирането.
Готино.
, то с голяма степен на вероятност може да се твърди, че е допусната грешка в хода на елементарни трансформации.
Да, ето подарък: 
.
Първата особеност е, че понякога някои променливи липсват в уравненията на системата, например: 
Как правилно да напишем разширената матрица на системата? Вече говорих за този момент в урока. Правилото на Крамер. Матричен метод. В разширената матрица на системата поставяме нули на мястото на липсващите променливи: 
Между другото, това е доста лесен пример, тъй като вече има една нула в първата колона и има по-малко елементарни трансформации за изпълнение. .
. Тук тройката на второто „стъпало“ също ни подхожда, тъй като 12 (мястото, където трябва да получим нула) се дели на 3 без остатък. Необходимо е да се извърши следната трансформация: към третия ред добавете втория ред, умножен по -4, в резултат на което ще се получи нулата, от която се нуждаем.
Извършени елементарни трансформации:
(1) Първият ред беше добавен към втория ред, умножен по -2. Първият ред беше добавен към третия ред, умножен по -1.Внимание!
Тук може да е изкушаващо да извадите първия от третия ред, силно не препоръчвам да изваждате - рискът от грешка се увеличава значително. Просто сгъваме!
(2) Знакът на втория ред е променен (умножен по -1). Вторият и третият ред са разменени.Забележка
че на „стъпките“ се задоволяваме не само с една, но и с -1, което е още по-удобно.
(3) Към третия ред добавете втория ред, умножен по 5.
(4) Знакът на втория ред е променен (умножен по -1). Третият ред беше разделен на 14.
Отговор: 
.
(1) Вторият ред беше добавен към първия ред. По този начин желаната единица е организирана в горната лява „стъпка“.
(2) Първият ред, умножен по 7, се добавя към втория ред. Първият ред, умножен по 6, се добавя към третия ред.
(4) Третият ред, умножен по -3, се добавя към втория ред.
Получава се необходимото на втората стъпка
.
(5) Към третия ред се добавя вторият, умножен по 6.
(6) Вторият ред беше умножен по -1, третият ред беше разделен на -83..Очевидно равнината се определя еднозначно от три различни точки, които не лежат на една права линия. Следователно трибуквените обозначения на равнините са доста популярни - според принадлежащите им точки, например; .Ако свободни членове
