Тази статия разкрива извеждането на уравнението на права линия, минаваща през две дадени точки в правоъгълна координатна система, разположена върху равнина. Извеждаме уравнението на права линия, минаваща през две дадени точки в правоъгълна координатна система. Нагледно ще покажем и решим няколко примера, свързани с обхванатия материал.

Yandex.RTB R-A-339285-1

Преди да се получи уравнението на права линия, минаваща през две дадени точки, е необходимо да се обърне внимание на някои факти. Има аксиома, която гласи, че през две несъвпадащи точки на равнина е възможно да се начертае права линия и само една. С други думи, две дадени точки от равнината се определят от права линия, минаваща през тези точки.

Ако равнината е дадена от правоъгълната координатна система Oxy, тогава всяка права линия, изобразена в нея, ще съответства на уравнението на правата линия на равнината. Съществува и връзка с насочващия вектор на правата линия.Тези данни са достатъчни за съставяне на уравнението на права линия, преминаваща през две дадени точки.

Помислете за пример за решаване на подобен проблем. Необходимо е да се състави уравнението на права линия a, минаваща през две несъответстващи точки M 1 (x 1, y 1) и M 2 (x 2, y 2), разположени в декартовата координатна система.

В каноничното уравнение на права линия на равнина, имаща формата x - x 1 a x \u003d y - y 1 a y , правоъгълна координатна система O x y е определена с права линия, която се пресича с нея в точка с координати M 1 (x 1, y 1) с направляващ вектор a → = (a x , a y) .

Необходимо е да се състави каноничното уравнение на правата а, която ще минава през две точки с координати M 1 (x 1, y 1) и M 2 (x 2, y 2) .

Правата линия a има насочващ вектор M 1 M 2 → с координати (x 2 - x 1, y 2 - y 1), тъй като пресича точките M 1 и M 2. Получихме необходимите данни, за да трансформираме каноничното уравнение с координатите на вектора на посоката M 1 M 2 → = (x 2 - x 1, y 2 - y 1) и координатите на точките M 1, лежащи върху тях (x 1, y 1) и M 2 (x 2, y 2) . Получаваме уравнение от вида x - x 1 x 2 - x 1 = y - y 1 y 2 - y 1 или x - x 2 x 2 - x 1 = y - y 2 y 2 - y 1 .

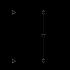
Помислете за фигурата по-долу.

След изчисленията записваме параметричните уравнения на права линия в равнина, която минава през две точки с координати M 1 (x 1, y 1) и M 2 (x 2, y 2) . Получаваме уравнение под формата x = x 1 + (x 2 - x 1) λ y = y 1 + (y 2 - y 1) λ или x = x 2 + (x 2 - x 1) λ y \u003d y 2 + (y 2 - y 1) λ.

Нека разгледаме по-подробно няколко примера.

Пример 1

Напишете уравнението на права линия, минаваща през 2 дадени точки с координати M 1 - 5 , 2 3 , M 2 1 , - 1 6 .

Решение

Каноничното уравнение за права линия, пресичаща се в две точки с координати x 1 , y 1 и x 2 , y 2 , приема формата x - x 1 x 2 - x 1 = y - y 1 y 2 - y 1 . Според условието на задачата имаме, че x 1 = 5, y 1 = 2 3, x 2 = 1, y 2 = 1 6. Необходимо е да се заменят числови стойности в уравнението x - x 1 x 2 - x 1 = y - y 1 y 2 - y 1 . От тук получаваме, че каноничното уравнение ще приеме формата x - (- 5) 1 - (- 5) = y - 2 3 - 1 6 - 2 3 ⇔ x + 5 6 = y - 2 3 - 5 6 .

Отговор: x + 5 6 = y - 2 3 - 5 6 .

Ако е необходимо да се реши проблем с различен тип уравнение, тогава за начало можете да преминете към каноничното, тъй като е по-лесно да стигнете до всяко друго от него.

Пример 2

Съставете общото уравнение на права линия, минаваща през точки с координати M 1 (1, 1) и M 2 (4, 2) в координатната система O x y.

Решение

Първо трябва да запишете каноничното уравнение на дадена права, която минава през дадените две точки. Получаваме уравнение от вида x - 1 4 - 1 = y - 1 2 - 1 ⇔ x - 1 3 = y - 1 1 .

Привеждаме каноничното уравнение до желаната форма, след което получаваме:

x - 1 3 = y - 1 1 ⇔ 1 x - 1 = 3 y - 1 ⇔ x - 3 y + 2 = 0

Отговор: x - 3 y + 2 = 0 .

Примери за такива задачи бяха разгледани в училищните учебници на уроците по алгебра. Училищните задачи се различаваха по това, че беше известно уравнението на права линия с коефициент на наклон, имащо формата y \u003d k x + b. Ако трябва да намерите стойността на наклона k и числото b, при което уравнението y \u003d k x + b дефинира права в системата O x y, която минава през точките M 1 (x 1, y 1) и M 2 (x 2, y 2) , където x 1 ≠ x 2 . Когато x 1 = x 2 , тогава наклонът придобива стойността на безкрайност, а правата линия M 1 M 2 се определя от общо непълно уравнение от вида x - x 1 = 0 .

Защото точките М 1и М 2са на права линия, то техните координати удовлетворяват уравнението y 1 = k x 1 + b и y 2 = k x 2 + b. Необходимо е да се реши системата от уравнения y 1 = k x 1 + b y 2 = k x 2 + b по отношение на k и b.

За да направите това, намираме k = y 2 - y 1 x 2 - x 1 b = y 1 - y 2 - y 1 x 2 - x 1 x 1 или k \u003d y 2 - y 1 x 2 - x 1 b \u003d y 2 - y 2 - y 1 x 2 - x 1 x 2 .

С такива стойности на k и b, уравнението на права линия, преминаваща през дадените две точки, приема следния вид y = y 2 - y 1 x 2 - x 1 x + y 2 - y 2 - y 1 x 2 - x 1 x 1 или y \u003d y 2 - y 1 x 2 - x 1 x + y 2 - y 2 - y 1 x 2 - x 1 x 2.

Запомнянето на такъв огромен брой формули наведнъж няма да работи. За да направите това, е необходимо да увеличите броя на повторенията при решаването на проблеми.

Пример 3

Напишете уравнението на права линия с наклон, минаваща през точки с координати M 2 (2, 1) и y = k x + b.

Решение

За да решим проблема, използваме формула с наклон, който има формата y \u003d k x + b. Коефициентите k и b трябва да приемат такава стойност, че това уравнение да съответства на права линия, минаваща през две точки с координати M 1 (- 7 , - 5) и M 2 (2 , 1) .

точки М 1и М 2разположени на права линия, тогава техните координати трябва да обърнат уравнението y = k x + b правилното равенство. От тук получаваме, че - 5 = k · (- 7) + b и 1 = k · 2 + b. Нека комбинираме уравнението в системата - 5 = k · - 7 + b 1 = k · 2 + b и решаваме.

При замяна получаваме това

5 = k - 7 + b 1 = k 2 + b ⇔ b = - 5 + 7 k 2 k + b = 1 ⇔ b = - 5 + 7 k 2 k - 5 + 7 k = 1 ⇔ ⇔ b = - 5 + 7 k k = 2 3 ⇔ b = - 5 + 7 2 3 k = 2 3 ⇔ b = - 1 3 k = 2 3

Сега стойностите k = 2 3 и b = - 1 3 се заменят в уравнението y = k x + b . Получаваме, че желаното уравнение, преминаващо през дадените точки, ще бъде уравнение с формата y = 2 3 x - 1 3 .

Този начин на решаване предопределя разхода на голям период от време. Има начин, по който задачата се решава буквално в две стъпки.

Записваме каноничното уравнение на права линия, минаваща през M 2 (2, 1) и M 1 (- 7, - 5) , имаща формата x - (- 7) 2 - (- 7) = y - (- 5 ) 1 - (- 5) ⇔ x + 7 9 = y + 5 6 .

Сега да преминем към уравнението на наклона. Получаваме, че: x + 7 9 = y + 5 6 ⇔ 6 (x + 7) = 9 (y + 5) ⇔ y = 2 3 x - 1 3 .

Отговор: y = 2 3 x - 1 3 .

Ако в триизмерното пространство има правоъгълна координатна система O x y z с две дадени несъвпадащи точки с координати M 1 (x 1, y 1, z 1) и M 2 (x 2, y 2, z 2), права линия M, преминаваща през тях 1 M 2 , е необходимо да се получи уравнението на тази права.

Имаме, че каноничните уравнения от вида x - x 1 a x = y - y 1 a y = z - z 1 a z и параметричните уравнения x = x 1 + a x λ y = y 1 + a y λ z = z 1 + a z λ са може да зададе права в координатната система O x y z, преминаваща през точки с координати (x 1, y 1, z 1) с насочващ вектор a → = (a x, a y, a z) .

Прави M 1 M 2 има вектор на посоката от вида M 1 M 2 → = (x 2 - x 1 , y 2 - y 1 , z 2 - z 1) , където правата минава през точката M 1 (x 1 , y 1 , z 1) и M 2 (x 2, y 2, z 2), следователно каноничното уравнение може да бъде от вида x - x 1 x 2 - x 1 = y - y 1 y 2 - y 1 = z - z 1 z 2 - z 1 или x - x 2 x 2 - x 1 \u003d y - y 2 y 2 - y 1 \u003d z - z 2 z 2 - z 1, на свой ред, параметричен x \u003d x 1 + (x 2 - x 1) λ y \u003d y 1 + (y 2 - y 1) λ z = z 1 + (z 2 - z 1) λ или x = x 2 + (x 2 - x 1) λ y = y 2 + (y 2 - y 1) λ z \u003d z 2 + (z 2 - z 1) λ.

Помислете за фигура, която показва 2 дадени точки в пространството и уравнението на права линия.

Пример 4

Напишете уравнението на права линия, дефинирана в правоъгълна координатна система O x y z на триизмерно пространство, минаваща през дадените две точки с координати M 1 (2, - 3, 0) и M 2 (1, - 3, - 5 ) .

Решение

Трябва да намерим каноничното уравнение. Тъй като говорим за триизмерно пространство, това означава, че когато права линия минава през дадени точки, желаното канонично уравнение ще приеме формата x - x 1 x 2 - x 1 = y - y 1 y 2 - y 1 = z - z 1 z 2 - z 1 .

По условие имаме, че x 1 = 2, y 1 = - 3, z 1 = 0, x 2 = 1, y 2 = - 3, z 2 = - 5. От това следва, че необходимите уравнения могат да бъдат записани, както следва:

x - 2 1 - 2 = y - (- 3) - 3 - (- 3) = z - 0 - 5 - 0 ⇔ x - 2 - 1 = y + 3 0 = z - 5

Отговор: x - 2 - 1 = y + 3 0 = z - 5.

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter

Определение.Всяка права в равнината може да бъде дадена от уравнение от първи ред

Ah + Wu + C = 0,

и константите A, B не са равни на нула едновременно. Това уравнение от първи ред се нарича общото уравнение на права линия.В зависимост от стойностите на константите A, B и C са възможни следните специални случаи:

C \u003d 0, A ≠ 0, B ≠ 0 - линията минава през началото

A = 0, B ≠ 0, C ≠ 0 (By + C = 0) - линията е успоредна на оста Ox

B \u003d 0, A ≠ 0, C ≠ 0 ( Ax + C = 0) - правата е успоредна на оста Oy

B \u003d C \u003d 0, A ≠ 0 - правата линия съвпада с оста Oy

A \u003d C \u003d 0, B ≠ 0 - правата линия съвпада с оста Ox

Уравнението на права линия може да бъде представено в различни форми в зависимост от дадени начални условия.

Уравнение на права линия от точка и нормален вектор

Определение.В декартова правоъгълна координатна система вектор с компоненти (A, B) е перпендикулярен на правата, дадена от уравнението Ax + By + C = 0.

Пример. Намерете уравнението на права линия, минаваща през точката A(1, 2), перпендикулярна на (3, -1).

Решение. При A = 3 и B = -1 съставяме уравнението на права линия: 3x - y + C = 0. За да намерим коефициента C, заместваме координатите на дадена точка A в получения израз. Получаваме: 3 - 2 + C = 0, следователно, C = -1 . Общо: желаното уравнение: 3x - y - 1 \u003d 0.

Уравнение на права, минаваща през две точки

Нека две точки M 1 (x 1, y 1, z 1) и M 2 (x 2, y 2, z 2) са дадени в пространството, тогава уравнението на права линия, минаваща през тези точки:

Ако някой от знаменателите е равен на нула, съответният числител трябва да бъде равен на нула. На равнината уравнението на права линия, написано по-горе, е опростено:

ако x 1 ≠ x 2 и x = x 1, ако x 1 = x 2.

Извиква се фракция = k фактор на наклонаправ.

Пример. Намерете уравнението на права линия, минаваща през точките A(1, 2) и B(3, 4).

Решение.Прилагайки горната формула, получаваме:

Уравнение на права линия от точка и наклон

Ако общият Ax + Wu + C = 0 води до формата:

и посочете , тогава полученото уравнение се нарича уравнение на права линия с наклонк.

Уравнение на права линия с вектор на точка и посока

По аналогия с точката, като се има предвид уравнението на права линия през нормалния вектор, можете да въведете присвояването на права линия през точка и насочващ вектор на права линия.

Определение.Всеки ненулев вектор (α 1, α 2), чиито компоненти удовлетворяват условието A α 1 + B α 2 = 0, се нарича насочващ вектор на правата

Ah + Wu + C = 0.

Пример. Намерете уравнението на права линия с вектор на посока (1, -1) и минаваща през точка A(1, 2).

Решение.Ще търсим уравнението на желаната права линия във вида: Ax + By + C = 0. В съответствие с определението коефициентите трябва да отговарят на условията:

1 * A + (-1) * B = 0, т.е. А = Б.

Тогава уравнението на права линия има вида: Ax + Ay + C = 0, или x + y + C / A = 0. за x = 1, y = 2 получаваме C / A = -3, т.е. желаното уравнение:

Уравнение на права линия в сегменти

Ако в общото уравнение на правата линия Ah + Wu + C = 0 C≠0, тогава, разделяйки на –C, получаваме: или

Геометричното значение на коефициентите е, че коефициентът ае координатата на точката на пресичане на правата с оста x, и б- координатата на пресечната точка на правата линия с оста Oy.

Пример.Дадено е общото уравнение на правата x - y + 1 = 0. Намерете уравнението на тази права в отсечките.

C \u003d 1, , a = -1, b = 1.

Нормално уравнение на права линия

Ако и двете страни на уравнението Ax + Vy + C = 0 се умножат по числото , което се нарича нормализиращ фактор, тогава получаваме

xcosφ + ysinφ - p = 0 –

нормално уравнение на права линия. Знакът ± на нормализиращия коефициент трябва да бъде избран така, че μ * С< 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Пример. Като се има предвид общото уравнение на правата 12x - 5y - 65 = 0. За тази права се изисква да се напишат различни видове уравнения.

уравнението на тази права линия в сегменти:

уравнението на тази права с наклона: (разделете на 5)

; cos φ = 12/13; sin φ= -5/13; р=5.

Трябва да се отбележи, че не всяка права линия може да бъде представена с уравнение на сегменти, например прави линии, успоредни на осите или минаващи през началото.

Пример. Правата линия отрязва равни положителни отсечки по координатните оси. Напишете уравнението на права линия, ако площта на триъгълника, образуван от тези сегменти, е 8 cm 2.

Решение.Правото уравнение има вида: , ab /2 = 8; ab=16; а=4, а=-4. а = -4< 0 не подходит по условию задачи. Итого: или х + у – 4 = 0.

Пример. Напишете уравнението на права линия, минаваща през точка А (-2, -3) и началото.

Решение. Уравнението на права линия има вида: , където x 1 = y 1 \u003d 0; x 2 \u003d -2; y 2 \u003d -3.

Ъгъл между линиите в равнина

Определение.Ако са дадени две линии y = k 1 x + b 1 , y = k 2 x + b 2 , тогава острият ъгъл между тези линии ще бъде определен като

.

Две прави са успоредни, ако k 1 = k 2 . Две прави са перпендикулярни, ако k 1 = -1/ k 2 .

Теорема.Правите линии Ax + Vy + C \u003d 0 и A 1 x + B 1 y + C 1 = 0 са успоредни, когато коефициентите A 1 = λA, B 1 = λB са пропорционални. Ако и С 1 = λС, тогава правите съвпадат. Координатите на пресечната точка на две прави се намират като решение на системата от уравнения на тези прави.

Уравнение на права, минаваща през дадена точка, перпендикулярна на дадена права

Определение.Правата, минаваща през точката M 1 (x 1, y 1) и перпендикулярна на правата y = kx + b, е представена от уравнението:

Разстояние от точка до линия

Теорема.Ако е дадена точка M(x 0, y 0), тогава разстоянието до правата Ax + Vy + C \u003d 0 се определя като

.

Доказателство.Нека точката M 1 (x 1, y 1) е основата на перпендикуляра, спуснат от точка M на дадената права. Тогава разстоянието между точките M и M 1:

(1)

Координатите x 1 и y 1 могат да бъдат намерени като решение на системата от уравнения:

Второто уравнение на системата е уравнението на права линия, минаваща през дадена точка M 0 перпендикулярно на дадена права линия. Ако трансформираме първото уравнение на системата във вида:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

тогава, решавайки, получаваме:

Замествайки тези изрази в уравнение (1), намираме:

Теоремата е доказана.

Пример. Определете ъгъла между правите: y = -3 x + 7; y = 2 x + 1.

k 1 \u003d -3; k2 = 2; tgφ = ; φ= π /4.

Пример. Покажете, че правите 3x - 5y + 7 = 0 и 10x + 6y - 3 = 0 са перпендикулярни.

Решение. Откриваме: k 1 = 3/5, k 2 = -5/3, k 1 * k 2 = -1, следователно линиите са перпендикулярни.

Пример. Дадени са върховете на триъгълника A(0; 1), B (6; 5), C (12; -1). Намерете уравнението за височината, изтеглена от връх C.

Решение. Намираме уравнението на страната AB: ; 4 х = 6 у - 6;

2x – 3y + 3 = 0;

Желаното уравнение за височина е: Ax + By + C = 0 или y = kx + b. k = . Тогава y = . Защото височината минава през точка C, тогава нейните координати удовлетворяват това уравнение: откъдето b = 17. Общо: .

Отговор: 3x + 2y - 34 = 0.

В тази статия ще разгледаме общото уравнение на права линия в равнина. Нека да дадем примери за построяване на общото уравнение на права линия, ако са известни две точки от тази права линия или ако са известни една точка и нормалният вектор на тази права линия. Нека представим методи за трансформиране на уравнение в общ вид в канонични и параметрични форми.

Нека е дадена произволна декартова правоъгълна координатна система Окси. Помислете за уравнение от първа степен или линейно уравнение:

Ax+By+C=0,

(1)

където А, Б, Вса някои константи и поне един от елементите Аи Бразличен от нула.

Ще покажем, че линейно уравнение в равнината дефинира права линия. Нека докажем следната теорема.

Теорема 1. В произволна декартова правоъгълна координатна система на равнина всяка права линия може да бъде дадена с линейно уравнение. Обратно, всяко линейно уравнение (1) в произволна декартова правоъгълна координатна система на равнината дефинира права линия.

Доказателство. Достатъчно е да се докаже, че линията Лсе определя от линейно уравнение за всяка една декартова правоъгълна координатна система, тъй като тогава ще се определя от линейно уравнение и за всеки избор на декартова правоъгълна координатна система.

Нека на равнината е дадена права линия Л. Избираме координатна система, така че оста волподравнени с линията Л, и оста ойбеше перпендикулярна на него. След това уравнението на правата Лще приеме следната форма:

y=0.

(2)

Всички точки на една права Лще удовлетвори линейното уравнение (2), а всички точки извън тази права линия няма да удовлетворяват уравнение (2). Първата част на теоремата е доказана.

Нека е дадена декартова правоъгълна координатна система и е дадено линейно уравнение (1), където поне един от елементите Аи Бразличен от нула. Намерете местоположението на точките, чиито координати удовлетворяват уравнение (1). Тъй като поне един от коефициентите Аи Бе различно от нула, то уравнение (1) има поне едно решение М(х 0 ,г 0). (Например кога А≠0, точка М 0 (−C/A, 0) принадлежи на даденото място на точки). Замествайки тези координати в (1), получаваме тъждеството

брадва 0 +от 0 +° С=0.

(3)

Нека извадим тъждество (3) от (1):

А(х−х 0)+Б(г−г 0)=0.

(4)

Очевидно уравнение (4) е еквивалентно на уравнение (1). Следователно е достатъчно да се докаже, че (4) дефинира някаква права.

Тъй като разглеждаме декартова правоъгълна координатна система, от равенство (4) следва, че векторът с компоненти ( x−x 0 , y−y 0 ) е ортогонална на вектора нс координати ( А, Б}.

Помислете за някаква линия Лпреминаване през точката М 0 (х 0 , г 0) и перпендикулярно на вектора н(Фиг. 1). Нека точката М(х,y) принадлежи на реда Л. След това векторът с координати x−x 0 , y−y 0 перпендикулярно ни уравнение (4) е изпълнено (скаларно произведение на векторите ни е равно на нула). Обратно, ако точката М(х,y) не лежи на права Л, след това векторът с координати x−x 0 , y−y 0 не е ортогонално на вектора ни уравнение (4) не е изпълнено. Теоремата е доказана.

Доказателство. Тъй като линии (5) и (6) дефинират една и съща линия, нормалните вектори н 1 ={А 1 ,Б 1) и н 2 ={А 2 ,Б 2) са колинеарни. Тъй като векторите н 1 ≠0, н 2 ≠ 0, тогава има число λ , Какво н 2 =н 1 λ . Следователно имаме: А 2 =А 1 λ , Б 2 =Б 1 λ . Нека докажем това ° С 2 =° С 1 λ . Очевидно е, че съвпадащите прави имат обща точка М 0 (х 0 , г 0). Умножаване на уравнение (5) по λ и като извадим уравнение (6) от него получаваме:

Тъй като първите две равенства от изрази (7) са изпълнени, то ° С 1 λ −° С 2=0. Тези. ° С 2 =° С 1 λ . Забележката е доказана.

Забележете, че уравнение (4) дефинира уравнението на права линия, минаваща през точката М 0 (х 0 , г 0) и има нормален вектор н={А, Б). Следователно, ако нормалният вектор на правата и точката, принадлежаща на тази права, са известни, тогава общото уравнение на правата може да бъде построено с помощта на уравнение (4).

Пример 1. Права минава през точка М=(4,−1) и има нормален вектор н=(3, 5). Построете общото уравнение на права линия.

Решение. Ние имаме: х 0 =4, г 0 =−1, А=3, Б=5. За да построим общото уравнение на права линия, ние заместваме тези стойности в уравнение (4):

Отговор:

Вектор, успореден на линията Ли следователно е перпендикулярна на нормалния вектор на правата Л. Нека построим нормален вектор Л, като се има предвид, че скаларното произведение на векторите ни е равно на нула. Можем да напишем напр. н={1,−3}.

За да построим общото уравнение на права линия, използваме формула (4). Нека заместим в (4) координатите на точката М 1 (можем да вземем и координатите на точката М 2) и нормален вектор н:

Заместване на координати на точката М 1 и М 2 в (9) можем да се уверим, че правата линия, дадена от уравнение (9), минава през тези точки.

Отговор:

Извадете (10) от (1):

Получихме каноничното уравнение на права линия. вектор q={−Б, А) е векторът на посоката на правата линия (12).

Вижте обратна трансформация.

Пример 3. Права линия в равнина се представя със следното общо уравнение:

Преместете втория член надясно и разделете двете страни на уравнението на 2 5.

Уравнение на права линия, минаваща през две точки. В статията" " Обещах ви да анализирате втория начин за решаване на представените задачи за намиране на производната, с дадена функционална графика и допирателна към тази графика. Ще проучим този метод в , не пропускайте! Защоследващия?

Факт е, че там ще се използва формулата на уравнението на права линия. Разбира се, човек може просто да покаже тази формула и да ви посъветва да я научите. Но е по-добре да се обясни откъде идва (как се получава). Необходимо е! Ако го забравите, бързо го възстановетеняма да е трудно. Всичко е подробно описано по-долу. И така, имаме две точки A в координатната равнина(x 1; y 1) и B (x 2; y 2), през посочените точки се начертава права линия:

Ето директната формула:

*Тоест при заместване на конкретните координати на точките получаваме уравнение от вида y=kx+b.

** Ако тази формула е просто „запомнена“, тогава има голяма вероятност да се объркате с индекси, когато х. В допълнение, индексите могат да бъдат обозначени по различни начини, например:

Ето защо е важно да разберете значението.

Сега извеждането на тази формула. Всичко е много просто!

Триъгълниците ABE и ACF са сходни по отношение на остър ъгъл (първият знак за сходство на правоъгълните триъгълници). От това следва, че съотношенията на съответните елементи са равни, тоест:

Сега просто изразяваме тези сегменти по отношение на разликата в координатите на точките:

Разбира се, няма да има грешка, ако напишете връзките на елементите в различен ред (основното нещо е да запазите съответствието):

Резултатът е същото уравнение на права линия. Това е всичко!

Тоест, независимо как са обозначени самите точки (и техните координати), разбирайки тази формула, винаги ще намерите уравнението на права линия.

Формулата може да се изведе с помощта на свойствата на векторите, но принципът на извеждане ще бъде същият, тъй като ще говорим за пропорционалността на техните координати. В този случай работи същото сходство на правоъгълни триъгълници. Според мен изводът, описан по-горе, е по-разбираем)).

Преглед на изхода чрез векторни координати >>>

Нека върху координатната равнина се построи права линия, минаваща през две дадени точки A (x 1; y 1) и B (x 2; y 2). Нека маркираме произволна точка C на правата с координати ( х; г). Ние също така означаваме два вектора:

Известно е, че за вектори, лежащи на успоредни прави (или на една права), съответните им координати са пропорционални, т.е.

- пишем равенството на съотношенията на съответните координати:

Помислете за пример:

Намерете уравнението на права линия, минаваща през две точки с координати (2;5) и (7:3).

Не можете дори да изградите самата линия. Прилагаме формулата:

Важно е да хванете кореспонденцията при съставянето на съотношението. Няма как да сбъркате, ако напишете:

Отговор: y=-2/5x+29/5 go y=-0.4x+5.8

За да се уверите, че полученото уравнение е намерено правилно, не забравяйте да го проверите - заменете координатите на данните в него в състоянието на точките. Трябва да получите правилни равенства.

Това е всичко. Надявам се материалът да ви е бил полезен.

С уважение, Александър.

P.S: Ще бъда благодарен, ако разкажете за сайта в социалните мрежи.

Уравнение на права линия върху равнина.
Векторът на посоката е прав. Нормален вектор

Правата линия на равнина е една от най-простите геометрични фигури, позната ви от началните класове и днес ще научим как да се справяме с нея, използвайки методите на аналитичната геометрия. За да овладеете материала, е необходимо да можете да изградите права линия; знаете кое уравнение определя права линия, по-специално права линия, минаваща през началото и прави линии, успоредни на координатните оси. Тази информация може да бъде намерена в ръководството. Графики и свойства на елементарни функции, аз го създадох за matan, но разделът за линейната функция се оказа много сполучлив и подробен. Затова, скъпи чайници, първо загрейте там. Освен това трябва да имате основни познания за векторив противен случай разбирането на материала ще бъде непълно.

В този урок ще разгледаме начините, по които можете да напишете уравнението на права линия в равнина. Препоръчвам да не пренебрегвате практическите примери (дори и да изглеждат много прости), тъй като ще ги снабдя с елементарни и важни факти, технически методи, които ще са необходими в бъдеще, включително в други раздели на висшата математика.

• Как да напиша уравнението на права линия с наклон?
• Как ?
• Как да намерим вектора на посоката по общото уравнение на права линия?
• Как да напиша уравнение на права линия с дадена точка и нормален вектор?

и започваме:

Линейно уравнение с наклон

Нарича се добре познатата "училищна" форма на уравнението на права линия уравнение на права линия с наклон. Например, ако правата линия е дадена от уравнението, тогава нейният наклон: . Помислете за геометричното значение на този коефициент и как неговата стойност влияе върху местоположението на линията:

В хода на геометрията се доказва, че наклонът на правата линия е тангенс на ъгълмежду положителна посока на оси дадена линия: , а ъгълът се „развива“ обратно на часовниковата стрелка.

За да не претрупвам чертежа, нарисувах ъгли само за две прави линии. Помислете за "червената" права линия и нейния наклон. Съгласно горното: (ъгълът "алфа" е обозначен със зелена дъга). За "синята" линия с наклона е вярно равенството (ъгълът "бета" е обозначен с кафявата дъга). И ако тангенсът на ъгъла е известен, тогава, ако е необходимо, е лесно да се намери и ъгълас помощта на обратната функция - дъгова допирателна. Както се казва, тригонометрична таблица или калкулатор в ръка. По този начин, наклонът характеризира степента на наклон на правата линия към оста x.

В този случай са възможни следните случаи:

1) Ако наклонът е отрицателен: , тогава линията, грубо казано, върви отгоре надолу. Примери са "сини" и "пурпурни" прави линии в чертежа.

2) Ако наклонът е положителен: , тогава линията върви отдолу нагоре. Примери са "черни" и "червени" прави линии в чертежа.

3) Ако наклонът е равен на нула: , тогава уравнението приема формата , а съответната права линия е успоредна на оста. Пример за това е "жълтата" линия.

4) За семейство прави линии, успоредни на оста (няма пример на чертежа, освен самата ос), наклонът не съществува (тангенс от 90 градуса не е дефиниран).

Колкото по-голям е модулът на наклона, толкова по-стръмна става линейната графика.

Например, помислете за две прави линии. Ето, така че правата линия има по-стръмен наклон. Напомням ви, че модулът ви позволява да игнорирате знака, само нас ни интересува абсолютни стойностиъглови коефициенти.

От своя страна правата линия е по-стръмна от правите. .

Обратно: колкото по-малък е наклонът по модул, правата линия е по-плоска.

За прави линии неравенството е вярно, така че правата линия е повече от балдахин. Детска пързалка, за да не се засаждат синини и подутини.

Защо е необходимо това?

Удължете мъките си Познаването на горните факти ви позволява незабавно да видите грешките си, по-специално грешките при начертаване на графики - ако чертежът се оказа „очевидно нещо не е наред“. Желателно е вие незабавнобеше ясно, че например правата линия е много стръмна и върви отдолу нагоре, а правата линия е много плоска, близо до оста и върви отгоре надолу.

В геометричните задачи често се появяват няколко прави линии, така че е удобно да ги обозначим по някакъв начин.

Нотация: правите линии са обозначени с малки латински букви: . Популярна опция е обозначаването на една и съща буква с естествени индекси. Например петте реда, които току-що разгледахме, могат да бъдат обозначени с .

Тъй като всяка линия е уникално определена от две точки, тя може да бъде обозначена с тези точки: и т.н. Нотацията съвсем очевидно предполага, че точките принадлежат на правата.

Време е да се отпуснете малко:

Как да напиша уравнението на права линия с наклон?

Ако е известна точка, която принадлежи на определена права, и наклонът на тази права, тогава уравнението на тази права се изразява с формулата:

Пример 1

Напишете уравнението на права линия с наклон, ако е известно, че точката принадлежи на тази права линия.

Решение: Ще съставим уравнението на права линия по формулата . В такъв случай:

Отговор:

Прегледизпълнени елементарно. Първо, разглеждаме полученото уравнение и се уверяваме, че нашият наклон е на мястото си. Второ, координатите на точката трябва да отговарят на даденото уравнение. Нека ги включим в уравнението:

Получава се правилното равенство, което означава, че точката удовлетворява полученото уравнение.

Заключение: Уравнението е намерено правилно.

По-сложен пример за решение "направи си сам":

Пример 2

Напишете уравнението на права линия, ако е известно, че нейният ъгъл на наклон към положителната посока на оста е , и точката принадлежи на тази права линия.

Ако имате някакви затруднения, прочетете отново теоретичния материал. По-точно, по-практично, пропускам много доказателства.

Последният звънец удари, абитуриентският бал утихна, а зад портите на родното ни училище всъщност ни чака аналитичната геометрия. Шегите свършиха... Може би тепърва започва =)

Носталгично размахваме дръжката на познатото и се запознаваме с общото уравнение на права линия. Тъй като в аналитичната геометрия се използва точно това:

Общото уравнение на права линия има вида: , къде са някои числа. В същото време коефициентите едновременноне са равни на нула, тъй като уравнението губи смисъла си.

Да се ​​облечем в костюм и да завържем уравнение с наклон. Първо, преместваме всички термини в лявата страна:

Терминът с "x" трябва да бъде поставен на първо място:

По принцип уравнението вече има формата , но според правилата на математическия етикет коефициентът на първия член (в този случай) трябва да е положителен. Промяна на знаците:

Запомнете тази техническа характеристика!Правим първия коефициент (най-често) положителен!

В аналитичната геометрия уравнението на права линия почти винаги ще бъде дадено в общ вид. Е, ако е необходимо, е лесно да го приведете до "училищна" форма с наклон (с изключение на прави линии, успоредни на оста y).

Да се ​​запитаме какво достатъчнознаете как да изградите права линия? Две точки. Но за този случай от детството по-късно, сега пръчки със стрелки правило. Всяка права линия има добре дефиниран наклон, към който е лесно да се "адаптира" вектор.

Вектор, който е успореден на права, се нарича вектор на посоката на тази права.. Очевидно всяка права линия има безкрайно много вектори на посоката и всички те ще бъдат колинеарни (ко-насочени или не - няма значение).

Ще обозначя вектора на посоката по следния начин: .

Но един вектор не е достатъчен за изграждане на права линия, векторът е свободен и не е прикрепен към нито една точка от равнината. Следователно е необходимо допълнително да се знае някаква точка, която принадлежи на правата.

Как да напиша уравнение на права линия с дадена точка и вектор на посоката?

Ако е известна точка, принадлежаща на правата, и насочващият вектор на тази права, тогава уравнението на тази права може да се състави по формулата:

Понякога се нарича канонично уравнение на правата .

Какво да правя кога една от координатитее нула, ще разгледаме практически примери по-долу. Между другото, забележете - и двете наведнъжкоординатите не могат да бъдат нула, тъй като нулевият вектор не определя конкретна посока.

Пример 3

Напишете уравнение на права линия с дадена точка и вектор на посоката

Решение: Ще съставим уравнението на права линия по формулата. В такъв случай:

Използвайки свойствата на пропорцията, ние се отърваваме от фракциите:

И привеждаме уравнението в общ вид:

Отговор:

Рисуването в такива примери, като правило, не е необходимо, но в името на разбирането:

На чертежа виждаме началната точка, оригиналния вектор на посоката (може да бъде отложен от всяка точка на равнината) и конструираната линия. Между другото, в много случаи изграждането на права линия се извършва най-удобно с помощта на уравнението на наклона. Нашето уравнение е лесно да се преобразува във формата и без никакви проблеми вземете още една точка, за да построите права линия.

Както беше отбелязано в началото на раздела, една линия има безкрайно много вектори на посоката и всички те са колинеарни. Например, нарисувах три такива вектора: . Който и вектор на посока да изберем, резултатът винаги ще бъде едно и също уравнение на права линия.

Нека съставим уравнението на права линия от точка и насочващ вектор:

Разбиване на пропорцията:

Разделете двете страни на -2 и получете познатото уравнение:

Желаещите могат по подобен начин да тестват вектори или всеки друг колинеарен вектор.

Сега нека решим обратната задача:

Как да намерим вектора на посоката по общото уравнение на права линия?

Много просто:

Ако права линия е дадена от общо уравнение в правоъгълна координатна система, тогава векторът е векторът на посоката на тази права линия.

Примери за намиране на вектори на посоката на прави линии:

Изявлението ни позволява да намерим само един вектор на посока от безкраен набор, но не се нуждаем от повече. Въпреки че в някои случаи е препоръчително да се намалят координатите на векторите на посоката:

И така, уравнението определя права линия, която е успоредна на оста, а координатите на получения направляващ вектор се разделят удобно на -2, като се получава точно основният вектор като управляващ вектор. Логично.

По същия начин, уравнението дефинира права линия, успоредна на оста, и разделяйки координатите на вектора на 5, получаваме орта като вектор на посоката.

Сега нека изпълним проверете пример 3. Примерът се повиши, така че ви напомням, че в него съставихме уравнението на права линия, използвайки точка и вектор на посока

Преди всичко, според уравнението на права линия, ние възстановяваме нейния насочващ вектор: - всичко е наред, получихме оригиналния вектор (в някои случаи той може да се окаже колинеарен с оригиналния вектор и това обикновено е лесно да се види от пропорционалността на съответните координати).

Второ, координатите на точката трябва да отговарят на уравнението. Заместваме ги в уравнението:

Получи се правилно равенство, от което сме много доволни.

Заключение: Работата е завършена правилно.

Пример 4

Напишете уравнение на права линия с дадена точка и вектор на посоката

Това е пример "направи си сам". Решение и отговор в края на урока. Много е желателно да се направи проверка според току-що разгледания алгоритъм. Опитайте се винаги (ако е възможно) да проверявате чернова. Глупаво е да правиш грешки там, където те могат да бъдат 100% избегнати.

В случай, че една от координатите на вектора на посоката е нула, е много лесно да се направи:

Пример 5

Решение: Формулата е невалидна, защото знаменателят от дясната страна е нула. Има изход! Използвайки свойствата на пропорцията, пренаписваме формулата във формата , а останалата част се търкаля по дълбока коловоза:

Отговор:

Преглед:

1) Възстановете вектора на посоката на правата линия:
– полученият вектор е колинеарен спрямо първоначалния вектор на посоката.

2) Заменете координатите на точката в уравнението:

Получава се правилното равенство

Заключение: работата е завършена правилно

Възниква въпросът, защо да се занимавате с формулата, ако има универсална версия, която така или иначе ще работи? Има две причини. Първо, дробната формула много по-добре да се запомни. И второ, недостатъкът на универсалната формула е това значително повишен риск от объркванепри заместване на координати.

Пример 6

Съставете уравнението на права линия с дадена точка и вектор на посоката.

Това е пример "направи си сам".

Нека се върнем към вездесъщите две точки:

Как да напиша уравнението на права линия с две точки?

Ако са известни две точки, тогава уравнението на права линия, минаваща през тези точки, може да се състави по формулата:

Всъщност това е един вид формула и ето защо: ако са известни две точки, тогава векторът ще бъде векторът на посоката на тази права. На урока Вектори за манекениразгледахме най-простия проблем - как да намерим координатите на вектор от две точки. Според този проблем координатите на вектора на посоката:

Забележка : точките могат да се "разменят" и да се използва формулата . Такова решение би било равностойно.

Пример 7

Напишете уравнението на права линия от две точки .

Решение: Използвайте формулата:

Сресваме знаменателите:

И разбъркайте тестето:

Сега е удобно да се отървете от дробни числа. В този случай трябва да умножите и двете части по 6:

Отворете скобите и си спомнете уравнението:

Отговор:

Прегледе очевидно - координатите на началните точки трябва да отговарят на полученото уравнение:

1) Заменете координатите на точката:

Истинско равенство.

2) Заменете координатите на точката:

Истинско равенство.

Заключение: уравнението на правата линия е правилно.

Ако поне единот точки не удовлетворява уравнението, потърсете грешка.

Струва си да се отбележи, че графичната проверка в този случай е трудна, тъй като да се изгради линия и да се види дали точките принадлежат към нея , не е толкова лесно.

Ще отбележа няколко технически точки на решението. Може би в този проблем е по-изгодно да се използва огледалната формула и за същите точки направи уравнение:

Има по-малко дроби. Ако искате, можете да завършите решението до края, като резултатът трябва да бъде същото уравнение.

Втората точка е да погледнете крайния отговор и да видите дали може да бъде допълнително опростен? Например, ако се получи уравнение, тогава е препоръчително да го намалите с две: - уравнението ще зададе същата права линия. Това обаче вече е тема за разговор взаимно подреждане на прави линии.

След като получи отговор в пример 7 за всеки случай проверих дали ВСИЧКИ коефициенти на уравнението се делят на 2, 3 или 7. Въпреки че най-често такива намаления се правят по време на решението.

Пример 8

Напишете уравнението на права линия, минаваща през точките .

Това е пример за независимо решение, което просто ще ви позволи да разберете и изработите по-добре техниката на изчисление.

Подобно на предишния параграф: ако във формулата един от знаменателите (координата на вектора на посоката) изчезва, след което го пренаписваме като . И отново забележете колко неудобна и объркана започна да изглежда. Не виждам голям смисъл да давам практически примери, тъй като вече сме решили такъв проблем (виж № 5, 6).

Права линия нормален вектор (нормален вектор)

Какво е нормално? Казано по-просто, нормата е перпендикуляр. Тоест нормалният вектор на права е перпендикулярен на дадената права. Очевидно е, че всяка права линия има безкраен брой от тях (както и насочващи вектори), а всички нормални вектори на правата линия ще бъдат колинеарни (съпосочени или не - няма значение).

Справянето с тях ще бъде дори по-лесно, отколкото с векторите на посоката:

Ако права линия е дадена от общо уравнение в правоъгълна координатна система, тогава векторът е нормален вектор на тази права линия.

Ако координатите на вектора на посоката трябва внимателно да бъдат „извадени“ от уравнението, тогава координатите на нормалния вектор могат просто да бъдат „отстранени“.

Нормалният вектор винаги е ортогонален на вектора на посоката на линията. Ще проверим ортогоналността на тези вектори с помощта на точков продукт:

Ще дам примери със същите уравнения като за вектора на посоката:

Възможно ли е да се напише уравнение на права линия, като се знае една точка и нормален вектор? Усеща се, че е възможно. Ако нормалният вектор е известен, тогава посоката на най-правата линия също се определя еднозначно - това е „твърда структура“ с ъгъл от 90 градуса.

Как да напиша уравнение на права линия с дадена точка и нормален вектор?

Ако някаква точка, принадлежаща на правата, и нормалният вектор на тази права са известни, тогава уравнението на тази права се изразява с формулата:

Тук всичко мина без дроби и други изненади. Такъв е нашият нормален вектор. Обичам го. И уважение =)

Пример 9

Съставете уравнението на права линия с дадена точка и нормален вектор. Намерете вектора на посоката на правата линия.

Решение: Използвайте формулата:

Получава се общото уравнение на правата линия, нека проверим:

1) „Премахнете“ координатите на нормалния вектор от уравнението: - да, наистина, оригиналният вектор се получава от условието (или векторът трябва да е колинеарен на оригиналния вектор).

2) Проверете дали точката отговаря на уравнението:

Истинско равенство.

След като сме се уверили, че уравнението е правилно, ще изпълним втората, по-лесна част от задачата. Изваждаме вектора на посоката на правата линия:

Отговор:

На чертежа ситуацията е следната:

За целите на обучението подобна задача за самостоятелно решение:

Пример 10

Съставете уравнението на права линия с дадена точка и нормален вектор. Намерете вектора на посоката на правата линия.

Последният раздел на урока ще бъде посветен на по-рядко срещани, но също така важни видове уравнения на права линия в равнина

Уравнение на права линия в сегменти.
Уравнение на права линия в параметрична форма

Уравнението на права линия в сегменти има вида , където са различни от нула константи. Някои видове уравнения не могат да бъдат представени в тази форма, например пряка пропорционалност (тъй като свободният член е нула и няма начин да се получи едно от дясната страна).

Това е, образно казано, "технически" тип уравнение. Обичайната задача е да се представи общото уравнение на права линия като уравнение на права линия на отсечки. Защо е удобно? Уравнението на права линия в сегменти ви позволява бързо да намерите точките на пресичане на права линия с координатни оси, което е много важно в някои проблеми на висшата математика.

Намерете пресечната точка на правата с оста. Нулираме „y“ и уравнението приема формата . Желаната точка се получава автоматично: .

Същото и с ос е точката, където правата пресича оста y.