Методи за намиране на матрица. Обратна матрица. Решаване на матрични уравнения

Подобно на обратната в много свойства.

Колегиален YouTube

1 / 5

✪ Как да намерим обратната страна на матрица - bezbotvy

✪ Обратна матрица (2 начина за намиране)

✪ Обратна матрица # 1

-2 28.01.2015 г. Обратна матрица 3x3

-2 27.01.2015 г. Обратна матрица 2x2

Субтитри

Свойства на обратната матрица

• det A - 1 = 1 det A (\ displaystyle \ det A ^ ( - 1) = (\ frac (1) (\ det A))), където det (\ displaystyle \ \ det)означава детерминанта.
• (A B) - 1 = B - 1 A - 1 (\ displaystyle \ (AB) ^ ( - 1) = B ^ ( - 1) A ^ ( - 1))за две квадратни обратими матрици A (\ displaystyle A)и B (\ displaystyle B).
• (A T) - 1 = (A - 1) T (\ displaystyle \ (A ^ (T)) ^ ( - 1) = (A ^ ( - 1)) ^ (T)), където (...) T (\ displaystyle (...) ^ (T))означава транспонирана матрица.
• (k A) - 1 = k - 1 A - 1 (\ displaystyle \ (kA) ^ ( - 1) = k ^ ( - 1) A ^ ( - 1))за всеки коефициент k ≠ 0 (\ displaystyle k \ not = 0).
• E - 1 = E (\ displaystyle \ E ^ ( - 1) = E).
• Ако е необходимо да се реши система от линейни уравнения, (b е ненулев вектор) където x (\ displaystyle x)е необходимия вектор и ако A - 1 (\ displaystyle A ^ ( - 1))съществува, значи x = A - 1 b (\ displaystyle x = A ^ ( - 1) b)... В противен случай или измерението на пространството на решенията е по -голямо от нула, или изобщо няма такива.

Методи за намиране на обратната матрица

Ако матрицата е обратима, тогава можете да използвате един от следните методи, за да намерите обратната страна на матрицата:

Точни (директни) методи

Метод на Гаус-Джордан

Да вземем две матрици: себе си Аи сингъл E... Нека дадем матрицата Акъм матрицата на идентичността по метода на Gauss-Jordan, прилагайки трансформации по редове (можете също да приложите трансформации по колони, но не и разбъркване). След като приложите всяка операция към първата матрица, приложете същата операция към втората. Когато редукцията на първата матрица до единичната форма приключи, втората матрица ще бъде равна на A −1.

Когато използвате метода на Гаус, първата матрица ще бъде умножена вляво с една от елементарните матрици Λ i (\ displaystyle \ Lambda _ (i))(трансвекционна или диагонална матрица с такива на основния диагонал, с изключение на една позиция):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A - 1 (\ displaystyle \ Lambda _ (1) \ cdot \ dots \ cdot \ Lambda _ (n) \ cdot A = \ Lambda A = E \ Rightarrow \ Lambda = A ^ (- 1)). Λ m = [1… 0 - a 1 m / amm 0… 0… 0… 1 - am - 1 m / amm 0… 0 0… 0 1 / amm 0… 0 0… 0 - am + 1 m / amm 1 … 0… 0… 0 - anm / amm 0… 1] (\ displaystyle \ Lambda _ (m) = (\ start (bmatrix) 1 & \ dots & 0 & -a_ (1m) / a_ (mm) & 0 & \ точки & 0 \\ &&& \ точки &&& \\ 0 & \ точки & 1 & -a_ (m -1m) / a_ (mm) & 0 & \ dots & 0 \\ 0 & \ dots & 0 & 1 / a_ (mm) & 0 & \ dots & 0 \\ 0 & \ dots & 0 & -a_ (m + 1m) / a_ (mm) & 1 & \ dots & 0 \\ &&& \ dots &&& \\ 0 & \ dots & 0 & -a_ (nm) / a_ (mm) & 0 & \ dots & 1 \ end (bmatrix))).

Втората матрица след прилагане на всички операции ще бъде равна на Λ (\ displaystyle \ Lambda), тоест ще бъде желаният. Сложност на алгоритъма - O (n 3) (\ displaystyle O (n ^ (3))).

Използване на матрицата на алгебрични допълнения

Матрица, обратна на матрицата A (\ displaystyle A), може да се представи като

A - 1 = adj (A) det (A) (\ displaystyle (A) ^ ( - 1) = (((\ mbox (adj)) (A)) \ over (\ det (A))))

където adj (A) (\ displaystyle (\ mbox (adj)) (A))- прикрепена матрица;

Сложността на алгоритъма зависи от сложността на алгоритъма за изчисляване на детерминанта O det и е равна на O (n²) · O det.

Използване на разлагане на LU / LUP

Матрично уравнение A X = I n (\ displaystyle AX = I_ (n))за обратната матрица X (\ displaystyle X)може да се разглежда като колекция n (\ displaystyle n)системи на формата A x = b (\ displaystyle Ax = b)... Ние обозначаваме i (\ displaystyle i)колона на матрицата X (\ displaystyle X)през X i (\ displaystyle X_ (i)); тогава A X i = e i (\ displaystyle AX_ (i) = e_ (i)), i = 1,…, n (\ displaystyle i = 1, \ ldots, n),дотолкова доколкото i (\ displaystyle i)колона на матрицата I n (\ displaystyle I_ (n))е единичният вектор e i (\ displaystyle e_ (i))... с други думи, намирането на обратната матрица се свежда до решаване на n уравнения с една матрица и различни дясни страни. След извършване на LUP-разлагане (време O (n³)), решаването на всяко от n уравнения отнема време O (n²), така че тази част от работата отнема време O (n³).

Ако матрицата A е недегенерирана, тогава LUP разлагането може да бъде изчислено за нея P A = L U (\ displaystyle PA = LU)... Нека бъде P A = B (\ displaystyle PA = B), B - 1 = D (\ displaystyle B ^ ( - 1) = D)... Тогава от свойствата на обратната матрица можем да напишем: D = U - 1 L - 1 (\ displaystyle D = U ^ ( - 1) L ^ ( - 1))... Ако умножим това равенство с U и L, тогава можем да получим две равенства на формата U D = L - 1 (\ displaystyle UD = L ^ ( - 1))и D L = U - 1 (\ displaystyle DL = U ^ ( - 1))... Първото от тези равенства е система от n² линейни уравнения за n (n + 1) 2 (\ displaystyle (\ frac (n (n + 1)) (2)))от които са известни дясните страни (от свойствата на триъгълни матрици). Вторият също представлява система от n² линейни уравнения за n (n - 1) 2 (\ displaystyle (\ frac (n (n -1)) (2)))от които са известни дясните страни (също от свойствата на триъгълни матрици). Заедно те представляват система от n² равенства. Използвайки тези равенства, можем рекурсивно да определим всички n² елементи на матрицата D. След това от равенството (PA) −1 = A −1 P −1 = B −1 = D. получаваме равенството A - 1 = D P (\ displaystyle A ^ ( - 1) = DP).

В случай на използване на LU-разлагане, не се изисква пермутация на колоните на матрицата D, но решението може да се разминава, дори ако матрицата A е недегенерирана.

Сложността на алгоритъма е O (n³).

Итеративни методи

Методи на Шулц

(Ψ k = E - AU k, U k + 1 = U k ∑ i = 0 n Ψ ki (\ displaystyle (\ start (случаи) \ Psi _ (k) = E -AU_ (k), \\ U_ ( k + 1) = U_ (k) \ sum _ (i = 0) ^ (n) \ Psi _ (k) ^ (i) \ end (случаи)))

Оценка на грешки

Избор на първоначално предположение

Проблемът за избор на първоначално приближение в разглежданите тук процеси на итеративна матрична инверсия не позволява да се третират като независими универсални методи, конкуриращи се с директни методи на инверсия, базирани например на LU-разлагане на матрици. Има някои препоръки за избор U 0 (\ displaystyle U_ (0))осигуряване изпълнението на условието ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (спектралният радиус на матрицата е по -малък от един), което е необходимо и достатъчно за конвергенцията на процеса. В този случай обаче първо е необходимо да се знае горната граница за спектъра на обърнатата матрица А или матрицата A A T (\ displaystyle AA ^ (T))(а именно, ако A е симетрична положително определена матрица и ρ (A) ≤ β (\ displaystyle \ rho (A) \ leq \ beta), тогава можете да вземете U 0 = α E (\ displaystyle U_ (0) = (\ alpha) E), където ; ако A е произволна невырождена матрица и ρ (A A T) ≤ β (\ displaystyle \ rho (AA ^ (T)) \ leq \ beta)тогава се вярва U 0 = α A T (\ displaystyle U_ (0) = (\ alpha) A ^ (T))къде също α ∈ (0, 2 β) (\ displaystyle \ alpha \ in \ left (0, (\ frac (2) (\ beta)) \ right)); разбира се, можете да опростите ситуацията и да се възползвате от факта, че ρ (A A T) ≤ k A A T k (\ displaystyle \ rho (AA ^ (T)) \ leq (\ mathcal (k)) AA ^ (T) (\ mathcal (k))), слагам U 0 = A T ‖ A A T ‖ (\ displaystyle U_ (0) = (\ frac (A ^ (T)) (\ | AA ^ (T) \ |)))). Второ, при такова определение на началната матрица няма гаранция, че ‖ Ψ 0 ‖ (\ displaystyle \ | \ Psi _ (0) \ |)ще бъде малък (може дори да бъде ‖ Ψ 0 ‖> 1 (\ displaystyle \ | \ Psi _ (0) \ |> 1)) и високата степен на конвергенция няма да бъде разкрита веднага.

Примери за

Матрица 2x2

A - 1 = [a b c d] - 1 = 1 det (A) [d - b - c a] = 1 a d - b c [d - b - c a]. (\ displaystyle \ mathbf (A) ^ (- 1) = (\ begin (bmatrix) a & b \\ c & d \\\ end (bmatrix)) ^ (- 1) = (\ frac (1) (\ det (\ mathbf (A)))) (\ begin (bmatrix) \, \, \, d & \! \! - b \\ - c & \, a \\\ end (bmatrix)) = (\ frac (1) (ad- bc)) (\ begin (bmatrix) \, \, \, d & \! \! - b \\ - c & \, a \\\ end (bmatrix)).)

Инверсията на 2x2 матрица е възможна само ако a d - b c = det A ≠ 0 (\ displaystyle ad -bc = \ det A \ neq 0).

Намиране на обратната матрица- задача, която често се решава по два метода:

• методът на алгебрични допълнения, при който се изисква намиране на детерминанти и транспониране на матрици;
• методът за елиминиране на неизвестен Гаус, при който се изисква да се извършат елементарни матрични трансформации (добавяне на редове, умножаване на редове със същия брой и т.н.).

За тези, които са особено любопитни, има и други методи, например методът на линейни трансформации. В този урок ще анализираме трите споменати метода и алгоритми за намиране на обратната матрица, използвайки тези методи.

Обратна матрица НО, такава матрица се нарича

НО
. (1)

Обратна матрица , което е необходимо за намиране за дадена квадратна матрица НО, такава матрица се нарича

продукт, чрез който матрици НОвдясно е матрицата на идентичността, т.е.
. (1)

Матрицата за идентичност е диагонална матрица, в която всички диагонални елементи са равни на едно.

Теорема.За всяка не-единична (не-дегенерирана, не-единична) квадратна матрица можете да намерите обратната матрица и освен това само една. За специална (изродена, единична) квадратна матрица обратното не съществува.

Квадратната матрица се нарича неспециални(или неизроден, не единствено число), ако неговата детерминанта не е нула, и специален(или изроден, единствено число), ако неговата детерминанта е нула.

Обратната матрица може да се намери само за квадратна матрица. Естествено, обратната матрица също ще бъде квадратна и в същия ред като дадената матрица. Матрица, за която може да се намери обратна матрица, се нарича обратима матрица.

За обратна матрица има подходяща аналогия с реципрочната. За всеки номер а, не е равно на нула, има такова число бче работата аи бравен на един: ab= 1. Номер бсе нарича обратен за числото б... Например за числото 7 обратното е 1/7, тъй като 7 * 1/7 = 1.

Намиране на обратната матрица по метода на алгебрични допълнения (обединена матрица)

За неособа квадратна матрица НОобратното е матрицата

където е детерминантата на матрицата НО, a е матрицата, съседна на матрицата НО.

Съюз с квадратна матрица Ае матрица от същия ред, чиито елементи са алгебричните допълнения на съответните елементи на детерминантата на матрицата, транспонирана по отношение на матрицата А. По този начин, ако

тогава

и

Алгоритъм за намиране на обратната матрица по метода на алгебрични допълнения

1. Намерете определителя на дадена матрица А... Ако детерминантата е равна на нула, търсенето на обратната матрица спира, тъй като матрицата е изродена и нейната обратна не съществува.

2. Намерете матрица, транспонирана по отношение на А.

3. Изчислете елементите на прилежащата матрица като алгебрични допълнения на Марица, намерени в стъпка 2.

4. Приложете формула (2): умножете обратната страна на детерминантата на матрицата А, към прилежащата матрица, намерена в стъпка 4.

5. Проверете резултата, получен в стъпка 4, като умножите тази матрица Акъм обратната матрица. Ако произведението на тези матрици е равно на матрицата на идентичността, тогава обратната матрица е намерена правилно. В противен случай стартирайте процеса на решение отново.

Пример 1.За матрица

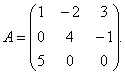
намери обратната страна на матрицата.

Решение. За да се намери обратната матрица, е необходимо да се намери детерминантата на матрицата НО... По правилото на триъгълниците намираме:

Оттук и матрицата НО-несингуларен (недегенериран, неособен) и за него има обратна.

Намерете матрицата, съседна на дадената матрица НО.

Намерете матрицата, транспонирана по отношение на матрицата А:

Изчислете елементите на прилежащата матрица като алгебрични допълнения на матрицата, транспонирана по отношение на матрицата А:

Следователно матрицата, съседна на матрицата А, има формата

Коментирайте.Редът на изчисляване на елементите и транспонирането на матрицата може да бъде различен. Първо може да се изчислят алгебричните допълнения на матрицата Аи след това транспонира матрицата на комплемента. Резултатът трябва да бъде същите елементи на матрицата на обединението.

Прилагайки формула (2), намираме матрицата, обратна на матрицата НО:

Намиране на обратната матрица чрез елиминиране по Гаус

Първата стъпка за намиране на обратната матрица по метода на елиминиране по Гаус е да се присвои на матрицата Аматрицата на идентичността от същия ред, като ги разделя с вертикална лента. Получаваме удвоена матрица. Умножаваме двете страни на тази матрица с, след което получаваме

,

Алгоритъм за намиране на обратната матрица чрез елиминиране по Гаус

1. Към матрицата Азадайте матрицата на идентичността на същия ред.

2. Трансформирайте получената двойна матрица, така че матрицата на идентичността да се получи от лявата й страна, тогава обратната матрица автоматично ще се окаже на мястото на матрицата на идентичността от дясната страна. Матрицата Аот лявата страна се трансформира в матрица на идентичността чрез елементарни матрични трансформации.

2. Ако в процес на матрично преобразуване Ав матрицата за идентичност във всеки ред или във всяка колона ще има само нули, тогава детерминантата на матрицата е равна на нула и следователно матрицата Аще се изроди и няма обратна матрица. В този случай по -нататъшното откриване на обратната матрица се прекратява.

Пример 2.За матрица

намери обратната страна на матрицата.

и ще го преобразуваме така, че от лявата страна да получим матрицата на идентичността. Започваме трансформации.

Умножете първия ред от лявата и дясната матрица с (-3) и го добавете към втория ред, след което умножете първия ред с (-4) и го добавете към третия ред, след което получаваме

.

Така че, ако е възможно, да няма дробни числа по време на последващи трансформации, първо създаваме единица във втория ред от лявата страна на удвоената матрица. За да направите това, умножете втория ред по 2 и извадете третия ред от него, след което получаваме

.

Добавете първия ред към втория и след това умножете втория ред с (-9) и го добавете към третия ред. Тогава получаваме

.

След това разделете третия ред на 8

.

Нека умножим третия ред по 2 и го добавим към втория ред. Оказва се:

.

Нека разменим втория и третия ред, след което най -накрая получаваме:

.

Виждаме, че матрицата на идентичността се получава от лявата страна, следователно, обратната матрица се получава от дясната страна. Поради това:

.

Можете да проверите правилността на изчисленията, като умножите оригиналната матрица с намерената обратна матрица:

Резултатът трябва да бъде обратна матрица.

Пример 3.За матрица

намери обратната страна на матрицата.

Решение. Съставяне на двойна матрица

и ние ще го трансформираме.

Умножаваме първия ред с 3, а вторият с 2 и изваждаме от втория, след което умножаваме първия ред с 5, а третият с 2 и изваждаме от третия ред, след което получаваме

.

Умножаваме първия ред по 2 и го добавяме към втория, след което изваждаме втория от третия ред, след което получаваме

.

Виждаме, че в третия ред вляво всички елементи се оказаха равни на нула. Следователно матрицата е изродена и няма обратна матрица. Спираме по -нататък намирането на обратната марица.

Матрицата $ A ^ (- 1) $ се нарича обратна по отношение на квадратната матрица $ A $, ако е изпълнено условието $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ , където $ E $ е матрицата на идентичността, чийто ред е равен на реда на матрицата $ A $.

Неизродена матрица - матрица, чиято детерминанта не е равна на нула. Съответно, дегенерирана матрица е тази, за която детерминантата е равна на нула.

Обратната матрица $ A ^ (- 1) $ съществува тогава и само ако матрицата $ A $ е неизродена. Ако съществува обратна матрица $ A ^ (- 1) $, тя е уникална.

Има няколко начина да намерите обратната страна на матрица и ще разгледаме два от тях. Тази страница ще обсъди метода на прилежащата матрица, който се счита за стандартен в повечето висши математически курсове. Вторият метод за намиране на обратната матрица (методът на елементарни трансформации), който включва използването на метода на Гаус или на метода на Гаус-Йордан, е разгледан във втората част.

Методът на прилежащата (съседна) матрица

Нека бъде дадена матрицата $ A_ (n \ times n) $. За да намерите обратната страна на матрицата $ A ^ (- 1) $, са необходими три стъпки:

1. Намерете детерминантата на матрицата $ A $ и се уверете, че $ \ Delta A \ neq 0 $, т.е. че матрицата А е невыродена.
2. Съставете алгебричните допълнения $ A_ (ij) $ на всеки елемент от матрицата $ A $ и напишете матрицата $ A_ (n \ times n) ^ (*) = \ наляво (A_ (ij) \ надясно) $ от намерени алгебрични допълнения.
3. Напишете обратната матрица, като вземете предвид формулата $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $.

Матрицата $ (A ^ (*)) ^ T $ често се споменава като свързана (реципрочна, съседна) към матрицата $ A $.

Ако решението се прави ръчно, тогава първият метод е добър само за матрици с относително малки поръчки: втори (), трети (), четвърти (). Други методи се използват за намиране на обратната страна на матрица от по-висок ред. Например методът на Гаус, който е разгледан във втората част.

Пример №1

Намерете обратната стойност на $ A = \ left (\ begin (array) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & - 1 & -9 & 0 \ end (масив) \ вдясно) $.

Тъй като всички елементи на четвъртата колона са равни на нула, тогава $ \ Delta A = 0 $ (т.е. матрицата $ A $ е изродена). Тъй като $ \ Delta A = 0 $, матрицата, обратна на матрицата $ A $, не съществува.

Пример №2

Намерете обратната страна на матрицата $ A = \ left (\ begin (array) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ right) $.

Използваме метода на прилежащата матрица. Първо откриваме детерминантата на дадената матрица $ A $:

$$ \ Delta A = \ наляво | \ begin (масив) (cc) -5 & 7 \\ 9 & 8 \ end (масив) \ вдясно | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

Тъй като $ \ Delta A \ neq 0 $, тогава съществува обратна матрица, затова ще продължим решението. Намиране на алгебрични допълнения

\ begin (подравнено) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = ( - 1) ^ 3 \ cdot 9 = -9; \\ & A_ (21) = ( - 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) =- 5. \\ \ край (подравнено)

Съставяме матрица от алгебрични допълнения: $ A ^ (*) = \ left (\ begin (array) (cc) 8 & -9 \\ -7 & -5 \ end (array) \ right) $.

Транспонирайте получената матрица: $ (A ^ (*)) ^ T = \ left (\ begin (array) (cc) 8 & -7 \\ -9 & -5 \ end (array) \ right) $ (получената матрица) матрица често се нарича съседна или прилежаща матрица към матрицата $ A $). Използвайки формулата $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, имаме:

$$ A ^ ( -1) = \ frac (1) ( -103) \ cdot \ left (\ begin (масив) (cc) 8 & -7 \\ -9 & -5 \ end (масив) \ вдясно) = \ наляво (\ begin (масив) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (масив) \ вдясно) $$

Значи е намерено обратното: $ A ^ ( - 1) = \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (array) \ right) $. За да проверите истинността на резултата, достатъчно е да проверите истинността на едно от равенствата: $ A ^ (- 1) \ cdot A = E $ или $ A \ cdot A ^ (- 1) = E $. Нека проверим равенството $ A ^ (- 1) \ cdot A = E $. За да работим по -малко с дроби, ще заменим матрицата $ A ^ ( - 1) $ не във формата $ \ left (\ begin (array) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (масив) \ вдясно) $ и като $ -\ frac (1) (103) \ cdot \ вляво (\ begin (масив) (cc) 8 & -7 \\ -9 & -5 \ end (масив) \ вдясно) $:

Отговор: $ A ^ ( - 1) = \ наляво (\ begin (масив) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (масив) \ вдясно) $.

Пример №3

Намерете обратната страна на матрицата $ A = \ вляво (\ begin (масив) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (масив) \ вдясно) $.

Нека започнем с изчисляване на детерминантата на матрицата $ A $. Така че детерминантата на матрицата $ A $ е следната:

$$ \ Delta A = \ наляво | \ begin (масив) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (масив) \ вдясно | = 18-36 + 56-12 = 26. $$

Тъй като $ \ Delta A \ neq 0 $, тогава съществува обратна матрица, затова ще продължим решението. Намираме алгебричните допълнения на всеки елемент от дадена матрица:

Съставяме матрица от алгебрични допълнения и я транспонираме:

$$ A ^ * = \ наляво (\ begin (масив) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ end (масив) \ вдясно); \; (A ^ *) ^ T = \ наляво (\ begin (масив) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (масив) \ вдясно) $$

Използвайки формулата $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, получаваме:

$$ A ^ ( -1) = \ frac (1) (26) \ cdot \ left (\ begin (array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37 \ end (масив) \ вдясно) = \ наляво (\ begin (масив) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ end (масив) \ вдясно) $$

Така че $ A ^ ( - 1) = \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \ end (масив) \ вдясно) $. За да проверите истинността на резултата, достатъчно е да проверите истинността на едно от равенствата: $ A ^ (- 1) \ cdot A = E $ или $ A \ cdot A ^ (- 1) = E $. Нека проверим равенството $ A \ cdot A ^ (- 1) = E $. За да работим по -малко с дроби, ще заменим матрицата $ A ^ ( - 1) $ не във формата $ \ left (\ begin (array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ end (масив) \ вдясно) $ и като $ \ frac (1) (26) \ cdot \ вляво (\ begin (масив) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (масив) \ вдясно) $:

Проверката беше успешна, обратният $ A ^ (- 1) $ беше намерен правилно.

Отговор: $ A ^ ( -1) = \ наляво (\ start (масив) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \ end (масив) \ вдясно) $.

Пример №4

Намерете обратната стойност на $ A = \ вляво (\ begin (масив) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8 & -8 & -3 \ end (масив) \ вдясно) $.

За матрица от четвърти ред намирането на обратната матрица с помощта на алгебрични допълнения е донякъде трудно. Такива примери обаче се намират в тестови документи.

За да намерите обратното на матрица, първо трябва да изчислите детерминантата на матрицата $ A $. Най -добрият начин да направите това в тази ситуация е да разширите детерминантата по ред (колона). Избираме всеки ред или колона и намираме алгебричните допълнения на всеки елемент от избрания ред или колона.

Матрична алгебра - Обратна матрица

обратна матрица

Обратна матрицасе нарича матрица, която, умножена както отдясно, така и отляво с дадена матрица, дава матрицата на идентичността.
Нека обозначим матрицата, обратна на матрицата НОчрез, тогава, според дефиницията, получаваме:

където EТова е матрицата на идентичността.
Квадратна матрицаНаречен неспециални (неизроден), ако неговата детерминанта не е нула. В противен случай се нарича специален (изроден) или единствено число.

Важи следната теорема: всяка неособена матрица има обратна.

Операцията за намиране на обратната матрица се нарича обжалванематрици. Помислете за алгоритъма за инверсия на матрицата. Нека бъде дадена неособена матрица н-та поръчка:

където Δ = det А ≠ 0.

Алгебрично допълнение на елементматрици н-та поръчка НОдетерминантата на матрицата ( н–1) та поръчка, получена чрез изтриване i-ти ред и йколона на матрицата НО:

Нека съставим т.нар приложенматрица:

където са алгебричните допълнения на съответните елементи на матрицата НО.
Обърнете внимание, че алгебричните допълнения на елементите от редовете на матрицата НОсе поставят в съответните колони на матрицата Ã , тоест матрицата се транспонира едновременно.
Чрез разделяне на всички елементи на матрицата Ã по Δ - стойността на детерминантата на матрицата НО, в резултат получаваме обратната матрица:

Отбелязваме редица специални свойства на обратната матрица:
1) за дадена матрица НОнеговата обратна матрица е единственият;
2) ако има обратна матрица, тогава десен заден ходи ляв заден ходматриците съвпадат с него;
3) специална (изродена) квадратна матрица няма обратна матрица.

Основни свойства на обратната матрица:
1) детерминантата на обратната матрица и определящата на оригиналната матрица са реципрочни стойности;
2) обратната матрица на произведението на квадратни матрици е равна на произведението на обратните матрици на фактори, взети в обратен ред:

3) транспонираната обратна на матрицата е равна на обратната на дадената транспонирана матрица:

ПРИМЕР Изчислете обратната страна на дадената матрица.

Нека има квадратна матрица от n -ти ред

Матрицата A -1 се нарича обратна матрицапо отношение на матрицата A, ако A * A -1 = E, където E е матрицата на идентичността на n -ти ред.

Единична матрица- такава квадратна матрица, в която всички елементи по главния диагонал, преминаващи от горния ляв ъгъл до долния десен ъгъл, са единици, а останалите са нули, например:

обратна матрицаможе да съществува само за квадратни матрицитези. за тези матрици със същия брой редове и колони.

Теоремата за условието за съществуване на обратна матрица

За да има матрица обратна матрица, е необходимо и достатъчно тя да е неизродена.

Извиква се матрицата A = (A1, A2, ... A n) неизроденако векторите на колоните са линейно независими. Броят на линейно независимите вектори на колони на матрица се нарича ранг на матрицата. Следователно можем да кажем, че за да съществува обратна матрица, е необходимо и достатъчно рангът на матрицата да бъде равен на нейното измерение, т.е. r = n.

Алгоритъм за намиране на обратната матрица

1. Напишете матрица А в таблицата за решаване на системи от уравнения по метода на Гаус и вдясно (на мястото на дясните страни на уравненията) задайте матрица Е.
2. Използвайки преобразуването на Джордан, намалете матрицата А до матрица, състояща се от единични колони; в този случай е необходимо едновременно да се трансформира матрицата Е.
3. Ако е необходимо, пренаредете редовете (уравненията) на последната таблица, така че единичната матрица E да се получи под матрицата A на оригиналната таблица.
4. Напишете обратната матрица A -1, която е в последната таблица под матрицата E на оригиналната таблица.

Пример 1

За матрица A намерете обратната матрица A -1

Решение: Записваме матрицата A и вдясно присвояваме матрицата на идентичността E. Използвайки Йордановите преобразувания, редуцираме матрицата A до матрицата на идентичността E. Изчисленията са показани в таблица 31.1.

Нека проверим правилността на изчисленията, като умножим оригиналната матрица A и обратната матрица A -1.

В резултат на умножението на матрицата се получава единичната матрица. Следователно изчисленията са правилни.

Отговор:

Решаване на матрични уравнения

Матричните уравнения могат да бъдат от вида:

AX = B, XA = B, AXB = C,

където A, B, C са посочените матрици, X е необходимата матрица.

Матричните уравнения се решават чрез умножаване на уравнението по неговите обратни матрици.

Например, за да намерите матрица от уравнение, умножавате това уравнение вляво.

Следователно, за да намерите решение на уравнението, трябва да намерите обратната матрица и да я умножите по матрицата от дясната страна на уравнението.

Други уравнения се решават по подобен начин.

Пример 2

Решете уравнението AX = B, ако

Решение: Тъй като обратната страна на матрицата е (вижте пример 1)

Матричен метод в икономическия анализ

Заедно с други те намират приложение и в матрични методи... Тези методи се основават на линейна и векторно-матрична алгебра. Такива методи се използват за анализ на сложни и многоизмерни икономически явления. Най -често тези методи се използват, когато е необходимо да се направи сравнителна оценка на функционирането на организациите и техните структурни звена.

В процеса на прилагане на матрични методи за анализ могат да се разграничат няколко етапа.

На първия етапосъществява се формирането на система от икономически показатели и въз основа на нея се съставя матрица от изходни данни, която представлява таблица, в която броят на системите е показан на отделните й редове (i = 1,2, ...., n), а по вертикалните колони - броят на показателите (j = 1,2, ...., m).

Във втория етапза всяка вертикална колона се разкрива най -голямата от наличните стойности на показателите, която се приема като единица.

След това всички суми, отразени в тази колона, се разделят на най -голямата стойност и се формира матрица от стандартизирани коефициенти.

В третия етапвсички съставни части на матрицата са на квадрат. Ако те имат различно значение, тогава на всеки индикатор на матрицата се присвоява определен коефициент на тежест к... Стойността на последната се определя с експертна преценка.

При последния, четвърти етапнамерени стойности на рейтинги R jса групирани по ред на увеличаване или намаляване.

Очертаните матрични методи трябва да се използват например при сравнителен анализ на различни инвестиционни проекти, както и при оценка на други икономически показатели за дейността на организациите.