Standard-Taylor-Reihenentwicklungen. Maclaurin-Reihe und Erweiterung einiger Funktionen
Wenn die Funktion f(x) hat auf einem Intervall mit dem Punkt ein, Ableitungen aller Ordnungen, dann kann die Taylor-Formel darauf angewendet werden:
wo r nein- der sogenannte Rest oder der Rest der Reihe, er kann mit der Lagrange-Formel geschätzt werden:
 , wobei die Zahl x zwischen . liegt NS und ein.
, wobei die Zahl x zwischen . liegt NS und ein.
Wenn für einen gewissen Wert x r n®0 für n® ¥, dann wird im Grenzfall die Taylor-Formel für diesen Wert konvergent Taylor-Reihe:
Also die Funktion f(x) kann an der betrachteten Stelle zu einer Taylor-Reihe erweitert werden NS, wenn:
1) es hat Derivate aller Ordnungen;
2) die konstruierte Reihe konvergiert an diesem Punkt.
Bei ein= 0 erhalten wir eine Reihe namens in der Nähe von Maclaurin:
Beispiel 1 f (x) = 2x.
Lösung... Finden wir die Werte der Funktion und ihrer Ableitungen bei NS=0
f(x) = 2x, F ( 0) = 2 0 =1;
f ¢ (x) = 2x ln2, f ¢ ( 0) = 2 0 ln2 = ln2;
f ¢¢ (x) = 2x ln 2 2, f ¢¢ ( 0) = 2 0 ln 2 2 = ln 2 2;
f (n) (x) = 2x ln n 2, f (n) ( 0) = 2 0 ln n 2 = ln n 2.
Wenn wir die erhaltenen Werte der Ableitungen in die Taylor-Reihenformel einsetzen, erhalten wir:
Der Konvergenzradius dieser Reihe ist gleich unendlich, daher gilt diese Entwicklung für - ¥<x<+¥.
Beispiel 2 NS+4) für die Funktion f (x) = e x.
Lösung... Finden Sie die Ableitungen der Funktion e x und ihre Werte an der Stelle NS=-4.
f(x)= e x, F (-4) = e -4 ;
f ¢ (x)= e x, f ¢ (-4) = e -4 ;
f ¢¢ (x)= e x, f ¢¢ (-4) = e -4 ;
f (n) (x)= e x, f (n) ( -4) = e -4 .
Daher hat die erforderliche Taylorreihe der Funktion die Form:
Diese Erweiterung gilt auch für - ¥<x<+¥.
Beispiel 3 ... Funktion erweitern f(x)= ln x in einer Reihe von Potenzen ( NS- 1),
(d.h. in der Taylor-Reihe in der Nähe des Punktes NS=1).
Lösung... Finden Sie die Ableitungen dieser Funktion.
![]()
![]()
![]()
![]()
![]()

Durch Einsetzen dieser Werte in die Formel erhalten wir die erforderliche Taylor-Reihe:
Mit dem d'Alembert-Test kann man sicherstellen, dass die Reihe für konvergiert
½ NS- 1½<1. Действительно,
Die Reihe konvergiert, wenn ½ NS- 1½<1, т.е. при 0<x<2. При NS= 2 erhalten wir eine alternierende Reihe, die die Bedingungen des Leibniz-Tests erfüllt. Bei NS= 0 Funktion ist nicht definiert. Somit ist der Konvergenzbereich der Taylor-Reihe das halboffene Intervall (0; 2].
Zeigen wir die in ähnlicher Weise erhaltenen Entwicklungen in der Maclaurin-Reihe (d. h. in der Nähe des Punktes NS= 0) für einige elementare Funktionen:
(2) ![]() ,
,
(3) 
![]() ,
,
( die letzte Zerlegung heißt Binomialreihe)
Beispiel 4 ... Erweitern einer Funktion in einer Potenzreihe
Lösung... In Erweiterung (1) ersetzen wir NS An - NS 2, wir erhalten:
Beispiel 5
... Erweitern Sie die Funktion der Maclaurin-Serie ![]()
Lösung... Wir haben ![]()
Mit Formel (4) können wir schreiben:
Ersatz für NS in die Formel -NS, wir bekommen:

Von hier aus finden wir:
Wenn wir die Klammern erweitern, die Terme der Reihe neu anordnen und ähnliche Terme reduzieren, erhalten wir
Diese Reihe konvergiert im Intervall
(-1; 1), da sie aus zwei Reihen erhalten wird, die jeweils in diesem Intervall konvergieren.
Kommentar .
Die Formeln (1) - (5) können auch verwendet werden, um die entsprechenden Funktionen in einer Taylor-Reihe zu entwickeln, d.h. für die Entwicklung von Funktionen in positiven ganzzahligen Potenzen ( Ha). Um dies zu tun, ist es notwendig, über eine gegebene Funktion solche identischen Transformationen durchzuführen, um eine der Funktionen (1) - (5) zu erhalten, in der anstelle von NS kostet k ( Ha) m, wobei k eine konstante Zahl ist, ist m eine positive ganze Zahl. Es ist oft praktisch, die Variable zu ändern T=Ha und entwickeln Sie die resultierende Funktion nach t in einer Maclaurin-Reihe.
Diese Methode veranschaulicht den Satz über die Eindeutigkeit der Entwicklung einer Funktion in einer Potenzreihe. Die Essenz dieses Theorems besteht darin, dass in der Nähe desselben Punktes keine zwei verschiedenen Potenzreihen erhalten werden können, die gegen dieselbe Funktion konvergieren, egal wie ihre Entwicklung durchgeführt wird.
Beispiel 6 ... Erweitere eine Funktion in einer Taylor-Reihe in einer Umgebung eines Punktes NS=3.
Lösung... Dieses Problem kann wie zuvor mit der Definition der Taylor-Reihe gelöst werden, für die es notwendig ist, die Ableitungen der Funktion und ihre Werte bei zu finden NS= 3. Es wird jedoch einfacher sein, die vorhandene Zerlegung (5) zu verwenden:

Die resultierende Reihe konvergiert für ![]() oder –3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.
oder –3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.
Beispiel 7
... Schreiben Sie die Taylor-Reihe in Potenzen ( NS-1) Funktionen ![]() .
.
Lösung.
Die Reihe konvergiert bei ![]() , oder 2< x£ 5.
, oder 2< x£ 5.
Wenn die Funktion f (x) Ableitungen aller Ordnungen auf einem Intervall hat, das den Punkt a enthält, dann kann die Taylor-Formel darauf angewendet werden:
,
wo r nein- der sogenannte Rest oder der Rest der Reihe, er kann mit der Lagrange-Formel geschätzt werden:
, wobei die Zahl x zwischen x und a liegt.
Regeln für die Funktionseingabe:
Wenn für einen gewissen Wert NS r nein→ 0 für n→ ∞, dann wird im Grenzfall die Taylor-Formel für diesen Wert konvergent Taylor-Reihe:
,
Damit lässt sich die Funktion f (x) im betrachteten Punkt x in einer Taylor-Reihe entwickeln, wenn:
1) es hat Derivate aller Ordnungen;
2) die konstruierte Reihe konvergiert an diesem Punkt.
Für a = 0 erhalten wir eine Reihe namens in der Nähe von Maclaurin:
,
Zerlegung der einfachsten (elementaren) Funktionen der Maclaurin-Reihe:
Hinweisfunktionen
, R =
Trigonometrische Funktionen ![]() , R =
, R = ![]() , R =
, R =
, (-π / 2< x < π/2), R=π/2
Die Funktion actgx expandiert nicht in Potenzen von x, da ctg0 = ∞
Hyperbolische Funktionen
Logarithmische Funktionen
, -1
Binomialreihe
![]() .
.
Beispiel 1. Erweitern einer Funktion in einer Potenzreihe f (x) = 2x.
Lösung... Finden wir die Werte der Funktion und ihrer Ableitungen bei NS=0
f(x) = 2x, F ( 0)
= 2 0
=1;
f"(x) = 2x ln2, F "( 0)
= 2 0
ln2 = ln2;
f"" (x) = 2x ln 2 2, F "" ( 0)
= 2 0
ln 2 2 = ln 2 2;
…
f (n) (x) = 2x ln n 2, f (n) ( 0)
= 2 0
ln n 2 = ln n 2.
Wenn wir die erhaltenen Werte der Ableitungen in die Taylor-Reihenformel einsetzen, erhalten wir:
Der Konvergenzradius dieser Reihe ist gleich unendlich, also gilt diese Entwicklung für -∞<x<+∞.
Beispiel # 2. Schreiben Sie die Taylor-Reihe in Potenzen ( NS+4) für die Funktion f (x) = e x.
Lösung... Finden Sie die Ableitungen der Funktion e x und ihre Werte an der Stelle NS=-4.
f(x)= e x, F (-4)
= e -4
;
f"(x)= e x, F "(-4)
= e -4
;
f"" (x)= e x, F "" (-4)
= e -4
;
…
f (n) (x)= e x, f (n) ( -4)
= e -4
.
Daher hat die erforderliche Taylorreihe der Funktion die Form:
Diese Zerlegung gilt auch für -∞<x<+∞.
Beispiel Nr. 3. Funktion erweitern f(x)= ln x in einer Reihe von Potenzen ( NS- 1),
(d.h. in der Taylor-Reihe in der Nähe des Punktes NS=1).
Lösung... Finden Sie die Ableitungen dieser Funktion.
f (x) = lnx,,,,
f (1) = ln1 = 0, f "(1) = 1, f" "(1) = - 1, f" "" (1) = 1 * 2, ..., f (n) = (- 1) n-1 (n-1)!
Durch Einsetzen dieser Werte in die Formel erhalten wir die erforderliche Taylor-Reihe:
Mit dem d'Alembert-Test kann man sicherstellen, dass die Reihe für ½x-1½ . konvergiert<1 . Действительно,
Die Reihe konvergiert, wenn ½ NS- 1½<1, т.е. при 0<x<2. При NS= 2 erhalten wir eine alternierende Reihe, die die Bedingungen des Leibniz-Tests erfüllt. Für x = 0 ist die Funktion undefiniert. Somit ist der Konvergenzbereich der Taylor-Reihe das halboffene Intervall (0; 2].
Beispiel Nr. 4. Erweitern Sie die Funktion in eine Potenzreihe. Beispiel Nr. 5. Erweitern Sie die Maclaurin-Funktion. Kommentar
.
Diese Methode basiert auf dem Eindeutigkeitssatz für die Entwicklung einer Funktion in einer Potenzreihe. Die Essenz dieses Theorems besteht darin, dass in der Nähe desselben Punktes keine zwei verschiedenen Potenzreihen erhalten werden können, die gegen dieselbe Funktion konvergieren, egal wie ihre Entwicklung durchgeführt wird. Beispiel Nr. 5a. Erweitern Sie die Funktion in eine Maclaurin-Reihe, geben Sie den Konvergenzbereich an. Der Bruch 3 / (1-3x) kann als Summe einer unendlich abnehmenden geometrischen Folge mit dem Nenner 3x betrachtet werden, wenn |3x |< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
Beispiel Nr. 6. Erweitern Sie die Funktion in eine Taylor-Reihe in der Nähe des Punktes x = 3. Beispiel Nr. 7. Schreiben Sie die Taylor-Reihe in Potenzen (x -1) der Funktion ln (x + 2). Beispiel Nr. 8. Entwickeln Sie die Funktion f (x) = sin (πx / 4) in eine Taylor-Reihe in der Nähe des Punktes x = 2. Beispiel 1. Berechnen Sie ln (3) auf die nächsten 0,01. Beispiel # 2. Berechnen Sie auf die nächsten 0,0001. Beispiel Nr. 3. Integral auswerten ∫ 0 1 4 sin (x) x bis 10 -5. Beispiel Nr. 4. Bewerten Sie das Integral ∫ 0 1 4 e x 2 auf 0,001 genau. In der Theorie der Funktionsreihen nimmt der Abschnitt über die Entwicklung einer Funktion in einer Reihe den zentralen Platz ein. Damit stellt sich das Problem: für eine gegebene Funktion
es ist erforderlich, eine solche Potenzreihe zu finden die auf einem Intervall konvergierte und deren Summe gleich war Diese Aufgabe heißt das Problem der Erweiterung einer Funktion in einer Potenzreihe. Eine notwendige Bedingung für die Entwicklung einer Funktion in einer Potenzreihe ist seine Differenzierbarkeit unendlich oft - dies folgt aus den Eigenschaften konvergierender Potenzreihen. Diese Bedingung ist in der Regel für elementare Funktionen in ihrem Definitionsbereich erfüllt. Angenommen, die Funktion Nehmen wir an, die Funktion wo ein 0 ,ein 1 ,ein 2 ,...,ein NS ,...
- (noch) undefinierte Koeffizienten. Wir setzen in Gleichheit (*) den Wert x = x 0 ,
dann bekommen wir Lassen Sie uns die Potenzreihe (*) Term für Term differenzieren und nehme hier an x = x 0 ,
werden Mit der nächsten Differenzierung erhalten wir die Reihe vorausgesetzt x = x 0 ,
werden Nach NS-fache Differenzierung, wir erhalten Einstellung in der letzten Gleichheit x = x 0 ,
werden Damit sind die Koeffizienten gefunden setzen wir sie in die Reihe (*) ein, erhalten wir Die resultierende Reihe heißt neben taylor
für Funktion
Damit haben wir festgestellt, dass wenn die Funktion in einer Potenzreihe in Potenzen (x - x 0 ), dann ist diese Entwicklung eindeutig und die resultierende Reihe ist notwendigerweise eine Taylorreihe. Beachten Sie, dass die Taylor-Reihe für jede Funktion mit Ableitungen beliebiger Ordnung im Punkt . erhalten werden kann x = x 0 .
Dies bedeutet jedoch nicht, dass zwischen der Funktion und der resultierenden Reihe ein Gleichheitszeichen gesetzt werden kann, d.h. dass die Summe der Reihe gleich der ursprünglichen Funktion ist. Erstens kann eine solche Gleichheit nur im Konvergenzbereich sinnvoll sein, und die für die Funktion erhaltene Taylor-Reihe kann divergieren, und zweitens, wenn die Taylor-Reihe konvergiert, kann ihre Summe nicht mit der ursprünglichen Funktion übereinstimmen. Wir formulieren eine Aussage, mit deren Hilfe die gestellte Aufgabe gelöst wird. Wenn die Funktion
woR n (NS)ist der Rest der Taylor-Formel - hat die Form (Lagrange-Form) wo
Punktξ
liegt zwischen x und x 0 . Beachten Sie, dass es einen Unterschied zwischen der Taylor-Reihe und der Taylor-Formel gibt: Die Taylor-Formel ist eine endliche Summe, d. NS - Feste Nummer. Denken Sie daran, dass die Summe der Reihe S(x)
kann als Grenzwert der Funktionsfolge von Teilsummen definiert werden S NS (x)
in gewissen Abständen NS: Dementsprechend bedeutet das Erweitern einer Funktion in einer Taylor-Reihe, eine Reihe zu finden, so dass für alle NSx Wir schreiben die Taylorsche Formel in der Form, wobei beachte das Wenn Damit haben wir bewiesen ein Kriterium für die Erweiterung einer Funktion in einer Taylor-Reihe.
Damit in einem bestimmten Intervall die FunktionF(x) zu einer Taylor-Reihe entwickelt, ist es notwendig und ausreichend, dass auf diesem Intervall
Mit dem formulierten Kriterium erhält man ausreichendBedingungen für die zu entwickelnde Funktion in einer Taylor-Reihe.
Wenn ineine Umgebung des Punktes x 0 die Absolutwerte aller Ableitungen der Funktion sind durch die gleiche Zahl M . begrenzt≥ 0, d.h. Aus obigem folgt AlgorithmusFunktionszerlegung
F(x) in der Taylor-Reihe in der Nähe des Punktes NS 0 :
1.
Finden Sie die Ableitungen der Funktion F(x):
f (x), f ’(x), f“ (x), f ’“ (x), f (n) (x), ... 2. Wir berechnen den Wert der Funktion und die Werte ihrer Ableitungen an der Stelle NS 0 f (x 0
), f ’(x 0
), f ”(x 0
), f ’“ (x 0
), F (n) (x 0
),…
3. Schreiben Sie die Taylor-Reihe formal auf und bestimmen Sie den Konvergenzbereich der resultierenden Potenzreihe. 4. Wir prüfen die Erfüllung hinreichender Bedingungen, d.h. wir stellen für wen NS aus dem Konvergenzbereich, der Rest R n (x)
tendiert gegen Null bei Die Entwicklung von Funktionen in einer Taylorreihe nach diesem Algorithmus heißt Entwicklung der Funktion in einer Taylor-Reihe per Definition oder direkte Zersetzung. Zeigen wir, dass wenn eine beliebige Funktion auf der Menge definiert ist dann können die Koeffizienten dieser Reihe gefunden werden. Ersatz in der Potenzreihe Finden Sie die erste Ableitung der Funktion Bei Für die zweite Ableitung erhalten wir: Bei Fortsetzung dieses Verfahrens n sobald wir bekommen: Damit erhalten wir eine Potenzreihe der Form: welches heisst neben taylor für Funktion Ein Spezialfall der Taylor-Reihe ist Maclaurin-Reihe bei Der Rest der Taylor (Maclaurin)-Reihe erhält man durch Verwerfen aus den Hauptreihen n erste Mitglieder und bezeichnet als Der Rest ist normalerweise Einer von ihnen ist in Form von Lagrange: Beachten Sie, dass in der Praxis die Maclaurin-Serie häufiger verwendet wird. Um also die Funktion zu schreiben 1) finde die Koeffizienten der Maclaurin (Taylor)-Reihe; 2) finde den Konvergenzbereich der erhaltenen Potenzreihe; 3) Beweisen Sie, dass die gegebene Reihe gegen die Funktion konvergiert Satz1
(eine notwendige und hinreichende Bedingung für die Konvergenz der Maclaurin-Reihe). Sei der Konvergenzradius der Reihe Satz 2. Wenn die Ableitungen beliebiger Ordnung der Funktion Beispiel1
.
Erweitern Sie in einer Taylor-Reihe um den Punkt Lösung. ....................................................................................................................................... Konvergenzregion Beispiel2
.
Funktion erweitern Lösung: Finden Sie den Wert der Funktion und ihrer Ableitungen bei ...........…………………………… Wir ersetzen diese Werte hintereinander. Wir bekommen: oder Finden wir den Konvergenzbereich dieser Reihe. Nach dem d'Alembert-Merkmal konvergiert die Reihe, wenn Daher für alle Betrachten wir einige Beispiele für die Erweiterung der Maclaurin-Reihe von elementaren Grundfunktionen. Denken Sie daran, dass die Maclaurin-Reihe: konvergiert auf dem Intervall Beachten Sie, dass zum Erweitern der Funktion in einer Reihe Folgendes erforderlich ist: a) finde die Koeffizienten der Maclaurin-Reihe für diese Funktion; b) Berechnen des Konvergenzradius für die resultierende Reihe; c) Beweisen Sie, dass die resultierende Reihe gegen die Funktion konvergiert Beispiel 3. Betrachten Sie die Funktion Lösung. Berechnen wir den Wert der Funktion und ihrer Ableitungen bei Dann sind die numerischen Koeffizienten der Reihe: für jeden n. Setze die gefundenen Koeffizienten in die Maclaurin-Reihe ein und erhalte: Bestimmen Sie den Konvergenzradius der resultierenden Reihe, nämlich: Folglich konvergiert die Reihe auf dem Intervall Diese Reihe konvergiert gegen die Funktion Beispiel4
.
Betrachten Sie die Funktion Lösung.
Es ist leicht zu sehen, dass die Ableitungen gerader Ordnung Finden wir das Konvergenzintervall dieser Reihe. Auf der Grundlage von d'Alembert: für jeden Diese Reihe konvergiert gegen die Funktion Beispiel5
.
Lösung. Finden wir den Wert der Funktion und ihrer Ableitungen bei Somit sind die Koeffizienten dieser Reihe: Ähnlich wie bei der vorherigen Reihe ist der Konvergenzbereich Beachten Sie, dass die Funktion Beispiel6
.
Binomialreihe: Lösung. Finden wir den Wert der Funktion und ihrer Ableitungen bei Daraus ist klar: Ersetzen Sie diese Werte der Koeffizienten in der Maclaurin-Reihe und erhalten Sie die Entwicklung dieser Funktion in eine Potenzreihe: Bestimmen Sie den Konvergenzradius dieser Reihe: Folglich konvergiert die Reihe auf dem Intervall Die untersuchte Reihe konvergiert auf dem Intervall Beispiel7
.
Erweitern wir in einer Maclaurin-Reihe die Funktion Lösung. Für die Reihenentwicklung dieser Funktion verwenden wir die Binomialreihe für Ausgehend von der Eigenschaft der Potenzreihe (die Potenzreihe kann im Bereich ihrer Konvergenz integriert werden) finden wir das Integral der linken und rechten Seite dieser Reihe: Finden Sie den Konvergenzbereich dieser Reihe: das heißt, der Konvergenzbereich dieser Reihe ist das Intervall Die Leibniz-Reihe konvergiert. Der Konvergenzbereich dieser Reihe ist also das Intervall Bei Näherungsrechnungen spielen Potenzreihen eine äußerst wichtige Rolle. Mit ihrer Hilfe wurden Tabellen trigonometrischer Funktionen, Logarithmentabellen, Wertetabellen anderer Funktionen erstellt, die in verschiedenen Wissensgebieten verwendet werden, beispielsweise in der Wahrscheinlichkeitstheorie und der mathematischen Statistik. Darüber hinaus ist die Erweiterung von Funktionen in einer Potenzreihe für deren theoretische Untersuchung nützlich. Das Hauptproblem bei der Verwendung von Potenzreihen in Näherungsrechnungen ist die Frage der Schätzung des Fehlers beim Ersetzen der Summe einer Reihe durch die Summe ihrer ersten n Mitglieder. Betrachten Sie zwei Fälle: die Funktion wird zu einer Reihe alternierender Zeichen erweitert; die Funktion wird zu einer konstanten Reihe erweitert. Lassen Sie die Funktion Beispiel8
.
Berechnung Lösung. Wir verwenden die Maclaurin-Reihe für Wenn wir den ersten und zweiten Term der Reihe mit einer gegebenen Genauigkeit vergleichen, dann gilt:. Der dritte Expansionsbegriff: kleiner als die angegebene Rechengenauigkeit. Daher zu berechnen Auf diese Weise Beispiel9
.
Berechnung Lösung. Wir verwenden die Binomialreihenformel. Schreiben Sie dazu In diesem Ausdruck Vergleichen wir jedes der Mitglieder der Reihe mit der angegebenen Genauigkeit. Es ist klar, dass Beispiel10
.
Berechnen Sie die Zahl Lösung. In einer Reihe für die Funktion Schätzen wir den Fehler ab, der entsteht, wenn die Summe der Reihe durch die Summe der ersten ersetzt wird das ist 2< Je nach Zustand des Problems müssen Sie finden n so dass folgende Ungleichung gilt: Es ist leicht zu überprüfen, dass für n= 6: Somit, Beispiel11
.
Berechnung Lösung. Beachten Sie, dass man zur Berechnung der Logarithmen die Reihe für die Funktion anwenden könnte Lass uns rechnen Somit, Um zu berechnen Rest der Reihe oder Somit reichte es in der Reihe, die für die Berechnung verwendet wurde, nur die ersten vier Terme anstelle von 9999 in der Reihe für die Funktion 1. Was ist eine Taylor-Reihe? 2. Welche Art hatte die Maclaurin-Reihe? 3. Formulieren Sie einen Satz über die Entwicklung einer Funktion in einer Taylor-Reihe. 4. Schreiben Sie die Maclaurin-Reihenentwicklung der Hauptfunktionen. 5. Geben Sie die Konvergenzbereiche der betrachteten Reihe an. 6. Wie kann man den Fehler bei Näherungsrechnungen mit Potenzreihen schätzen? Unter den Funktionsreihen nehmen die Potenzreihen den wichtigsten Platz ein. Die Reihe wird Potenzreihe genannt deren Terme Potenzfunktionen sind, die in aufsteigenden ganzzahligen nichtnegativen Potenzen angeordnet sind x, ein C0
, C 1
, C 2
, C n
- konstante Werte. Die Zahlen C1
, C 2
, C n
- die Koeffizienten der Mitglieder der Reihe, C0
- Freies Mitglied. Die Mitglieder der Potenzreihe werden auf dem ganzen Zahlenstrahl definiert. Machen wir uns mit dem Konzept vertraut Konvergenzbereich der Potenzreihe.
Dies ist der Satz von Variablenwerten x für die die Reihe konvergiert. Potenzreihen haben einen relativ einfachen Konvergenzbereich. Für reelle Werte der Variablen x der Konvergenzbereich besteht entweder aus einem Punkt oder ist ein Intervall (Konvergenzintervall) oder fällt mit der gesamten Achse zusammen Ochse
. Bei Substitution in einer Potenzreihe sind die Werte x= 0 erhältst du eine Zahlenreihe C0
+0+0+...+0+...
, die zusammenläuft. Daher für x= 0 jede Potenzreihe konvergiert und daher sein Konvergenzbereich
kann nicht leer sein. Die Struktur des Konvergenzbereichs aller Potenzreihen ist gleich. Sie lässt sich mit dem folgenden Theorem herstellen. Satz 1 (Satz von Abel)... Konvergiert die Potenzreihe für einen Wert x = x 0
ungleich Null, dann konvergiert sie, und zwar absolut für alle Werte |x| < |x 0
|
... Achtung: Sowohl der Startwert "x ist Null" als auch ein beliebiger Wert von "x", der mit dem Startwert verglichen wird, werden modulo - ohne Berücksichtigung des Vorzeichens - berücksichtigt. Folge. Wenn Potenzreihe divergiert
zu einem gewissen Wert x = x 1
, dann divergiert es für alle Werte |x| > |x 1
|
. Wie wir bereits herausgefunden haben, konvergiert jede Potenzreihe um den Wert x= 0. Es gibt Potenzreihen, die nur für . konvergieren x= 0 und divergieren für andere Werte NS... Wenn wir diesen Fall aus der Betrachtung eliminieren, nehmen wir an, dass die Potenzreihe für einen Wert . konvergiert x = x 0
ungleich null. Dann konvergiert es nach dem Satz von Abel an allen Punkten des Intervalls] - | x0
|, |x 0
|[
(das Intervall, dessen linke und rechte Grenze die x-Werte sind, bei denen die Potenzreihe konvergiert, jeweils mit Minus- und Pluszeichen), symmetrisch zum Ursprung. Wenn die Potenzreihe bei einem bestimmten Wert divergiert x = x 1
, dann divergiert sie nach dem Korollar zum Satz von Abel auch an allen Punkten außerhalb des Segments [- | x1
|, |x 1
|]
... Daraus folgt, dass es für jede Potenzreihe ein um den Ursprung symmetrisches Intervall gibt, genannt Konvergenzintervall
, an jedem Punkt, an dem die Reihe konvergiert, an den Rändern kann sie konvergieren und divergieren, und zwar nicht notwendigerweise gleichzeitig, aber außerhalb des Segments divergiert die Reihe. Nummer R heißt Konvergenzradius der Potenzreihe. In besonderen Fällen Konvergenzintervall der Potenzreihen
zu einem Punkt entarten kann (dann konvergiert die Reihe nur für x= 0 und es wird angenommen, dass R= 0) oder den gesamten Zahlenstrahl darstellen (dann konvergiert die Reihe an allen Punkten des Zahlenstrahls und es wird davon ausgegangen). Die Definition des Konvergenzbereichs einer Potenzreihe besteht also in der Definition ihrer Konvergenzradius
R und das Studium der Konvergenz der Reihe an den Grenzen des Konvergenzintervalls (at). Satz 2. Wenn alle Koeffizienten der Potenzreihe, beginnend mit einer Reihe, ungleich null sind, ist ihr Konvergenzradius gleich der Grenze im Verhältnis der absoluten Werte der Koeffizienten der gesamten folgenden Terme der Reihe, d.h. Beispiel 1. Bestimmen Sie den Konvergenzbereich einer Potenzreihe Lösung. Hier Mit Formel (28) finden wir den Konvergenzradius dieser Reihe: Untersuchen wir die Konvergenz der Reihe an den Enden des Konvergenzintervalls. Beispiel 13 zeigt, dass diese Reihe für konvergiert x= 1 und divergiert bei x= -1. Folglich ist der Konvergenzbereich ein halbes Intervall. Beispiel 2. Bestimmen Sie den Konvergenzbereich einer Potenzreihe Lösung. Die Reihenkoeffizienten sind positiv, und Finden wir die Grenze dieses Verhältnisses, d.h. Konvergenzradius der Potenzreihe: Untersuchen wir die Konvergenz der Reihe an den Enden des Intervalls. Austausch von Werten x= -1/5 und x= 1/5 in einer bestimmten Zeile ergibt: Die erste dieser Reihen konvergiert (siehe Beispiel 5). Aber dann konvergiert aufgrund des Satzes im Abschnitt "Absolute Konvergenz" auch die zweite Reihe, und der Bereich ihrer Konvergenz ist das Segment Beispiel 3. Bestimmen Sie den Konvergenzbereich einer Potenzreihe Lösung. Hier Mit Formel (28) ermitteln wir den Konvergenzradius der Reihe: Untersuchen wir die Konvergenz der Reihe für Werte. Setzen wir sie in dieser Zeile ein, erhalten wir jeweils Beide Reihen divergieren, da die notwendige Konvergenzbedingung nicht erfüllt ist (ihre gemeinsamen Terme streben bei nicht gegen Null). An beiden Enden des Konvergenzintervalls divergiert die gegebene Reihe, und der Bereich ihrer Konvergenz ist das Intervall. Beispiel 5. Bestimmen Sie den Konvergenzbereich einer Potenzreihe Lösung. Finden Sie die Beziehung, wo und Nach Formel (28) ist der Konvergenzradius dieser Reihe das heißt, die Reihe konvergiert nur für x= 0 und divergiert für andere Werte NS. Beispiele zeigen, dass sich die Reihen an den Enden des Konvergenzintervalls unterschiedlich verhalten. In Beispiel 1 konvergiert die Reihe an einem Ende des Konvergenzintervalls und divergiert am anderen; in Beispiel 2 konvergiert sie an beiden Enden; in Beispiel 3 divergiert sie an beiden Enden. Die Formel für den Konvergenzradius einer Potenzreihe wird unter der Annahme erhalten, dass alle Koeffizienten der Terme der Reihe, beginnend bei einem, von Null verschieden sind. Daher ist die Verwendung von Formel (28) nur in diesen Fällen zulässig. Wird diese Bedingung verletzt, so sollte der Konvergenzradius der Potenzreihe mit d'Alembert-Zeichen, oder durch Ändern der Variablen die Reihe in die Form umwandeln, in der die angegebene Bedingung erfüllt ist. Beispiel 6. Bestimmen Sie das Konvergenzintervall einer Potenzreihe Lösung. Diese Reihe enthält keine Elemente mit ungeraden Graden. NS... Daher transformieren wir die Reihe durch Setzen. Dann bekommen wir die Serie den Konvergenzradius zu finden, auf den Formel (28) angewendet werden kann. Da a, dann ist der Konvergenzradius dieser Reihe Aus der Gleichheit, die wir erhalten, konvergiert diese Reihe also auf dem Intervall. Lassen Sie für eine Potenzreihe Konvergenzradius R> 0, d.h. diese Reihe konvergiert auf dem Intervall. Dann jeder Wert NS aus dem Konvergenzintervall entspricht eine bestimmte Summe der Reihe. Daher ist die Summe der Potenzreihen eine Funktion von NS auf dem Konvergenzintervall. Bezeichne es durch F(x), können wir die Gleichheit schreiben es in dem Sinne zu verstehen, dass die Summe der Reihen an jedem Punkt NS aus dem Konvergenzintervall ist gleich dem Wert der Funktion F(x) An diesem Punkt. Im gleichen Sinne werden wir sagen, dass die Potenzreihe (29) gegen die Funktion F(x) auf dem Konvergenzintervall. Außerhalb des Konvergenzintervalls ist die Gleichheit (30) bedeutungslos. Beispiel 7. Finde die Summe der Summe einer Potenzreihe Lösung. Dies ist eine geometrische Reihe mit ein= 1, und Q= x... Daher ist seine Summe eine Funktion gilt nur für Werte, obwohl die Funktion Es kann bewiesen werden, dass die Summe der Potenzreihen F(x) ist auf jedem Segment innerhalb des Konvergenzintervalls stetig und differenzierbar, insbesondere an jedem Punkt des Konvergenzintervalls der Reihe. Lassen Sie uns Theoreme zur Term-für-Term-Differenzierung und Integration von Potenzreihen präsentieren. Satz 1. Potenzreihen (30) im Intervall ihrer Konvergenz können beliebig oft termweise differenziert werden, und die resultierenden Potenzreihen haben den gleichen Konvergenzradius wie die ursprüngliche Reihe, und ihre Summen sind jeweils gleich. Satz 2. Leistungsserie (30) kann im Bereich von 0 bis unbegrenzt oft integriert werden NS, falls und die resultierende Potenzreihe denselben Konvergenzradius wie die ursprüngliche Reihe hat und ihre Summen jeweils gleich sind Gegeben sei eine Funktion F(x), die in einer Potenzreihe erweitert werden muss, d.h. in der Form (30) darstellen: Die Aufgabe besteht darin, die Koeffizienten zu bestimmen ……………………………………………….. (31) Einstellung in Gleichheiten (30) und (31) NS= 0, wir finden Setzen wir die gefundenen Ausdrücke in die Gleichheit (30) ein, erhalten wir Finden wir die Entwicklung einiger elementarer Funktionen in der Maclaurin-Reihe. Beispiel 8. Erweitern Sie die Funktion der Maclaurin-Serie Lösung. Die Ableitungen dieser Funktion sind die gleichen wie die Funktion selbst: Daher bei NS= 0 wir haben Setzen wir diese Werte in Formel (32) ein, erhalten wir die erforderliche Erweiterung: Diese Reihe konvergiert auf der ganzen Zahlengeraden (ihrem Konvergenzradius).
Lösung... In der Erweiterung (1) ersetzen wir x durch -x 2 und erhalten:
, -∞
Lösung... Wir haben
Mit Formel (4) können wir schreiben:
Wenn wir in der Formel -x anstelle von x einsetzen, erhalten wir:
Von hier aus finden wir: ln (1 + x) -ln (1-x) = -
Wenn wir die Klammern erweitern, die Terme der Reihe neu anordnen und ähnliche Terme reduzieren, erhalten wir
... Diese Reihe konvergiert im Intervall (-1; 1), da sie sich aus zwei Reihen ergibt, die jeweils in diesem Intervall konvergieren.
Die Formeln (1) - (5) können auch verwendet werden, um die entsprechenden Funktionen in einer Taylor-Reihe zu entwickeln, d.h. für die Entwicklung von Funktionen in positiven ganzzahligen Potenzen ( Ha). Um dies zu tun, ist es notwendig, über eine gegebene Funktion solche identischen Transformationen durchzuführen, um eine der Funktionen (1) - (5) zu erhalten, in der anstelle von NS kostet k ( Ha) m, wobei k eine konstante Zahl ist, ist m eine positive ganze Zahl. Es ist oft praktisch, die Variable zu ändern T=Ha und entwickeln Sie die resultierende Funktion nach t in einer Maclaurin-Reihe.
Lösung. Finden Sie zuerst 1-x-6x 2 = (1-3x) (1 + 2x).
zu elementar:
mit dem Konvergenzbereich | x |< 1/3.
Lösung... Dieses Problem kann wie zuvor mit der Definition der Taylor-Reihe gelöst werden, für die es notwendig ist, die Ableitungen der Funktion und ihre Werte bei zu finden NS= 3. Es wird jedoch einfacher sein, die vorhandene Zerlegung (5) zu verwenden:
=
Die resultierende Reihe konvergiert bei oder –3
Lösung.
Die Reihe konvergiert bei oder -2< x < 5.
Lösung... Nehmen wir die Substitution t = x-2 vor:
Mit der Entwicklung (3), bei der wir π / 4 t anstelle von x einsetzen, erhalten wir:
Die resultierende Reihe konvergiert gegen eine gegebene Funktion bei -∞< π / 4 t<+∞, т.е. при (-∞
, (-∞Ungefähre Berechnungen mit Potenzreihen
Potenzreihen werden häufig in Näherungsrechnungen verwendet. Mit ihrer Hilfe können Sie mit einer bestimmten Genauigkeit die Werte von Wurzeln, trigonometrischen Funktionen, Logarithmen von Zahlen und bestimmten Integralen berechnen. Die Reihen werden auch bei der Integration von Differentialgleichungen verwendet.
Betrachten Sie die Entwicklung einer Funktion in einer Potenzreihe:
Um den Näherungswert der Funktion an einem bestimmten Punkt zu berechnen NS zum Konvergenzbereich der angegebenen Reihe gehörend, die erste n Mitglieder ( n ist eine endliche Zahl) und die restlichen Terme werden verworfen:
Um den Fehler des erhaltenen Näherungswerts abzuschätzen, ist es notwendig, den verworfenen Rest r n (x) zu schätzen. Dazu werden folgende Techniken verwendet:
Lösung... Lassen Sie uns die Zerlegung verwenden, wobei x = 1/2 (siehe Beispiel 5 im vorherigen Thema):
Prüfen wir, ob wir den Rest nach den ersten drei Termen der Entwicklung verwerfen können, dazu schätzen wir ihn mit der Summe einer unendlich abnehmenden geometrischen Progression:
Also können wir diesen Rest verwerfen und erhalten
Lösung... Verwenden wir die Binomialreihe. Da 5 3 der Kubus einer ganzen Zahl ist, die 130 am nächsten kommt, ist es ratsam, die Zahl 130 als 130 = 5 3 +5 darzustellen. 
da bereits der vierte Term der resultierenden alternierenden Reihe, die das Leibniz-Kriterium erfüllt, unter der geforderten Genauigkeit liegt:
, daher können sie und die ihr folgenden Mitglieder verworfen werden.
Viele praktisch notwendige bestimmte oder uneigentliche Integrale können mit der Newton-Leibniz-Formel nicht berechnet werden, da ihre Anwendung mit der Suche nach einer Stammfunktion verbunden ist, die oft keinen Ausdruck in elementaren Funktionen hat. Es kommt auch vor, dass das Auffinden der Stammfunktion zwar möglich, aber unnötig mühsam ist. Wenn der Integrand jedoch zu einer Potenzreihe erweitert werden kann und die Integrationsgrenzen zum Konvergenzintervall dieser Reihe gehören, dann ist eine näherungsweise Berechnung des Integrals mit einer vorgegebenen Genauigkeit möglich.
Lösung... Das entsprechende unbestimmte Integral lässt sich nicht in elementaren Funktionen ausdrücken, d.h. ist ein "unzerbrechliches Integral". Die Anwendung der Newton-Leibniz-Formel ist hier nicht möglich. Wir berechnen das Integral näherungsweise.
Durch Teilen der Reihe für sin x An x, wir bekommen: 
Integriert man diese Reihe Term für Term (dies ist möglich, da die Integrationsgrenzen zum Konvergenzintervall dieser Reihe gehören), erhalten wir:
Da die resultierende Reihe die Leibniz-Bedingungen erfüllt, reicht es aus, die Summe der ersten beiden Terme zu bilden, um den gewünschten Wert mit einer bestimmten Genauigkeit zu erhalten.
Somit finden wir  .
.
Lösung.

![]() ... Lassen Sie uns prüfen, ob wir den Rest nach dem zweiten Term der resultierenden Reihe verwerfen können.
... Lassen Sie uns prüfen, ob wir den Rest nach dem zweiten Term der resultierenden Reihe verwerfen können.
0,0001<0.001. Следовательно,  .
. ,
jene.
,
jene. =
..
=
..
 hat Ableitungen beliebiger Ordnung. Ist es möglich, es in einer Potenzreihe zu erweitern, wenn möglich, wie findet man dann diese Reihe? Der zweite Teil des Problems ist einfacher zu lösen, und wir fangen damit an.
hat Ableitungen beliebiger Ordnung. Ist es möglich, es in einer Potenzreihe zu erweitern, wenn möglich, wie findet man dann diese Reihe? Der zweite Teil des Problems ist einfacher zu lösen, und wir fangen damit an. kann als Summe einer Potenzreihe dargestellt werden, die in dem Intervall konvergiert, das den Punkt enthält NS 0 :
kann als Summe einer Potenzreihe dargestellt werden, die in dem Intervall konvergiert, das den Punkt enthält NS 0 :
 =
..
(*)
=
..
(*) .
. =
..
=
..
 .
. =
..
=
..
 , wo
, wo  .
. , wo
, wo
 ,
,
 ,
,
 ,
…,
,
…,
 ,….,
,…., .
.
3.2. Genügende Bedingungen für die Entwicklung einer Funktion in einer Taylor-Reihe
 in einer Umgebung des Punktes x 0 hat Derivate bis zu (n+
1) der Bestellung inklusive, dann in dieser NachbarschaftFormel
Taylor
in einer Umgebung des Punktes x 0 hat Derivate bis zu (n+
1) der Bestellung inklusive, dann in dieser NachbarschaftFormel
Taylor

 .
.
 definiert den Fehler, den wir erhalten, ersetzen Sie die Funktion F(x)
Polynom S n (x).
definiert den Fehler, den wir erhalten, ersetzen Sie die Funktion F(x)
Polynom S n (x).
 , dann
, dann  ,jene. die Funktion entwickelt sich zu einer Taylor-Reihe. Umgekehrt, wenn
,jene. die Funktion entwickelt sich zu einer Taylor-Reihe. Umgekehrt, wenn  , dann
, dann  .
. , woR n (x) ist der Rest der Taylor-Reihe.
, woR n (x) ist der Rest der Taylor-Reihe. , To in dieser Umgebung entwickelt sich die Funktion in einer Taylor-Reihe.
, To in dieser Umgebung entwickelt sich die Funktion in einer Taylor-Reihe. oder
oder
 .
.16.1. Erweiterung elementarer Funktionen in Taylorreihen und
Maclaurin
 , in der Nähe des Punktes
, in der Nähe des Punktes  hat viele Ableitungen und ist die Summe einer Potenzreihe:
hat viele Ableitungen und ist die Summe einer Potenzreihe: ... Dann
... Dann  .
. :
: :
: .
. :
: .
. .
.

 ,
, in der Nähe des Punktes
in der Nähe des Punktes  .
. :
:


 ... Dann die Funktion
... Dann die Funktion  kann als Summe geschrieben werden n frühe Mitglieder einer Reihe
kann als Summe geschrieben werden n frühe Mitglieder einer Reihe  und der Rest
und der Rest  :,
:, .
. in verschiedenen Formeln ausgedrückt.
in verschiedenen Formeln ausgedrückt. , wo
, wo  .
. .
. in Form einer Summe einer Potenzreihe ist es notwendig:
in Form einer Summe einer Potenzreihe ist es notwendig: .
. ... Damit diese Reihe im Intervall konvergiert
... Damit diese Reihe im Intervall konvergiert  Funktionieren
Funktionieren  , ist es notwendig und ausreichend, dass die Bedingung erfüllt ist:
, ist es notwendig und ausreichend, dass die Bedingung erfüllt ist:  im angegebenen Intervall.
im angegebenen Intervall. in einigen intervallen
in einigen intervallen  im absoluten Wert durch die gleiche Zahl begrenzt m, also
im absoluten Wert durch die gleiche Zahl begrenzt m, also  , dann ist in diesem Intervall die Funktion
, dann ist in diesem Intervall die Funktion  kann zu einer Maclaurin-Reihe erweitert werden.
kann zu einer Maclaurin-Reihe erweitert werden. Funktion.
Funktion. .
. ,;
,; ,
, ;
; ,
, ;
; ,
,
 ,
, ;
; .
. in Taylors Reihe um den Punkt
in Taylors Reihe um den Punkt  .
. .
. ,
, ;
; ,
, ;
; ,
, .
. .
. .
. dieser Grenzwert ist kleiner als 1, und daher ist der Konvergenzbereich der Reihe:
dieser Grenzwert ist kleiner als 1, und daher ist der Konvergenzbereich der Reihe:  .
.

 .
. Funktionieren
Funktionieren  .
. .
. .
. .
.
 .
. .
. für beliebige Werte
für beliebige Werte  weil jede Lücke
weil jede Lücke  Funktion
Funktion  und seine Ableitungen im absoluten Wert sind durch die Zahl begrenzt
und seine Ableitungen im absoluten Wert sind durch die Zahl begrenzt  .
. .
. :
:
 , und die Ableitungen sind von ungerader Ordnung. Wir setzen die gefundenen Koeffizienten in die Maclaurin-Reihe ein und erhalten die Entwicklung:
, und die Ableitungen sind von ungerader Ordnung. Wir setzen die gefundenen Koeffizienten in die Maclaurin-Reihe ein und erhalten die Entwicklung: ... Folglich konvergiert die Reihe auf dem Intervall
... Folglich konvergiert die Reihe auf dem Intervall  .
. , weil alle seine Ableitungen auf eins beschränkt sind.
, weil alle seine Ableitungen auf eins beschränkt sind. .
. :
:
 und
und  , somit:
, somit: ... Die Reihe konvergiert gegen die Funktion
... Die Reihe konvergiert gegen die Funktion  , weil alle seine Ableitungen auf eins beschränkt sind.
, weil alle seine Ableitungen auf eins beschränkt sind. ungerade und Reihenentwicklung in ungeraden Potenzen, die Funktion
ungerade und Reihenentwicklung in ungeraden Potenzen, die Funktion  - gerade und Reihenausdehnung in geraden Potenzen.
- gerade und Reihenausdehnung in geraden Potenzen. .
. :
:


 ... An den Grenzpunkten bei
... An den Grenzpunkten bei  und
und  die Reihe kann je nach Exponenten konvergieren oder nicht
die Reihe kann je nach Exponenten konvergieren oder nicht  .
. Funktionieren
Funktionieren  , also die Summe der Ladung
, also die Summe der Ladung  bei
bei  .
. .
. ... Wir bekommen:
... Wir bekommen: 
 ,
, ... Definieren wir die Konvergenz der Reihe an den Enden des Intervalls. Bei
... Definieren wir die Konvergenz der Reihe an den Enden des Intervalls. Bei 
 ... Diese Reihe ist eine harmonische Reihe, dh sie divergiert. Bei
... Diese Reihe ist eine harmonische Reihe, dh sie divergiert. Bei  wir erhalten eine Zahlenreihe mit einem gemeinsamen Begriff
wir erhalten eine Zahlenreihe mit einem gemeinsamen Begriff  .
. .
.16.2. Anwenden von Potenzreihen in ungefähren Berechnungen
Berechnung mit alternierenden Reihen
 zu einer Wechselstromreihe erweitert. Wenn dann diese Funktion für einen bestimmten Wert berechnet wird
zu einer Wechselstromreihe erweitert. Wenn dann diese Funktion für einen bestimmten Wert berechnet wird  erhalten wir eine Zahlenreihe, auf die der Leibniz-Test angewendet werden kann. Wenn gemäß diesem Merkmal die Summe der Reihe durch die Summe ihrer ersten ersetzt wird n Terme, dann überschreitet der absolute Fehler nicht den ersten Term des Rests dieser Reihe, d. h.:
erhalten wir eine Zahlenreihe, auf die der Leibniz-Test angewendet werden kann. Wenn gemäß diesem Merkmal die Summe der Reihe durch die Summe ihrer ersten ersetzt wird n Terme, dann überschreitet der absolute Fehler nicht den ersten Term des Rests dieser Reihe, d. h.:  .
. auf 0,0001 genau.
auf 0,0001 genau. , den Wert des Winkels im Bogenmaß ersetzen:
, den Wert des Winkels im Bogenmaß ersetzen:
 es reicht aus, zwei Mitglieder der Serie zu verlassen, das heißt
es reicht aus, zwei Mitglieder der Serie zu verlassen, das heißt .
. .
. mit einer Genauigkeit von 0,001.
mit einer Genauigkeit von 0,001. als:
als:  .
. ,
,
 ... Daher zu berechnen
... Daher zu berechnen  es reicht aus, drei Mitglieder der Reihe zu verlassen.
es reicht aus, drei Mitglieder der Reihe zu verlassen. oder
oder  .
.Berechnung mit Positivreihen
 genau auf 0,001.
genau auf 0,001. Ersatz
Ersatz  ... Wir bekommen:
... Wir bekommen:
 Mitglieder. Schreiben wir die offensichtliche Ungleichung auf:
Mitglieder. Schreiben wir die offensichtliche Ungleichung auf: <3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
<3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
 ,
, .
. oder
oder  .
. .
. .
. mit einer Genauigkeit von 0,0001.
mit einer Genauigkeit von 0,0001. , aber diese Reihe konvergiert sehr langsam und es müssten 9999 Terme verwendet werden, um die angegebene Genauigkeit zu erreichen! Daher wird zur Berechnung von Logarithmen in der Regel eine Reihe für die Funktion verwendet
, aber diese Reihe konvergiert sehr langsam und es müssten 9999 Terme verwendet werden, um die angegebene Genauigkeit zu erreichen! Daher wird zur Berechnung von Logarithmen in der Regel eine Reihe für die Funktion verwendet  die gegen das Intervall konvergiert
die gegen das Intervall konvergiert  .
. diese Zeile verwenden. Lassen
diese Zeile verwenden. Lassen  , dann
, dann  .
. ,
, mit einer gegebenen Genauigkeit nehmen wir die Summe der ersten vier Terme:
mit einer gegebenen Genauigkeit nehmen wir die Summe der ersten vier Terme:  .
. verwerfen. Schätzen wir den Fehler ab. Es ist klar, dass
verwerfen. Schätzen wir den Fehler ab. Es ist klar, dass 
 .
.
 .
.Fragen zum Selbsttest
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]() :
:![]()
![]() ,
,![]()
![]()
![]()
Die Summe der Potenzreihen. Differenzierung und Integration von Leistungsreihen
![]()
![]() ... Die Reihe konvergiert, wenn, und ist ihr Konvergenzintervall. Daher ist die Gleichheit
... Die Reihe konvergiert, wenn, und ist ihr Konvergenzintervall. Daher ist die Gleichheit![]()
![]() für alle Werte definiert NS, außer NS= 1.
für alle Werte definiert NS, außer NS= 1.
Erweiterung der Funktionen in Leistungsreihen
![]() Reihe (30). Dazu differenzieren wir die Gleichheit (30) Term für Term und finden sukzessive:
Reihe (30). Dazu differenzieren wir die Gleichheit (30) Term für Term und finden sukzessive:![]()
![]()
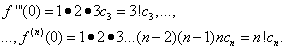
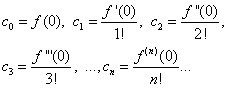
 (32)
(32)
![]() (33)
(33)