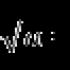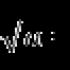Свойства на сбора от корени. Аритметичен квадратен корен и неговите свойства

Коренни формули. свойства на квадратни корени.

Внимание!
Има допълнителни
материал в специален раздел 555.
За тези, които силно "не много..."
И за тези, които "много...")

В предишния урок разбрахме какво е корен квадратен. Време е да разберем какви са формули за корени, какво са коренови свойстваи какво може да се направи за всичко това.

Основни формули, коренни свойства и правила за действия с корени- по същество е едно и също нещо. Формули за квадратни корениизненадващо малко. Което, разбира се, радва! По-скоро можете да напишете много всякакви формули, но само три са достатъчни за практична и уверена работа с корени. Всичко останало произтича от тези три. Въпреки че много се отклоняват в трите формули на корените, да...

Нека започнем с най-простото. Ето я:

Ако харесвате този сайт...

Между другото, имам още няколко интересни сайта за вас.)

Можете да практикувате решаването на примери и да разберете нивото си. Тестване с незабавна проверка. Учене - с интерес!)

можете да се запознаете с функции и производни.

Площта на квадратен парцел е 81 дм². Намерете неговата страна. Да предположим, че дължината на страната на квадрата е хдециметри. Тогава площта на парцела е х² квадратни дециметри. Тъй като според условието тази площ е 81 dm², то х² = 81. Дължината на страната на квадрат е положително число. Положително число, чийто квадрат е 81, е числото 9. При решаването на задачата се изискваше да се намери числото x, чийто квадрат е 81, т.е. да се реши уравнението х² = 81. Това уравнение има два корена: х 1 = 9 и х 2 = - 9, тъй като 9² = 81 и (- 9)² = 81. И двете числа 9 и - 9 се наричат квадратни корени от числото 81.

Забележете, че един от квадратните корени х= 9 е положително число. Нарича се аритметичен квадратен корен от 81 и се обозначава √81, така че √81 = 9.

Аритметичен квадратен корен от число ае неотрицателно число, чийто квадрат е равен на а.

Например числата 6 и -6 са квадратни корени от 36. Числото 6 е аритметичен квадратен корен от 36, тъй като 6 е неотрицателно число и 6² = 36. Числото -6 не е аритметичен корен.

Аритметика Корен квадратенот номера аозначени както следва: √ а.

Знакът се нарича аритметичен знак квадратен корен; асе нарича коренен израз. Израз √ аПрочети така: аритметичният квадратен корен от число а.Например, √36 = 6, √0 = 0, √0,49 = 0,7. В случаите, когато е ясно, че говорим сиза аритметичния корен те накратко казват: „корен квадратен от а«.

Актът за намиране на квадратен корен от число се нарича вземане на квадратен корен. Това действие е обратното на квадратурата.

Всяко число може да бъде на квадрат, но не всяко число може да бъде квадратен корен. Например, не е възможно да се извлече корен квадратен от числото - 4. Ако такъв корен е съществувал, тогава, обозначавайки го с буквата х, ще получим грешно равенство x² = - 4, тъй като отляво има неотрицателно число, а отдясно - отрицателно.

Израз √ аима смисъл само когато а ≥ 0. Определението на квадратния корен може да се запише накратко като: √ а ≥ 0, (√а)² = а. Равенство (√ а)² = авалидно за а ≥ 0. По този начин, за да се уверите, че корен квадратен от неотрицателно число аравно на б, т.е. че √ а =б, трябва да проверите дали са изпълнени следните две условия: b ≥ 0, б² = а.

Корен квадратен от дроб

Да изчислим. Обърнете внимание, че √25 = 5, √36 = 6 и проверете дали равенството е валидно.

Защото и , тогава равенството е вярно. Така, .

теорема:Ако а≥ 0 и б> 0, тоест коренът на дроба е равен на корена на числителя, разделен на корена на знаменателя. Необходимо е да се докаже, че: и .

Тъй като √ а≥0 и √ б> 0, тогава .

Чрез свойството да се повдига дроб на степен и да се определя квадратен корен теоремата е доказана. Нека разгледаме няколко примера.

Изчислете според доказаната теорема .

Втори пример: Докажете това , ако а ≤ 0, б < 0. .

Друг пример: Изчислете .

Преобразуване на квадратен корен

Изваждане на множителя изпод знака на корена. Нека бъде даден израз. Ако а≥ 0 и б≥ 0, тогава по теоремата за корена на произведението можем да запишем:

Такава трансформация се нарича разлагане на основния знак. Помислете за пример;

Изчислете при х= 2. Директно заместване х= 2 в радикалния израз води до сложни изчисления. Тези изчисления могат да бъдат опростени, ако първо премахнем факторите под основния знак: . Сега замествайки x = 2, получаваме:.

И така, когато се изважда факторът под коренния знак, радикалният израз се представя като произведение, в което един или повече фактори са квадратите на неотрицателни числа. След това се прилага теоремата за коренното произведение и се взема коренът на всеки фактор. Помислете за пример: Опростете израза A = √8 + √18 - 4√2, като извадим факторите под знака за корен в първите два члена, получаваме:. Подчертаваме, че равенството валидно само когато а≥ 0 и б≥ 0. ако а < 0, то .

Урок и презентация по темата:
"Свойства на квадратен корен. Формули. Примери за решения, задачи с отговори"

Допълнителни материали
Уважаеми потребители, не забравяйте да оставите вашите коментари, отзиви, предложения. Всички материали се проверяват от антивирусна програма.

Учебни помагала и симулатори в онлайн магазин "Интеграл" за 8 клас
Интерактивно учебно помагало "Геометрия за 10 минути" за 8 клас
Образователен комплекс "1C: Училище. Геометрия, 8 клас"

Свойства квадратен корен

Продължаваме да изучаваме квадратни корени. Днес ще разгледаме основните свойства на корените. Всички основни свойства са интуитивни и в съответствие с всички операции, които сме правили преди.

Свойство 1. Коренът квадратен от произведението на две неотрицателни числа е равен на произведението на корените квадратни от тези числа: $\sqrt(a*b)=\sqrt(a)*\sqrt(b)$.

Прието е да се доказват всякакви свойства, нека го направим.
Нека $\sqrt(a*b)=x$, $\sqrt(a)=y$, $\sqrt(b)=z$. Тогава трябва да докажем, че $x=y*z$.
Нека квадратурираме всеки израз.
Ако $\sqrt(a*b)=x$, тогава $a*b=x^2$.
Ако $\sqrt(a)=y$, $\sqrt(b)=z$, след това възлагайки на квадрат двата израза, получаваме: $a=y^2$, $b=z^2$.
$a*b=x^2=y^2*z^2$, т.е. $x^2=(y*z)^2$. Ако квадратите на две неотрицателни числа са равни, тогава самите числа са равни, което трябваше да се докаже.

От нашето свойство следва, че например $\sqrt(5)*\sqrt(3)=\sqrt(15)$.

Забележка 1. Свойството е валидно и за случая, когато под корена има повече от два неотрицателни фактора.
Свойство 2. Ако $a≥0$ и $b>0$, тогава е валидно следното равенство: $\sqrt(\frac(a)(b))=\frac(\sqrt(a))(\sqrt(b))$

Тоест коренът на частното е равен на частното от корените.
Доказателство.
Нека използваме таблицата и накратко докажем нашето свойство.

Примери за използване на свойства на квадратен корен

Пример 1
Изчислете: $\sqrt(81*25*121)$.

Решение.
Разбира се, можем да вземем калкулатор, да умножим всички числа под корен и да извършим операцията по извличане на квадратен корен. И ако няма калкулатор под ръка, какво тогава?
$\sqrt(81*25*121)=\sqrt(81)*\sqrt(25)*\sqrt(121)=9*5*11=495$.
Отговор: 495.

Пример 2. Изчислете: $\sqrt(11\frac(14)(25))$.

Решение.
Представяме радикалното число като неправилна дроб: $11\frac(14)(25)=\frac(11*25+14)(25)=\frac(275+14)(25)=\frac(289)( 25) $.
Нека използваме свойство 2.
$\sqrt(\frac(289)(25))=\frac(\sqrt(289))(\sqrt(25))=\frac(17)(5)=3\frac(2)(5)= 3,4 $.
Отговор: 3.4.

Пример 3
Изчислете: $\sqrt(40^2-24^2)$.

Решение.
Можем да оценим нашия израз директно, но почти винаги може да бъде опростен. Нека се опитаме да направим това.
$40^2-24^2=(40-24)(40+24)=16*64$.
И така, $\sqrt(40^2-24^2)=\sqrt(16*64)=\sqrt(16)*\sqrt(64)=4*8=32$.
Отговор: 32.

Момчета, имайте предвид, че няма формули за операциите събиране и изваждане на радикални изрази и изразите по-долу не са правилни.
$\sqrt(a+b)≠\sqrt(a)+\sqrt(b)$.
$\sqrt(a-b)≠\sqrt(a)-\sqrt(b)$.

Пример 4
Изчислете: а) $\sqrt(32)*\sqrt(8)$; б) $\frac(\sqrt(32))(\sqrt(8))$.
Решение.
Представените по-горе свойства работят както отляво надясно, така и в обратен ред, тоест:
$\sqrt(a)*\sqrt(b)=\sqrt(a*b)$.
$\frac(\sqrt(a))(\sqrt(b))=\sqrt(\frac(a)(b))$.
Нека използваме това, за да разрешим нашия пример.
а) $\sqrt(32)*\sqrt(8)=\sqrt(32*8)=\sqrt(256)=16.$

Б) $\frac(\sqrt(32))(\sqrt(8))=\sqrt(\frac(32)(8))=\sqrt(4)=2$.

Отговор: а) 16; б) 2.

Свойство 3. Ако $a≥0$ и n е естествено число, тогава е валидно следното равенство: $\sqrt(a^(2n))=a^n$.

Например. $\sqrt(a^(16))=a^8$, $\sqrt(a^(24))=a^(12)$ и така нататък.

Пример 5
Изчислете: $\sqrt(129600)$.

Решение.
Представеното ни число е доста голямо, нека го разложим на прости множители.
Получаваме: $129600=5^2*2^6*3^4$ или $\sqrt(129600)=\sqrt(5^2*2^6*3^4)=5*2^3*3^2 =5*8*9=360$.
Отговор: 360.

Задачи за самостоятелно решаване

1. Изчислете: $\sqrt(144*36*64)$.
2. Изчислете: $\sqrt(8\frac(1)(36))$.
3. Изчислете: $\sqrt(52^2-48^2)$.
4. Изчислете:
а) $\sqrt(128*\sqrt(8))$;
б) $\frac(\sqrt(128))(\sqrt(8))$.

Свойства на квадратните корени

Досега сме извършили пет аритметични операции върху числата: събиране, изваждане, умножение, деление и степенуване, както и в изчисленията, които активно са използвали различни свойстватези операции, например, a + b = b + a, an-bn = (ab) n и т.н.

Тази глава въвежда нова операция - вземане на корен квадратен от неотрицателно число. За да го използвате успешно, трябва да се запознаете със свойствата на тази операция, което ще направим в този раздел.

Доказателство. Нека въведем следната нотация: https://pandia.ru/text/78/290/images/image005_28.jpg" alt="(!LANG:Равенство" width="120" height="25 id=">!}.

Ето как формулираме следната теорема.

(Кратка формулировка, която е по-удобна за използване на практика: коренът на фракцията равно на дробот корените или коренът на частното е равен на частното от корените.)

Този път само ще представим кратка бележкадоказателство и се опитвате да направите подходящи коментари, подобни на тези, които съставляват същността на доказателството на теорема 1.

Забележка 3. Разбира се, този пример може да бъде решен по различен начин, особено ако имате калкулатор: умножете числата 36, 64, 9 и след това вземете корен квадратен от получения продукт. Въпреки това ще се съгласите, че предложеното по-горе решение изглежда по-културно.

Забележка 4. При първия метод направихме челни изчисления. Вторият начин е по-елегантен:
кандидатствахме формула a2 - b2 = (a - b) (a + b) и използва свойството квадратен корен.

Забележка 5. Някои "горещи глави" понякога предлагат следното "решение" на Пример 3:

Това, разбира се, не е вярно: виждате - резултатът не е същият като в нашия пример 3. Факт е, че няма свойство https://pandia.ru/text/78/290/images/image014_6.jpg" alt="(!LANG:Task" width="148" height="26 id=">!}Има само свойства, отнасящи се до умножение и деление на квадратни корени. Бъдете внимателни и внимателни, не си мислете за пожелания.

В заключение на параграфа отбелязваме още едно доста просто и в същото време важно свойство:
ако a > 0 и n - естествено число, тогава

Преобразуване на изрази, съдържащи операция квадратен корен

Досега сме извършвали само трансформации рационални изрази, използвайки за това правилата за операции върху полиноми и алгебрични дроби, съкратени формули за умножение и др. В тази глава въведохме нова операция - операцията за извличане на квадратен корен; установихме това

където, припомнете си, a, b са неотрицателни числа.

Използвайки тези формули, можете да извършвате различни трансформации на изрази, съдържащи операция квадратен корен. Нека разгледаме няколко примера и във всички примери ще приемем, че променливите приемат само неотрицателни стойности.

Пример 3Въведете коефициент под знака квадратен корен:

Пример 6. Опростете израза Решение. Нека извършим последователни трансформации:

Тази статия е колекция от подробна информация, която се занимава с темата за свойствата на корените. Разглеждайки темата, ще започнем със свойствата, ще проучим всички формулировки и ще дадем доказателства. За да затвърдим темата, ще разгледаме свойствата на n-та степен.

Yandex.RTB R-A-339285-1

Свойства на корена

Ще говорим за имоти.

Имот умножени числа аи б, което се представя като равенството a · b = a · b . Може да се представи като множители, положителни или равни на нула a 1 , a 2 , … , a kкато a 1 a 2 … a k = a 1 a 2 … a k ;
от частно a: b = a: b, a ≥ 0, b > 0, може да се запише и в този вид a b = a b ;
Свойство от степента на число ас четен показател a 2 m = a m за произволно число а, например, свойство от квадрата на число a 2 = a .

Във всяко от представените уравнения можете да размените частите преди и след знака тире, например равенството a · b = a · b се трансформира като a · b = a · b . Свойствата на равенството често се използват за опростяване на сложни уравнения.

Доказателството на първите свойства се основава на дефиницията на квадратния корен и свойствата на степени с естествен степен. За да се обоснове третото свойство, е необходимо да се обърнем към определението на модула на число.

На първо място е необходимо да се докажат свойствата на квадратния корен a · b = a · b . Според дефиницията е необходимо да се има предвид, че a b е число, положително или равно на нула, което ще бъде равно на а бпо време на строителството в квадрат. Стойността на израза a · b е положителна или равна на нула като произведение на неотрицателни числа. Свойството на степента на умножените числа ни позволява да представим равенството във вида (a · b) 2 = a 2 · b 2 . По дефиницията на квадратния корен a 2 \u003d a и b 2 \u003d b, след това a b \u003d a 2 b 2 \u003d a b.

По подобен начин може да се докаже това от продукта кмножители a 1 , a 2 , … , a kще бъде равно на произведението на квадратните корени на тези фактори. Наистина, a 1 · a 2 · … · ak 2 = a 1 2 · a 2 2 · … · ak 2 = a 1 · a 2 · … · a k .

От това равенство следва, че a 1 · a 2 · … · a k = a 1 · a 2 · … · a k .

Нека разгледаме няколко примера, за да подсилим темата.

Пример 1

3 5 2 5 = 3 5 2 5 , 4 , 2 13 1 2 = 4 , 2 13 1 2 и 2 , 7 4 12 17 0 , 2 (1) = 2 , 7 4 12 17 0. 2 (1) .

Необходимо е да се докаже свойството на аритметичния квадратен корен от частното: a: b = a: b, a ≥ 0, b > 0. Свойството ви позволява да запишете равенството a: b 2 = a 2: b 2 и a 2: b 2 = a: b , докато a: b е положително число или равно на нула. Този израз ще бъде доказателството.

Например 0:16 = 0:16, 80:5 = 80:5 и 30, 121 = 30, 121.

Помислете за свойството на квадратния корен от квадрата на число. Може да се запише като равенство като a 2 = a За да се докаже това свойство, е необходимо да разгледаме подробно няколко равенства за а ≥ 0и при а< 0 .

Очевидно е, че за a ≥ 0, равенството a 2 = a е вярно. В а< 0 равенството a 2 = - a ще бъде вярно. Всъщност в този случай − a > 0и (− a) 2 = a 2 . Можем да заключим, че a 2 = a , a ≥ 0 - a , a< 0 = a . Именно это и требовалось доказать.

Нека разгледаме няколко примера.

Пример 2

5 2 = 5 = 5 и - 0. 36 2 = - 0. 36 = 0. 36.

Доказаното свойство ще помогне да се обоснове a 2 m = a m , където а- истински и м-естествено число. Всъщност свойството на степенуване ни позволява да заменим степента а 2 мизразяване (ам) 2, тогава a 2 · m = (a m) 2 = a m .

Пример 3

3 8 = 3 4 = 3 4 и (- 8 , 3) 14 = - 8 , 3 7 = (8 , 3) 7 .

Свойства на n-тия корен

Първо трябва да разгледате основните свойства на корените от n-та степен:

Свойство от произведението на числата аи б, които са положителни или равни на нула, могат да се изразят като равенството a b n = a n b n , това свойство е валидно за произведението кчисла a 1 , a 2 , … , a kкато a 1 a 2 … a k n = a 1 n a 2 n … a k n ;
от дробно число има свойството a b n = a n b n , където ае всяко реално число, което е положително или равно на нула, и бе положително реално число;
За всякакви аи четни числа n = 2 m a 2 m 2 m = a е вярно, а за нечетно n = 2 m − 1е изпълнено равенството a 2 · m - 1 2 · m - 1 = a.
Свойство за извличане от a m n = a n m , където а- произволно число, положително или равно на нула, ни мса естествени числа, това свойство може да бъде представено и като . . a n k n 2 n 1 = a n 1 · n 2 . . . nk ;
За всяко неотрицателно a и произволно ни м, които са естествени, може да се дефинира и справедливото равенство a m n · m = a n ;
степен имот нот силата на число а, което е положително или равно на нула, в натура м, дефиниран от равенството a m n = a n m ;
Свойство за сравнение, които имат еднакви експоненти: за всякакви положителни числа аи бтакъв, че а< b , неравенството a n< b n ;
Свойството за сравнение, което притежава същите числакорен: ако ми н-естествени числа, които m > n, след това при 0 < a < 1 неравенството a m > a n е валидно и за а > 1а м< a n .

Горните уравнения са валидни, ако частите преди и след знака за равенство са обърнати. Те могат да се използват и в тази форма. Това често се използва по време на опростяване или трансформиране на изрази.

Доказателството за горните свойства на корена се основава на определението, свойствата на степента и определението на модула на число. Тези свойства трябва да бъдат доказани. Но всичко е наред.

Преди всичко ще докажем свойствата на корена от n-та степен от произведението a · b n = a n · b n . За аи б, коетоса положителен или нула , стойността a n · b n също е положителна или равна на нула, тъй като е следствие от умножение на неотрицателни числа. Свойството на естествено степенно произведение ни позволява да запишем равенството a n · b n n = a n n · b n n . По дефиниция на root нстепен a n n = a и b n n = b , следователно a n · b n n = a · b . Полученото равенство е точно това, което се изискваше да се докаже.

Това свойство се доказва по подобен начин за продукта кфактори: за неотрицателни числа a 1 , a 2 , … , a n a 1 n · a 2 n · … · a k n ≥ 0 .

Ето примери за използване на свойството root нй степен от произведението: 5 2 1 2 7 = 5 7 2 1 2 7 и 8 , 3 4 17 , (21) 4 3 4 5 7 4 = 8 , 3 17 , (21) 3 5 7 4 .

Нека докажем свойството на корена на частното a b n = a n b n . В а ≥ 0и b > 0условието a n b n ≥ 0 е изпълнено и a n b n n = a n n b n n = a b .

Нека покажем примери:

Пример 4

8 27 3 = 8 3 27 3 и 2 , 3 10: 2 3 10 = 2 , 3: 2 3 10 .

За Следваща стъпканеобходимо е да се докажат свойствата на n-та степен от числото до степента н. Представяме това като равенство a 2 m 2 m = a и a 2 m - 1 2 m - 1 = a за всяко реално аи естествено м. В а ≥ 0получаваме a = a и a 2 m = a 2 m , което доказва равенството a 2 m 2 m = a , а равенството a 2 m - 1 2 m - 1 = a е очевидно. В а< 0 получаваме съответно a = - a и a 2 m = (- a) 2 m = a 2 m . Последната трансформация на числото е валидна според свойството на степента. Това доказва равенството a 2 m 2 m \u003d a и a 2 m - 1 2 m - 1 \u003d a ще бъде вярно, тъй като - c 2 m - 1 = - c 2 m се счита за нечетно степен - 1 за произволно число ° С ,положителен или равен на нула.

За да консолидирате получената информация, разгледайте няколко примера за използване на свойството:

Пример 5

7 4 4 = 7 = 7 , (- 5) 12 12 = - 5 = 5 , 0 8 8 = 0 = 0 , 6 3 3 = 6 и (- 3 , 39) 5 5 = - 3 , 39 .

Нека докажем следното равенство a m n = a n · m . За да направите това, трябва да промените числата преди знака за равенство и след него на места a n · m = a m n . Ще означава правилно вписване. За а ,което е положително или равно на нула , от формата a m n е положително число или равно на нула. Нека се обърнем към свойството да се издига степен до степен и определението. С тяхна помощ можете да трансформирате равенства във формата a m n n · m = a m n n m = a m m = a . Това доказва разглежданото свойство на корен от корен.

Други свойства се доказват по подобен начин. Наистина ли, . . . a n k n 2 n 1 n 1 n 2 . . . nk = . . . a n k n 3 n 2 n 2 n 3 . . . nk = . . . a nk n 4 n 3 n 3 n 4 . . . nk = . . . = a n k n k = a .

Например 7 3 5 = 7 5 3 и 0 . 0009 6 = 0 . 0009 2 2 6 = 0 . 0009 24 .

Да докажем следващ имот a m n · m = a n . За да направите това, е необходимо да се покаже, че n е число, което е положително или равно на нула. Когато се повдигне на степен n m е а м. Ако номер атогава е положително или нула нта степен измежду ае положително число или равно на нула Освен това a n · m n = a n n m , което трябваше да се докаже.

За да затвърдите придобитите знания, разгледайте няколко примера.

Нека докажем следното свойство – свойството на корена на степента на вида a m n = a n m . Очевидно е, че при а ≥ 0степента a n m е неотрицателно число. Освен това тя н-та степен е равна на а м, наистина, a n m n = a n m · n = a n n m = a m . Това доказва разглежданото свойство на степента.

Например, 2 3 5 3 = 2 3 3 5 .

Трябва да докажем това за всякакви положителни числа аи б а< b . Да разгледаме неравенството a n< b n . Воспользуемся методом от противного a n ≥ b n . Тогда, согласно свойству, о котором говорилось выше, неравенство считается верным a n n ≥ b n n , то есть, a ≥ b . Но это не соответствует условию а< b . Следователно, a n< b n при а< b .

Например даваме 12 4< 15 2 3 4 .

Помислете за коренното свойство н-та степен. Първо, разгледайте първата част от неравенството. В m > nи 0 < a < 1 вярно a m > a n . Да предположим, че a m ≤ a n. Свойствата ще опростят израза до a n m · n ≤ a m m · n . Тогава, според свойствата на степен с естествен експонент, неравенството a n m n m n ≤ a m m n m n е изпълнено, т.е. a n ≤ a m. Получената стойност при m > nи 0 < a < 1 не съответства на свойствата по-горе.

По същия начин може да се докаже това m > nи а > 1състояние a m< a n .

За да коригирате горните свойства, разгледайте няколко конкретни примери. Помислете за неравенствата, като използвате конкретни числа.

Пример 6

0 , 7 3 < 0 , 7 5 и 12 > 12 7 .

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter