Серия Тейлър, квадратен корен. Степенни редове, тяхното сближаване, разширяване на функциите в степенни редове

Студентите от висшата математика трябва да знаят, че сумата от определена степенна серия, принадлежаща към интервала на сходимост на дадената ни поредица, е непрекъсната и безкраен брой пъти диференцирана функция. Възниква въпросът: възможно ли е да се твърди, че дадена произволна функция f (x) е сумата от определен степенен ред? Тоест, при какви условия f-ija f (x) може да бъде представена от степенна серия? Важността на такъв въпрос се крие във факта, че е възможно приблизително да се замени f-yu f (x) със сумата от първите няколко члена на степенния ред, тоест с полином. Тази подмяна на функция с доста прост израз - полином - също е удобна при решаване на някои проблеми, а именно: при решаване на интеграли, при изчисляване и т.н.

Доказано е, че за някои fu и f (x), при които е възможно да се изчислят производни до (n + 1) -и ред, включително последния, в околността (α - R; x 0 + R) на някаква точка x = α е валидна формула:

Тази формула носи името на известния учен Брук Тейлър. Поредицата, получена от предишната, се нарича серия Маклаурин:

Правилото, което позволява да се извърши разширяването в серията Maclaurin:

1. Определете производни на първи, втори, трети ... ред.
2. Изчислете на какво са равни производните при x = 0.
3. Запишете поредицата Маклаурин за тази функция и след това определете интервала на нейната конвергенция.
4. Определете интервала (-R; R), където остатъчната част от формулата на Маклаурин

R n (x) -> 0 като n -> безкрайност. Ако такава съществува, функцията f (x) в нея трябва да съвпада със сумата от поредицата Маклорен.

Нека сега разгледаме поредицата Maclaurin за отделни функции.

1. И така, първият ще бъде f (x) = e x. Разбира се, по своите характеристики, такава функция има производни на различни порядки и f (k) (x) = e x, където k е равно на всички.Заместете x = 0. Получаваме f (k) (0) = e 0 = 1, k = 1,2 ... Въз основа на горното редът e x ще изглежда така:

2. Серия Макларен за функцията f (x) = sin x. Нека веднага изясним, че f -s за всички неизвестни ще има производни, освен f "(x) = cos x = sin (x + n / 2), f" "(x) = -sin x = sin (x + 2 * n / 2) ..., f (k) (x) = sin (x + k * n / 2), където k е равно на всяко естествено число. че редът за f (x) = sin x ще бъде от този вид:

3. Сега нека се опитаме да разгледаме f-yu f (x) = cos x. За всички неизвестни има производни от произволен ред и | f (k) (x) | = | cos (x + k * n / 2) |<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

И така, ние изброихме най -важните функции, които могат да бъдат разширени в серия Maclaurin, но те се допълват от серия Taylor за някои функции. Сега ще ги изброим и тях. Също така си струва да се отбележи, че поредиците Тейлър и Макларин са важна част от семинара за решаване на серии по висша математика. И така, Тейлър се нарежда.

1. Първият ще бъде редът за f-ii f (x) = ln (1 + x). Както в предишните примери, за дадено f (x) = ln (1 + x), можем да добавим серия, използвайки общата форма на серията Maclaurin. обаче серията Maclaurin може да се получи много по -просто за тази функция. Чрез интегриране на определена геометрична серия получаваме серия за f (x) = ln (1 + x) на такава извадка:

2. И второто, което ще бъде окончателно в нашата статия, ще бъде серията за f (x) = arctan x. За х, принадлежащи към интервала [-1; 1], разлагането е валидно:

Това е всичко. Тази статия разглежда най -използваните серии на Тейлър и Маклаурин във висшата математика, по -специално в икономическите и техническите университети.

Как да вмъкнете математически формули в уебсайт?

Ако някога се наложи да добавите една или две математически формули към уеб страница, тогава най -лесният начин да направите това е както е описано в статията: математическите формули лесно се вмъкват в сайта под формата на картини, които Wolfram Alpha автоматично генерира. В допълнение към простотата, този универсален метод ще помогне за подобряване на видимостта на вашия сайт в търсачките. Работи отдавна (и мисля, че ще работи вечно), но вече е морално остаряло.

Ако редовно използвате математически формули на вашия сайт, препоръчвам ви да използвате MathJax, специална JavaScript библиотека, която показва математическа нотация в уеб браузъри, използвайки MathML, LaTeX или ASCIIMathML маркировка.

Има два начина да започнете да използвате MathJax: (1) с прост код, можете бързо да свържете скрипт MathJax към вашия сайт, който автоматично ще се зареди от отдалечен сървър в точното време (списък със сървъри); (2) качете скрипта MathJax от отдалечен сървър към вашия сървър и го свържете с всички страници на вашия сайт. Вторият метод, който е по-сложен и отнема много време, ще ускори зареждането на страниците на вашия сайт и ако родителският сървър MathJax по някаква причина временно стане недостъпен, това няма да повлияе по никакъв начин на вашия собствен сайт. Въпреки тези предимства, аз избрах първия метод, тъй като е по -прост, по -бърз и не изисква технически умения. Следвайте моя пример и след 5 минути ще можете да използвате всички функции на MathJax на вашия сайт.

Можете да свържете скрипта на библиотеката MathJax от отдалечен сървър, като използвате две версии на кода, взет от основния сайт на MathJax или от страницата с документация:

Един от тези варианти на код трябва да бъде копиран и поставен в кода на вашата уеб страница, за предпочитане между маркерите иили веднага след етикета ... Според първия вариант MathJax се зарежда по -бързо и забавя страницата по -малко. Но втората опция автоматично проследява и зарежда най -новите версии на MathJax. Ако вмъкнете първия код, той ще трябва периодично да се актуализира. Ако вмъкнете втория код, страниците ще се зареждат по -бавно, но няма да е необходимо постоянно да следите актуализациите на MathJax.

Най-лесният начин да свържете MathJax е в Blogger или WordPress: в таблото за управление на вашия сайт добавете приспособление за вмъкване на JavaScript код на трета страна, копирайте първата или втората версия на кода за зареждане, представен по-горе, и го поставете по-близо до началото на шаблона (между другото, това изобщо не е необходимо, защото скриптът MathJax се зарежда асинхронно). Това е всичко. Сега научете синтаксиса за маркиране на MathML, LaTeX и ASCIIMathML и сте готови да вградите математически формули в уеб страниците на вашия уебсайт.

Всеки фрактал е изграден по определено правило, което се прилага последователно неограничен брой пъти. Всеки такъв момент се нарича итерация.

Итеративният алгоритъм за конструиране на гъбата Менгер е доста прост: оригиналният куб със страна 1 е разделен от равнини, успоредни на лицата му, на 27 равни кубчета. Един централен куб и 6 съседни кубчета се отстраняват от него. Резултатът е комплект, състоящ се от останалите 20 по -малки кубчета. Правейки същото с всяко от тези кубчета, получаваме комплект, който вече се състои от 400 по -малки кубчета. Продължавайки този процес безкрайно, получаваме гъба Menger.

Сред функционалните серии най -важното място заемат степенните серии.

Серията се нарича степенна серия

чиито членове са степенни функции, подредени в увеличаващи се цели неотрицателни степени х, а ° С0 , ° С 1 , ° С 2 , ° Сн - постоянни стойности. Числата ° С1 , ° С 2 , ° Сн - коефициентите на членовете на поредицата, ° С0 - безплатен член. Членовете на степенния ред са дефинирани в цялата числова линия.

Нека се запознаем с концепцията областта на сходимост на степенните редове. Това е набор от променливи стойности хза които поредицата се сближава. Степените серии имат сравнително проста област на конвергенция. За реални стойности на променливата хдомейнът на сходимост се състои или от една точка, или представлява някакъв интервал (интервал на конвергенция), или съвпада с цялата ос Вол .

Когато се заменят в степенна серия, стойностите х= 0 получавате числова серия

° С0 +0+0+...+0+... ,

който се сближава.

Следователно, за х= 0 всяка степенна серия се сближава и следователно, зоната му на сближаване не може да бъде празно. Структурата на областта на сходимост на всички степенни серии е една и съща. Това може да се установи, като се използва следната теорема.

Теорема 1 (теоремата на Абел)... Ако степенният ред се сближи за някаква стойност х = х 0 ненулева, тогава тя се сближава и освен това абсолютно за всички стойности |х| < |х 0 | ... Обърнете внимание: както началната стойност "x е нула", така и всяка стойност на "x", която се сравнява с началната стойност, се вземат по модул - без да се отчита знакът.

Последица. Ако степенните серии се разминават на някаква стойност х = х 1 , след това се различава за всички стойности |х| > |х 1 | .

Както разбрахме по -рано, всяка степенна серия се сближава по стойността х= 0. Има степенни серии, които се сближават само за х= 0 и се разминават за други стойности NS... Премахвайки този случай от разглеждане, приемаме, че степенният ред се сближава за някаква стойност х = х 0 ненулева. Тогава, по теоремата на Абел, тя се сближава във всички точки на интервала] - | х0 |, |х 0 |[ (интервалът, чиято лява и дясна граница са стойностите на x, при които степенният ред се сближава, взети съответно със знаците минус и плюс), симетрични спрямо произхода.

Ако степенният ред се разминава при някаква стойност х = х 1 , тогава, въз основа на следствието от теоремата на Абел, тя също се разминава във всички точки извън сегмента [- | х1 |, |х 1 |] ... От това следва, че за всяка степенна серия има интервал, симетричен за произхода, т.нар интервал на сближаване , във всяка точка, от която редът се сближава, по границите може да се сближи и може да се отклони, и не непременно едновременно, но извън сегмента серията се разминава. Номер Rсе нарича радиусът на сходимост на степенния ред.

В конкретни случаи интервал на сходимост на степенните редове може да се изроди до точка (тогава поредицата се сближава само за х= 0 и се приема, че R= 0) или представляват цялата числова линия (тогава серията се сближава във всички точки на числовата линия и се приема, че).

По този начин дефиницията на областта на сходимост на степенна серия се състои в дефиницията на нейната радиус на конвергенция Rи изследване на сходимостта на редовете по границите на интервала на сходимост (в).

Теорема 2.Ако всички коефициенти на степенния ред, започвайки с някакъв, са ненулеви, тогава радиусът му на сходимост е равен на границата при съотношението на абсолютните стойности на коефициентите на общите следващи членове на поредицата, т.е.

Пример 1. Намерете областта на сходимост на степенния ред

Решение. Тук

Използвайки формула (28), намираме радиуса на сходимост на тази серия:

Нека изследваме сходимостта на редовете в краищата на интервала на сходимост. Пример 13 показва, че тази серия се сближава за х= 1 и се разминава при х= -1. Следователно районът на конвергенция е половин интервал.

Пример 2. Намерете областта на сходимост на степенния ред

Решение. Серийните коефициенти са положителни и

Нека намерим границата на това съотношение, т.е. радиус на сходимост на степенния ред:

Нека изследваме сходимостта на редовете в краищата на интервала. Замяна на стойности х= -1/5 и х= 1/5 в даден ред дава:

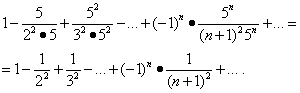
Първата от тези серии се сближава (виж пример 5). Но след това, по силата на теоремата в раздела "Абсолютна конвергенция", втората серия също се сближава, а областта на нейната конвергенция е сегментът

Пример 3. Намерете областта на сходимост на степенния ред

Решение. Тук

Използвайки формула (28), намираме радиуса на сходимост на серията:

Нека изследваме сближаването на серията за стойности. Замествайки ги в този ред, съответно получаваме

И двете серии се разминават, тъй като необходимото условие за сходимост не е изпълнено (общите им условия нямат тенденция към нула при). И така, в двата края на интервала на конвергенция дадената серия се разминава, а областта на нейната конвергенция е интервалът.

Пример 5. Намерете областта на сходимост на степенния ред

Решение. Намерете връзката, къде и :

Съгласно формула (28) радиусът на сходимост на тази серия е

,

тоест поредицата се сближава само за х= 0 и се разминава за други стойности NS.

Примерите показват, че сериите се държат по различен начин в краищата на интервала на конвергенция. В пример 1, серията се сближава в единия край на интервала на конвергенция и се разминава в другия; в пример 2, тя се сближава в двата края; в пример 3, се разминава в двата края.

Формулата за радиуса на сходимост на степенна серия се получава при предположението, че всички коефициенти на членовете на серията, започвайки от някакъв, са ненулеви. Следователно използването на формула (28) е допустимо само в тези случаи. Ако това условие е нарушено, тогава трябва да се търси радиусът на сходимост на степенния ред знак на д'Аламбер, или чрез промяна на променливата, преобразуване на серията във формата, в която посоченото условие е изпълнено.

Пример 6. Намерете интервала на сходимост на степенния ред

Решение. Тази серия не съдържа членове с нечетни степени. NS... Следователно, ние преобразуваме серията чрез настройка. Тогава получаваме поредицата

за да се намери радиусът на сходимост, към която може да се приложи формула (28). Тъй като, a, тогава радиусът на сходимост на тази серия

Следователно от равенството, което получаваме, тази серия се сближава на интервала.

Сумата от степенния ред. Диференциране и интегриране на Power Series

Нека за степенна серия

радиус на конвергенция R> 0, т.е. тази серия се сближава на интервала.

След това всяка стойност NSот интервала на сходимост съответства определена сума от поредицата. Следователно сумата от степенния ред е функция на NSна интервала на сближаване. Обозначавайки го чрез е(х), можем да напишем равенството

разбиране в смисъл, че сумата от поредицата във всяка точка NSот интервала на сходимост е равна на стойността на функцията е(х) в този момент. В същия смисъл ще кажем, че степенният ред (29) се сближава с функцията е(х) върху интервала на сближаване.

Извън интервала на сближаване равенството (30) е безсмислено.

Пример 7.Намерете сумата от сумата на степенния ред

Решение. Това е геометричен ред с а= 1 и q= х... Следователно неговата сума е функция ... Поредицата се сближава ако и е нейният интервал на сближаване. Следователно, равенството

е валиден само за стойности, въпреки че функцията дефинирани за всички стойности NS, с изключение NS= 1.

Може да се докаже, че сумата от степенните редове е(х) е непрекъснат и диференцируем на всеки сегмент в интервала на сходимост, по -специално във всяка точка от интервала на сходимост на поредицата.

Нека представим теореми за терминологично диференциране и интегриране на степенни редове.

Теорема 1.Степенните редове (30) в интервала на неговата сходимост могат да бъдат терминово диференцирани неограничен брой пъти, а получените степенни редове имат същия радиус на сходимост като оригиналния ред и техните суми съответно са равни.

Теорема 2.Мощните серии (30) могат да бъдат интегрирани неограничен брой пъти в диапазона от 0 до NS, if и получените степенни серии имат същия радиус на сходимост като оригиналната серия и техните суми съответно са равни

Разширяване на функциите в степенни серии

Дадена функция е(х), която се изисква да бъде разгърната в степенна серия, т.е. представляват под формата (30):

Задачата е да се определят коефициентите ред (30). За това, разграничавайки равенството (30) термин по термин, последователно намираме:

……………………………………………….. (31)

Настройка на равенства (30) и (31) NS= 0, намираме

Подменяйки намерените изрази в равенство (30), получаваме

(32)

Нека открием разширяването на някои елементарни функции в поредицата Макларин.

Пример 8.Разгънете функцията Maclaurin series

Решение. Производните на тази функция са същите като самата функция:

Следователно, при NS= 0 имаме

Замествайки тези стойности във формула (32), получаваме необходимото разширение:

(33)

Тази серия се сближава по цялата числова линия (нейният радиус на сходимост).

16.1. Разширяване на елементарни функции в сериите на Тейлър и

Маклаурин

Нека покажем, че ако на множеството е дефинирана произволна функция
, в близост до точката
има много производни и е сумата от степенна серия:

тогава могат да се намерят коефициентите на тази серия.

Заместник в силовия ред
... Тогава
.

Намерете първата производна на функцията
:

При
:
.

За втората производна получаваме:

При
:
.

Продължаването на тази процедура нслед като получим:
.

По този начин получаваме степенни серии от вида:

,

който се нарича до Тейлърза функция
в близост до точката
.

Специален случай от поредицата Тейлър е Серия Макларинв
:

Остатъкът от поредицата Тейлър (Макларин) се получава чрез изхвърляне на основните редове нпърви членове и означени като
... След това функцията
може да се запише като сума нранни членове на дадено число
и останалата част
:,

.

Остатъкът обикновено е
изразени в различни формули.

Един от тях е под формата на Лагранж:

, където
.
.

Имайте предвид, че на практика серията Maclaurin се използва по -често. По този начин, за да се напише функцията
под формата на сума от степенни серии е необходимо:

1) намерете коефициентите на поредицата Макларин (Тейлър);

2) намерете областта на сходимост на получената степенна серия;

3) докажете, че дадената серия се сближава с функцията
.

Теорема1 (необходимо и достатъчно условие за сходимостта на поредицата Маклаурин). Нека радиусът на сходимост на поредицата
... За да може тази серия да се сближи в интервала
да функционира
, е необходимо и достатъчно, за да бъде изпълнено условието:
в посочения интервал.

Теорема 2.Ако производни на произволен ред на функцията
в някакъв интервал
ограничени по абсолютна стойност със същия номер М, това е
, тогава в този интервал функцията
може да бъде разгърнат в серия Maclaurin.

Пример1 . Разгънете в ред на Тейлър около точката
функция.

Решение.

.

,;

,
;

,
;

,

.......................................................................................................................................

,
;

Регион на конвергенция
.

Пример2 . Разширете функцията в реда на Тейлър около точката
.

Решение:

Намерете стойността на функцията и нейните производни при
.

,
;

,
;

...........……………………………

,
.

Заместваме тези стойности подред. Получаваме:

или
.

Нека намерим района на сходимост на тази серия. Според характеристиката на д'Аламбер поредицата се сближава, ако

.

Следователно, за всеки тази граница е по -малка от 1 и следователно районът на сближаване на серията ще бъде:
.

Нека разгледаме няколко примера за разширяване в основни елементарни функции в поредицата Макларен. Припомнете си, че поредицата Maclaurin:

.

се сближава на интервала
да функционира
.

Имайте предвид, че за да се разшири функцията в серия, е необходимо:

а) намерете коефициентите на серията Макларин за тази функция;

б) изчислява радиуса на сходимост за получената серия;

в) докажете, че получената серия се сближава с функцията
.

Пример 3.Помислете за функцията
.

Решение.

Нека изчислим стойността на функцията и нейните производни при
.

Тогава числовите коефициенти на серията са:

за всеки н.Заместете намерените коефициенти в серията Maclaurin и получете:

Намерете радиуса на сходимост на получената серия, а именно:

.

Следователно поредицата се сближава на интервала
.

Тази серия се сближава с функцията за всякакви стойности защото всяка празнина
функция и нейните производни в абсолютна стойност са ограничени от броя .

Пример4 . Помислете за функцията
.

Решение.

:

Лесно е да се види, че дериватите са равномерни
, а дериватите са в нечетен ред. Заместваме намерените коефициенти в серията Макларин и получаваме разширението:

Нека намерим интервала на сходимост на тази серия. Въз основа на d'Alembert:

за всеки ... Следователно поредицата се сближава на интервала
.

Тази серия се сближава с функцията
, тъй като всички негови производни са ограничени до едно.

Пример5 .
.

Решение.

Нека намерим стойността на функцията и нейните производни при
:

По този начин коефициентите на тази серия:
и
, следователно:

Подобно на предишната серия, регионът на конвергенция
... Поредицата се сближава с функцията
, тъй като всички негови производни са ограничени до едно.

Обърнете внимание, че функцията
нечетно и серийно разширение в нечетни степени, функцията
- равномерно и серийно разширяване в четни правомощия.

Пример6 . Биномни серии:
.

Решение.

Нека намерим стойността на функцията и нейните производни при
:

От това става ясно, че:

Заместете тези стойности на коефициентите в серията Maclaurin и получете разширението на тази функция в степенна серия:

Намерете радиуса на сходимост на тази серия:

Следователно поредицата се сближава на интервала
... В граничните точки при
и
серията може или не може да се сближи в зависимост от степента
.

Изследваната поредица се сближава на интервала
да функционира
, тоест сумата на таксата
в
.

Пример7 . Нека разширим функцията в поредица Макларин
.

Решение.

За да разширим тази функция в серия, използваме биномиалната серия за
... Получаваме:

Въз основа на свойството на степенните серии (степенните серии могат да бъдат интегрирани в областта на нейната конвергенция), намираме интеграла от лявата и дясната страна на този ред:

Намерете района на конвергенция на тази серия:
,

т.е. регионът на сходимост на тази серия е интервалът
... Нека определим сходимостта на поредицата в краищата на интервала. При

... Този ред е хармоничен ред, тоест се разминава. При
получаваме числови серии с общ термин
.

Серията Leibniz се сближава. По този начин районът на сближаване на тази серия е интервалът
.

16.2. Прилагане на степенни серии при приблизителни изчисления

При приблизителни изчисления, степенните серии играят изключително важна роля. С тяхна помощ бяха съставени таблици с тригонометрични функции, таблици с логаритми, таблици със стойности на други функции, които се използват в различни области на знанието, например в теорията на вероятностите и математическата статистика. Освен това разширяването на функциите в степенни редове е полезно за тяхното теоретично изследване. Основният проблем при използване на степенни серии при приблизителни изчисления е въпросът за оценката на грешката при замяна на сумата на серия със сумата на първата нчленове.

Помислете за два случая:

функцията се разширява в поредица от редуващи се знаци;

функцията се разгръща в постоянна серия.

Изчисляване с помощта на редуващи се серии

Нека функцията
разширени в променлива серия мощности. След това, когато се изчислява тази функция за конкретна стойност получаваме числова серия, към която може да се приложи тестът на Лайбниц. В съответствие с тази функция, ако сумата от поредицата се замени със сумата от първата нусловия, тогава абсолютната грешка не надвишава първия член на остатъка от тази поредица, тоест:
.

Пример8 . Изчисли
с точност до 0,0001.

Решение.

Ще използваме серията Maclaurin за
, замествайки стойността на ъгъла в радиани:

Ако сравним първия и втория член на поредицата с дадена точност, тогава :.

Третият срок на разширяване:

по -малка от посочената точност на изчисление. Следователно, за да се изчисли
достатъчно е да оставите двама членове на поредицата, т.е.

.

Поради това
.

Пример9 . Изчисли
с точност 0,001.

Решение.

Ще използваме формулата за биномиални редове. За да направите това, пишете
като:
.

В този израз
,

Нека сравним всеки от членовете на поредицата с посочената точност. Ясно е, че
... Следователно, за да се изчисли
достатъчно е да оставите трима членове на реда.

или
.

Изчисление с помощта на положителни редове

Пример10 . Изчислете броя с точност до 0,001.

Решение.

Поред за функцията
заместител
... Получаваме:

Нека да оценим грешката, която възниква, когато сумата от поредицата се замени с сумата на първата членове. Нека запишем очевидното неравенство:

това е 2<<3. Используем формулу остаточного члена ряда в форме Лагранжа:
,
.

Според състоянието на проблема трябва да намерите нтака че важи следното неравенство:
или
.

Това е лесно да се провери за н= 6:
.

Следователно,
.

Пример11 . Изчисли
с точност 0,0001.

Решение.

Имайте предвид, че за да се изчислят логаритмите, може да се приложи серия за функцията
, но тази серия се сближава много бавно и за да се постигне дадената точност би било необходимо да се вземат 9999 термина! Следователно за изчисляване на логаритми като правило се използва серия за функцията
която се сближава на интервала
.

Нека изчислим
използвайки този ред. Нека бъде
, тогава .

Следователно,
,

За да се изчисли
с дадена точност вземаме сумата от първите четири члена:
.

Остатък от реда
изхвърлете. Нека преценим грешката. Очевидно е, че

или
.

По този начин в поредицата, използвана за изчислението, беше достатъчно да се вземат само първите четири члена вместо 9999 в поредицата за функцията
.

Въпроси за самодиагностика

1. Какво е поредицата на Тейлър?

2. Какъв вид имаше поредицата Maclaurin?

3. Формулирайте теорема за разгръщането на функция в ред на Тейлър.

4. Напишете разширението на Maclaurin за основните функции.

5. Посочете областите на конвергенция на разглежданите серии.

6. Как да оценим грешката в приблизителните изчисления, използвайки степенни серии?

Ако функцията f (x)има на някакъв интервал, съдържащ точката а, производни на всички поръчки, тогава формулата на Тейлър може да се приложи към нея:

където r n- така нареченият остатък или остатъкът от поредицата, той може да бъде оценен с помощта на формулата на Лагранж:

, където числото x е между NSи а.

Ако за някаква стойност x r n®0 за н® ¥, тогава в лимита формулата на Тейлър се превръща за тази стойност в конвергентна Поредицата на Тейлър:

Така че функцията f (x)могат да бъдат разширени в серия Тейлър в разглеждания момент NS, ако:

1) има деривати на всички поръчки;

2) построената серия се сближава в тази точка.

При а= 0 получаваме наречена серия близо до Макларин:

Пример 1 f (x) = 2х.

Решение... Нека намерим стойностите на функцията и нейните производни при NS=0

f (x) = 2х, f (f 0) = 2 0 =1;

f ¢ (x) = 2х ln2, f ¢ ( 0) = 2 0 ln2 = ln2;

f ¢¢ (x) = 2хв 2 2, f ¢¢ ( 0) = 2 0 ln 2 2 = ln 2 2;

f (n) (x) = 2хИн н 2, f (n) ( 0) = 2 0 Ин н 2 = ln н 2.

Замествайки получените стойности на производни във формулата на серията Тейлър, получаваме:

Радиусът на сходимост на тази серия е равен на безкрайността; следователно това разширение е валидно за - ¥<х<+¥.

Пример 2 NS+4) за функцията f (x) =д х.

Решение... Намерете производни на функцията e хи техните стойности в точката NS=-4.

f (x)= д х, f (f-4) = д -4 ;

f ¢ (x)= д х, f ¢ (-4) = д -4 ;

f ¢¢ (x)= д х, f ¢¢ (-4) = д -4 ;

f (n) (x)= д х, f (n) ( -4) = д -4 .

Следователно необходимата серия Тейлър на функцията има формата:

Това разширение е валидно и за - ¥<х<+¥.

Пример 3 ... Разширете функцията f (x)= ln хв поредица от правомощия ( NS- 1),

(т.е. в поредицата Тейлър в близост до точката NS=1).

Решение... Намерете производни на тази функция.

Замествайки тези стойности във формулата, получаваме необходимите серии на Тейлър:

Използвайки теста на d'Alembert, човек може да се увери, че поредицата се сближава за

½ NS- 1½<1. Действительно,

Поредицата се сближава, ако ½ NS- 1½<1, т.е. при 0<х<2. При NS= 2 получаваме променлив ред, отговарящ на условията на теста на Лайбниц. При NS= 0 функция е неопределена. По този начин, областта на сходимост на серията Тейлър е полуотвореният интервал (0; 2].

Нека представим разширенията, получени по подобен начин в серията Маклаурин (т.е. в близост до точката NS= 0) за някои елементарни функции:

(2) ,

(3) ,

(се нарича последното разлагане биномиални серии)

Пример 4 ... Разгънете функция в степенна серия

Решение... В разширение (1) заменяме NSНа - NS 2, получаваме:

Пример 5 ... Разгънете функцията Maclaurin series

Решение... Ние имаме

Използвайки формула (4), можем да напишем:

заместващи за NSвъв формулата -NS, получаваме:

От тук намираме:

Разширявайки скобите, пренареждайки условията на поредицата и намалявайки подобни термини, получаваме

Тази серия се сближава в интервала

(-1; 1), тъй като се получава от две серии, всяка от които се сближава в този интервал.

Коментирайте .

Формули (1) - (5) могат да се използват и за разширяване на съответните функции в редица на Тейлър, т.е. за разширяване на функциите в положителни цели числа ( Ха). За да направите това, над дадена функция е необходимо да извършите подобни идентични трансформации, за да получите една от функциите (1) - (5), в която вместо NSразходи k ( Ха) m, където k е постоянно число, m е положително цяло число. Често е удобно да променяте променливата T=Хаи разгънете получената функция по отношение на t в ред на Маклорен.

Този метод илюстрира теоремата за единствеността на разгъването на функция в степенния ред. Същността на тази теорема е, че в близост до една и съща точка не могат да бъдат получени две различни степенни серии, които биха се сближили до една и съща функция, без значение как се извършва нейното разширение.

Пример 6 ... Разгънете функция от поредица на Тейлър в съседство на точка NS=3.

Решение... Този проблем може да бъде решен, както и преди, с помощта на дефиницията на поредицата Тейлър, за която е необходимо да се намерят производни на функцията и техните стойности при NS= 3. Въпреки това ще бъде по -лесно да се използва съществуващото разлагане (5):

Получената серия се сближава за или –3<х- 3<3, 0<х< 6 и является искомым рядом Тейлора для данной функции.

Пример 7 ... Напишете поредицата Тейлър в правомощия ( NS-1) функции .

Решение.

Серията се сближава в , или 2< х 5 паунда.