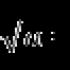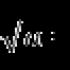Raskite tiesės, einančios per taškus internete, lygtį. Tiesės, einančios per tašką, lygtis, tiesės, einančios per du taškus, kampo tarp dviejų tiesių, tiesės nuolydžio lygtis

Tiesės, einančios per du taškus, lygtis. Straipsnyje" " Pažadėjau išanalizuoti antrąjį pateiktų išvestinės radimo uždavinių sprendimo būdą su duotu funkcijos grafiku ir šio grafiko liestine. Išnagrinėsime šį metodą , Nepraleisk! Kodėl Kitas?

Faktas yra tas, kad ten bus naudojama tiesės lygties formulė. Žinoma, galima tiesiog parodyti šią formulę ir patars to išmokti. Bet geriau paaiškinti, iš kur jis kilęs (kaip jis gaunamas). Tai būtina! Jei pamiršite, greitai atkurkitenebus sunku. Viskas išsamiai aprašyta žemiau. Taigi koordinačių plokštumoje turime du taškus A(x 1; y 1) ir B (x 2; y 2), per nurodytus taškus nubrėžiama tiesi linija:

Čia yra tiesioginė formulė:

*Tai yra, pakeitę konkrečias taškų koordinates, gauname y=kx+b formos lygtį.

** Jei ši formulė tiesiog „įsiminta“, yra didelė tikimybė susipainioti su indeksais, kai X. Be to, indeksai gali būti žymimi įvairiais būdais, pavyzdžiui:

Štai kodėl svarbu suprasti prasmę.

Dabar šios formulės išvedimas. Viskas labai paprasta!

Trikampiai ABE ir ACF yra panašūs smailiojo kampo požiūriu (pirmasis stačiųjų trikampių panašumo ženklas). Iš to išplaukia, kad atitinkamų elementų santykiai yra lygūs, tai yra:

Dabar mes tiesiog išreiškiame šiuos segmentus taškų koordinačių skirtumu:

Žinoma, klaidų nebus, jei elementų ryšius parašysite kita tvarka (svarbiausia, kad atitiktų):

Rezultatas yra ta pati tiesės lygtis. Tai viskas!

Tai yra, kad ir kaip būtų pažymėti patys taškai (ir jų koordinatės), suprasdami šią formulę, visada rasite tiesės lygtį.

Formulę galima išvesti naudojant vektorių savybes, tačiau išvedimo principas bus tas pats, nes kalbėsime apie jų koordinačių proporcingumą. Šiuo atveju veikia tas pats stačiųjų trikampių panašumas. Mano nuomone, aukščiau aprašyta išvada yra suprantamesnė)).

Peržiūrėkite išvestį per vektorines koordinates >>>

Koordinačių plokštumoje, einančioje per du duotus taškus A (x 1; y 1) ir B (x 2; y 2), nubrėžkite tiesę. Pažymėkime savavališką tašką C tiesėje koordinatėmis ( x; y). Taip pat žymime du vektorius:

Yra žinoma, kad vektoriams, esantiems lygiagrečiose tiesėse (arba vienoje tiesėje), jų atitinkamos koordinatės yra proporcingos, tai yra:

- rašome atitinkamų koordinačių santykių lygybę:

Apsvarstykite pavyzdį:

Raskite tiesės, einančios per du taškus, kurių koordinatės (2;5) ir (7:3), lygtį.

Jūs netgi negalite sukurti pačios linijos. Taikome formulę:

Sudarant santykį svarbu, kad gautumėte korespondenciją. Negalite suklysti, jei rašote:

Atsakymas: y=-2/5x+29/5 eiti y=-0,4x+5,8

Norėdami įsitikinti, kad gauta lygtis rasta teisingai, būtinai ją patikrinkite – pakeiskite į ją duomenų koordinates taškų sąlygoje. Turėtumėte gauti teisingas lygybes.

Tai viskas. Tikiuosi, kad medžiaga jums buvo naudinga.

Pagarbiai Aleksandras.

P.S. Būčiau dėkingas, jei papasakotumėte apie svetainę socialiniuose tinkluose.

Tegul tiesė eina per taškus M 1 (x 1; y 1) ir M 2 (x 2; y 2). Tiesės, einančios per tašką M 1, lygtis yra y- y 1 \u003d k (x - x 1), (10,6)

kur k – dar nežinomas koeficientas.

Kadangi tiesė eina per tašką M 2 (x 2 y 2), šio taško koordinatės turi atitikti (10.6) lygtį: y 2 -y 1 \u003d k (x 2 - x 1).

Iš čia randame Rastos vertės pakeitimą k į (10.6) lygtį gauname tiesės, einančios per taškus M 1 ir M 2, lygtį:

Daroma prielaida, kad šioje lygtyje x 1 ≠ x 2, y 1 ≠ y 2

Jei x 1 \u003d x 2, tai tiesė, einanti per taškus M 1 (x 1, y I) ir M 2 (x 2, y 2), yra lygiagreti y ašiai. Jo lygtis yra x = x 1 .

Jei y 2 \u003d y I, tada tiesės lygtis gali būti parašyta kaip y \u003d y 1, tiesė M 1 M 2 yra lygiagreti x ašiai.

Tiesios linijos atkarpose lygtis

Tegul tiesė kerta Ox ašį taške M 1 (a; 0), o Oy ašį - taške M 2 (0; b). Lygtis bus tokia:
tie.
. Ši lygtis vadinama tiesės lygtis atkarpose, nes skaičiai a ir b rodo, kuriuos atkarpas tiesia linija nukerta koordinačių ašyse.

Tiesės, einančios per tam tikrą tašką, statmeną tam tikram vektoriui, lygtis

Raskite tiesės, einančios pro ją, lygtį duotas taškas Mo (x O; y o) yra statmenas duotam nuliniam vektoriui n = (A; B).

Paimkite savavališką tiesės tašką M(x; y) ir apsvarstykite vektorių M 0 M (x - x 0; y - y o) (žr. 1 pav.). Kadangi vektoriai n ir M o M yra statmeni, jų skaliarinė sandauga yra lygi nuliui: tai yra,

A(x – xo) + B(y – yo) = 0. (10.8)

Lygtis (10.8) vadinama einančios tiesės lygtis duotas taškas statmenai duotam vektoriui .

Vektorius n = (A; B), statmenas tiesei, vadinamas normaliuoju šios linijos normalusis vektorius .

Lygtį (10.8) galima perrašyti kaip Ah + Wu + C = 0 , (10.9)

kur A ir B yra normaliojo vektoriaus koordinatės, C \u003d -Ax o - Vu o - laisvasis narys. Lygtis (10.9) yra bendroji tiesės lygtis(žr. 2 pav.).

1 pav.2 pav

Kanoninės tiesės lygtys

Kur
yra taško, per kurį eina linija, koordinatės ir
- krypties vektorius.

Antros eilės apskritimo kreivės

Apskritimas yra visų plokštumos taškų, nutolusių vienodu atstumu nuo nurodyto taško, vadinamo centru, rinkinys.

Kanoninė spindulio apskritimo lygtis R sutelktas į tašką
:

Visų pirma, jei statymo centras sutampa su kilme, lygtis atrodys taip:

Elipsė

Elipsė yra plokštumos taškų rinkinys, atstumų nuo kiekvieno iš jų iki dviejų nurodytų taškų suma ir , kurie vadinami židiniais, yra pastovi reikšmė
, didesnis nei atstumas tarp židinių
.

Elipsės, kurios židiniai yra ant Jaučio ašies ir kurios pradžia yra viduryje tarp židinių, kanoninė lygtis turi formą
G de a didžiosios pusašios ilgis; b yra mažosios pusašios ilgis (2 pav.).

Pamoka iš serijos „Geometriniai algoritmai“

Sveiki, mielas skaitytojau!

Šiandien pradėsime mokytis su geometrija susijusių algoritmų. Faktas yra tai, kad kompiuterių moksle yra gana daug olimpiadų uždavinių, susijusių su skaičiavimo geometrija, ir tokių problemų sprendimas dažnai sukelia sunkumų.

Keliose pamokose apsvarstysime keletą elementarių subproblemų, kuriais grindžiamas daugumos skaičiavimo geometrijos uždavinių sprendimas.

Šioje pamokoje parašysime programą, skirtą tiesios lygties radimas einantis per duotą du taškai. Norint išspręsti geometrines problemas, mums reikia tam tikrų skaičiavimo geometrijos žinių. Dalį pamokos skirsime jų pažinimui.

Informacija iš skaičiavimo geometrijos

Skaičiavimo geometrija – kompiuterių mokslo šaka, tirianti geometrinių uždavinių sprendimo algoritmus.

Pradiniai tokių problemų duomenys gali būti taškų rinkinys plokštumoje, atkarpų rinkinys, daugiakampis (pateiktas, pavyzdžiui, jo viršūnių sąrašu pagal laikrodžio rodyklę) ir kt.

Rezultatas gali būti atsakymas į kokį nors klausimą (pvz., ar taškas priklauso atkarpai, ar du atkarpos susikerta, ...), arba koks nors geometrinis objektas (pavyzdžiui, mažiausias išgaubtas daugiakampis, jungiantis duotus taškus, plotas daugiakampis ir pan.).

Skaičiavimo geometrijos uždavinius nagrinėsime tik plokštumoje ir tik Dekarto koordinačių sistemoje.

Vektoriai ir koordinatės

Norint taikyti skaičiavimo geometrijos metodus, reikia geometrinius vaizdus išversti į skaičių kalbą. Darysime prielaidą, kad plokštumoje pateikta Dekarto koordinačių sistema, kurioje sukimosi kryptis prieš laikrodžio rodyklę vadinama teigiama.

Dabar geometriniai objektai gauna analitinę išraišką. Taigi, norint nustatyti tašką, pakanka nurodyti jo koordinates: skaičių porą (x; y). Atkarpą galima nurodyti nurodant jo galų koordinates, tiesę – nurodant jos taškų poros koordinates.

Tačiau pagrindinis problemų sprendimo įrankis bus vektoriai. Todėl leiskite jums priminti tam tikrą informaciją apie juos.

Skyrius AB, kuris turi prasmę A laikoma pradžia (taikymo tašku) ir tašku V- galas vadinamas vektoriumi AB ir žymi arba , arba paryškintą mažosios raidės, Pavyzdžiui a .

Norėdami pažymėti vektoriaus ilgį (tai yra atitinkamo segmento ilgį), naudosime modulio simbolį (pavyzdžiui, ).

Savavališkas vektorius turės koordinates, lygias skirtumui tarp atitinkamų jo pabaigos ir pradžios koordinačių:

taškai čia A ir B turėti koordinates atitinkamai.

Skaičiavimams naudosime sąvoką orientuotas kampas, tai yra kampas, kuriame atsižvelgiama į santykinę vektorių padėtį.

Orientuotas kampas tarp vektorių a ir b teigiamas, jei sukimas yra toli nuo vektoriaus a į vektorių b daroma teigiama kryptimi (prieš laikrodžio rodyklę), o neigiama kitu atveju. Žr. 1a pav., 1b pav. Taip pat sakoma, kad vektorių pora a ir b teigiamai (neigiamai) orientuotas.

Taigi, orientuoto kampo reikšmė priklauso nuo vektorių surašymo tvarkos ir gali įgauti reikšmes intervale .

Daugelis skaičiavimo geometrijos uždavinių naudoja vektorinių (kreipinių arba pseudoskaliarinių) vektorių sandaugų sąvoką.

Vektorių a ir b vektorinė sandauga yra šių vektorių ilgių ir kampo tarp jų sinuso sandauga:

Vektorių sandauga koordinatėse:

Dešinėje esanti išraiška yra antros eilės determinantas:

Skirtingai nuo apibrėžimo, pateikto analitinėje geometrijoje, tai yra skaliarinis.

Kryžminės sandaugos ženklas nustato vektorių padėtį vienas kito atžvilgiu:

a ir b pozityviai orientuotas.

Jei reikšmė yra , tada vektorių pora a ir b neigiamai orientuotas.

Nulinių vektorių kryžminė sandauga yra lygi nuliui tada ir tik tada, kai jie yra kolineariniai ( ). Tai reiškia, kad jie yra toje pačioje linijoje arba lygiagrečiose linijose.

Panagrinėkime keletą paprastų užduočių, reikalingų sudėtingesnėms išspręsti.

Apibrėžkime tiesės lygtį dviejų taškų koordinatėmis.

Tiesės, einančios per du skirtingus taškus, lygtis, nurodyta jų koordinatėmis.

Tegu tiesėje pateikti du nesutampantys taškai: su koordinatėmis (x1;y1) ir su koordinatėmis (x2; y2). Atitinkamai, vektorius, kurio pradžia taške ir pabaiga taške, turi koordinates (x2-x1, y2-y1). Jei P(x, y) yra savavališkas taškas mūsų tiesėje, tai vektoriaus koordinatės yra (x-x1, y - y1).

Kryžminės sandaugos pagalba vektorių kolineariškumo sąlygą galima parašyti taip:

Tie. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0

(y2-y1)x + (x1-x2)y + x1 (y1-y2) + y1 (x2-x1) = 0

Paskutinę lygtį perrašome taip:

ax + by + c = 0, (1)

c = x1(y1-y2) + y1(x2-x1)

Taigi, tiesią liniją galima pateikti pagal (1) formos lygtį.

Užduotis 1. Pateikiamos dviejų taškų koordinatės. Raskite jo atvaizdavimą forma ax + by + c = 0.

Šioje pamokoje susipažinome su tam tikra informacija iš skaičiavimo geometrijos. Išsprendėme tiesės lygties radimo pagal dviejų taškų koordinates uždavinį.

Kitoje pamokoje parašysime programą, kaip rasti dviejų tiesių, pateiktų mūsų lygtimis, susikirtimo tašką.

Šis straipsnis tęsia tiesės lygties plokštumoje temą: apsvarstykite tokio tipo lygtį kaip bendrą tiesės lygtį. Apibrėžkime teoremą ir pateikime jos įrodymą; Išsiaiškinkime, kas yra neišsami bendroji tiesės lygtis ir kaip atlikti perėjimus iš bendrosios lygties į kitų tipų tiesės lygtis. Visą teoriją įtvirtinsime iliustracijomis ir spręsdami praktines problemas.

Yandex.RTB R-A-339285-1

Tegu plokštumoje pateikta stačiakampė koordinačių sistema O x y.

1 teorema

Bet kuri pirmojo laipsnio lygtis, turinti formą A x + B y + C \u003d 0, kur A, B, C yra kai kurie realieji skaičiai (A ir B tuo pačiu metu nėra lygūs nuliui), apibrėžia tiesę stačiakampė koordinačių sistema plokštumoje. Savo ruožtu bet kuri tiesė stačiakampėje koordinačių sistemoje plokštumoje yra nustatoma pagal lygtį, kurios forma yra A x + B y + C = 0 tam tikram reikšmių rinkiniui A, B, C.

Įrodymas

Ši teorema susideda iš dviejų punktų, kiekvieną iš jų įrodysime.

Įrodykime, kad lygtis A x + B y + C = 0 apibrėžia tiesę plokštumoje.

Tebūnie koks nors taškas M 0 (x 0, y 0), kurio koordinatės atitinka lygtį A x + B y + C = 0. Taigi: A x 0 + B y 0 + C = 0 . Iš kairės ir dešinės lygčių A x + B y + C \u003d 0 atimkite lygties A x 0 + B y 0 + C \u003d 0 kairę ir dešinę puses, gausime naują lygtį, kuri atrodo kaip A (x - x 0) + B (y - y 0) = 0 . Jis lygus A x + B y + C = 0 .

Gauta lygtis A (x - x 0) + B (y - y 0) = 0 yra būtina ir pakankama vektorių n → = (A, B) ir M 0 M → = (x - x) statmenumo sąlyga. 0, y - y 0) . Taigi taškų aibė M (x, y) stačiakampėje koordinačių sistemoje apibrėžia tiesę, statmeną vektoriaus n → = (A, B) krypčiai. Galime manyti, kad taip nėra, bet tada vektoriai n → = (A, B) ir M 0 M → = (x - x 0, y - y 0) nebūtų statmeni, o lygybė A (x - x 0 ) + B (y - y 0) = 0 nebūtų teisinga.

Todėl lygtis A (x - x 0) + B (y - y 0) \u003d 0 apibrėžia tam tikrą tiesę stačiakampėje koordinačių sistemoje plokštumoje, todėl lygiavertė lygtis A x + B y + C \u003d 0 apibrėžia tą pačią liniją. Taigi mes įrodėme pirmąją teoremos dalį.

Įrodykime, kad bet kurią tiesę stačiakampėje koordinačių sistemoje plokštumoje galima pateikti pirmojo laipsnio lygtimi A x + B y + C = 0 .

Stačiakampėje koordinačių sistemoje plokštumoje nustatykime tiesę a; taškas M 0 (x 0 , y 0), per kurį eina ši tiesė, taip pat šios tiesės normalusis vektorius n → = (A , B) .

Tegu taip pat egzistuoja tam tikras taškas M (x , y) – tiesės slankusis taškas. Šiuo atveju vektoriai n → = (A , B) ir M 0 M → = (x - x 0 , y - y 0) yra statmeni vienas kitam, o jų skaliarinė sandauga lygi nuliui:

n → , M 0 M → = A (x - x 0) + B (y - y 0) = 0

Perrašykime lygtį A x + B y - A x 0 - B y 0 = 0 , apibrėžkime C: C = - A x 0 - B y 0 ir galiausiai gaukime lygtį A x + B y + C = 0 .

Taigi, mes įrodėme antrąją teoremos dalį ir įrodėme visą teoremą kaip visumą.

1 apibrėžimas

Lygtis, kuri atrodo kaip A x + B y + C = 0 - tai bendroji tiesės lygtis stačiakampės koordinačių sistemos plokštumojeO x y .

Remdamiesi įrodyta teorema, galime daryti išvadą, kad tiesė, duota plokštumoje fiksuotoje stačiakampėje koordinačių sistemoje, ir jos bendroji lygtis yra neatsiejamai susijusios. Kitaip tariant, pradinė eilutė atitinka jos bendrąją lygtį; bendroji tiesės lygtis atitinka duotąją tiesę.

Iš teoremos įrodymo taip pat išplaukia, kad kintamųjų x ir y koeficientai A ir B yra tiesės normaliojo vektoriaus koordinatės, kurią pateikia bendroji tiesės lygtis A x + B y + C = 0.

Apsvarstykite konkretus pavyzdys bendroji tiesės lygtis.

Tegu yra lygtis 2 x + 3 y - 2 = 0, kuri atitinka tiesę duotoje stačiakampėje koordinačių sistemoje. Normalus šios linijos vektorius yra vektorius n → = (2 , 3) . Brėžinyje nubrėžkite nurodytą tiesią liniją.

Taip pat galima ginčytis: tiesė, kurią matome brėžinyje, yra nulemta bendrosios lygties 2 x + 3 y - 2 = 0, nes visų duotosios tiesės taškų koordinatės atitinka šią lygtį.

Lygtį λ · A x + λ · B y + λ · C = 0 galime gauti padauginę abi bendrosios tiesės lygties puses iš nulinio skaičiaus λ. Gauta lygtis yra lygiavertė pradinei bendrajai lygčiai, todėl ji aprašys tą pačią tiesę plokštumoje.

2 apibrėžimas

Pilna bendroji tiesės lygtis- tokia bendroji eilutės A x + B y + C \u003d 0 lygtis, kurioje skaičiai A, B, C nėra lygūs nuliui. Priešingu atveju lygtis yra Nebaigtas.

Išanalizuokime visus nepilnos bendrosios tiesės lygties variantus.

Kai A \u003d 0, B ≠ 0, C ≠ 0, bendroji lygtis tampa B y + C \u003d 0. Tokia nepilna bendroji lygtis apibrėžia tiesę stačiakampėje koordinačių sistemoje O x y, kuri yra lygiagreti O x ašiai, nes bet kuriai realiajai x vertei kintamasis y įgis reikšmę. - C B. Kitaip tariant, bendroji tiesės A x + B y + C \u003d 0 lygtis, kai A \u003d 0, B ≠ 0, apibrėžia taškų (x, y), kurių koordinatės yra lygios tam pačiam skaičiui, vietą. - C B.
Jei A \u003d 0, B ≠ 0, C \u003d 0, bendroji lygtis tampa y \u003d 0. Tokia nepilna lygtis apibrėžia x ašies O x .
Kai A ≠ 0, B \u003d 0, C ≠ 0, gauname neišsamią bendrąją lygtį A x + C \u003d 0, apibrėžiančią tiesę, lygiagrečią y ašiai.
Tegul A ≠ 0, B \u003d 0, C \u003d 0, tada nepilna bendroji lygtis bus x \u003d 0, ir tai yra koordinačių linijos O y lygtis.
Galiausiai, kai A ≠ 0, B ≠ 0, C \u003d 0, nepilna bendroji lygtis įgauna formą A x + B y \u003d 0. Ir ši lygtis apibūdina tiesią liniją, kuri eina per pradžią. Iš tiesų skaičių pora (0 , 0) atitinka lygybę A x + B y = 0 , nes A · 0 + B · 0 = 0 .

Grafiškai pavaizduokime visus aukščiau išvardintus nepilnos bendrosios tiesės lygties tipus.

1 pavyzdys

Yra žinoma, kad duotoji tiesė yra lygiagreti y ašiai ir eina per tašką 2 7 , - 11 . Būtina užrašyti bendrąją duotosios tiesės lygtį.

Sprendimas

Tiesi linija, lygiagreti y ašiai, pateikiama A x + C \u003d 0 formos lygtimi, kurioje A ≠ 0. Sąlyga taip pat nurodo taško, per kurį eina tiesė, koordinates, o šio taško koordinatės atitinka nepilnos bendrosios lygties A x + C = 0 sąlygas, t.y. lygybė teisinga:

A 2 7 + C = 0

Iš jo galima nustatyti C, suteikiant A kokią nors nulinę reikšmę, pavyzdžiui, A = 7 . Šiuo atveju gauname: 7 2 7 + C \u003d 0 ⇔ C \u003d - 2. Žinome abu koeficientus A ir C, pakeisime juos lygtimi A x + C = 0 ir gauname reikiamą tiesės lygtį: 7 x - 2 = 0

Atsakymas: 7 x - 2 = 0

2 pavyzdys

Brėžinyje pavaizduota tiesė, būtina užrašyti jos lygtį.

Sprendimas

Pateiktas brėžinys leidžia lengvai paimti pradinius duomenis problemai išspręsti. Brėžinyje matome, kad duota linija yra lygiagreti O x ašiai ir eina per tašką (0 , 3).

Tiesi linija, kuri yra lygiagreti abscisei, nustatoma pagal nepilną bendrąją lygtį B y + С = 0. Raskite B ir C reikšmes. Taško (0, 3) koordinatės, kadangi per jį eina duota tiesė, tenkins tiesės B y + С = 0 lygtį, tada galioja lygybė: В · 3 + С = 0. Nustatykime B vertę, kuri skiriasi nuo nulio. Tarkime, B \u003d 1, šiuo atveju iš lygybės B · 3 + C \u003d 0 galime rasti C: C \u003d - 3. Mes naudojame žinomos vertės B ir C, gauname reikiamą tiesės lygtį: y - 3 = 0.

Atsakymas: y-3 = 0.

Bendroji tiesės, einančios per tam tikrą plokštumos tašką, lygtis

Tegu duotoji tiesė eina per tašką M 0 (x 0, y 0), tada jos koordinatės atitinka bendrąją tiesės lygtį, t.y. lygybė teisinga: A x 0 + B y 0 + C = 0 . Atimkite kairę ir dešinę šios lygties puses iš kairės ir dešinės bendrosios pusės pilna lygtis tiesiai. Gauname: A (x - x 0) + B (y - y 0) + C \u003d 0, ši lygtis yra lygiavertė pradinei bendrajai, eina per tašką M 0 (x 0, y 0) ir turi normalusis vektorius n → \u003d (A, B) .

Gautas rezultatas leidžia parašyti bendrąją tiesės lygtį žinomoms normalaus tiesės vektoriaus koordinatėms ir tam tikro šios tiesės taško koordinatėms.

3 pavyzdys

Duotas taškas M 0 (- 3, 4), per kurį eina tiesė, ir šios tiesės normalusis vektorius n → = (1 , - 2) . Būtina užrašyti duotosios tiesės lygtį.

Sprendimas

Pradinės sąlygos leidžia gauti reikiamus duomenis lygčiai sudaryti: A \u003d 1, B \u003d - 2, x 0 \u003d - 3, y 0 \u003d 4. Tada:

A (x - x 0) + B (y - y 0) = 0 ⇔ 1 (x - (- 3)) - 2 y (y - 4) = 0 ⇔ ⇔ x - 2 y + 22 = 0

Problema galėjo būti išspręsta kitaip. Bendroji tiesės lygtis yra tokia: A x + B y + C = 0 . Pateiktas normalus vektorius leidžia gauti koeficientų A ir B reikšmes, tada:

A x + B y + C = 0 ⇔ 1 x - 2 y + C = 0 ⇔ x - 2 y + C = 0

Dabar suraskime C reikšmę, naudodami tašką M 0 (- 3, 4), pateiktą uždavinio sąlygos, per kurią eina tiesė. Šio taško koordinatės atitinka lygtį x - 2 · y + C = 0 , t.y. - 3 - 2 4 + C \u003d 0. Taigi C = 11. Reikalinga tiesės lygtis yra tokia: x - 2 · y + 11 = 0 .

Atsakymas: x - 2 y + 11 = 0 .

4 pavyzdys

Duota tiesė 2 3 x - y - 1 2 = 0 ir taškas M 0, esantis šioje tiesėje. Žinoma tik šio taško abscisė ir ji lygi – 3. Būtina nustatyti duoto taško ordinates.

Sprendimas

Taško M 0 koordinačių žymėjimą nustatykime kaip x 0 ir y 0 . Pradiniai duomenys rodo, kad x 0 \u003d - 3. Kadangi taškas priklauso duotai tiesei, tai jo koordinatės atitinka bendrąją šios tiesės lygtį. Tada bus teisinga tokia lygybė:

2 3 x 0 – y 0 – 1 2 = 0

Apibrėžkite y 0: 2 3 (- 3) - y 0 - 1 2 = 0 ⇔ - 5 2 - y 0 = 0 ⇔ y 0 = - 5 2

Atsakymas: - 5 2

Perėjimas iš bendrosios tiesės lygties į kitų tipų tiesės lygtis ir atvirkščiai

Kaip žinome, yra keli tos pačios tiesės plokštumoje lygčių tipai. Lygties tipo pasirinkimas priklauso nuo uždavinio sąlygų; galima pasirinkti jo sprendimui patogesnį. Čia labai praverčia įgūdžiai konvertuoti vienos rūšies lygtį į kitos rūšies lygtį.

Pirmiausia apsvarstykite perėjimą nuo bendrosios A x + B y + C = 0 lygties į kanoninę lygtį x - x 1 a x = y - y 1 a y .

Jei A ≠ 0, tai terminą B y perkeliame į dešinę bendrosios lygties pusę. Kairėje pusėje iš skliaustų išimame A. Dėl to gauname: A x + C A = - B y .

Šią lygybę galima užrašyti kaip proporciją: x + C A - B = y A .

Jei B ≠ 0, kairėje bendrosios lygties pusėje paliekame tik terminą A x, kitus perkeliame į dešinę, gauname: A x \u003d - B y - C. Iš skliaustų išimame - B, tada: A x \u003d - B y + C B.

Perrašykime lygybę kaip proporciją: x - B = y + C B A .

Žinoma, nereikia įsiminti gautų formulių. Pakanka žinoti veiksmų algoritmą pereinant nuo bendrosios lygties prie kanoninės.

5 pavyzdys

Pateikta bendroji tiesės 3 lygtis y - 4 = 0. Ją reikia konvertuoti į kanoninę lygtį.

Sprendimas

Pradinę lygtį užrašome kaip 3 y - 4 = 0 . Toliau veikiame pagal algoritmą: terminas 0 x lieka kairėje pusėje; ir dešinėje pusėje išimame - 3 iš skliaustų; gauname: 0 x = - 3 y - 4 3 .

Gautą lygybę parašykime proporcija: x - 3 = y - 4 3 0 . Taigi, mes gavome kanoninės formos lygtį.

Atsakymas: x - 3 = y - 4 3 0.

Norint paversti bendrąją tiesės lygtį į parametrines, pirmiausia pereinama prie kanoninės formos, o po to pereinama iš kanoninė lygtis tiesiogiai į parametrines lygtis.

6 pavyzdys

Tiesi linija pateikiama lygtimi 2 x - 5 y - 1 = 0 . Užrašykite šios tiesės parametrines lygtis.

Sprendimas

Pereikime nuo bendrosios lygties prie kanoninės:

2 x - 5 y - 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

Dabar paimkime abi gautos kanoninės lygties dalis, lygias λ, tada:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 λ y = - 1 5 + 2 λ , λ ∈ R

Atsakymas:x = 5 λ y = - 1 5 + 2 λ , λ ∈ R

Bendrąją lygtį galima konvertuoti į tiesią lygtį, kurios nuolydis y = k x + b, bet tik tada, kai B ≠ 0. Perėjimui kairėje pusėje paliekame terminą B y , likusieji perkeliami į dešinę. Gauname: B y = - A x - C . Abi gautos lygybės dalis padalinkime iš B , kuri skiriasi nuo nulio: y = - A B x - C B .

7 pavyzdys

Pateikiama bendroji tiesės lygtis: 2 x + 7 y = 0 . Turite konvertuoti šią lygtį į nuolydžio lygtį.

Sprendimas

Gaminkime būtini veiksmai pagal algoritmą:

2 x + 7 y = 0 ⇔ 7 y - 2 x ⇔ y = - 2 7 x

Atsakymas: y = - 2 7 x .

Iš bendrosios tiesės lygties pakanka tiesiog gauti lygtį x a + y b \u003d 1 formos segmentuose. Norėdami atlikti tokį perėjimą, skaičių C perkeliame į dešinę lygybės pusę, abi gautos lygybės dalis padaliname iš - С ir galiausiai perkeliame kintamųjų x ir y koeficientus į vardiklius:

A x + B y + C = 0 ⇔ A x + B y = - C ⇔ ⇔ A - C x + B - C y = 1 ⇔ x - C A + y - C B = 1

8 pavyzdys

Reikia paversti bendrąją tiesės x - 7 y + 1 2 = 0 lygtį į tiesės lygtį atkarpomis.

Sprendimas

Perkelkime 1 2 į dešinę pusę: x - 7 y + 1 2 = 0 ⇔ x - 7 y = - 1 2 .

Padalinkite iš -1/2 abiejų lygties pusių: x - 7 y = - 1 2 ⇔ 1 - 1 2 x - 7 - 1 2 y = 1 .

Atsakymas: x - 1 2 + y 1 14 = 1 .

Apskritai atvirkštinis perėjimas taip pat yra lengvas: nuo kitų tipų lygčių prie bendrosios.

Tiesios linijos lygtis atkarpomis ir lygtis su nuolydžiu gali būti lengvai konvertuojama į bendrą, tiesiog surinkus visus terminus kairėje lygties pusėje:

x a + y b ⇔ 1 a x + 1 b y - 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y - k x - b = 0 ⇔ A x + B y + C = 0

Kanoninė lygtis konvertuojama į bendrąją pagal šią schemą:

x - x 1 ax = y - y 1 ay ⇔ ay (x - x 1) = ax (y - y 1) ⇔ ⇔ ayx - axy - ayx 1 + axy 1 = 0 ⇔ A x + B y + C = 0

Norėdami pereiti nuo parametrinio, pirmiausia pereinama prie kanoninio, o tada prie bendro:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x - x 1 a x = y - y 1 a y ⇔ A x + B y + C = 0

9 pavyzdys

Pateikiamos tiesės x = - 1 + 2 · λ y = 4 parametrinės lygtys. Būtina užrašyti bendrąją šios tiesės lygtį.

Sprendimas

Pereikime nuo parametrinių lygčių prie kanoninių:

x = - 1 + 2 λ y = 4 ⇔ x = - 1 + 2 λ y = 4 + 0 λ ⇔ λ = x + 1 2 λ = y - 4 0 ⇔ x + 1 2 = y - 4 0

Pereikime nuo kanoninio prie bendro:

x + 1 2 = y - 4 0 ⇔ 0 (x + 1) = 2 (y - 4) ⇔ y - 4 = 0

Atsakymas: y – 4 = 0

10 pavyzdys

Pateikta tiesės lygtis atkarpose x 3 + y 1 2 = 1. Būtina pereiti prie bendras vaizdas lygtys.

Sprendimas:

Tiesiog perrašykime lygtį reikiama forma:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y - 1 = 0

Atsakymas: 1 3 x + 2 y - 1 = 0 .

Bendrosios tiesės lygties sudarymas

Aukščiau sakėme, kad bendrąją lygtį galima parašyti žinomomis normalaus vektoriaus koordinatėmis ir taško, per kurį eina linija, koordinatėmis. Tokia tiesė apibrėžiama lygtimi A (x - x 0) + B (y - y 0) = 0 . Toje pačioje vietoje analizavome atitinkamą pavyzdį.

Dabar pažvelkime į daugiau sudėtingų pavyzdžių, kuriame pirmiausia reikia nustatyti normaliojo vektoriaus koordinates.

11 pavyzdys

Duota tiesė, lygiagreti tiesei 2 x - 3 y + 3 3 = 0 . Taip pat žinomas taškas M 0 (4 , 1), per kurį eina duotoji tiesė. Būtina užrašyti duotosios tiesės lygtį.

Sprendimas

Pradinės sąlygos mums sako, kad tiesės yra lygiagrečios, o kaip normalų tiesės, kurios lygtį reikia parašyti, vektorių, imame tiesės nukreipimo vektorių n → \u003d (2, - 3) : 2 x - 3 y + 3 3 \u003d 0. Dabar mes žinome visus reikalingus duomenis, kad sudarytume bendrą tiesės lygtį:

A (x - x 0) + B (y - y 0) = 0 ⇔ 2 (x - 4) - 3 (y - 1) = 0 ⇔ 2 x - 3 y - 5 = 0

Atsakymas: 2 x - 3 y - 5 = 0 .

12 pavyzdys

Duota tiesė eina per pradžią statmenai tiesei x - 2 3 = y + 4 5 . Būtina parašyti bendrąją duotosios tiesės lygtį.

Sprendimas

Duotos tiesės normalusis vektorius bus tiesės x - 2 3 = y + 4 5 krypties vektorius.

Tada n → = (3 , 5) . Tiesi linija eina per pradžią, t.y. per tašką O (0, 0) . Sudarykime bendrąją duotosios tiesės lygtį:

A (x - x 0) + B (y - y 0) = 0 ⇔ 3 (x - 0) + 5 (y - 0) = 0 ⇔ 3 x + 5 y = 0

Atsakymas: 3 x + 5 y = 0 .

Jei tekste pastebėjote klaidą, pažymėkite ją ir paspauskite Ctrl+Enter

Bendroji tiesės lygtis:

Konkretūs bendrosios tiesės lygties atvejai:

ir jeigu C= 0, (2) lygtis turės formą

Ax + Autorius = 0,

o šia lygtimi apibrėžta tiesė eina per pradžios tašką, nes pradžios koordinatės x = 0, y= 0 tenkina šią lygtį.

b) Jei yra bendroji lygtis tiesus (2) B= 0, tada lygtis įgauna formą

Ax + SU= 0 arba .

Lygtyje nėra kintamojo y, o šia lygtimi apibrėžta tiesė yra lygiagreti ašiai Oy.

c) Jei bendrojoje tiesės lygtyje (2) A= 0, tada ši lygtis įgauna formą

Autorius + SU= 0 arba ;

lygtyje nėra kintamojo x, o jo apibrėžta tiesė yra lygiagreti ašiai Jautis.

Reikėtų prisiminti: jei tiesė yra lygiagreti bet kuriai koordinačių ašiai, tada jos lygtyje nėra termino, kuriame būtų to paties pavadinimo koordinatė su šia ašimi.

d) Kada C= 0 ir A= 0 (2) lygtis įgauna formą Autorius= 0 arba y = 0.

Tai yra ašies lygtis Jautis.

e) Kada C= 0 ir B= 0 lygtis (2) gali būti įrašyta forma Ax= 0 arba x = 0.

Tai yra ašies lygtis Oy.

Abipusis tiesių išdėstymas plokštumoje. Kampas tarp linijų plokštumoje. Lygiagrečių linijų būklė. Linijų statmenumo sąlyga.

l 1 l 2 l 1: A 1 x + B 1 y + C 1 = 0
l 2: A 2 x + B 2 y + C 2 = 0

S 2 S 1 Vektoriai S 1 ir S 2 vadinami jų linijų kreiptuvais.

Kampas tarp tiesių l 1 ir l 2 nustatomas pagal kampą tarp krypties vektorių.
1 teorema: cos kampas tarp l 1 ir l 2 \u003d cos (l 1; l 2) \u003d

2 teorema: Kad 2 eilutės būtų lygios, būtina ir pakanka:

3 teorema: kad 2 linijos būtų statmenos, būtina ir pakanka:

L 1 l 2 – A 1 A 2 + B 1 B 2 = 0

Bendroji plokštumos lygtis ir jos specialieji atvejai. Plokštumos atkarpomis lygtis.

Bendroji plokštumos lygtis:

Ax + By + Cz + D = 0

Ypatingi atvejai:

1. D=0 Ax+By+Cz = 0 - plokštuma eina per pradžią

2. С=0 Ax+By+D = 0 – plokštuma || oz

3. В=0 Ax+Cz+d = 0 – plokštuma || OY

4. A=0 By+Cz+D = 0 – plokštuma || JAUTIS

5. A=0 ir D=0 By+Cz = 0 - plokštuma eina per OX

6. B=0 ir D=0 Ax+Cz = 0 - plokštuma eina per OY

7. C=0 ir D=0 Ax+By = 0 - plokštuma eina per OZ

Abipusis plokštumų ir tiesių išdėstymas erdvėje:

1. Kampas tarp tiesių erdvėje yra kampas tarp jų krypties vektorių.

Cos (l 1 ; l 2) = cos (S 1 ; S 2) = =

2. Kampas tarp plokštumų nustatomas per kampą tarp jų normaliųjų vektorių.

Cos (l 1 ; l 2) = cos (N 1 ; N 2) = =

3. Kampo tarp tiesės ir plokštumos kosinusą galima rasti per kampo tarp tiesės krypties vektoriaus ir plokštumos normaliojo vektoriaus sin.

4. 2 eilutės || erdvėje, kai jų || vektoriniai vadovai

5. 2 lėktuvai || kada || normalūs vektoriai

6. Panašiai įvedamos tiesių ir plokštumų statmenumo sąvokos.

Klausimas #14

Skirtingos rūšys tiesės lygtis plokštumoje (tiesės lygtis atkarpose, su nuolydžiu ir kt.)

Tiesios linijos atkarpomis lygtis:
Tarkime, kad bendrojoje tiesės lygtyje:

1. C \u003d 0 Ah + Wu \u003d 0 - tiesi linija eina per pradžią.

2. a \u003d 0 Wu + C \u003d 0 y \u003d

3. in \u003d 0 Ax + C \u003d 0 x \u003d

4. v \u003d C \u003d 0 Ax \u003d 0 x \u003d 0

5. a \u003d C \u003d 0 Wu \u003d 0 y \u003d 0

Tiesios linijos su nuolydžiu lygtis:

Bet kuri tiesi linija, kuri nėra lygi y ašiai (B ne = 0), gali būti parašyta toliau. forma:

k = tgα α yra kampas tarp tiesės ir teigiamai nukreiptos linijos ОХ

b - tiesės susikirtimo taškas su OS ašimi

Doc-in:

Ax+By+C = 0

Wu \u003d -Ax-C |: B

Dviejų taškų tiesės lygtis:

16 klausimas

Baigtinė funkcijos riba taške ir x→∞

Pabaigos riba taške x 0:

Skaičius A vadinamas funkcijos y \u003d f (x) riba, kai x → x 0, jei bet kurio E > 0 atveju yra b > 0, kad esant x ≠ x 0, tenkinama nelygybė |x - x 0 |< б, выполняется условие |f(x) - A| < Е

Riba žymima: = A

Pabaigos riba taške +∞:

Skaičius A vadinamas funkcijos y = f(x) riba x → + ∞ , jei bet kuriam E > 0 egzistuoja C > 0, kad x > C nelygybė |f(x) - A|< Е

Riba žymima: = A

Pabaigos riba taške -∞:

Skaičius A vadinamas funkcijos y = f(x) for riba x→-∞, jei dėl kokių nors E< 0 существует С < 0 такое, что при х < -С выполняется неравенство |f(x) - A| < Е