Тейлорын цуврал, квадрат язгуур. Эрчим хүчний цуваа, тэдгээрийн нэгдэл, чадлын цуваа дахь функцүүдийн өргөтгөл

Дээд математикийн оюутнууд бидэнд өгөгдсөн цувааг нэгтгэх интервалд хамаарах тодорхой чадлын цувааны нийлбэр нь тасралтгүй, хязгааргүй олон удаа дифференциаллагдсан функц гэдгийг мэдэх ёстой. Асуулт гарч ирнэ: өгөгдсөн дурын функц f (x) нь тодорхой чадлын цувралын нийлбэр гэж батлах боломжтой юу? Өөрөөр хэлбэл, ямар нөхцөлд f-ija f (x) хүчийг хүчний цуваагаар төлөөлж болох вэ? Ийм асуултын ач холбогдол нь f-yu f (x) -ийг хүчний цувааны эхний хэдэн гишүүний нийлбэрээр, өөрөөр хэлбэл олон гишүүнтээр орлуулах боломжтой байдагт оршино. Функцийг нэлээд энгийн илэрхийлэл буюу олон гишүүнтээр солих нь зарим асуудлыг шийдвэрлэхэд тохиромжтой, тухайлбал: интегралыг шийдвэрлэх, тооцоолох гэх мэт.

Зарим fu ба f (x)-ийн хувьд (n + 1)-р дараалал хүртэлх деривативыг, түүний дотор сүүлчийнх нь хөрш (α - R; x 0 + R) -ийг тооцоолох боломжтой болох нь батлагдсан. зарим цэг x = α энэ нь зөв томъёо юм:

Энэ томъёог нэрт эрдэмтэн Брук Тэйлорын нэрээр нэрлэсэн. Өмнөх цувралаас олж авсан цувралыг Маклаурин цуврал гэж нэрлэдэг.

Маклаурин цувралд өргөтгөл хийх боломжтой болгодог дүрэм:

1. Нэгдүгээр, хоёр дахь, гурав дахь ... эрэмбийн деривативуудыг тодорхойл.
2. x = 0 дээрх деривативууд хэдтэй тэнцүү болохыг тооцоол.
3. Энэ функцийн Маклаурины цувралыг бичээд дараа нь түүний нийлэх интервалыг тодорхойл.
4. Маклаурины томъёоны үлдэгдэл хэсгийг (-R; R) тодорхойлно

R n (x) -> 0 гэж n -> хязгааргүй. Хэрэв ийм байгаа бол f (x) функц нь Маклаурины цувралын нийлбэртэй давхцах ёстой.

Одоо бие даасан функцүүдийн хувьд Маклаурин цувралыг авч үзье.

1. Тэгэхээр эхнийх нь f (x) = e x болно. Мэдээжийн хэрэг, онцлог шинжээрээ ийм функц нь янз бүрийн эрэмбийн деривативтай ба f (k) (x) = e x, k нь бүгд тэнцүү байна. x = 0-ийг орлуулна. Бид f (k) (0) = e 0 = 1, k = 1,2-ийг авна ... Дээр дурдсан зүйлс дээр үндэслэн e x мөр дараах байдлаар харагдах болно.

2. f (x) = sin x функцийн Маклаурины цуваа. Бүх үл мэдэгдэх f-s нь f "(x) = cos x = sin (x + n / 2), f" "(x) = -sin x = sin (x + 2) -аас гадна деривативтай байх болно гэдгийг нэн даруй тодруулцгаая. * n / 2) ..., f (k) (x) = sin (x + k * n / 2), энд k нь ямар ч натурал тоотой тэнцүү байна. Өөрөөр хэлбэл, энгийн тооцооллыг хийсний дараа бид хүрч болно. f (x) = sin x цуврал нь дараах хэлбэртэй байна гэсэн дүгнэлт:

3. Одоо f-yu f (x) = cos x гэж үзэхийг оролдъё. Бүх үл мэдэгдэхийн хувьд энэ нь дурын дарааллын деривативтай ба | f (k) (x) | = | cos (x + k * n / 2) |<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

Тиймээс, бид Маклаурины цуврал болгон өргөжүүлж болох хамгийн чухал функцуудыг жагсаасан боловч зарим функцийг Тэйлорын цувралаар дүүргэсэн болно. Одоо бид тэдгээрийг бас жагсаах болно. Тейлор ба Маклаурин цувралууд нь дээд математикийн цувралыг шийдвэрлэх семинарын чухал хэсэг гэдгийг тэмдэглэх нь зүйтэй. Тиймээс, Тейлор жагсаж байна.

1. Эхнийх нь f-ii f (x) = ln (1 + x) -ийн цуваа байх болно. Өмнөх жишээнүүдийн нэгэн адил өгөгдсөн f (x) = ln (1 + x) хувьд бид Маклаурин цувралын ерөнхий хэлбэрийг ашиглан цуваа нэмж болно. Гэсэн хэдий ч, Маклаурины цувралыг энэ функцэд илүү хялбараар авч болно. Тодорхой геометрийн цувралыг нэгтгэсний дараа бид ийм түүврийн f (x) = ln (1 + x) цувралыг авна.

2. Мөн бидний өгүүлэлд эцсийн байх хоёр дахь нь f (x) = arctan x-ийн цуврал байх болно. [-1; 1] интервалд хамаарах x-ийн хувьд задрал хүчинтэй байна:

Тэгээд л болоо. Энэ нийтлэлд дээд математик, ялангуяа эдийн засаг, техникийн их сургуулиудад хамгийн их хэрэглэгддэг Тейлор, Маклаурин цувралуудыг авч үзсэн.

Вэбсайтад математикийн томъёог хэрхэн оруулах вэ?

Хэрэв та хэзээ нэгэн цагт вэб хуудсанд нэг эсвэл хоёр математикийн томьёо нэмэх шаардлагатай бол үүнийг хийх хамгийн хялбар арга бол нийтлэлд тайлбарласны дагуу: математикийн томьёог Вольфрам Альфа автоматаар үүсгэсэн зураг хэлбэрээр сайтад хялбархан оруулдаг. Энгийн байдлаас гадна энэхүү олон талын арга нь хайлтын системд таны сайтын харагдах байдлыг сайжруулахад тусална. Энэ нь удаан хугацаанд ажиллаж байгаа (мөн үүрд ажиллах болно гэж бодож байна), гэхдээ энэ нь ёс суртахууны хувьд хоцрогдсон.

Хэрэв та өөрийн сайт дээр математикийн томъёог тогтмол ашигладаг бол MathML, LaTeX эсвэл ASCIIMathML тэмдэглэгээг ашиглан вэб хөтчүүдэд математикийн тэмдэглэгээг харуулдаг тусгай JavaScript номын сан болох MathJax-г ашиглахыг зөвлөж байна.

MathJax-г ашиглаж эхлэх хоёр арга бий: (1) энгийн код ашиглан та MathJax скриптийг өөрийн сайт руу хурдан холбох боломжтой бөгөөд энэ нь зөв цагт алсын серверээс автоматаар ачаалагдах болно (серверийн жагсаалт); (2) MathJax скриптийг алсын серверээс сервертээ байршуулж, сайтынхаа бүх хуудсанд холбоно уу. Хоёрдахь арга нь илүү төвөгтэй бөгөөд цаг хугацаа их шаарддаг бөгөөд таны сайтын хуудсуудын ачааллыг хурдасгах бөгөөд хэрэв эх MathJax сервер ямар нэг шалтгаанаар түр ажиллахгүй бол энэ нь таны сайтад ямар ч байдлаар нөлөөлөхгүй. Эдгээр давуу талуудыг үл харгалзан би илүү хялбар, хурдан бөгөөд техникийн ур чадвар шаарддаггүй тул эхний аргыг сонгосон. Миний жишээг дагаж, 5 минутын дараа та MathJax-ийн бүх боломжуудыг сайт дээрээ ашиглах боломжтой болно.

Та MathJax номын сангийн скриптийг үндсэн MathJax сайт эсвэл баримт бичгийн хуудаснаас авсан кодын хоёр хувилбарыг ашиглан алсын серверээс холбож болно.

Эдгээр кодын хувилбаруудын аль нэгийг хуулж аваад вэб хуудасныхаа код руу, шошгонуудын хооронд оруулах нь дээр. болонэсвэл шошгоны дараа ... Эхний хувилбарын дагуу MathJax илүү хурдан ачаалж, хуудсыг бага удаашруулдаг. Гэхдээ хоёр дахь сонголт нь MathJax-ийн хамгийн сүүлийн хувилбаруудыг автоматаар дагаж, ачаалдаг. Хэрэв та эхний кодыг оруулбал үүнийг үе үе шинэчлэх шаардлагатай болно. Хэрэв та хоёр дахь кодыг оруулбал хуудаснууд илүү удаан ачаалах боловч MathJax-ийн шинэчлэлтийг байнга хянах шаардлагагүй болно.

MathJax-г холбох хамгийн хялбар арга бол Blogger эсвэл WordPress дээр: өөрийн сайтын хяналтын самбарт гуравдагч этгээдийн JavaScript код оруулах зориулалттай виджет нэмж, дээр дурдсан ачаалах кодын эхний эсвэл хоёр дахь хувилбарыг хуулж, виджетийг дараах руу ойртуулна уу. загварын эхлэл (дашрамд хэлэхэд, MathJax скрипт асинхроноор ачаалагдсан тул энэ нь огт шаардлагагүй). Тэгээд л болоо. Одоо MathML, LaTeX, ASCIIMathML тэмдэглэгээний синтаксийг сурснаар та математикийн томьёог вэбсайтынхаа вэб хуудсанд оруулахад бэлэн боллоо.

Аливаа фрактал нь тодорхой дүрмийн дагуу баригдсан бөгөөд үүнийг хязгааргүй олон удаа тогтмол хэрэглэдэг. Ийм цаг бүрийг давталт гэж нэрлэдэг.

Менгер хөвөнг бүтээх давталтын алгоритм нь маш энгийн: 1-р талтай анхны шоо нь нүүртэйгээ параллель хавтгайгаар хуваагдаж, 27 тэнцүү шоо болж хуваагдана. Үүнээс нэг төв шоо болон зэргэлдээ 6 шоо хасагдана. Үр дүн нь үлдсэн 20 жижиг шооноос бүрдсэн багц юм. Эдгээр шоо тус бүртэй ижил зүйлийг хийснээр бид 400 жижиг шооноос бүрдсэн багцыг авна. Энэ үйл явцыг эцэс төгсгөлгүй үргэлжлүүлснээр бид Menger хөвөн авдаг.

Функциональ цувралуудын дунд хамгийн чухал байрыг цахилгаан цуваа эзэлдэг.

Цувралыг хүчирхэг цуврал гэж нэрлэдэг

Нөхцөлүүд нь бүхэл тооны сөрөг бус утгуудыг нэмэгдүүлэх замаар зохион байгуулагдсан чадлын функцууд юм х, a в0 , в 1 , в 2 , в n - тогтмол утга. Тоонууд в1 , в 2 , в n - цувралын гишүүдийн коэффициент; в0 - чөлөөт гишүүн. Цахилгаан цувааны гишүүдийг бүхэл тооны шулуун дээр тодорхойлно.

Ингээд ойлголттой танилцацгаая хүчний цувааны нийлмэл байдлын муж. Энэ бол хувьсагчийн утгуудын багц юм хүүний төлөө цуврал нийлдэг. Эрчим хүчний цуваа нь нэлээн энгийн нэгдэх мужтай байдаг. Хувьсагчийн бодит утгуудын хувьд хнийлэх талбар нь нэг цэгээс бүрдэх, эсвэл ямар нэгэн интервал (нэгдэх интервал) эсвэл бүх тэнхлэгтэй давхцах Үхэр .

Хүч чадлын цуваагаар орлуулах үед утгууд х= 0 тоон цуваа авах болно

в0 +0+0+...+0+... ,

нийлдэг.

Тиймээс, төлөө х= 0 аливаа чадлын цуваа нийлдэг тул түүний нэгдэх талбар хоосон байж болохгүй. Бүх чадлын цувааг нэгтгэх бүсийн бүтэц ижил байна. Үүнийг дараах теоремыг ашиглан тогтоож болно.

Теорем 1 (Абелийн теорем)... Хэрэв чадлын цуваа ямар нэг утгаараа нийлбэл х = х 0 тэг биш бол энэ нь нийлдэг бөгөөд үүнээс гадна бүх утгын хувьд туйлын хувьд нийлдэг |х| < |х 0 | ... Анхаарна уу: "x нь тэг" гэсэн эхлэлийн утга ба эхлэлтэй харьцуулсан "x"-ийн аль ч утгыг модулиар авна - тэмдгийг харгалзахгүйгээр.

Үр дагавар. Хэрэв хүчний цуваа зөрүүтэй байна ямар нэг үнэ цэнээр х = х 1 , дараа нь энэ нь бүх утгын хувьд ялгаатай байна |х| > |х 1 | .

Бидний урьд нь олж мэдсэнээр аливаа чадлын цуваа утгаараа нийлдэг х= 0. Зөвхөн нийлдэг хүчний цуваа байдаг х= 0 ба бусад утгуудын хувьд ялгаатай NS... Энэ тохиолдлыг авч үзэхээс хасч, бид чадлын цуваа тодорхой утгаараа нийлдэг гэж таамаглаж байна х = х 0 тэг биш. Дараа нь Абелийн теоремоор интервалын бүх цэгүүдэд нийлдэг] - | х0 |, |х 0 |[ (зүүн ба баруун хил нь х утгууд болох интервал, хасах ба нэмэх тэмдгээр тус тус нийлдэг хүчний цуваа), гарал үүслийн тэгш хэмтэй.

Хэрэв чадлын цуваа ямар нэгэн утгаар зөрөөд байвал х = х 1 , тэгвэл Абелын теоремын үр дүнд тулгуурлан энэ нь мөн сегментийн гаднах бүх цэгүүдэд хуваагдана [- | х1 |, |х 1 |] ... Эндээс аливаа чадлын цувааны хувьд гарал үүслийн тэгш хэмтэй интервал гэж нэрлэгддэг нийлэх интервал , цуваа нийлэх цэг бүрд, хил хязгаарт нь нийлж, салж болох ба заавал нэгэн зэрэг биш, харин сегментээс гадуур цуваа зөрөх болно. Тоо Рхүчийг цуваа нийлэх радиус гэнэ.

Ялангуяа тохиолдолд чадлын цувааны нэгдэх интервал цэг хүртэл доройтож болно (дараа нь цуваа зөвхөн нийлдэг х= 0 гэсэн таамаг байна Р= 0) эсвэл бүхэл тооны шугамыг төлөөлнө (дараа нь тоон шулууны бүх цэгүүдэд цуваа нийлдэг бөгөөд энэ нь тийм гэж үздэг).

Тиймээс чадлын цувааны ойртох мужийн тодорхойлолт нь түүний тодорхойлолтоос бүрдэнэ нэгдэх радиус Рба нийлэх интервалын зааг дээрх цувааны нийлэлтийг судлах (at).

Теорем 2.Хэрэв зарим нэгээс эхлэн хүч чадлын цувралын бүх коэффициентүүд тэгээс өөр байвал түүний нэгдэх радиус нь цувралын дараах нийт нөхцлийн коэффициентүүдийн абсолют утгын харьцааны хязгаартай тэнцүү байна, өөрөөр хэлбэл.

Жишээ 1. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Энд

(28) томъёог ашиглан бид энэ цувралын нэгдэх радиусыг олно.

Нэгдэх интервалын төгсгөлд цувааны нийлэлтийг судалъя. Жишээ 13-аас харахад энэ цуврал нь нийлдэг х= 1 ба зөрүүтэй байна х= -1. Иймээс нэгдэх бүс нь хагас интервал юм.

Жишээ 2. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Цувралын коэффициентүүд эерэг, ба

Энэ харьцааны хязгаарыг олъё, өөрөөр хэлбэл. Хүчний цувааны ойртох радиус:

Интервалын төгсгөлд цувааны нийлэлтийг судалж үзье. Үнэт зүйлсийг орлуулах х= -1/5 ба х= Өгөгдсөн эгнээний 1/5 нь:

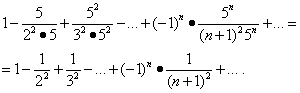
Эдгээр цувралын эхнийх нь нийлдэг (5-р жишээг үз). Харин дараа нь "Үнэмлэхүй нийлэх" хэсгийн теоремын дагуу хоёр дахь цуваа бас нийлдэг бөгөөд түүний нийлэх муж нь сегмент юм.

Жишээ 3. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Энд

Томъёо (28) ашиглан бид цувралын нэгдэх радиусыг олно.

Цувралуудын утгын нийлэлтийг судалж үзье. Тэдгээрийг энэ эгнээнд орлуулж, бид тус тусад нь авна

Шаардлагатай нийлэх нөхцөл хангагдаагүй (тэдгээрийн нийтлэг нэр томъёо нь тэг байх хандлагатай байдаггүй) тул хоёр цуваа зөрүүтэй байдаг. Тэгэхээр нийлэх интервалын хоёр төгсгөлд өгөгдсөн цуваа нь салж, түүний нийлэх муж нь интервал болно.

Жишээ 5. Хүчний цувааны нийлэх мужийг ол

Шийдэл. Хаана, ба хамаарлыг ол :

Томъёоны дагуу (28) энэ цувралын нэгдэх радиус нь байна

,

өөрөөр хэлбэл, цуврал нь зөвхөн төлөө нийлдэг х= 0 ба бусад утгуудын хувьд ялгаатай NS.

Жишээ нь нийлбэрийн интервалын төгсгөлд цуваа өөр өөрөөр ажилладаг болохыг харуулж байна. 1-р жишээнд цуваа нь нийлбэрийн интервалын нэг төгсгөлд нийлж, нөгөө талд нь хуваагддаг; жишээ 2-т хоёр төгсгөлд нийлдэг; жишээ 3-т хоёр төгсгөлд хуваагддаг.

Хүчин чадлын цувааны нийлэх радиусын томъёог зарим нэгээс эхлэн цувралын нөхцлийн бүх коэффициентүүд тэгээс өөр байна гэсэн таамаглалаар гарна. Тиймээс (28) томъёог зөвхөн эдгээр тохиолдолд ашиглахыг зөвшөөрнө. Хэрэв энэ нөхцөл зөрчигдсөн бол хүч чадлын цуваа нийлэх радиусыг ашиглан хайх хэрэгтэй. д'Аламберт тэмдэг, эсвэл хувьсагчийг өөрчилснөөр цувааг заасан нөхцөл хангагдсан хэлбэрт шилжүүлнэ.

Жишээ 6. Хүчний цувааны нийлэх интервалыг ол

Шийдэл. Энэ цувралд сондгой зэрэгтэй гишүүд байхгүй. NS... Тиймээс бид цувралыг тохируулах замаар хувиргадаг. Дараа нь бид цувралыг авна

(28) томъёог хэрэглэж болох нэгдэх радиусыг олох. Учир нь, a, дараа нь энэ цувралын нэгдэх радиус

Тиймээс бидний олж авсан тэгш байдлын дагуу энэ цуврал интервал дээр нийлдэг.

Эрчим хүчний цувааны нийлбэр. Эрчим хүчний цувааг ялгах, нэгтгэх

Эрчим хүчний цувралыг үзье

нэгдэх радиус Р> 0, өөрөөр хэлбэл. энэ цуврал интервал дээр нийлдэг.

Дараа нь утга бүр NSнийлэх интервалаас цувааны тодорхой нийлбэр тохирно. Үүний үр дүнд чадлын цувааны нийлбэр нь функц юм NSнийлэх интервал дээр. Үүнийг дамжуулан тэмдэглэж байна е(х), бид тэгш байдлыг бичиж болно

цэг бүр дэх цувааны нийлбэр гэсэн утгаар ойлгох NSнийлэх интервалаас функцийн утгатай тэнцүү байна е(х) энэ үед. Үүнтэй ижил утгаараа бид чадлын цуваа (29) функцэд нийлдэг гэж хэлэх болно е(х) нэгдэх интервал дээр.

Нэгдэх интервалаас гадуур тэгш байдал (30) утгагүй болно.

Жишээ 7.Хүчний цувааны нийлбэрийн нийлбэрийг ол

Шийдэл. Энэ бол геометрийн цуврал юм а= 1, ба q= х... Тиймээс түүний нийлбэр нь функц юм ... Цуврал нийлдэг if, and бол түүний нийлэх интервал. Тиймээс тэгш байдал

функц хэдий ч зөвхөн утгуудад хүчинтэй бүх утгын хувьд тодорхойлогдсон NS, бусад NS= 1.

Хүчний цувааны нийлбэр болохыг баталж болно е(х) нь нийлэх интервал доторх аль ч сегмент дээр, тухайлбал цувааны нийлэх интервалын аль ч цэг дээр тасралтгүй ба ялгагдах боломжтой.

Хүчний цувааг гишүүнээр нь ялгах, интеграци хийх теоремуудыг танилцуулъя.

Теорем 1.Хүчний цуваа (30) нь нийлэх интервалд хязгааргүй олон удаа нэр томъёогоор ялгагдах боломжтой ба үр дүнд бий болсон хүчнүүдийн цуваа нь анхны цуваатай ижил нийлэлтийн радиустай бөгөөд тэдгээрийн нийлбэрүүд тус тус тэнцүү байна.

Теорем 2.Эрчим хүчний цувралыг (30) 0-ээс хязгааргүй олон удаа нэгтгэж болно NS, хэрэв, ба үр дүнгийн зэрэглэлийн цуваа нь анхны цуваатай ижил нийлэх радиустай бөгөөд тэдгээрийн нийлбэрүүд нь тус тус тэнцүү байна.

Эрчим хүчний цуваа дахь функцуудыг өргөжүүлэх

Функц өгье е(х), эрчим хүчний цувралд өргөтгөх шаардлагатай, i.e. (30) хэлбэрээр илэрхийлнэ:

Даалгавар бол коэффициентийг тодорхойлох явдал юм эгнээ (30). Үүний тулд тэгш байдлыг (30) нэр томьёогоор нь ялгаж үзвэл бид дараалан олж авна:

……………………………………………….. (31)

(30) ба (31) тэнцүү байдлын тохиргоо NS= 0, бид олдог

Олсон илэрхийллийг тэгш байдал (30) болгон орлуулснаар бид олж авна

(32)

Зарим энгийн функцүүдийн Маклаурин цувралын өргөтгөлийг олцгооё.

Жишээ 8.Маклаурин цуврал функцийг өргөжүүлэх

Шийдэл. Энэ функцийн деривативууд нь функцтэй ижил байна:

Тиймээс, at NS= 0 бидэнд байна

Эдгээр утгыг томъёогоор (32) орлуулснаар бид шаардлагатай өргөтгөлийг олж авна.

(33)

Энэ цуваа нь бүхэл тооны шулуун дээр нийлдэг (түүний нэгдэх радиус).

16.1. Тейлорын цувралын энгийн функцүүдийн өргөтгөл ба

Маклаурин

Хэрэв олонлог дээр дурын функц тодорхойлогдсон бол гэдгийг харуулъя
, цэгийн ойролцоо
нь олон деривативтай ба зэрэглэлийн цувааны нийлбэр юм:

дараа нь энэ цувралын коэффициентүүдийг олж болно.

Эрчим хүчний цувралд орлуулах
... Дараа нь
.

Функцийн эхний деривативыг ол
:

At
:
.

Хоёр дахь деривативын хувьд бид дараахь зүйлийг авна.

At
:
.

Энэ процедурыг үргэлжлүүлнэ nнэг удаа бид:
.

Тиймээс бид дараах хэлбэрийн чадлын цувралыг авсан.

,

гэж нэрлэдэг Тейлорын хажуудфункцийн хувьд
цэгийн ойролцоо
.

Тейлорын цувралын онцгой тохиолдол бол Маклаурин цувралцагт
:

Тейлор (Маклаурин) цувралын үлдсэн хэсгийг үндсэн мөрүүдийг хаях замаар олж авна. nэхний гишүүд ба гэж тэмдэглэнэ
... Дараа нь функц
нийлбэр гэж бичиж болно nтооны анхны гишүүд
болон үлдсэн
:,

.

Үлдсэн хэсэг нь ихэвчлэн байдаг
янз бүрийн томъёогоор илэрхийлэгддэг.

Тэдний нэг нь Лагранж хэлбэртэй:

, хаана
.
.

Практикт Maclaurin цувралыг илүү олон удаа ашигладаг болохыг анхаарна уу. Тиймээс функцийг бичихийн тулд
Эрчим хүчний цувралын нийлбэр хэлбэрээр дараахь зүйлийг хийх шаардлагатай.

1) Маклаурин (Тейлор) цувралын коэффициентийг олох;

2) олж авсан чадлын цувааны нийлэх мужийг олох;

3) өгөгдсөн цуваа функцэд нийлдэг болохыг батал
.

Теорем1 (Маклаурины цувралыг нэгтгэхэд шаардлагатай бөгөөд хангалттай нөхцөл). Цувралын нийлэх радиусыг үзье
... Энэ цуваа интервалд нийлэхийн тулд
ажиллах
, нөхцөлийг хангахад шаардлагатай бөгөөд хангалттай:
заасан интервалд.

Теорем 2.Хэрэв функцийн аль нэг эрэмбийн деривативууд
тодорхой интервалд
үнэмлэхүй утгаараа ижил тоогоор хязгаарлагдана М, тэр бол
, дараа нь энэ интервалд функц
Маклаурин цуврал болгон өргөжүүлж болно.

Жишээ1 . Цэгний эргэн тойронд Тейлорын эгнээнд тэлэх
функц.

Шийдэл.

.

,;

,
;

,
;

,

.......................................................................................................................................

,
;

Конвергенцийн бүс нутаг
.

Жишээ2 . Функцийг өргөжүүлэх цэгийн эргэн тойронд Тейлорын эгнээнд
.

Шийдэл:

Функцийн утга ба түүний деривативын утгыг ол
.

,
;

,
;

...........……………………………

,
.

Бид эдгээр утгыг дараалан орлуулдаг. Бид авах:

эсвэл
.

Энэ цувралын нэгдэх мужийг олцгооё. d'Alembert онцлог дагуу, цуврал converges бол

.

Тиймээс, аливаад Энэ хязгаар нь 1-ээс бага тул цувралын нийлэх муж нь:
.

Маклаурины цувралын үндсэн үндсэн функцүүдийн өргөтгөлийн хэд хэдэн жишээг авч үзье. Маклаурин цувралыг эргэн санацгаая.

.

интервал дээр нийлдэг
ажиллах
.

Функцийг цувралаар өргөжүүлэхийн тулд дараахь зүйлийг хийх шаардлагатайг анхаарна уу.

a) энэ функцийн Маклаурины цувралын коэффициентийг олох;

б) үүссэн цувралын нийлэгжилтийн радиусыг тооцоолох;

в) гарсан цуваа нь функцэд нийлдэг болохыг нотол
.

Жишээ 3.Функцийг авч үзье
.

Шийдэл.

Функцийн утга ба түүний деривативын утгыг тооцоолъё
.

Дараа нь цувралын тоон коэффициентүүд нь:

хэний ч төлөө n.Олдсон коэффициентүүдийг Маклаурин цувралд орлуулж дараахийг авна уу:

Үүссэн цувааны нэгдэх радиусыг ол, тухайлбал:

.

Үүний үр дүнд цувралууд интервал дээр нийлдэг
.

Энэ цуврал функцэд нийлдэг аливаа үнэт зүйлсийн хувьд учир нь ямар ч цоорхой
функц мөн үнэмлэхүй утга дахь түүний дериватив нь тоогоор хязгаарлагддаг .

Жишээ4 . Функцийг авч үзье
.

Шийдэл.

:

Энэ нь жигд дарааллын дериватив гэдгийг харахад хялбар байдаг
, мөн деривативууд нь сондгой дараалалтай байна. Бид олсон коэффициентүүдийг Маклаурин цувралд орлуулж, өргөтгөлийг олж авна.

Энэ цувралын нийлэх интервалыг олцгооё. Д'Аламберт үндэслэн:

хэний ч төлөө ... Үүний үр дүнд цувралууд интервал дээр нийлдэг
.

Энэ цуврал функцэд нийлдэг
, учир нь түүний бүх дериватив нь нэгээр хязгаарлагддаг.

Жишээ5 .
.

Шийдэл.

Функцийн утга ба түүний деривативын утгыг олъё
:

Тиймээс энэ цувралын коэффициентүүд:
болон
, иймээс:

Өмнөх цувралын нэгэн адил нийлмэл байдлын бүс
... Цуврал нь функцэд нийлдэг
, учир нь түүний бүх дериватив нь нэгээр хязгаарлагддаг.

функц гэдгийг анхаарна уу
сондгой ба цуваа сондгой градусаар өргөтгөх, функц
- тэгш эрх мэдэлд тэгш ба цуврал өргөтгөл.

Жишээ6 . бином цуврал:
.

Шийдэл.

Функцийн утга ба түүний деривативын утгыг олъё
:

Үүнээс үзэхэд:

Маклаурины цуврал дахь коэффициентүүдийн эдгээр утгыг орлуулж, энэ функцийн өргөтгөлийг хүчирхэг цувралд авна уу.

Энэ цувралын нэгдэх радиусыг ол:

Үүний үр дүнд цувралууд интервал дээр нийлдэг
... Хязгаарлалтын цэгүүдэд
болон
Цуврал нь илтгэгчээс хамаарч нийлэх эсвэл нийлэхгүй байж болно
.

Судалж буй цувралууд нь интервал дээр нийлдэг
ажиллах
, өөрөөр хэлбэл хураамжийн нийлбэр
цагт
.

Жишээ7 . Маклаурины цувралд функцийг өргөжүүлье
.

Шийдэл.

Энэ функцийн цуврал өргөтгөлийн хувьд бид хоёр нэрийн цувааг ашигладаг
... Бид авах:

Эрчим хүчний цувралын шинж чанарт үндэслэн (цахилгаан цувааг нэгтгэх бүсэд нэгтгэж болно) бид энэ цувралын зүүн ба баруун талуудын салшгүй хэсгийг олно.

Энэ цувралын нэгдэх мужийг олцгооё.
,

өөрөөр хэлбэл энэ цувааны нийлэх муж нь интервал юм
... Интервалын төгсгөлд цуваа нийлэхийг тодорхойлъё. At

... Энэ эгнээ нь эв нэгдэлтэй эгнээ, өөрөөр хэлбэл хуваагддаг. At
Бид нийтлэг нэр томъёо бүхий тооны цувралыг авдаг
.

Лейбницийн цуврал нийлдэг. Тиймээс энэ цувралын нийлэх муж нь интервал юм
.

16.2. Ойролцоогоор тооцоололд эрчим хүчний цуваа хэрэглэх

Ойролцоогоор тооцоололд эрчим хүчний цуваа нь маш чухал үүрэг гүйцэтгэдэг. Тэдгээрийн тусламжтайгаар тригонометрийн функцүүдийн хүснэгтүүд, логарифмын хүснэгтүүд, бусад функцүүдийн утгын хүснэгтүүдийг эмхэтгэсэн бөгөөд эдгээрийг мэдлэгийн янз бүрийн салбарт, жишээлбэл, магадлалын онол, математик статистикт ашигладаг. Нэмж дурдахад хүчин чадлын цуваа дахь функцүүдийн өргөтгөл нь тэдний онолын судалгаанд ашигтай байдаг. Ойролцоогоор тооцоололд хүч чадлын цуваа ашиглах гол асуудал бол цувралын нийлбэрийг эхнийх нь нийлбэрээр солих үед гарсан алдааг тооцоолох асуудал юм. nгишүүд.

Хоёр тохиолдлыг авч үзье:

функцийг ээлжлэн цуврал болгон өргөжүүлсэн;

функцийг тогтмол цуврал болгон өргөжүүлсэн.

Ээлжит цуваа ашиглан тооцоолох

Функцийг зөвшөөр
ээлжлэн эрчим хүчний цуврал болгон өргөжүүлсэн. Дараа нь энэ функцийг тодорхой утгыг тооцоолохдоо Бид Лейбницийн тестийг ашиглаж болох тоон цувралыг олж авдаг. Энэ онцлогийн дагуу цувралын нийлбэрийг эхнийх нь нийлбэрээр сольсон бол nНөхцөлүүдийн хувьд үнэмлэхүй алдаа нь энэ цувралын үлдсэн хэсгийн эхний гишүүнээс хэтрэхгүй, өөрөөр хэлбэл:
.

Жишээ8 . Тооцоол
0.0001 хүртэл нарийвчлалтай.

Шийдэл.

Бид Маклаурин цувралыг ашиглах болно
, радиан дахь өнцгийн утгыг орлуулах:

Хэрэв бид цувралын нэг ба хоёрдугаар гишүүнийг өгөгдсөн нарийвчлалтайгаар харьцуулж үзвэл:.

Гурав дахь өргөтгөлийн хугацаа:

тогтоосон тооцооллын нарийвчлалаас бага. Тиймээс тооцоолох
цувралын хоёр гишүүнийг орхиход хангалттай, өөрөөр хэлбэл

.

Тиймээс
.

Жишээ9 . Тооцоол
0.001 нарийвчлалтай.

Шийдэл.

Бид бином цувралын томъёог ашиглана. Үүнийг хийхийн тулд бичнэ үү
зэрэг:
.

Энэ илэрхийлэлд
,

Цувралын гишүүн бүрийг заасан нарийвчлалтайгаар харьцуулж үзье. Энэ нь ойлгомжтой
... Тиймээс тооцоолох
эгнээний гурван гишүүнийг орхиход л хангалттай.

эсвэл
.

Эерэг цуваа ашиглан тооцоолох

Жишээ10 . Тоогоо тооцоол 0.001 хүртэл нарийвчлалтай.

Шийдэл.

Функцийн хувьд дараалан
орлуулах
... Бид авах:

Цувралын нийлбэрийг эхнийх нь нийлбэрээр солиход гарах алдааг тооцоолъё гишүүд. Илэрхий тэгш бус байдлыг бичье:

энэ нь 2<<3. Используем формулу остаточного члена ряда в форме Лагранжа:
,
.

Асуудлын нөхцөл байдлын дагуу та олох хэрэгтэй nДараахь тэгш бус байдал үүснэ.
эсвэл
.

Үүнийг шалгах нь амархан n= 6:
.

Тиймээс,
.

Жишээ11 . Тооцоол
0.0001 нарийвчлалтай.

Шийдэл.

Логарифмыг тооцоолохын тулд функцэд цуврал ашиглаж болно гэдгийг анхаарна уу
, гэхдээ энэ цуврал нь маш удаан нийлдэг бөгөөд өгөгдсөн нарийвчлалд хүрэхийн тулд 9999 нөхцөлийг авах шаардлагатай болно! Тиймээс логарифмыг тооцоолохын тулд дүрмээр бол функцийн цуваа
интервал дээр нийлдэг
.

Тооцоод үзье
энэ мөрийг ашиглан. Байцгаая
, дараа нь .

Тиймээс,
,

Тооцоолохын тулд
Өгөгдсөн нарийвчлалтайгаар бид эхний дөрвөн гишүүний нийлбэрийг авна.
.

Эгнээний үлдэгдэл
хаях. Алдаагаа тооцоод үзье. Энэ нь ойлгомжтой

эсвэл
.

Тиймээс, тооцоололд ашигласан цувралд функцийн цувралд 9999-ийн оронд зөвхөн эхний дөрвөн гишүүнийг авахад хангалттай байсан.
.

Өөрийгөө шалгах асуултууд

1. Тейлорын цуврал гэж юу вэ?

2. Маклаурин цуврал ямар төрлийн байсан бэ?

3. Тейлорын цуваа дахь функцийн өргөтгөлийн теоремыг томъёол.

4. Үндсэн функцүүдийн Маклаурины цуврал өргөтгөлийг бич.

5. Харгалзан үзсэн цувааны нийлэх талбаруудыг заана уу.

6. Хүчний цуваа ашиглан ойролцоогоор тооцооллын алдааг хэрхэн тооцох вэ?

Хэрэв функц f (x)цэгийг агуулсан зарим интервалтай байна а, бүх дарааллын деривативууд, тэгвэл Тэйлорын томъёог түүнд хэрэглэж болно:

хаана r n- цувралын үлдэгдэл буюу үлдэгдэл гэж нэрлэгддэгийг Лагранжийн томъёогоор тооцоолж болно.

, энд x тоо хоёрын хооронд байна NSболон а.

Хэрэв ямар нэг үнэ цэнийн хувьд x r n®0 нь n® ¥, дараа нь хязгаарт Тейлорын томъёо нь энэ утгыг нэгтгэгч болгон хувиргадаг Тейлорын цуврал:

Тиймээс функц f (x)авч үзэж буй цэг дээр Тейлорын цуврал болгон өргөжүүлж болно NS, хэрэв:

1) бүх захиалгын деривативтай;

2) баригдсан цувралууд энэ цэг дээр нийлдэг.

At а= 0 гэж нэрлэгддэг цуврал гарч ирнэ Маклаурины ойролцоо:

Жишээ 1 f (x) = 2х.

Шийдэл... Функцийн утгууд ба түүний деривативуудыг олъё NS=0

f (x) = 2х, f ( 0) = 2 0 =1;

f ¢ (x) = 2х ln2, f ¢ ( 0) = 2 0 ln2 = ln2;

f ¢¢ (x) = 2х ln 2 2, f ¢¢ ( 0) = 2 0 ln 2 2 = ln 2 2;

f (n) (x) = 2х ln n 2, f (n) ( 0) = 2 0 ln n 2 = ln n 2.

Деривативын олж авсан утгыг Тейлорын цувралын томъёонд орлуулснаар бид дараахь зүйлийг авна.

Энэ цувралын нэгдэх радиус нь хязгааргүйтэй тэнцүү тул энэ өргөтгөл нь -¥-д хүчинтэй байна.<х<+¥.

Жишээ 2 NS+4) функцийн хувьд f (x) =д х.

Шийдэл... Функцийн деривативуудыг олоорой e хболон тэдний үнэ цэнэ NS=-4.

f (x)= e х, f (-4) = e -4 ;

f ¢ (x)= e х, f ¢ (-4) = e -4 ;

f ¢¢ (x)= e х, f ¢¢ (-4) = e -4 ;

f (n) (x)= e х, f (n) ( -4) = e -4 .

Тиймээс функцийн шаардлагатай Тейлор цуврал дараах хэлбэртэй байна.

Энэ өргөтгөл нь - ¥-д мөн хүчинтэй<х<+¥.

Жишээ 3 ... Функцийг өргөжүүлэх f (x)= ln хэрх мэдлийн цувралд ( NS- 1),

(өөрөөр хэлбэл, цэгийн ойролцоох Тейлорын цувралд NS=1).

Шийдэл... Энэ функцийн деривативуудыг ол.

Эдгээр утгыг томъёонд орлуулснаар бид шаардлагатай Тейлор цувралыг авна.

D'Alembert тестийг ашиглан цувралууд хоорондоо нийлж байгаа эсэхийг шалгаж болно

½ NS- 1½<1. Действительно,

½ бол цуваа нийлнэ NS- 1½<1, т.е. при 0<х<2. При NS= 2 Бид Лейбницийн тестийн нөхцлийг хангасан ээлжлэн цуваа олж авна. At NS= 0 функц тодорхойгүй байна. Тиймээс Тейлорын цувралын нийлэх муж нь хагас нээлттэй интервал юм (0; 2).

Үүнтэй ижил аргаар олж авсан өргөтгөлүүдийг Маклаурины цувралд (жишээ нь, цэгийн ойролцоо) танилцуулъя. NS= 0) зарим энгийн функцүүдийн хувьд:

(2) ,

(3) ,

(сүүлчийн задрал гэж нэрлэдэг бином цуврал)

Жишээ 4 ... Хүч чадлын цуваа дахь функцийг өргөжүүлэх

Шийдэл... Өргөтгөх хэсэгт (1) бид солино NSдээр - NS 2, бид авна:

Жишээ 5 ... Маклаурин цуврал функцийг өргөжүүлэх

Шийдэл... Бидэнд байгаа

Томъёо (4) ашиглан бид дараахь зүйлийг бичиж болно.

орлуулж байна NSтомъёонд оруулна -Н.С, бид авах:

Эндээс бид олж мэднэ:

Хаалтуудыг өргөжүүлж, цувралын нөхцлүүдийг дахин цэгцэлж, ижил төстэй нөхцлүүдийг бууруулснаар бид олж авна.

Энэ цуврал интервалд нийлдэг

(-1; 1), учир нь тус бүр нь энэ интервалд нийлдэг хоёр цувралаас авсан.

Сэтгэгдэл .

Формула (1) - (5) нь мөн Тейлорын цувралын харгалзах функцуудыг өргөтгөхөд ашиглагдаж болно, жишээлбэл. эерэг бүхэл тоон дахь функцуудыг өргөтгөхөд ( Ха). Үүнийг хийхийн тулд өгөгдсөн функц дээр (1) - (5) функцүүдийн аль нэгийг олж авахын тулд ижил төстэй хувиргалтыг хийх шаардлагатай байдаг. NSзардал k ( Ха) m, k нь тогтмол тоо, m нь эерэг бүхэл тоо. Хувьсагчийг өөрчлөх нь ихэвчлэн тохиромжтой байдаг т=Хамөн Маклаурины цуврал дахь t-тэй холбоотой үүссэн функцийг өргөжүүлнэ.

Энэ арга нь чадлын цуваа дахь функцийн тэлэлтийн өвөрмөц байдлын тухай теоремыг харуулж байна. Энэ теоремын мөн чанар нь нэг цэгийн ойролцоо түүний тэлэлт хэрхэн хийгдсэнээс үл хамааран ижил функцэд нийлэх хоёр өөр чадлын цуваа олж авах боломжгүй юм.

Жишээ 6 ... Тейлорын цувралын функцийг цэгийн ойролцоо өргөжүүл NS=3.

Шийдэл... Энэ асуудлыг өмнөх шигээ Тейлорын цувралын тодорхойлолтыг ашиглан шийдэж болох бөгөөд үүний тулд функцийн дериватив ба тэдгээрийн утгыг олох шаардлагатай. NS= 3. Гэсэн хэдий ч одоо байгаа задралыг ашиглах нь илүү хялбар байх болно (5):

Үр дүнд нь цуваа нь нийлдэг эсвэл -3<х- 3<3, 0<х< 6 и является искомым рядом Тейлора для данной функции.

Жишээ 7 ... Тейлорын цувралыг хүчээр бичнэ үү ( NS-1) функцууд .

Шийдэл.

Цуврал нэгдэн нийлдэг , эсвэл 2< х£ 5.