Матрицыг олох аргууд. Урвуу матриц. Матрицын тэгшитгэлийг шийдвэрлэх

Олон шинж чанараараа урвуутай төстэй.

Коллежийн YouTube

1 / 5

✪ Матрицын урвуу утгыг хэрхэн олох вэ - bezbotvy

✪ Урвуу матриц (олох 2 арга)

✪ Урвуу матриц №1

✪ 2015-01-28. Урвуу 3х3 матриц

✪ 2015-01-27. Урвуу 2х2 матриц

Хадмал орчуулга

Урвуу матрицын шинж чанарууд

det A - 1 = 1 det A (\ displaystyle \ det A ^ (- 1) = (\ frac (1) (\ det A))), хаана det (\ displaystyle \ \ det)тодорхойлогчийг илэрхийлдэг.
(A B) - 1 = B - 1 A - 1 (\ displaystyle \ (AB) ^ (- 1) = B ^ (- 1) A ^ (- 1))хоёр квадрат урвуу матрицын хувьд A (\ дэлгэцийн хэв маяг A)болон B (\ дэлгэцийн хэв маяг B).
(A T) - 1 = (A - 1) T (\ displaystyle \ (A ^ (T)) ^ (- 1) = (A ^ (- 1)) ^ (T)), хаана (...) T (\ displaystyle (...) ^ (T))шилжүүлсэн матрицыг илэрхийлнэ.
(k A) - 1 = k - 1 A - 1 (\ displaystyle \ (kA) ^ (- 1) = k ^ (- 1) A ^ (- 1))аливаа коэффициентийн хувьд k ≠ 0 (\ displaystyle k \ not = 0).
E - 1 = E (\ дэлгэцийн хэв маяг \ E ^ (- 1) = E).
Шугаман тэгшитгэлийн системийг шийдвэрлэх шаардлагатай бол (b нь тэгээс ялгаатай вектор) энд x (\ displaystyle x)нь шаардлагатай вектор бөгөөд хэрэв A - 1 (\ displaystyle A ^ (- 1))тэр үед байдаг x = A - 1 b (\ displaystyle x = A ^ (- 1) b)... Үгүй бол шийдлийн орон зайн хэмжээ нь тэгээс их эсвэл огт байхгүй.

Урвуу матрицыг олох аргууд

Хэрэв матриц урвуу бол матрицын урвуу утгыг олохын тулд та дараах аргуудын аль нэгийг ашиглаж болно.

Яг (шууд) аргууд

Гаусс-Жорданы арга

Хоёр матрицыг авъя: өөрөө Амөн ганц бие Э... Матриц өгье АГаусс-Жорданы аргаар таних матрицыг мөр болгон хувиргах (та мөн баганаар хувиргах боломжтой, гэхдээ холих боломжгүй). Эхний матрицад үйлдэл бүрийг хэрэглэсний дараа хоёр дахь матрицад ижил үйлдлийг хийнэ. Эхний матрицыг нэгж хэлбэрт буулгаж дуусахад хоёр дахь матриц нь тэнцүү болно A -1.

Гауссын аргыг ашиглах үед эхний матрицыг зүүн талаас нь энгийн матрицуудын аль нэгээр нь үржүүлнэ. Λ би (\ displaystyle \ Lambda _ (i))(нэг байрлалаас бусад нь үндсэн диагональ дээр байгаа нэг нь трансвекц эсвэл диагональ матриц):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A - 1 (\ displaystyle \ Lambda _ (1) \ cdot \ dots \ cdot \ Lambda _ (n) \ cdot A = \ Lambda A = E \ Баруун сум \ Ламбда = A ^ (- 1)). Λ m = [1… 0 - a 1 м / амм 0… 0… 0… 1 - цаг - 1 м / амм 0… 0 0… 0 1 / амм 0… 0 0… 0 - ам + 1 м / амм 1 … 0… 0… 0 - anm / amm 0… 1] (\ displaystyle \ Lambda _ (m) = (\ begin (bmatrix) 1 & \ цэгүүд & 0 & -a_ (1м) / a_ (мм) & 0 & \ цэгүүд & 0 \\ &&& \ цэгүүд &&& \\ 0 & \ цэгүүд & 1 & -a_ (м-1м) / a_ (мм) & 0 & \ цэгүүд & 0 \\ 0 & \ цэгүүд & 0 & 1 / a_ (мм) & 0 & \ цэгүүд & 0 \\ 0 & \ цэгүүд & 0 & -a_ ( м + 1м) / a_ (мм) & 1 & \ цэгүүд & 0 \\ &&& \ цэгүүд &&& \\ 0 & \ цэгүүд & 0 & -a_ (нм) / a_ (мм) & 0 & \ цэгүүд & 1 \ төгсгөл (бматриц))).

Бүх үйлдлүүдийг хэрэгжүүлсний дараа хоёр дахь матриц нь тэнцүү байх болно Λ (\ дэлгэцийн хэв маяг \ Ламбда), энэ нь хүссэн зүйл байх болно. Алгоритмын нарийн төвөгтэй байдал - O (n 3) (\ displaystyle O (n ^ (3))).

Алгебрийн нэмэлтүүдийн матрицыг ашиглах

Матрицаас урвуу матриц A (\ дэлгэцийн хэв маяг A), хэлбэрээр төлөөлж болно

A - 1 = adj (A) det (A) (\ displaystyle (A) ^ (- 1) = (((\ mbox (adj)) (A)) \ over (\ det (A))))

хаана adj (A) (\ displaystyle (\ mbox (adj)) (A))- хавсаргасан матриц;

Алгоритмын нарийн төвөгтэй байдал нь тодорхойлогч O det-ийг тооцоолох алгоритмын нарийн төвөгтэй байдлаас хамаарах ба O (n²) · O det-тэй тэнцүү байна.

LU / LUP задралыг ашиглах

Матрицын тэгшитгэл A X = I n (\ displaystyle AX = I_ (n))урвуу матрицын хувьд X (\ дэлгэцийн X)цуглуулга гэж үзэж болно n (\ displaystyle n)хэлбэрийн системүүд A x = b (\ displaystyle Ax = b)... Бид тэмдэглэж байна i (\ displaystyle i)матрицын багана X (\ дэлгэцийн X)хөндлөн X i (\ дэлгэцийн хэв маяг X_ (i)); тэгээд A X i = e i (\ displaystyle AX_ (i) = e_ (i)), i = 1,…, n (\ displaystyle i = 1, \ ldots, n)гэх мэт i (\ displaystyle i)матрицын багана I n (\ displaystyle I_ (n))нэгж вектор юм e i (\ displaystyle e_ (i))... Өөрөөр хэлбэл урвуу матрицыг олох нь нэг матрицтай, өөр өөр баруун талтай n тэгшитгэлийг шийдвэрлэхэд буурдаг. LUP задралыг (O (n³) хугацаа) хийсний дараа n тэгшитгэл бүрийг шийдвэрлэхэд O (n²) хугацаа шаардагддаг тул ажлын энэ хэсэгт мөн O (n³) хугацаа шаардагдана.

Хэрэв А матриц муудаагүй бол түүнд зориулж LUP задралыг тооцоолж болно P A = L U (\ displaystyle PA = LU)... Байцгаая P A = B (\ displaystyle PA = B), B - 1 = D (\ displaystyle B ^ (- 1) = D)... Дараа нь урвуу матрицын шинж чанаруудаас бид дараахь зүйлийг бичиж болно. D = U - 1 L - 1 (\ displaystyle D = U ^ (- 1) L ^ (- 1))... Хэрэв бид энэ тэгшитгэлийг U ба L-ээр үржүүлбэл бид хоёр хэлбэрийн тэгшитгэлийг олж авах боломжтой U D = L - 1 (\ displaystyle UD = L ^ (- 1))болон D L = U - 1 (\ displaystyle DL = U ^ (- 1))... Эдгээр тэгшитгэлүүдийн эхнийх нь n² шугаман тэгшитгэлийн систем юм n (n + 1) 2 (\ displaystyle (\ frac (n (n + 1)) (2)))баруун тал нь мэдэгдэж байгаа (гурвалжин матрицын шинж чанараас). Хоёр дахь нь мөн n² шугаман тэгшитгэлийн системийг төлөөлдөг n (n - 1) 2 (\ displaystyle (\ frac (n (n-1)) (2)))баруун тал нь мэдэгдэж байгаа (мөн гурвалжин матрицын шинж чанараас). Тэд хамтдаа n² тэгш байдлын системийг төлөөлдөг. Эдгээр тэгш байдлыг ашиглан бид D матрицын бүх n² элементийг рекурсив аргаар тодорхойлж болно. Дараа нь тэгшитгэлээс (PA) −1 = A −1 P −1 = B −1 = D. тэгш байдлыг олж авна. A - 1 = D P (\ displaystyle A ^ (- 1) = DP).

LU-задралыг ашиглах тохиолдолд D матрицын багануудыг солих шаардлагагүй, гэхдээ А матриц муудсан ч гэсэн шийдэл нь салж болно.

Алгоритмын нарийн төвөгтэй байдал нь O (n³) юм.

Давталтын аргууд

Шульцын аргууд

(Ψ k = E - AU k, U k + 1 = U k ∑ i = 0 n Ψ ki (\ displaystyle (\ эхлэл (тохиолдлууд) \ Psi _ (k) = E-AU_ (k), \\ U_ () k + 1) = U_ (k) \ нийлбэр _ (i = 0) ^ (n) \ Psi _ (k) ^ (i) \ төгсгөл (тохиолдлууд)))

Алдааны тооцоо

Анхны таамаглалыг сонгох

Энд авч үзсэн давталттай матрицын урвуу процессын анхны ойролцооллыг сонгох асуудал нь тэдгээрийг жишээлбэл матрицын LU задралд суурилсан шууд инверцийн аргуудтай өрсөлддөг бие даасан бүх нийтийн арга гэж үзэх боломжийг олгодоггүй. Сонгох зарим зөвлөмжүүд байдаг U 0 (\ displaystyle U_ (0))нөхцөлийн биелэлтийг хангах ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (матрицын спектрийн радиус нь нэгээс бага) бөгөөд энэ нь процессыг нэгтгэхэд шаардлагатай бөгөөд хангалттай юм. Гэхдээ энэ тохиолдолд эхлээд урвуутай А матриц эсвэл матрицын спектрийн дээд хязгаарыг мэдэх шаардлагатай. A A T (\ displaystyle AA ^ (T))(жишээлбэл, хэрэв А нь тэгш хэмт эерэг тодорхой матриц ба ρ (A) ≤ β (\ displaystyle \ rho (A) \ leq \ бета), дараа нь та авч болно U 0 = α E (\ displaystyle U_ (0) = (\ альфа) E), хаана; хэрэв А нь дур зоргоороо доройтдоггүй матриц ба ρ (A A T) ≤ β (\ displaystyle \ rho (AA ^ (T)) \ leq \ бета)тэгвэл итгэдэг U 0 = α A T (\ displaystyle U_ (0) = (\ альфа) A ^ (T))бас хаана α ∈ (0, 2 β) (\ дэлгэцийн хэв маяг \ альфа \ зүүн талд (0, (\ frac (2) (\ бета)) \ баруун)); Мэдээжийн хэрэг та нөхцөл байдлыг хялбаршуулж, давуу талыг ашиглаж болно ρ (A A T) ≤ k A A T k (\ displaystyle \ rho (AA ^ (T)) \ leq (\ mathcal (k)) AA ^ (T) (\ mathcal (k))), тавих U 0 = A T ‖ A A T ‖ (\ displaystyle U_ (0) = (\ frac (A ^ (T)) (\ | AA ^ (T) \ |)))). Хоёрдугаарт, анхны матрицын ийм тодорхойлолттой бол тийм баталгаа байхгүй ‖ Ψ 0 ‖ (\ displaystyle \ | \ Psi _ (0) \ |)жижиг байх болно (энэ нь бүр байж болно ‖ Ψ 0 ‖> 1 (\ дэлгэцийн хэв маяг \ | \ Psi _ (0) \ |> 1)), мөн нийлэх хурдны өндөр дарааллыг шууд илрүүлэхгүй.

Жишээ нь

Матриц 2х2

A - 1 = [a b c d] - 1 = 1 det (A) [d - b - c a] = 1 a d - b c [d - b - c a]. (\ displaystyle \ mathbf (A) ^ (- 1) = (\ эхлэл (бматриц) a & b \\ c & d \\\ төгсгөл (бматриц)) ^ (- 1) = (\ frac (1) (\ det (\ mathbf (A))) (\ эхлэл (бматриц) \, \, \, d & \! \! - b \\ - c & \, a \\\ төгсгөл (бматриц)) = (\ frac (1) (ad- bc)) (\ эхлэл (bматриц) \, \, \, d & \! \! - b \\ - c & \, a \\\ төгсгөл (бматриц)).)

2х2 матрицыг урвуу болгох нь зөвхөн тохиолдолд л боломжтой a d - b c = det A ≠ 0 (\ displaystyle ad-bc = \ det A \ neq 0).

Урвуу матрицыг олох- ихэвчлэн хоёр аргаар шийдэгддэг даалгавар:

тодорхойлогчийг олох, матрицыг шилжүүлэх шаардлагатай алгебрийн нэмэлтүүдийн арга;
үл мэдэгдэх Gauss-ийг арилгах аргаар, үүнд энгийн матрицын хувиргалт хийх шаардлагатай (мөр нэмэх, мөрийг ижил тоогоор үржүүлэх гэх мэт).

Ялангуяа сониуч хүмүүсийн хувьд бусад аргууд байдаг, жишээлбэл, шугаман хувиргалтын арга. Энэ хичээлээр бид урвуу матрицыг олох гурван арга, алгоритмд дүн шинжилгээ хийх болно.

Урвуу матриц А, ийм матриц гэж нэрлэдэг

А
. (1)

Урвуу матриц өгөгдсөн квадрат матрицыг олоход шаардлагатай А, ийм матриц гэж нэрлэдэг

матрицын бүтээгдэхүүн Абаруун талд нь таних матриц, өөрөөр хэлбэл,
. (1)

Таних матриц нь диагональ матриц бөгөөд бүх диагональ элементүүд нь нэгтэй тэнцүү байна.

Теорем.Ганц бус (мууддаггүй, ганц бие биш) квадрат матриц бүрийн хувьд урвуу матрицыг олж болно, үүнээс гадна зөвхөн нэгийг нь олж болно. Тусгай (муухайлсан, ганц бие) квадрат матрицын хувьд урвуу тал байхгүй.

Квадрат матриц гэж нэрлэдэг тусгай бус(эсвэл доройтдоггүй, дан бус) хэрэв түүний тодорхойлогч нь тэг биш бол ба Онцгой(эсвэл доройтох, ганц бие) хэрэв түүний тодорхойлогч нь тэг байвал.

Урвуу матрицыг зөвхөн квадрат матрицад л олж болно. Мэдээжийн хэрэг урвуу матриц нь өгөгдсөн матрицтай ижил дарааллаар дөрвөлжин байх болно. Урвуу матрицыг олж болох матрицыг урвуу матриц гэнэ.

Учир нь урвуу матриц харилцан адилтгалтай зүйрлэл бий. Тоо бүрийн хувьд а, тэгтэй тэнцүү биш, ийм тоо байдаг бтэр ажил аболон бнэгтэй тэнцүү: ab= 1. Тоо бтоог урвуу гэж нэрлэдэг б... Жишээлбэл, 7-ын тооны хувьд урвуу нь 1/7, учир нь 7 * 1/7 = 1.

Алгебрийн нэмэлтүүдийн аргаар урвуу матрицыг олох (нэгдэл матриц)

Ганц бус квадрат матрицын хувьд Аурвуу нь матриц юм

матрицын тодорхойлогч хаана байна А, a нь матрицтай хавсарсан матриц юм А.

Квадрат матрицтай нэгдэл Ань ижил дарааллын матриц гэж нэрлэгддэг ба түүний элементүүд нь А матрицад шилжүүлсэн матрицын тодорхойлогчийн харгалзах элементүүдийн алгебрийн нэмэлтүүд юм. Тиймээс хэрэв

тэгээд

болон

Алгебрийн нэмэлтүүдийн аргаар урвуу матрицыг олох алгоритм

1. Өгөгдсөн матрицын тодорхойлогчийг ол А... Хэрэв тодорхойлогч нь тэг байвал урвуу матрицыг хайх нь зогсдог, учир нь матриц нь доройтсон бөгөөд урвуу нь байхгүй.

2. Харьцуулан шилжүүлсэн матрицыг ол А.

3. 2-р алхамд олдсон Марицагийн алгебрийн нэмэлтүүд болох хавсарсан матрицын элементүүдийг тооцоол.

4. Томъёо (2) хэрэглэнэ: матрицын тодорхойлогчийн урвуу тоог үржүүлнэ А, 4-р алхамаас олдсон хавсарсан матриц руу.

5. Энэ матрицыг үржүүлэх замаар 4-р алхам дээр олж авсан үр дүнг шалгана уу Аурвуу матриц руу. Хэрэв эдгээр матрицын үржвэр нь таних матрицтай тэнцүү бол урвуу матриц зөв олдсон байна. Үгүй бол шийдлийн процессыг дахин эхлүүлнэ үү.

Жишээ 1.Матрицын хувьд

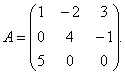
матрицын урвуу утгыг ол.

Шийдэл. Урвуу матрицыг олохын тулд матрицын тодорхойлогчийг олох шаардлагатай А... Бид гурвалжны дүрмээр олдог:

Тиймээс матриц А- дан бус (мууддаггүй, ганц бие биш) ба түүний хувьд урвуу байдаг.

Өгөгдсөн матрицтай залгаа матрицыг ол А.

Матрицтай харьцуулан шилжүүлсэн матрицыг ол А:

Зэргэлдээ матрицын элементүүдийг матрицтай харьцуулан шилжүүлсэн матрицын алгебрийн нэмэлтүүд гэж тооцоол. А:

Тиймээс матрицтай зэргэлдээх матриц А, хэлбэртэй байна

Сэтгэгдэл.Элементүүдийг тооцоолох дараалал ба матрицын шилжүүлэг өөр байж болно. Эхлээд матрицын алгебрийн нэмэлтүүдийг тооцоолж болно Адараа нь комплемент матрицыг шилжүүлнэ. Үр дүн нь нэгдлийн матрицын ижил элементүүд байх ёстой.

Томъёо (2) ашиглан бид матрицын урвуу матрицыг олно А:

Гауссын хасалтаар урвуу матрицыг олох

Гауссын арилгах аргаар урвуу матрицыг олох эхний алхам бол матрицыг оноох явдал юм. Аижил эрэмбийн таних матриц, тэдгээрийг босоо зураасаар тусгаарлана. Бид давхар матрицыг авдаг. Бид энэ матрицын хоёр талыг үржүүлээд дараа нь авна

Үл мэдэгдэхийг Гауссын аргаар арилгах урвуу матрицыг олох алгоритм

1. Матриц руу Аижил эрэмбийн таних матрицыг онооно.

2. Үүссэн давхар матрицыг зүүн талд нь таних матриц авахаар хувиргавал урвуу матриц нь баруун талд байгаа таних матрицын оронд автоматаар гарч ирнэ. Матриц Азүүн талд нь энгийн матрицын хувиргалтаар таних матриц болж хувирдаг.

2. Хэрэв матрицыг хувиргах явцад Ааль ч мөрөнд эсвэл аль ч баганад таних матрицад зөвхөн тэг байх болно, дараа нь матрицын тодорхойлогч нь тэгтэй тэнцүү байх тул матриц болно. Адоройтох бөгөөд урвуу матрицгүй болно. Энэ тохиолдолд урвуу матрицын цаашдын хайлтыг зогсооно.

Жишээ 2.Матрицын хувьд

матрицын урвуу утгыг ол.

мөн бид үүнийг хувиргаж, зүүн талд нь таних матрицыг авах болно. Бид өөрчлөлтүүдийг эхлүүлдэг.

Зүүн ба баруун матрицын эхний мөрийг (-3) үржүүлж, хоёр дахь эгнээнд нэмээд дараа нь эхний мөрийг (-4) үржүүлж, гурав дахь эгнээнд нэмнэ.

Боломжтой бол дараагийн хувиргалтуудын үед бутархай тоо байхгүй тул эхлээд хоёр дахин нэмэгдсэн матрицын зүүн талд хоёр дахь эгнээнд нэгж үүсгэнэ. Үүнийг хийхийн тулд хоёр дахь мөрийг 2-оор үржүүлж, түүнээс гурав дахь мөрийг хасвал бид авна

Эхний мөрийг хоёр дахь эгнээнд нэмж, дараа нь хоёр дахь мөрийг (-9) үржүүлж, гурав дахь эгнээнд нэмнэ. Дараа нь бид авна

Гурав дахь мөрийг 8-аар хуваа

Гурав дахь эгнээ 2-оор үржүүлж, хоёр дахь эгнээнд нэмнэ. Энэ нь харагдаж байна:

Хоёр ба гурав дахь мөрүүдийг сольж, эцэст нь бид дараах зүйлийг авна.

Нэгж матрицыг зүүн талд нь олж авдаг тул урвуу матрицыг баруун талд нь олж авдаг. Тиймээс:

Та анхны матрицыг олсон урвуу матрицаар үржүүлэх замаар тооцооллын зөв эсэхийг шалгаж болно.

Үр дүн нь урвуу матриц байх ёстой.

Жишээ 3.Матрицын хувьд

матрицын урвуу утгыг ол.

Шийдэл. Давхар матриц зохиох

мөн бид үүнийг өөрчлөх болно.

Бид эхний мөрийг 3-аар, хоёр дахь мөрийг 2-оор үржүүлж, хоёр дахь мөрийг хасч, дараа нь эхний мөрийг 5-аар, гурав дахь мөрийг 2-оор үржүүлж, гурав дахь эгнээнээс хасна.

Бид эхний мөрийг 2-оор үржүүлж, хоёр дахь мөрөнд нэмээд гурав дахь мөрөөс хоёр дахь мөрийг хасаад дараа нь бид гарна.

Зүүн талын гурав дахь мөрөнд бүх элементүүд тэгтэй тэнцүү болохыг бид харж байна. Үүний үр дүнд матриц нь доройтож, урвуу матрицгүй байна. Бид урвуу марица олохоо больсон.

$ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ нөхцөл хангагдсан бол $ A ^ (- 1) $ матрицыг $ A $ квадрат матрицтай харьцуулахад урвуу гэж нэрлэдэг. , Энд $ E $ нь таних матриц бөгөөд дараалал нь $ A $ матрицын дараалалтай тэнцүү байна.

Муу бус матриц - тодорхойлогч нь тэгтэй тэнцүү биш матриц. Үүний дагуу доройтсон матриц нь тодорхойлогч нь тэгтэй тэнцүү байх нэг юм.

Урвуу матриц $ A ^ (- 1) $ нь зөвхөн $ A $ матриц доройтоогүй тохиолдолд л оршино. Хэрэв урвуу матриц $ A ^ (- 1) $ байгаа бол энэ нь өвөрмөц байна.

Матрицын урвуу утгыг олох хэд хэдэн арга байдаг бөгөөд бид хоёрыг нь авч үзэх болно. Энэ хуудсанд ихэнх дээд математикийн хичээлүүдэд стандарт гэж тооцогддог нэмэлт матрицын аргыг хэлэлцэх болно. Гауссын арга эсвэл Гаусс-Жорданы аргыг ашигладаг урвуу матрицыг олох хоёр дахь аргыг (элементийн хувиргалтын арга) хоёрдугаар хэсэгт авч үзнэ.

Хавсаргасан (зэргэлдээ) матрицын арга

$ A_ (n \ дахин n) $ матрицыг өгье. $ A ^ (- 1) $-ын урвуу утгыг олохын тулд гурван алхам хийх шаардлагатай.

$ A $ матрицын тодорхойлогчийг олоод $ \ Delta A \ neq 0 $, i.e. А матриц доройтдоггүй.
$ A_ матрицын элемент бүрийн $ A_ (ij) $ алгебрийн нэмэлтүүдийг бүрдүүлж $ A_ (n \ үржвэр n) ^ (*) = \ зүүн (A_ (ij) \ баруун) $ матрицыг бичнэ үү. алгебрийн нэмэлтүүдийг олсон.
$ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ томьёог харгалзан урвуу матрицыг бич.

$ (A ^ (*)) ^ T $ матрицыг ихэвчлэн $ A $ матрицтай залгаа (харилцан, залгаа) гэж нэрлэдэг.

Хэрэв шийдлийг гараар хийсэн бол эхний арга нь зөвхөн харьцангуй бага эрэмбийн матрицуудад тохиромжтой: хоёрдугаарт (), гурав дахь (), дөрөв дэх (). Дээд эрэмбийн матрицын урвуу утгыг олохын тулд өөр аргуудыг ашигладаг. Жишээлбэл, хоёр дахь хэсэгт авч үзсэн Гауссын арга.

Жишээ №1

$ A = \ зүүн (\ эхлэл (массив) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & -ийн урвууг ол. - 1 & -9 & 0 \ төгсгөл (массив) \ баруун) $.

Дөрөв дэх баганын бүх элементүүд тэгтэй тэнцүү тул $ \ Delta A = 0 $ (өөрөөр хэлбэл $ A $ матриц нь доройтсон байна). $ \ Delta A = 0 $ тул $ A $ матрицын урвуу матриц байхгүй.

Жишээ №2

$ A = \ left (\ begin (массив) (cc) -5 & 7 \\ 9 & 8 \ end (массив) \ баруун) $ матрицын урвууг ол.

Бид нэмэлт матрицын аргыг ашигладаг. Эхлээд бид $ A $ матрицын тодорхойлогчийг олно.

$$ \ Дельта А = \ зүүн | \ эхлэл (массив) (cc) -5 & 7 \\ 9 & 8 \ төгсгөл (массив) \ баруун | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

$ \ Delta A \ neq 0 $ тул урвуу матриц байгаа тул бид шийдлийг үргэлжлүүлэх болно. Алгебрийн нэмэлтүүдийг олох

\ эхлэл (зэрэгцүүлсэн) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9; \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ төгсгөл (зэрэгцүүлсэн)

Бид алгебрийн нэмэлтүүдээс матриц зохиодог: $ A ^ (*) = \ зүүн (\ эхлэл (массив) (cc) 8 & -9 \\ -7 & -5 \ төгсгөл (массив) \ баруун) $.

Гарсан матрицыг шилжүүлнэ: $ (A ^ (*)) ^ T = \ зүүн (\ эхлэл (массив) (cc) 8 & -7 \\ -9 & -5 \ төгсгөл (массив) \ баруун) $ (үр дүн матрицыг ихэвчлэн $ A $ матрицтай хавсарсан эсвэл хавсарсан матриц гэж нэрлэдэг). $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ томъёог ашиглан бид дараах байдалтай байна:

$$ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ зүүн (\ эхлэл (массив) (cc) 8 & -7 \\ -9 & -5 \ төгсгөл (массив) \ баруун) = \ зүүн (\ эхлэл (массив) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ төгсгөл (массив) \ баруун) $$

Тиймээс урвуу нь олддог: $ A ^ (- 1) = \ зүүн (\ эхлэл (массив) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ төгсгөл (массив) \ баруун) доллар. Үр дүнгийн үнэнийг шалгахын тулд $ A ^ (- 1) \ cdot A = E $ эсвэл $ A \ cdot A ^ (- 1) = E $ гэсэн тэгш байдлын аль нэгний үнэнийг шалгахад хангалттай. $ A ^ (- 1) \ cdot A = E $ тэгш байдлыг шалгая. Бутархайтай бага ажиллахын тулд бид $ A ^ (- 1) $ матрицыг $ \ орхисон (\ эхлэл (массив) (cc) -8/103 & 7/103 \\ 9/103 хэлбэрээр орлуулах болно. & 5/103 \ төгсгөл (массив) \ баруун) $, мөн $ - \ frac (1) (103) \ cdot \ зүүн (\ эхлэл (массив) (cc) 8 & -7 \\ -9 & -5 \ төгсгөл (массив) \ баруун) $:

Хариулах: $ A ^ (- 1) = \ зүүн (\ эхлэл (массив) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ төгсгөл (массив) \ баруун) $.

Жишээ №3

$ A = \ left (\ begin (массив) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (массив) \ баруун) $ матрицын урвууг ол.

$ A $ матрицын тодорхойлогчийг тооцоолж эхэлцгээе. Тэгэхээр $ A $ матрицын тодорхойлогч дараах байдалтай байна.

$$ \ Дельта А = \ зүүн | \ эхлэл (массив) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ төгсгөл (массив) \ баруун | = 18-36 + 56-12 = 26. $$

$ \ Delta A \ neq 0 $ тул урвуу матриц байгаа тул бид шийдлийг үргэлжлүүлэх болно. Өгөгдсөн матрицын элемент бүрийн алгебрийн нэмэлтүүдийг олно:

Бид алгебрийн нэмэлтүүдийн матрицыг бүрдүүлж, шилжүүлнэ.

$$ A ^ * = \ зүүн (\ эхлэл (массив) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ төгсгөл (массив) \ баруун); \; (A ^ *) ^ T = \ зүүн (\ эхлэл (массив) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ төгсгөл (массив) \ баруун) $$

$ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ томъёог ашиглан бид дараахь зүйлийг авна.

$$ A ^ (- 1) = \ frac (1) (26) \ cdot \ зүүн (\ эхлэл (массив) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37 \ төгсгөл (массив) \ баруун) = \ зүүн (\ эхлэл (массив) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ төгсгөл (массив) \ баруун) $$

Тэгэхээр $ A ^ (- 1) = \ зүүн (\ эхлэл (массив) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \ төгсгөл (массив) \ баруун) $. Үр дүнгийн үнэнийг шалгахын тулд $ A ^ (- 1) \ cdot A = E $ эсвэл $ A \ cdot A ^ (- 1) = E $ гэсэн тэгш байдлын аль нэгний үнэнийг шалгахад хангалттай. $ A \ cdot A ^ (- 1) = E $ тэгш байдлыг шалгацгаая. Бутархайтай бага ажиллахын тулд бид $ A ^ (- 1) $ матрицыг $ \ орхисон (\ эхлэл (массив) (ccc) 3/13 & -5/26 & 1/26 \" хэлбэрээр орлуулах болно. \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ төгсгөл (массив) \ баруун) $, мөн $ \ frac (1) (26) \ cdot \ left ( \ эхлэл (массив) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ төгсгөл (массив) \ баруун) $:

Шалгалт амжилттай болсон тул урвуу $ A ^ (- 1) $ зөв олдсон.

Хариулах: $ A ^ (- 1) = \ зүүн (\ эхлэл (массив) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 / 13 & -3/26 & 37/26 \ төгсгөл (массив) \ баруун) $.

Жишээ № 4

$ A = \ зүүн (\ эхлэл (массив) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8-ийн урвууг ол. & -8 & -3 \ төгсгөл (массив) \ баруун) $.

Дөрөвдүгээр эрэмбийн матрицын хувьд алгебрийн нэмэлтүүдийг ашиглан урвуу матрицыг олох нь зарим талаараа хэцүү байдаг. Гэсэн хэдий ч ийм жишээг туршилтын баримт бичгүүдээс олж болно.

Матрицын урвуу утгыг олохын тулд эхлээд $A $ матрицын тодорхойлогчийг тооцоолох хэрэгтэй. Энэ нөхцөлд үүнийг хийх хамгийн сайн арга бол тодорхойлогчийг мөр (багана) болгон өргөжүүлэх явдал юм. Бид дурын мөр, баганыг сонгож, сонгосон мөр, баганын элемент бүрийн алгебрийн нэмэлтүүдийг олдог.

Матриц алгебр - Урвуу матриц

урвуу матриц

Урвуу матрицбаруун болон зүүн талд хоёуланг нь өгөгдсөн матрицаар үржүүлэхэд таних матрицыг өгдөг матриц гэж нэрлэдэг.
Матрицын урвуу матрицыг тэмдэглэе АДараа нь тодорхойлолтын дагуу бид дараахь зүйлийг авна.

хаана ЭЭнэ нь таних матриц юм.
Квадрат матрицдуудсан тусгай бус (доройтдоггүй) хэрэв түүний тодорхойлогч нь тэг биш бол. Үгүй бол үүнийг дууддаг Онцгой (доройтох) эсвэл ганц бие.

Дараах теоремыг баримтална. Ганц бус матриц бүр урвуу утгатай.

Урвуу матрицыг олох үйлдлийг гэнэ давж заалдахматрицууд. Матрицын урвуу алгоритмыг авч үзье. Ганц бус матриц өгөгдсөн байг n--р захиалга:

Энд Δ = det А ≠ 0.

Элементийн алгебрийн нэмэлтматрицууд n--р захиалга Аматрицын тодорхойлогч ( n–1) устгаснаар олж авсан дараалал би-р мөр ба жматрицын багана А:

гэж нэрлэгддэг зүйлийг зохиоё хавсаргасанматриц:

матрицын харгалзах элементүүдийн алгебрийн нэмэлтүүд хаана байна А.
Матрицын эгнээний элементүүдийн алгебрийн нэмэлтүүд гэдгийг анхаарна уу Аматрицын харгалзах баганад байрлуулна Ã , өөрөөр хэлбэл матрицыг нэгэн зэрэг шилжүүлдэг.
Матрицын бүх элементүүдийг хуваах замаар Ã Δ-ээр - матрицын тодорхойлогчийн утга А, бид урвуу матрицыг олж авна:

Бид урвуу матрицын хэд хэдэн тусгай шинж чанарыг тэмдэглэж байна.
1) өгөгдсөн матрицын хувьд Атүүний урвуу матриц цорын ганц;
2) урвуу матриц байвал баруун урвууболон зүүн урвууматрицууд үүнтэй давхцдаг;
3) тусгай (муудсан) квадрат матриц нь урвуу матрицгүй.

Урвуу матрицын үндсэн шинж чанарууд:
1) урвуу матрицын тодорхойлогч ба анхны матрицын тодорхойлогч нь харилцан хамааралтай утгууд;
2) квадрат матрицын үржвэрийн урвуу матриц нь урвуу дарааллаар авсан хүчин зүйлийн урвуу матрицын үржвэртэй тэнцүү байна.

3) матрицын шилжүүлсэн урвуу нь өгөгдсөн шилжүүлсэн матрицын урвуутай тэнцүү байна:

ЖИШЭЭ Өгөгдсөн матрицын урвуу утгыг тооцоол.

n-р эрэмбийн квадрат матриц байг

А -1 матрицыг дуудна урвуу матрицА матрицын хувьд хэрэв A * A -1 = E бол E нь n-р эрэмбийн нэгж матриц юм.

Нэгж матриц- зүүн дээд булангаас баруун доод булан руу дамжих үндсэн диагональ дээрх бүх элементүүд нэг, үлдсэн хэсэг нь тэг байх ийм дөрвөлжин матриц, жишээлбэл:

урвуу матрицбайж болно зөвхөн квадрат матрицын хувьдтэдгээр. ижил тооны мөр, баганатай матрицуудын хувьд.

Урвуу матриц байх нөхцөлийн тухай теорем

Матриц урвуу матрицтай байхын тулд энэ нь доройтоогүй байх нь зайлшгүй бөгөөд хангалттай юм.

A = (A1, A2, ... A n) матрицыг дуудна доройтдоггүйбаганын векторууд шугаман хамааралгүй бол. Матрицын шугаман бие даасан баганын векторуудын тоог матрицын зэрэг гэнэ. Тиймээс урвуу матриц оршин тогтнохын тулд матрицын зэрэглэл нь түүний хэмжээстэй тэнцүү байх шаардлагатай бөгөөд хангалттай гэж хэлж болно. r = n.

Урвуу матрицыг олох алгоритм

Гауссын аргаар тэгшитгэлийн системийг шийдвэрлэх хүснэгтэд А матрицыг бичиж, баруун талд (тэгшитгэлийн баруун талын оронд) Е матрицыг онооно.
Жорданы хувиргалтыг ашиглан А матрицыг нэгж баганаас бүрдэх матриц болгон бууруул; Энэ тохиолдолд E матрицыг нэгэн зэрэг хувиргах шаардлагатай.
Шаардлагатай бол анхны хүснэгтийн А матрицын доор бид Е нэгж матрицыг авахын тулд сүүлчийн хүснэгтийн мөрүүдийг (тэгшитгэл) дахин зохион байгуул.
Анхны хүснэгтийн Е матрицын доорх хамгийн сүүлийн хүснэгтэд байгаа A -1 урвуу матрицыг бичнэ үү.

Жишээ 1

А матрицын хувьд урвуу А -1 матрицыг ол

Шийдэл: Бид А матрицыг бичиж, баруун талд нь таних матриц Е-г онооно. Жорданы хувиргалтуудыг ашиглан бид А матрицыг E таних матриц руу буулгана. Тооцооллыг 31.1-р хүснэгтэд үзүүлэв.

Анхны А матриц болон урвуу матриц А -1-ийг үржүүлж тооцоолол зөв эсэхийг шалгая.

Матрицын үржүүлгийн үр дүнд нэгж матрицыг олж авна. Тиймээс тооцоолол нь зөв юм.

Хариулт:

Матрицын тэгшитгэлийг шийдвэрлэх

Матрицын тэгшитгэл нь дараах хэлбэртэй байж болно.

AX = B, XA = B, AXB = C,

Энд A, B, C нь заасан матрицууд, X нь шаардлагатай матрицууд юм.

Матрицын тэгшитгэлийг урвуу матрицаар нь үржүүлэх замаар шийддэг.

Жишээлбэл, тэгшитгэлээс матрицыг олохын тулд тэр тэгшитгэлийг зүүн тийш үржүүлнэ.

Тиймээс тэгшитгэлийн шийдийг олохын тулд урвуу матрицыг олж, тэгшитгэлийн баруун талд байгаа матрицаар үржүүлэх хэрэгтэй.

Бусад тэгшитгэлийг ижил төстэй байдлаар шийддэг.

Жишээ 2

AX = B тэгшитгэлийг шийд

Шийдэл: Матрицын урвуу нь (жишээ 1-ийг үзнэ үү)

Эдийн засгийн шинжилгээнд матрицын арга

Бусадтай зэрэгцэн тэд мөн програмыг олдог матрицын аргууд... Эдгээр аргууд нь шугаман болон вектор матрицын алгебр дээр суурилдаг. Ийм аргуудыг эдийн засгийн цогц, олон талт үзэгдлүүдийг шинжлэхэд ашигладаг. Ихэнхдээ эдгээр аргуудыг байгууллага, тэдгээрийн бүтцийн нэгжийн үйл ажиллагаанд харьцуулсан үнэлгээ хийх шаардлагатай үед ашигладаг.

Матрицын шинжилгээний аргыг хэрэглэх явцад хэд хэдэн үе шатыг ялгаж салгаж болно.

Эхний шатандэдийн засгийн үзүүлэлтүүдийн тогтолцоог бүрдүүлж, түүний үндсэн дээр системийн дугаарыг тусад нь мөрөнд харуулсан хүснэгт болох анхны мэдээллийн матрицыг бүрдүүлдэг. (i = 1,2, ...., n), босоо баганын дагуу - үзүүлэлтүүдийн тоо (j = 1,2, ...., m).

Хоёр дахь шатандбосоо багана бүрийн хувьд боломжит үзүүлэлтүүдийн хамгийн том утгыг нэгж болгон авч үзнэ.

Үүний дараа энэ баганад тусгагдсан бүх дүнг хамгийн том утгад хувааж, стандартчилагдсан коэффициентүүдийн матриц үүснэ.

Гурав дахь шатандматрицын бүх бүрэлдэхүүн хэсгүүд квадрат хэлбэртэй байна. Хэрэв тэдгээр нь өөр өөр ач холбогдолтой бол матрицын үзүүлэлт бүрт тодорхой жингийн хүчин зүйл оноогддог к... Сүүлчийн үнэ цэнийг шинжээчийн дүгнэлтээр тодорхойлно.

Хамгийн сүүлд, дөрөв дэх үе шатүнэлгээний утгыг олсон Р жөсөх, буурах дарааллаар бүлэглэв.

Тодорхойлсон матрицын аргуудыг жишээлбэл, янз бүрийн хөрөнгө оруулалтын төслүүдийн харьцуулсан дүн шинжилгээ хийх, түүнчлэн байгууллагын үйл ажиллагааны эдийн засгийн бусад үзүүлэлтүүдийг үнэлэхэд ашиглах ёстой.