سری تیلور، ریشه مربع. سری های توان، همگرایی آنها، گسترش توابع در سری های توانی

دانش آموزان ریاضی بالاتر باید بدانند که مجموع یک سری توانی معین متعلق به بازه همگرایی سری که به ما داده شده است یک تابع متمایز پیوسته و بی نهایت است. این سوال مطرح می شود: آیا می توان ادعا کرد که تابع دلخواه f (x) مجموع یک سری توان معین است؟ یعنی تحت چه شرایطی f-ija f (x) را می توان با یک سری توانی نشان داد؟ اهمیت چنین سؤالی در این واقعیت نهفته است که تقریباً می توان f-yu f (x) را با مجموع چند جمله اول سری توان، یعنی با یک چند جمله ای جایگزین کرد. این جایگزینی یک تابع با یک عبارت نسبتاً ساده - یک چند جمله ای - هنگام حل برخی مسائل نیز راحت است، یعنی: هنگام حل انتگرال، هنگام محاسبه و غیره.

ثابت شده است که برای برخی از fu و f (x)، که در آنها می توان مشتقات را تا مرتبه (n + 1) ام، از جمله دومی، در یک همسایگی (α - R؛ x 0 + R) محاسبه کرد. یک نقطه x = α فرمول معتبر است:

این فرمول به نام دانشمند معروف بروک تیلور نامگذاری شده است. سری که از قبلی بدست می آید سری Maclaurin نام دارد:

قانونی که امکان اجرای بسط را در سری Maclaurin می دهد:

1. مشتقات مرتبه اول، دوم، سوم ... را تعیین کنید.
2. مشتقات x = 0 را محاسبه کنید.
3. سری Maclaurin را برای این تابع بنویسید و سپس فاصله همگرایی آن را تعیین کنید.
4. بازه (-R; R)، جایی که بخش باقیمانده از فرمول Maclaurin را تعیین کنید

R n (x) -> 0 به عنوان n -> بی نهایت. اگر چنین وجود داشته باشد، تابع f (x) باید با مجموع سری Maclaurin منطبق باشد.

اجازه دهید اکنون سری Maclaurin را برای توابع فردی در نظر بگیریم.

1. بنابراین، اولین مورد f (x) = e x خواهد بود. البته چنین تابعی با توجه به ویژگی هایش مشتقاتی از مرتبه های مختلف دارد و f (k) (x) = e x که k برابر با همه است. x=0 را جایگزین کنید. f (k) (0) = e 0 = 1, k = 1,2 ... بر اساس موارد فوق، سطر e x به شکل زیر خواهد بود:

2. سری Maclaurin برای تابع f (x) = sin x. اجازه دهید بلافاصله روشن کنیم که f-s برای همه مجهولات مشتقاتی خواهد داشت، علاوه بر f "(x) = cos x = sin (x + n / 2)، f" "(x) = -sin x = sin (x + 2 * n / 2) ...، f (k) (x) = sin (x + k * n / 2)، که k برابر هر عدد طبیعی است. یعنی پس از انجام محاسبات ساده می توان به این نتیجه رسید. که سری f (x) = sin x به این شکل خواهد بود:

3. حالا بیایید سعی کنیم f-yu f (x) = cos x را در نظر بگیریم. برای همه مجهولات مشتقاتی از نظم دلخواه دارد و | f (k) (x) | = | cos (x + k * n / 2) |<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

بنابراین، ما مهم‌ترین توابعی را که می‌توان در سری Maclaurin گسترش داد، فهرست کرده‌ایم، اما برای برخی از توابع با سری تیلور تکمیل می‌شوند. اکنون آنها را نیز فهرست می کنیم. همچنین شایان ذکر است که سری تیلور و مکلارین بخش مهمی از کارگاه حل سری در ریاضیات عالی هستند. بنابراین، تیلور در رتبه بندی قرار می گیرد.

1. اولین سری برای f-ii f (x) = ln (1 + x) خواهد بود. مانند مثال‌های قبلی، برای f (x) = ln (1 + x)، می‌توانیم یک سری با استفاده از شکل کلی سری Maclaurin اضافه کنیم. با این حال، سری Maclaurin را می توان بسیار ساده تر برای این عملکرد به دست آورد. با ادغام یک سری هندسی خاص، یک سری برای f (x) = ln (1 + x) از چنین نمونه ای دریافت می کنیم:

2. و دومی که در مقاله ما نهایی خواهد شد، سری f (x) = arctan x خواهد بود. برای x متعلق به بازه [-1؛ 1]، تجزیه معتبر است:

همین. این مقاله به بررسی پرکاربردترین سری های تیلور و مکلارین در ریاضیات عالی، به ویژه در دانشگاه های اقتصاد و فنی پرداخته است.

چگونه فرمول های ریاضی را در وب سایت قرار دهیم؟

اگر زمانی نیاز دارید که یک یا دو فرمول ریاضی را به یک صفحه وب اضافه کنید، ساده ترین راه برای انجام این کار همانگونه است که در مقاله توضیح داده شده است: فرمول های ریاضی به راحتی به شکل تصاویری که Wolfram Alpha به طور خودکار تولید می کند در سایت قرار می گیرند. این روش همه کاره علاوه بر سادگی، به بهبود دید سایت شما در موتورهای جستجو کمک می کند. مدت زیادی است که کار می کند (و، فکر می کنم، برای همیشه کار خواهد کرد)، اما از نظر اخلاقی منسوخ شده است.

اگر به طور مرتب از فرمول های ریاضی در سایت خود استفاده می کنید، پس توصیه می کنم از MathJax استفاده کنید، یک کتابخانه جاوا اسکریپت ویژه که نمادهای ریاضی را در مرورگرهای وب با استفاده از نشانه گذاری MathML، LaTeX یا ASCIIMathML نمایش می دهد.

دو راه برای شروع استفاده از MathJax وجود دارد: (1) با استفاده از یک کد ساده، می توانید به سرعت یک اسکریپت MathJax را به سایت خود متصل کنید، که به طور خودکار از یک سرور راه دور در زمان مناسب بارگذاری می شود (لیست سرور). (2) اسکریپت MathJax را از یک سرور راه دور به سرور خود آپلود کنید و آن را به تمام صفحات سایت خود متصل کنید. روش دوم که پیچیده‌تر و زمان‌برتر است، سرعت بارگذاری صفحات سایت شما را افزایش می‌دهد و اگر سرور مادر MathJax به دلایلی موقتاً از دسترس خارج شود، به هیچ وجه روی سایت شما تأثیری نخواهد داشت. با وجود این مزایا، من روش اول را انتخاب کردم زیرا ساده تر، سریع تر است و به مهارت های فنی نیاز ندارد. از من پیروی کنید و در عرض 5 دقیقه می توانید از تمام ویژگی های MathJax در سایت خود استفاده کنید.

می توانید اسکریپت کتابخانه MathJax را از یک سرور راه دور با استفاده از دو نسخه کد گرفته شده از سایت اصلی MathJax یا از صفحه مستندات متصل کنید:

یکی از این انواع کد باید کپی و در کد صفحه وب شما جایگذاری شود، ترجیحاً بین تگ ها ویا درست بعد از برچسب ... طبق گزینه اول MathJax سریعتر لود می شود و سرعت صفحه را کمتر می کند. اما گزینه دوم به طور خودکار آخرین نسخه های MathJax را ردیابی و بارگذاری می کند. اگر اولین کد را وارد کنید، باید به صورت دوره ای به روز شود. اگر کد دوم را وارد کنید، صفحات کندتر بارگذاری می شوند، اما نیازی به نظارت مداوم به روز رسانی MathJax ندارید.

ساده ترین راه برای اتصال MathJax در بلاگر یا وردپرس است: در داشبورد سایت خود، ویجتی را که برای درج کد جاوا اسکریپت شخص ثالث طراحی شده است، اضافه کنید، نسخه اول یا دوم کد بارگیری ارائه شده در بالا را در آن کپی کنید و ویجت را نزدیکتر به آن قرار دهید. ابتدای قالب (به هر حال، این به هیچ وجه ضروری نیست زیرا اسکریپت MathJax به صورت ناهمزمان بارگیری می شود). همین. اکنون، نحو نشانه گذاری MathML، LaTeX و ASCIIMathML را یاد بگیرید، و آماده هستید تا فرمول های ریاضی را در صفحات وب سایت خود جاسازی کنید.

هر فراکتال بر اساس قانون خاصی ساخته می شود که به طور مداوم تعداد نامحدودی بارها اعمال می شود. هر یک از این زمان ها یک تکرار نامیده می شود.

الگوریتم تکراری برای ساخت اسفنج منگر بسیار ساده است: مکعب اصلی با ضلع 1 توسط صفحات موازی با وجوه خود به 27 مکعب مساوی تقسیم می شود. یک مکعب مرکزی و 6 مکعب مجاور از آن جدا می شود. نتیجه مجموعه ای متشکل از 20 مکعب کوچکتر باقی مانده است. با انجام همین کار با هر یک از این مکعب ها، مجموعه ای به دست می آوریم که قبلاً از 400 مکعب کوچکتر تشکیل شده است. با ادامه این روند بی انتها، یک اسفنج منگر به دست می آوریم.

در بین سری های فانکشنال، مهم ترین جایگاه را سری های پاور به خود اختصاص داده اند.

این سری یک سری قدرت نامیده می شود

که عبارت‌های آن توابع توانی هستند که در توان‌های غیر منفی افزایشی عدد صحیح مرتب شده‌اند ایکس، آ ج0 , ج 1 , ج 2 , ج n - مقادیر ثابت شماره ج1 , ج 2 , ج n - ضرایب اعضای مجموعه، ج0 - عضو رایگان اعضای سری توان روی خط اعداد کامل تعریف می شوند.

بیایید با مفهوم آشنا شویم دامنه همگرایی سری توان. این مجموعه مقادیر یک متغیر است ایکسکه برای آن مجموعه همگرا می شود. سری های قدرت دارای یک منطقه همگرایی نسبتاً ساده هستند. برای مقادیر واقعی متغیر ایکسدامنه همگرایی یا از یک نقطه تشکیل شده است، یا مقداری بازه (فاصله همگرایی)، یا منطبق بر کل محور است. گاو نر .

وقتی در یک سری توان جایگزین می شوند، مقادیر ایکس= 0 یک سری اعداد دریافت می کنید

ج0 +0+0+...+0+... ,

که همگرا می شود.

بنابراین، برای ایکس= 0 هر سری توان همگرا می شود و بنابراین، منطقه همگرایی آن نمیتواند خالی باشد. ساختار منطقه همگرایی تمام سری های توان یکسان است. با استفاده از قضیه زیر می توان آن را ایجاد کرد.

قضیه 1 (قضیه هابیل)... اگر سری توان برای مقداری همگرا شود ایکس = ایکس 0 غیر صفر، سپس همگرا می شود، و علاوه بر این، مطلقاً برای همه مقادیر |ایکس| < |ایکس 0 | ... توجه کنید: هم مقدار شروع "x صفر است" و هم هر مقدار "x" که با مقدار شروع مقایسه می شود مدولو گرفته می شود - بدون در نظر گرفتن علامت.

نتیجه. اگر سری قدرت واگرا می شود به مقداری ایکس = ایکس 1 ، سپس برای همه مقادیر واگرا می شود |ایکس| > |ایکس 1 | .

همانطور که قبلا متوجه شدیم، هر سری توان در مقدار همگرا می شود ایکس= 0. سری های توانی وجود دارند که فقط برای همگرا هستند ایکس= 0 و برای مقادیر دیگر واگرا می شوند NS... با حذف این مورد از در نظر گرفتن، فرض می کنیم که سری توان برای مقداری همگرا می شود ایکس = ایکس 0 غیر صفر سپس با قضیه هابیل در تمام نقاط بازه همگرا می شود] - | ایکس0 |, |ایکس 0 |[ (فاصله ای که مرزهای چپ و راست آن مقادیر x هستند که در آن سری توانی به ترتیب با علامت منفی و مثبت همگرا می شود)، متقارن در مورد مبدا.

اگر سری توان در مقداری واگرا شود ایکس = ایکس 1 ، سپس بر اساس نتیجه قضیه آبل، در تمام نقاط خارج از بخش نیز واگرا می شود [- | ایکس1 |, |ایکس 1 |] ... از این رو نتیجه می شود که برای هر سری توان یک بازه متقارن در مورد مبدا وجود دارد که نامیده می شود فاصله همگرایی ، در هر نقطه ای که سری همگرا می شود، در مرزها ممکن است همگرا شود و ممکن است واگرا شود، و نه لزوماً همزمان، اما خارج از بخش، سری واگرا می شود. عدد آرشعاع همگرایی سری توان نامیده می شود.

در موارد خاص فاصله همگرایی سری توان می تواند تا یک نقطه منحط شود (سپس سری فقط برای ایکس= 0 و فرض می شود که آر= 0) یا کل خط اعداد را نشان می دهد (سپس این سری در تمام نقاط خط اعداد همگرا می شود و فرض می شود).

بنابراین، تعریف منطقه همگرایی یک سری توان شامل تعریف آن است شعاع همگرایی آرو بررسی همگرایی سری بر روی مرزهای فاصله همگرایی (at).

قضیه 2.اگر تمام ضرایب سری توان، از یک عدد شروع شود، غیر صفر باشد، شعاع همگرایی آن برابر است با حد نسبت مقادیر مطلق ضرایب مجموع عبارت‌های زیر مجموعه، یعنی.

مثال 1. ناحیه همگرایی یک سری توان را بیابید

راه حل. اینجا

با استفاده از فرمول (28) شعاع همگرایی این سری را پیدا می کنیم:

اجازه دهید همگرایی سری را در انتهای بازه همگرایی بررسی کنیم. مثال 13 نشان می دهد که این سری برای ایکس= 1 و در واگرایی است ایکس= -1. در نتیجه، منطقه همگرایی یک نیمه بازه است.

مثال 2. ناحیه همگرایی یک سری توان را بیابید

راه حل. ضرایب سری مثبت هستند و

اجازه دهید حد این نسبت را پیدا کنیم، یعنی. شعاع همگرایی سری توان:

اجازه دهید همگرایی سری را در انتهای بازه بررسی کنیم. جایگزینی ارزش ها ایکس= -1/5 و ایکس= 1/5 در یک ردیف داده شده نشان می دهد:

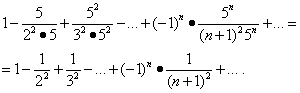
اولین مورد از این سری همگرا می شود (به مثال 5 مراجعه کنید). اما پس از آن، به موجب قضیه در بخش "همگرایی مطلق"، سری دوم نیز همگرا می شوند و منطقه همگرایی آن قطعه است.

مثال 3. ناحیه همگرایی یک سری توان را بیابید

راه حل. اینجا

با استفاده از فرمول (28)، شعاع همگرایی سری را پیدا می کنیم:

اجازه دهید همگرایی سری برای مقادیر را بررسی کنیم. با جایگزینی آنها در این ردیف، به ترتیب به دست می آوریم

هر دو سری واگرا می شوند، زیرا شرط همگرایی لازم برآورده نمی شود (شرایط مشترک آنها به صفر تمایل ندارند). بنابراین، در هر دو انتهای بازه همگرایی، سری داده شده واگرا می شود و منطقه همگرایی آن بازه است.

مثال 5. ناحیه همگرایی یک سری توان را بیابید

راه حل. رابطه، کجا، و را پیدا کنید :

طبق فرمول (28) شعاع همگرایی این سری است

,

یعنی سریال فقط برای همگرا می شود ایکس= 0 و برای مقادیر دیگر واگرا می شود NS.

مثال ها نشان می دهد که سری ها در انتهای بازه همگرایی متفاوت رفتار می کنند. در مثال 1، سری در یک انتهای بازه همگرایی همگرا می شود، و در سر دیگر واگرا می شود؛ در مثال 2، در هر دو انتها همگرا می شود، در مثال 3، در هر دو انتها واگرا می شود.

فرمول شعاع همگرایی یک سری توانی با این فرض به دست می‌آید که تمام ضرایب عبارت‌های سری، که از یک عدد شروع می‌شوند، غیر صفر هستند. بنابراین استفاده از فرمول (28) فقط در این موارد جایز است. اگر این شرط نقض شد، باید شعاع همگرایی سری توان را با استفاده از علامت دالامبر، یا با تغییر متغیر، سری را به شکلی تبدیل کنید که در آن شرط مشخص شده برآورده شود.

مثال 6. بازه همگرایی یک سری توان را بیابید

راه حل. این مجموعه دارای اعضایی با درجات فرد نیست. NS... بنابراین، سری را با تنظیم تغییر شکل می دهیم. سپس سریال را دریافت می کنیم

برای یافتن شعاع همگرایی که فرمول (28) را می توان اعمال کرد. از آنجا که، a، پس شعاع همگرایی این سری

بنابراین، از برابری که به دست می آوریم، این سری در بازه همگرا می شود.

مجموع سری توان. تمایز و ادغام سری های قدرت

اجازه دهید برای یک سری قدرت

شعاع همگرایی آر> 0، یعنی این سری در بازه همگرا می شود.

سپس هر مقدار NSاز بازه همگرایی، مجموع معینی از سری مطابقت دارد. در نتیجه، مجموع سری توان تابعی از NSدر بازه همگرایی نشان دادن آن از طریق f(ایکس) می توانیم برابری را بنویسیم

درک آن به این معنا که مجموع سری در هر نقطه NSاز فاصله همگرایی برابر با مقدار تابع است f(ایکس) در این مرحله. به همین معنا خواهیم گفت که سری توان (29) به تابع همگرا می شود f(ایکس) در بازه همگرایی.

در خارج از فاصله همگرایی، برابری (30) بی معنی است.

مثال 7.مجموع مجموع یک سری توان را پیدا کنید

راه حل. این یک سری هندسی با آ= 1 و q= ایکس... بنابراین مجموع آن یک تابع است ... سری همگرا می شود اگر، و بازه همگرایی آن است. بنابراین، برابری

فقط برای مقادیر معتبر است، اگرچه تابع برای همه مقادیر تعریف شده است NS، جز NS= 1.

می توان ثابت کرد که مجموع سری توان f(ایکس) پیوسته و قابل تمایز در هر بخش در داخل بازه همگرایی، به ویژه، در هر نقطه از بازه همگرایی سری است.

اجازه دهید قضایایی را در مورد تمایز ترم به ترم و ادغام سری های توان ارائه کنیم.

قضیه 1.سری توانی (30) در بازه همگرایی خود را می توان تعداد نامحدودی از نظر اصطلاحی متمایز کرد و سری توانی حاصله شعاع همگرایی مشابه سری اصلی دارند و مجموع آنها به ترتیب برابر است.

قضیه 2.سری توان (30) را می توان تعداد نامحدودی بار در محدوده 0 تا ادغام کرد NS، اگر، و سری توانی حاصل شعاع همگرایی مشابه سری اصلی دارند و مجموع آنها به ترتیب برابر است

گسترش توابع در سری های توانی

اجازه دهید یک تابع داده شود f(ایکس) که باید در یک سری قدرت گسترش یابد، یعنی. به شکل (30):

وظیفه تعیین ضرایب است ردیف (30). برای این، با تمایز برابری (30) ترم به ترم، به طور متوالی در می یابیم:

……………………………………………….. (31)

تنظیم برابری (30) و (31) NS= 0، پیدا می کنیم

با جایگزینی عبارات یافت شده به برابری (30)، به دست می آوریم

(32)

اجازه دهید یک بسط در یک سری Maclaurin از برخی توابع ابتدایی پیدا کنیم.

مثال 8.تابع سری Maclaurin را گسترش دهید

راه حل. مشتقات این تابع مانند خود تابع است:

بنابراین، در NS= 0 داریم

با جایگزینی این مقادیر به فرمول (32)، بسط مورد نیاز را بدست می آوریم:

(33)

این سری روی خط اعداد کامل (شعاع همگرایی آن) همگرا می شود.

16.1. بسط توابع ابتدایی در سری تیلور و

ماکلورین

اجازه دهید نشان دهیم که اگر یک تابع دلخواه در مجموعه تعریف شده باشد
، در مجاورت نقطه
مشتقات زیادی دارد و مجموع یک سری توان است:

سپس ضرایب این سری را می توان یافت.

جایگزین در سری پاور
... سپس
.

اولین مشتق تابع را پیدا کنید
:

در
:
.

برای مشتق دوم بدست می آوریم:

در
:
.

ادامه این رویه nزمانی که می گیریم:
.

بنابراین، ما یک سری قدرت از فرم به دست آوردیم:

,

که نامیده می شود در کنار تیلوربرای عملکرد
در مجاورت نقطه
.

یک مورد خاص از سری تیلور است سری Maclaurinدر
:

باقی مانده سری تیلور (Maclaurin) با دور انداختن ردیف های اصلی به دست می آید nاولین اعضا و نشان داده شده به عنوان
... سپس تابع
را می توان به صورت مجموع نوشت nاعضای اولیه یک شماره
و بقیه
:,

.

باقی مانده معمولا
در فرمول های مختلف بیان می شود.

یکی از آنها به شکل لاگرانژ است:

، جایی که
.
.

توجه داشته باشید که در عمل از سری Maclaurin بیشتر استفاده می شود. بنابراین، برای نوشتن تابع
در قالب مجموع یک سری توان لازم است:

1) ضرایب سری Maclaurin (Taylor) را پیدا کنید.

2) ناحیه همگرایی سری توان به دست آمده را پیدا کنید.

3) ثابت کنید که سری داده شده به تابع همگرا می شود
.

قضیه1 (شرط لازم و کافی برای همگرایی سری Maclaurin). اجازه دهید شعاع همگرایی سری
... برای اینکه این سری در بازه همگرا شوند
برای عملکرد
، لازم و کافی است برای شرط:
در بازه زمانی مشخص شده

قضیه 2.اگر مشتقات هر مرتبه ای از تابع
در یک فاصله زمانی
محدود به مقدار مطلق به همان تعداد م، به این معنا که
، سپس در این بازه تابع
را می توان به یک سری Maclaurin گسترش داد.

مثال1 . در یک ردیف تیلور اطراف نقطه را باز کنید
عملکرد.

راه حل.

.

,;

,
;

,
;

,

.......................................................................................................................................

,
;

منطقه همگرایی
.

مثال2 . گسترش تابع در ردیف تیلور در اطراف نقطه
.

راه حل:

مقدار تابع و مشتقات آن را در پیدا کنید
.

,
;

,
;

...........……………………………

,
.

ما این مقادیر را در یک ردیف جایگزین می کنیم. ما گرفتیم:

یا
.

بیایید منطقه همگرایی این سری را پیدا کنیم. با توجه به ویژگی d'Alembert، سریال همگرا می شود اگر

.

بنابراین، برای هر این حد کمتر از 1 است و بنابراین منطقه همگرایی سری خواهد بود:
.

اجازه دهید چندین مثال از بسط در سری توابع ابتدایی ابتدایی Maclaurin را در نظر بگیریم. به یاد بیاورید که سری Maclaurin:

.

روی بازه همگرا می شود
برای عملکرد
.

توجه داشته باشید که برای گسترش تابع در یک سری، لازم است:

الف) ضرایب سری Maclaurin را برای این تابع پیدا کنید.

ب) شعاع همگرایی سری حاصل را محاسبه کنید.

ج) ثابت کنید که سری حاصل به تابع همگرا می شود
.

مثال 3.تابع را در نظر بگیرید
.

راه حل.

اجازه دهید مقدار تابع و مشتقات آن را در محاسبه کنیم
.

سپس ضرایب عددی سری عبارتند از:

برای هرکس nضرایب پیدا شده را جایگزین سری Maclaurin کنید و بدست آورید:

شعاع همگرایی سری حاصل را پیدا کنید، یعنی:

.

در نتیجه، مجموعه در فاصله زمانی همگرا می شود
.

این سری به تابع همگرا می شود برای هر ارزشی زیرا هر شکافی
عملکرد و مشتقات آن در مقدار مطلق محدود به تعداد است .

مثال4 . تابع را در نظر بگیرید
.

راه حل.

:

به راحتی می توان فهمید که مشتقات مرتبه زوج هستند
، و مشتقات از ترتیب فرد هستند. ضرایب پیدا شده را جایگزین سری Maclaurin می کنیم و بسط را بدست می آوریم:

بیایید فاصله همگرایی این سری را پیدا کنیم. بر اساس دالامبر:

برای هرکس ... در نتیجه، مجموعه در فاصله زمانی همگرا می شود
.

این سری به تابع همگرا می شود
، زیرا تمام مشتقات آن محدود به یک است.

مثال5 .
.

راه حل.

اجازه دهید مقدار تابع و مشتقات آن را در پیدا کنیم
:

بنابراین، ضرایب این سری:
و
، از این رو:

به طور مشابه با سری قبلی، منطقه همگرایی
... سری به تابع همگرا می شود
، زیرا تمام مشتقات آن محدود به یک است.

توجه داشته باشید که تابع
بسط فرد و سری در درجات فرد، تابع
- گسترش یکنواخت و سری در قدرت های زوج.

مثال6 . سری دو جمله ای:
.

راه حل.

اجازه دهید مقدار تابع و مشتقات آن را در پیدا کنیم
:

از اینجا مشخص می شود که:

این مقادیر ضرایب را در سری Maclaurin جایگزین کنید و بسط این تابع را در یک سری توان بدست آورید:

شعاع همگرایی این سری را بیابید:

در نتیجه، مجموعه در فاصله زمانی همگرا می شود
... در نقاط حد در
و
مجموعه ممکن است بسته به توان همگرا شود یا نباشد
.

سری مورد مطالعه در فاصله زمانی همگرا می شود
برای عملکرد
، یعنی مجموع شارژ
در
.

مثال7 . اجازه دهید در یک سری Maclaurin این تابع را گسترش دهیم
.

راه حل.

برای گسترش این تابع به صورت سری، از سری دو جمله ای برای استفاده می کنیم
... ما گرفتیم:

بر اساس ویژگی سری توان (سری توان را می توان در ناحیه همگرایی آن یکپارچه کرد) انتگرال سمت چپ و راست این سری را پیدا می کنیم:

بیایید منطقه همگرایی این سری را پیدا کنیم:
,

یعنی منطقه همگرایی این سری بازه است
... اجازه دهید همگرایی سری را در انتهای بازه تعریف کنیم. در

... این ردیف یک ردیف هماهنگ است، یعنی واگرا می شود. در
ما یک سری اعداد با یک عبارت مشترک دریافت می کنیم
.

سری لایب نیتس همگرا می شوند. بنابراین، منطقه همگرایی این سری فاصله است
.

16.2. استفاده از سری قدرت در محاسبات تقریبی

در محاسبات تقریبی، سری های قدرت نقش فوق العاده مهمی دارند. با کمک آنها جداول توابع مثلثاتی، جداول لگاریتم، جداول مقادیر سایر توابع گردآوری شد که در زمینه های مختلف دانش، به عنوان مثال، در تئوری احتمالات و آمار ریاضی استفاده می شود. علاوه بر این، بسط توابع در یک سری توان برای مطالعه نظری آنها مفید است. مسئله اصلی هنگام استفاده از سری توان در محاسبات تقریبی، مسئله تخمین خطا هنگام جایگزینی مجموع یک سری با مجموع اولین آن است. nاعضا.

دو مورد را در نظر بگیرید:

تابع به سری های متناوب گسترش می یابد.

تابع به یک سری ثابت گسترش می یابد.

محاسبه با استفاده از سری های متناوب

اجازه دهید تابع
به یک سری توان متناوب گسترش یافته است. سپس، هنگام محاسبه این تابع برای یک مقدار خاص ما یک سری عددی به دست می آوریم که می توان آزمون لایب نیتس را برای آن اعمال کرد. مطابق با این ویژگی، اگر مجموع سری با مجموع اولین آن جایگزین شود nشرایط، پس خطای مطلق از جمله اول باقیمانده این سری تجاوز نمی کند، یعنی:
.

مثال8 . محاسبه
دقت 0.0001

راه حل.

ما از سری Maclaurin برای
، جایگزینی مقدار زاویه بر حسب رادیان:

اگر ترم اول و دوم سریال را با دقت مشخصی مقایسه کنیم، آنگاه:.

دوره سوم گسترش:

کمتر از دقت محاسباتی تعیین شده بنابراین، برای محاسبه
کافی است دو نفر از سریال را ترک کنید، یعنی

.

بدین ترتیب
.

مثال9 . محاسبه
با دقت 0.001

راه حل.

ما از فرمول سری دوجمله ای استفاده خواهیم کرد. برای این کار بنویسید
مانند:
.

در این بیان
,

بیایید هر یک از اعضای سریال را با دقت مشخص شده مقایسه کنیم. واضح است که
... بنابراین، برای محاسبه
کافی است سه نفر از ردیف را ترک کنید.

یا
.

محاسبه با استفاده از سری های مثبت

مثال10 . عدد را محاسبه کنید دقت 0.001

راه حل.

در یک ردیف برای تابع
جایگزین
... ما گرفتیم:

اجازه دهید خطایی را تخمین بزنیم که وقتی مجموع سری با مجموع اولی جایگزین می شود ایجاد می شود اعضا. بیایید نابرابری آشکار را بنویسیم:

یعنی 2<<3. Используем формулу остаточного члена ряда в форме Лагранжа:
,
.

با توجه به شرایط مشکل، باید پیدا کنید nبه طوری که نابرابری زیر برقرار است:
یا
.

بررسی آن آسان است n= 6:
.

از این رو،
.

مثال11 . محاسبه
با دقت 0.0001

راه حل.

توجه داشته باشید که برای محاسبه لگاریتم ها می توان یک سری برای تابع اعمال کرد
، اما این سری بسیار کند همگرا می شود و برای دستیابی به دقت داده شده باید 9999 ترم گرفته شود! بنابراین، برای محاسبه لگاریتم، به عنوان یک قاعده، یک سری برای تابع
که روی بازه همگرا می شود
.

بیایید محاسبه کنیم
با استفاده از این ردیف بگذار باشد
، سپس .

از این رو،
,

به منظور محاسبه
با دقت معین، مجموع چهار جمله اول را می گیریم:
.

باقیمانده ردیف
دور انداختن بیایید خطا را تخمین بزنیم. بدیهی است که

یا
.

بنابراین، در سری هایی که برای محاسبه استفاده شد، به جای 9999 در سری برای تابع، فقط چهار عبارت اول را در نظر گرفت.
.

سوالات خودآزمایی

1. سریال تیلور چیست؟

2. سری Maclaurin چه نوع داشت؟

3. یک قضیه بسط یک تابع در یک سری تیلور را فرموله کنید.

4. بسط سری Maclaurin از توابع اصلی را بنویسید.

5. مناطق همگرایی سری در نظر گرفته شده را مشخص کنید.

6. چگونه می توان خطا در محاسبات تقریبی را با استفاده از سری توان تخمین زد؟

اگر تابع f (x)در برخی از بازه های حاوی نقطه است آ، مشتقات همه سفارشات، سپس فرمول تیلور را می توان برای آن اعمال کرد:

جایی که r n- به اصطلاح باقی مانده یا باقیمانده سری را می توان با استفاده از فرمول لاگرانژ تخمین زد:

، جایی که عدد x بین آن قرار دارد NSو آ.

اگر برای مقداری ارزش x r n®0 برای n® ¥، سپس در حد، فرمول تیلور برای این مقدار به یک همگرا تبدیل می شود سریال تیلور:

بنابراین تابع f (x)را می توان در یک سری تیلور در نقطه مورد بررسی گسترش داد NS، اگر:

1) دارای مشتقات تمام سفارشات است.

2) سری ساخته شده در این نقطه همگرا می شود.

در آ= 0 یک سری به نام دریافت می کنیم نزدیک مکلارین:

مثال 1 f (x) = 2ایکس.

راه حل... اجازه دهید مقادیر تابع و مشتقات آن را در پیدا کنیم NS=0

f (x) = 2ایکس, f ( 0) = 2 0 =1;

f ¢ (x) = 2ایکس ln2، f ¢ ( 0) = 2 0 ln2 = ln2;

f ¢¢ (x) = 2ایکس ln 2 2, f ¢¢ ( 0) = 2 0 ln 2 2 = ln 2 2;

f (n) (x) = 2ایکسلوگاریتم n 2, f (n) ( 0) = 2 0 لوگاریتم n 2 = ln n 2.

با جایگزینی مقادیر به دست آمده از مشتقات به فرمول سری تیلور، به دست می آوریم:

شعاع همگرایی این سری برابر با بی نهایت است؛ بنابراین، این بسط برای - ¥ معتبر است.<ایکس<+¥.

مثال 2 NS+4) برای تابع f (x) =ه ایکس.

راه حل... مشتقات تابع e را بیابید ایکسو ارزش آنها در نقطه NS=-4.

f (x)= e ایکس, f (-4) = e -4 ;

f ¢ (x)= e ایکس, f ¢ (-4) = e -4 ;

f ¢¢ (x)= e ایکس, f ¢¢ (-4) = e -4 ;

f (n) (x)= e ایکس, f (n) ( -4) = e -4 .

بنابراین، سری تیلور مورد نیاز تابع به شکل زیر است:

این بسط برای - ¥ نیز معتبر است<ایکس<+¥.

مثال 3 ... گسترش تابع f (x)= ln ایکسدر یک سری در قدرت ( NS- 1),

(یعنی در سری تیلور در مجاورت نقطه NS=1).

راه حل... مشتقات این تابع را بیابید.

با جایگزینی این مقادیر در فرمول، سری تیلور مورد نیاز را دریافت می کنیم:

با استفاده از آزمون d'Alembert، می توان مطمئن شد که سری برای همگرا هستند

½ NS- 1 ½<1. Действительно,

سری همگرا می شود اگر ½ NS- 1 ½<1, т.е. при 0<ایکس<2. При NS= 2 یک سری متناوب به دست می آوریم که شرایط آزمون لایب نیتس را برآورده می کند. در NS= 0 تابع تعریف نشده است. بنابراین، دامنه همگرایی سری تیلور بازه نیمه باز است (0؛ 2).

اجازه دهید بسط های به دست آمده را به روشی مشابه در سری Maclaurin (یعنی در مجاورت نقطه) ارائه کنیم. NS= 0) برای برخی از توابع ابتدایی:

(2) ,

(3) ,

(آخرین تجزیه نامیده می شود سری دوجمله ای)

مثال 4 ... یک تابع را در یک سری توان بسط دهید

راه حل... در بسط (1) جایگزین می کنیم NSبر - NS 2، دریافت می کنیم:

مثال 5 ... تابع سری Maclaurin را گسترش دهید

راه حل... ما داریم

با استفاده از فرمول (4) می توانیم بنویسیم:

جایگزین کردن برای NSبه فرمول -NS، ما گرفتیم:

از اینجا متوجه می شویم:

با گسترش براکت ها، مرتب کردن مجدد اصطلاحات سری و کاهش اصطلاحات مشابه، به دست می آوریم

این سری در بازه همگرا می شود

(-1؛ 1)، زیرا از دو سری به دست می آید که هر کدام در این بازه همگرا می شوند.

اظهار نظر .

از فرمول های (1) - (5) نیز می توان برای گسترش توابع مربوطه در یک سری تیلور استفاده کرد. برای بسط توابع در توان های عدد صحیح مثبت ( ها). برای انجام این کار، بر روی یک تابع معین، لازم است چنین تبدیل های یکسانی انجام شود تا یکی از توابع (1) - (5) به دست آید، که در آن، به جای NSهزینه های k ( ها) m، جایی که k یک عدد ثابت است، m یک عدد صحیح مثبت است. اغلب تغییر متغیر راحت است تی=هاو تابع حاصل را با توجه به t در یک سری Maclaurin گسترش دهید.

این روش قضیه منحصر به فرد بودن بسط یک تابع در یک سری توانی را نشان می دهد. ماهیت این قضیه این است که در مجاورت یک نقطه، دو سری توان متفاوت را نمی توان به دست آورد که به یک تابع همگرا شوند، مهم نیست که چگونه بسط آن انجام شود.

مثال 6 ... یک تابع را در یک سری تیلور در همسایگی یک نقطه بسط دهید NS=3.

راه حل... این مشکل را می توان مانند قبل با استفاده از تعریف سری تیلور حل کرد که برای آن لازم است مشتقات تابع و مقادیر آنها را در NS= 3. با این حال، استفاده از تجزیه موجود آسان تر خواهد بود (5):

سری به دست آمده برای همگرا می شود یا -3<ایکس- 3<3, 0<ایکس< 6 и является искомым рядом Тейлора для данной функции.

مثال 7 ... سری تیلور را با قدرت بنویسید ( NS-1) توابع .

راه حل.

مجموعه در همگرا می شود ، یا 2< ایکس 5 پوند