روش های یافتن ماتریس ماتریس معکوس حل معادلات ماتریسی

در بسیاری از خواص مشابه معکوس است.

یوتیوب دانشگاهی

1 / 5

✪ نحوه پیدا کردن معکوس یک ماتریس - bezbotvy

✪ ماتریس معکوس (2 راه برای پیدا کردن)

✪ ماتریس معکوس شماره 1

✪ 2015/01/28. ماتریس معکوس 3x3

✪ 2015/01/27. ماتریس معکوس 2x2

زیرنویس

خواص ماتریس معکوس

• det A - 1 = 1 det A (\ displaystyle \ det A ^ (- 1) = (\ frac (1) (\ det A)))، جایی که det (\ displaystyle \\ det)تعیین کننده را نشان می دهد.
• (A B) - 1 = B - 1 A - 1 (\ displaystyle \ (AB) ^ (- 1) = B ^ (- 1) A ^ (- 1))برای دو ماتریس معکوس مربع A (\ displaystyle A)و B (\ سبک نمایش B).
• (A T) - 1 = (A - 1) T (\ displaystyle \ (A ^ (T)) ^ (- 1) = (A ^ (- 1)) ^ (T))، جایی که (...) T (\ نمایش سبک (...) ^ (T))نشان دهنده یک ماتریس جابجا شده است.
• (k A) - 1 = k - 1 A - 1 (\ displaystyle \ (kA) ^ (- 1) = k ^ (- 1) A ^ (- 1))برای هر ضریب k ≠ 0 (\ displaystyle k \ not = 0).
• E - 1 = E (\ displaystyle \ E ^ (- 1) = E).
• اگر حل یک سیستم معادلات خطی ضروری باشد، (b بردار غیر صفر است) که در آن x (\ displaystyle x)بردار مورد نیاز است و اگر A - 1 (\ displaystyle A ^ (- 1))آن زمان وجود دارد x = A - 1 b (\ سبک نمایش x = A ^ (- 1) b)... در غیر این صورت، یا ابعاد فضای راه حل ها بزرگتر از صفر است یا اصلا وجود ندارد.

روشهای یافتن ماتریس معکوس

اگر ماتریس معکوس باشد، می توانید از یکی از روش های زیر برای یافتن معکوس ماتریس استفاده کنید:

روش های دقیق (مستقیم).

روش گاوس-اردن

بیایید دو ماتریس بگیریم: خودش آو مجرد E... بیایید یک ماتریس بدهیم آبه ماتریس هویت با استفاده از روش گاوس-جردن، با استفاده از تبدیل ها توسط ردیف (شما همچنین می توانید تبدیل ها را بر اساس ستون ها اعمال کنید، اما نه به هم زدن). پس از اعمال هر عملیات بر روی ماتریس اول، همان عملیات را بر روی ماتریس دوم اعمال کنید. هنگامی که کاهش ماتریس اول به فرم واحد تکمیل شد، ماتریس دوم برابر خواهد بود A-1.

هنگام استفاده از روش گاوسی، ماتریس اول از سمت چپ در یکی از ماتریس های ابتدایی ضرب می شود. Λ i (\ displaystyle \ Lambda _ (i))(ماتریس ترابری یا مورب با ماتریس های روی مورب اصلی به جز یک موقعیت):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A - 1 (\ displaystyle \ Lambda _ (1) \ cdot \ dots \ cdot \ Lambda _ (n) \ cdot A = \ Lambda A = E \ Rightarrow \ Lambda = A ^ (- 1)). Λ m = [1… 0 - a 1 m / amm 0… 0… 0… 1 - am - 1 m / amm 0… 0 0… 0 1 / amm 0… 0 0… 0 - am + 1 m / amm 1 … 0… 0… 0 - anm / amm 0… 1] (\ displaystyle \ Lambda _ (m) = (\ start (bmatrix) 1 & \ نقطه & 0 & -a_ (1m) / a_ (mm) & 0 & \ نقطه & 0 \\ &&& \ نقطه &&& \\ 0 & \ نقطه & 1 & -a_ (m-1m) / a_ (mm) & 0 & \ نقطه & 0 \\ 0 & \ نقطه & 0 & 1 / a_ (mm) & 0 & \ نقطه & 0 \\ 0 & \ نقطه & 0 & -a_ ( m + 1m) / a_ (mm) & 1 & \ نقطه & 0 \\ &&& \ نقطه &&& \\ 0 & \ نقطه & 0 & -a_ (nm) / a_ (mm) & 0 & \ نقطه & 1 \ انتهای (bmatrix))).

ماتریس دوم پس از اعمال تمامی عملیات برابر خواهد بود با Λ (\ displaystyle \ Lambda)یعنی مورد نظر خواهد بود. پیچیدگی الگوریتم - O (n 3) (\ displaystyle O (n ^ (3))).

استفاده از ماتریس متمم های جبری

ماتریس معکوس به ماتریس A (\ displaystyle A)، می تواند به صورت نمایش داده شود

A - 1 = adj (A) det (A) (\ displaystyle (A) ^ (- 1) = ((\ mbox (adj)) (A)) \ over (\ det (A))))

جایی که adj (A) (\ displaystyle (\ mbox (adj)) (A))- ماتریس پیوست؛

پیچیدگی الگوریتم به پیچیدگی الگوریتم برای محاسبه تعیین کننده O det بستگی دارد و برابر است با O (n²) · O det.

با استفاده از تجزیه LU / LUP

معادله ماتریسی A X = I n (\ شیوه نمایش AX = I_ (n))برای ماتریس معکوس X (\ displaystyle X)را می توان به عنوان یک مجموعه مشاهده کرد n (\ displaystyle n)سیستم های فرم A x = b (\ شیوه نمایش Ax = b)... نشان می دهیم i (\ displaystyle i)ستون هفتم ماتریس X (\ displaystyle X)در سراسر X i (\ displaystyle X_ (i)); سپس A X i = e i (\ شیوه نمایش AX_ (i) = e_ (i)), i = 1،…، n (\ displaystyle i = 1، \ ldots، n)، تا جایی که i (\ displaystyle i)ستون هفتم ماتریس I n (\ displaystyle I_ (n))بردار واحد است e i (\ displaystyle e_ (i))... به عبارت دیگر، یافتن ماتریس معکوس به حل n معادله با یک ماتریس و ضلع های مختلف سمت راست تقلیل می یابد. پس از انجام تجزیه LUP (زمان O (n³))، حل هر یک از n معادله به زمان O (n²) نیاز دارد، بنابراین این بخش از کار نیز به زمان O (n³) نیاز دارد.

اگر ماتریس A غیر دژنره باشد، تجزیه LUP را می توان برای آن محاسبه کرد P A = L U (\ سبک نمایش PA = LU)... بگذار باشد P A = B (\ سبک نمایش PA = B), B - 1 = D (\ سبک نمایش B ^ (- 1) = D)... سپس از خواص ماتریس معکوس می توانیم بنویسیم: D = U - 1 L - 1 (\ سبک نمایش D = U ^ (- 1) L ^ (- 1))... اگر این تساوی را در U و L ضرب کنیم، می توانیم دو برابری از فرم را بدست آوریم U D = L - 1 (\ style display UD = L ^ (- 1))و D L = U - 1 (\ displaystyle DL = U ^ (- 1))... اولین مورد از این برابری ها، سیستمی از معادلات خطی n² است n (n + 1) 2 (\ displaystyle (\ frac (n (n + 1)) (2)))که اضلاع سمت راست آن مشخص است (از خواص ماتریس های مثلثی). دومی نیز سیستمی از معادلات خطی n² را نشان می دهد n (n - 1) 2 (\ displaystyle (\ frac (n (n-1)) (2)))که اضلاع سمت راست آن مشخص است (همچنین از ویژگی های ماتریس های مثلثی). آنها با هم سیستمی از برابری های n² را نشان می دهند. با استفاده از این برابری‌ها، می‌توانیم به صورت بازگشتی همه عناصر n² ماتریس D را تعیین کنیم. سپس از برابری (PA) -1 = A -1 P -1 = B -1 = D. برابری را بدست می‌آوریم. A - 1 = D P (\ displaystyle A ^ (- 1) = DP).

در مورد استفاده از تجزیه LU، هیچ جایگشتی برای ستون‌های ماتریس D مورد نیاز نیست، اما راه‌حل می‌تواند واگرا شود حتی اگر ماتریس A غیردژنراته باشد.

پیچیدگی الگوریتم O (n³) است.

روش های تکراری

روش های شولتز

(Ψ k = E - AU k، U k + 1 = U k ∑ i = 0 n Ψ ki (\ سبک نمایش (\ شروع (موارد) \ Psi _ (k) = E-AU_ (k)، \\ U_ ( k + 1) = U_ (k) \ جمع _ (i = 0) ^ (n) \ Psi _ (k) ^ (i) \ پایان (موارد)))

تخمین خطا

انتخاب یک حدس اولیه

مشکل انتخاب یک تقریب اولیه در فرآیندهای وارونگی ماتریس تکراری در نظر گرفته شده در اینجا اجازه نمی دهد که آنها را به عنوان روش های جهانی مستقل در رقابت با روش های مستقیم وارونگی مبتنی بر، به عنوان مثال، بر روی تجزیه LU ماتریس ها در نظر بگیریم. توصیه هایی برای انتخاب وجود دارد U 0 (\ displaystyle U_ (0))حصول اطمینان از تحقق شرط ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (شعاع طیفی ماتریس کمتر از یک است) که برای همگرایی فرآیند لازم و کافی است. با این حال، در این مورد، ابتدا لازم است کران بالایی برای طیف ماتریس معکوس A یا ماتریس بدانیم. A A T (\ displaystyle AA ^ (T))(یعنی اگر A یک ماتریس قطعی مثبت متقارن باشد و ρ (A) ≤ β (\ displaystyle \ rho (A) \ leq \ بتا)، سپس می توانید بگیرید U 0 = α E (\ نمایش سبک U_ (0) = (\ آلفا) E)، جایی که ؛ اگر A یک ماتریس غیرمنحط دلخواه باشد و ρ (A A T) ≤ β (\ displaystyle \ rho (AA ^ (T)) \ leq \ بتا)سپس باور می شود U 0 = α A T (\ displaystyle U_ (0) = (\ alpha) A ^ (T))کجا نیز α ∈ (0، 2 β) (\ نمایش سبک \ آلفا \ در \ چپ (0، (\ فراک (2) (\ بتا)) \ راست)); البته می توانید شرایط را ساده کنید و از این واقعیت استفاده کنید ρ (A A T) ≤ k A A T k (\ displaystyle \ rho (AA ^ (T)) \ leq (\ mathcal (k)) AA ^ (T) (\ mathcal (k)))، قرار دادن U 0 = A T ‖ A A T ‖ (\ displaystyle U_ (0) = (\ frac (A ^ (T)) (\ | AA ^ (T) \ |)))). دوم، با چنین تعریفی از ماتریس اولیه، هیچ تضمینی وجود ندارد ‖ Ψ 0 ‖ (\ displaystyle \ | \ Psi _ (0) \ |)کوچک خواهد بود (حتی ممکن است باشد ‖ Ψ 0 ‖> 1 (\ displaystyle \ | \ Psi _ (0) \ |> 1)، و مرتبه بالای نرخ همگرایی فوراً آشکار نخواهد شد.

نمونه هایی از

ماتریس 2x2

A - 1 = [a b c d] - 1 = 1 det (A) [d - b - c a] = 1 a d - b c [d - b - c a]. (\ displaystyle \ mathbf (A) ^ (- 1) = (\ start (bmatrix) a & b \\ c & d \\\ end (bmatrix)) ^ (- 1) = (\ frac (1) (\ det (\ mathbf (A)))) (\ begin (bmatrix) \, \, \, d & \! \! - b \\ - c & \, a \\\ end (bmatrix)) = (\ frac (1) (ad- bc)) (\ begin (bmatrix) \, \, \, d & \! \! - b \\ - c & \, a \\\ end (bmatrix)).)

وارونگی یک ماتریس 2x2 فقط در صورتی امکان پذیر است a d - b c = det A ≠ 0 (\ displaystyle ad-bc = \ det A \ neq 0).

پیدا کردن ماتریس معکوس- کاری که اغلب با دو روش حل می شود:

• روش متمم های جبری، که در آن نیاز به یافتن عوامل تعیین کننده و جابجایی ماتریس ها است.
• با روش حذف مجهولات توسط گاوس، که در آن لازم است تبدیل های ماتریس ابتدایی را انجام دهید (افزودن ردیف ها، ضرب ردیف ها در همان تعداد و غیره).

برای کسانی که به ویژه کنجکاو هستند، روش های دیگری نیز وجود دارد، به عنوان مثال، روش تبدیل های خطی. در این درس سه روش و الگوریتم ذکر شده برای یافتن ماتریس معکوس با این روش ها را تحلیل خواهیم کرد.

ماتریس معکوس آ، چنین ماتریسی نامیده می شود

آ
. (1)

ماتریس معکوس ، که برای یافتن ماتریس مربع داده شده لازم است آ، چنین ماتریسی نامیده می شود

محصولی که توسط آن ماتریس ها آدر سمت راست ماتریس هویت است، یعنی
. (1)

ماتریس هویت یک ماتریس مورب است که در آن همه عناصر مورب برابر با یک هستند.

قضیه.برای هر ماتریس مربع غیر مفرد (غیر منحط، غیر مفرد)، می توانید ماتریس معکوس و علاوه بر این، تنها یک را پیدا کنید. برای یک ماتریس مربع خاص (منحط، منفرد)، معکوس وجود ندارد.

ماتریس مربع نامیده می شود غیر خاص(یا غیر منحط, غیر مفرد) اگر تعیین کننده آن صفر نباشد و خاص(یا منحط, مفرد) اگر تعیین کننده آن صفر باشد.

ماتریس معکوس را فقط برای یک ماتریس مربع می توان یافت. به طور طبیعی، ماتریس معکوس نیز مربع و از همان ترتیب ماتریس داده شده خواهد بود. ماتریسی که می توان برای آن ماتریس معکوس پیدا کرد، ماتریس معکوس نامیده می شود.

برای ماتریس معکوس یک قیاس مناسب با متقابل وجود دارد. برای هر عدد آ، برابر با صفر نیست، چنین عددی وجود دارد بکه کار آو ببرابر یک: اب= 1. عدد بمعکوس عدد نامیده می شود ب... به عنوان مثال، برای عدد 7، معکوس 1/7 است، زیرا 7 * 1/7 = 1 است.

یافتن ماتریس معکوس به روش متمم های جبری (ماتریس اتحاد)

برای یک ماتریس مربع غیر منفرد آمعکوس ماتریس است

تعیین کننده ماتریس کجاست آ، a ماتریس الحاقی با ماتریس است آ.

اتحاد با ماتریس مربع آماتریسی از همان مرتبه نامیده می شود که عناصر آن مکمل های جبری عناصر متناظر تعیین کننده ماتریس با توجه به ماتریس A هستند. بنابراین، اگر

سپس

و

الگوریتم یافتن ماتریس معکوس به روش متمم های جبری

1. تعیین کننده یک ماتریس داده شده را پیدا کنید آ... اگر تعیین کننده صفر باشد، جستجو برای ماتریس معکوس متوقف می شود، زیرا ماتریس منحط است و معکوس آن وجود ندارد.

2. ماتریس جابجا شده با توجه به آ.

3. عناصر ماتریس الحاقی را به عنوان مکمل های جبری Maritsa موجود در مرحله 2 محاسبه کنید.

4. اعمال فرمول (2): معکوس دترمینان ماتریس را ضرب کنید آ، به ماتریس الحاقی موجود در مرحله 4.

5. نتیجه به دست آمده در مرحله 4 را با ضرب این ماتریس بررسی کنید آبه ماتریس معکوس اگر حاصل ضرب این ماتریس ها برابر با ماتریس هویت باشد، ماتریس معکوس به درستی پیدا شده است. در غیر این صورت، روند حل را دوباره شروع کنید.

مثال 1.برای ماتریس

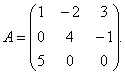
معکوس ماتریس را پیدا کنید

راه حل. برای یافتن ماتریس معکوس، باید تعیین کننده ماتریس را پیدا کرد آ... با قانون مثلث ها می یابیم:

از این رو ماتریس آ- غیر مفرد (غیر منحط، غیر مفرد) و برای آن معکوس وجود دارد.

ماتریس مجاور ماتریس داده شده را پیدا کنید آ.

ماتریس جابجا شده با توجه به ماتریس را پیدا کنید آ:

محاسبه عناصر ماتریس الحاقی به عنوان مکمل های جبری ماتریس جابجا شده با توجه به ماتریس آ:

بنابراین، ماتریس مجاور ماتریس آ، فرم را دارد

اظهار نظر.ترتیب محاسبه عناصر و جابجایی ماتریس می تواند متفاوت باشد. ابتدا می توان مکمل های جبری ماتریس را محاسبه کرد آو سپس ماتریس متمم را جابجا کنید. نتیجه باید همان عناصر ماتریس اتحاد باشد.

با استفاده از فرمول (2)، ماتریس را معکوس به ماتریس می یابیم آ:

یافتن ماتریس معکوس با حذف گاوسی

اولین قدم برای یافتن ماتریس معکوس با روش حذف گاوسی، تخصیص به ماتریس است. آماتریس هویت از همان ترتیب، آنها را با یک نوار عمودی جدا می کند. ما یک ماتریس دوتایی دریافت می کنیم. هر دو طرف این ماتریس را در ضرب می کنیم، سپس به دست می آوریم

,

الگوریتم یافتن ماتریس معکوس با حذف گاوسی مجهولات

1. به ماتریس آماتریس هویت را به همان ترتیب اختصاص دهید.

2. ماتریس دوگانه حاصل را طوری تبدیل کنید که ماتریس هویت در سمت چپ آن به دست آید، سپس ماتریس معکوس به طور خودکار در جای ماتریس هویت در سمت راست قرار می گیرد. ماتریس آدر سمت چپ با تبدیل ماتریس ابتدایی به ماتریس هویت تبدیل می شود.

2. اگر در طول تبدیل ماتریس آدر ماتریس هویت در هر سطر یا در هر ستون فقط صفر وجود خواهد داشت، سپس تعیین کننده ماتریس برابر با صفر است، و بنابراین، ماتریس آمنحط خواهد بود و ماتریس معکوس ندارد. در این مورد، یافتن بیشتر ماتریس معکوس خاتمه می یابد.

مثال 2.برای ماتریس

معکوس ماتریس را پیدا کنید

و آن را طوری تبدیل می کنیم که در سمت چپ ماتریس هویت را بدست آوریم. ما تحولات را شروع می کنیم.

سطر اول ماتریس چپ و راست را در (-3) ضرب می کنیم و به ردیف دوم اضافه می کنیم و سپس ردیف اول را در (4-) ضرب می کنیم و به سطر سوم اضافه می کنیم، سپس به دست می آید.

.

به طوری که در صورت امکان، هیچ اعداد کسری در طول تبدیل های بعدی وجود نداشته باشد، ابتدا یک واحد در ردیف دوم در سمت چپ ماتریس دو برابر شده ایجاد می کنیم. برای این کار، ردیف دوم را در 2 ضرب کرده و ردیف سوم را از آن کم کنید، سپس به دست می آوریم

.

ردیف اول را به ردیف دوم اضافه کنید و سپس ردیف دوم را در (9-) ضرب کنید و به ردیف سوم اضافه کنید. سپس می گیریم

.

سپس خط سوم را بر 8 تقسیم کنید

.

سطر سوم را در 2 ضرب می کنیم و به ردیف دوم اضافه می کنیم. معلوم می شود:

.

بیایید خط دوم و سوم را با هم عوض کنیم، سپس در نهایت می‌گیریم:

.

می بینیم که ماتریس واحد در سمت چپ به دست می آید، بنابراین ماتریس معکوس در سمت راست به دست می آید. بدین ترتیب:

.

می توانید صحت محاسبات را با ضرب ماتریس اصلی در ماتریس معکوس یافت شده بررسی کنید:

نتیجه باید یک ماتریس معکوس باشد.

مثال 3.برای ماتریس

معکوس ماتریس را پیدا کنید

راه حل. ساختن یک ماتریس دوگانه

و ما آن را متحول خواهیم کرد.

ردیف اول را در 3 و ردیف دوم را در 2 ضرب می کنیم و از دومی کم می کنیم و سپس ردیف اول را در 5 و ردیف سوم را در 2 ضرب می کنیم و از ردیف سوم کم می کنیم سپس به دست می آید.

.

خط اول را در 2 ضرب می کنیم و به دومی اضافه می کنیم و دومی را از خط سوم کم می کنیم و به دست می آید.

.

می بینیم که در خط سوم سمت چپ، همه عناصر برابر با صفر هستند. در نتیجه، ماتریس منحط است و ماتریس معکوس ندارد. ما دیگر از یافتن ماریتزا معکوس جلوگیری می کنیم.

اگر شرط $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ برآورده شود، ماتریس $ A ^ (- 1) $ نسبت به ماتریس مربع $ A $ معکوس نامیده می شود. ، که در آن $ E $ ماتریس هویت است که ترتیب آن برابر با ترتیب ماتریس $ A $ است.

ماتریس غیر منحط - ماتریسی که تعیین کننده آن برابر با صفر نیست. بر این اساس، یک ماتریس منحط، ماتریسی است که تعیین کننده آن برابر با صفر است.

ماتریس معکوس $ A ^ (- 1) $ وجود دارد اگر و فقط در صورتی که ماتریس $ A $ منحط نباشد. اگر ماتریس معکوس $ A ^ (- 1) $ وجود داشته باشد، یکتا است.

چندین راه برای یافتن معکوس یک ماتریس وجود دارد که ما به دو مورد از آنها خواهیم پرداخت. در این صفحه روش ماتریس الحاقی که در اکثر دروس ریاضیات عالی استاندارد در نظر گرفته می شود، بحث خواهد شد. روش دوم برای یافتن ماتریس معکوس (روش تبدیل های ابتدایی) که شامل استفاده از روش گاوس یا روش گاوس-جردن است، در قسمت دوم مورد بحث قرار گرفته است.

روش ماتریس الحاقی (الحاقی).

اجازه دهید ماتریس $ A_ (n \ بار n) $ داده شود. برای یافتن معکوس $ A ^ (- 1) $، سه مرحله لازم است:

1. تعیین کننده ماتریس $ A $ را بیابید و مطمئن شوید که $ \ دلتا A \ neq 0 $ ، یعنی. که ماتریس A غیر منحط است.
2. مکمل های جبری $ A_ (ij) $ از هر عنصر ماتریس $ A $ را بسازید و ماتریس $ A_ (n \ بار n) ^ (*) = \ چپ (A_ (ij) \ راست) $ را از مکمل های جبری پیدا کرد.
3. ماتریس معکوس را با در نظر گرفتن فرمول $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $ بنویسید.

ماتریس $ (A ^ (*)) ^ T $ اغلب به عنوان الحاق (مقابل، الحاق) به ماتریس $ A $ نامیده می شود.

اگر راه حل به صورت دستی انجام شود، روش اول فقط برای ماتریس های سفارشات نسبتا کوچک مناسب است: دوم ()، سوم ()، چهارم (). روش های دیگری برای یافتن معکوس یک ماتریس مرتبه بالاتر استفاده می شود. برای مثال روش گاوس که در قسمت دوم به آن پرداخته شده است.

مثال شماره 1

معکوس $ A = \ چپ (\ شروع (آرایه) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & - 1 و -9 و 0 \ انتهای (آرایه) \ سمت راست) $.

از آنجایی که تمام عناصر ستون چهارم برابر با صفر هستند، پس $ \ دلتا A = 0 $ (یعنی ماتریس $ A $ منحط است). از آنجایی که $ \ دلتا A = 0 $، ماتریس معکوس ماتریس $ A $ وجود ندارد.

مثال شماره 2

معکوس ماتریس $ A = \ چپ (\ شروع (آرایه) (cc) -5 & 7 \\ 9 & 8 \ پایان (آرایه) \ سمت راست) $.

ما از روش ماتریس الحاقی استفاده می کنیم. ابتدا، ما تعیین کننده ماتریس داده شده $ A $ را پیدا می کنیم:

$$ \ دلتا A = \ چپ | \ begin (آرایه) (cc) -5 & 7 \\ 9 & 8 \ end (array) \ سمت راست | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

از آنجایی که $ \ دلتا A \ neq 0 $ است، پس ماتریس معکوس وجود دارد، بنابراین راه حل را ادامه می دهیم. یافتن مکمل های جبری

\ شروع (تراز شده) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9؛ \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ انتهای (تراز شده)

ما یک ماتریس از مکمل های جبری می سازیم: $ A ^ (*) = \ چپ (\ شروع (آرایه) (cc) 8 & -9 \\ -7 & -5 \ پایان (آرایه) \ سمت راست) $.

ماتریس حاصل را جابه‌جا کنید: $ (A ^ (*)) ^ T = \ چپ (\ شروع (آرایه) (cc) 8 & -7 \\ -9 و -5 \ پایان (آرایه) \ راست) $ (نتیجه ماتریس اغلب به عنوان ماتریس الحاقی یا الحاقی به ماتریس $ A $ نامیده می شود. با استفاده از فرمول $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $، داریم:

$$ A ^ (- 1) = \ فرک (1) (- 103) \ cdot \ چپ (\ شروع (آرایه) (cc) 8 & -7 \\ -9 و -5 \ پایان (آرایه) \ راست) = \ چپ (\ شروع (آرایه) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ پایان (آرایه) \ راست) $$

بنابراین معکوس پیدا می شود: $ A ^ (- 1) = \ چپ (\ شروع (آرایه) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (آرایه) \ راست) $. برای بررسی صحت نتیجه کافی است صحت یکی از برابری ها را بررسی کنید: $ A ^ (- 1) \ cdot A = E $ یا $ A \ cdot A ^ (- 1) = E $. اجازه دهید برابری $ A ^ (- 1) \ cdot A = E $ را بررسی کنیم. برای اینکه کمتر با کسرها کار کنیم، ماتریس $ A ^ (- 1) $ را جایگزین می کنیم نه به شکل $ \ left (\ begin (آرایه) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ end (آرایه) \ راست) $، و به صورت $ - \ frac (1) (103) \ cdot \ چپ (\ شروع (آرایه) (cc) 8 & -7 \\ -9 و -5 \ پایان (آرایه) \ سمت راست) $:

پاسخ: $ A ^ (- 1) = \ چپ (\ شروع (آرایه) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ پایان (آرایه) \ راست) $.

مثال شماره 3

معکوس ماتریس $ A = \ چپ (\ شروع (آرایه) (cccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (آرایه) \ سمت راست) $ را بیابید.

بیایید با محاسبه تعیین کننده ماتریس $ A $ شروع کنیم. بنابراین، تعیین کننده ماتریس $ A $ به شرح زیر است:

$$ \ دلتا A = \ چپ | \ شروع (آرایه) (cccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (array) \ سمت راست | = 18-36 + 56-12 = 26. $$

از آنجایی که $ \ دلتا A \ neq 0 $ است، پس ماتریس معکوس وجود دارد، بنابراین راه حل را ادامه می دهیم. ما مکمل های جبری هر عنصر از یک ماتریس معین را پیدا می کنیم:

ماتریسی از متمم های جبری می سازیم و آن را جابجا می کنیم:

$$ A ^ * = \ چپ (\ شروع (آرایه) (cccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ پایان (آرایه) \ سمت راست); \; (A ^ *) ^ T = \ چپ (\ شروع (آرایه) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ پایان (آرایه) \ راست) $$

با استفاده از فرمول $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $، دریافت می کنیم:

$$ A ^ (- 1) = \ فراک (1) (26) \ cdot \ چپ (\ شروع (آرایه) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 و 37 \ پایان (آرایه) \ راست) = \ چپ (\ شروع (آرایه) (cccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ انتهای (آرایه) \ سمت راست) $$

بنابراین $ A ^ (- 1) = \ چپ (\ شروع (آرایه) (cccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \ end (آرایه) \ سمت راست) $. برای بررسی صحت نتیجه کافی است صحت یکی از برابری ها را بررسی کنید: $ A ^ (- 1) \ cdot A = E $ یا $ A \ cdot A ^ (- 1) = E $. اجازه دهید برابری $ A \ cdot A ^ (- 1) = E $ را بررسی کنیم. برای اینکه کمتر با کسرها کار کنیم، ماتریس $ A ^ (- 1) $ را جایگزین می کنیم نه به شکل $ \ left (\ begin (آرایه) (cc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ end (آرایه) \ سمت راست) $ و به صورت $ \ فراک (1) (26) \ cdot \ چپ ( \ شروع (آرایه) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ end (آرایه) \ سمت راست) $:

چک با موفقیت انجام شد، معکوس $ A ^ (- 1) $ به درستی پیدا شد.

پاسخ: $ A ^ (- 1) = \ چپ (\ شروع (آرایه) (cccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 / 13 & -3/26 & 37/26 \ end (آرایه) \ سمت راست) $.

مثال شماره 4

معکوس $ A = \ چپ (\ شروع (آرایه) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8 را پیدا کنید & -8 & -3 \ end (آرایه) \ سمت راست) $.

برای یک ماتریس مرتبه چهارم، یافتن ماتریس معکوس با استفاده از مکمل های جبری تا حدودی دشوار است. با این حال، چنین نمونه هایی در مقالات آزمون یافت می شود.

برای پیدا کردن معکوس یک ماتریس، ابتدا باید تعیین کننده ماتریس $ A $ را محاسبه کنید. بهترین راه برای انجام این کار در این شرایط این است که تعیین کننده را به ردیف (ستون) بسط دهید. هر سطر یا ستونی را انتخاب می کنیم و مکمل های جبری هر عنصر سطر یا ستون انتخاب شده را پیدا می کنیم.

جبر ماتریسی - ماتریس معکوس

ماتریس معکوس

ماتریس معکوسماتریسی نامیده می شود که وقتی در سمت راست و چپ در یک ماتریس معین ضرب شود، ماتریس هویت به دست می آید.
اجازه دهید ماتریس را معکوس به ماتریس نشان دهیم آاز طریق، سپس، طبق تعریف، دریافت می کنیم:

جایی که Eماتریس هویت است.
ماتریس مربعتماس گرفت غیر خاص (غیر منحط) اگر تعیین کننده آن صفر نباشد. در غیر این صورت نامیده می شود خاص (منحط) یا مفرد.

قضیه زیر صادق است: هر ماتریس غیر مفرد یک معکوس دارد.

عملیات یافتن ماتریس معکوس نامیده می شود درخواستماتریس ها الگوریتم وارونگی ماتریس را در نظر بگیرید. بگذارید یک ماتریس غیرمفرد داده شود n- مرتبه:

جایی که Δ = det آ ≠ 0.

مکمل جبری یک عنصرماتریس ها n- مرتبه آتعیین کننده ماتریس ( n-1) مرتبه ای که با حذف به دست می آید من-خط و jستون هفتم ماتریس آ:

به اصطلاح بسازیم پیوست شده استماتریس:

مکمل های جبری عناصر مربوطه ماتریس کجا هستند آ.
توجه داشته باشید که مکمل های جبری عناصر ردیف های ماتریس آدر ستون های مربوطه ماتریس قرار می گیرند Ã ، یعنی ماتریس در همان زمان جابجا می شود.
با تقسیم تمام عناصر ماتریس Ã توسط Δ - مقدار تعیین کننده ماتریس آ، ماتریس معکوس را در نتیجه بدست می آوریم:

ما تعدادی از خواص ویژه ماتریس معکوس را یادداشت می کنیم:
1) برای یک ماتریس معین آماتریس معکوس آن تنها است؛
2) اگر ماتریس معکوس وجود داشته باشد، پس سمت راست معکوسو سمت چپ معکوسماتریس ها با آن منطبق هستند.
3) یک ماتریس مربعی خاص (منحط) ماتریس معکوس ندارد.

ویژگی های اصلی ماتریس معکوس:
1) تعیین کننده ماتریس معکوس و تعیین کننده ماتریس اصلی مقادیر متقابل هستند.
2) ماتریس معکوس حاصل ضرب ماتریس های مربع برابر است با حاصل ضرب ماتریس معکوس عوامل به ترتیب معکوس:

3) معکوس جابجایی ماتریس برابر است با معکوس ماتریس انتقال داده شده:

مثال معکوس ماتریس داده شده را محاسبه کنید.

بگذارید یک ماتریس مربع از مرتبه n وجود داشته باشد

ماتریس A -1 نامیده می شود ماتریس معکوسبا توجه به ماتریس A، اگر A * A -1 = E، که در آن E ماتریس واحد مرتبه n است.

ماتریس واحد- چنین ماتریس مربعی، که در آن تمام عناصر در امتداد مورب اصلی که از گوشه سمت چپ بالا به گوشه سمت راست پایین می گذرد یک هستند و بقیه صفر هستند، به عنوان مثال:

ماتریس معکوسممکن است وجود داشته باشد فقط برای ماتریس های مربعآن ها برای آن ماتریس هایی با تعداد سطر و ستون یکسان.

قضیه شرط وجود ماتریس معکوس

برای اینکه یک ماتریس دارای ماتریس معکوس باشد، لازم و کافی است که غیر منحط باشد.

ماتریس A = (A1, A2, ... A n) نامیده می شود غیر منحطاگر بردارهای ستون به صورت خطی مستقل باشند. تعداد بردارهای ستون مستقل خطی یک ماتریس را رتبه ماتریس می گویند. بنابراین می توان گفت که برای وجود یک ماتریس معکوس، لازم و کافی است که رتبه ماتریس برابر با بعد آن باشد، یعنی. r = n

الگوریتم یافتن ماتریس معکوس

1. ماتریس A را در جدول حل سیستم معادلات به روش گاوس بنویسید و در سمت راست (به جای سمت راست معادلات) ماتریس E را اختصاص دهید.
2. با استفاده از تبدیل جردن، ماتریس A را به ماتریسی متشکل از ستون های واحد کاهش دهید. در این حالت، لازم است همزمان ماتریس E را تبدیل کنیم.
3. در صورت لزوم، ردیف ها (معادلات) آخرین جدول را به گونه ای تنظیم کنید که در زیر ماتریس A جدول اصلی، ماتریس واحد E را بدست آوریم.
4. ماتریس معکوس A -1 را که در آخرین جدول زیر ماتریس E جدول اصلی قرار دارد، بنویسید.

مثال 1

برای ماتریس A، ماتریس معکوس A -1 را پیدا کنید

راه حل: ماتریس A را یادداشت می کنیم و در سمت راست ماتریس هویت E را اختصاص می دهیم. با استفاده از تبدیل های Jordan، ماتریس A را به ماتریس هویت E کاهش می دهیم. محاسبات در جدول 31.1 نشان داده شده است.

بیایید صحت محاسبات را با ضرب ماتریس اصلی A و ماتریس معکوس A -1 بررسی کنیم.

در نتیجه ضرب ماتریس، ماتریس واحد به دست می آید. بنابراین محاسبات صحیح است.

پاسخ:

حل معادلات ماتریسی

معادلات ماتریسی می توانند به شکل زیر باشند:

AX = B، XA = B، AXB = C،

در جایی که A، B، C ماتریس های مشخص شده هستند، X ماتریس مورد نیاز است.

معادلات ماتریسی با ضرب معادله در ماتریس های معکوس آن حل می شود.

به عنوان مثال، برای پیدا کردن یک ماتریس از یک معادله، آن معادله را در سمت چپ ضرب کنید.

بنابراین، برای یافتن راه حل معادله، باید ماتریس معکوس را پیدا کنید و آن را در ماتریس سمت راست معادله ضرب کنید.

سایر معادلات نیز به همین ترتیب حل می شوند.

مثال 2

اگر معادله AX = B را حل کنید

راه حل: از آنجایی که معکوس ماتریس است (به مثال 1 مراجعه کنید)

روش ماتریسی در تحلیل اقتصادی

در کنار دیگران، آنها نیز کاربرد پیدا می کنند روش های ماتریسی... این روش ها بر اساس جبر خطی و ماتریس برداری هستند. چنین روش هایی برای تجزیه و تحلیل پدیده های پیچیده و چند بعدی اقتصادی استفاده می شود. بیشتر اوقات، این روش ها زمانی مورد استفاده قرار می گیرند که ارزیابی مقایسه ای از عملکرد سازمان ها و واحدهای ساختاری آنها ضروری باشد.

در فرآیند بکارگیری روش های تحلیل ماتریسی، مراحل مختلفی را می توان تشخیص داد.

در مرحله اولسیستمی از شاخص های اقتصادی تشکیل می شود و بر اساس آن ماتریسی از داده های اولیه تهیه می شود که جدولی است که در آن اعداد سیستم در خطوط جداگانه آن نشان داده شده است. (i = 1،2، ....، n)، و در امتداد ستون های عمودی - تعداد نشانگرها (j = 1،2، ....، m).

در مرحله دومبرای هر ستون عمودی، بزرگترین مقدار شاخص های موجود نشان داده می شود که به عنوان یک واحد در نظر گرفته می شود.

پس از آن، تمام مقادیر منعکس شده در این ستون بر بزرگترین مقدار تقسیم شده و ماتریسی از ضرایب استاندارد تشکیل می شود.

در مرحله سومتمام اجزای تشکیل دهنده ماتریس مربع هستند. اگر آنها اهمیت متفاوتی داشته باشند، به هر شاخص ماتریس یک فاکتور وزنی خاص اختصاص داده می شود ک... ارزش دومی با قضاوت متخصص تعیین می شود.

در آخرین مورد، مرحله چهارممقادیر یافت شده رتبه بندی R jبه ترتیب افزایش یا کاهش گروه بندی می شوند.

روش‌های ماتریسی مشخص شده باید به‌عنوان مثال در تحلیل مقایسه‌ای پروژه‌های سرمایه‌گذاری مختلف و همچنین در ارزیابی سایر شاخص‌های اقتصادی فعالیت‌های سازمان‌ها مورد استفاده قرار گیرد.