بردار ویژه یک ماتریس مربع، بردار ویژه ای است که وقتی در یک ماتریس معین ضرب می شود، یک بردار خطی ایجاد می کند. به عبارت ساده، هنگامی که یک ماتریس در یک بردار ویژه ضرب می شود، دومی ثابت می ماند، اما در عددی ضرب می شود.

تعریف

بردار ویژه یک بردار غیرصفر V است که وقتی در ماتریس مربع M ضرب می شود به خودش تبدیل می شود و عدد معینی λ افزایش می یابد. در نماد جبری، به نظر می رسد:

M × V = λ × V،

جایی که λ مقدار ویژه ماتریس M است.

بیایید به یک مثال عددی نگاه کنیم. برای راحتی، اعداد در ماتریس با یک نقطه ویرگول از هم جدا می شوند. بیایید یک ماتریس داشته باشیم:

• M = 0; 4
• 6; 10.

بیایید آن را در یک بردار ستون ضرب کنیم:

• V = -2;

وقتی یک ماتریس را در بردار ستونی ضرب می کنیم، یک بردار ستونی نیز بدست می آوریم. در شرایط دقیق ریاضی، فرمول ضرب یک ماتریس 2 × 2 در بردار ستونی به صورت زیر خواهد بود:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 به معنای عنصر ماتریس M است که در ردیف اول و ستون اول قرار دارد و M22 - عنصر واقع در ردیف دوم و ستون دوم. برای ماتریس ما، این عناصر برابر است با M11 = 0، M12 = 4، M21 = 6، M22 10. برای یک بردار ستون، این مقادیر V11 = –2، V21 = 1 است. طبق این فرمول، ما به دست می آوریم. نتیجه زیر حاصل ضرب یک ماتریس مربع با یک بردار:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

برای راحتی، بردار ستون را در یک ردیف بنویسیم. بنابراین، ماتریس مربع را در بردار (-2; 1) ضرب کردیم و به بردار (4; -2) رسیدیم. بدیهی است که این همان بردار ضرب در λ = -2 است. Lambda در این مورد نشان دهنده مقدار ویژه ماتریس است.

بردار ویژه یک ماتریس یک بردار خطی است، یعنی جسمی که با ضرب در یک ماتریس، موقعیت خود را در فضا تغییر نمی دهد. خط خطی در جبر برداری مشابه موازی بودن در هندسه است. در تفسیر هندسی، بردارهای خطی، پاره خط های جهت دار موازی با طول های مختلف هستند. از زمان اقلیدس، می دانیم که یک خط مستقیم دارای بی نهایت خطوط مستقیم موازی است، بنابراین منطقی است که فرض کنیم هر ماتریس دارای تعداد نامتناهی بردار ویژه است.

از مثال قبلی، می توانید ببینید که بردارهای ویژه می توانند (-8؛ 4)، و (16؛ -8)، و (32، -16) باشند. همه اینها بردارهای خطی مربوط به مقدار ویژه λ = -2 هستند. وقتی ماتریس اصلی را در این بردارها ضرب می کنیم، باز هم برداری را دریافت می کنیم که 2 برابر با اصلی تفاوت دارد. به همین دلیل است که هنگام حل مسائل یافتن بردار ویژه، باید فقط اشیاء بردار مستقل خطی را پیدا کرد. اغلب، برای یک ماتریس n × n، تعداد n بردار ویژه وجود دارد. ماشین حساب ما برای تجزیه و تحلیل ماتریس های مربع مرتبه دوم طراحی شده است، بنابراین، تقریباً همیشه در نتیجه، دو بردار ویژه پیدا می شود، به جز مواردی که با هم همخوانی دارند.

در مثال بالا، ما از قبل بردار ویژه ماتریس اصلی را می دانستیم و عدد لامبدا را به وضوح تعیین می کردیم. با این حال، در عمل، همه چیز برعکس اتفاق می افتد: مقادیر ویژه در ابتدا پیدا می شوند و تنها پس از آن بردارهای ویژه هستند.

الگوریتم برای حل

بیایید دوباره به ماتریس اصلی M نگاه کنیم و سعی کنیم هر دو بردار ویژه آن را پیدا کنیم. بنابراین ماتریس به نظر می رسد:

• M = 0; 4
• 6; 10.

ابتدا باید مقدار ویژه λ را تعیین کنیم که برای آن باید تعیین کننده ماتریس زیر را محاسبه کنیم:

• (0 - λ)؛ 4
• 6 (10 - λ).

این ماتریس با کم کردن λ مجهول از عناصر روی قطر اصلی به دست می آید. تعیین کننده با استفاده از فرمول استاندارد تعیین می شود:

• detA = M11 × M21 - M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

از آنجایی که بردار ما نباید صفر باشد، معادله حاصل را به صورت خطی وابسته در نظر می گیریم و detA تعیین کننده خود را با صفر برابر می کنیم.

(0 - λ) × (10 - λ) - 24 = 0

بیایید براکت ها را باز کنیم و معادله مشخصه ماتریس را بدست آوریم:

λ 2 - 10λ - 24 = 0

این معادله درجه دوم استاندارد است که باید با استفاده از تفکیک حل شود.

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

ریشه تشخیص sqrt (D) = 14 است، بنابراین، λ1 = -2، λ2 = 12. حال، برای هر مقدار لامبدا، باید یک بردار ویژه پیدا کنید. اجازه دهید ضرایب سیستم را برای λ = -2 بیان کنیم.

• M - λ × E = 2; 4
• 6; 12.

در این فرمول E ماتریس هویت است. بر اساس ماتریس به دست آمده، سیستمی از معادلات خطی را می سازیم:

2x + 4y = 6x + 12y،

که در آن x و y عناصر بردار ویژه هستند.

تمام X ها را در سمت چپ و همه بازیکنان را در سمت راست جمع کنید. بدیهی است - 4x = 8y. عبارت را بر - 4 تقسیم کنید و x = –2y را بدست آورید. اکنون می‌توانیم اولین بردار ویژه ماتریس را با گرفتن مقادیر مجهولات تعیین کنیم (بی نهایت بردارهای ویژه وابسته به خطی را به خاطر بسپاریم). بیایید y = 1 و سپس x = –2 را در نظر بگیریم. بنابراین، اولین بردار ویژه شبیه V1 = (–2; 1) است. به ابتدای مقاله برگردید. روی این شی برداری است که ماتریس را برای نشان دادن مفهوم بردار ویژه ضرب کردیم.

اکنون بردار ویژه λ = 12 را خواهیم یافت.

• M - λ × E = -12; 4
• 6; -2.

بیایید همان سیستم معادلات خطی را بسازیم.

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x = y.

حال اجازه دهید x = 1 را بگیریم، از این رو y = 3. بنابراین، بردار ویژه دوم شبیه V2 = (1؛ 3) است. هنگامی که ماتریس اصلی در این بردار ضرب می شود، نتیجه همیشه همان بردار ضرب در 12 خواهد بود. این نتیجه الگوریتم حل است. اکنون می دانید که چگونه به صورت دستی بردار ویژه یک ماتریس را تعریف کنید.

• تعیین کننده؛
• ردیابی، یعنی مجموع عناصر روی مورب اصلی؛
• رتبه، یعنی حداکثر تعداد سطر/ستون مستقل خطی.

این برنامه طبق الگوریتم فوق عمل می کند و فرآیند حل را به حداقل می رساند. ذکر این نکته ضروری است که لامبدا با حرف "c" در برنامه مشخص می شود. بیایید یک مثال عددی در نظر بگیریم.

نمونه ای از برنامه

بیایید سعی کنیم بردارهای ویژه را برای ماتریس زیر تعریف کنیم:

• M = 5; 13;
• 4; 14.

بیایید این مقادیر را در سلول های ماشین حساب وارد کرده و به شکل زیر پاسخ را دریافت کنیم:

• رتبه ماتریس: 2
• تعیین کننده ماتریس: 18;
• ردیابی ماتریس: 19;
• محاسبه بردار ویژه: c 2 - 19.00c + 18.00 (معادله مشخصه)؛
• محاسبه بردار ویژه: 18 (مقدار لامبدا اول).
• محاسبه بردار ویژه: 1 (مقدار لامبدا دوم)؛
• سیستم معادلات برای بردار 1: -13x1 + 13y1 = 4x1 - 4y1.
• سیستم معادلات برای بردار 2: 4x1 + 13y1 = 4x1 + 13y1.
• بردار ویژه 1: (1; 1);
• بردار ویژه 2: (-3.25؛ 1).

بنابراین، ما دو بردار ویژه مستقل خطی به دست آورده ایم.

نتیجه

جبر خطی و هندسه تحلیلی دروس استاندارد برای هر دانشجوی سال اول مهندسی هستند. تعداد زیاد بردارها و ماتریس ها وحشتناک است و به راحتی می توان در چنین محاسبات دست و پا گیر اشتباه کرد. برنامه ما به دانش آموزان اجازه می دهد تا محاسبات خود را بررسی کنند یا به طور خودکار مشکل پیدا کردن بردار خود را حل می کند. ماشین حساب های جبر خطی دیگری در کاتالوگ ما وجود دارد، از آنها در مطالعه یا کار خود استفاده کنید.

بخش اول حداقل مقررات را برای درک شیمی سنجی ارائه می کند و بخش دوم حاوی حقایقی است که برای درک عمیق تر از روش های تجزیه و تحلیل چند متغیره باید بدانید. Matrix.xlsکه همراه این سند است.

ارجاع به مثال ها به عنوان اشیاء اکسل در متن قرار می گیرند. این مثال ها ماهیت انتزاعی دارند و به هیچ وجه به مسائل شیمی تجزیه گره نمی خورند. نمونه های واقعی استفاده از جبر ماتریسی در شیمی سنجی در سایر متون اختصاص داده شده به کاربردهای مختلف شیمی سنجی در نظر گرفته شده است.

اکثر اندازه گیری های انجام شده در شیمی تجزیه مستقیم نیستند، اما غیر مستقیم... یعنی در آزمایش به جای مقدار آنالیت مورد نظر C (غلظت)، مقدار دیگری به دست می آید. ایکس(سیگنال) مرتبط اما برابر با C نیست، یعنی. ایکس(C) ≠ C. به عنوان یک قاعده، نوع وابستگی ایکس(C) شناخته شده نیست، با این حال، خوشبختانه در شیمی تجزیه، اکثر اندازه گیری ها متناسب هستند. این بدان معنی است که با افزایش غلظت C در آبار، سیگنال X به همان مقدار افزایش می یابد. ایکس(آج) = تبر(C). علاوه بر این، سیگنال ها نیز افزودنی هستند، به طوری که سیگنال از یک نمونه حاوی دو ماده با غلظت های C 1 و C 2 برابر با مجموع سیگنال های هر جزء خواهد بود، یعنی. ایکس(C 1 + C 2) = ایکس(C 1) + ایکس(ج 2). تناسب و افزایش با هم می دهد خطی بودن... مثال های زیادی برای نشان دادن اصل خطی بودن وجود دارد، اما کافی است به دو نمونه از بارزترین نمونه ها اشاره کنیم - کروماتوگرافی و طیف سنجی. دومین ویژگی آزمایش در شیمی تجزیه است چند کاناله... تجهیزات تحلیلی مدرن به طور همزمان سیگنال های بسیاری از کانال ها را اندازه گیری می کنند. به عنوان مثال، شدت عبور نور برای چندین طول موج به طور همزمان اندازه گیری می شود، یعنی. طیف بنابراین در آزمایش با سیگنال های زیادی سروکار داریم ایکس 1 , ایکس 2 ,...., ایکس n، مشخص کننده مجموعه ای از غلظت های C 1، C 2، ...، C m از مواد موجود در سیستم مورد مطالعه.

برنج. 1 طیف

بنابراین، یک آزمایش تحلیلی با خطی بودن و چند بعدی بودن مشخص می شود. بنابراین، راحت است که داده های تجربی را به عنوان بردار و ماتریس در نظر بگیریم و آنها را با استفاده از دستگاه جبر ماتریسی دستکاری کنیم. ثمربخشی این رویکرد با مثال نشان داده شده در نشان داده شده است، که سه طیف ثبت شده برای 200 طول موج از 4000 تا 4796 سانتی متر – 1 را نشان می دهد. اولین ( ایکس 1) و دومی ( ایکس 2) طیف برای نمونه های استاندارد به دست آمد که در آنها غلظت دو ماده A و B مشخص است: در نمونه اول [A] = 0.5، [B] = 0.1، و در نمونه دوم [A] = 0.2، [B] ] = 0.6. در مورد یک نمونه جدید و ناشناخته که طیف آن مشخص شده است، چه می توان گفت ایکس 3 ?

سه طیف تجربی را در نظر بگیرید ایکس 1 , ایکس 2 و ایکس 3 به عنوان سه بردار بعد 200. با استفاده از جبر خطی می توان به راحتی نشان داد که ایکس 3 = 0.1 ایکس 1 +0.3 ایکس 2؛ بنابراین، نمونه سوم بدیهی است که تنها حاوی مواد A و B در غلظت های [A] = 0.5 × 0.1 + 0.2 × 0.3 = 0.11 و [B] = 0.1 × 0.1 + 0.6 × 0.3 = 0.19 است.

1. اطلاعات اولیه

1.1 ماتریس

ماتریسبه عنوان مثال یک جدول مستطیلی از اعداد نامیده می شود

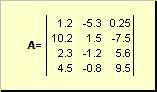
برنج. 2 ماتریس

ماتریس ها با حروف بزرگ درشت مشخص شده اند ( آ، و عناصر آنها - حروف کوچک مربوطه با شاخص ها، یعنی. آ ij. شاخص اول ردیف ها را شماره گذاری می کند و دومی ستون ها را شماره گذاری می کند. در شیمی سنجی، مرسوم است که حداکثر مقدار شاخص را با همان حرف خود شاخص، اما با حروف بزرگ نشان می دهند. بنابراین ماتریس آهمچنین می توان به صورت ( آ ij , من = 1,..., من; j = 1,..., جی). برای ماتریس نشان داده شده در مثال من = 4, جی= 3 و آ 23 = −7.5.

جفت اعداد منو جیبعد ماتریس نامیده می شود و به عنوان نشان داده می شود من× جی... نمونه ای از یک ماتریس در شیمی سنجی مجموعه ای از طیف های به دست آمده برای مننمونه بر روی جیطول موج

1.2. عملیات ماتریس ساده

ماتریس ها می توانند ضرب در اعداد... در این حالت هر عنصر در این عدد ضرب می شود. مثلا -

برنج. 3 ضرب ماتریس در عدد

دو ماتریس از یک بعد می توانند از نظر عنصر باشند تا کردنو کم کردن... مثلا،

برنج. 4 اضافه کردن ماتریس

در نتیجه ضرب در عدد و جمع، ماتریسی با همان ابعاد به دست می آید.

ماتریس صفر ماتریسی متشکل از صفر است. نشان داده شده است O... بدیهی است که آ+O = آ, آ−آ = Oو 0 آ = O.

ماتریس می تواند باشد جابجا کردن... در طی این عملیات، ماتریس برگردانده می شود، یعنی. سطرها و ستون ها با هم عوض می شوند. انتقال با سکته مغزی نشان داده می شود، آ"یا شاخص آتی بنابراین اگر آ = {آ ij , من = 1,..., من; j = 1,...,جی)، سپس آ t = ( آ جی , j = 1,...,جی; i = 1، ...، من). مثلا

برنج. 5 ماتریس را جابجا کنید

واضح است که ( آ t) t = آ, (آ+ب) t = A t + بتی

1.3. ضرب ماتریس

ماتریس ها می توانند تکثیر کردن، اما به شرطی که دارای ابعاد مناسب باشند. چرایی این چنین است از تعریف مشخص خواهد شد. حاصل ضرب ماتریس آ، بعد، ابعاد، اندازه من× کو ماتریس ها ب، بعد، ابعاد، اندازه ک× جیماتریس نامیده می شود سی، بعد، ابعاد، اندازه من× جیکه عناصر آن اعداد هستند

بنابراین، برای تولید ABلازم است که تعداد ستون ها در ماتریس سمت چپ آبرابر تعداد سطرهای ماتریس سمت راست بود ب... نمونه ای از محصول ماتریس -

شکل 6 محصول ماتریس

قانون ضرب ماتریس را می توان به صورت زیر فرموله کرد. برای پیدا کردن یک عنصر از یک ماتریس سیایستاده در تقاطع من-خط و jستون -ام ( ج ij) باید عنصر به عنصر ضرب شود منسطر اول ماتریس آبر jستون هفتم ماتریس دوم بو تمام نتایج را جمع کنید. بنابراین در مثال نشان داده شده، یک عنصر از ردیف سوم و ستون دوم به عنوان مجموع حاصلضرب های عنصری ردیف سوم به دست می آید. آو ستون دوم ب

شکل 7 عنصر محصول ماتریس

حاصل ضرب ماتریس ها به ترتیب بستگی دارد، یعنی. AB ≠ BA، اگر فقط به دلایل بعد. می گویند غیر قابل تعویض است. با این حال، محصولات ماتریسی انجمنی هستند. معنیش اینه که ABC = (AB)سی = آ(قبل از میلاد مسیح). علاوه بر این، توزیعی نیز هست، یعنی. آ(ب+سی) = AB+AC... بدیهی است که AO = O.

1.4. ماتریس های مربعی

اگر تعداد ستون های ماتریس برابر با تعداد سطرهای آن باشد ( من = J = N، پس چنین ماتریسی مربع نامیده می شود. در این بخش، ما فقط چنین ماتریس هایی را در نظر خواهیم گرفت. از بین این ماتریس ها می توان ماتریس هایی با ویژگی های خاص را مشخص کرد.

تنهاماتریس (نشان داده شده است من،و گاهی اوقات E) ماتریسی است که در آن همه عناصر برابر با صفر هستند، به جز عناصر مورب که برابر با 1 هستند، یعنی.

به طور مشخص Ai = IA = آ.

ماتریس نامیده می شود مورباگر همه عناصر آن، به جز عناصر مورب ( آ ii) برابر با صفر هستند. مثلا

برنج. 8 ماتریس مورب

ماتریس آبالا نامیده می شود مثلثیاگر تمام عناصر آن زیر قطر برابر با صفر باشد، یعنی. آ ij= 0، برای من>j... مثلا

برنج. 9 ماتریس مثلثی بالا

ماتریس مثلثی پایین به طور مشابه تعریف شده است.

ماتریس آتماس گرفت متقارن، اگر آ t = آ... به عبارت دیگر آ ij = آ جی... مثلا

برنج. 10 ماتریس متقارن

ماتریس آتماس گرفت ارتودنسی، اگر

آتی آ = AA t = من.

ماتریس نامیده می شود طبیعیاگر

1.5. ردیابی و تعیین کننده

ذیلماتریس مربع آ(با Tr ( آ) یا Sp ( آ)) مجموع عناصر مورب آن است،

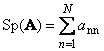
مثلا،

برنج. 11 ردیابی ماتریسی

بدیهی است که

Sp (α آ) = α Sp ( آ) و

Sp ( آ+ب) = Sp ( آ) + Sp ( ب).

می توان نشان داد که

Sp ( آ) = Sp ( آ t)، Sp ( من) = ن,

و همچنین آن

Sp ( AB) = Sp ( BA).

یکی دیگر از ویژگی های مهم ماتریس مربعی بودن آن است تعیین کننده(نشان داده شده با det ( آ)). تعیین تعیین کننده در حالت کلی بسیار دشوار است، بنابراین ما با ساده ترین نسخه - ماتریس شروع می کنیم. آابعاد (2×2). سپس

برای یک ماتریس (3×3)، تعیین کننده خواهد بود

در مورد ماتریس ( ن× ن) تعیین کننده به صورت مجموع 1 2 3 محاسبه می شود ... ن= ن! شرایط، که هر یک برابر است

شاخص ها ک 1 , ک 2 ,..., k Nبه عنوان همه جایگشت های مرتب شده ممکن تعریف می شوند rاعداد در مجموعه (1، 2، ...، ن). محاسبه تعیین کننده یک ماتریس یک روش پیچیده است که در عمل با استفاده از برنامه های خاص انجام می شود. مثلا،

برنج. 12 تعیین کننده ماتریس

ما فقط به ویژگی های آشکار توجه می کنیم:

دت ( من) = 1، دت ( آ) = دت ( آت)

دت ( AB) = دت ( آ) دت ( ب).

1.6. بردارها

اگر ماتریس فقط از یک ستون تشکیل شده باشد ( جی= 1)، سپس چنین شیئی فراخوانی می شود بردار... به طور دقیق تر، یک بردار ستونی. مثلا

به عنوان مثال می توان ماتریس هایی متشکل از یک ردیف را نیز در نظر گرفت

این شی نیز بردار است، اما وکتور ردیف... هنگام تجزیه و تحلیل داده ها، مهم است که بفهمیم با کدام بردارها سروکار داریم - ستون ها یا ردیف ها. بنابراین طیف گرفته شده برای یک نمونه را می توان به عنوان بردار ردیف در نظر گرفت. سپس مجموعه شدت های طیفی در یک طول موج معین برای همه نمونه ها باید به عنوان بردار ستون در نظر گرفته شود.

بعد یک بردار تعداد عناصر آن است.

واضح است که هر بردار ستونی را می توان با جابجایی به بردار ردیفی تبدیل کرد، یعنی.

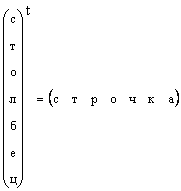
در مواردی که شکل یک بردار به طور خاص مشخص نشده است، بلکه صرفاً یک بردار گفته می شود، منظور آنها بردار ستونی است. ما نیز به این قانون پایبند خواهیم بود. یک بردار با یک حروف پررنگ مستقیم و کوچک نشان داده می شود. بردار صفر برداری است که همه عناصر آن صفر هستند. تعیین شده است 0 .

1.7. عملیات اساسی با بردارها

بردارها را می توان مانند ماتریس ها با اعداد اضافه و ضرب کرد. مثلا،

برنج. 13 عملیات بردار

دو بردار ایکسو yنامیده می شوند خط خطیاگر عدد α وجود داشته باشد به طوری که

1.8. محصولات بردارها

دو بردار با ابعاد یکسان نقابل ضرب است. بگذارید دو بردار وجود داشته باشد ایکس = (ایکس 1 , ایکس 2 ,...,ایکسن) t و y = (y 1 , y 2 ,...,yن) تی. با هدایت قاعده ضرب "ردیف به ستون"، می توانیم دو محصول از آنها بسازیم: ایکستی yو xyتی قطعه اول

تماس گرفت اسکالریا درونی؛ داخلی... نتیجه آن یک عدد است. همچنین از علامت گذاری ( ایکس,y)= ایکستی y... مثلا،

برنج. 14 محصول داخلی (محصول نقطه ای)

قطعه دوم

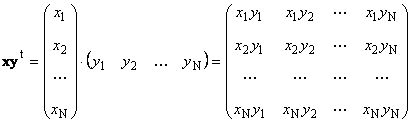
تماس گرفت خارجی... نتیجه آن یک ماتریس بعد است ( ن× ن). مثلا،

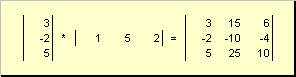
برنج. 15 کار خارجی

بردارهایی که حاصل ضرب اسکالر آنها برابر با صفر است نامیده می شوند ارتودنسی.

1.9. هنجار برداری

حاصل ضرب اسکالر یک بردار به خودی خود مربع اسکالر نامیده می شود. این مقدار

مربع را تعریف می کند طولبردار ایکس... برای نشان دادن طول (همچنین نامیده می شود عرفبردار)، از نماد استفاده می شود

مثلا،

برنج. 16 هنجار برداری

بردار واحد طول (|| ایکس|| = 1) نرمال شده نامیده می شود. یک بردار غیر صفر ( ایکس ≠ 0 ) را می توان با تقسیم آن بر طول نرمال کرد، یعنی. ایکس = ||ایکس|| (ایکس /||ایکس||) = ||ایکس|| ه... اینجا ه = ایکس /||ایکس|| بردار نرمال شده است.

بردارها را در صورتی متعامد می نامند که همگی نرمال شده و متعامد به صورت زوجی باشند.

1.10. زاویه بین بردارها

محصول نقطه ای و تزریقφ بین دو بردار ایکسو y

اگر بردارها متعامد باشند، cosφ = 0 و φ = π / 2، و اگر آنها خطی باشند، cosφ = 1 و φ = 0.

1.11. نمایش برداری از یک ماتریس

هر ماتریس آاندازه من× جیرا می توان به صورت مجموعه ای از بردارها نشان داد

در اینجا هر بردار آ jهست یک jستون و بردار سطر ب منهست یک منردیف -امین ماتریس آ

1.12. بردارهای وابسته خطی

بردارهای یک بعد ( ن) را می توان مانند ماتریس ها در یک عدد اضافه و ضرب کرد. نتیجه یک بردار با همان ابعاد خواهد بود. بگذارید چندین بردار با یک بعد وجود داشته باشد ایکس 1 , ایکس 2 ,...,ایکس K و همان تعداد اعداد α α 1، α 2، ...، α ک... بردار

y= α 1 ایکس 1 + α 2 ایکس 2 + ... + α ک ایکس ک

تماس گرفت ترکیب خطیبردارها ایکس ک .

اگر اعداد غیرصفر α وجود داشته باشد ک ≠ 0, ک = 1,..., ک، چی y = 0 ، سپس چنین مجموعه ای از بردارها ایکس کتماس گرفت وابسته به خط... در غیر این صورت، بردارها مستقل خطی نامیده می شوند. به عنوان مثال بردارها ایکس 1 = (2، 2) t و ایکس 2 = (-1، -1) t به صورت خطی وابسته هستند، زیرا ایکس 1 +2ایکس 2 = 0

1.13. رتبه ماتریسی

مجموعه ای را در نظر بگیرید کبردارها ایکس 1 , ایکس 2 ,...,ایکس کابعاد ن... رتبه این سیستم از بردارها حداکثر تعداد بردارهای مستقل خطی است. مثلا در مجموعه

برای مثال فقط دو بردار مستقل خطی وجود دارد ایکس 1 و ایکس 2، پس رتبه آن 2 است.

بدیهی است که اگر تعداد بردارها در مجموعه بیشتر از ابعاد آنها باشد ( ک>ن، پس آنها لزوماً به طور خطی وابسته هستند.

با رتبه ماتریس(نشان داده شده با رتبه ( آ)) رتبه سیستم بردارهایی است که از آن تشکیل شده است. اگرچه هر ماتریس را می توان به دو صورت (بردارهای ستونی یا ردیف) نشان داد، این بر مقدار رتبه تأثیر نمی گذارد، زیرا

1.14. ماتریس معکوس

ماتریس مربع آدر صورتی که منحصر به فرد باشد، غیر منحط نامیده می شود معکوسماتریس آ-1 با شرایط تعیین می شود

AA −1 = آ −1 آ = من.

ماتریس معکوس برای همه ماتریس ها وجود ندارد. شرط لازم و کافی برای عدم انحطاط است

دت ( آ) ≠ 0 یا رتبه ( آ) = ن.

وارونگی ماتریس یک روش پیچیده است که برنامه های خاصی برای آن وجود دارد. مثلا،

برنج. 17 وارونگی ماتریس

اجازه دهید فرمول هایی را برای ساده ترین حالت - ماتریس های 2×2 ارائه کنیم

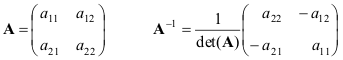
اگر ماتریس ها آو بپس غیر منحط

(AB) −1 = ب −1 آ −1 .

1.15. ماتریس شبه معکوس

اگر ماتریس آمنحط است و ماتریس معکوس وجود ندارد، پس در برخی موارد می توانید استفاده کنید شبه معکوسماتریسی که به عنوان چنین ماتریسی تعریف می شود آ+ اون

AA + آ = آ.

ماتریس شبه معکوس تنها نیست و نوع آن به روش ساخت بستگی دارد. به عنوان مثال، برای یک ماتریس مستطیلی، می توانید از روش مور-پنروز استفاده کنید.

اگر تعداد ستون ها کمتر از تعداد ردیف ها باشد، پس

آ + =(آتی آ) −1 آتی

مثلا،

برنج. 17a شبه وارونگی ماتریس

اگر تعداد ستون ها از تعداد سطرها بیشتر باشد، پس

آ + =آتی ( AAت) −1

1.16. ضرب یک بردار در یک ماتریس

بردار ایکسرا می توان در یک ماتریس ضرب کرد آبعد مناسب در این حالت بردار ستون در سمت راست ضرب می شود تبرو بردار ردیف در سمت چپ است ایکستی آ... اگر بعد بردار جی، و بعد ماتریس من× جیسپس نتیجه یک بردار بعد است من... مثلا،

برنج. 18 بردار با ضرب ماتریس

اگر ماتریس آ- مربع ( من× من، سپس بردار y = تبرهمان ابعاد را دارد ایکس... بدیهی است که

آ(α 1 ایکس 1 + α 2 ایکس 2) = α 1 تبر 1 + α 2 تبر 2 .

بنابراین، ماتریس ها را می توان به عنوان تبدیل خطی بردارها مشاهده کرد. به خصوص IX = ایکس, گاو نر = 0 .

2. اطلاعات تکمیلی

2.1. سیستم های معادلات خطی

بگذار باشد آ- اندازه ماتریس من× جی، آ ب- بردار بعد جی... معادله را در نظر بگیرید

تبر = ب

با توجه به بردار ایکس، ابعاد من... در واقع، این یک سیستم از منمعادلات خطی با جیناشناس ایکس 1 ,...,ایکس جی... راه حل وجود دارد اگر و فقط اگر

رتبه ( آ) = رتبه ( ب) = آر,

جایی که بیک ماتریس بعد توسعه یافته است من×( J + 1) متشکل از ماتریس آپر شده با ستون ب, ب = (آ ب). در غیر این صورت، معادلات ناسازگار هستند.

اگر آر = من = جی، سپس راه حل منحصر به فرد است

ایکس = آ −1 ب.

اگر آر < من، سپس راه حل های مختلفی وجود دارد که می توان آنها را بر حسب ترکیب خطی بیان کرد جی−آربردارها سیستم معادلات همگن تبر = 0 ماتریس مربع آ (ن× ن) یک راه حل غیر ضروری دارد ( ایکس ≠ 0 ) اگر و فقط اگر det ( آ) = 0. اگر آر= رتبه ( آ)<نسپس وجود داشته باشد ن−آرراه حل های مستقل خطی

2.2. اشکال دو خطی و درجه دوم

اگر آیک ماتریس مربع است و ایکسو yبردارهای بعد مربوطه، سپس حاصل ضرب اسکالر فرم هستند ایکستی آیتماس گرفت دو خطیشکل تعریف شده توسط ماتریس آ... در ایکس = yاصطلاح ایکستی تبرتماس گرفت درجه دومفرم.

2.3. ماتریس های قطعی مثبت

ماتریس مربع آتماس گرفت مثبت تعریف شده استاگر برای هر بردار غیر صفر ایکس ≠ 0 ,

ایکستی تبر > 0.

به همین ترتیب، منفی (ایکستی تبر < 0), غیر منفی (ایکستی تبر≥ 0) و مثبت نیست (ایکستی تبر≤ 0) ماتریس های خاص.

2.4. تجزیه کولسکی

اگر یک ماتریس متقارن آمثبت قطعی است، پس یک ماتریس مثلثی منحصر به فرد وجود دارد Uبا عناصر مثبت، که برای آن

آ = Uتی U.

مثلا،

برنج. 19 تجزیه کولسکی

2.5. تجزیه قطبی

بگذار باشد آیک ماتریس مربع غیر منحط ابعاد است ن× ن... سپس یک به یک وجود دارد قطبیکارایی

آ = SR،

جایی که اسیک ماتریس متقارن غیر منفی است و آریک ماتریس متعامد است. ماتریس ها اسو آررا می توان به صراحت تعریف کرد:

اس 2 = AA t یا اس = (AAت) ½ و آر = اس −1 آ = (AAت) -1 آ.

مثلا،

برنج. 20 تجزیه قطبی

اگر ماتریس آمنحط است، پس گسترش منحصر به فرد نیست - یعنی: اسهنوز تنهاست اما آرشاید خیلی تجزیه قطبی نشان دهنده ماتریس است آبه عنوان ترکیبی از فشرده سازی / کشش اسو چرخش آر.

2.6. بردارهای ویژه و مقادیر ویژه

بگذار باشد آیک ماتریس مربع است. بردار vتماس گرفت بردار خودماتریس ها آ، اگر

Av = λ v,

جایی که عدد λ نامیده می شود معنی خودماتریس ها آ... بنابراین، تبدیلی که ماتریس انجام می دهد آبیش از بردار v، به کشش یا فشرده سازی ساده با ضریب λ کاهش می یابد. بردار ویژه تا ضرب در ثابت α ≠ 0 تعیین می شود، یعنی. اگر vیک بردار ویژه است، سپس α vهمچنین یک بردار ویژه است.

2.7. مقادیر ویژه

ماتریس آ، بعد، ابعاد، اندازه ( ن× ن) نمی تواند بیشتر از نمقادیر ویژه راضی می کنند معادله مشخصه

دت ( آ − λ من) = 0,

که یک معادله جبری است نمرتبه به طور خاص، برای یک ماتریس 2 × 2، معادله مشخصه شکل دارد

مثلا،

برنج. 21 مقادیر ویژه

مجموعه مقادیر ویژه λ 1، ...، λ نماتریس ها آتماس گرفت طیف آ.

طیف دارای خواص مختلفی است. به خصوص

دت ( آ) = λ 1 × ... × λ ن, Sp ( آ) = λ 1 + ... + λ ن.

مقادیر ویژه یک ماتریس دلخواه می تواند اعداد مختلط باشد، اما اگر ماتریس متقارن باشد ( آ t = آ، سپس مقادیر ویژه آن واقعی هستند.

2.8. بردارهای خود

ماتریس آ، بعد، ابعاد، اندازه ( ن× ن) نمی تواند بیشتر از نبردارهای ویژه که هر کدام با مقدار خود مطابقت دارد. برای تعیین بردار ویژه v nشما باید یک سیستم معادلات همگن را حل کنید

(آ − λ n من)v n = 0 .

این یک راه حل غیر ضروری دارد، زیرا آ -λ n من) = 0.

مثلا،

برنج. 22 بردار ویژه

بردارهای ویژه یک ماتریس متقارن متعامد هستند.

تعریف 9.3.بردار NS تماس گرفت بردار خودماتریس ها آاگر چنین عددی وجود داشته باشد λ, که برابری وجود دارد: آ NS= λ NS, یعنی نتیجه اعمال به NS تبدیل خطی داده شده توسط ماتریس آ، ضرب این بردار در عدد است λ ... خود شماره λ تماس گرفت شماره خودماتریس ها آ.

جایگزینی به فرمول (9.3) x` j = λx j،ما سیستمی از معادلات را برای تعیین مختصات بردار ویژه به دست می آوریم:

. (9.5)

این سیستم همگن خطی تنها در صورتی یک راه حل غیر ضروری خواهد داشت که تعیین کننده اصلی آن 0 باشد (قانون کرامر). نوشتن این شرط به شکل:

معادله تعیین مقادیر ویژه را بدست می آوریم λ تماس گرفت معادله مشخصه... به طور خلاصه می توان آن را به شرح زیر ارائه کرد:

| A - λE | = 0, (9.6)

از آنجایی که سمت چپ آن دارای تعیین کننده ماتریس است A-λE... چند جمله ای با توجه به λ | A - λE| تماس گرفت چند جمله ای مشخصهماتریس های A.

ویژگی های چند جمله ای مشخص:

1) چند جمله ای مشخصه تبدیل خطی به انتخاب مبنا بستگی ندارد. اثبات (نگاه کنید به (9.4))، اما از این رو، . بنابراین، به انتخاب پایه بستگی ندارد. از این رو، و | A-λE| هنگام تغییر به یک پایه جدید تغییر نمی کند.

2) اگر ماتریس آتبدیل خطی است متقارن(آنها و ij = یک جی، پس تمام ریشه های معادله مشخصه (9.6) اعداد واقعی هستند.

ویژگی های مقادیر ویژه و بردارهای ویژه:

1) اگر مبنایی از بردارهای ویژه انتخاب کنیم x 1، x 2، x 3 مربوط به مقادیر ویژه λ 1، λ 2، λ 3ماتریس ها آ، پس بر این اساس تبدیل خطی A دارای ماتریسی به شکل مورب است:

(9.7) اثبات این ویژگی از تعریف بردارهای ویژه حاصل می شود.

2) اگر مقادیر ویژه تبدیل آمتفاوت هستند، سپس بردارهای ویژه مربوطه به صورت خطی مستقل هستند.

3) اگر چند جمله ای مشخصه ماتریس آدارای سه ریشه متفاوت است، سپس در برخی موارد ماتریس آفرم مورب دارد.

اجازه دهید مقادیر ویژه و بردارهای ویژه ماتریس را پیدا کنیم بیایید معادله مشخصه را بسازیم: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0، λ 1 = -2, λ 2 = 3, λ 3 = 6.

اجازه دهید مختصات بردارهای ویژه مربوط به هر مقدار یافت شده را پیدا کنیم λ. از (9.5) بر می آید که اگر NS (1) ={x 1، x 2، x 3) آیا بردار ویژه مربوط است λ 1 = -2، سپس

- یک سیستم مشارکتی اما تعریف نشده. راه حل آن را می توان به صورت NS (1) ={آ,0,-آ) که در آن a هر عددی است. به ویژه، اگر ما به آن نیاز داشته باشیم | ایکس (1) |=1, NS (1) =

جایگزینی در سیستم (9.5) λ 2 = 3، سیستمی برای تعیین مختصات بردار ویژه دوم به دست می آوریم - ایکس (2) ={y 1، y 2، y 3}:

، جایی که NS (2) ={ب، -ب، ب) یا، موضوع | ایکس (2) |=1, ایکس (2) =

برای λ 3 = 6 بردار ویژه را پیدا کنید ایکس (3) ={z 1، z 2، z 3}:

, ایکس (3) ={ج,2c، c) یا در نسخه عادی

x (3) = شما می توانید آن را ببینید NS (1) NS (2) = ab - ab= 0, ایکس (1) ایکس (3) = ac - ac= 0, ایکس (2) ایکس (3) = قبل از میلاد مسیح- 2قبل از میلاد + قبل از میلاد= 0. بنابراین، بردارهای ویژه این ماتریس متعامد به صورت زوجی هستند.

سخنرانی 10.

فرم های درجه دوم و رابطه آنها با ماتریس های متقارن. ویژگی های بردارهای ویژه و مقادیر ویژه یک ماتریس متقارن. تقلیل شکل درجه دوم به شکل متعارف.

تعریف 10.1.فرم درجه دوممتغیرهای واقعی x 1، x 2، ...، x nیک چند جمله ای درجه دوم نسبت به این متغیرها است که شامل یک عبارت آزاد و عبارت درجه اول نیست.

نمونه هایی از فرم های درجه دوم:

(n = 2),

(n = 3). (10.1)

بیایید تعریف یک ماتریس متقارن را که در آخرین سخنرانی ارائه شد را به یاد بیاوریم:

تعریف 10.2.ماتریس مربع نامیده می شود متقارن، اگر، یعنی اگر عناصر ماتریس متقارن نسبت به قطر اصلی برابر باشند.

ویژگی های مقادیر ویژه و بردارهای ویژه یک ماتریس متقارن:

1) تمام مقادیر ویژه ماتریس متقارن واقعی هستند.

اثبات (برای n = 2).

اجازه دهید ماتریس آبه نظر می رسد: ... بیایید معادله مشخصه را بسازیم:

(10.2) ممیز را بیابید:

بنابراین، معادله فقط ریشه واقعی دارد.

2) بردارهای ویژه ماتریس متقارن متعامد هستند.

اثبات (برای n= 2).

مختصات بردارهای ویژه و باید معادلات را برآورده کند.

با یک ماتریس A، اگر یک عدد l وجود داشته باشد که AX = lX باشد.

علاوه بر این، عدد l نامیده می شود معنی خودعملگر (ماتریس A) مربوط به بردار X.

به عبارت دیگر، بردار ویژه برداری است که تحت عمل یک عملگر خطی، به یک بردار خطی تبدیل می شود، یعنی. فقط در یک عدد ضرب می شود در مقابل، تبدیل بردارهای نامناسب دشوارتر است.

اجازه دهید تعریف بردار ویژه را در قالب یک سیستم معادلات بنویسیم:

همه عبارت ها را به سمت چپ منتقل کنید:

سیستم اخیر را می توان به صورت ماتریسی به صورت زیر نوشت:

(A - lE) X = O

سیستم به دست آمده همیشه یک جواب صفر دارد X = O. چنین سیستم هایی که در آنها تمام عبارات آزاد برابر با صفر هستند نامیده می شوند. همگن... اگر ماتریس چنین سیستمی مربع باشد و تعیین کننده آن برابر با صفر نباشد، با استفاده از فرمول های کرامر همیشه یک راه حل منحصر به فرد - صفر به دست می آوریم. می توان ثابت کرد که سیستم راه حل های غیر صفر دارد اگر و تنها در صورتی که تعیین کننده این ماتریس برابر با صفر باشد، یعنی.

| A - LE | = = 0

این معادله با l مجهول نامیده می شود معادله مشخصه (چند جمله ای مشخصه) از ماتریس A (عملگر خطی).

می توان نشان داد که چند جمله ای مشخصه یک عملگر خطی به انتخاب مبنا بستگی ندارد.

برای مثال، اجازه دهید مقادیر ویژه و بردارهای ویژه عملگر خطی را که توسط ماتریس A = ارائه شده است، پیدا کنیم.

برای این، معادله مشخصه | A - lЕ | را می سازیم = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; مقادیر ویژه l 1 = (2 - 12) / 2 = -5؛ l 2 = (2 + 12) / 2 = 7.

برای یافتن بردارهای ویژه، دو سیستم معادله را حل می کنیم

(A + 5E) X = O

(A - 7E) X = O

برای اولین مورد، ماتریس گسترش یافته شکل می گیرد

,

از آنجا x 2 = c، x 1 + (2/3) c = 0; x 1 = - (2/3) s، یعنی. X (1) = (- (2/3) s؛ s).

برای دومی از آنها، ماتریس گسترش یافته شکل می گیرد

,

از آنجا x 2 = c 1، x 1 - (2/3) c 1 = 0; x 1 = (2/3) s 1، یعنی. X (2) = ((2/3) s 1؛ s 1).

بنابراین، بردارهای ویژه این عملگر خطی همه بردارهایی به شکل (- (2/3) с؛ с) با مقدار ویژه (-5) و همه بردارهای شکل ((2/3) с 1؛ с 1) هستند. با مقدار ویژه 7 ...

می توان ثابت کرد که ماتریس عملگر A در پایه متشکل از بردارهای ویژه آن مورب است و به شکل زیر است:

,

جایی که l i مقادیر ویژه این ماتریس هستند.

عکس آن نیز صادق است: اگر ماتریس A در برخی از پایه ها مورب باشد، آنگاه همه بردارهای این مبنا بردارهای ویژه این ماتریس خواهند بود.

همچنین می توان ثابت کرد که اگر یک عملگر خطی دارای n مقدار ویژه جفتی متفاوت باشد، بردارهای ویژه متناظر به صورت خطی مستقل هستند و ماتریس این عملگر در مبنای متناظر دارای فرم مورب است.

اجازه دهید این را با مثال قبلی توضیح دهیم. مقادیر غیر صفر دلخواه с و с 1 را می گیریم، اما به گونه ای که بردارهای X (1) و X (2) به صورت خطی مستقل هستند، یعنی. اساس را تشکیل خواهد داد. برای مثال، اجازه دهید c = c 1 = 3، سپس X (1) = (-2؛ 3)، X (2) = (2؛ 3).

اجازه دهید استقلال خطی این بردارها را تأیید کنیم:

12 ≠ 0. در این مبنای جدید، ماتریس A به شکل A * = خواهد بود.

برای تأیید این موضوع، از فرمول A * = C -1 AC استفاده می کنیم. ابتدا C -1 را پیدا می کنیم.

С -1 = ;

فرم های درجه دوم

فرم درجه دوم f (x 1, x 2, xn) از n متغیر مجموعی نامیده می شود که هر جمله آن یا مجذور یکی از متغیرها است یا حاصل ضرب دو متغیر مختلف با یک ضریب معین: f (x 1 ، x 2، xn) = (اِ ایج = یک جی).

ماتریس A متشکل از این ضرایب نامیده می شود ماتریسفرم درجه دوم همیشه متقارنماتریس (یعنی یک ماتریس متقارن در مورد قطر اصلی، a ij = a ji).

در نمادگذاری ماتریسی، شکل درجه دوم f (X) = X T AX است، که در آن

در واقع

به عنوان مثال، اجازه دهید شکل درجه دوم را به صورت ماتریسی بنویسیم.

برای انجام این کار، ماتریسی از فرم درجه دوم را پیدا می کنیم. عناصر مورب آن برابر با ضرایب مربع های متغیرها و عناصر باقی مانده برابر با نیمی از ضرایب متناظر شکل درجه دوم است. از همین رو

اجازه دهید ماتریس-ستون متغیرهای X با تبدیل خطی غیر منحط ماتریس-ستون Y به دست آید، یعنی. X = CY، جایی که С یک ماتریس غیر منحط از مرتبه n است. سپس فرم درجه دوم f (X) = X T AX = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y.

بنابراین، با یک تبدیل خطی غیر منحط C، ماتریس شکل درجه دوم به شکل A * = C T AC می باشد.

برای مثال، بیایید شکل درجه دوم f (y 1, y 2) را که از شکل درجه دوم f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 با تبدیل خطی به دست می آید، پیدا کنیم.

شکل درجه دوم نامیده می شود ابتدایی(این دارد دیدگاه متعارف) اگر تمام ضرایب آن a ij = 0 برای i ≠ j، یعنی،
f (x 1، x 2، x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

ماتریس آن مورب است.

قضیه(در اینجا هیچ مدرکی ارائه نشده است). هر شکل درجه دوم را می توان با استفاده از تبدیل خطی غیر منحط به شکل متعارف کاهش داد.

به عنوان مثال، می توانیم شکل درجه دوم را به شکل متعارف کاهش دهیم
f (x 1، x 2، x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

برای این کار ابتدا یک مربع کامل با متغیر x 1 انتخاب کنید:

f (x 1، x 2، x 3) = 2 (x 1 2 + 2 x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2 (x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

حالا یک مربع کامل با متغیر x 2 انتخاب می کنیم:

f (x 1، x 2، x 3) = 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 =
= 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

سپس تبدیل خطی غیر منحط y 1 = x 1 + x 2، y 2 = x 2 + (1/10) x 3 و y 3 = x 3 این شکل درجه دوم را به شکل متعارف f (y 1, y 2) کاهش می دهد. ، y 3) = 2y 1 2 - 5y 2 2 + (1/20) y 3 2.

توجه داشته باشید که شکل متعارف یک فرم درجه دوم به طور مبهم تعیین می شود (یک شکل درجه دوم را می توان به روش های مختلف به شکل متعارف کاهش داد). با این حال، اشکال متعارف به‌دست‌آمده از راه‌های مختلف، تعدادی ویژگی مشترک دارند. به طور خاص، تعداد عبارت های دارای ضرایب مثبت (منفی) شکل درجه دوم به روش کاهش فرم به این شکل بستگی ندارد (مثلاً در مثال در نظر گرفته شده همیشه دو ضریب منفی و یک ضریب مثبت وجود خواهد داشت). . این ویژگی را قانون اینرسی اشکال درجه دوم می نامند.

اجازه دهید این را با کاهش همان شکل درجه دوم به شکل متعارف به روشی دیگر تأیید کنیم. اجازه دهید تبدیل را با متغیر x 2 شروع کنیم:

f (x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3 (x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
= -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 = f (y 1، y 2، y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2، که در آن y 1 = - (2/3) x 1 + x 2 + (1/6) x 3، y 2 = (2/3) x 1 + (1/6) x 3 و y 3 = x 1. در اینجا یک ضریب منفی -3 برای y 1 و دو ضریب مثبت 3 و 2 برای y 2 و y 3 (و هنگام استفاده از روش دیگری، ضریب منفی (-5) برای y 2 و دو ضریب مثبت دریافت کردیم: 2 برای y 1 و 1/20 برای y 3).

همچنین لازم به ذکر است که رتبه ماتریس فرم درجه دوم، به نام رتبه فرم درجه دوم، برابر با تعداد ضرایب غیر صفر شکل متعارف است و تحت تبدیل های خطی تغییر نمی کند.

شکل درجه دوم f (X) نامیده می شود مثبت (منفی) معیناگر برای تمام مقادیر متغیرهایی که در یک زمان برابر با صفر نیستند، مثبت است، یعنی. f (X)> 0 (منفی، یعنی.
f (X)< 0).

به عنوان مثال، شکل درجه دوم f 1 (X) = x 1 2 + x 2 2 مثبت است، زیرا مجموع مربع ها است و شکل درجه دوم f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 منفی است، زیرا نشان می دهد که می توان آن را به صورت f 2 (X) = - (x 1 - x 2) 2 نشان داد.

در بیشتر موقعیت های عملی، تعیین قطعیت یک شکل درجه دوم تا حدودی دشوارتر است، بنابراین یکی از قضایای زیر برای این مورد استفاده می شود (ما آنها را بدون اثبات فرمول بندی می کنیم).

قضیه... یک شکل درجه دوم مثبت (منفی) قطعی است اگر و فقط در صورتی که همه مقادیر ویژه ماتریس آن مثبت (منفی) باشند.

قضیه(معیار سیلوستر). یک فرم درجه دوم قطعی مثبت است اگر و فقط در صورتی که همه جزئی های اصلی ماتریس این شکل مثبت باشند.

ماژور (گوشه) جزئیمرتبه k ام ماتریس A از مرتبه n را تعیین کننده ماتریس می گویند که از k ردیف و ستون اول ماتریس A () تشکیل شده است.

توجه داشته باشید که برای اشکال درجه دوم قطعی منفی، علائم مینورهای اصلی متناوب هستند و صغیر مرتبه اول باید منفی باشد.

برای مثال، اجازه دهید شکل درجه دوم f (x 1، x 2) = 2x 1 2 + 4x 1 x 2 + 3x2 2 را برای قطعیت علامت بررسی کنیم.

= (2 - l) *
* (3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
... بنابراین، شکل درجه دوم مثبت قطعی است.

روش 2. مینور اصلی مرتبه اول ماتریس А D 1 = a 11 = 2> 0. مینور اصلی مرتبه دوم D 2 = = 6 - 4 = 2> 0. بنابراین با توجه به معیار سیلوستر، شکل درجه دوم مثبت قطعی است.

اجازه دهید شکل درجه دوم دیگری را برای قطعیت نشانه بررسی کنیم، f (x 1، x 2) = -2x 1 2 + 4x 1 x 2 - 3x2 2.

روش 1. بیایید یک ماتریس از شکل درجه دوم A = بسازیم. معادله مشخصه شکل خواهد داشت = (-2 - l) *
* (- 3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
... بنابراین، شکل درجه دوم قطعی منفی است.

روش 2. مینور اصلی مرتبه اول ماتریس A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. بنابراین، طبق معیار سیلوستر، صورت درجه دوم قطعی منفی است (علائم صغیر اصلی متناوب، با منهای شروع می شود).

و به عنوان مثالی دیگر، اجازه دهید شکل درجه دوم f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 را برای قطعیت علامت بررسی کنیم.

روش 1. بیایید یک ماتریس از شکل درجه دوم A = بسازیم. معادله مشخصه شکل خواهد داشت = (2 - l) *
* (- 3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

یکی از این اعداد منفی و دیگری مثبت است. نشانه های مقادیر ویژه متفاوت است. در نتیجه، شکل درجه دوم نه می تواند معین منفی باشد و نه مثبت، یعنی. این شکل درجه دوم قطعی نیست (می تواند مقادیر هر علامتی را بگیرد).

روش 2. مینور اصلی مرتبه اول ماتریس A D 1 = a 11 = 2> 0. مینور اصلی مرتبه دوم D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

ماتریس های مورب ساده ترین هستند. این سوال مطرح می شود که آیا می توان مبنایی را پیدا کرد که در آن ماتریس یک عملگر خطی شکل مورب داشته باشد؟ چنین مبنایی وجود دارد.
اجازه دهید یک فضای خطی R n و یک عملگر خطی A در آن داده شود. در این حالت عملگر A R n را در خود می گیرد، یعنی A: R n → R n.

تعریف. یک بردار غیرصفر بردار ویژه عملگر A نامیده می شود که عملگر A به بردار هم خط با آن تبدیل شود، یعنی. عدد λ را مقدار ویژه یا مقدار ویژه عملگر A می نامند که مربوط به بردار ویژه است.
اجازه دهید به برخی از ویژگی های مقادیر ویژه و بردارهای ویژه توجه کنیم.
1. هر ترکیب خطی از بردارهای ویژه از عملگر A مربوط به مقدار ویژه λ یک بردار ویژه با مقدار ویژه یکسان است.
2. بردارهای ویژه از عملگر A با مقادیر ویژه جفتی مختلف λ 1، λ 2،…، λ m به صورت خطی مستقل هستند.
3. اگر مقادیر ویژه λ 1 = λ 2 = λ m = λ، آنگاه مقدار ویژه λ با حداکثر m بردارهای ویژه مستقل خطی مطابقت دارد.

بنابراین، اگر n بردار ویژه مستقل خطی وجود داشته باشد مربوط به مقادیر ویژه مختلف λ 1، λ 2، ...، λ n، سپس آنها به صورت خطی مستقل هستند، بنابراین، می توان آنها را به عنوان مبنای فضای R n در نظر گرفت. اجازه دهید شکل ماتریس عملگر خطی A را بر اساس بردارهای ویژه آن پیدا کنیم، که برای آن توسط عملگر A بر اساس بردارهای پایه عمل می کنیم: سپس .
بنابراین، ماتریس عملگر خطی A بر اساس بردارهای ویژه آن شکل مورب دارد و مقادیر ویژه عملگر A بر روی قطر قرار دارند.
آیا مبنای دیگری وجود دارد که در آن ماتریس مورب باشد؟ پاسخ این سوال با قضیه زیر داده می شود.

قضیه. ماتریس یک عملگر خطی A در پایه (i = 1..n) شکل مورب دارد اگر و فقط اگر همه بردارهای مبنا بردارهای ویژه عملگر A باشند.

قانون برای یافتن مقادیر ویژه و بردارهای ویژه

بگذارید یک بردار داده شود ، که در آن x 1، x 2، ...، x n مختصات بردار نسبت به پایه هستند. و بردار ویژه عملگر خطی A مربوط به مقدار ویژه λ است، یعنی. این رابطه را می توان به صورت ماتریسی نوشت

. (*)

معادله (*) را می توان به عنوان معادله ای برای یافتن در نظر گرفت، علاوه بر این، ما به راه حل های غیر پیش پا افتاده علاقه مند هستیم، زیرا بردار ویژه نمی تواند صفر باشد. مشخص است که راه حل های غیر ضروری یک سیستم همگن معادلات خطی وجود دارند اگر و فقط اگر det (A - λE) = 0 باشد. بنابراین، برای اینکه λ یک مقدار ویژه عملگر A باشد، لازم و کافی است که det (A - λE) = 0.
اگر معادله (*) با جزئیات به صورت مختصات نوشته شده باشد، سیستم معادلات همگن خطی به دست می آید:

(1)
جایی که ماتریس عملگر خطی است.

اگر سیستم (1) تعیین کننده D برابر با صفر باشد، جواب غیر صفر دارد

معادله ای برای یافتن مقادیر ویژه دریافت کرد.
این معادله را معادله مشخصه و سمت چپ آن را چند جمله ای مشخصه ماتریس (عملگر) A می نامند. اگر چند جمله ای مشخصه ریشه واقعی نداشته باشد، ماتریس A فاقد بردار ویژه است و نمی توان آن را به صورت مورب تقلیل داد. .
فرض کنید λ 1، λ 2،...، λ n ریشه های واقعی معادله مشخصه باشند و در بین آنها ممکن است چندین ریشه وجود داشته باشد. با جایگزینی این مقادیر به نوبه خود با سیستم (1)، بردارهای ویژه را پیدا می کنیم.

مثال 12. عملگر خطی A در R 3 طبق قانون عمل می کند، که در آن x 1، x 2، ..، x n مختصات بردار در پایه هستند. , , ... مقادیر ویژه و بردارهای ویژه این عملگر را پیدا کنید.
راه حل. ماتریس این عملگر را می سازیم:
.
ما یک سیستم برای تعیین مختصات بردارهای ویژه می سازیم:

یک معادله مشخصه ترسیم می کنیم و آن را حل می کنیم:

.
λ 1،2 = -1، λ 3 = 3.
با جایگزینی λ = -1 در سیستم، داریم:
یا
زیرا ، سپس دو متغیر وابسته و یک متغیر آزاد وجود دارد.
پس اجازه دهید x 1 یک مجهول رایگان باشد ما این سیستم را به هر طریقی حل می کنیم و یک راه حل کلی برای این سیستم پیدا می کنیم: سیستم اساسی راه حل ها از یک راه حل تشکیل شده است، زیرا n - r = 3 - 2 = 1.
مجموعه بردارهای ویژه متناظر با مقدار ویژه λ = -1 به شکل: است، که در آن x 1 هر عدد غیر صفر است. اجازه دهید از این مجموعه یک بردار را انتخاب کنیم، برای مثال x 1 = 1 را قرار دهیم: .
با استدلال مشابه، بردار ویژه مربوط به مقدار ویژه λ = 3 را می یابیم: .
در فضای R 3 اساس از سه بردار مستقل خطی تشکیل شده است، اما ما فقط دو بردار ویژه خطی مستقل دریافت کرده‌ایم که اساس R3 را نمی‌توان از آنها تشکیل داد. در نتیجه، ماتریس A عملگر خطی را نمی توان به شکل مورب کاهش داد.

مثال 13. با توجه به یک ماتریس .
1. ثابت کنید که بردار یک بردار ویژه از ماتریس A است. مقدار ویژه مربوط به این بردار ویژه را پیدا کنید.
2. مبنایی را پیدا کنید که در آن ماتریس A شکل مورب داشته باشد.
راه حل.
1. اگر، پس - بردار ویژه

.
بردار (1, 8, -1) یک بردار ویژه است. مقدار ویژه λ = -1.
ماتریس دارای یک فرم مورب در پایه است که از بردارهای ویژه تشکیل شده است. یکی از آنها معروف است. بیا بقیه رو پیدا کنیم
ما بردارهای ویژه را از سیستم جستجو می کنیم:

معادله مشخصه: ;
(3 + λ) [- 2 (2-λ) (2 + λ) +3] = 0; (3 + λ) (λ 2 - 1) = 0
λ 1 = -3، λ 2 = 1، λ 3 = -1.
اجازه دهید بردار ویژه مربوط به مقدار ویژه λ = -3 را پیدا کنیم:

رتبه ماتریس این سیستم برابر با دو و برابر با تعداد مجهولات است، بنابراین این سیستم فقط یک جواب صفر دارد x 1 = x 3 = 0. x 2 در اینجا می تواند هر غیر صفر باشد، به عنوان مثال، x 2 = 1. بنابراین، بردار (0، 1،0) یک بردار ویژه مربوط به λ = -3 است. بیایید بررسی کنیم:
.
اگر λ = 1، سیستم را بدست می آوریم
رتبه ماتریس دو است. معادله آخر را حذف می کنیم.
اجازه دهید x 3 یک مجهول رایگان باشد. سپس x 1 = -3x 3، 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3، x 2 = -9x 3.
با تنظیم x 3 = 1، (-3، -9،1) داریم - بردار ویژه مربوط به مقدار ویژه λ = 1. تأیید:

.
از آنجایی که مقادیر ویژه واقعی و متفاوت هستند، بردارهای مربوط به آنها به صورت خطی مستقل هستند، بنابراین می توان آنها را به عنوان پایه در R3 در نظر گرفت. بنابراین، در اساس , , ماتریس A به شکل زیر است:
.
همه ماتریس های یک عملگر خطی A: Rn → Rn را نمی توان به شکل مورب کاهش داد، زیرا برای برخی از عملگرهای خطی بردارهای ویژه مستقل خطی می توانند کمتر از n باشند. با این حال، اگر ماتریس متقارن باشد، دقیقاً m بردار مستقل خطی با ریشه معادله مشخصه تعدد m مطابقت دارد.

تعریف. ماتریس متقارن یک ماتریس مربعی است که در آن عناصر متقارن نسبت به قطر اصلی برابر هستند، یعنی در آن.
ملاحظات. 1. تمام مقادیر ویژه یک ماتریس متقارن واقعی هستند.
2. بردارهای ویژه یک ماتریس متقارن متناظر با مقادیر ویژه مختلف جفتی متعامد هستند.
به عنوان یکی از کاربردهای فراوان دستگاه مورد مطالعه، اجازه دهید مسئله تعیین شکل یک منحنی مرتبه دوم را در نظر بگیریم.