Онлайн калкулатор Лимит решение. Решаване на онлайн ограничения

Правилото на L'Hôpital (стр. L.) улеснява изчисляването на границите на функциите. Например, трябва да намерите границата на функция, която е съотношението на функциите, стремящи се към нула. Тези. съотношението на функцията е 0/0 несигурност. Ще помогне да се разкрие. В предела съотношението на функциите може да бъде заменено със съотношението на производните на тези функции. Тези. е необходимо да се раздели производната на числителя на производната на знаменателя и да се вземе границата от тази дроб.

1. Несигурност 0/0. Първи артикул L.

Ако = 0, тогава ако последното съществува.

2. Несигурност на формата ∞ / ∞ Втори раздел L.

Намирането на граници от този тип се нарича разкриване на несигурности.

Ако = ∞, тогава ако последното съществува.

3. Несигурностите 0⋅∞, ∞- ∞, 1 ∞ и 0 0 се редуцират до неопределености 0/0 и ∞ / ∞ чрез трансформации. Този запис служи като кратка индикация за случая при намиране на лимита. Всяка несигурност се разкрива по свой собствен начин. Правилото на L'Hôpital може да се приложи няколко пъти, докато не се отървем от несигурността. Прилагането на правилото на L'Hôpital е полезно, когато съотношението на производните може да се преобразува в по-удобна форма по-лесно от съотношението на функциите.

0⋅∞ е произведение на две функции, първата клони към нула, втората към безкрайност;
∞- ∞ е разликата на функциите, стремящи се към безкрайност;
1 ∞ степен, основата му клони към единица, а степента клони към безкрайност;
∞ 0 градус, основата му клони към безкрайност, а степента към нула;
0 0 градус, основата му клони към 0, а степента също клони към нула.

Пример 1. В този пример несигурността е 0/0

Пример 2. Тук ∞ / ∞

В тези примери ние разделяме производните на числителя на производните на знаменателя и заместваме граничната стойност за x.

Пример 3. Вид на неопределеността 0⋅∞ .

Преобразуваме неопределеността 0⋅∞ в ∞ / ∞, за това прехвърляме x в знаменателя като дроб 1 / x, записваме производната на числителя в числителя и производната на знаменателя в знаменателя.

Пример 4 Изчислете границата на функция

Тук неопределеността на формата ∞ 0 Първо логаритмираме функцията, след това намираме границата от нея

За да получите отговора, трябва да повишите e на степен -1, получаваме e -1.

Пример 5. Изчислете границата на ако x → 0

Решение. Тип неопределеност ∞ -∞ Свеждайки дроба до общ знаменател, преминаваме от ∞-∞ към 0/0. Прилагаме правилото на L'Hôpital, но отново получаваме несигурност от 0/0, така че L. трябва да се приложи втори път. Решението изглежда така:

= = = =
= =

Пример 6 Решете

Решение. Типът на несигурността е ∞ / ∞, като я отворим, получаваме

В случаите 3), 4), 5) първо функцията се логаритмизира и се намира границата на логаритъма, а след това търсената граница e се повишава до получената степен.

Пример 7. Изчислете лимита

Решение. Тук неопределеността е 1 ∞. Означаваме A =

Тогава lnA = = = = 2.

Основата на логаритъма е e, така че за да получите отговора, който трябва да квадратирате e, получаваме e 2.

Понякога има случаи, когато съотношението на функциите има граница, за разлика от съотношението на производните, което няма.

Нека разгледаме пример:

Защото sinx е ограничен и x расте неограничено, вторият член е 0.

Тази функция няма ограничение, тъй като той постоянно се колебае между 0 и 2, p.L. не е приложимо за този пример.

Разкриване на несигурности от формата 0/0 или ∞ / ∞ и някои други несигурности, възникващи при изчислението лимитвръзката на две безкрайно малки или безкрайно големи функции е значително опростена с помощта на правилото на L'Hôpital (всъщност две правила и забележки към тях).

Същността Правилата на L'Hôpital е, че в случай, когато изчисляването на границата на съотношенията на две безкрайно малки или безкрайно големи функции дава несигурности от вида 0/0 или ∞ / ∞, границата на съотношението на две функции може да бъде заменена с границата на техните съотношение производнии по този начин да получите определен резултат.

Да преминем към формулирането на правилата на L'Hôpital.

Правилото на L'Hôpital за случая на границата на две безкрайно малки количества... Ако функции е(х) и ж(х аа, и в този квартал ж"(х аравни една на друга и равни на нула

().

Правилото на L'Hôpital за случая на границата на две безкрайно големи количества... Ако функции е(х) и ж(х) са диференцируеми в някаква околност на точката а, с възможно изключение на самата точка а, и в този квартал ж"(х) ≠ 0 и ако и ако границите на тези функции като x клонят към стойността на функцията в точката аравни един на друг и равни на безкрайност

(),

тогава границата на отношението на тези функции е равна на границата на отношението на техните производни

().

С други думи, за неопределености от вида 0/0 или ∞ / ∞ границата на съотношението на две функции е равна на границата на съотношението на техните производни, ако последната съществува (крайна или безкрайна).

Забележки.

1. Правилата на L'Hôpital са приложими и когато функциите е(х) и ж(х) не са дефинирани за х = а.

2. Ако при изчисляване на границата на отношението на производните на функциите е(х) и ж(х) отново стигаме до несигурност от формата 0/0 или ∞ / ∞, тогава правилата на L'Hôpital трябва да се прилагат многократно (поне два пъти).

3. Правилата на L'Hôpital са приложими и когато аргументът на функциите (x) не клони към крайно число а, и до безкрайност ( х → ∞).

Несигурността от други типове също може да се сведе до несигурност от тип 0/0 и ∞ / ∞.

Разкриване на несигурности от типовете "нула, разделена на нула" и "безкрайност, разделена на безкрайност"

Пример 1.

х= 2 води до несигурност от вида 0/0. Следователно, производната на всяка функция и получаваме

Производната на полинома е изчислена в числителя, а в знаменателя - производна на комплексна логаритмична функция... Преди последния знак за равенство, обичайното лимит, замествайки две вместо x.

Пример 2.Изчислете границата на съотношението на две функции, като използвате правилото на L'Hôpital:

Решение. Замяна на стойност в дадена функция х

Пример 3.Изчислете границата на съотношението на две функции, като използвате правилото на L'Hôpital:

Решение. Замяна на стойност в дадена функция х= 0 води до несигурност от вида 0/0. Следователно, ние изчисляваме производните на функциите в числителя и знаменателя и получаваме:

Пример 4.Изчисли

Решение. Заместването на стойността x равна на плюс безкрайност в дадената функция води до несигурност от вида ∞ / ∞. Следователно ние прилагаме правилото на L'Hôpital:

Коментирайте. Нека се обърнем към примери, в които правилото на L'Hôpital трябва да се приложи два пъти, тоест да се стигне до границата на съотношенията на вторите производни, тъй като границата на съотношението на първите производни е несигурност от вида 0 /0 или ∞ / ∞.

Приложете сами правилото на L'Hôpital и след това вижте решението

Разкриване на несигурности от формата "нула по безкрайност"

Пример 12.Изчисли

Решение. Получаваме

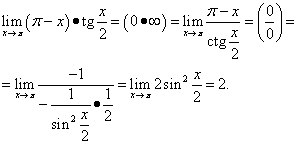
Този пример използва тригонометрична идентичност.

Разкриване на несигурности от типовете "нула в степен на нула", "безкрайност в степен на нула" и "едно в степен на безкрайност"

Несигурността на формата или обикновено се свежда до формата 0/0 или ∞ / ∞ с помощта на логаритъма на функция от формата

За да се изчисли границата на израз, трябва да се използва логаритмичната идентичност, чийто специален случай е свойството на логаритъма .

Използвайки логаритмичната идентичност и свойството за непрекъснатост на функцията (за да се премине отвъд знака на границата), границата трябва да се изчисли, както следва:

Отделно, трябва да намерите границата на изразяване в експонента и да изградите ддо намерената степен.

Пример 13.

Решение. Получаваме

Пример 14.Изчислете, като използвате правилото на L'Hôpital

Решение. Получаваме

Изчисляваме границата на изразяване в степента

Пример 15.Изчислете, като използвате правилото на L'Hôpital

Правилото на L'Hôpital и разкриването на несигурността
Разкриване на несигурности от типовете "нула, разделена на нула" и "безкрайност, разделена на безкрайност"
Разкриване на несигурности от формата "нула по безкрайност"
Разкриване на несигурности от типовете "нула в степен на нула", "безкрайност в степен на нула" и "едно в степен на безкрайност"
Разкриване на несигурности от формата "безкрайност минус безкрайност"

Правилото на L'Hôpital и разкриването на несигурността

Разкриването на несигурности от формата 0/0 или ∞ / ∞ и някои други несигурности е значително опростено с помощта на правилото на L'Hôpital.

Същността Правилата на L'Hôpital е, че в случай, когато изчисляването на границата на съотношенията на две функции дава несигурности от вида 0/0 или ∞ / ∞, границата на съотношението на две функции може да бъде заменена с границата на съотношението на техните производни и по този начин може да се получи определен резултат.

Като цяло правилата на L'Hôpital означават няколко теореми, които могат да бъдат предадени в следващата формулировка.

Правилото на L'Hôpital... Ако функции е(х) и ж(х) са диференцируеми в някаква околност на точката, с изключение може би на самата точка и в тази окръжност

(1)

В равенство (1) стойността, към която клони променливата, може да бъде или крайно число, или безкрайност, или минус безкрайност.

Несигурността от други типове също може да се сведе до несигурност от тип 0/0 и ∞ / ∞.

Разкриване на несигурности от типовете "нула, разделена на нула" и "безкрайност, разделена на безкрайност"

Пример 1.Изчисли

х= 2 води до несигурност от вида 0/0. Следователно ние прилагаме правилото на L'Hôpital:

Пример 2.Изчисли

Решение. Замяна на стойност в дадена функция х

Пример 3.Изчисли

Решение. Замяна на стойност в дадена функция х= 0 води до несигурност от вида 0/0. Следователно ние прилагаме правилото на L'Hôpital:

Пример 4.Изчисли

Решение. Заместването на стойността x, равна на плюс безкрайност в дадената функция, води до несигурност от вида ∞ / ∞. Следователно ние прилагаме правилото на L'Hôpital:

Коментирайте. Ако границата на коефициента на производната е несигурност от формата 0/0 или ∞ / ∞, тогава правилото на L'Hôpital може да се приложи отново, т.е. отидете до границата на съотношението на вторите производни и т.н.

Пример 5.Изчисли

Решение. Намираме

Тук правилото на L'Hôpital се прилага два пъти, тъй като и границата на съотношението на функциите, и границата на съотношението на производните дават несигурност от вида ∞ / ∞.

Пример 6.Изчисли

Представете си ято врабчета с изпъкнали очи. Не, това не е гръм, не е ураган или дори малко момче с прашка в ръцете си. Просто огромно, огромно гюле хвърчи всред пиленцата. Точно Правилата на L'Hôpitalсправят се с границите, в които има несигурност или.

Правилата на L'Hôpital са много мощен метод, който ви позволява бързо и ефективно да елиминирате посочените несигурности, не е случайно, че в колекциите от проблеми, при тестове, тестове често се среща стабилно клише: „изчислете лимита, не използвайки правилото на L'Hôpital". Изискването, подчертано с удебелен шрифт, може да бъде приписано с чиста съвест към всяка граница на уроците. Ограничения. Примери за решения, Прекрасни граници. Ограничете методи за решаване, Забележителни еквивалентности, където се среща несигурността "нула до нула" или "безкрайност до безкрайност". Дори ако задачата е формулирана накратко - „изчислете границите“, имплицитно се подразбира, че ще използвате всичко, всичко, но не и правилата на L'Hôpital.

Има общо две правила и те са много сходни едно с друго, както по същество, така и по начин на приложение. В допълнение към преките примери по темата, ще изучаваме и допълнителен материал, който ще бъде полезен при по-нататъшното изучаване на математическия анализ.

Веднага ще направя резервация, че правилата ще бъдат дадени в сбита "практическа" форма, а ако трябва да преминете теория, препоръчвам да се обърнете към учебника за по-строги изчисления.

Първото правило на L'Hôpital

Помислете за функциите, които безкрайно малъкв някакъв момент. Ако има ограничение за връзката им, тогава, за да премахнете несигурността, можете да вземете две производни- от числителя и от знаменателя. при което: , това е .

Забележка : ограничението също трябва да съществува, в противен случай правилото не се прилага.

Какво следва от горното?

Първо, трябва да можете да намерите производни на функции, и колкото по-добре - толкова по-добре =)

Второ, производните се вземат ОТДЕЛНО от числителя и ОТДЕЛНО от знаменателя. Моля, не се бъркайте с правилото за диференциране на коефициента !!!

И, трето, "X" може да се стреми навсякъде, включително до безкрайност - само ако има несигурност.

Нека се върнем към пример 5 от първата статия относно границите, при което се получи следният резултат:

Първото правило на L'Hôpital се прилага за несигурността 0:0:

Както можете да видите, диференцирането на числителя и знаменателя ни доведе до отговор на половин оборот: намерихме две прости производни, заместихме „две“ в тях и се оказа, че несигурността изчезна безследно!

Не е необичайно, когато правилата на L'Hôpital трябва да се прилагат последователно два или повече пъти (това важи и за второто правило). Нека го извадим за ретро вечер Пример 2 урок за прекрасните граници:

Два геврека отново се разхлаждат на двуетажното легло. Нека приложим правилото на L'Hôpital:

Моля, имайте предвид, че в първата стъпка се взема знаменателят производна на съставна функция... След това извършваме редица междинни опростявания, по-специално се отърваваме от косинуса, което показва, че той има тенденция към единство. Несигурността не е елиминирана, затова отново прилагаме правилото на L'Hôpital (втори ред).

Умишлено избрах не най-лесния пример, за да можете да проведете малък самотест. Ако не е съвсем ясно как са открити производни, трябва да укрепите техниката си за диференциране, ако фокусът с косинус не е ясен, моля, върнете се към прекрасни граници... Не виждам голям смисъл в коментарите стъпка по стъпка, тъй като вече говорих достатъчно подробно за производните и ограниченията. Новостта на статията се крие в самите правила и някои технически решения.

Както вече беше отбелязано, в повечето случаи правилата на L'Hôpital не е необходимо да се използват, но често е препоръчително да ги използвате за груба проверка на решението. Често, но не винаги. Така например, току-що разгледаният пример е много по-изгоден за проверка чудесни еквивалентности.

Второто правило на L'Hôpital

Брат 2 се бие с две спящи осмици. По същия начин:

Ако има граница на връзката безкрайно голямв точката на функциите:, тогава, за да премахнете несигурността, можете да вземете две производни- ОТДЕЛЕНО от числителя и ОТДЕЛЕНО от знаменателя. при което: , това е при диференциране на числителя и знаменателя, стойността на границата не се променя.

Забележка : ограничението трябва да съществува

Отново в различни практически примери значението може да бъде различно, включително безкрайни. Важно е да има несигурност.

Нека проверим Пример № 3 от първия урок: ... Използваме второто правило на L'Hôpital:

Веднага щом говорим за гиганти, ще анализираме две канонични граници:

Пример 1

Изчислете лимит

Не е лесно да се получи отговор чрез „обичайни“ методи, следователно, за да разкрием неопределеността „от безкрайност до безкрайност“, използваме правилото на L'Hôpital:

Поради това, линейна функция от по-висок порядък на растеж от логаритъм с основа по-голяма от единица(и др.). Разбира се, "x" в по-високи степени също ще "плъзне" такива логаритми. Всъщност функцията расте доста бавно и нейната графике по-плоска спрямо същото "x".

Пример 2

Изчислете лимит

Още един познат кадър. За да премахнем неяснотата, ние използваме правилото на L'Hôpital, освен това два пъти подред:

Експоненциална функция с основа по-голяма от единица(и др.) от по-висок порядък на растеж от степенна функция с положителна степен.

Подобни ограничения се срещат по време на пълно функционално изследване, а именно при намиране асимптоти на графики... Те се забелязват и в някои задачи на теория на вероятностите... Съветвам ви да вземете под внимание двата разгледани примера, това е един от малкото случаи, когато няма нищо по-добро от разграничаването на числителя и знаменателя.

По-нататък в текста няма да правя разлика между първото и второто правило на L'Hôpital, това е направено само с цел структуриране на статията. Като цяло, от моя гледна точка, е донякъде вредно да се номерират ненужно математически аксиоми, теореми, правила, свойства, тъй като фрази като "съгласно следствие 3 от теорема 19 ..." са информативни само в рамките на конкретен учебник . В друг източник на информация същото би било "Следствие 2 и теорема 3". Такива изявления са формални и удобни само за самите автори. В идеалния случай най-добре е да се позовава на същността на математически факт. Изключение са исторически установените термини, напр. първата чудесна границаили второ прекрасно ограничение.

Продължаваме да развиваме тема, предложена от член на Парижката академия на науките, маркиз Гийом Франсоа дьо Л'Хопитал. Статията придобива ясно изразена практическа конотация и в доста често срещана задача се изисква:

За да се затоплим, нека се справим с няколко малки врабчета:

Пример 3

Границата може да се опрости предварително, като се отървете от косинуса, но покажете уважение към условието и веднага разграничете числителя и знаменателя:

В процеса на намиране на производни няма нищо нестандартно, така че в знаменателя обичайното правило за диференциациявърши работа .

Разгледаният пример е уреден и след прекрасни граници, подобен случай е разгледан в края на статията за трудни граници.

Пример 4

Изчислете лимита по правилото на L'Hôpital

Това е пример за решение "направи си сам". Пошегувах се добре =)

Типична ситуация е, когато след диференциране се получават три- или четириетажни дроби:

Пример 5

Изчислете лимита с помощта на правилото на L'Hôpital

Приложението се подсказва забележителна еквивалентност, но пътят е строго предварително дефиниран от условието:

След диференцирането силно препоръчвам да се отървете от многоетажната фракция и да извършите максималните опростявания.... Разбира се, по-напредналите ученици могат да пропуснат последната стъпка и веднага да напишат: , но в някои граници дори отличниците ще се объркат.

Пример 6

Изчислете лимита с помощта на правилото на L'Hôpital

Пример 7

Изчислете лимита с помощта на правилото на L'Hôpital

Това са примери за решение „направи си сам“. В пример 7 нищо не може да се опрости, дробът е твърде проста след диференциране. Но в пример 8, след прилагане на правилото на L'Hôpital, е много желателно да се отървете от триетажната структура, тъй като изчисленията няма да са най-удобни. Пълно решение и отговор в края на урока. Ако имате някакви затруднения - тригонометрична таблицада помогна.

И опростяванията са абсолютно необходими, когато след диференциране несигурността не е елиминиран.

Пример 8

Изчислете лимита с помощта на правилото на L'Hôpital

Отивам:

Интересното е, че първоначалната несигурност след първото диференциране се превърна в несигурност и правилото на L'Hôpital се прилага спокойно по-нататък. Също така забележете как след всяко "приближаване" четириетажната фракция се елиминира и константите се преместват извън знака за граница. В по-прости примери е по-удобно да не понасяме константи, но когато границата е сложна, ние опростяваме всичко, всичко, всичко. Коварството на разкрития пример се крие и в това, че за , а, следователно, в хода на елиминирането на синусите, не е изненадващо да се объркате в знаците. В предпоследния ред синусите не биха могли да бъдат убити, но примерът е доста труден, простим.

Онзи ден попаднах на интересна задача:

Пример 9

Честно казано, малко се съмнявах на какво ще бъде равна тази граница. Както беше показано по-горе, „x“ е от по-висок порядък на растеж от логаритъма, но дали ще „плъзне“ куба на логаритъма? Опитайте се сами да разберете кой ще спечели.

Да, правилата на L'Hôpital са не само стрелба по врабчета от оръдие, но и старателна работа...

За да се прилагат правилата на L'Hôpital, несигурността на вида се свежда до гевреци или уморени осмици.

Репресията с несигурност е разгледана подробно в Примери № 9-13 от урока Ограничете методи за решаване... Нека вземем още едно за формата:

Пример 10

Изчислете границата на функция, като използвате правилото на L'Hôpital

На първата стъпка привеждаме израза към общ знаменател, като по този начин трансформираме несигурността в несигурност. След това зареждаме правилото на L'Hôpital:

Тук, между другото, е случаят, когато е безсмислено да се докосва до четириетажния израз.

Несигурността също не устоява да се превърне в или:

Пример 11

Изчислете границата на функция, като използвате правилото на L'Hôpital

Ограничението тук е едностранно и такива ограничения вече са обсъждани в ръководството Функционални графики и свойства... Както си спомняте, графиката на "класическия" логаритъм не съществува отляво на оста, така че можем да се приближим до нула само отдясно.

Правилата на L'Hôpital за едностранни ограничения работят, но първо трябва да се справите с несигурността. На първата стъпка правим триетажна дроб, получавайки несигурност, след което решението следва шаблонна схема:

След като разграничим числителя и знаменателя, се отърваваме от четириетажната дроб, за да опростим. В резултат на това се появи несигурност. Повтаряме трика: отново правим дроба триетажна и отново прилагаме правилото на L'Hôpital към получената несигурност:

Готов.

Първоначалният лимит може да се опита да бъде намален до два геврека:

Но, първо, производната в знаменателя е по-трудна, и второ, нищо добро няма да излезе от това.

Поради това, преди да решите подобни примери, трябва да анализирате(устно или на чернова) КАКВА несигурност е по-изгодно да се намали - до "нула до нула" или до "безкрайност до безкрайност".

На свой ред другарите по пиене и по-екзотичните другари са изтеглени към светлината. Методът на трансформация е прост и стандартен.