Собственият вектор на квадратна матрица е този, който, когато се умножи по дадена матрица, води до колинеарен вектор. С прости думи, когато една матрица се умножи по собствен вектор, последният остава същият, но умножен по някакво число.

Определение

Собственият вектор е ненулев вектор V, който, когато се умножи по квадратна матрица M, се превръща в себе си, увеличен с определено число λ. В алгебричната нотация изглежда така:

M × V = λ × V,

където λ е собствената стойност на матрицата M.

Нека разгледаме числен пример. За удобство числата в матрицата ще бъдат разделени с точка и запетая. Нека имаме матрица:

• М = 0; 4;
• 6; 10.

Нека го умножим по вектор колона:

• V = -2;

Когато умножим матрица по вектор колона, получаваме и вектор колона. В строги математически термини, формулата за умножаване на матрица 2 × 2 по вектор колона ще изглежда така:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 означава елементът от матрицата M, разположен в първия ред и първата колона, а M22 - елементът, разположен във втория ред и втората колона. За нашата матрица тези елементи са равни на M11 = 0, M12 = 4, M21 = 6, M22 10. За вектор колона тези стойности са V11 = –2, V21 = 1. Съгласно тази формула получаваме следния резултат от произведението на квадратна матрица от вектор:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

За удобство нека запишем вектора на колоната в ред. И така, умножихме квадратната матрица по вектора (-2; 1), което води до вектора (4; -2). Очевидно това е същият вектор, умножен по λ = -2. Ламбда в този случай означава собствената стойност на матрицата.

Собственият вектор на матрицата е колинеарен вектор, тоест обект, който не променя позицията си в пространството, когато се умножи по матрица. Колинеарността във векторната алгебра е подобна на паралелизма в геометрията. В геометричната интерпретация колинеарните вектори са успоредни насочени отсечки с различни дължини. От времето на Евклид знаем, че една права линия има безкраен брой успоредни прави линии, така че е логично да приемем, че всяка матрица има безкраен брой собствени вектори.

От предишния пример можете да видите, че собствените вектори могат да бъдат (-8; 4), и (16; -8) и (32, -16). Всичко това са колинеарни вектори, съответстващи на собствената стойност λ = -2. Когато умножим оригиналната матрица по тези вектори, ние все пак ще получим вектор, който се различава от оригинала 2 пъти. Ето защо при решаване на задачи за намиране на собствен вектор се изисква намиране само на линейно независими векторни обекти. Най-често за n × n матрица има n-ти брой собствени вектори. Нашият калкулатор е пригоден за анализ на квадратни матрици от втори ред, следователно почти винаги в резултат ще бъдат намерени два собствени вектора, с изключение на случаите, когато те съвпадат.

В примера по-горе, ние знаехме предварително собствения вектор на оригиналната матрица и ясно определихме ламбда числото. На практика обаче всичко се случва обратното: собствените стойности се намират в началото и едва след това са собствените вектори.

Алгоритъм за решаване

Нека да разгледаме отново оригиналната матрица M и да се опитаме да намерим и двата нейни собствени вектора. Така матрицата изглежда така:

• М = 0; 4;
• 6; 10.

Първо, трябва да определим собствената стойност λ, за която трябва да изчислим детерминанта на следната матрица:

• (0 - λ); 4;
• 6; (10 - λ).

Тази матрица се получава чрез изваждане на неизвестното λ от елементите на главния диагонал. Детерминантата се определя по стандартната формула:

• detA = M11 × M21 - M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

Тъй като нашият вектор не трябва да е нула, ние приемаме полученото уравнение като линейно зависимо и приравняваме нашата детерминанта detA на нула.

(0 - λ) × (10 - λ) - 24 = 0

Нека отворим скобите и ще получим характеристичното уравнение на матрицата:

λ 2 - 10λ - 24 = 0

Това е стандартното квадратно уравнение, което трябва да се реши с помощта на дискриминанта.

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

Коренът на дискриминанта е sqrt (D) = 14, следователно, λ1 = -2, λ2 = 12. Сега, за всяка ламбда стойност, трябва да намерите собствен вектор. Нека изразим коефициентите на системата за λ = -2.

• M - λ × E = 2; 4;
• 6; 12.

В тази формула E е идентичната матрица. Въз основа на получената матрица съставяме система от линейни уравнения:

2x + 4y = 6x + 12y,

където x и y са елементи на собствения вектор.

Съберете всички X отляво и всички играчи отдясно. Очевидно - 4x = 8y. Разделете израза на -4 и получете x = –2y. Сега можем да определим първия собствен вектор на матрицата, като вземем всякакви стойности на неизвестните (запомнете безкрайността на линейно зависими собствени вектори). Да вземем y = 1, тогава x = –2. Следователно първият собствен вектор изглежда като V1 = (–2; 1). Върнете се в началото на статията. Именно върху този векторен обект ние умножихме матрицата, за да демонстрираме концепцията за собствен вектор.

Сега ще намерим собствения вектор за λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Нека съставим същата система от линейни уравнения;

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x = y.

Сега нека вземем x = 1, следователно y = 3. По този начин вторият собствен вектор изглежда като V2 = (1; 3). Когато оригиналната матрица се умножи по този вектор, резултатът винаги ще бъде същият вектор, умножен по 12. Това завършва алгоритъма на решението. Вече знаете как да дефинирате ръчно собствения вектор на матрица.

• детерминант;
• следа, тоест сумата от елементите на главния диагонал;
• ранг, тоест максималният брой линейно независими редове/колони.

Програмата работи съгласно горния алгоритъм, минимизирайки процеса на решение. Важно е да се отбележи, че ламбдата се обозначава с буквата "c" в програмата. Да вземем числен пример.

Пример за програмата

Нека се опитаме да дефинираме собствени вектори за следната матрица:

• М = 5; 13;
• 4; 14.

Нека да въведете тези стойности в клетките на калкулатора и да получите отговора в следната форма:

• Матричен ранг: 2
• Детерминанта на матрицата: 18;
• Матрична следа: 19;
• Изчисляване на собствения вектор: c 2 - 19.00c + 18.00 (характерно уравнение);
• Изчисляване на собствен вектор: 18 (първа ламбда стойност);
• Изчисляване на собствен вектор: 1 (втора ламбда стойност);
• Системата от уравнения за вектор 1: -13x1 + 13y1 = 4x1 - 4y1;
• Системата от уравнения за вектор 2: 4x1 + 13y1 = 4x1 + 13y1;
• Собствен вектор 1: (1; 1);
• Собствен вектор 2: (-3,25; 1).

Така получихме два линейно независими собствени вектора.

Заключение

Линейната алгебра и аналитичната геометрия са стандартни предмети за всеки първокурсник по инженерство. Големият брой вектори и матрици е ужасяващ и е лесно да се направи грешка в такива тромави изчисления. Нашата програма ще позволи на учениците да проверят своите изчисления или автоматично ще реши проблема с намирането на собствен вектор. В нашия каталог има и други калкулатори за линейна алгебра, използвайте ги в обучението или работата си.

". Първата част излага минималните разпоредби за разбиране на химиометрията, а втората част съдържа факти, които трябва да знаете за по-задълбочено разбиране на методите на многовариантния анализ. Презентацията е илюстрирана с примери, извършени в работна книга на Excel Matrix.xlsкоято придружава този документ.

Препратките към примери се поставят в текста като обекти на Excel. Тези примери са абстрактни по природа, те по никакъв начин не са свързани с проблемите на аналитичната химия. Реални примери за използване на матричната алгебра в химометрията са разгледани в други текстове, посветени на различни химометрични приложения.

Повечето измервания, направени в аналитичната химия, не са директни, но непряк... Това означава, че в експеримента вместо стойността на желания аналит C (концентрация) се получава друга стойност х(сигнал) свързан, но не е равен на C, т.е. х(C) ≠ C. Като правило, вид зависимост х(C) не е известно, но за щастие в аналитичната химия, повечето измервания са пропорционални. Това означава, че с увеличаване на концентрацията на C in апъти, сигнал X ще се увеличи със същото количество. х(аВ) = а х(° С). Освен това сигналите също са адитивни, така че сигналът от проба, съдържаща две вещества с концентрации C 1 и C 2, ще бъде равен на сумата от сигнали от всеки компонент, т.е. х(C 1 + C 2) = х(C 1) + х(С 2). Пропорционалността и адитивността заедно дават линейност... Има много примери за илюстриране на принципа на линейността, но е достатъчно да споменем два от най-ярките примери – хроматографията и спектроскопията. Втората характеристика на експеримента по аналитична химия е многоканален... Съвременното аналитично оборудване едновременно измерва сигнали за много канали. Например, интензитетът на пропускане на светлината се измерва за няколко дължини на вълната наведнъж, т.е. спектър. Следователно, в експеримента, ние се занимаваме с много сигнали х 1 , х 2 ,...., х n, характеризиращ набора от концентрации C 1, C 2, ..., C m на вещества, присъстващи в изследваната система.

Ориз. 1 Спектри

И така, аналитичният експеримент се характеризира с линейност и многоизмерност. Следователно е удобно експерименталните данни да се разглеждат като вектори и матрици и да се манипулират с помощта на апарата на матричната алгебра. Плодотворността на този подход се илюстрира от показания пример, който показва три спектра, записани за 200 дължини на вълната от 4000 до 4796 cm – 1. Първо ( х 1) и вторият ( х 2) получени са спектри за стандартни проби, в които е известна концентрацията на две вещества А и В: в първата проба [A] = 0,5, [B] = 0,1, а във втората проба [A] = 0,2, [B ] = 0,6. Какво може да се каже за нова, неизвестна проба, чийто спектър е обозначен х 3 ?

Помислете за три експериментални спектра х 1 , х 2 и х 3 като три вектора с размерност 200. С помощта на линейна алгебра може лесно да се покаже, че х 3 = 0.1 х 1 +0.3 х 2; следователно, третата проба очевидно съдържа само вещества А и В при концентрации [A] = 0,5 × 0,1 + 0,2 × 0,3 = 0,11 и [B] = 0,1 × 0,1 + 0,6 × 0,3 = 0,19.

1. Основна информация

1.1 Матрици

Матрицанаречена например правоъгълна таблица с числа

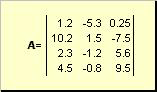
Ориз. 2 Матрица

Матриците са обозначени с удебелен шрифт с главни букви ( А), и техните елементи - съответни малки букви с индекси, т.е. а ij. Първият индекс номерира редовете, а вторият номерира колоните. В химиометрията е обичайно максималната стойност на индекса да се обозначава със същата буква като самия индекс, но с главни букви. Следователно матрицата Аможе да се запише и като ( а ij , и = 1,..., аз; j = 1,..., Дж). За матрицата, показана в примера аз = 4, Дж= 3 и а 23 = −7.5.

Двойка числа ази Джсе нарича размерност на матрицата и се обозначава като аз× Дж... Пример за матрица в химиометрията е наборът от спектри, получени за азпроби върху Дждължини на вълните.

1.2. Прости матрични операции

Матриците могат умножете по числа... В този случай всеки елемент се умножава по това число. Например -

Ориз. 3 Матрично умножение по число

Две матрици с една и съща размерност могат да бъдат елементарно сгънетеи извади... Например,

Ориз. 4 Добавяне на матрица

В резултат на умножение по число и събиране се получава матрица със същата размерност.

Нулевата матрица е матрица, състояща се от нули. Обозначава се О... Очевидно е, че А+О = А, А−А = Ои 0 А = О.

Матрицата може да бъде транспониране... По време на тази операция матрицата се обръща, т.е. редовете и колоните се разменят. Транспонирането е обозначено с щрих, А"или индекс А T. Така че, ако А = {а ij , и = 1,..., аз; j = 1,...,Дж), тогава А t = ( а ji , j = 1,...,Дж; i = 1, ..., аз). Например

Ориз. 5 Транспонирана матрица

Очевидно е, че ( А t) t = А, (А+Б) T = А t + Б T.

1.3. Матрично умножение

Матриците могат умножете, но само ако имат съответните размери. Защо това е така, ще стане ясно от определението. Продуктът на матрицата А, измерение аз× К, и матрици Б, измерение К× Джсе нарича матрица ° С, измерение аз× Джчиито елементи са числа

Така да произвежда ABнеобходимо е броят на колоните в лявата матрица Ае равно на броя на редовете в дясната матрица Б... Пример за матричен продукт -

Фиг. 6 Матричен продукт

Правилото за умножение на матрицата може да бъде формулирано по следния начин. За намиране на елемент от матрица ° Сстои на кръстовището и-ти ред и j-та колона ( ° С ij) трябва да се умножи елемент по елемент ити ред от първата матрица АНа jта колона на втората матрица Би сумирайте всички резултати. Така че в показания пример елемент от третия ред и втората колона се получава като сума от поелементните произведения на третия ред Аи втората колона Б

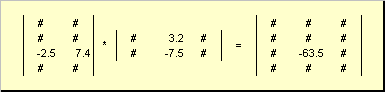
Фиг. 7 Елемент на матричен продукт

Продуктът на матриците зависи от реда, т.е. AB ≠ BA, макар и само поради размери. Казва се, че е некомутативна. Въпреки това, матричните продукти са асоциативни. Означава, че ABC = (AB)° С = А(пр.н.е). Освен това е и разпределителен, т.е. А(Б+° С) = AB+AC... Очевидно е, че АО = О.

1.4. Квадратни матрици

Ако броят на колоните на матрицата е равен на броя на нейните редове ( аз = J = N), тогава такава матрица се нарича квадратна. В този раздел ще разгледаме само такива матрици. Сред тези матрици могат да се отделят матрици със специални свойства.

Нежененматрица (означена аз,и понякога Е) е матрица, в която всички елементи са равни на нула, с изключение на диагоналните, които са равни на 1, т.е.

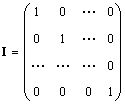
Очевидно Ai = IA = А.

Матрицата се нарича диагоналако всички негови елементи, с изключение на диагоналните ( а ii) са равни на нула. Например

Ориз. 8 Диагонална матрица

Матрица Анаречено върха триъгълнаако всички негови елементи под диагонала са равни на нула, т.е. а ij= 0, за и>j... Например

Ориз. 9 Горна триъгълна матрица

Долната триъгълна матрица се дефинира по подобен начин.

Матрица АНаречен симетрични, ако А t = А... С други думи а ij = а ji... Например

Ориз. 10 Симетрична матрица

Матрица АНаречен ортогонална, ако

А T А = AA t = аз.

Матрицата се нарича нормалноако

1.5. Следа и детерминанта

Следванеквадратна матрица А(означено с Tr ( А) или Sp ( А)) е сумата от диагоналните му елементи,

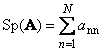
Например,

Ориз. 11 Матрична следа

Очевидно е, че

Sp (α А) = α Sp ( А) и

Sp ( А+Б) = Sp ( А) + Sp ( Б).

Може да се покаже, че

Sp ( А) = Sp ( А t), Sp ( аз) = н,

а също и това

Sp ( AB) = Sp ( BA).

Друга важна характеристика на квадратната матрица е нейната детерминанта(означено с det ( А)). Определянето на детерминанта в общия случай е доста трудно, така че ще започнем с най-простата версия - матрицата Аразмер (2 × 2). Тогава

За матрица (3 × 3) детерминантата ще бъде

В случая на матрицата ( н× н) детерминантата се изчислява като сбор от 1 2 3 ... н= н! членове, всеки от които е равен на

Индекси к 1 , к 2 ,..., k Nсе дефинират като всички възможни подредени пермутации rчисла в набора (1, 2, ..., н). Изчисляването на детерминанта на матрица е сложна процедура, която на практика се извършва с помощта на специални програми. Например,

Ориз. 12 Матричен детерминант

Отбелязваме само очевидните свойства:

дет ( аз) = 1, дет ( А) = дет ( А T),

дет ( AB) = дет ( А) дет ( Б).

1.6. вектори

Ако матрицата се състои само от една колона ( Дж= 1), тогава такъв обект се нарича вектор... По-точно, вектор колона. Например

Може да се разгледат и матрици, състоящи се от един ред, например

Този обект също е вектор, но вектор ред... Когато анализирате данни, е важно да разберем с кои вектори имаме работа – колони или редове. Така че спектърът, взет за една проба, може да се разглежда като вектор-ред. Тогава наборът от спектрални интензитети при определена дължина на вълната за всички проби трябва да се третира като колонен вектор.

Размерността на вектора е броят на неговите елементи.

Ясно е, че всеки вектор колона може да бъде трансформиран в вектор ред чрез транспониране, т.е.

В случаите, когато формата на вектор не е конкретно посочена, а просто се казва вектор, тогава те означават вектор колона. Ние също ще се придържаме към това правило. Векторът се обозначава с малка права удебелена буква. Нулев вектор е вектор, всички елементи на който са нула. Той е обозначен 0 .

1.7. Основни операции с вектори

Векторите могат да се добавят и умножават по числа по същия начин като матриците. Например,

Ориз. 13 Векторни операции

Два вектора хи гса наречени колинеарнаако има число α такова, че

1.8. Продукти на вектори

Два вектора с една и съща размерност нможе да се умножи. Нека има два вектора х = (х 1 , х 2 ,...,х N) t и г = (г 1 , г 2 ,...,г N) т. Водени от правилото за умножение "ред по колона", можем да съставим два продукта от тях: х T ги xy T. Първо парче

Наречен скаларенили вътрешни... Неговият резултат е число. Той също така използва нотацията ( х,г)= х T г... Например,

Ориз. 14 Вътрешен продукт (точков продукт)

Второ парче

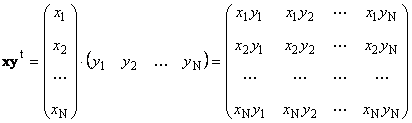
Наречен външен... Неговият резултат е матрица с измерение ( н× н). Например,

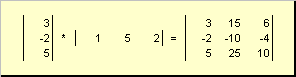
Ориз. 15 Външна работа

Наричат ​​се вектори, чието скаларно произведение е равно на нула ортогонална.

1.9. Векторна норма

Скаларното произведение на вектор сам по себе си се нарича скаларен квадрат. Тази стойност

определя квадрат дължинавектор х... За обозначаване на дължина (нарича се още норматавектор), се използва обозначението

Например,

Ориз. 16 Векторна норма

Вектор с единична дължина (|| х|| = 1) се нарича нормализиран. Ненулев вектор ( х ≠ 0 ) може да се нормализира, като се раздели на дължината, т.е. х = ||х|| (х /||х||) = ||х|| д... Тук д = х /||х|| е нормализираният вектор.

Векторите се наричат ​​ортонормирани, ако всички са нормализирани и ортогонални по двойки.

1.10. Ъгъл между векторите

Точковият продукт определя и инжекцияφ между два вектора хи г

Ако векторите са ортогонални, тогава cosφ = 0 и φ = π / 2, а ако са колинеарни, тогава cosφ = 1 и φ = 0.

1.11. Векторно представяне на матрица

Всяка матрица Аразмер аз× Джможе да се представи като набор от вектори

Тук всеки вектор а jе jта колона и вектора ред б ие и-ти ред на матрицата А

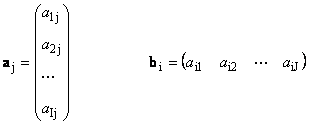
1.12. Линейно зависими вектори

Вектори със същото измерение ( н) може да се добавя и умножава по число, точно като матрици. Резултатът ще бъде вектор със същото измерение. Нека има няколко вектора с една и съща размерност х 1 , х 2 ,...,х K и същия брой числа α α 1, α 2, ..., α К... вектор

г= α 1 х 1 + α 2 х 2 + ... + α К х К

Наречен линейна комбинациявектори х к .

Ако има ненулеви числа α к ≠ 0, к = 1,..., К, Какво г = 0 , тогава такъв набор от вектори х кНаречен линейно зависими... В противен случай векторите се наричат ​​линейно независими. Например вектори х 1 = (2, 2) t и х 2 = (−1, −1) t са линейно зависими, тъй като х 1 +2х 2 = 0

1.13. Матричен ранг

Помислете за набор от Квектори х 1 , х 2 ,...,х Кразмери н... Рангът на тази система от вектори е максималният брой линейно независими вектори. Например в комплекта

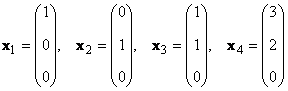
има само два линейно независими вектора, например х 1 и х 2, така че рангът му е 2.

Очевидно, ако в множеството има повече вектори от тяхната измерение ( К>н), тогава те непременно са линейно зависими.

По ранга на матрицата(означено с ранг ( А)) е рангът на системата от вектори, от която се състои. Въпреки че всяка матрица може да бъде представена по два начина (вектори на колони или редове), това не засяга стойността на ранга, тъй като

1.14. обратна матрица

Квадратна матрица Асе нарича неизроден, ако има уникален обратенматрица А-1 се определя от условията

AA −1 = А −1 А = аз.

Обратна матрица не съществува за всички матрици. Необходимо и достатъчно условие за неизраждане е

дет ( А) ≠ 0 или ранг ( А) = н.

Обръщането на матрицата е сложна процедура, за която има специални програми. Например,

Ориз. 17 Матрична инверсия

Нека представим формули за най-простия случай - 2 × 2 матрици

Ако матрици Аи Бнедегенерати, значи

(AB) −1 = Б −1 А −1 .

1.15. Псевдообратна матрица

Ако матрицата Ае изродено и обратната матрица не съществува, тогава в някои случаи можете да използвате псевдо-обратенматрица, която се дефинира като такава матрица А+ това

AA + А = А.

Псевдо-инверсната матрица не е единствената и нейният вид зависи от метода на изграждане. Например, за правоъгълна матрица можете да използвате метода на Мур-Пенроуз.

Ако броят на колоните е по-малък от броя на редовете, тогава

А + =(А T А) −1 А T

Например,

Ориз. 17a Псевдо-инверсия на матрицата

Ако броят на колоните е по-голям от броя на редовете, тогава

А + =А T ( AA T) −1

1.16. Умножаване на вектор по матрица

вектор хможе да се умножи по матрица Аподходящ размер. В този случай векторът на колоната се умножава отдясно брадваи векторът на реда е отляво х T А... Ако размерността на вектора Дж, и размерността на матрицата аз× Джтогава резултатът е вектор на измерението аз... Например,

Ориз. 18 Вектор по матрично умножение

Ако матрицата А- квадрат ( аз× аз), след това векторът г = брадваима същото измерение като х... Очевидно е, че

А(α 1 х 1 + α 2 х 2) = α 1 брадва 1 + α 2 брадва 2 .

Следователно матриците могат да се разглеждат като линейни трансформации на вектори. В частност Ix = х, вол = 0 .

2. Допълнителна информация

2.1. Системи от линейни уравнения

Нека бъде А- размер на матрицата аз× Дж, а б- вектор на измерението Дж... Помислете за уравнението

брадва = б

по отношение на вектора х, размери аз... Всъщност това е система от азлинейни уравнения с Джнеизвестен х 1 ,...,х Дж... Решението съществува тогава и само ако

ранг ( А) = ранг ( Б) = Р,

където Бе матрица с разширено измерение аз×( J + 1), състояща се от матрицата Аподплатен с колона б, Б = (А б). В противен случай уравненията са непоследователни.

Ако Р = аз = Дж, то решението е уникално

х = А −1 б.

Ако Р < аз, тогава има много различни решения, които могат да бъдат изразени чрез линейната комбинация Дж−Рвектори. Система от хомогенни уравнения брадва = 0 квадратна матрица А (н× н) има нетривиално решение ( х ≠ 0 ) ако и само ако det ( А) = 0. Ако Р= ранг ( А)<нтогава съществуват н−Рлинейно независими решения.

2.2. Билинейни и квадратни форми

Ако Ае квадратна матрица и хи гса вектори със съответната размерност, тогава скаларното произведение на формата х T ДаНаречен билинеенформата, дефинирана от матрицата А... В х = гизразяване х T брадваНаречен квадратичнаформа.

2.3. Положително определени матрици

Квадратна матрица АНаречен положително дефиниранако за всеки ненулев вектор х ≠ 0 ,

х T брадва > 0.

По същия начин, отрицателно (х T брадва < 0), неотрицателен (х T брадва≥ 0) и не положително (х T брадва≤ 0) определени матрици.

2.4. Разлагане на Холецки

Ако е симетрична матрица Ае положително определена, тогава има уникална триъгълна матрица Ус положителни елементи, за които

А = У T У.

Например,

Ориз. 19 Разлагане на Холецки

2.5. Полярно разлагане

Нека бъде Ае неизродена квадратна матрица с размерност н× н... След това има едно към едно полярнипроизводителност

А = SR,

където Се неотрицателна симетрична матрица и Ре ортогонална матрица. Матрици Си Рможе да се дефинира изрично:

С 2 = AA t или С = (AA t) ½ и Р = С −1 А = (AA t) −1 А.

Например,

Ориз. 20 Полярно разлагане

Ако матрицата Ае изродено, то разширението не е уникално - а именно: Свсе още сам, но Рможе би много. Полярното разлагане представлява матрицата Акато комбинация от компресия/разтягане Си обръщане Р.

2.6. Собствени вектори и собствени стойности

Нека бъде Ае квадратна матрица. вектор vНаречен собствен векторматрици А, ако

Av = λ v,

където се извиква числото λ собствен смисълматрици А... По този начин, трансформацията, която матрицата извършва Анад вектор v, се свежда до просто разтягане или компресия с коефициент λ. Собственият вектор се определя до умножение по константата α ≠ 0, т.е. ако vе собствен вектор, тогава α vсъщо е собствен вектор.

2.7. Собствени стойности

Матрица А, измерение ( н× н) не може да бъде повече от нсобствени стойности. Те удовлетворяват характеристично уравнение

дет ( А − λ аз) = 0,

което е алгебрично уравнение нта поръчка. По-специално, за 2 × 2 матрица, характеристичното уравнение има формата

Например,

Ориз. 21 Собствени стойности

Множеството от собствени стойности λ 1, ..., λ нматрици АНаречен спектър А.

Спектърът има различни свойства. В частност

дет ( А) = λ 1 × ... × λ н, Sp ( А) = λ 1 + ... + λ н.

Собствените стойности на произволна матрица могат да бъдат комплексни числа, но ако матрицата е симетрична ( А t = А), тогава неговите собствени стойности са реални.

2.8. Собствени вектори

Матрица А, измерение ( н× н) не може да бъде повече от нсобствени вектори, всеки от които съответства на собствената си стойност. За определяне на собствения вектор v нтрябва да решите система от хомогенни уравнения

(А − λ н аз)v н = 0 .

Той има нетривиално решение, тъй като det ( А -λ н аз) = 0.

Например,

Ориз. 22 собствени вектора

Собствените вектори на симетрична матрица са ортогонални.

Определение 9.3.вектор NS Наречен собствен векторматрици Аако има такъв номер λ, че равенството важи: А NS= λ NS, т.е. резултатът от кандидатстването към NS линейна трансформация, дадена от матрицата А, е умножението на този вектор по числото λ ... Самото число λ Наречен собствен номерматрици А.

Заместване във формули (9.3) x` j = λx j,получаваме система от уравнения за определяне на координатите на собствения вектор:

. (9.5)

Тази линейна хомогенна система ще има нетривиално решение само ако главният й детерминант е 0 (правилото на Крамер). Записване на това условие във формата:

получаваме уравнението за определяне на собствените стойности λ Наречен характеристично уравнение... Накратко може да се представи по следния начин:

| A - λE | = 0, (9.6)

тъй като лявата му страна съдържа детерминантата на матрицата A-λE... Полином по отношение на λ | A - λE| Наречен характеристичен полиномматрици А.

Характерни полиномни свойства:

1) Характеристичният полином на линейна трансформация не зависи от избора на основата. Доказателство. (виж (9.4)), но следователно,. По този начин не зависи от избора на основата. Следователно и | A-λE| не се променя при преминаване към нова основа.

2) Ако матрицата Алинейната трансформация е симетрично(тези. и ij = a ji), тогава всички корени на характеристичното уравнение (9.6) са реални числа.

Свойства на собствените стойности и собствените вектори:

1) Ако изберем база от собствени вектори х 1, х 2, х 3 съответстващи на собствените стойности λ 1, λ 2, λ 3матрици А, то в тази база линейната трансформация A има матрица с диагонална форма:

(9.7) Доказателството на това свойство следва от определението на собствените вектори.

2) Ако собствените стойности на трансформацията Аса различни, то съответните собствени вектори са линейно независими.

3) Ако характеристичният полином на матрицата Аима три различни корена, тогава в някаква основа матрицата Аима диагонална форма.

Нека намерим собствените стойности и собствените вектори на матрицата Нека съставим характеристичното уравнение: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Нека намерим координатите на собствените вектори, съответстващи на всяка намерена стойност λ. От (9.5) следва, че ако NS (1) ={х 1, х 2, х 3) Съответен ли е собственият вектор λ 1 = -2, тогава

- съвместна, но недефинирана система. Неговото решение може да се запише като NS (1) ={а,0,-а), където a е произволно число. По-специално, ако изискваме, че | х (1) |=1, NS (1) =

Заместване в системата (9.5) λ 2 = 3, получаваме система за определяне на координатите на втория собствен вектор - х (2) ={y 1, y 2, y 3}:

, където NS (2) ={б, -б, б) или при спазване на | х (2) |=1, х (2) =

За λ 3 = 6 намерете собствения вектор х (3) ={z 1, z 2, z 3}:

, х (3) ={° С,2в, в) или в нормализираната версия

х (3) = Можете да видите това NS (1) NS (2) = ab - аб= 0, х (1) х (3) = ac - ac= 0, х (2) х (3) = пр. н. е- 2пр. н. е. + пр. н. е= 0. Така собствените вектори на тази матрица са ортогонални по двойки.

Лекция 10.

Квадратни форми и връзката им със симетрични матрици. Свойства на собствени вектори и собствени стойности на симетрична матрица. Свеждане на квадратичната форма до каноничната форма.

Определение 10.1.Квадратична формареални променливи x 1, x 2, ..., x nе полином от втора степен по отношение на тези променливи, който не съдържа свободен член и членове от първа степен.

Примери за квадратични форми:

(н = 2),

(н = 3). (10.1)

Нека си припомним определението за симетрична матрица, дадено в последната лекция:

Определение 10.2.Квадратната матрица се нарича симетрично, ако, тоест, ако матричните елементи, симетрични спрямо главния диагонал, са равни.

Свойства на собствените стойности и собствените вектори на симетрична матрица:

1) Всички собствени стойности на симетрична матрица са реални.

Доказателство (за н = 2).

Нека матрицата Аизглежда като: ... Нека съставим характеристичното уравнение:

(10.2) Намерете дискриминанта:

Следователно уравнението има само реални корени.

2) Собствените вектори на симетричната матрица са ортогонални.

Доказателство (за н= 2).

Координатите на собствените вектори и трябва да отговарят на уравненията.

С матрица A, ако има число l такова, че AX = lX.

Освен това се нарича числото l собствен смисълоператор (матрица A), съответстващ на вектор X.

С други думи, собствен вектор е вектор, който под действието на линеен оператор се трансформира в колинеарен вектор, т.е. просто умножено по някакво число. За разлика от тях, неправилните вектори са по-трудни за трансформиране.

Нека напишем определението на собствен вектор под формата на система от уравнения:

Преместете всички термини в лявата страна:

Последната система може да бъде написана в матрична форма, както следва:

(A - lE) X = O

Получената система винаги има нулево решение X = O. Такива системи, в които всички свободни членове са равни на нула, се наричат хомогенна... Ако матрицата на такава система е квадратна и детерминантата й не е равна на нула, тогава с помощта на формулите на Крамер винаги получаваме уникално решение - нула. Може да се докаже, че системата има ненулеви решения, ако и само ако детерминантът на тази матрица е равен на нула, т.е.

| A - LE | = = 0

Това уравнение с неизвестно l се нарича характеристично уравнение (характеристичен полином) на матрицата A (линеен оператор).

Може да се покаже, че характеристичният полином на линеен оператор не зависи от избора на базата.

Например, нека намерим собствените стойности и собствените вектори на линейния оператор, даден от матрицата A =.

За това съставяме характеристичното уравнение | A - lЕ | = = (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; собствени стойности l 1 = (2 - 12) / 2 = -5; l 2 = (2 + 12) / 2 = 7.

За да намерим собствените вектори, решаваме две системи от уравнения

(A + 5E) X = O

(A - 7E) X = O

За първия от тях разширената матрица приема формата

,

откъдето x 2 = c, x 1 + (2/3) c = 0; x 1 = - (2/3) s, т.е. X (1) = (- (2/3) s; s).

За втория от тях разширената матрица приема формата

,

откъдето x 2 = c 1, x 1 - (2/3) c 1 = 0; x 1 = (2/3) s 1, т.е. X (2) = ((2/3) s 1; s 1).

По този начин, собствените вектори на този линеен оператор са всички вектори от вида (- (2/3) с; с) със собствена стойност (-5) и всички вектори от вида ((2/3) с 1; с 1) със собствена стойност 7...

Може да се докаже, че матрицата на оператор A в базиса, състояща се от неговите собствени вектори, е диагонална и има вида:

,

където l i са собствените стойности на тази матрица.

Обратното също е вярно: ако матрицата A в някаква основа е диагонална, тогава всички вектори на тази база ще бъдат собствени вектори на тази матрица.

Възможно е също да се докаже, че ако линеен оператор има n по двойки различни собствени стойности, тогава съответните собствени вектори са линейно независими и матрицата на този оператор в съответната база има диагонална форма.

Нека обясним това с предишния пример. Взимаме произволни ненулеви стойности с и с 1, но такива, че векторите X (1) и X (2) са линейно независими, т.е. ще формират основата. Например, нека c = c 1 = 3, тогава X (1) = (-2; 3), X (2) = (2; 3).

Нека проверим линейната независимост на тези вектори:

12 ≠ 0. В тази нова база матрицата A ще приеме формата A * =.

За да проверим това, използваме формулата A * = C -1 AC. Първо, намираме C -1.

С -1 = ;

Квадратни форми

Квадратична форма f (x 1, x 2, xn) от n променливи се нарича сбор, всеки член на който е или квадратът на една от променливите, или произведението на две различни променливи, взети с определен коефициент: f (x 1 , x 2, xn) = (a ij = a ji).

Матрицата A, съставена от тези коефициенти, се нарича матрицаквадратна форма. То винаги симетричноматрица (т.е. матрица, симетрична спрямо главния диагонал, a ij = a ji).

В матричната нотация квадратичната форма е f (X) = X T AX, където

Наистина

Например, нека запишем квадратичната форма в матрична форма.

За да направим това, намираме матрица с квадратична форма. Неговите диагонални елементи са равни на коефициентите на квадратите на променливите, а останалите елементи са равни на половината от съответните коефициенти на квадратната форма. Ето защо

Нека матрицата-колона от променливи X се получава чрез неизродена линейна трансформация на матрицата-колона Y, т.е. X = CY, където С е неизродена матрица от порядък n. Тогава квадратичната форма f (X) = X T AX = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y.

По този начин, при неизродена линейна трансформация C, матрицата на квадратната форма приема формата: A * = C T AC.

Например, нека намерим квадратната форма f (y 1, y 2), получена от квадратната форма f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 чрез линейно преобразуване.

Квадратната форма се нарича каноничен(То има каноничен възглед) ако всичките му коефициенти a ij = 0 за i ≠ j, т.е.
f (x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Матрицата му е диагонална.

Теорема(тук не са дадени доказателства). Всяка квадратна форма може да бъде редуцирана до канонична, като се използва недегенерирана линейна трансформация.

Например, можем да намалим квадратичната форма до канонична
f (x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

За да направите това, първо изберете пълен квадрат с променлива x 1:

f (x 1, x 2, x 3) = 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2 (x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

Сега избираме пълен квадрат с променлива x 2:

f (x 1, x 2, x 3) = 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 =
= 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Тогава недегенерираното линейно преобразуване y 1 = x 1 + x 2, y 2 = x 2 + (1/10) x 3 и y 3 = x 3 редуцира тази квадратична форма до каноничната форма f (y 1, y 2 , y 3) = 2y 1 2 - 5y 2 2 + (1/20) y 3 2.

Имайте предвид, че каноничната форма на квадратна форма се определя нееднозначно (една и същата квадратична форма може да бъде сведена до канонична форма по различни начини). Въпреки това, каноничните форми, получени по различни начини, имат редица общи свойства. По-специално, броят на членовете с положителни (отрицателни) коефициенти на квадратната форма не зависи от метода за редуциране на формата до тази форма (например в разглеждания пример винаги ще има два отрицателни и един положителен коефициент) . Това свойство се нарича закон за инерцията на квадратичните форми.

Нека проверим това, като намалим същата квадратична форма до каноничната форма по различен начин. Нека започнем трансформацията с променлива x 2:

f (x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3 (x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
= -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 = f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, където y 1 = - (2/3) x 1 + x 2 + (1/6) x 3, y 2 = (2/3) x 1 + (1/6) x 3 и y 3 = x 1. Тук има отрицателен коефициент -3 за y 1 и два положителни коефициента 3 и 2 за y 2 и y 3 (и когато използваме друг метод, получаваме отрицателен коефициент (-5) за y 2 и два положителни: 2 за y 1 и 1/20 за y 3).

Трябва също да се отбележи, че рангът на матрицата на квадратната форма, наречен рангът на квадратната форма, е равно на броя на ненулевите коефициенти на каноничната форма и не се променя при линейни трансформации.

Квадратната форма f (X) се нарича положително (отрицателно) сигуренако за всички стойности на променливите, които не са равни на нула едновременно, той е положителен, т.е. f (X)> 0 (отрицателно, т.е.
е (X)< 0).

Например, квадратната форма f 1 (X) = x 1 2 + x 2 2 е положително определена, тъй като е сумата от квадрати, а квадратната форма f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 е отрицателно определена, тъй като представлява, може да се представи като f 2 (X) = - (x 1 - x 2) 2.

В повечето практически ситуации е малко по-трудно да се установи определеността на квадратична форма, затова за това се използва една от следните теореми (ще ги формулираме без доказателства).

Теорема... Квадратната форма е положителна (отрицателна) определена, ако и само ако всички собствени стойности на нейната матрица са положителни (отрицателни).

Теорема(критерий на Силвестър). Квадратната форма е положително определена, ако и само ако всички големи минорни числа на матрицата на тази форма са положителни.

Мажор (ъгъл) минор K-тият ред на матрицата A от n-тия ред се нарича детерминанта на матрицата, съставена от първите k редове и колони на матрицата A ().

Обърнете внимание, че за отрицателно определени квадратни форми знаците на главните минори се редуват и минорът от първи ред трябва да бъде отрицателен.

Например, нека разгледаме квадратната форма f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 за определеност на знака.

= (2 - l) *
* (3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; D = 25 - 8 = 17;
... Следователно квадратичната форма е положително определена.

Метод 2. Главен минор от първи ред на матрицата А D 1 = a 11 = 2> 0. Главен минор от втори ред D 2 = = 6 - 4 = 2> 0. Следователно, според критерия на Силвестър, квадратичната форма е положително определена.

Нека да изследваме друга квадратична форма за определеност на знака, f (x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Метод 1. Да построим матрица на квадратната форма A =. Характеристичното уравнение ще има формата = (-2 - l) *
* (- 3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
... Следователно квадратичната форма е отрицателно определена.

Метод 2. Главен минор от първи ред на матрицата A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Следователно, според критерия на Силвестър, квадратичната форма е отрицателно определена (знаците на главните минорни се редуват, започвайки с минус).

И като друг пример, нека разгледаме квадратната форма f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 за определеност на знака.

Метод 1. Да построим матрица на квадратната форма A =. Характеристичното уравнение ще има формата = (2 - l) *
* (- 3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Едно от тези числа е отрицателно, а другото е положително. Знаците на собствените стойности са различни. Следователно квадратичната форма не може да бъде нито отрицателна, нито положително определена, т.е. тази квадратична форма не е определена (може да приема стойности от всеки знак).

Метод 2. Главен минор от първи ред на матрицата A D 1 = a 11 = 2> 0. Основен минор от втори ред D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

Най-прости са диагоналните матрици. Възниква въпросът дали е възможно да се намери база, в която матрицата на линеен оператор да има диагонална форма. Такава основа съществува.
Нека има дадено линейно пространство R n и линеен оператор A, действащ в него; в този случай операторът A взема R n в себе си, тоест A: R n → R n.

Определение. Ненулев вектор се нарича собствен вектор на оператор A, ако операторът A се трансформира във вектор, колинеарен спрямо него, т.е. Числото λ се нарича собствена стойност или собствена стойност на оператора A, съответстваща на собствения вектор.
Нека отбележим някои свойства на собствените стойности и собствените вектори.
1. Всяка линейна комбинация от собствени вектори на оператора A, съответстващ на същата собствена стойност λ, е собствен вектор със същата собствена стойност.
2. Собствени вектори на оператор A с различни по двойки собствени стойности λ 1, λ 2,…, λ m са линейно независими.
3. Ако собствените стойности λ 1 = λ 2 = λ m = λ, тогава собствената стойност λ съответства на най-много m линейно независими собствени вектори.

Така че, ако има n линейно независими собствени вектори съответстващи на различни собствени стойности λ 1, λ 2,..., λ n, то те са линейно независими, следователно могат да се вземат за основа на пространството R n. Нека намерим формата на матрицата на линейния оператор A в основата на неговите собствени вектори, за които действаме от оператор A на базисни вектори: тогава .
По този начин матрицата на линейния оператор A в основата на неговите собствени вектори има диагонална форма, а собствените стойности на оператор A са разположени на диагонала.
Има ли друга основа, в която матрицата е диагонална? Отговорът на този въпрос се дава от следната теорема.

Теорема. Матрицата на линеен оператор A в основата (i = 1..n) има диагонална форма тогава и само ако всички вектори на основата са собствени вектори на оператор A.

Правилото за намиране на собствени стойности и собствени вектори

Нека е даден вектор , където x 1, x 2, ..., x n са координатите на вектора спрямо основата и е собственият вектор на линеен оператор A, съответстващ на собствената стойност λ, т.е. Тази връзка може да се запише в матрична форма

. (*)

Уравнение (*) може да се разглежда като уравнение за намиране, освен това, тоест ние се интересуваме от нетривиални решения, тъй като собственият вектор не може да бъде нула. Известно е, че нетривиални решения на хомогенна система от линейни уравнения съществуват само ако det (A - λE) = 0. Следователно, за да бъде λ собствена стойност на оператора A, е необходимо и достатъчно det (A - λE) = 0.
Ако уравнението (*) е написано подробно в координатна форма, тогава получаваме система от линейни хомогенни уравнения:

(1)
където е матрицата на линейния оператор.

Система (1) има ненулево решение, ако детерминантата й D е равна на нула

Получава се уравнение за намиране на собствените стойности.
Това уравнение се нарича характеристично уравнение, а лявата му страна се нарича характеристичен полином на матрицата (оператор) A. Ако характеристичният полином няма реални корени, тогава матрицата A няма собствени вектори и не може да бъде сведена до диагонална форма .
Нека λ 1, λ 2,…, λ n са реални корени на характеристичното уравнение и сред тях може да има множество корени. Замествайки тези стойности на свой ред в система (1), намираме собствените вектори.

Пример 12. Линейният оператор A действа в R 3 съгласно закона, където x 1, x 2, .., x n са координатите на вектора в основата , , ... Намерете собствените стойности и собствените вектори на този оператор.
Решение. Изграждаме матрицата на този оператор:
.
Съставяме система за определяне на координатите на собствените вектори:

Съставяме характеристично уравнение и го решаваме:

.
λ 1,2 = -1, λ 3 = 3.
Замествайки λ = -1 в системата, имаме:
или
Защото , тогава има две зависими променливи и една свободна променлива.
Тогава нека x 1 е свободно неизвестно Решаваме тази система по всякакъв начин и намираме общо решение на тази система: Основната система от решения се състои от едно решение, тъй като n - r = 3 - 2 = 1.
Множеството от собствени вектори, съответстващи на собствената стойност λ = -1, има формата:, където x 1 е всяко ненулево число. Нека изберем един вектор от това множество, например, като поставим x 1 = 1: .
Разсъждавайки по подобен начин, намираме собствения вектор, съответстващ на собствената стойност λ = 3: .
В пространството R 3 базата се състои от три линейно независими вектора, но сме получили само два линейно независими собствени вектора, от които не може да се състави базата в R 3. Следователно матрицата A на линейния оператор не може да бъде сведена до диагонална форма.

Пример 13. Дадена матрица .
1. Докажете, че векторът е собствен вектор на матрицата A. Намерете собствената стойност, съответстваща на този собствен вектор.
2. Намерете основа, в която матрицата A има диагонална форма.
Решение.
1. Ако, тогава - собствен вектор

.
Вектор (1, 8, -1) е собствен вектор. Собствена стойност λ = -1.
Матрицата има диагонална форма в основата, състояща се от собствени вектори. Един от тях е известен. Да намерим останалото.
Търсим собствени вектори от системата:

Характерно уравнение: ;
(3 + λ) [- 2 (2-λ) (2 + λ) +3] = 0; (3 + λ) (λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Нека намерим собствения вектор, съответстващ на собствената стойност λ = -3:

Рангът на матрицата на тази система е равен на две и е равен на броя неизвестни, следователно тази система има само нулево решение x 1 = x 3 = 0. x 2 тук може да бъде всяко различно от нула, например x 2 = 1. По този начин векторът (0 , 1,0) е собствен вектор, съответстващ на λ = -3. Да проверим:
.
Ако λ = 1, тогава получаваме системата
Рангът на матрицата е два. Изтриваме последното уравнение.
Нека x 3 е свободно неизвестно. Тогава x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Задавайки x 3 = 1, имаме (-3, -9,1) - собствения вектор, съответстващ на собствената стойност λ = 1. Проверка:

.
Тъй като собствените стойности са реални и различни, векторите, съответстващи на тях, са линейно независими, така че могат да се вземат за основа в R 3. Така в основата , , матрица А има вида:
.
Не всяка матрица на линеен оператор A: R n → R n може да бъде сведена до диагонална форма, тъй като за някои линейни оператори линейно независимите собствени вектори могат да бъдат по-малки от n. Ако обаче матрицата е симетрична, тогава точно m линейно независими вектори съответстват на корена на характеристичното уравнение на кратност m.

Определение. Симетрична матрица е квадратна матрица, в която елементите, симетрични по отношение на главния диагонал, са равни, тоест в която.
Забележки. 1. Всички собствени стойности на симетрична матрица са реални.
2. Собствените вектори на симетрична матрица, съответстващи на по двойки различни собствени стойности, са ортогонални.
Като едно от многото приложения на изследвания апарат нека разгледаме проблема за определяне на формата на крива от втори ред.