Užduotys su išvestiniu egzamine. Meistriškumo klasė „Funkcijos išvestinė egzamino užduotyse. geometrinė ir fizinė išvestinės reikšmė; funkcijos grafiko liestinės lygtis; funkcijos tyrimas naudojant išvestinę

Funkcijos išvestinė yra viena iš sudėtingiausių temų mokyklos programoje. Ne kiekvienas abiturientas atsakys į klausimą, kas yra darinys.

Šiame straipsnyje paprastai ir aiškiai paaiškinama, kas yra išvestinė priemonė ir kodėl ji reikalinga.. Dabar nesieksime matematinio pateikimo griežtumo. Svarbiausia suprasti prasmę.

Prisiminkime apibrėžimą:

Išvestinė yra funkcijos kitimo greitis.

Paveikslėlyje pavaizduoti trijų funkcijų grafikai. Kaip manote, kuris iš jų auga greičiausiai?

Atsakymas akivaizdus – trečias. Ji turi didžiausią pokyčio greitį, ty didžiausią išvestinę priemonę.

Štai dar vienas pavyzdys.

Kostya, Grisha ir Matvey gavo darbus tuo pačiu metu. Pažiūrėkime, kaip per metus pasikeitė jų pajamos:

Jūs galite pamatyti viską diagramoje iš karto, tiesa? Kostjos pajamos per šešis mėnesius išaugo daugiau nei dvigubai. Ir Grišos pajamos taip pat padidėjo, bet tik šiek tiek. O Mato pajamos sumažėjo iki nulio. Paleidimo sąlygos tos pačios, tačiau funkcijos kitimo greitis, t.y. išvestinė, - kitoks. Kalbant apie Matvey, jo pajamų išvestinė suma paprastai yra neigiama.

Intuityviai galime lengvai įvertinti funkcijos kitimo greitį. Bet kaip tai padaryti?

Mes iš tikrųjų žiūrime į tai, kaip staigiai funkcijos grafikas kyla aukštyn (arba žemyn). Kitaip tariant, kaip greitai y keičiasi su x. Akivaizdu, kad ta pati funkcija skirtinguose taškuose gali turėti skirtingą išvestinės reikšmę – tai yra, ji gali keistis greičiau arba lėčiau.

Funkcijos išvestinė žymima .

Parodykime, kaip rasti naudojant grafiką.

Nubraižytas kokios nors funkcijos grafikas. Paimkite tašką ant jo abscise. Šiame taške nubrėžkite funkcijos grafiko liestinę. Norime įvertinti, kaip staigiai kyla funkcijos grafikas. Patogi vertė yra liestinės nuolydžio liestinė.

Funkcijos išvestinė taške yra lygi liestinės, nubrėžtos į funkcijos grafiką tame taške, nuolydžio liestei.

Atkreipkite dėmesį - kaip liestinės pasvirimo kampas, mes imame kampą tarp liestinės ir teigiamos ašies krypties.

Kartais mokiniai klausia, kokia yra funkcijos grafiko liestinė. Tai tiesi linija, turinti vienintelį bendrą tašką su diagrama šioje dalyje, be to, kaip parodyta mūsų paveikslėlyje. Tai atrodo kaip apskritimo liestinė.

Raskime. Prisimename, kad stačiojo trikampio smailiojo kampo liestinė yra lygi priešingos kojos ir gretimos kojos santykiui. Iš trikampio:

Išvestinę radome naudodamiesi grafiku, net nežinodami funkcijos formulės. Tokios užduotys dažnai randamos matematikos egzamine po numeriu.

Yra dar viena svarbi koreliacija. Prisiminkite, kad tiesią liniją suteikia lygtis

Šioje lygtyje esantis dydis vadinamas tiesios linijos nuolydis. Jis lygus tiesės polinkio į ašį kampo liestinei.

Mes tai suprantame

Prisiminkime šią formulę. Ji išreiškia geometrinę išvestinės reikšmę.

Funkcijos išvestinė taške yra lygi to taško funkcijos grafiko liestinės nuolydžiui.

Kitaip tariant, išvestinė lygi liestinės nuolydžio liestinei.

Jau sakėme, kad ta pati funkcija skirtinguose taškuose gali turėti skirtingus išvestinius. Pažiūrėkime, kaip išvestinė yra susijusi su funkcijos veikimu.

Nubraižykime kokios nors funkcijos grafiką. Tegul ši funkcija vienose srityse didėja, o kitose mažėja ir skirtingais tempais. Ir tegul ši funkcija turi didžiausius ir mažiausius taškus.

Tam tikru momentu funkcija didėja. Taške nubrėžta grafiko liestinė sudaro smailųjį kampą su teigiama ašies kryptimi. Taigi išvestinė taške yra teigiama.

Šiuo metu mūsų funkcija mažėja. Šiame taške liestinė sudaro bukąjį kampą su teigiama ašies kryptimi. Kadangi bukojo kampo liestinė yra neigiama, išvestinė taške yra neigiama.

Štai kas nutinka:

Jei funkcija didėja, jos išvestinė yra teigiama.

Jei jis mažėja, jo išvestinė yra neigiama.

O kas bus didžiausiame ir minimaliame taške? Matome, kad (maksimaliajame taške) ir (minimaliame taške) liestinė yra horizontali. Todėl liestinės nuolydžio liestinė šiuose taškuose lygi nuliui, o išvestinė taip pat lygi nuliui.

Taškas yra maksimalus taškas. Šiuo metu funkcijos padidėjimas pakeičiamas sumažėjimu. Vadinasi, išvestinės ženklas taške pasikeičia iš „pliuso“ į „minusą“.

Taške – minimaliame taške – išvestinė taip pat lygi nuliui, tačiau jos ženklas keičiasi iš „minuso“ į „pliusą“.

Išvada: naudodamiesi išvestine, galite sužinoti viską, kas mus domina, apie funkcijos veikimą.

Jei išvestinė yra teigiama, tada funkcija didėja.

Jei išvestinė yra neigiama, tada funkcija mažėja.

Didžiausiame taške išvestinė yra nulis ir keičia ženklą iš pliuso į minusą.

Minimaliame taške išvestinė taip pat yra nulis ir keičia ženklą iš minuso į pliusą.

Šias išvadas rašome lentelės pavidalu:

	dideja	maksimalus taškas	mažėja	minimalus taškas	dideja
+	0	-	0	+

Padarykime du nedidelius patikslinimus. Vieno iš jų prireiks sprendžiant egzamino uždavinius. Kitas – pirmame kurse, su rimtesniu funkcijų ir darinių studijavimu.

Galimas atvejis, kai funkcijos išvestinė tam tikru momentu lygi nuliui, bet funkcija šiuo metu neturi nei maksimumo, nei minimumo. Šis vadinamasis :

Taške grafiko liestinė yra horizontali, o išvestinė lygi nuliui. Tačiau prieš tašką funkcija padidėjo, o po taško ji toliau didėja. Darinio ženklas nesikeičia – išliko teigiamas toks, koks buvo.

Taip pat atsitinka, kad maksimumo ar minimumo taške išvestinė neegzistuoja. Grafike tai atitinka staigų pertrauką, kai tam tikrame taške neįmanoma nubrėžti liestinės.

Bet kaip rasti išvestinę, jei funkcija pateikta ne grafiku, o formule? Šiuo atveju tai taikoma

Funkcijos $y = f(x)$ išvestinė duotame taške $x_0$ yra funkcijos prieaugio santykio su atitinkamu argumento prieaugiu riba, jei pastarasis linkęs į nulį:

$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$

Diferencijavimas – tai išvestinės paieškos operacija.

Kai kurių elementariųjų funkcijų išvestinių lentelė

Funkcija	Darinys
$c$	$0$
$x$	$1$
$x^n$	$nx^(n-1)$
$(1)/(x)$	$-(1)/(x^2)$
$√x$	$(1)/(2√x)$
$e^x$	$e^x$
$lnx$	$(1)/(x)$
$sinx$	$cosx$
$cosx$	$-sinx $
$tgx$	$(1)/(cos^2x)$
$ctgx$	$-(1)/(sin^2x)$

Pagrindinės diferenciacijos taisyklės

1. Sumos (skirtumo) išvestinė lygi išvestinių sumai (skirtumui)

$(f(x) ± g(x))"= f"(x)±g"(x)$

Raskite funkcijos $f(x)=3x^5-cosx+(1)/(x)$ išvestinę

Sumos (skirtumo) išvestinė yra lygi išvestinių sumai (skirtumui).

$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + sinx - (1)/(x^2)$

2. Produkto darinys

$(f(x) g(x))"= f"(x) g(x)+ f(x) g(x)"$

Raskite išvestinę $f(x)=4x cosx$

$f"(x)=(4x)" cosx+4x (cosx)"=4 cosx-4x sinx$

3. Dalinio išvestinė

$((f(x))/(g(x)))"=(f"(x) g(x)-f(x) g(x)")/(g^2(x)) $

Raskite išvestinę $f(x)=(5x^5)/(e^x)$

$f"(x)=((5x^5)" e^x-5x^5 (e^x)")/((e^x)^2)=(25x^4 e^x- 5x^5 e^x)/((e^x)^2)$

4. Sudėtinės funkcijos išvestinė lygi išorinės funkcijos išvestinės ir vidinės funkcijos išvestinės sandaugai

$f(g(x))"=f"(g(x)) g"(x)$

$f"(x)=cos"(5x) (5x)"=-sin(5x) 5 = -5sin(5x)$

Išvestinio fizinė reikšmė

Jeigu materialus taškas juda tiesia linija ir jo koordinatė keičiasi priklausomai nuo laiko pagal dėsnį $x(t)$, tai šio taško momentinis greitis lygus funkcijos išvestinei.

Taškas juda koordinačių linija pagal dėsnį $x(t)= 1,5t^2-3t + 7$, kur $x(t)$ yra koordinatė momentu $t$. Kuriuo momentu taško greitis bus lygus 12 USD?

1. Greitis yra $x(t)$ išvestinė, todėl suraskime duotosios funkcijos išvestinę

$v(t) = x"(t) = 1,5 2t -3 = 3t -3 $

2. Norėdami sužinoti, kuriuo momentu $t$ greitis buvo lygus $12$, sudarome ir išsprendžiame lygtį:

Išvestinės geometrinė reikšmė

Prisiminkite, kad tiesės, kuri nėra lygiagrečios koordinačių ašims, lygtis gali būti parašyta $y = kx + b$, kur $k$ yra tiesės nuolydis. Koeficientas $k$ lygus nuolydžio tarp tiesės ir teigiamos $Ox$ ašies krypties liestinės.

Funkcijos $f(x)$ išvestinė taške $x_0$ yra lygi grafiko liestinės duotame taške $k$ nuolydžiui:

Todėl galime padaryti bendrą lygybę:

$f"(x_0) = k = tgα$

Paveiksle funkcijos $f(x)$ liestinė didėja, taigi koeficientas $k > 0$. Kadangi $k > 0$, tai $f"(x_0) = tgα > 0$. Kampas $α$ tarp liestinės ir teigiamos krypties $Ox$ yra smailusis.

Paveiksle funkcijos $f(x)$ liestinė mažėja, taigi koeficientas $k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

Paveiksle funkcijos $f(x)$ liestinė yra lygiagreti $Ох$ ašiai, taigi koeficientas $k = 0$, taigi $f"(x_0) = tg α = 0$. Taškas $ x_0$, kai $f "(x_0) = 0$, iškviečiama ekstremumas.

Paveiksle pavaizduotas funkcijos $y=f(x)$ grafikas ir šio grafiko liestinė, nubrėžta taške su abscise $x_0$. Raskite funkcijos $f(x)$ išvestinės reikšmę taške $x_0$.

Grafiko liestinė didėja, todėl $f"(x_0) = tg α > 0$

Norėdami rasti $f"(x_0)$, randame nuolydžio liestinę tarp liestinės ir teigiamos $Ox$ ašies krypties. Norėdami tai padaryti, užbaigiame trikampio $ABC$ liestinę.

Raskite kampo $BAC$ liestinę. (Smailaus kampo liestinė stačiakampiame trikampyje yra priešingos kojos ir gretimos kojos santykis.)

$tg BAC = (BC) / (AC) = (3) / (12) = (1) / (4) = 0,25 $

$f"(x_0) = tg JŪS = 0,25 $

Atsakymas: 0,25 USD

Išvestinė taip pat naudojama didėjančių ir mažėjančių funkcijų intervalams rasti:

Jei intervale $f"(x) > 0$, tai funkcija $f(x)$ šiame intervale didėja.

Jei $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

Paveiksle parodytas funkcijos $y = f(x)$ grafikas. Tarp taškų $х_1,х_2,х_3…х_7$ raskite tuos taškus, kuriuose funkcijos išvestinė yra neigiama.

Atsakydami užrašykite duomenų taškų skaičių.

PRAKTINIAI PRAKTINIAI DARBAI 2

Funkcijų grafikų transformacija.

Tikslas

Nubraižykite funkcijų grafikus naudodami įvairias transformacijas, atsakykite į problemos klausimą.

Darbo užbaigimas

Gairės

Darbas skirtas 10 variantų, pasirinkimo numeris sutampa su paskutiniu sąraše esančio serijos numerio skaitmeniu. Pavyzdžiui, 1, 11, 21, 31 ... atlikite 1 parinktį, 2, 12, 22 ... - 2 parinktį ir pan.

Darbas susideda iš dviejų dalių: pirmoji 1-5 užduočių dalis, tai užduotys, kurias būtina atlikti norint gauti įskaitą, jei šios užduotys atliktos su klaida, jas reikia pataisyti ir vėl pateikti darbą patikrinimui . Antroje dalyje pateikiamos užduotys, kurias atlikę galite uždirbti papildomą pažymį: pagrindinė dalis +2 užduotys - "4", pagrindinė dalis +3 užduotys - "5".

Užduotis 1. Tiesinės funkcijos grafikas yra tiesė, jai sukurti pakanka dviejų taškų. (argumento x reikšmes imame savavališkai ir apsvarstykite galimybę funkcijos y reikšmę pakeisti formule).

Norėdami patikrinti, ar funkcijos grafikas eina per nurodytą tašką, vietoj x ir y reikia pakeisti taško koordinates, jei gaunate teisingą lygybę, tai tiesė eina per nurodytą tašką, kitaip ji neperžengia .

2, 3, 4 užduotis. Nurodytų funkcijų grafikai gauti iš funkcijų grafikų , naudojant poslinkį išilgai x arba y ašies.

, pirmiausia nubraižykite funkciją arba , tada perkeliame jį „a“ vienetais į dešinę arba į kairę (+ a - į kairę, - a į dešinę), tada perkeliame „b“ vienetais aukštyn arba žemyn (+ in - up, - in - žemyn)

Panašiai ir su kitomis funkcijomis:

5 užduotis Norėdami nubrėžti funkcijos grafiką: , jums reikia: 1) sudaryti funkcijos grafiką , 2) grafiko dalis, esanti virš x ašies, paliekama nepakeista, 3) grafiko dalis, esanti žemiau x ašies, atspindima.

Savarankiško sprendimo užduotys.

Privaloma dalis

Užduotis 1. Nubraižykite tiesinės funkcijos grafiką, nustatykite, ar funkcijos grafikas eina per nurodytą tašką:

2 užduotis. Nubraižykite kvadratinės funkcijos grafiką, nurodykite šios funkcijos reikšmių rinkinį.

3 užduotis. Sudarykite funkcijos grafiką, nustatykite, ar nurodyta funkcija didėja, ar mažėja.

4 užduotis. Sudarykite funkcijos grafiką, atsakykite į užduoties klausimą.

5 užduotis. Sudarykite funkcijos grafiką, kuriame yra modulio ženklas.

Užduotys papildomam įvertinimui.

6 užduotis. Nubraižykite pateiktos funkcijos grafiką dalimis, nustatykite, ar ši funkcija turi lūžio tašką:

7 užduotis. Nustatykite, kiek sprendinių turi lygčių sistema, pagrįskite atsakymą. Padarykite išvadas atsakydami į klausimus.

Kokių funkcijų grafikus sukūrėte šiame darbe?

Kaip vadinasi tiesinės funkcijos grafikas?

Kaip vadinasi kvadratinės funkcijos grafikas?

Kokias diagramos transformacijas žinote?

Kaip koordinačių sistemoje yra lyginės funkcijos grafikas? Nelyginės funkcijos grafikas?

Vieningo valstybinio egzamino bazinio lygio matematikos užduotyje Nr. 13 turėsite pademonstruoti vienos iš funkcijos elgsenos sąvokų įgūdžius ir žinias: išvestines taške arba didėjimo ar mažėjimo tempus. Šios užduoties teorija bus pridėta šiek tiek vėliau, tačiau tai netrukdys mums išsamiai išanalizuoti kelių tipinių variantų.

Bazinio lygio matematikos užduočių Nr. 14 tipinių variantų analizė

Variantas 14MB1

Grafike parodyta temperatūros priklausomybė nuo laiko, kai šildomas automobilio variklis. Horizontali ašis rodo laiką minutėmis, praėjusį nuo variklio užvedimo; vertikalioje ašyje yra variklio temperatūra Celsijaus laipsniais.

Naudodamiesi diagrama, kiekvieną laiko intervalą suderinkite su variklio įšilimo proceso charakteristikomis šiuo intervalu.

Lentelėje po kiekviena raide nurodykite atitinkamą skaičių.

Vykdymo algoritmas:

Pasirinkite laiko intervalą, per kurį temperatūra nukrito.
Pritvirtinkite liniuotę prie 30°C ir nustatykite laiko intervalą, per kurį temperatūra buvo žemesnė nei 30°C.

Sprendimas:

Pasirenkame laiko intervalą, per kurį temperatūra nukrito. Ši sekcija matoma plika akimi, ji prasideda praėjus 8 minutėms nuo variklio užvedimo.

Uždėkite liniuotę iki 30°C ir nustatykite laiko intervalą, per kurį temperatūra buvo žemesnė nei 30°C.

Po liniuote bus sekcija, atitinkanti laiko intervalą 0 - 1 min.

Pieštuko ir liniuote pagalba nustatome, kokiu laiko intervalu temperatūra buvo nuo 40 ° C iki 80 ° C.

Iš taškų, atitinkančių 40°C ir 80°C, statmenus metame į grafiką, o iš gautų taškų – į laiko ašį.

Matome, kad šis temperatūros intervalas atitinka 3 - 6,5 min laiko intervalą. Tai yra, iš pateiktų sąlygoje 3 - 6 min.

Pašalinimo metodu pasirinkite trūkstamą atsakymą.

Variantas 14MB2

Sprendimas:

Išanalizuokime funkcijos A grafiką. Jei funkcija didėja, tai išvestinė yra teigiama ir atvirkščiai. Funkcijos išvestinė yra lygi nuliui ekstremumo taškuose.

Pirma, funkcija A didėja, t.y. išvestinė yra teigiama. Tai atitinka 2 ir 3 išvestinių grafikus. Maksimaliame funkcijos x = -2 taške, tai yra, šiame taške išvestinė turėtų būti lygi nuliui. Ši sąlyga atitinka grafiko numerį 3.

Pirma, funkcija B mažėja, t.y. išvestinė yra neigiama. Tai atitinka 1 ir 4 išvestinių grafikus. Maksimalus funkcijos x \u003d -2 taškas, tai yra, šiuo metu išvestinė turi būti lygi nuliui. Ši sąlyga atitinka grafiko numerį 4.

Pirma, funkcija B didėja, t.y. išvestinė yra teigiama. Tai atitinka 2 ir 3 išvestinių grafikus. Funkcijos x = 1 maksimalus taškas, tai yra, šiuo metu išvestinė turi būti lygi nuliui. Ši sąlyga atitinka grafiko numerį 2.

Eliminavimo metodu galime nustatyti, kad funkcijos Г grafikas atitinka išvestinės, esančios skaičiumi 1, grafiką.

Atsakymas: 3421.

Variantas 14MB3

Kiekvienos funkcijos vykdymo algoritmas:

Nustatykite didėjančių ir mažėjančių funkcijų intervalus.
Nustatykite maksimalius ir mažiausius funkcijų taškus.
Padarykite išvadas, suderinkite siūlomus grafikus.

Sprendimas:

Išanalizuokime funkcijos A grafiką.

Jei funkcija didėja, tada išvestinė yra teigiama ir atvirkščiai. Funkcijos išvestinė yra lygi nuliui ekstremumo taškuose.

Ekstremalumo taškas yra taškas, kuriame pasiekiama maksimali arba mažiausia funkcijos reikšmė.

Pirma, funkcija A didėja, t.y. išvestinė yra teigiama. Tai atitinka 3 ir 4 išvestinių grafikus. Maksimaliame funkcijos x=0 taške, tai yra, šiame taške išvestinė turėtų būti lygi nuliui. Ši sąlyga atitinka grafiko numerį 4.

Išanalizuokime funkcijos B grafiką.

Pirma, funkcija B mažėja, t.y. išvestinė yra neigiama. Tai atitinka 1 ir 2 išvestinių grafikus. Funkcijos x=-1 mažiausias taškas, tai yra, šiuo metu išvestinė turi būti lygi nuliui. Ši sąlyga atitinka grafiko numerį 2.

Išanalizuokime funkcijos B grafiką.

Pirma, funkcija B sumažėja, t.y. išvestinė yra neigiama. Tai atitinka 1 ir 2 išvestinių grafikus. Mažiausias funkcijos x \u003d 0 taškas, tai yra, šiuo metu išvestinė turi būti lygi nuliui. Ši sąlyga atitinka grafiko numerį 1.

Eliminavimo būdu galime nustatyti, kad funkcijos Г grafikas atitinka išvestinės, esančios skaičiumi 3, grafiką.

Atsakymas: 4213.

Variantas 14MB4

Paveikslėlyje parodytas funkcijos grafikas ir jai nubrėžtos liestinės taškuose su abscisėmis A, B, C ir D.Dešiniajame stulpelyje rodomos išvestinės reikšmės taškuose A, B, C ir D. Naudodami grafiką suderinkite kiekvieną tašką su jame esančios funkcijos išvestinės reikšme.

TAŠKAI
BET
AT
Su
D

IŠVESTINĖS VERTĖS
1) –4
2) 3
3) 2/3
4) -1/2

Prisiminkite, ką reiškia išvestinė, būtent jos vertę taške - išvestinės funkcijos reikšmė taške lygi liestinės nuolydžio (koeficiento) liestinei.

Atsakymuose turime du teigiamus ir du neigiamus variantus. Kaip prisimename, jei koeficientas yra tiesioginis (grafika y = kx + b) yra teigiamas, tada linija didėja, jei ji yra neigiama, tada linija mažėja.

Turime dvi didėjančias linijas – taškuose A ir D. Dabar prisiminkime, ką reiškia koeficiento k reikšmė?

Koeficientas k parodo, kaip greitai funkcija didėja arba mažėja (iš tikrųjų pats koeficientas k yra funkcijos y = kx + b išvestinė).

Todėl k \u003d 2/3 atitinka švelnesnę tiesią liniją - D, o k \u003d 3 - A.

Panašiai ir neigiamų verčių atveju: taškas B atitinka statesnę tiesę, kurios k = -4, o taškas C - -1/2.

Variantas 14MB5

Paveikslėlyje taškai rodo mėnesinių šildytuvų pardavimo apimtis buitinės technikos parduotuvėje. Mėnesiai nurodomi horizontaliai, parduotų šildytuvų skaičius – vertikaliai. Aiškumo dėlei taškai yra sujungti linija.

Naudodamiesi paveikslu, kiekvieną nurodytą laikotarpį suderinkite su šildytuvų pardavimo charakteristikomis.

Vykdymo algoritmas

Analizuojame skirtingus metų laikus atitinkančias grafiko dalis. Suformuluojame grafike rodomas situacijas. Mes randame jiems tinkamiausius atsakymus.

Sprendimas:

Žiemą pardavimų skaičius viršijo 120 vnt/mėn., ir jis nuolat didėjo. Ši situacija atitinka 3 atsakymą. Tie. mes gauname: A-3.

Pavasarį pardavimai palaipsniui sumažėjo nuo 120 šildytuvų per mėnesį iki 50. 2 variantas yra artimiausias šiai formulei. Mes turime: B–2.

Vasarą pardavimų skaičius nesikeitė ir buvo minimalus. 2-oji šios formuluotės dalis atsakymuose neatsispindi, o pirmajai tinka tik Nr.4. Taigi mes turime: 4 val.

Rudenį pardavimai augo, tačiau jų skaičius neviršijo 100 vienetų nei vieną mėnesį. Ši situacija aprašyta 1 variante. Mes gauname: G-1.

Variantas 14MB6

Grafike parodyta reguliaraus autobuso greičio priklausomybė nuo laiko. Vertikalioje ašyje rodomas autobuso greitis km/h, horizontalioje – laikas minutėmis nuo autobuso pradžios.

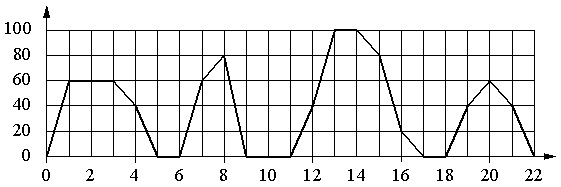
Naudodamiesi diagrama, kiekvieną laiko intervalą suderinkite su magistralės judėjimo šiuo intervalu charakteristika.

Vykdymo algoritmas

Padalinimo kainą nustatome ant horizontalios ir vertikalios skalės.
Mes paeiliui analizuojame siūlomus 1–4 teiginius iš dešiniojo stulpelio („Charakteristikos“). Juos lyginame su laiko intervalais iš kairiojo lentelės stulpelio, atsakymui randame poras „raidės-skaičiaus“.

Sprendimas:

Horizontalios skalės padalijimo reikšmė – 1 s, vertikalios – 20 km/val.

Autobusui sustojus jo greitis lygus 0. 2 minutes iš eilės autobusas nuliniu greičiu važiavo tik nuo 9 iki 11 minutės. Šis laikas patenka į 8–12 minučių intervalą. Taigi atsakymui turime porą: B–1.
Keletą laikotarpių autobusas važiavo 20 km/h ar didesniu greičiu. Be to, A variantas čia netinka, nes, pavyzdžiui, 7 minutę greitis buvo 60 km/h, B variantas – nes jis jau pritaikytas, D variantas – nes intervalo pradžioje ir pabaigoje autobusas turėjo nulinį greitį. Šiuo atveju tinka B variantas (12–16 min.); šiuo intervalu autobusas pradeda važiuoti 40 km/h greičiu, tada įsibėgėja iki 100 km/m ir po to palaipsniui mažina greitį iki 20 km/h. Taigi mes turime: 2.
Čia yra nustatytas greičio apribojimas. B ir C variantų nesvarstome. Likę intervalai A ir G yra tinkami. Todėl būtų teisinga pirmiausia apsvarstyti 4-ąjį variantą, o tada vėl grįžti prie 3-iojo.
Iš dviejų likusių intervalų charakteristikai Nr. 4 tinka tik 4–8 minutės, nes šiuo intervalu (6 minutę) buvo sustojimas. Per 18–22 minučių intervalą sustojimų nebuvo. Mes gauname: A-4. Iš to išplaukia, kad charakteristikai Nr.3 reikia imti intervalą Г, t.y. pasirodo pora G-3.

Variantas 14MB7

Taškinė figūra rodo Kinijos gyventojų skaičiaus augimą nuo 2004 iki 2013 m. Metai nurodomi horizontaliai, gyventojų prieaugis procentais (gyventojų skaičiaus padidėjimas, palyginti su praėjusiais metais) – vertikaliai. Aiškumo dėlei taškai yra sujungti linija.

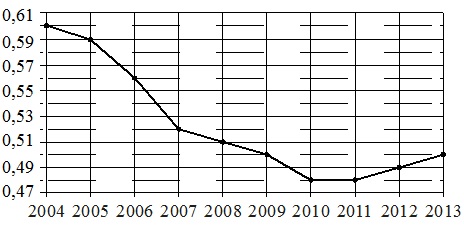
Naudodamiesi diagrama, kiekvieną nurodytą laikotarpį suderinkite su Kinijos gyventojų skaičiaus augimo per šį laikotarpį charakteristika..

Vykdymo algoritmas

Nustatykite paveikslo vertikalios skalės padalijimo reikšmę. Jis randamas kaip skirtumas tarp gretimų skalės verčių poros, padalytos iš 2 (nes tarp dviejų gretimų verčių yra 2 padalos).
Analizuojame 1–4 charakteristikas, pateiktas sąlygoje (kairysis lentelės stulpelis). Kiekvieną iš jų lyginame su konkrečiu laikotarpiu (dešinysis lentelės stulpelis).

Sprendimas:

Vertikalios skalės padalijimo reikšmė yra 0,01%.

Augimo mažėjimas tęsėsi nuo 2004 iki 2010 m. 2010–2011 m. augimas buvo nuolat minimalus, o nuo 2012 m. pradėjo didėti. Tie. Augimas sustojo 2010 m. Šie metai yra 2009–2011 m. Atitinkamai, mes turime: 1.
Didžiausias augimo kritimas turėtų būti laikomas „stačiausiai“ krentančia diagramos linija paveiksle. Jis patenka į 2006–2007 m. laikotarpį. ir yra 0,04 proc. per metus (2006 m. – 0,59–0,56=0,04 proc., o 2007 m. – 0,56–0,52=0,04 proc.). Iš čia gauname: A-2.
3 charakteristikoje nurodytas augimas prasidėjo 2007 m., tęsėsi 2008 m. ir baigėsi 2009 m. Tai atitinka B laiko tarpą, t.y. mes turime: B–3.
Gyventojų skaičius pradėjo didėti po 2011 m., t.y. 2012–2013 metais Todėl gauname: G 4.

Variantas 14MB8

Paveikslėlyje parodytas funkcijų grafikas ir į jį nubrėžtos liestinės taškuose su abscisėmis A, B, C ir D.

Dešiniajame stulpelyje rodomos funkcijos išvestinės reikšmės taškuose A, B, C ir D. Naudodami diagramą suderinkite kiekvieną tašką su funkcijos išvestinės reikšme jame.

Vykdymo algoritmas

Mes laikome liestinių porą, kurios turi smailų kampą su teigiama x ašies kryptimi. Mes juos palyginame, randame atitiktį tarp atitinkamų išvestinių verčių poros.
Nagrinėjame liestinių porą, sudarančių bukąjį kampą su teigiama x ašies kryptimi. Palyginame juos modulio, nustatome išvestinių išvestinių verčių atitiktį tarp dviejų likusių dešiniajame stulpelyje.

Sprendimas:

Smailusis kampas su teigiama x ašies kryptimi susidaro išvestinėmis t.B ir t.C. Šios išvestinės priemonės turi teigiamas vertes. Todėl čia reikėtų rinktis tarp reikšmių Nr. 1 ir 3. Taikant taisyklę, kad jei kampas yra mažesnis nei 45 0, tai išvestinė yra mažesnė už 1, o jei daugiau, tai daugiau nei 1, darome išvadą: t.B modulio išvestinė yra didesnė nei 1 t.C - mažesnė nei 1. Tai reiškia, kad atsakymui galite sudaryti poras: 3 DALYJE ir S-1.

Išvestinės t.A ir t.D sudaro bukąjį kampą su teigiama x ašies kryptimi. Ir čia taikome tą pačią taisyklę, šiek tiek perfrazuodami: kuo labiau taške esanti liestinė „prispaudžiama“ prie abscisių ašies linijos (į neigiamą jos kryptį), tuo ji yra didesnė absoliučia verte. Tada gauname: išvestinė taške A yra mažesnė absoliučia verte nei išvestinė taške D. Iš čia mes turime poras atsakymui: A-2 ir D–4.

Variantas 14MB9

Paveiksle esantys taškai rodo vidutinę paros oro temperatūrą Maskvoje 2011 m. sausio mėn. Mėnesio datos nurodomos horizontaliai, temperatūra Celsijaus laipsniais – vertikaliai. Aiškumo dėlei taškai yra sujungti linija.

Naudodamiesi paveikslu, kiekvieną nurodytą laikotarpį suderinkite su temperatūros pokyčio charakteristika.

Vykdymo algoritmas

Mes analizuojame 1–4 charakteristikas nuosekliai (dešinysis stulpelis), naudodami diagramą paveikslėlyje. Kiekvieną iš jų išdėstome pagal tam tikrą laikotarpį (kairysis stulpelis).

Sprendimas:

Temperatūra pakilo tik laikotarpio pabaigoje sausio 22–28 d. Čia 27 ir 28 dienomis pakilo atitinkamai 1 ir 2 laipsniais. Laikotarpio pabaigoje sausio 1–7 dienomis temperatūra buvo pastovi (–10 laipsnių), sausio 8–14 ir 15–21 pabaigoje nukrito (nuo –1 iki –2 ir nuo –11 iki –12). laipsniais, atitinkamai). Todėl gauname: G-1.
Kadangi kiekvienas laikotarpis apima 7 dienas, temperatūra turėtų būti analizuojama pradedant nuo kiekvieno laikotarpio 4 dienos. Temperatūra nepakito 3–4 dienas tik nuo sausio 4 iki 7 d. Taigi gauname atsakymą: A-2.
Minimali mėnesio temperatūra buvo stebima sausio 17 d. Šis skaičius patenka į sausio 15–21 d. Iš čia turime porą: 3 DALYJE.
Maksimali temperatūra nukrito sausio 10 dieną ir siekė +1 laipsnį. Ši data patenka į sausio 8–14 d. Taigi mes turime: B-4.

Variantas 14MB10

Vykdymo algoritmas

Funkcijos reikšmė taške yra teigiama, jei šis taškas yra virš Ox ašies.
Išvestinė taške yra didesnė už nulį, jei to taško liestinė sudaro smailųjį kampą su teigiama x ašies kryptimi.

Sprendimas:

Taškas A. Jis yra žemiau Ox ašies, o tai reiškia, kad funkcijos reikšmė jame yra neigiama. Jeigu joje nubrėžsime liestinę, tai kampas tarp jos ir teigiamos krypties Ox bus apie 90 0, t.y. sudaro smailų kampą. Taigi šiuo atveju tinka charakteristikos numeris 3. Tie. mes turime: A-3.

Taškas B. Jis yra virš Jaučio ašies, t.y. taškas turi teigiamą funkcijos reikšmę. Šiame taške liestinė bus gana arti abscisių ašies, sudarydama bukąjį kampą (šiek tiek mažesnį nei 180 0) su savo teigiama kryptimi. Atitinkamai, išvestis šiuo metu yra neigiama. Taigi čia tinka charakteristika 1. Gauname atsakymą: 1.

Taškas C. Taškas yra žemiau Ox ašies, jame esanti liestinė sudaro didelį bukąjį kampą su teigiama abscisių ašies kryptimi. Tie. t.C ir funkcijos, ir išvestinės reikšmės yra neigiamos, kas atitinka charakteristiką Nr. Atsakymas: S-2.

Taškas D. Taškas yra virš Ox ašies, o jame esanti liestinė sudaro smailųjį kampą su teigiama ašies kryptimi. Tai rodo, kad ir funkcijos reikšmė, ir išvestinės vertės čia yra didesnės už nulį. Atsakymas: D–4.

Variantas 14MB11

Paveiksle taškeliai rodo mėnesinių šaldytuvų pardavimų apimtis buitinės technikos parduotuvėje. Mėnesiai nurodomi horizontaliai, parduotų šaldytuvų skaičius – vertikaliai. Aiškumo dėlei taškai yra sujungti linija.

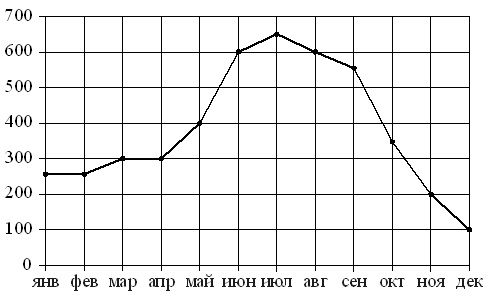
Naudodamiesi paveikslu, kiekvieną nurodytą laikotarpį suderinkite su šaldytuvų pardavimo charakteristikomis.

Pirmiausia pabandykite rasti funkcijos apimtį:

Ar susitvarkei? Palyginkime atsakymus:

Gerai? Šauniai padirbėta!

Dabar pabandykime rasti funkcijos diapazoną:

Rasti? Palyginti:

Ar sutiko? Šauniai padirbėta!

Vėl dirbkime su grafikais, tik dabar šiek tiek sunkiau – rasti ir funkcijos sritį, ir funkcijos diapazoną.

Kaip rasti domeną ir funkcijos diapazoną (išplėstinė)

Štai kas atsitiko:

Su grafika, manau, jūs tai supratote. Dabar pabandykime rasti funkcijos domeną pagal formules (jei nežinote, kaip tai padaryti, skaitykite skyrių apie):

Ar susitvarkei? Tikrinama atsakymai:

, nes šaknies išraiška turi būti didesnė arba lygi nuliui.
, nes padalyti iš nulio neįmanoma, o radikalioji išraiška negali būti neigiama.
, kadangi, atitinkamai, visiems.
nes negalima dalyti iš nulio.

Tačiau turime dar vieną momentą, kuris dar neišspręstas...

Leiskite man pakartoti apibrėžimą ir sutelkti dėmesį į jį:

Pastebėjote? Žodis „tik“ yra labai, labai svarbus mūsų apibrėžimo elementas. Pabandysiu tau ant pirštų galų paaiškinti.

Tarkime, kad turime funkciją, kurią pateikia tiesia linija. . Kai mes pakeičiame šią reikšmę į savo „taisyklę“ ir gauname ją. Viena reikšmė atitinka vieną reikšmę. Mes netgi galime sudaryti įvairių reikšmių lentelę ir nubrėžti tam tikrą funkciją, kad tai patikrintume.

„Žiūrėk! - tu sakai, - "" susitinka du kartus!" Tai gal parabolė nėra funkcija? Ne, tai yra!

Tai, kad „“ pasitaiko du kartus, toli gražu nėra priežastis apkaltinti parabolę dviprasmiškumu!

Faktas yra tas, kad skaičiuodami gavome vieną žaidimą. O skaičiuojant su gavome vieną žaidimą. Taigi, parabolė yra funkcija. Pažiūrėkite į diagramą:

Supratau? Jei ne, štai jums realus pavyzdys, toli nuo matematikos!

Tarkime, turime grupę pareiškėjų, kurie susitiko teikdami dokumentus, kurių kiekvienas pokalbio metu pasakojo, kur gyvena:

Sutikite, visai realu, kad tame pačiame mieste gyvena keli vaikinai, tačiau vienam žmogui keliuose miestuose vienu metu gyventi neįmanoma. Tai tarsi loginis mūsų „parabolės“ vaizdas – Keli skirtingi x atitinka tą patį y.

Dabar pateiksime pavyzdį, kai priklausomybė nėra funkcija. Tarkime, tie patys vaikinai papasakojo, į kokias specialybes pretendavo:

Čia yra visiškai kitokia situacija: vienas žmogus gali nesunkiai kreiptis į vieną ar kelias kryptis. T.y vienas elementas rinkiniai dedami į korespondenciją keli elementai rinkiniai. Atitinkamai, tai ne funkcija.

Išbandykime savo žinias praktiškai.

Iš paveikslėlių nustatykite, kas yra funkcija, o kas ne:

Supratau? Ir štai atsakymai:

Funkcija yra - B,E.
Ne funkcija – A, B, D, D.

Klausiate kodėl? Taip, štai kodėl:

Visuose paveiksluose, išskyrus AT) ir E) yra keli už vieną!

Esu tikras, kad dabar galite lengvai atskirti funkciją nuo nefunkcijos, pasakyti, kas yra argumentas ir kas yra priklausomas kintamasis, taip pat nustatyti argumento ir funkcijos apimtį. Pereikime prie kito skyriaus – kaip apibrėžti funkciją?

Funkcijos nustatymo būdai

Ką, jūsų nuomone, reiškia žodžiai "nustatyti funkciją"? Teisingai, tai reiškia visiems paaiškinti, apie kokią funkciją šiuo atveju kalbame. Be to, paaiškink taip, kad visi tave teisingai suprastų ir žmonių nubraižyti funkcijų grafikai pagal tavo paaiškinimą būtų vienodi.

Kaip aš tai galėčiau padaryti? Kaip nustatyti funkciją? Paprasčiausias būdas, kuris šiame straipsnyje jau buvo naudojamas ne kartą - naudojant formulę. Rašome formulę ir, pakeisdami į ją reikšmę, apskaičiuojame reikšmę. Ir kaip pamenate, formulė yra dėsnis, taisyklė, pagal kurią mums ir kitam žmogui tampa aišku, kaip X virsta Y.

Paprastai jie daro būtent tai - užduotyse matome paruoštas funkcijas, apibrėžtas formulėmis, tačiau yra ir kitų būdų nustatyti funkciją, apie kurią visi pamiršta, todėl kyla klausimas „kaip kitaip galite nustatyti funkciją? painioja. Pažvelkime į viską iš eilės ir pradėkime nuo analizės metodo.

Analitinis funkcijos apibrėžimo būdas

Analitinis metodas yra funkcijos užduotis naudojant formulę. Tai pats universaliausias ir išsamiausias bei nedviprasmiškiausias būdas. Jei turite formulę, tuomet apie funkciją žinote absoliučiai viską – galite joje sudaryti reikšmių lentelę, sudaryti grafiką, nustatyti, kur funkcija didėja, o kur mažėja, apskritai, tyrinėkite ją. pilnai.

Panagrinėkime funkciją. Ka tai reiskia?

"Ką tai reiškia?" - Jūs klausiate. Aš dabar paaiškinsiu.

Priminsiu, kad žymėjime skliausteliuose esanti išraiška vadinama argumentu. Ir šis argumentas gali būti bet kokia išraiška, nebūtinai paprasta. Atitinkamai, kad ir koks būtų argumentas (išraiška skliausteliuose), mes jį parašysime reiškinyje.

Mūsų pavyzdyje tai atrodys taip:

Apsvarstykite kitą užduotį, susijusią su analitiniu metodu, nurodant funkciją, kurią atliksite per egzaminą.

Raskite išraiškos reikšmę at.

Esu tikras, kad iš pradžių išsigandote, kai pamatėte tokią išraišką, bet tame nėra visiškai nieko baisaus!

Viskas yra taip pat, kaip ir ankstesniame pavyzdyje: kad ir koks būtų argumentas (išraiška skliausteliuose), mes jį parašysime reiškinyje. Pavyzdžiui, funkcijai.

Ką reikėtų daryti mūsų pavyzdyje? Vietoj to reikia rašyti, o vietoj -:

sutrumpinkite gautą išraišką:

Tai viskas!

Savarankiškas darbas

Dabar pabandykite patys surasti šių posakių reikšmę:

, jei
, jei

Ar susitvarkei? Palyginkime savo atsakymus: Esame įpratę, kad funkcija turi formą

Netgi savo pavyzdžiuose funkciją apibrėžiame tokiu būdu, tačiau analitiškai funkciją galima apibrėžti netiesiogiai, pvz.

Pabandykite sukurti šią funkciją patys.

Ar susitvarkei?

Štai kaip aš jį sukūriau.

Su kokia lygtimi mes atsidūrėme?

Teisingai! Tiesinis, tai reiškia, kad grafikas bus tiesi linija. Padarykime lentelę, kad nustatytų, kurie taškai priklauso mūsų linijai:

Kaip tik apie tai ir kalbėjome... Vienas atitinka kelis.

Pabandykime nupiešti, kas atsitiko:

Ar tai, ką turime, yra funkcija?

Teisingai, ne! Kodėl? Pabandykite atsakyti į šį klausimą paveikslėliu. Ką tu gavai?

„Kadangi viena reikšmė atitinka kelias reikšmes!

Kokią išvadą galime padaryti iš to?

Tiesa, funkcija ne visada gali būti aiškiai išreikšta, o tai, kas „užmaskuota“ kaip funkcija, ne visada yra funkcija!

Lentelinis funkcijos apibrėžimo būdas

Kaip rodo pavadinimas, šis metodas yra paprasta plokštelė. Taip taip. Kaip ir tą, kurią jau padarėme. Pavyzdžiui:

Čia jūs iš karto pastebėjote modelį - Y yra tris kartus didesnis nei X. O dabar užduotis „pagalvok labai gerai“: ar manote, kad lentelės pavidalu pateikta funkcija yra lygiavertė funkcijai?

Ilgai nekalbėkime, o pieškime!

Taigi. Nubrėžiame funkciją, pateiktą abiem būdais:

Ar matote skirtumą? Tai ne apie pažymėtus taškus! Pažiūrėk atidžiau:

Ar dabar matėte? Kai nustatome funkciją lentelės būdu, grafike atspindime tik tuos taškus, kuriuos turime lentelėje, o linija (kaip ir mūsų atveju) eina tik per juos. Kai funkciją apibrėžiame analitiniu būdu, galime paimti bet kokius taškus, ir mūsų funkcija jais neapsiriboja. Štai tokia funkcija. Prisiminti!

Grafinis būdas sukurti funkciją

Ne mažiau patogus ir grafinis funkcijos konstravimo būdas. Nubraižome savo funkciją, ir kitas suinteresuotas asmuo gali rasti, kam y yra lygus tam tikrame x ir pan. Grafiniai ir analitiniai metodai yra vieni iš labiausiai paplitusių.

Tačiau čia reikia prisiminti, apie ką kalbėjome pačioje pradžioje - ne kiekvienas koordinačių sistemoje nubrėžtas „skraidymas“ yra funkcija! Prisiminėte? Tik tuo atveju, nukopijuosiu čia funkcijos apibrėžimą:

Paprastai žmonės dažniausiai įvardija būtent tuos tris funkcijos nurodymo būdus, kuriuos mes analizavome – analitinį (naudojant formulę), lentelę ir grafinį, visiškai pamiršdami, kad funkciją galima apibūdinti žodžiu. Kaip šitas? Taip, labai lengva!

Žodinis funkcijos aprašymas

Kaip apibūdinti funkciją žodžiu? Paimkime mūsų naujausią pavyzdį - . Šią funkciją galima apibūdinti kaip „kiekviena tikroji x reikšmė atitinka jos trigubą reikšmę“. Tai viskas. Nieko sudėtingo. Žinoma, jūs prieštarausite - „yra tokių sudėtingų funkcijų, kurių tiesiog neįmanoma nustatyti žodžiu! Taip, yra keletas, bet yra funkcijų, kurias lengviau aprašyti žodžiu, nei nustatyti formule. Pavyzdžiui: "kiekviena natūrali x reikšmė atitinka skirtumą tarp skaitmenų, iš kurių ji susideda, o didžiausias skaitmuo, esantis skaičiaus įvestyje, laikomas minuendu." Dabar apsvarstykite, kaip mūsų žodinis funkcijos aprašymas įgyvendinamas praktiškai:

Didžiausias tam tikro skaičiaus skaitmuo - atitinkamai - sumažinamas, tada:

Pagrindiniai funkcijų tipai

Dabar pereikime prie įdomiausių - mes apsvarstysime pagrindinius funkcijų tipus, su kuriais dirbote / dirbate ir dirbsite mokyklinėje ir instituto matematikoje, tai yra, mes susipažinsime su jomis, taip sakant, ir trumpai apibūdinkite juos. Daugiau apie kiekvieną funkciją skaitykite atitinkamame skyriuje.

Linijinė funkcija

Formos funkcija, kur yra tikrieji skaičiai.

Šios funkcijos grafikas yra tiesi linija, todėl tiesinės funkcijos konstrukcija sumažinama iki dviejų taškų koordinačių radimo.

Tiesės padėtis koordinačių plokštumoje priklauso nuo nuolydžio.

Funkcijos apimtis (dar žinoma kaip argumentų diapazonas) - .

Vertybių diapazonas yra.

kvadratinė funkcija

Formos funkcija, kur

Funkcijos grafikas yra parabolė, kai parabolės šakos nukreiptos žemyn, kai - aukštyn.

Daugelis kvadratinės funkcijos savybių priklauso nuo diskriminanto reikšmės. Diskriminantas apskaičiuojamas pagal formulę

Parabolės padėtis koordinačių plokštumoje vertės ir koeficiento atžvilgiu parodyta paveikslėlyje:

Domenas

Reikšmių diapazonas priklauso nuo nurodytos funkcijos ekstremumo (parabolės viršūnės) ir koeficiento (parabolės šakų krypties)

Atvirkštinis proporcingumas

Funkcija, pateikta formule, kur

Skaičius vadinamas atvirkštinio proporcingumo koeficientu. Priklausomai nuo reikšmės, hiperbolės šakos yra skirtinguose kvadratuose:

Domenas - .

Vertybių diapazonas yra.

SANTRAUKA IR PAGRINDINĖ FORMULĖ

1. Funkcija – tai taisyklė, pagal kurią kiekvienam aibės elementui priskiriamas unikalus aibės elementas.

- tai formulė, žyminti funkciją, tai yra, vieno kintamojo priklausomybę nuo kito;
- kintamasis arba argumentas;
- priklausoma reikšmė - keičiasi pasikeitus argumentui, tai yra pagal kažkokią konkrečią formulę, kuri atspindi vienos reikšmės priklausomybę nuo kitos.

2. Tinkamos argumentų reikšmės, arba funkcijos apimtis, yra tai, kas yra susijusi su galimybe, pagal kurią funkcija turi prasmę.

3. Funkcijos reikšmių diapazonas- štai kokių verčių reikia su galiojančiomis vertėmis.

4. Yra 4 būdai nustatyti funkciją:

analitinis (naudojant formules);
lentelės;
grafinis
žodinis aprašymas.

5. Pagrindiniai funkcijų tipai:

: , kur yra tikrieji skaičiai;
: , kur;
: , kur.