Aufgaben mit einem Derivat in der Prüfung. Meisterklasse „Die Ableitung einer Funktion in den Aufgaben der Prüfung. geometrische und physikalische Bedeutung der Ableitung; die Gleichung der Tangente an den Graphen der Funktion; das Studium der Funktion unter Verwendung der Ableitung

Die Ableitung einer Funktion ist eines der schwierigsten Themen im Schullehrplan. Nicht jeder Absolvent wird die Frage beantworten, was ein Derivat ist.

Dieser Artikel erklärt einfach und klar, was ein Derivat ist und warum es benötigt wird.. Wir werden jetzt keine mathematische Strenge der Darstellung anstreben. Das Wichtigste ist, die Bedeutung zu verstehen.

Erinnern wir uns an die Definition:

Die Ableitung ist die Änderungsrate der Funktion.

Die Abbildung zeigt Graphen von drei Funktionen. Welche wächst deiner Meinung nach am schnellsten?

Die Antwort liegt auf der Hand - die dritte. Es hat die höchste Änderungsrate, dh die größte Ableitung.

Hier ist ein weiteres Beispiel.

Kostya, Grisha und Matvey bekamen gleichzeitig Jobs. Mal sehen, wie sich ihr Einkommen im Laufe des Jahres verändert hat:

Sie können sofort alles auf dem Diagramm sehen, richtig? Kostyas Einkommen hat sich in sechs Monaten mehr als verdoppelt. Und Grishas Einkommen stieg auch, aber nur ein bisschen. Und Matthews Einkommen ging auf null zurück. Die Startbedingungen sind die gleichen, aber die Änderungsrate der Funktion, d.h. Derivat, - anders. Bei Matvey ist die Ableitung seines Einkommens im Allgemeinen negativ.

Intuitiv können wir die Änderungsrate einer Funktion leicht abschätzen. Aber wie machen wir das?

Was wir wirklich sehen, ist, wie steil der Graph der Funktion nach oben (oder nach unten) geht. Mit anderen Worten, wie schnell sich y mit x ändert. Offensichtlich kann dieselbe Funktion an verschiedenen Punkten einen anderen Wert der Ableitung haben – das heißt, sie kann sich schneller oder langsamer ändern.

Die Ableitung einer Funktion wird mit bezeichnet.

Lassen Sie uns zeigen, wie man mithilfe des Diagramms findet.

Ein Graph einer Funktion wird gezeichnet. Nehmen Sie einen Punkt darauf mit einer Abszisse. Zeichnen Sie an dieser Stelle eine Tangente an den Graphen der Funktion. Wir wollen auswerten, wie steil der Graph der Funktion nach oben geht. Ein praktischer Wert dafür ist Tangente der Steigung der Tangente.

Die Ableitung einer Funktion an einem Punkt ist gleich der Tangente der Steigung der Tangente, die an diesem Punkt an den Graphen der Funktion gezogen wird.

Bitte beachten Sie - als Neigungswinkel der Tangente nehmen wir den Winkel zwischen der Tangente und der positiven Richtung der Achse.

Manchmal fragen die Schüler, was die Tangente an den Graphen einer Funktion ist. Dies ist eine gerade Linie, die außerdem den einzigen gemeinsamen Punkt mit dem Diagramm in diesem Abschnitt hat, wie in unserer Abbildung gezeigt. Es sieht aus wie eine Tangente an einen Kreis.

Lass uns finden . Wir erinnern uns, dass die Tangente eines spitzen Winkels in einem rechtwinkligen Dreieck gleich dem Verhältnis des gegenüberliegenden Schenkels zum benachbarten ist. Aus Dreieck:

Wir haben die Ableitung mithilfe des Diagramms gefunden, ohne die Formel der Funktion zu kennen. Solche Aufgaben finden sich oft in der Klausur in Mathematik unter der Nummer.

Es gibt noch einen weiteren wichtigen Zusammenhang. Denken Sie daran, dass die Gerade durch die Gleichung gegeben ist

Die Menge in dieser Gleichung heißt Steigung einer Geraden. Sie ist gleich der Tangente des Neigungswinkels der Geraden zur Achse.

Das verstehen wir

Erinnern wir uns an diese Formel. Es drückt die geometrische Bedeutung der Ableitung aus.

Die Ableitung einer Funktion an einem Punkt ist gleich der Steigung der Tangente, die an diesem Punkt an den Graphen der Funktion gezogen wird.

Mit anderen Worten, die Ableitung ist gleich der Tangente der Steigung der Tangente.

Wir haben bereits gesagt, dass dieselbe Funktion an verschiedenen Stellen unterschiedliche Ableitungen haben kann. Mal sehen, wie die Ableitung mit dem Verhalten der Funktion zusammenhängt.

Lassen Sie uns einen Graphen einer Funktion zeichnen. Lassen Sie diese Funktion in einigen Bereichen zunehmen und in anderen abnehmen, und zwar mit unterschiedlichen Raten. Und lassen Sie diese Funktion maximale und minimale Punkte haben.

An einem Punkt nimmt die Funktion zu. Die am Punkt gezeichnete Tangente an den Graphen bildet mit der positiven Richtung der Achse einen spitzen Winkel. Also ist die Ableitung an dem Punkt positiv.

An diesem Punkt nimmt unsere Funktion ab. Die Tangente an diesem Punkt bildet mit der positiven Richtung der Achse einen stumpfen Winkel. Da der Tangens eines stumpfen Winkels negativ ist, ist die Ableitung am Punkt negativ.

Folgendes passiert:

Wenn eine Funktion wächst, ist ihre Ableitung positiv.

Wenn es abnimmt, ist seine Ableitung negativ.

Und was passiert bei den Höchst- und Mindestpunkten? Wir sehen, dass bei (Maximalpunkt) und (Minimalpunkt) die Tangente horizontal ist. Daher ist die Tangente der Steigung der Tangente an diesen Punkten Null, und die Ableitung ist ebenfalls Null.

Der Punkt ist der Maximalpunkt. An dieser Stelle wird die Zunahme der Funktion durch eine Abnahme ersetzt. Folglich ändert sich das Vorzeichen der Ableitung an der Stelle von „Plus“ auf „Minus“.

Am Punkt – dem Minimalpunkt – ist die Ableitung ebenfalls gleich Null, ändert aber ihr Vorzeichen von „minus“ auf „plus“.

Fazit: Mit Hilfe der Ableitung erfahren Sie alles, was uns über das Verhalten der Funktion interessiert.

Wenn die Ableitung positiv ist, dann steigt die Funktion.

Wenn die Ableitung negativ ist, dann ist die Funktion fallend.

Am Maximalpunkt ist die Ableitung Null und wechselt das Vorzeichen von Plus nach Minus.

Am Minimalpunkt ist die Ableitung ebenfalls Null und wechselt das Vorzeichen von Minus zu Plus.

Wir schreiben diese Erkenntnisse in Form einer Tabelle:

	erhöht sich	Höchstpunkt	abnehmend	Mindestpunkt	erhöht sich
+	0	-	0	+

Machen wir zwei kleine Klarstellungen. Sie werden eine davon benötigen, wenn Sie Prüfungsaufgaben lösen. Ein anderer - im ersten Jahr mit einer ernsthafteren Untersuchung von Funktionen und Derivaten.

Es ist ein Fall möglich, in dem die Ableitung einer Funktion irgendwann gleich Null ist, die Funktion aber an dieser Stelle weder ein Maximum noch ein Minimum hat. Diese sog :

An einem Punkt ist die Tangente an den Graphen horizontal und die Ableitung ist Null. Vor dem Punkt nahm die Funktion jedoch zu - und nach dem Punkt steigt sie weiter an. Das Vorzeichen der Ableitung ändert sich nicht – es ist positiv geblieben wie es war.

Es kommt auch vor, dass am Punkt des Maximums oder Minimums die Ableitung nicht existiert. In der Grafik entspricht dies einem scharfen Bruch, wenn es unmöglich ist, an einem bestimmten Punkt eine Tangente zu zeichnen.

Aber wie findet man die Ableitung, wenn die Funktion nicht durch einen Graphen, sondern durch eine Formel gegeben ist? In diesem Fall gilt es

Die Ableitung einer Funktion $y = f(x)$ an einem gegebenen Punkt $x_0$ ist die Grenze des Verhältnisses des Inkrements der Funktion zum entsprechenden Inkrement ihres Arguments, sofern letzteres gegen Null geht:

$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$

Differenzieren ist die Operation, eine Ableitung zu finden.

Tabelle der Ableitungen einiger elementarer Funktionen

Funktion	Derivat
$c$	$0$
$x$	$1$
$x^n$	$nx^(n-1)$
$(1)/(x)$	$-(1)/(x^2)$
$√x$	$(1)/(2√x)$
$e^x$	$e^x$
$lnx$	$(1)/(x)$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	$(1)/(cos^2x)$
$ctgx$	$-(1)/(sin^2x)$

Grundregeln der Differenzierung

1. Die Ableitung der Summe (Differenz) ist gleich der Summe (Differenz) der Ableitungen

$(f(x) ± g(x))"= f"(x)±g"(x)$

Finden Sie die Ableitung der Funktion $f(x)=3x^5-cosx+(1)/(x)$

Die Ableitung der Summe (Differenz) ist gleich der Summe (Differenz) der Ableitungen.

$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + sinx - (1)/(x^2)$

2. Derivat eines Produkts

$(f(x) g(x))"= f"(x) g(x)+ f(x) g(x)"$

Finde die Ableitung $f(x)=4x cosx$

$f"(x)=(4x)" cosx+4x (cosx)"=4 cosx-4x sinx$

3. Ableitung des Quotienten

$((f(x))/(g(x)))"=(f"(x) g(x)-f(x) g(x)")/(g^2(x)) $

Finde die Ableitung $f(x)=(5x^5)/(e^x)$

$f"(x)=((5x^5)" e^x-5x^5 (e^x)")/((e^x)^2)=(25x^4 e^x- 5x^5 e^x)/((e^x)^2)$

4. Die Ableitung einer komplexen Funktion ist gleich dem Produkt der Ableitung der externen Funktion und der Ableitung der internen Funktion

$f(g(x))"=f"(g(x)) g"(x)$

$f"(x)=cos"(5x) (5x)"=-sin(5x) 5= -5sin(5x)$

Die physikalische Bedeutung der Ableitung

Bewegt sich ein materieller Punkt geradlinig und ändert sich seine Koordinate mit der Zeit nach dem Gesetz $x(t)$, so ist die Momentangeschwindigkeit dieses Punktes gleich der Ableitung der Funktion.

Der Punkt bewegt sich entlang der Koordinatenlinie nach dem Gesetz $x(t)= 1,5t^2-3t + 7$, wobei $x(t)$ die Koordinate zum Zeitpunkt $t$ ist. Zu welchem Zeitpunkt wird die Geschwindigkeit des Punktes gleich $12$ sein?

1. Geschwindigkeit ist eine Ableitung von $x(t)$, also finden wir die Ableitung der gegebenen Funktion

$v(t) = x"(t) = 1,5 2t -3 = 3t -3$

2. Um herauszufinden, zu welchem Zeitpunkt $t$ die Geschwindigkeit gleich $12$ war, stellen wir die Gleichung auf und lösen sie:

Die geometrische Bedeutung der Ableitung

Erinnern Sie sich, dass die Gleichung einer geraden Linie, die nicht parallel zu den Koordinatenachsen ist, geschrieben werden kann als $y = kx + b$, wobei $k$ die Steigung der geraden Linie ist. Der Koeffizient $k$ ist gleich der Tangente der Steigung zwischen der Geraden und der positiven Richtung der $Ox$-Achse.

Die Ableitung der Funktion $f(x)$ am Punkt $x_0$ ist gleich der Steigung $k$ der Tangente an den Graphen am gegebenen Punkt:

Daher können wir eine allgemeine Gleichstellung machen:

$f"(x_0) = k = tgα$

In der Abbildung steigt die Tangente an die Funktion $f(x)$, daher ist der Koeffizient $k > 0$. Da $k > 0$ ist, ist $f"(x_0) = tgα > 0$. Der Winkel $α$ zwischen der Tangente und der positiven Richtung $Ox$ ist spitz.

In der Abbildung nimmt die Tangente an die Funktion $f(x)$ ab, daher der Koeffizient $k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

In der Abbildung ist die Tangente an die Funktion $f(x)$ parallel zur $Ох$-Achse, daher ist der Koeffizient $k = 0$, also $f"(x_0) = tg α = 0$. Der Punkt $ x_0$ bei dem $f"(x_0) = 0$, genannt extrem.

Die Abbildung zeigt den Graphen der Funktion $y=f(x)$ und die Tangente an diesen Graphen, gezeichnet an der Stelle mit der Abszisse $x_0$. Finde den Wert der Ableitung der Funktion $f(x)$ am Punkt $x_0$.

Die Tangente an den Graphen steigt, also $f"(x_0) = tg α > 0$

Um $f"(x_0)$ zu finden, finden wir die Tangente der Steigung zwischen der Tangente und der positiven Richtung der $Ox$-Achse. Dazu vervollständigen wir die Tangente an das Dreieck $ABC$.

Finde den Tangens des Winkels $BAC$. (Der Tangens eines spitzen Winkels in einem rechtwinkligen Dreieck ist das Verhältnis des gegenüberliegenden Schenkels zum benachbarten Schenkel.)

$tg BAC = (BC)/(AC) = (3)/(12)= (1)/(4)=0,25$

$f"(x_0) = tg SIE = 0,25 $

Antwort: 0,25 $

Die Ableitung wird auch verwendet, um die Intervalle von steigenden und fallenden Funktionen zu finden:

Wenn $f"(x) > 0$ in einem Intervall, dann erhöht sich die Funktion $f(x)$ in diesem Intervall.

Wenn $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

Die Abbildung zeigt den Graphen der Funktion $y = f(x)$. Finden Sie unter den Punkten $х_1,х_2,х_3…х_7$ die Punkte, an denen die Ableitung der Funktion negativ ist.

Notieren Sie als Antwort die Anzahl der Datenpunkte.

AUßERSCHULLICHE PRAKTISCHE ARBEIT 2

Transformation von Funktionsgraphen.

Ziel

Zeichnen Sie Funktionsgraphen mit verschiedenen Transformationen, beantworten Sie die Frage des Problems.

Abschluss der Arbeiten

Richtlinien

Das Werk ist für 10 Optionen ausgelegt, die Optionsnummer entspricht der letzten Ziffer der Seriennummer in der Liste. Zum Beispiel 1, 11, 21, 31 ... führen 1 Option aus, 2,12, 22 ... - 2 Option usw.

Die Arbeit besteht aus zwei Teilen: Der erste Teil der Aufgaben 1 - 5, dies sind Aufgaben, die abgeschlossen werden müssen, um eine Anerkennung zu erhalten. Wenn diese Aufgaben mit einem Fehler abgeschlossen wurden, müssen Sie sie korrigieren und die Arbeit erneut zur Überprüfung einreichen . Der zweite Teil enthält Aufgaben, durch deren Erfüllung Sie eine zusätzliche Note erhalten können: Hauptteil +2 Aufgaben - "4", Hauptteil +3 Aufgaben - "5".

Aufgabe 1. Der Graph einer linearen Funktion ist eine Gerade, zwei Punkte genügen, um sie zu konstruieren. (Wir nehmen die Werte des Arguments x willkürlich und erwägen, den Wert der Funktion y in die Formel einzusetzen).

Um zu überprüfen, ob der Graph der Funktion durch den angegebenen Punkt verläuft, müssen Sie die Koordinaten des Punkts anstelle von x und y ersetzen. Wenn Sie die richtige Gleichheit erhalten, verläuft die Linie durch den angegebenen Punkt, andernfalls verläuft sie nicht .

Aufgabe 2, 3, 4. Die Graphen der angegebenen Funktionen erhält man aus den Graphen der Funktionen , mit einer Verschiebung entlang der x- oder y-Achse.

, zeichnen Sie zuerst die Funktion oder , dann verschieben wir es um „a“ Einheiten nach rechts oder links (+ a - nach links, - a nach rechts), dann verschieben wir es um „b“ Einheiten nach oben oder unten (+ in - nach oben, - in - Nieder)

Ähnlich bei anderen Funktionen:

Aufgabe 5 So stellen Sie einen Funktionsgraphen dar: , müssen Sie: 1) einen Graphen der Funktion erstellen , 2) der Teil des Graphen, der oberhalb der x-Achse liegt, bleibt unverändert, 3) der Teil des Graphen, der unterhalb der x-Achse liegt, wird gespiegelt.

Aufgaben zur selbstständigen Lösung.

Pflichtteil

Aufgabe 1. Zeichnen Sie einen Graphen einer linearen Funktion und bestimmen Sie, ob der Graph der Funktion durch den angegebenen Punkt verläuft:

Aufgabe 2. Zeichnen Sie einen Graphen einer quadratischen Funktion und geben Sie den Wertesatz für diese Funktion an.

Aufgabe 3. Erstellen Sie ein Diagramm einer Funktion und bestimmen Sie, ob die angegebene Funktion zunimmt oder abnimmt.

Aufgabe 4. Erstellen Sie einen Graphen der Funktion, beantworten Sie die Frage der Aufgabe.

Aufgabe 5. Erstellen Sie einen Graphen einer Funktion, die das Vorzeichen des Moduls enthält.

Aufgaben zur zusätzlichen Bewertung.

Aufgabe 6. Zeichne einen Graphen einer stückweise gegebenen Funktion und bestimme, ob diese Funktion einen Bruchpunkt hat:

Aufgabe 7. Bestimmen Sie, wie viele Lösungen das Gleichungssystem hat, begründen Sie die Antwort. Ziehen Sie Schlussfolgerungen, indem Sie die Fragen beantworten.

Welche Funktionsgraphen haben Sie in dieser Arbeit gebaut?

Wie heißt der Graph einer linearen Funktion?

Wie heißt der Graph einer quadratischen Funktion?

Welche Diagrammtransformationen kennen Sie?

Wie liegt der Graph einer geraden Funktion im Koordinatensystem? Graph einer ungeraden Funktion?

In Aufgabe Nr. 13 der Einheitlichen Staatsprüfung Mathematik der Grundstufe müssen Sie die Fähigkeiten und Kenntnisse eines der Konzepte des Verhaltens einer Funktion nachweisen: Ableitungen an einem Punkt oder Anstiegs- oder Abfallraten. Die Theorie für diese Aufgabe wird etwas später hinzugefügt, aber das hindert uns nicht daran, einige typische Optionen im Detail zu analysieren.

Analyse typischer Optionen für Aufgaben Nr. 14 VERWENDUNG in Mathematik auf Grundniveau

Option 14MB1

Die Grafik zeigt die Abhängigkeit der Temperatur von der Zeit beim Aufwärmen des Motors eines Autos. Die horizontale Achse gibt die Zeit in Minuten an, die vergangen ist, seit der Motor gestartet wurde; auf der vertikalen Achse ist die Motortemperatur in Grad Celsius aufgetragen.

Ordnen Sie unter Verwendung des Diagramms jedes Zeitintervall den Eigenschaften des Motoraufwärmvorgangs in diesem Intervall zu.

Geben Sie in der Tabelle unter jedem Buchstaben die entsprechende Zahl an.

Ausführungsalgorithmus:

Wählen Sie das Zeitintervall, in dem die Temperatur gesunken ist.
Bringen Sie ein Lineal an 30 °C an und bestimmen Sie das Zeitintervall, in dem die Temperatur unter 30 °C lag.

Entscheidung:

Wählen wir das Zeitintervall, in dem die Temperatur gefallen ist. Dieser Abschnitt ist mit bloßem Auge sichtbar und beginnt 8 Minuten nach dem Starten des Motors.

Legen Sie ein Lineal auf 30 °C und bestimmen Sie das Zeitintervall, in dem die Temperatur unter 30 °C lag.

Unterhalb des Lineals befindet sich ein Abschnitt, der dem Zeitintervall 0 - 1 min entspricht.

Mit Hilfe eines Bleistifts und eines Lineals finden wir heraus, in welchem Zeitintervall die Temperatur im Bereich von 40 ° C bis 80 ° C lag.

Von den Punkten, die 40°C und 80°C entsprechen, lassen wir die Senkrechten auf den Graphen fallen, und von den erhaltenen Punkten lassen wir die Senkrechten auf die Zeitachse fallen.

Wir sehen, dass dieses Temperaturintervall einem Zeitintervall von 3 - 6,5 min entspricht. Das heißt, von den in der Bedingung angegebenen 3 - 6 min.

Wählen Sie die fehlende Antwort mit der Eliminierungsmethode aus.

Option 14MB2

Entscheidung:

Analysieren wir den Graphen der Funktion A. Wenn die Funktion zunimmt, ist die Ableitung positiv und umgekehrt. Die Ableitung der Funktion ist an den Extrempunkten gleich Null.

Zunächst steigt die Funktion A, d.h. die Ableitung ist positiv. Dies entspricht den Graphen der Ableitungen 2 und 3. Am Maximum der Funktion x = -2, also an dieser Stelle, soll die Ableitung gleich Null sein. Diese Bedingung entspricht der Grafik Nummer 3.

Zuerst nimmt die Funktion B ab, d.h. die Ableitung ist negativ. Dies entspricht den Graphen der Ableitungen 1 und 4. Der maximale Punkt der Funktion x \u003d -2, dh an diesem Punkt sollte die Ableitung gleich Null sein. Diese Bedingung entspricht der Grafik Nummer 4.

Zunächst steigt die Funktion B, d.h. die Ableitung ist positiv. Dies entspricht den Graphen der Ableitungen 2 und 3. Der Maximalpunkt der Funktion x = 1, dh an dieser Stelle sollte die Ableitung gleich Null sein. Diese Bedingung entspricht der Grafik Nummer 2.

Durch die Eliminationsmethode können wir feststellen, dass der Graph der Funktion Г dem Graphen der Ableitung bei Nummer 1 entspricht.

Antwort: 3421.

Option 14MB3

Der Ausführungsalgorithmus für jede der Funktionen:

Bestimmen Sie die Intervalle steigender und fallender Funktionen.
Bestimmen Sie die maximalen und minimalen Punkte der Funktionen.
Ziehen Sie Schlussfolgerungen, passen Sie die vorgeschlagenen Zeitpläne an.

Entscheidung:

Analysieren wir den Graphen der Funktion A.

Wenn die Funktion steigt, dann ist die Ableitung positiv und umgekehrt. Die Ableitung der Funktion ist an den Extrempunkten gleich Null.

Der Extremumpunkt ist der Punkt, an dem der maximale oder minimale Wert der Funktion erreicht wird.

Zunächst steigt die Funktion A, d.h. die Ableitung ist positiv. Dies entspricht den Graphen der Ableitungen 3 und 4. Am Maximum der Funktion x=0, dh an dieser Stelle soll die Ableitung gleich Null sein. Diese Bedingung entspricht der Grafik Nummer 4.

Analysieren wir den Graphen der Funktion B.

Zuerst nimmt die Funktion B ab, d.h. die Ableitung ist negativ. Dies entspricht den Graphen der Ableitungen 1 und 2. Der Minimalpunkt der Funktion x=-1, dh an diesem Punkt muss die Ableitung gleich Null sein. Diese Bedingung entspricht der Grafik Nummer 2.

Analysieren wir den Graphen der Funktion B.

Zuerst nimmt die Funktion B ab, d.h. die Ableitung ist negativ. Dies entspricht den Graphen der Ableitungen 1 und 2. Der Mindestpunkt der Funktion x \u003d 0, dh an diesem Punkt sollte die Ableitung gleich Null sein. Diese Bedingung entspricht der Grafik Nummer 1.

Durch die Eliminationsmethode können wir bestimmen, dass der Graph der Funktion Г dem Graphen der Ableitung bei Nummer 3 entspricht.

Antwort: 4213.

Option 14MB4

Die Abbildung zeigt einen Graphen einer Funktion und daran an Punkten mit den Abszissen A, B, C und D gezogene Tangenten.Die rechte Spalte zeigt die Werte der Ableitung an den Punkten A, B, C und D. Ordnen Sie jeden Punkt mithilfe des Diagramms dem Wert der Ableitung der Funktion an ihm zu.

PUNKTE
SONDERN
BEIM
Mit
D

DERIVATIVE WERTE
1) –4
2) 3
3) 2/3
4) -1/2

Erinnern Sie sich, was die Ableitung bedeutet, nämlich ihren Wert an dem Punkt - Der Wert der Ableitungsfunktion an einem Punkt ist gleich der Tangente der Steigung (Koeffizient) der Tangente.

Bei den Antworten haben wir zwei positive und zwei negative Optionen. Wie wir uns erinnern, wenn der Koeffizient direkt ist (Grafik y = kx + b) positiv ist, dann steigt die Linie, ist sie negativ, dann fällt die Linie.

Wir haben zwei aufsteigende Linien - an den Punkten A und D. Erinnern wir uns nun, was der Wert des Koeffizienten k bedeutet?

Der Koeffizient k zeigt, wie schnell die Funktion zu- oder abnimmt (tatsächlich ist der Koeffizient k selbst die Ableitung der Funktion y = kx + b).

Daher entspricht k \u003d 2/3 einer sanfteren geraden Linie - D und k \u003d 3 - A.

Analog gilt bei negativen Werten: Punkt B entspricht einer steileren Geraden mit k = -4 und Punkt C - -1/2.

Option 14MB5

In der Abbildung zeigen die Punkte das monatliche Verkaufsvolumen von Heizungen in einem Haushaltsgerätegeschäft. Monate sind horizontal angegeben, die Anzahl der verkauften Heizungen ist vertikal angegeben. Zur Verdeutlichung sind die Punkte durch eine Linie verbunden.

Ordnen Sie anhand der Abbildung jedem der angegebenen Zeiträume die Merkmale des Heizgeräteverkaufs zu.

Ausführungsalgorithmus

Wir analysieren die Teile des Diagramms, die den verschiedenen Jahreszeiten entsprechen. Wir formulieren die in der Grafik dargestellten Situationen. Wir finden die passenden Antworten für sie.

Entscheidung:

Im Winter überstieg die Anzahl der Verkäufe 120 Stück / Monat und stieg ständig. Diese Situation entspricht Antwort 3. Jene. wir bekommen: A-3.

Im Frühjahr ging der Absatz sukzessive von 120 Heizgeräten pro Monat auf 50 zurück. Option Nr. 2 kommt dieser Formulierung am nächsten. Wir haben: B–2.

Im Sommer änderte sich die Anzahl der Verkäufe nicht und war minimal. Der 2. Teil dieser Formulierung spiegelt sich nicht in den Antworten wider, und nur Nr. 4 ist für den ersten geeignet. Daher haben wir: UM 4.

Im Herbst stiegen die Verkäufe, aber ihre Zahl überschritt in keinem der Monate 100 Stück. Diese Situation wird in Option #1 beschrieben. Wir bekommen: G–1.

Option 14MB6

Die Grafik zeigt die Abhängigkeit der Geschwindigkeit eines Linienbusses von der Zeit. Die vertikale Achse zeigt die Geschwindigkeit des Busses in km/h, die horizontale Achse zeigt die Zeit in Minuten seit dem Start des Busses.

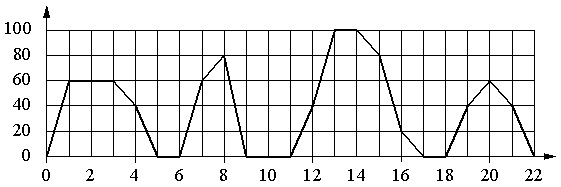
Ordnen Sie unter Verwendung des Diagramms jedes Zeitintervall der Charakteristik der Busbewegung in diesem Intervall zu.

Ausführungsalgorithmus

Wir ermitteln den Teilungspreis auf der horizontalen und vertikalen Skala.
Wir analysieren der Reihe nach die vorgeschlagenen Aussagen 1–4 aus der rechten Spalte („Merkmale“). Wir vergleichen sie mit Zeitintervallen aus der linken Spalte der Tabelle, wir finden Paare von "Buchstaben-Zahlen" für die Antwort.

Entscheidung:

Der Teilungswert der horizontalen Skala beträgt 1 s, die vertikale Skala 20 km/h.

Wenn der Bus anhält, ist seine Geschwindigkeit 0. Für 2 Minuten hintereinander hatte der Bus nur von der 9. bis zur 11. Minute eine Geschwindigkeit von null. Diese Zeit fällt in das Intervall von 8–12 min. Also haben wir ein paar für die Antwort: B–1.
Der Bus hatte mehrere Zeiträume eine Geschwindigkeit von 20 km/h oder mehr. Außerdem ist Option A hier nicht geeignet, weil z. B. in der 7. Minute die Geschwindigkeit 60 km/h betrug, Option B - weil sie bereits angewendet wurde, Option D - weil am Anfang und am Ende des Intervalls der Bus fährt hatte Nullgeschwindigkeit. In diesem Fall ist Option B geeignet (12–16 Minuten); In diesem Intervall setzt sich der Bus mit einer Geschwindigkeit von 40 km/h in Bewegung, beschleunigt dann auf 100 km/m und reduziert die Geschwindigkeit dann allmählich auf 20 km/h. Also haben wir: IN 2.
Hier wird die Geschwindigkeitsbegrenzung festgelegt. Wir ziehen die Optionen B und C nicht in Betracht. Die verbleibenden Intervalle A und G sind beide geeignet. Daher wäre es richtig, zuerst die 4. Option zu prüfen und dann wieder auf die 3. zurückzukommen.
Von den beiden verbleibenden Intervallen sind nur noch 4–8 Minuten für Merkmal Nr. 4 geeignet, da in diesem Intervall (bei der 6. Minute) gestoppt wurde. Zwischen 18 und 22 Minuten gab es keine Stopps. Wir bekommen: A-4. Daraus folgt, dass für das Merkmal Nr. 3 das Intervall Г genommen werden muss, d.h. es stellt sich heraus, ein paar G–3.

Option 14MB7

Die gepunktete Abbildung zeigt Chinas Bevölkerungswachstum von 2004 bis 2013. Horizontal ist das Jahr angegeben, vertikal ist das Bevölkerungswachstum in Prozent (eine Zunahme der Bevölkerung gegenüber dem Vorjahr) angegeben. Zur Verdeutlichung sind die Punkte durch eine Linie verbunden.

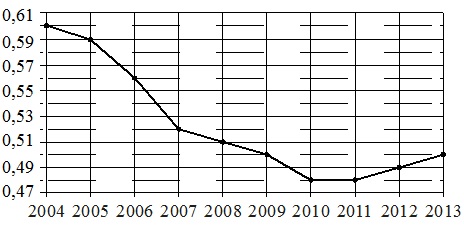
Ordnen Sie anhand des Diagramms jedem der angegebenen Zeiträume ein Merkmal des Bevölkerungswachstums in China in diesem Zeitraum zu..

Ausführungsalgorithmus

Bestimmen Sie den Wert der Teilung der vertikalen Skala des Bildes. Es wird als die Differenz zwischen einem Paar benachbarter Skalenwerte geteilt durch 2 gefunden (weil es 2 Divisionen zwischen zwei benachbarten Werten gibt).
Wir analysieren die in der Bedingung nacheinander angegebenen Merkmale 1–4 (linke Tabellenspalte). Wir vergleichen sie jeweils mit einem bestimmten Zeitraum (rechte Tabellenspalte).

Entscheidung:

Der Teilungswert der vertikalen Skala beträgt 0,01 %.

Von 2004 bis 2010 setzte sich der Wachstumsrückgang kontinuierlich fort. In den Jahren 2010-2011 war der Anstieg durchweg minimal, und ab 2012 begann er zu steigen. Jene. 2010 stoppte das Wachstum. Dieses Jahr fällt in den Zeitraum 2009-2011. Dementsprechend haben wir: IN 1.
Als größter Wachstumseinbruch ist die am „steilsten“ fallende Linie der Grafik in der Abbildung zu betrachten. Es fällt auf den Zeitraum 2006-2007. und beträgt 0,04 % pro Jahr (0,59–0,56 = 0,04 % im Jahr 2006 und 0,56–0,52 = 0,04 % im Jahr 2007). Von hier erhalten wir: A-2.
Das in Merkmal Nr. 3 angegebene Wachstum begann im Jahr 2007, setzte sich im Jahr 2008 fort und endete im Jahr 2009. Dies entspricht dem Zeitraum B, d.h. wir haben: B–3.
Das Bevölkerungswachstum begann nach 2011 zu steigen, d.h. 2012–2013 Daher erhalten wir: G–4.

Option 14MB8

Die Abbildung zeigt einen Funktionsgraphen und daran gezogene Tangenten an Punkten mit den Abszissen A, B, C und D.

Die rechte Spalte zeigt die Werte der Ableitung der Funktion an den Punkten A, B, C und D. Ordnen Sie jeden Punkt mithilfe des Diagramms dem Wert der Ableitung der Funktion an ihm zu.

Ausführungsalgorithmus

Wir betrachten ein Tangentenpaar, das mit der positiven Richtung der x-Achse einen spitzen Winkel bildet. Wir vergleichen sie, finden eine Übereinstimmung zwischen dem Paar der entsprechenden Werte der Ableitungen.
Wir betrachten ein Tangentenpaar, das mit der positiven Richtung der x-Achse einen stumpfen Winkel bildet. Wir vergleichen sie modulo, wir bestimmen die Entsprechung zu ihren Werten der Ableitungen unter den beiden verbleibenden in der rechten Spalte.

Entscheidung:

Ein spitzer Winkel mit positiver Richtung der x-Achse wird durch Ableitungen in t.B und t.C gebildet. Diese Derivate haben positive Werte. Daher sollte man hier zwischen den Werten Nr. 1 und 3 wählen. Wendet man die Regel an, dass, wenn der Winkel kleiner als 45 0 ist, die Ableitung kleiner als 1 ist und wenn mehr, dann größer als 1, wir schließen daraus: in t.B ist die Modulo-Ableitung größer als 1 in t.C - kleiner als 1. Das bedeutet, dass Sie Paare für die Antwort bilden können: IN 3 und S-1.

Die Ableitungen in t.A und t.D bilden mit der positiven Richtung der x-Achse einen stumpfen Winkel. Und hier wenden wir die gleiche Regel an, leicht umschrieben: Je mehr die Tangente am Punkt auf die Linie der Abszissenachse (in ihre negative Richtung) „gedrückt“ wird, desto größer ist ihr absoluter Wert. Dann erhalten wir: Die Ableitung am Punkt A ist betragsmäßig kleiner als die Ableitung am Punkt D. Ab hier haben wir Paare für die Antwort: A-2 und D-4.

Option 14MB9

Die Punkte in der Abbildung zeigen die durchschnittliche tägliche Lufttemperatur in Moskau im Januar 2011. Monatsdaten sind horizontal, Temperaturen in Grad Celsius sind vertikal angegeben. Zur Verdeutlichung sind die Punkte durch eine Linie verbunden.

Ordnen Sie anhand der Abbildung jedem der angegebenen Zeiträume ein Merkmal der Temperaturänderung zu.

Ausführungsalgorithmus

Wir analysieren nacheinander die Merkmale 1–4 (rechte Spalte) anhand der Grafik in der Abbildung. Wir haben sie jeweils einem bestimmten Zeitraum zugeordnet (linke Spalte).

Entscheidung:

Ein Temperaturanstieg wurde nur am Ende des Zeitraums vom 22. bis 28. Januar beobachtet. Hier stieg sie am 27. und 28. um 1 bzw. 2 Grad. Am Ende des Zeitraums vom 1. bis 7. Januar war die Temperatur stabil (–10 Grad), am Ende des 8. bis 14. und 15. bis 21. Januar sank sie (von –1 auf –2 und von –11 auf –12 Grad bzw.). Daher erhalten wir: G–1.
Da jeder Zeitraum 7 Tage umfasst, sollte die Temperatur ab dem 4. Tag jedes Zeitraums analysiert werden. Nur vom 4. bis 7. Januar blieb die Temperatur für 3–4 Tage unverändert. Also bekommen wir die Antwort: A-2.
Die monatliche Tiefsttemperatur wurde am 17. Januar beobachtet. Diese Zahl fällt in den Zeitraum vom 15. bis 21. Januar. Von hier haben wir ein paar: IN 3.
Das Temperaturmaximum fiel auf den 10. Januar und betrug +1 Grad. Dieses Datum fällt in den Zeitraum vom 8. bis 14. Januar. Also haben wir: B-4.

Option 14MB10

Ausführungsalgorithmus

Der Funktionswert an einem Punkt ist positiv, wenn dieser Punkt oberhalb der Ox-Achse liegt.
Die Ableitung an einem Punkt ist größer als Null, wenn die Tangente an diesen Punkt einen spitzen Winkel mit der positiven Richtung der x-Achse bildet.

Entscheidung:

Punkt A. Er liegt unterhalb der Ox-Achse, was bedeutet, dass der Wert der darin enthaltenen Funktion negativ ist. Wenn wir eine Tangente darin zeichnen, beträgt der Winkel zwischen ihr und der positiven Richtung Ox ungefähr 90 0, d.h. bildet einen spitzen Winkel. In diesem Fall ist also Kennzahl 3 geeignet. Jene. wir haben: A-3.

Punkt B. Er befindet sich oberhalb der Ochsenachse, d.h. der Punkt hat einen positiven Funktionswert. Die Tangente liegt an diesem Punkt ziemlich nahe an der Abszissenachse und bildet einen stumpfen Winkel (etwas weniger als 180°) mit ihrer positiven Richtung. Dementsprechend ist die Ableitung an dieser Stelle negativ. Hier eignet sich also Merkmal 1. Wir erhalten die Antwort: IN 1.

Punkt C. Der Punkt befindet sich unterhalb der Ox-Achse, die Tangente darin bildet einen großen stumpfen Winkel mit der positiven Richtung der Abszissenachse. Jene. in t.C ist der Wert sowohl der Funktion als auch der Ableitung negativ, was Merkmal Nr. 2 entspricht. Antworten: S-2.

Punkt D. Der Punkt befindet sich über der Ochsenachse und die Tangente darin bildet einen spitzen Winkel mit der positiven Richtung der Achse. Dies deutet darauf hin, dass hier sowohl der Wert der Funktion als auch der Wert der Ableitung größer Null sind. Antworten: D-4.

Option 14MB11

In der Abbildung zeigen die Punkte das monatliche Verkaufsvolumen von Kühlschränken in einem Haushaltsgerätegeschäft. Monate sind horizontal angegeben, die Anzahl der verkauften Kühlschränke ist vertikal angegeben. Zur Verdeutlichung sind die Punkte durch eine Linie verbunden.

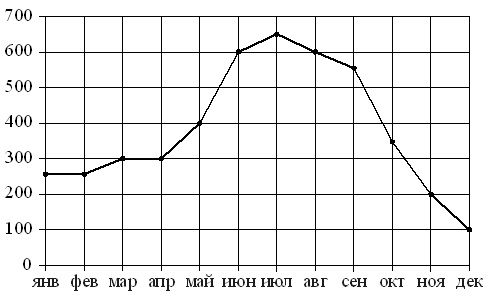
Ordnen Sie anhand der Abbildung jedem der angegebenen Zeiträume die Merkmale des Verkaufs von Kühlschränken zu.

Versuchen Sie zunächst, den Umfang der Funktion zu finden:

Hast du es geschafft? Vergleichen wir die Antworten:

Alles ist richtig? Gut erledigt!

Versuchen wir nun, den Bereich der Funktion zu finden:

Gefunden? Vergleichen:

Hat es zugestimmt? Gut erledigt!

Lassen Sie uns wieder mit den Graphen arbeiten, nur ist es jetzt etwas schwieriger - sowohl den Definitionsbereich der Funktion als auch den Wertebereich der Funktion zu finden.

So finden Sie sowohl die Domäne als auch den Bereich einer Funktion (Fortgeschrittene)

Folgendes ist passiert:

Mit Grafiken, denke ich, hast du es herausgefunden. Versuchen wir nun, den Definitionsbereich der Funktion gemäß den Formeln zu finden (wenn Sie nicht wissen, wie das geht, lesen Sie den Abschnitt über):

Hast du es geschafft? Überprüfung Antworten:

, da der Wurzelausdruck größer oder gleich Null sein muss.
, da es unmöglich ist, durch Null zu teilen, und der Wurzelausdruck nicht negativ sein kann.
, da bzw. für alle.
weil man nicht durch null teilen kann.

Wir haben jedoch noch einen weiteren Moment, der nicht geklärt wurde ...

Lassen Sie mich die Definition wiederholen und mich darauf konzentrieren:

Bemerkte? Das Wort „nur“ ist ein sehr, sehr wichtiges Element unserer Definition. Ich werde versuchen, es Ihnen an den Fingern zu erklären.

Nehmen wir an, wir haben eine Funktion, die durch eine gerade Linie gegeben ist. . Wann setzen wir diesen Wert in unsere "Regel" ein und erhalten das. Ein Wert entspricht einem Wert. Wir können sogar eine Tabelle mit verschiedenen Werten erstellen und eine bestimmte Funktion darstellen, um dies zu überprüfen.

"Suchen! - sagst du, - "trifft sich zweimal!" Vielleicht ist die Parabel also keine Funktion? Nein es ist!

Die Tatsache, dass "" zweimal vorkommt, ist noch lange kein Grund, der Parabel Mehrdeutigkeit vorzuwerfen!

Tatsache ist, dass wir bei der Berechnung ein Spiel bekommen haben. Und wenn wir mit rechnen, haben wir ein Spiel bekommen. Das ist also richtig, die Parabel ist eine Funktion. Schauen Sie sich das Diagramm an:

Ich habs? Wenn nicht, hier ist ein Beispiel aus dem wirklichen Leben für Sie, fernab von Mathematik!

Nehmen wir an, wir haben eine Gruppe von Bewerbern, die sich beim Einreichen von Dokumenten kennengelernt haben und denen jeder in einem Gespräch erzählt hat, wo er wohnt:

Stimmen Sie zu, es ist ziemlich real, dass mehrere Männer in derselben Stadt leben, aber es ist unmöglich, dass eine Person gleichzeitig in mehreren Städten lebt. Dies ist sozusagen eine logische Darstellung unserer "Parabel" - Mehrere verschiedene x entsprechen demselben y.

Lassen Sie uns nun ein Beispiel finden, bei dem die Abhängigkeit keine Funktion ist. Nehmen wir an, dieselben Typen haben erzählt, für welche Fachrichtungen sie sich beworben haben:

Hier haben wir eine ganz andere Situation: Eine Person kann sich problemlos für eine oder mehrere Richtungen bewerben. Also ein Element Sätze werden in Korrespondenz gebracht mehrere Elemente setzt. Bzw, es ist keine Funktion.

Lassen Sie uns Ihr Wissen in der Praxis testen.

Bestimmen Sie anhand der Bilder, was eine Funktion ist und was nicht:

Ich habs? Und hier ist Antworten:

Die Funktion ist - B,E.
Keine Funktion - A, B, D, D.

Du fragst warum? Ja, hier ist der Grund:

In allen Zahlen außer BEIM) und E) es gibt mehrere für einen!

Ich bin sicher, dass Sie jetzt leicht eine Funktion von einer Nichtfunktion unterscheiden, sagen können, was ein Argument und was eine abhängige Variable ist, und auch den Gültigkeitsbereich des Arguments und den Gültigkeitsbereich der Funktion bestimmen können. Kommen wir zum nächsten Abschnitt – wie definiert man eine Funktion?

Möglichkeiten, eine Funktion einzustellen

Was denkst du, was die Worte bedeuten "Funktion einstellen"? Das ist richtig, es bedeutet, jedem zu erklären, von welcher Funktion wir in diesem Fall sprechen. Erklären Sie außerdem so, dass jeder Sie richtig versteht und die Funktionsgraphen, die von Personen gemäß Ihrer Erklärung gezeichnet wurden, dieselben waren.

Wie kann ich das machen? Wie stelle ich eine Funktion ein? Der einfachste Weg, der in diesem Artikel bereits mehr als einmal verwendet wurde - mit einer Formel. Wir schreiben eine Formel, und indem wir einen Wert darin einsetzen, berechnen wir den Wert. Und wie Sie sich erinnern, ist eine Formel ein Gesetz, eine Regel, nach der uns und einem anderen klar wird, wie aus einem X ein Y wird.

Normalerweise tun sie genau das – in Aufgaben sehen wir vorgefertigte Funktionen, die durch Formeln definiert sind, es gibt jedoch andere Möglichkeiten, eine Funktion festzulegen, die jeder vergisst, und daher die Frage „Wie kann man sonst eine Funktion festlegen?“. verwirrt. Schauen wir uns alles der Reihe nach an und beginnen mit der analytischen Methode.

Analytische Art, eine Funktion zu definieren

Die analytische Methode ist die Aufgabe einer Funktion, die eine Formel verwendet. Dies ist der universellste und umfassendste und eindeutigste Weg. Wenn Sie eine Formel haben, wissen Sie absolut alles über die Funktion - Sie können eine Wertetabelle darauf erstellen, Sie können ein Diagramm erstellen, bestimmen, wo die Funktion zunimmt und wo sie abnimmt, im Allgemeinen, untersuchen Sie sie vollständig.

Betrachten wir eine Funktion. Was macht es aus?

"Was bedeutet das?" - du fragst. Ich werde es jetzt erklären.

Ich möchte Sie daran erinnern, dass in der Notation der Ausdruck in Klammern als Argument bezeichnet wird. Und dieses Argument kann jeder Ausdruck sein, nicht unbedingt einfach. Dementsprechend schreiben wir es unabhängig vom Argument (Ausdruck in Klammern) stattdessen in den Ausdruck.

In unserem Beispiel sieht das so aus:

Stellen Sie sich eine andere Aufgabe vor, die sich auf die analytische Methode zum Spezifizieren einer Funktion bezieht, die Sie in der Prüfung haben werden.

Ermitteln Sie den Wert des Ausdrucks at.

Ich bin mir sicher, dass Sie zuerst Angst hatten, als Sie einen solchen Ausdruck sahen, aber es ist absolut nichts Beängstigendes daran!

Alles ist dasselbe wie im vorherigen Beispiel: Unabhängig vom Argument (Ausdruck in Klammern) schreiben wir es stattdessen in den Ausdruck. Zum Beispiel für eine Funktion.

Was ist in unserem Beispiel zu tun? Stattdessen müssen Sie schreiben und anstelle von -:

Kürzen Sie den resultierenden Ausdruck:

Das ist alles!

Selbstständige Arbeit

Versuchen Sie nun selbst, die Bedeutung der folgenden Ausdrücke zu finden:

, Wenn
, Wenn

Hast du es geschafft? Vergleichen wir unsere Antworten: Wir sind daran gewöhnt, dass die Funktion die Form hat

Auch in unseren Beispielen definieren wir die Funktion auf diese Weise, aber analytisch ist es beispielsweise möglich, die Funktion implizit zu definieren.

Versuchen Sie, diese Funktion selbst zu erstellen.

Hast du es geschafft?

Hier ist, wie ich es gebaut habe.

Auf welche Gleichung sind wir gekommen?

Korrekt! Linear, was bedeutet, dass der Graph eine gerade Linie ist. Lassen Sie uns eine Tabelle erstellen, um zu bestimmen, welche Punkte zu unserer Linie gehören:

Genau darüber haben wir gesprochen ... Eins entspricht mehreren.

Versuchen wir zu zeichnen, was passiert ist:

Ist das, was wir haben, eine Funktion?

Richtig, nein! Wieso den? Versuchen Sie diese Frage mit einem Bild zu beantworten. Was hast du bekommen?

„Denn ein Wert entspricht mehreren Werten!“

Welche Schlussfolgerung können wir daraus ziehen?

Das ist richtig, eine Funktion kann nicht immer explizit ausgedrückt werden, und was als Funktion "getarnt" ist, ist nicht immer eine Funktion!

Tabellarische Art, eine Funktion zu definieren

Wie der Name schon sagt, handelt es sich bei dieser Methode um eine einfache Platte. Ja Ja. Wie die, die wir bereits gemacht haben. Zum Beispiel:

Hier ist Ihnen sofort ein Muster aufgefallen – Y ist dreimal größer als X. Und jetzt die „Denke sehr gut“-Aufgabe: Glaubst du, dass eine Funktion, die in Form einer Tabelle gegeben ist, einer Funktion entspricht?

Reden wir nicht lange, sondern zeichnen wir!

So. Wir zeichnen eine auf beide Arten gegebene Funktion:

Sehen Sie den Unterschied? Es geht nicht um die markierten Punkte! Schau genauer hin:

Hast du es jetzt gesehen? Wenn wir die Funktion tabellarisch einstellen, spiegeln wir nur die Punkte in der Tabelle wider, die wir in der Tabelle haben, und die Linie (wie in unserem Fall) verläuft nur durch sie. Wenn wir eine Funktion auf analytische Weise definieren, können wir beliebige Punkte nehmen, und unsere Funktion ist nicht auf sie beschränkt. Hier ist eine solche Funktion. Erinnern!

Grafische Methode zum Erstellen einer Funktion

Nicht weniger bequem ist die grafische Art, eine Funktion zu konstruieren. Wir zeichnen unsere Funktion, und eine andere interessierte Person kann herausfinden, womit y bei einem bestimmten x gleich ist, und so weiter. Graphische und analytische Methoden gehören zu den gebräuchlichsten.

Hier müssen Sie sich jedoch daran erinnern, worüber wir ganz am Anfang gesprochen haben - nicht jeder im Koordinatensystem gezeichnete „Schnörkel“ ist eine Funktion! Fiel ein? Für alle Fälle kopiere ich hier die Definition dessen, was eine Funktion ist:

In der Regel nennen die Leute genau die drei Möglichkeiten, eine Funktion zu spezifizieren, die wir analysiert haben - analytisch (mit einer Formel), tabellarisch und grafisch, wobei völlig vergessen wird, dass eine Funktion verbal beschrieben werden kann. Wie ist es? Ja, ganz einfach!

Verbale Beschreibung der Funktion

Wie kann man die Funktion verbal beschreiben? Nehmen wir unser aktuelles Beispiel - . Diese Funktion kann beschrieben werden als „jeder reelle Wert von x entspricht seinem dreifachen Wert“. Das ist alles. Nichts kompliziertes. Natürlich werden Sie einwenden: „Es gibt so komplexe Funktionen, dass es einfach unmöglich ist, sie mündlich einzustellen!“ Ja, es gibt einige, aber es gibt Funktionen, die sich einfacher verbal beschreiben als mit einer Formel einstellen lassen. Zum Beispiel: "Jeder natürliche Wert von x entspricht der Differenz zwischen den Ziffern, aus denen er besteht, während die größte Ziffer, die in der Zahleneingabe enthalten ist, als Minuend genommen wird." Betrachten Sie nun, wie unsere verbale Beschreibung der Funktion in der Praxis umgesetzt wird:

Die größte Ziffer in einer bestimmten Zahl - bzw. - wird reduziert, dann:

Haupttypen von Funktionen

Kommen wir nun zu den interessantesten - wir werden die Haupttypen von Funktionen betrachten, mit denen Sie gearbeitet haben / arbeiten und im Rahmen der Schul- und Institutsmathematik arbeiten werden, das heißt, wir werden sie sozusagen kennenlernen und Geben Sie ihnen eine kurze Beschreibung. Lesen Sie mehr über jede Funktion im entsprechenden Abschnitt.

Lineare Funktion

Eine Funktion der Form, wobei reelle Zahlen sind.

Der Graph dieser Funktion ist eine gerade Linie, daher reduziert sich die Konstruktion einer linearen Funktion darauf, die Koordinaten von zwei Punkten zu finden.

Die Lage der Geraden auf der Koordinatenebene hängt von der Steigung ab.

Funktionsumfang (auch bekannt als Argumentbereich) - .

Der Wertebereich ist .

quadratische Funktion

Funktion des Formulars, wo

Der Graph der Funktion ist eine Parabel, wenn die Zweige der Parabel nach unten gerichtet sind, wenn - nach oben.

Viele Eigenschaften einer quadratischen Funktion hängen vom Wert der Diskriminante ab. Die Diskriminante wird durch die Formel berechnet

Die Position der Parabel auf der Koordinatenebene relativ zum Wert und Koeffizienten ist in der Abbildung dargestellt:

Domain

Der Wertebereich hängt vom Extremum der gegebenen Funktion (dem Scheitelpunkt der Parabel) und dem Koeffizienten (der Richtung der Zweige der Parabel) ab.

Umgekehrte Proportionalität

Die durch die Formel gegebene Funktion, wo

Die Zahl wird als inverser Proportionalitätsfaktor bezeichnet. Je nach Wert liegen die Äste der Hyperbel in unterschiedlichen Quadraten:

Domäne - .

Der Wertebereich ist .

ZUSAMMENFASSUNG UND GRUNDFORMEL

1. Eine Funktion ist eine Regel, nach der jedem Element einer Menge ein eindeutiges Element der Menge zugeordnet wird.

- Dies ist eine Formel, die eine Funktion bezeichnet, dh die Abhängigkeit einer Variablen von einer anderen;
- Variable oder Argument;
- abhängiger Wert - ändert sich, wenn sich das Argument ändert, dh gemäß einer bestimmten Formel, die die Abhängigkeit eines Werts von einem anderen widerspiegelt.

2. Gültige Argumentwerte, oder der Umfang einer Funktion, bezieht sich auf das Mögliche, unter dem die Funktion sinnvoll ist.

3. Bereich der Funktionswerte- das sind die Werte, die es braucht, mit gültigen Werten.

4. Es gibt 4 Möglichkeiten, die Funktion einzustellen:

analytisch (unter Verwendung von Formeln);
tabellarisch;
Grafik
verbale Beschreibung.

5. Hauptarten von Funktionen:

: , wo, reelle Zahlen sind;
: , wo;
: , wo.