Онлайн тооцоолуур. Шийдлийн хязгаар. Онлайн хязгаарыг шийдвэрлэх

L'Hôpital -ийн дүрэм (p. L.) нь функцын хязгаарыг тооцоолоход хялбар болгодог. Жишээлбэл, та тэг рүү чиглэсэн функцүүдийн харьцаа болох функцийн хязгаарыг олох хэрэгтэй. Тэдгээр нь. Функцийн хамаарал нь 0/0 тодорхойгүй байдал юм. Үүнийг илчлэхэд тусална. Хязгаарлалтын хувьд функцуудын харьцааг эдгээр функцүүдийн деривативын харьцаагаар сольж болно. Тэдгээр нь. тоологчийн деривативыг хуваагчийн деривативт хувааж, энэ фракцын хязгаарыг авах шаардлагатай байна.

1. Тодорхой бус байдал 0/0. Эхний зүйл Л.

Хэрэв = 0 бол хэрэв сүүлийнх нь байгаа бол.

2. ∞ / ∞ хэлбэрийн тодорхойгүй байдал Хоёрдугаар сек. Л.

Энэ төрлийн хязгаарыг олох нь тодорхой бус байдлыг илчлэх гэж нэрлэдэг.

Хэрэв = ∞ байвал сүүлчийнх нь байгаа бол.

3. 0⋅∞, ∞- ∞, 1 ∞ ба 0 0 тодорхойгүй байдал нь хувиргалтаар 0/0 ба ∞ / ∞ тодорхойгүй болж буурдаг. Энэ оруулга нь хязгаарыг олох үед тухайн хэргийн товч заалт болдог. Тодорхой бус байдал бүр өөрийнхөөрөө илэрдэг. L'Hôpital -ийн дүрмийг бид тодорхойгүй байдлаас ангижрах хүртэл хэд хэдэн удаа хэрэглэж болно. L'Hôpital -ийн дүрмийг хэрэгжүүлэх нь деривативуудын хамаарлыг функцүүдийн хамаарлаас илүү хялбар хэлбэрт хөрвүүлэх тохиолдолд ашигтай байдаг.

• 0⋅∞ нь хоёр функцын үр дүн бөгөөд эхнийх нь тэг, хоёрдугаарт хязгааргүй байх хандлагатай байдаг;
• ∞- ∞ нь хязгааргүй байх чиг үүргийн ялгаа юм;
• 1 ∞ градус, түүний суурь нь нэг рүү, экспонент нь хязгааргүй байх хандлагатай байдаг;
• ∞ 0 градус, түүний суурь хязгааргүй, градус нь тэг хүртэл байх хандлагатай;
• 0 0 градус, түүний суурь нь 0, экспонент нь тэг рүү ханддаг.

Жишээ 1. Энэ жишээнд тодорхой бус байдал 0/0 байна

Жишээ 2. Энд ∞ / ∞ байна

Эдгээр жишээн дээр тоологчийн деривативыг хуваарийн деривативуудад хувааж, хязгаарын утгыг x -ээр орлуулна.

Жишээ 3. Тодорхойгүй байдлын төрөл 0⋅∞ .

Бид 0⋅∞ эргэлзээг ∞ / ∞ болгон өөрчилдөг, үүний тулд бид x -ийг хуваагч руу 1 / x бутархай болгон хувааж, тоологчны деривативыг тоонд хувааж, хуваагчийн деривативыг бичнэ.

Жишээ 4 Функцийн хязгаарыг тооцоол

Энд тодорхойгүй байдал нь ∞ 0 хэлбэртэй байна.Эхлээд бид функцийг логарифм хийж, үүний хязгаарыг олдог.

Хариултыг авахын тулд та e -г -1 болгож өсгөх хэрэгтэй, бид e -1 авна.

Жишээ 5. if x → 0 гэсэн хязгаарыг тооцоол

Шийдэл. Тодорхойгүй байдлын төрөл ∞ -∞ Бутархайг нийтлэг хуваагч болгон бууруулснаар бид ∞ -∞ -ээс 0/0 хүртэл шилждэг. Бид L'Hôpital -ийн дүрмийг мөрддөг боловч дахин 0/0 гэсэн тодорхойгүй байдлыг олж авдаг тул L. -ийг хоёр дахь удаагаа хэрэглэх ёстой. Шийдэл нь иймэрхүү харагдаж байна:

= = = =
= =

Жишээ 6 Шийдэх

Шийдэл. Тодорхойгүй байдлын төрөл ∞ / ∞, үүнийг өргөжүүлэхийн тулд бид олж авдаг

3), 4), 5) тохиолдлуудад эхлээд функцийг логарифмжуулж, логарифмын хязгаарыг олоод дараа нь эрэлттэй e хязгаарыг үр дүнгийн хэмжээнд хүргэнэ.

Жишээ 7. Хязгаарыг тооцоол

Шийдэл. Энд тодорхойгүй байдал 1 is байна. Бид A = гэж тэмдэглэв

Дараа нь lnA = = = = 2.

Логарифмын үндэс нь e бөгөөд хариултыг авахын тулд e -ийг квадрат болгохын тулд бид e 2 -ийг авна.

Заримдаа функцуудын харьцаа нь хязгаартай байх тохиолдол байдаг бөгөөд энэ нь деривативын харьцаанаас ялгаатай байдаг.

Жишээ авч үзье:

Учир нь sinx нь хязгаарлагдмал бөгөөд x нь хязгааргүй ургадаг, хоёр дахь гишүүн нь 0 болно.

Энэ функцэд хязгаар байхгүй энэ нь 0 -ээс 2 хооронд тогтмол хэлбэлздэг, энэ жишээнд p.L хамаарахгүй.

0/0 эсвэл ∞ / ∞ хэлбэрийн тодорхой бус байдал болон тооцоололд гарч буй бусад тодорхой бус байдлыг тодруулах хязгаархоёр хязгааргүй эсвэл хязгааргүй том функцын хамаарлыг L'Hôpital -ийн дүрмийн тусламжтайгаар ихээхэн хялбаршуулсан болно (үнэндээ тэдэнд хоёр дүрэм, тайлбар).

Мөн чанар L'Hôpital -ийн дүрэм хоёр хязгааргүй эсвэл хязгааргүй том функцийн харьцааны хязгаарыг тооцоолохдоо 0/0 эсвэл ∞ / ∞ хэлбэрийн тодорхой бус байдлыг өгдөг тохиолдолд хоёр функцийн харьцааны хязгаарыг тэдгээрийн хязгаараар сольж болно. харьцаа деривативуудтэгээд тодорхой үр дүнд хүрдэг.

L'Hôpital -ийн дүрмийн томъёолол руу шилжье.

Хязгааргүй хоёр хэмжигдэхүүний хязгаарын хувьд L'Hôpital -ийн дүрэм... Хэрэв функцууд f(x) ба g(x aa, мөн энэ хороололд g"(x aбие биетэйгээ тэнцүү, тэгтэй тэнцүү

().

Хязгааргүй их хэмжээгээр хязгаарлах тохиолдолд L'Hôpital -ийн дүрэм... Хэрэв функцууд f(x) ба g(x) цэгийн зарим хөрш хэсэгт ялгаатай байдаг a, цэгийг өөрөө эс тооцвол a, мөн энэ хороололд g"(x) ≠ 0 ба хэрэв эдгээр функцүүдийн x гэсэн хязгаар нь тухайн цэг дээрх функцийн утга руу ханддаг aбие биетэйгээ тэнцүү, хязгааргүйтэй тэнцүү

(),

Дараа нь эдгээр функцүүдийн харьцааны хязгаар нь тэдгээрийн деривативуудын харьцааны хязгаартай тэнцүү байна

().

Өөрөөр хэлбэл 0/0 эсвэл ∞ / ∞ хэлбэрийн тодорхой бус байдлын хувьд хоёр функцийн харьцааны хязгаар нь тэдгээрийн үүсмэл зүйлийн харьцааны хязгаартай тэнцүү бөгөөд хэрэв сүүлийнх нь (хязгаартай эсвэл хязгааргүй) байвал.

Тэмдэглэл.

1. L'Hôpital -ийн дүрмийг функцүүдийн хувьд мөн хэрэглэнэ f(x) ба g(x) -д зориулагдаагүй болно x = a.

2. Хэрэв функцийн деривативын харьцааны хязгаарыг тооцоолохдоо f(x) ба g(x) дахин бид 0/0 эсвэл ∞ / ∞ хэлбэрийн тодорхойгүй байдалд хүрч, L'Hôpital -ийн дүрмийг олон удаа (дор хаяж хоёр удаа) хэрэглэх ёстой.

3. L'Hôpital -ийн дүрмүүд (x) функцийн аргумент нь хязгаарлагдмал тоо биш байх үед мөн хамаарна. a, мөн хязгааргүй ( x → ∞).

Бусад төрлийн тодорхой бус байдлыг мөн 0/0 ба ∞ / ∞ төрлийн тодорхой бус байдал болгон бууруулж болно.

"Тэгийг тэг рүү хуваах" ба "хязгааргүй байдлыг хязгааргүйд хуваах" гэсэн тодорхойгүй байдлын талаар тодруулах.

Жишээ 1.

x= 2 нь 0/0 хэлбэрийн тодорхойгүй байдалд хүргэдэг. Тиймээс, функц бүрийн дериватив ба бид олж авдаг

Полиномын деривативыг тоологч, хуваагчаар тооцоолсон болно. Логарифмын нарийн төвөгтэй функцийн дериватив... Сүүлийн тэнцүү тэмдгийн өмнө ердийн хязгаар, x -ийн оронд хоёрыг орлуулах.

Жишээ 2. L'Hôpital дүрмийг ашиглан хоёр функцын харьцааны хязгаарыг тооцоолно уу.

Шийдэл. Өгөгдсөн функцэд утгыг орлуулах x

Жишээ 3. L'Hôpital дүрмийг ашиглан хоёр функцын харьцааны хязгаарыг тооцоолно уу.

Шийдэл. Өгөгдсөн функцэд утгыг орлуулах x= 0 нь 0/0 хэлбэрийн тодорхойгүй байдалд хүргэдэг. Тиймээс бид тоологч ба хуваагч дахь функцуудын деривативыг тооцоолж дараахь зүйлийг авна.

Жишээ 4.Тооцоолох

Шийдэл. Өгөгдсөн функцэд хязгааргүй нэмэхтэй тэнцүү x утгыг орлуулах нь ∞ / ∞ хэлбэрийн тодорхойгүй байдалд хүргэдэг. Тиймээс бид L'Hôpital -ийн дүрмийг баримталдаг.

Сэтгэгдэл. Эхний деривативын харьцааны хязгаар нь 0 хэлбэрийн тодорхойгүй байдал тул L'Hôpital -ийн дүрмийг хоёр удаа хэрэглэх, өөрөөр хэлбэл хоёр дахь деривативын харьцааны хязгаарт хүрэх шаардлагатай жишээг авч үзье. / 0 эсвэл ∞ / ∞.

L'Hôpital -ийн дүрмийг өөрөө хэрэгжүүлээд дараа нь шийдлийг нь үзээрэй

"Хязгааргүй 0 дахин" хэлбэрийн тодорхой бус байдлын талаар тодруулах

Жишээ 12.Тооцоолох

.

Шийдэл. Бид авдаг

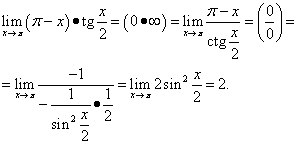
Энэ жишээ нь тригонометрийн өвөрмөц байдлыг ашигладаг.

"Тэгээс тэг хүртэл хүч чадал", "хязгааргүй байдлаас тэг хүртэл", "нэг нь хязгааргүй байдлын хүч хүртэл" гэсэн тодорхойгүй байдлын талаар тодруулах.

Хэлбэрийн тодорхойгүй байдал, эсвэл хэлбэрийн функцийн логарифмыг ашиглан 0/0 эсвэл ∞ / ∞ хэлбэр хүртэл буурдаг.

Илэрхийллийн хязгаарыг тооцоолохын тулд логарифмын шинж чанарыг ашиглах ёстой бөгөөд онцгой тохиолдол нь логарифмын шинж чанар юм. .

Логарифмын өвөрмөц байдал ба функцийн тасралтгүй байдлын шинж чанарыг ашиглан (хязгаарын тэмдгээс давж гарахын тулд) хязгаарыг дараах байдлаар тооцоолно.

Тус тусад нь та экспонентын илэрхийлэлийн хязгаарыг олж, бүтээх хэрэгтэй долдсон хэмжээнд хүртэл.

Жишээ 13.

Шийдэл. Бид авдаг

.

.

Жишээ 14. L'Hôpital дүрмийг ашиглан тооцоолно уу

Шийдэл. Бид авдаг

Бид экспонентын илэрхийлэлийн хязгаарыг тооцоолно

.

.

Жишээ 15. L'Hôpital дүрмийг ашиглан тооцоолно уу

• L'Hôpital -ийн дүрэм ба тодорхойгүй байдлын талаархи мэдээлэл
• "Тэгийг тэг рүү хуваах" ба "хязгааргүй байдлыг хязгааргүйд хуваах" гэсэн тодорхойгүй байдлын талаар тодруулах.
• "Хязгааргүй 0 дахин" хэлбэрийн тодорхой бус байдлын талаар тодруулах
• "Тэгээс тэг хүртэл хүч чадал", "хязгааргүй байдлаас тэг хүртэл", "нэг нь хязгааргүй байдлын хүч хүртэл" гэсэн тодорхойгүй байдлын талаар тодруулах.
• "Хязгааргүй ба хязгааргүй" хэлбэрийн тодорхой бус байдлын талаар тодруулах

L'Hôpital -ийн дүрэм ба тодорхойгүй байдлын талаархи мэдээлэл

0/0 эсвэл ∞ / ∞ хэлбэрийн тодорхой бус байдал болон бусад тодорхой бус байдлын талаар тодруулахыг L'Hôpital дүрмийг ашиглан ихээхэн хялбаршуулсан болно.

Мөн чанар L'Hôpital -ийн дүрэм хоёр функцын харьцааны хязгаарыг тооцоолохдоо 0/0 эсвэл ∞ / ∞ хэлбэрийн тодорхой бус байдлыг өгсөн тохиолдолд хоёр функцийн харьцааны хязгаарыг харьцааны хязгаараар сольж болно. тэдгээрийн деривативуудаас тодорхой үр дүнд хүрч болно.

Ерөнхийдөө L'Hôpital -ийн дүрмүүд нь дараагийн нэг томъёололд дамжуулж болох хэд хэдэн теоремыг хэлнэ.

L'Hôpital -ийн дүрэм... Хэрэв функцууд f(x) ба g(x) цэгийн зарим хөрш зэргээс ялгагдах боломжтой бөгөөд энэ цэгийг өөрөө эс тооцвол, мөн энэ хороололд

(1)

Өөрөөр хэлбэл 0/0 эсвэл ∞ / ∞ хэлбэрийн тодорхой бус байдлын хувьд хоёр функцийн харьцааны хязгаар нь тэдгээрийн үүсмэл зүйлийн харьцааны хязгаартай тэнцүү бөгөөд хэрэв сүүлийнх нь (хязгаартай эсвэл хязгааргүй) байвал.

Тэгш байдлын хувьд (1) хувьсагчийн ханддаг утга нь хязгаартай тоо, хязгааргүй эсвэл хасах хязгааргүй байж болно.

Бусад төрлийн тодорхой бус байдлыг мөн 0/0 ба ∞ / ∞ төрлийн тодорхой бус байдал болгон бууруулж болно.

"Тэгийг тэг рүү хуваах" ба "хязгааргүй байдлыг хязгааргүйд хуваах" гэсэн тодорхойгүй байдлын талаар тодруулах.

Жишээ 1.Тооцоолох

x= 2 нь 0/0 хэлбэрийн тодорхойгүй байдалд хүргэдэг. Тиймээс бид L'Hôpital -ийн дүрмийг баримталдаг.

Жишээ 2.Тооцоолох

Шийдэл. Өгөгдсөн функцэд утгыг орлуулах x

Жишээ 3.Тооцоолох

Шийдэл. Өгөгдсөн функцэд утгыг орлуулах x= 0 нь 0/0 хэлбэрийн тодорхойгүй байдалд хүргэдэг. Тиймээс бид L'Hôpital -ийн дүрмийг баримталдаг.

Жишээ 4.Тооцоолох

Шийдэл. Өгөгдсөн функцэд хязгааргүй нэмэхтэй тэнцүү x утгыг орлуулах нь ∞ / ∞ хэлбэрийн тодорхойгүй байдалд хүргэдэг. Тиймээс бид L'Hôpital -ийн дүрмийг баримталдаг.

Сэтгэгдэл. Хэрэв үүсмэл харьцааны хязгаар нь 0/0 эсвэл ∞ / ∞ хэлбэрийн тодорхой бус байдал байвал L'Hôpital дүрмийг дахин хэрэглэж болно, өөрөөр хэлбэл. хоёрдахь деривативын харьцааны хязгаар руу очих.

Жишээ 5.Тооцоолох

Шийдэл. Олоорой

Энд L'Hôpital -ийн дүрмийг хоёр удаа хэрэглэнэ, учир нь функцийн харьцаа ба деривативын харьцааны хязгаар хоёулаа ∞ / ∞ хэлбэрийн тодорхой бус байдлыг өгдөг.

Жишээ 6.Тооцоолох

Нүд нь бүлтийсэн бор шувуу гэж төсөөлөөд үз дээ. Үгүй ээ, энэ бол аянга биш, хар салхи, тэр ч байтугай гартаа дүүгүүртэй бяцхан хүү биш юм. Зүгээр л асар том, их бууны бөмбөг дэгдээхэйнүүдийн дунд нисдэг. Яг л L'Hôpital -ийн дүрэмэргэлзээтэй байгаа хязгаарыг шийдвэрлэх буюу.

L'Hôpital -ийн дүрмүүд нь заасан тодорхой бус байдлыг хурдан бөгөөд үр дүнтэй арилгах боломжийг олгодог маш хүчирхэг арга юм. L'Hôpital -ийн дүрмийг ашиглахгүй байх". Зоригтойгоор тодруулсан шаардлагыг аливаа хичээлийн хязгаарлагдмал ухамсартай холбож болно Хязгаар. Шийдлийн жишээ, Гайхамшигтай хязгаарлалтууд. Шийдвэрлэх аргуудыг хязгаарлах, Гайхалтай эквивалентууд, "тэгээс тэг хүртэл" эсвэл "хязгааргүй байдлаас хязгааргүй" гэсэн эргэлзээтэй тулгардаг. Даалгаврыг "хязгаарыг тооцоол" гэж товч томъёолсон байсан ч гэсэн та L'Hôpital -ийн дүрмийг ашиглахгүйгээр бүх зүйлийг, ямар ч зүйлийг ашиглах болно гэсэн шууд утгаар илэрхийлж байна.

Нийтдээ хоёр дүрэм байдаг бөгөөд тэдгээр нь мөн чанар, хэрэглээний аргын хувьд хоорондоо маш төстэй юм. Энэ сэдвээр шууд жишээ авахаас гадна математикийн анализын цаашдын судалгаанд хэрэг болох нэмэлт материалыг судлах болно.

Дүрмийг товчхон "практик" хэлбэрээр өгөх болно гэдгийг би тэр даруйд нь тэмдэглэх болно, хэрэв та онолоо батлах шаардлагатай бол илүү нарийвчлалтай тооцоолохын тулд сурах бичигт хандахыг зөвлөж байна.

L'Hôpital -ийн анхны дүрэм

Үүний чиг үүргийг анхаарч үзээрэй хязгааргүй жижигхэзээ нэгэн цагт Хэрэв тэдний харилцаанд хязгаар байгаа бол тодорхойгүй байдлыг арилгахын тулд та үүнийг авч болно хоёр деривативууд- тоологч ба хуваагчаас. Үүнд: , тэр бол .

Тэмдэглэл : хязгаар нь бас байх ёстой, эс тэгвээс дүрэм үйлчлэхгүй.

Дээрхээс юу гарах вэ?

Нэгдүгээрт, та олох чадвартай байх ёстой функцийн деривативууд, илүү сайн - илүү сайн =)

Хоёрдугаарт, деривативыг тоологчоос ЗӨВЛӨГӨӨ, хуваагчаас тусад нь авна. Хуваарийг ялгах дүрмийг андуурч болохгүй !!!

Гуравдугаарт, "X" нь тодорхой бус байдал байгаа бол хаана ч хамаагүй, хязгааргүй хүртэл хичээж чаддаг.

Эхний нийтлэлийн 5 -р жишээ рүү буцъя хязгаарын тухай, Үүний үр дүнд дараахь үр дүнд хүрсэн болно.

Эхний L'Hôpital дүрэм нь 0: 0 эргэлзээнд хамаарна.

Таны харж байгаагаар тоологч ба хуваарилагчийн ялгаа нь биднийг хагас ээлжээр хариулахад хүргэсэн: бид хоёр энгийн деривативыг олж, дотор нь "хоёр" -ыг орлуулсан бөгөөд тодорхойгүй байдал ул мөргүй алга болсон нь харагдаж байна!

L'Hôpital -ийн дүрмийг хоёр ба түүнээс дээш удаа дараалан хэрэглэх шаардлагатай болдог (энэ нь хоёрдахь дүрэмд бас хамаатай). Үүнийг чимэг орой болгон авч үзье Жишээ 2 хичээл гайхалтай хязгаарын тухай:

Давхар орон дээр хоёр боов дахин хөрч байна. L'Hôpital -ийн дүрмийг хэрэгжүүлье.

Эхний алхамд хуваарийг авсан болохыг анхаарна уу нийлмэл функцийн дериватив... Үүний дараа бид хэд хэдэн завсрын хялбаршуулалтыг хийж, тухайлбал косинусаас ангижрах нь эв нэгдэлтэй болохыг харуулж байна. Тодорхойгүй байдлыг арилгаагүй тул бид L'Hôpital -ийн дүрмийг дахин хэрэгжүүлнэ (хоёр дахь мөр).

Би жижиг тест хийх боломжтой байхын тулд би хамгийн хялбар жишээг санаатайгаар сонгосонгүй. Хэрэв тэд хэрхэн олдсон нь бүрэн тодорхой болоогүй бол деривативууд, хэрэв та косинусын анхаарал тодорхойгүй байвал буцаж очно уу гайхалтай хязгаар... Би дериватив ба хязгаарын талаар хангалттай нарийвчлан ярьсан болохоор алхам алхмаар тайлбарлахад тийм ч их ач холбогдол өгөхгүй байна. Өгүүллийн шинэлэг зүйл бол дүрмүүд болон техникийн зарим шийдлүүд юм.

Өмнө дурьдсанчлан, ихэнх тохиолдолд L'Hôpital -ийн дүрмийг ашиглах шаардлагагүй байдаг ч шийдлийг нарийвчлан шалгахын тулд тэдгээрийг ашиглах нь зүйтэй. Ихэнхдээ, гэхдээ үргэлж биш. Тиймээс, жишээлбэл, одоо авч үзсэн жишээг шалгах нь илүү ашигтай юм гайхалтай эквивалентууд.

L'Hôpital -ийн хоёр дахь дүрэм

Ах 2 унтаж буй хоёр найман тулаан хийж байна. Үүнтэй адил:

Хэрэв харилцаанд хязгаар байгаа бол хязгааргүй томфункцүүдийн цэг дээр :, дараа нь тодорхойгүй байдлыг арилгахын тулд та авч болно хоёр дериватив- Тоолуураас салгаж, хуваах хэсгээс салгах. Үүнд: , тэр бол тоологч ба хуваагчийг ялгахад хязгаарын утга өөрчлөгддөггүй.

Тэмдэглэл : хязгаар байх ёстой

Дахин хэлэхэд янз бүрийн практик жишээн дээр утга өөр байж болнотүүний дотор эцэс төгсгөлгүй. Тодорхой бус байдал байгаа нь чухал юм.

Эхний хичээлийн №3 жишээг шалгая. ... Бид L'Hôpital -ийн хоёрдахь дүрмийг ашигладаг.

Аварга хүмүүсийн тухай ярьж эхэлмэгц бид хоёр каноник хязгаарыг шинжлэх болно.

Жишээ 1

Хязгаарыг тооцоолох

"Ердийн" аргаар хариулт авах нь тийм ч амар биш тул "хязгааргүй байдлаас хязгааргүй" гэсэн тодорхой бус байдлыг тодруулахын тулд бид L'Hôpital -ийн дүрмийг ашигладаг.

Тиймээс, нэгээс дээш суурьтай логарифмаас илүү өндөр дараалсан өсөлтийн шугаман функц(гэх мэт). Мэдээжийн хэрэг, "x" нь илүү өндөр түвшинд ийм логарифмыг "чирэх" болно. Үнэн хэрэгтээ энэ функц нь аажмаар ургадаг хуваарьижил "x" -тэй харьцуулахад хавтгай байна.

Жишээ 2

Хязгаарыг тооцоолох

Бас нэг танил цохилт. Тодорхойгүй байдлыг арилгахын тулд бид L'Hôpital дүрмийг хоёр удаа дараалан ашигладаг.

Суурь нь нэгээс дээш хэмжээтэй экспоненциал функц(гэх мэт) эерэг зэрэгтэй хүчний функцээс илүү өндөр дарааллын өсөлт.

Үүнтэй төстэй хязгаарлалтууд энэ хугацаанд тохиолддог бүрэн функцийг судлахтухайлбал, олохдоо графикийн асимптотууд... Тэд мөн зарим ажлуудад анзаарагддаг магадлалын онол... Тооцоолсон хоёр жишээг анхаарч үзэхийг танд зөвлөж байна, энэ бол тоологч ба ялгааг ялгахаас өөр сайн зүйл байдаггүй цөөн тохиолдлын нэг юм.

Цаашид текстэд би L'Hôpital -ийн эхний болон хоёрдахь дүрмийг ялгахгүй, үүнийг зөвхөн өгүүллийг бүтээх зорилгоор хийсэн болно. Ерөнхийдөө миний үзэж байгаагаар математикийн аксиом, теорем, дүрэм, шинж чанарыг шаардлагагүй тоогоор тоолох нь зарим талаар хор хөнөөлтэй байдаг, учир нь "3 -р теоремоос 19 -р теоремын дагуу ..." гэх мэт хэллэгүүд нь зөвхөн тодорхой сурах бичгийн хүрээнд мэдээлэл өгөх чадвартай байдаг. . Мэдээллийн өөр эх сурвалжид мөн адил "Үр дүн 2 ба теорем 3" байх болно. Ийм мэдэгдэл нь албан ёсны бөгөөд зөвхөн зохиогчид өөрсдөдөө тохиромжтой байдаг. Хамгийн тохиромжтой нь математикийн баримтын мөн чанарыг авч үзэх нь зүйтэй юм. Үл хамаарах зүйл бол түүхэнд тогтсон нэр томъёо юм, жишээлбэл. анхны гайхалтай хязгаарэсвэл хоёр дахь гайхалтай хязгаар.

Бид Парисын Шинжлэх Ухааны Академийн гишүүн Маркиз Гийом Франсуа де Л'Хопиталын санал болгосон сэдвийг үргэлжлүүлэн боловсруулж байна. Нийтлэл нь тодорхой практик будаг олж авдаг бөгөөд нэлээд түгээмэл ажил бол дараахь зүйлийг шаарддаг.

Дулаарахын тулд хэдэн жижиг бор шувуутай харьцъя.

Жишээ 3

Косинусаас ангижрах замаар хязгаарыг урьдчилан хялбарчилж болох боловч нөхцөлийг хүндэтгэж, тоологч ба хуваагчийг нэн даруй ялгаж салгаж болно.

Деривативыг хайж олох явцад стандарт бус зүйл гэж байдаггүй, тиймээс хуваарь дээр ердийн зүйл байдаггүй. ялгах дүрэмажилладаг .

Харуулсан жишээг тогтоож, дараа нь шийддэг гайхалтай хязгаар, Үүнтэй төстэй хэргийг "Хэцүү хязгаар" нийтлэлийн төгсгөлд авч үзсэн болно.

Жишээ 4

L'Hôpital дүрмээр хязгаарыг тооцоол

Энэ бол өөрөө хийх шийдлийн жишээ юм. Тоглосон нь сайн =)

Ердийн нөхцөл байдал бол ялгаатай байдлаас хойш гурван эсвэл дөрвөн давхар бутархайг олж авах явдал юм.

Жишээ 5

L'Hôpital дүрмийг ашиглан хязгаарыг тооцоол

Аппликешн нь өөрөө санал болгож байна гайхалтай эквивалент, гэхдээ замыг дараах нөхцлөөр хатуу тодорхойлсон болно.

Ялгаварласны дараа би олон давхар фракцаас салж, хамгийн хялбарчлалыг хийхийг зөвлөж байна.... Мэдээжийн хэрэг, илүү дэвшилтэт оюутнууд сүүлийн алхамыг алгасаад шууд дараах зүйлийг бичиж болно. , гэхдээ зарим хязгаарт онц сурагчид хүртэл эргэлзэх болно.

Жишээ 6

L'Hôpital дүрмийг ашиглан хязгаарыг тооцоол

Жишээ 7

L'Hôpital дүрмийг ашиглан хязгаарыг тооцоол

Эдгээр нь өөрөө хийх шийдлийн жишээ юм. 7 -р жишээнд юу ч хялбарчилж болохгүй, ялгасны дараа бутархай нь хэтэрхий энгийн байна. Гэхдээ 8-р жишээнд L'Hôpital дүрмийг хэрэглэсний дараа гурван давхар бүтэцээс ангижрах нь зүйтэй юм, учир нь тооцоолол нь тийм ч тохиромжтой биш юм. Бүрэн шийдэл, сургалтын төгсгөлд хариулна уу. Хэрэв танд ямар нэгэн бэрхшээл тулгарвал - тригонометрийн хүснэгттуслах.

Тодорхой бус байдлыг ялгаж салгасны дараа хялбарчлах нь туйлын зайлшгүй шаардлагатай болно арилгаагүй.

Жишээ 8

L'Hôpital дүрмийг ашиглан хязгаарыг тооцоол

Явах:

Сонирхолтой нь, анхны ялгаварлалтын дараах анхны тодорхойгүй байдал нь эргэлзээ болж хувирсан бөгөөд L'Hôpital -ийн дүрмийг цаашид тайван байдлаар хэрэгжүүлдэг. Түүнчлэн "ойртох" бүрийн дараа дөрвөн давхар бутархайг хэрхэн арилгаж, тогтмолуудыг хязгаарын тэмдгээс гаргаж авдаг болохыг анхаарна уу. Энгийн жишээн дээр тогтмол байдлыг тэсвэрлэхгүй байх нь илүү тохиромжтой байдаг, гэхдээ хязгаар нь нарийн төвөгтэй байх үед бид бүх зүйл, бүх зүйл, бүх зүйлийг хялбаршуулдаг. Шийдэгдсэн жишээнүүдийн хуурамч байдал нь мөн , а, тиймээс синусыг арилгах явцад шинж тэмдгүүдэд төөрөлдөх нь гайхах зүйл биш юм. Эцсийн мөрөнд синусуудыг алах боломжгүй байсан боловч жишээ нь нэлээд хэцүү бөгөөд уучлагдах болно.

Нөгөө өдөр би нэгэн сонирхолтой даалгавартай таарлаа.

Жишээ 9

Үнэнийг хэлэхэд энэ хязгаар нь юутай тэнцэх вэ гэдэгт би бага зэрэг эргэлзэж байлаа. Дээр үзүүлсэнчлэн "x" нь логарифмаас илүү өндөр өсөлтийн дараалалтай боловч логарифмын кубыг "чирэх" болов уу? Хэн ялахыг өөрөө олж мэдэхийг хичээгээрэй.

Тийм ээ, L'Hôpital -ийн дүрэм бол их буунаас бор шувуу руу буудахаас гадна шаргуу хөдөлмөр юм.

L'Hôpital -ийн дүрмийг хэрэгжүүлэхийн тулд зүйлийн тодорхой бус байдлыг багел эсвэл ядарсан найман болгож бууруулдаг.

Тодорхой бус байдлаар шийтгэлийг хичээлийн 9-13-р жишээнд нарийвчлан авч үзсэн болно Шийдвэрлэх аргуудыг хязгаарлах... Хэлбэрийн хувьд дахиад нэгийг авч үзье.

Жишээ 10

L'Hôpital дүрмийг ашиглан функцийн хязгаарыг тооцоол

Эхний алхам дээр бид илэрхийлэлийг нийтлэг зүйл рүү авчирдаг бөгөөд ингэснээр тодорхой бус байдлыг эргэлзээ болгон хувиргадаг. Тэгээд бид L'Hôpital -ийн дүрмийг ачаалж байна.

Дашрамд хэлэхэд дөрвөн давхар илэрхийлэлд хүрэх нь утгагүй зүйл юм.

Тодорхой бус байдал нь дараахь зүйлийг өөрчлөхийг эсэргүүцдэггүй.

Жишээ 11

L'Hôpital дүрмийг ашиглан функцийн хязгаарыг тооцоол

Энд байгаа хязгаар нь нэг талыг барьсан бөгөөд ийм хязгаарлалтыг гарын авлагад аль хэдийн хэлэлцсэн болно Функцийн график ба шинж чанарууд... Таны санаж байгаагаар "сонгодог" логарифмын график тэнхлэгийн зүүн талд байдаггүй тул бид зөвхөн тэгээс баруун тийш ойртож чадна.

L'Hôpital-ийн нэг талыг барьсан хязгаарлалт хийх дүрэм нь ажилладаг боловч тодорхой бус байдлыг эхлээд шийдэх хэрэгтэй. Эхний алхам дээр бид тодорхой бус байдлыг олж авахын тулд гурван давхар фракц хийж, дараа нь шийдэл нь загвар схемийн дагуу явагдана.

Тоолуур ба хуваагчийг ялгаж салгасны дараа бид хялбарчлахын тулд дөрвөн давхар фракцаас салдаг. Үүний үр дүнд тодорхой бус байдал үүсэв. Бид заль мэхийг давтан хэлье: дахин бутархайг гурван давхар болгож, үүссэн эргэлзээнд L'Hôpital дүрмийг дахин хэрэглэнэ.

Бэлэн.

Анхны хязгаарыг хоёр багел болгохыг оролдож болно.

Гэхдээ нэгдүгээрт, хуваагч дахь дериватив нь илүү хэцүү бөгөөд хоёрдугаарт үүнээс сайн зүйл гарахгүй.

Тиймээс, ижил төстэй жишээг шийдэхийн өмнө дүн шинжилгээ хийх хэрэгтэй(амаар эсвэл ноорог дээр) Ямар эргэлзээг багасгах нь илүү ашигтай байдаг - "тэгээс тэг хүртэл" эсвэл "хязгааргүй байдлаас хязгааргүй" хүртэл.

Хариуд нь архи уудаг хамтрагчид болон чамин тансаг нөхдийг гэрэл рүү татдаг. Өөрчлөлтийн арга нь энгийн бөгөөд стандарт юм.