Սահմանում 9.3.Վեկտոր X կանչեց սեփական վեկտորըմատրիցներ Աեթե այդպիսի թիվ կա λ, այդ հավասարությունը գործում է. Ա X= λ X, այսինքն՝ դիմելու արդյունքը X գծային փոխակերպում, որը տրված է մատրիցով Ա, այս վեկտորի բազմապատկումն է թվով λ ... Թիվն ինքնին λ կանչեց սեփական համարըմատրիցներ Ա.

Փոխարինելով բանաձևերով (9.3) x` j = λx j,մենք ստանում ենք հավասարումների համակարգ սեփական վեկտորի կոորդինատները որոշելու համար.

. (9.5)

Այս գծային միատարր համակարգը կունենա ոչ տրիվիալ լուծում միայն այն դեպքում, եթե նրա հիմնական որոշիչը 0-ն է (Կրամերի կանոն): Այս պայմանը գրելով հետևյալ ձևով.

մենք ստանում ենք սեփական արժեքները որոշելու հավասարումը λ կանչեց բնորոշ հավասարում... Այն հակիրճ կարելի է ներկայացնել հետևյալ կերպ.

| A - λE | = 0, (9.6)

քանի որ նրա ձախ կողմը պարունակում է մատրիցայի որոշիչը A-λE... Բազմանդամի նկատմամբ λ | A - λE| կանչեց բնորոշ բազմանդամմատրիցներ Ա.

Բնութագրական բազմանդամ հատկություններ.

1) Գծային փոխակերպման բնորոշ բազմանդամը կախված չէ հիմքի ընտրությունից. Ապացույց. (տես (9.4)), բայց հետևաբար, . Այսպիսով, դա կախված չէ հիմքի ընտրությունից: Հետևաբար, և | A-λE| չի փոխվում նոր հիմքի անցնելիս:

2) Եթե մատրիցը Ագծային փոխակերպումն է սիմետրիկ(դրանք. եւ ij = a ji), ապա բնորոշ հավասարման (9.6) բոլոր արմատները իրական թվեր են։

Սեփական արժեքների և սեփական վեկտորների հատկությունները.

1) Եթե ընտրենք սեփական վեկտորների հիմքը x 1, x 2, x 3 սեփական արժեքներին համապատասխան λ 1, λ 2, λ 3մատրիցներ Ա, ապա այս հիմքում A գծային փոխակերպումն ունի անկյունագծային ձևի մատրիցա.

(9.7) Այս հատկության ապացույցը բխում է սեփական վեկտորների սահմանումից:

2) Եթե վերափոխման սեփական արժեքները Ատարբեր են, ապա համապատասխան սեփական վեկտորները գծային անկախ են:

3) Եթե մատրիցի բնորոշ բազմանդամը Աունի երեք տարբեր արմատներ, ապա որոշ հիմքերով մատրիցա Աունի անկյունագծային ձև.

Եկեք գտնենք մատրիցայի սեփական արժեքները և սեփական վեկտորները. Կազմենք բնորոշ հավասարումը. (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Եկեք գտնենք յուրաքանչյուր գտած արժեքին համապատասխան սեփական վեկտորների կոորդինատները λ. (9.5)-ից հետևում է, որ եթե X (1) ={x 1, x 2, x 3) Արդյո՞ք սեփական վեկտորը համապատասխանում է λ 1 = -2, ապա

- համագործակցային, բայց չսահմանված համակարգ: Դրա լուծումը կարելի է գրել այսպես X (1) ={ա,0,-ա), որտեղ a-ն ցանկացած թիվ է: Մասնավորապես, եթե մենք պահանջում ենք, որ | x (1) |=1, X (1) =

Համակարգում փոխարինում (9.5) λ 2 = 3, մենք ստանում ենք համակարգ երկրորդ սեփական վեկտորի կոորդինատները որոշելու համար. x (2) ={y 1, y 2, y 3}:

, որտեղ X (2) ={բ, -բ, բ) կամ, ենթակա | x (2) |=1, x (2) =

Համար λ 3 = 6 գտնել սեփական վեկտորը x (3) ={z 1, z 2, z 3}:

, x (3) ={գ,2c, c) կամ նորմալացված տարբերակով

x (3) = Դուք կարող եք դա տեսնել X (1) X (2) = աբ - աբ= 0, x (1) x (3) = ac - ac= 0, x (2) x (3) = մ.թ.ա- 2մ.թ.ա. + մ.թ.ա= 0. Այսպիսով, այս մատրիցայի սեփական վեկտորները զույգերով ուղղանկյուն են:

Դասախոսություն 10.

Քառակուսային ձևերը և դրանց կապը սիմետրիկ մատրիցների հետ: Սիմետրիկ մատրիցայի սեփական վեկտորների և սեփական արժեքների հատկությունները: Քառակուսի ձևի կրճատում մինչև կանոնական ձև:

Սահմանում 10.1.Քառակուսի ձևիրական փոփոխականներ x 1, x 2, ..., x nայս փոփոխականների նկատմամբ երկրորդ աստիճանի բազմանդամ է, որը չի պարունակում առաջին աստիճանի ազատ անդամ և անդամներ։

Քառակուսի ձևերի օրինակներ.

(n = 2),

(n = 3). (10.1)

Եկեք հիշենք վերջին դասախոսության մեջ տրված սիմետրիկ մատրիցայի սահմանումը.

Սահմանում 10.2.Քառակուսի մատրիցը կոչվում է սիմետրիկ, եթե, այսինքն, եթե հիմնական անկյունագծի նկատմամբ սիմետրիկ մատրիցային տարրերը հավասար են։

Սիմետրիկ մատրիցայի սեփական արժեքների և սեփական վեկտորների հատկությունները.

1) Սիմետրիկ մատրիցայի բոլոր սեփական արժեքները իրական են:

Ապացույց (համար n = 2).

Թող մատրիցը Անման է: ... Կազմենք բնորոշ հավասարումը.

(10.2) Գտեք տարբերակիչ.

Հետևաբար, հավասարումը միայն իրական արմատներ ունի:

2) Սիմետրիկ մատրիցայի սեփական վեկտորները ուղղանկյուն են.

Ապացույց (համար n= 2).

Սեփական վեկտորների կոորդինատները և պետք է բավարարեն հավասարումները:

Սեփական արժեքներ (թվեր) և սեփական վեկտորներ:
Լուծումների օրինակներ

Մնա ինչպիսին կաս

Երկու հավասարումներից էլ հետևում է, որ.

Ենթադրենք, ապա. .

Որպես արդյունք: Երկրորդ սեփական վեկտորն է:

Կրկնենք լուծման կարևոր կետերը.

- ստացված համակարգը, անշուշտ, ունի ընդհանուր լուծում (հավասարումները գծային կախված են);

- «Խաղը» ընտրում ենք այնպես, որ այն ամբողջական լինի, իսկ առաջին «x» կոորդինատը լինի ամբողջական, դրական և հնարավորինս փոքր:

- ստուգեք, որ կոնկրետ լուծումը բավարարում է համակարգի յուրաքանչյուր հավասարումը:

Պատասխանել .

Բավականին բավականաչափ միջանկյալ «հսկիչ կետեր» կային, հետևաբար հավասարության ստուգումը, սկզբունքորեն, ավելորդ գործ է։

Տեղեկատվության տարբեր աղբյուրներում սեփական վեկտորների կոորդինատները հաճախ գրվում են ոչ թե սյունակներում, այլ տողերում, օրինակ. (և, ճիշտն ասած, ես սովոր եմ դրանք տողերով գրել)... Այս տարբերակն ընդունելի է, բայց թեմայի լույսի ներքո գծային փոխակերպումներտեխնիկապես ավելի հարմար է օգտագործման համար սյունակի վեկտորներ.

Միգուցե լուծումը ձեզ շատ երկար թվաց, բայց դա միայն այն պատճառով, որ ես շատ մանրամասն մեկնաբանեցի առաջին օրինակը:

Օրինակ 2

Մատրիցներ

Մենք ինքներս ենք մարզվում։ Դասի վերջում առաջադրանքն ավարտելու մոտավոր օրինակ.

Երբեմն պահանջվում է կատարել լրացուցիչ առաջադրանք, մասնավորապես.

գրեք կանոնական մատրիցային տարրալուծումը

Ինչ է դա?

Եթե ​​մատրիցայի սեփական վեկտորները ձևավորվեն հիմք, ապա այն կարող է ներկայացվել որպես.

Որտեղ է մատրիցը, որը կազմված է սեփական վեկտորների կոորդինատներից, - անկյունագծայինմատրիցա՝ համապատասխան սեփական արժեքներով։

Նման մատրիցային տարրալուծումը կոչվում է կանոնականկամ անկյունագծային.

Դիտարկենք առաջին օրինակի մատրիցը: Իր սեփական վեկտորները գծային անկախ(ոչ գծային) և հիմք են կազմում: Եկեք նրանց կոորդինատներից կազմենք մատրիցա.

Վրա հիմնական անկյունագիծմատրիցներ համապատասխան կարգովսեփական արժեքները գտնվում են, իսկ մնացած տարրերը հավասար են զրոյի.
- ևս մեկ անգամ շեշտում եմ կարգի կարևորությունը. «երկու»-ը համապատասխանում է 1-ին վեկտորին և հետևաբար գտնվում է 1-ին սյունակում, «երեք»-ը՝ 2-րդ վեկտորին:

Գտնելու սովորական ալգորիթմի համաձայն հակադարձ մատրիցակամ Գաուս-Հորդանանի մեթոդգտնել ... Ոչ, սա տառասխալ չէ։ - Ձեր առջև հազվագյուտ իրադարձություն, ինչպես արևի խավարումը, երբ հակադարձը համընկավ սկզբնական մատրիցի հետ:

Մնում է գրել մատրիցայի կանոնական տարրալուծումը.

Համակարգը կարելի է լուծել տարրական փոխակերպումների միջոցով, և հաջորդ օրինակներում մենք կօգտագործենք այս մեթոդը։ Բայց այստեղ «դպրոցական» մեթոդը շատ ավելի արագ է աշխատում։ 3-րդ հավասարումից կարտահայտենք՝ - երկրորդ հավասարման մեջ կփոխարինենք.

Քանի որ առաջին կոորդինատը զրո է, մենք ստանում ենք մի համակարգ, որի յուրաքանչյուր հավասարումից բխում է.

Եւ կրկին ուշադրություն դարձրեք գծային կախվածության պարտադիր առկայությանը... Եթե ​​դուք ստանում եք միայն չնչին լուծում , ապա կամ սեփական արժեքը սխալ է հայտնաբերվել, կամ համակարգը կազմվել/լուծվել է սխալմամբ։

Կոմպակտ կոորդինատները իմաստ են տալիս

Սեփական վեկտոր:

Եվ ևս մեկ անգամ մենք ստուգում ենք, որ գտնված լուծումը բավարարում է համակարգի յուրաքանչյուր հավասարումը... Հետևյալ պարբերություններում և հաջորդ առաջադրանքներում ես խորհուրդ եմ տալիս այս ցանկությունն ընդունել որպես պարտադիր կանոն:

2) Սեփական արժեքի համար նույն սկզբունքով ստանում ենք հետևյալ համակարգը.

Համակարգի 2-րդ հավասարումից արտահայտում ենք՝ - փոխարինել երրորդ հավասարմամբ.

Քանի որ «զետա» կոորդինատը հավասար է զրոյի, ուրեմն ստանում ենք համակարգ, որի յուրաքանչյուր հավասարումից բխում է գծային կախվածություն։

Թող

Մենք ստուգում ենք, որ լուծումը բավարարում է համակարգի բոլոր հավասարումները:

Այսպիսով, սեփական վեկտորը հետևյալն է.

3) Եվ, վերջապես, համակարգը համապատասխանում է սեփական արժեքին.

Երկրորդ հավասարումը թվում է ամենապարզը, ուստի մենք արտահայտում ենք դրանից և այն փոխարինում 1-ին և 3-րդ հավասարումներով.

Ամեն ինչ լավ է. առաջացել է գծային հարաբերություն, որը մենք փոխարինում ենք արտահայտությամբ.

Արդյունքում «x»-ը և «igrek»-ը արտահայտվել են «z»-ի միջոցով: Գործնականում անհրաժեշտ չէ հասնել հենց այդպիսի հարաբերությունների, որոշ դեպքերում ավելի հարմար է արտահայտվել ինչպես միջոցով, այնպես էլ միջոցով: Կամ նույնիսկ «գնացք», օրինակ՝ «X»-ը «իգրեկ»-ով, իսկ «իգրեկ»-ը՝ «զ»-ով:

Ենթադրենք, ապա.

Մենք ստուգում ենք, որ գտնված լուծումը բավարարում է համակարգի յուրաքանչյուր հավասարումը և գրում երրորդ սեփական վեկտորը

Պատասխանելսեփական վեկտորներ:

Երկրաչափական առումով այս վեկտորները սահմանում են երեք տարբեր տարածական ուղղություններ: («Այնտեղ և նորից հետ»)ըստ որի գծային փոխակերպումոչ զրոյական վեկտորները (սեփական վեկտորները) վերածում է նրանց համագծի վեկտորների:

Եթե ​​պայմանը պահանջվում է կանոնական տարրալուծում գտնելու համար, ապա դա հնարավոր է այստեղ, քանի որ տարբեր սեփական արժեքները համապատասխանում են տարբեր գծային անկախ սեփական վեկտորներին: Մատրիցայի կազմում դրանց կոորդինատներից՝ անկյունագծային մատրիցը -ից համապատասխանսեփական արժեքներ և գտնել հակադարձ մատրիցա .

Եթե ​​պայմանի համաձայն պետք է գրել Գծային փոխակերպման մատրիցա սեփական վեկտորների հիմքում, ապա պատասխանը տալիս ենք ձևով։ Տարբերություն կա, և տարբերությունը զգալի է։Այս մատրիցայի համար «de» մատրիցն է:

Անկախ լուծման համար ավելի պարզ հաշվարկներով խնդիր.

Օրինակ 5

Գտե՛ք մատրիցով տրված գծային փոխակերպման սեփական վեկտորները

Սեփական արժեքները գտնելիս աշխատեք գործը չհասցնել 3-րդ աստիճանի բազմանդամի։ Բացի այդ, ձեր համակարգերի լուծումները կարող են տարբերվել իմ լուծումներից. այստեղ ոչ մի անորոշություն չկա. և ձեր գտած վեկտորները կարող են տարբերվել նմուշային վեկտորներից մինչև դրանց համապատասխան կոորդինատների համաչափությունը: Օրինակ, և. Պատասխանը ձևով ներկայացնելն ավելի էսթետիկ է, բայց նորմալ է, եթե կանգ առնես երկրորդ տարբերակի վրա։ Այնուամենայնիվ, ամեն ինչի համար կան ողջամիտ սահմաններ, տարբերակն այլևս այնքան էլ լավ տեսք չունի:

Դասի վերջում առաջադրանքի մոտավոր վերջնական նմուշ.

Ինչպե՞ս լուծել խնդիրը բազմաթիվ սեփական արժեքների դեպքում:

Ընդհանուր ալգորիթմը մնում է նույնը, բայց այն ունի իր առանձնահատկությունները, և խորհուրդ է տրվում լուծման որոշ հատվածներ պահպանել ավելի խիստ ակադեմիական ոճով.

Օրինակ 6

Գտեք սեփական արժեքներ և սեփական վեկտորներ

Լուծում

Իհարկե, մենք մեծատառով գրում ենք առասպելական առաջին սյունակը.

Եվ քառակուսի եռանկյունը գործակցելուց հետո.

Արդյունքում ստացվում են սեփական արժեքներ, որոնցից երկուսը բազմապատիկ են:

Գտնենք սեփական վեկտորները.

1) Միայնակ զինվորի հետ գործ կունենանք «պարզեցված» սխեմայով.

Վերջին երկու հավասարումներից հստակ երևում է հավասարությունը, որն ակնհայտորեն պետք է փոխարինել համակարգի 1-ին հավասարմամբ.

Ավելի լավ համադրություն չկա.
Սեփական վեկտոր:

2-3) Այժմ կրակեք մի քանի ժամապահների վրա: Այս դեպքում կարող է ստացվել կա՛մ երկու, կա՛մ մեկըսեփական վեկտոր. Անկախ արմատների բազմակիությունից՝ մենք արժեքը փոխարինում ենք որոշիչով որը մեզ բերում է հետևյալը գծային հավասարումների միատարր համակարգ:

Սեփական վեկտորները հենց վեկտորներ են
հիմնարար որոշումների համակարգ

Փաստորեն, ամբողջ դասի ընթացքում մենք զբաղվում էինք միայն հիմնարար համակարգի վեկտորները գտնելով: Պարզապես այս տերմինն առայժմ առանձնապես պահանջված չէր։ Ի դեպ, այն խելացի ուսանողները, որոնք սայթաքեցին թեման կամուֆլյաժ վերարկուներով միատարր հավասարումներհիմա ստիպված կլինեն ուտել այն:

Միակ գործողությունը լրացուցիչ տողերի ջնջումն էր։ Արդյունքը մեկ-երեք մատրիցան է, որի մեջտեղում կա պաշտոնական «դահլիճ»:
- հիմնական փոփոխական, - ազատ փոփոխականներ: Կան երկու ազատ փոփոխականներ, հետևաբար, Հիմնարար համակարգի վեկտորները նույնպես երկու են.

Եկեք արտահայտենք հիմնական փոփոխականը ազատ փոփոխականներով. «x»-ի դիմաց զրոյական գործակիցը թույլ է տալիս վերցնել բացարձակապես ցանկացած արժեք (ինչը հստակ երևում է հավասարումների համակարգից):

Այս խնդրի համատեքստում ավելի հարմար է ընդհանուր լուծումը գրել ոչ թե անընդմեջ, այլ սյունակով.

Սեփական վեկտորը համապատասխանում է զույգին.
Սեփական վեկտորը համապատասխանում է զույգին.

Նշում Բարդ ընթերցողները կարող են ընտրել այս վեկտորները և բանավոր՝ պարզապես վերլուծելով համակարգը , բայց այստեղ անհրաժեշտ է որոշակի գիտելիքներ. կան երեք փոփոխականներ. համակարգի մատրիցային դասակարգում- միավոր, ինչը նշանակում է հիմնարար որոշումների համակարգբաղկացած է 3 - 1 = 2 վեկտորից: Այնուամենայնիվ, հայտնաբերված վեկտորները կատարելապես տեսանելի են նույնիսկ առանց այդ գիտելիքի, զուտ ինտուիտիվ մակարդակով: Այս դեպքում երրորդ վեկտորը կգրվի նույնիսկ «ավելի գեղեցիկ»: Այնուամենայնիվ, զգուշացնում եմ ձեզ, որ մեկ այլ օրինակում պարզ ընտրությունը կարող է չհայտնվել, ինչի պատճառով էլ հերքումը նախատեսված է փորձառու մարդկանց համար։ Բացի այդ, ինչո՞ւ չընդունել, ասենք, որպես երրորդ վեկտոր։ Ի վերջո, նրա կոորդինատները նույնպես բավարարում են համակարգի յուրաքանչյուր հավասարումը և վեկտորները գծային անկախ. Այս տարբերակը, սկզբունքորեն, հարմար է, բայց «ծուռ», քանի որ «մյուս» վեկտորը հիմնարար համակարգի վեկտորների գծային համակցություն է:

Պատասխանելսեփական արժեքներ:, սեփական վեկտորներ:

Նմանատիպ օրինակ ինքնուրույն լուծման համար.

Օրինակ 7

Գտեք սեփական արժեքներ և սեփական վեկտորներ

Դասի վերջում ավարտելու կոպիտ օրինակ.

Հարկ է նշել, որ և՛ 6-րդ, և՛ 7-րդ օրինակներում ստացվում է գծային անկախ սեփական վեկտորների եռակի, և, հետևաբար, սկզբնական մատրիցը ներկայացված է կանոնական տարրալուծման մեջ: Բայց նման ազնվամորիները ոչ բոլոր դեպքերում են լինում.

Օրինակ 8

ԼուծումԿազմել և լուծել բնորոշ հավասարումը.

Մենք բացում ենք որոշիչը առաջին սյունակով.

Հետագա պարզեցումները կատարվում են դիտարկված մեթոդի համաձայն՝ խուսափելով 3-րդ աստիճանի բազմանդամից.

- սեփական արժեքներ.

Գտնենք սեփական վեկտորները.

1) Արմատի հետ կապված դժվարություններ չկան.

Մի զարմացեք, բացի հանդերձանքից, օգտագործվում են նաև փոփոխականներ՝ այստեղ տարբերություն չկա։

3-րդ հավասարումից մենք կարտահայտենք - 1-ին և 2-րդ հավասարումներում կփոխարինենք.

Երկու հավասարումներից էլ հետևում է.

Ուրեմն թող.

2-3) Բազմաթիվ արժեքների համար մենք ստանում ենք համակարգը .

Եկեք գրենք համակարգի մատրիցը և, օգտագործելով տարրական փոխակերպումներ, բերենք այն աստիճանական ձևի.

Առաջին մասը սահմանում է նվազագույն դրույթները քիմիոմետրիկությունը հասկանալու համար, իսկ երկրորդ մասը պարունակում է փաստեր, որոնք դուք պետք է իմանաք բազմաչափ վերլուծության մեթոդները ավելի խորը հասկանալու համար: Ներկայացումը պատկերված է Excel-ի աշխատանքային գրքում կատարված օրինակներով: Matrix.xlsորը ուղեկցում է այս փաստաթղթին:

Օրինակների հղումները տեքստում տեղադրվում են որպես Excel օբյեկտներ: Այս օրինակներն իրենց բնույթով վերացական են, դրանք ոչ մի կերպ կապված չեն անալիտիկ քիմիայի խնդիրների հետ։ Քիմիոմետրիկության մեջ մատրիցային հանրահաշվի կիրառման իրական օրինակները դիտարկված են քիմիաչափական տարբեր կիրառություններին նվիրված այլ տեքստերում:

Անալիտիկ քիմիայում կատարված չափումների մեծ մասը ուղղակի չեն, այլ անուղղակի... Սա նշանակում է, որ փորձի ժամանակ ցանկալի անալիտի C արժեքի փոխարեն (կոնցենտրացիան) ստացվում է մեկ այլ արժեք. x(ազդանշան) կապված, բայց ոչ հավասար C-ին, այսինքն. x(C) ≠ C. Որպես կանոն, կախվածության տեսակը x(C) հայտնի չէ, սակայն, բարեբախտաբար, անալիտիկ քիմիայում, չափումների մեծ մասը համամասնական է: Սա նշանակում է, որ C-ի կոնցենտրացիայի աճով աանգամ, X ազդանշանը կաճի նույնքանով: x(աԳ) = կացին(C). Բացի այդ, ազդանշանները նաև հավելում են, այնպես որ C 1 և C 2 կոնցենտրացիաներով երկու նյութեր պարունակող նմուշից ազդանշանը հավասար կլինի յուրաքանչյուր բաղադրիչի ազդանշանների գումարին, այսինքն. x(C 1 + C 2) = x(C 1) + x(C 2): Համաչափությունն ու հավելյալությունը միասին տալիս են գծայինություն... Գծայինության սկզբունքը լուսաբանելու համար կան բազմաթիվ օրինակներ, սակայն բավական է նշել ամենաակնառու օրինակներից երկուսը` քրոմատագրությունը և սպեկտրոսկոպիան: Անալիտիկ քիմիայի փորձի երկրորդ հատկանիշն է բազմալիքային... Ժամանակակից վերլուծական սարքավորումները միաժամանակ չափում են ազդանշանները բազմաթիվ ալիքների համար: Օրինակ, լույսի հաղորդման ինտենսիվությունը չափվում է միանգամից մի քանի ալիքի երկարությունների համար, այսինքն. միջակայք. Հետևաբար, փորձի ժամանակ մենք գործ ունենք բազմաթիվ ազդանշանների հետ x 1 , x 2 ,...., x n, որը բնութագրում է ուսումնասիրվող համակարգում առկա նյութերի C 1, C 2, ..., C m կոնցենտրացիաների հավաքածուն:

Բրինձ. 1 Սպեկտրա

Այսպիսով, վերլուծական փորձը բնութագրվում է գծայինությամբ և բազմաչափությամբ: Հետևաբար, հարմար է փորձարարական տվյալները դիտարկել որպես վեկտորներ և մատրիցներ և շահարկել դրանք՝ օգտագործելով մատրիցային հանրահաշվի ապարատը։ Այս մոտեցման արդյունավետությունը ցույց է տրված օրինակով, որը ցույց է տալիս երեք սպեկտրներ, որոնք գրանցված են 200 ալիքի երկարությունների համար 4000-ից 4796 սմ – 1: Առաջին ( x 1) և երկրորդը ( x 2) սպեկտրներ են ստացվել ստանդարտ նմուշների համար, որոնցում հայտնի է երկու նյութերի A և B կոնցենտրացիան՝ առաջին նմուշում [A] = 0,5, [B] = 0,1, իսկ երկրորդ նմուշում [A] = 0,2, [B. ] = 0,6: Ինչ կարելի է ասել նոր, անհայտ նմուշի մասին, որի սպեկտրը նշանակված է x 3 ?

Դիտարկենք երեք փորձարարական սպեկտր x 1 , x 2 և x 3-ը որպես 200 չափման երեք վեկտոր: Գծային հանրահաշվի միջոցով կարելի է հեշտությամբ ցույց տալ, որ x 3 = 0.1 x 1 +0.3 x 2; հետևաբար, երրորդ նմուշն ակնհայտորեն պարունակում է միայն A և B նյութեր [A] = 0,5 × 0,1 + 0,2 × 0,3 = 0,11 և [B] = 0,1 × 0,1 + 0,6 × 0,3 = 0,19 կոնցենտրացիաներում:

1. Հիմնական տեղեկատվություն

1.1 Մատրիցներ

Մատրիցակոչվում է թվերի ուղղանկյուն աղյուսակ, օրինակ

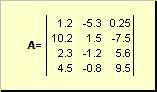
Բրինձ. 2 Մատրիցա

Մատրիցները նշված են թավ մեծատառերով ( Ա), իսկ դրանց տարրերը՝ համապատասխան փոքրատառերը՝ ինդեքսներով, այսինքն. ա ij. Առաջին ինդեքսը համարակալում է տողերը, իսկ երկրորդը՝ սյունակները։ Քիմիոմետրիկայի մեջ ընդունված է ինդեքսի առավելագույն արժեքը նշել նույն տառով, ինչ ինդեքսը, բայց մեծատառով։ Հետևաբար մատրիցը Ակարելի է գրել նաև որպես ( ա ij , ես = 1,..., Ի; ժ = 1,..., Ջ): Օրինակում ներկայացված մատրիցայի համար Ի = 4, Ջ= 3 և ա 23 = −7.5.

Զույգ թվեր Իև Ջկոչվում է մատրիցայի չափ և նշվում է որպես Ի× Ջ... Քիմիոմետրիկության մեջ մատրիցայի օրինակ է ստացված սպեկտրների բազմությունը Ինմուշների վրա Ջալիքի երկարություններ.

1.2. Պարզ մատրիցային գործողություններ

Մատրիցները կարող են բազմապատկել թվերով... Այս դեպքում յուրաքանչյուր տարր բազմապատկվում է այս թվով: Օրինակ -

Բրինձ. 3 Մատրիցային բազմապատկում թվով

Նույն չափման երկու մատրիցա կարող է լինել տարրական առումով ծալելև հանել... Օրինակ,

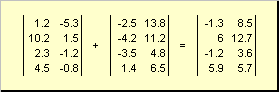
Բրինձ. 4 Մատրիցայի ավելացում

Թվով բազմապատկելու և գումարման արդյունքում ստացվում է նույն չափի մատրիցա։

Զրոյական մատրիցը զրոյից բաղկացած մատրից է: Նշվում է Օ... Ակնհայտ է, որ Ա+Օ = Ա, Ա−Ա = Օև 0 Ա = Օ.

Մատրիցը կարող է լինել փոխադրել... Այս գործողության ընթացքում մատրիցը շրջվում է, այսինքն. տողերն ու սյունակները փոխանակվում են: Տրանսպոզիցիան նշվում է կաթվածով, Ա«կամ ինդեքս Ատ. Այսպիսով, եթե Ա = {ա ij , ես = 1,..., Ի; ժ = 1,...,Ջ), ապա Ա t = ( ա ջի , ժ = 1,...,Ջ; i = 1, ..., Ի): օրինակ

Բրինձ. 5 Փոխադրել մատրիցը

Ակնհայտ է, որ ( Ատ) տ = Ա, (Ա+Բ) տ = Ա t + Բտ.

1.3. Մատրիցային բազմապատկում

Մատրիցները կարող են բազմապատկել, բայց միայն այն դեպքում, եթե դրանք ունենան համապատասխան չափսեր։ Թե ինչու է դա այդպես, պարզ կլինի սահմանումից: Մատրիցայի արտադրյալը Ա, չափս Ի× Կ, և մատրիցներ Բ, չափս Կ× Ջկոչվում է մատրիցա Գ, չափս Ի× Ջորի տարրերը թվերն են

Այսպիսով, արտադրել ԱԲանհրաժեշտ է, որ ձախ մատրիցայի սյունակների քանակը Ահավասար էր աջ մատրիցի տողերի թվին Բ... Մատրիցային արտադրանքի օրինակ.

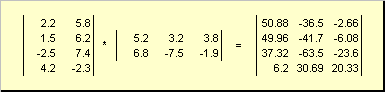
Նկ. 6 Մատրիցային արտադրանք

Մատրիցային բազմապատկման կանոնը կարելի է ձևակերպել հետևյալ կերպ. Մատրիցայի տարր գտնելու համար Գկանգնած խաչմերուկում ես-րդ գիծը և ժ-րդ սյունակ ( գ ij) պետք է բազմապատկել տարր առ տարր եսառաջին մատրիցայի րդ շարքը Ավրա ժերկրորդ մատրիցայի սյունակ Բև ավելացրեք բոլոր արդյունքները: Այսպիսով, ցույց տրված օրինակում երրորդ տողից և երկրորդ սյունակից տարրը ստացվում է որպես երրորդ շարքի տարրական արտադրյալների գումար։ Աև երկրորդ սյունակը Բ

Նկ. 7 Մատրիցային արտադրանքի տարր

Մատրիցների արտադրյալը կախված է հերթականությունից, այսինքն. ԱԲ ≠ ԲԱ, եթե միայն չափման նկատառումներով։ Ասվում է, որ այն ոչ փոխադարձ է: Այնուամենայնիվ, մատրիցային արտադրանքները ասոցիատիվ են: Դա նշանակում է որ ABC = (ԱԲ)Գ = Ա(մ.թ.ա): Բացի այդ, այն նաև բաշխիչ է, այսինքն. Ա(Բ+Գ) = ԱԲ+AC... Ակնհայտ է, որ ԱՕ = Օ.

1.4. Քառակուսի մատրիցներ

Եթե ​​մատրիցայի սյունակների թիվը հավասար է նրա տողերի թվին ( Ի = J = N), ապա նման մատրիցը կոչվում է քառակուսի: Այս բաժնում մենք կքննարկենք միայն այդպիսի մատրիցները: Այս մատրիցներից կարելի է առանձնացնել հատուկ հատկություններով մատրիցներ։

Միայնակմատրիցա (նշված է ես,և երբեմն Ե) մատրից է, որտեղ բոլոր տարրերը հավասար են զրոյի, բացառությամբ անկյունագծերի, որոնք հավասար են 1-ի, այսինքն.

Ակնհայտորեն Աի = ԻԱ = Ա.

Մատրիցը կոչվում է անկյունագծայինեթե նրա բոլոր տարրերը, բացառությամբ շեղանկյունների ( ա ii) հավասար են զրոյի։ օրինակ

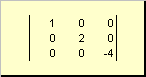
Բրինձ. 8 Անկյունագծային մատրիցա

Մատրիցա Ակոչվում է գագաթ եռանկյունաձեւեթե շեղանկյունից ներքեւ նրա բոլոր տարրերը հավասար են զրոյի, այսինքն. ա ij= 0, համար ես>ժ... օրինակ

Բրինձ. 9 Վերին եռանկյունաձև մատրիցա

Ստորին եռանկյուն մատրիցը սահմանվում է նույն կերպ:

Մատրիցա Ականչեց սիմետրիկ, եթե Ա t = Ա... Այլ կերպ ասած ա ij = ա ջի... օրինակ

Բրինձ. 10 Սիմետրիկ մատրիցա

Մատրիցա Ականչեց ուղղանկյուն, եթե

Ատ Ա = ԱԱ t = Ի.

Մատրիցը կոչվում է նորմալեթե

1.5. Հետք և որոշիչ

Հետևելովքառակուսի մատրիցա Ա(նշվում է Tr-ով Ա) կամ Sp ( Ա)) նրա անկյունագծային տարրերի գումարն է,

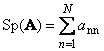
Օրինակ,

Բրինձ. 11 Մատրիցային հետք

Ակնհայտ է, որ

Sp (α Ա) = α Sp ( Ա) և

Սպ ( Ա+Բ) = Սպ ( Ա) + Սպ ( Բ).

Կարելի է ցույց տալ, որ

Սպ ( Ա) = Սպ ( Ա t), Sp ( Ի) = Ն,

և նաև այն

Սպ ( ԱԲ) = Սպ ( ԲԱ).

Քառակուսի մատրիցայի մեկ այլ կարևոր բնութագիր այն է որոշիչ(նշվում է det-ով ( Ա)): Ընդհանուր դեպքում որոշիչի որոշումը բավականին դժվար է, ուստի մենք կսկսենք ամենապարզ տարբերակից՝ մատրիցով Աչափս (2 × 2): Հետո

(3 × 3) մատրիցայի համար որոշիչը կլինի

Մատրիցայի դեպքում ( Ն× Ն) որոշիչը հաշվարկվում է որպես 1 2 3 ... Ն= Ն! պայմաններ, որոնցից յուրաքանչյուրը հավասար է

Ցուցանիշներ կ 1 , կ 2 ,..., կ Նսահմանվում են որպես բոլոր հնարավոր պատվիրված փոխարկումներ rթվեր հավաքածուում (1, 2, ..., Ն): Մատրիցայի որոշիչի հաշվարկը բարդ ընթացակարգ է, որը գործնականում իրականացվում է հատուկ ծրագրերի միջոցով: Օրինակ,

Բրինձ. 12 Մատրիցային որոշիչ

Մենք միայն նշում ենք ակնհայտ հատկությունները.

դետ ( Ի) = 1, det ( Ա) = դետ ( Ատ),

դետ ( ԱԲ) = դետ ( Ա) դետ ( Բ).

1.6. Վեկտորներ

Եթե ​​մատրիցը բաղկացած է միայն մեկ սյունակից ( Ջ= 1), ապա կոչվում է այդպիսի օբյեկտ վեկտոր... Ավելի ճիշտ՝ սյունակի վեկտոր։ օրինակ

Կարելի է նաև դիտարկել, օրինակ, մեկ տողից բաղկացած մատրիցներ

Այս օբյեկտը նույնպես վեկտոր է, բայց շարքի վեկտոր... Տվյալները վերլուծելիս կարևոր է հասկանալ, թե որ վեկտորների հետ գործ ունենք՝ սյունակների, թե տողերի: Այսպիսով, մեկ նմուշի համար վերցված սպեկտրը կարելի է համարել որպես տող վեկտոր: Այնուհետև բոլոր նմուշների համար որոշակի ալիքի երկարության սպեկտրային ինտենսիվությունների բազմությունը պետք է դիտարկվի որպես սյունակի վեկտոր:

Վեկտորի չափը նրա տարրերի քանակն է։

Հասկանալի է, որ ցանկացած սյունակային վեկտոր կարող է փոխակերպվել տողի վեկտորի փոխադրման միջոցով, այսինքն.

Այն դեպքերում, երբ վեկտորի ձևը հատուկ չի նշվում, այլ ուղղակի վեկտոր է ասվում, ապա դրանք նշանակում են սյունակային վեկտոր։ Մենք նույնպես կպահպանենք այս կանոնը. Վեկտորը նշվում է փոքրատառ ուղիղ թավ տառով: Զրոյական վեկտորը վեկտոր է, որի բոլոր տարրերը զրո են: Նշանակված է 0 .

1.7. Հիմնական գործողություններ վեկտորների հետ

Վեկտորները կարելի է ավելացնել և բազմապատկել թվերով այնպես, ինչպես մատրիցները: Օրինակ,

Բրինձ. 13 Վեկտորային գործողություններ

Երկու վեկտոր xև yկոչվում են համաչափեթե կա α այնպիսի թիվ, որ

1.8. Վեկտորների արտադրանք

Նույն հարթության երկու վեկտոր Նկարելի է բազմապատկել։ Թող լինի երկու վեկտոր x = (x 1 , x 2 ,...,xՆ) տ և y = (y 1 , y 2 ,...,yՆ) տ. Ղեկավարվելով «տող առ սյունակ» բազմապատկման կանոնով՝ մենք կարող ենք դրանցից կազմել երկու արտադրյալ. xտ yև xyտ. Առաջին կտոր

կանչեց սկալյարկամ ներքին... Դրա արդյունքը մի թիվ է: Այն նաև օգտագործում է նշումը ( x,y)= xտ y... Օրինակ,

Բրինձ. 14 Ներքին արտադրանք (կետային արտադրանք)

Երկրորդ կտոր

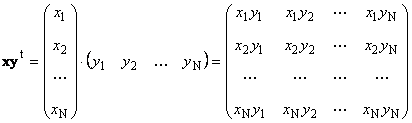
կանչեց արտաքին... Դրա արդյունքը չափումների մատրիցն է ( Ն× Ն): Օրինակ,

Բրինձ. 15 Արտաքին աշխատանք

Վեկտորները, որոնց սկալյար արտադրյալը հավասար է զրոյի, կոչվում են ուղղանկյուն.

1.9. Վեկտորի նորմ

Վեկտորի սկալյար արտադրյալն ինքնին կոչվում է սկալյար քառակուսի: Այս արժեքը

սահմանում է քառակուսի երկարությունըվեկտոր x... Երկարությունը նշելու համար (նաև կոչվում է նորմըվեկտոր), օգտագործվում է նշումը

Օրինակ,

Բրինձ. 16 Վեկտորային նորմ

Միավոր երկարության վեկտոր (|| x|| = 1) կոչվում է նորմալացված: Ոչ զրոյական վեկտոր ( x ≠ 0 ) կարելի է նորմալացնել՝ բաժանելով երկարության վրա, այսինքն. x = ||x|| (x /||x||) = ||x|| ե... Այստեղ ե = x /||x|| նորմալացված վեկտորն է:

Վեկտորները կոչվում են օրթոնորմալ, եթե դրանք բոլորը նորմալացված են և զույգերով ուղղանկյուն:

1.10. Անկյուն վեկտորների միջև

Կետային արտադրանքը սահմանում է և ներարկումφ երկու վեկտորների միջև xև y

Եթե ​​վեկտորները ուղղանկյուն են, ապա cosφ = 0 և φ = π / 2, իսկ եթե դրանք համագիծ են, ապա cosφ = 1 և φ = 0:

1.11. Մատրիցայի վեկտորային ներկայացում

Յուրաքանչյուր մատրիցա Աչափը Ի× Ջկարող է ներկայացվել որպես վեկտորների մի շարք

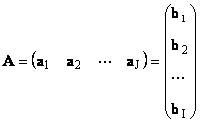
Այստեղ յուրաքանչյուր վեկտոր ա ժէ ժ-րդ սյունակը և տողի վեկտորը բ եսէ ես- մատրիցայի-րդ շարքը Ա

1.12. Գծային կախված վեկտորներ

Նույն չափի վեկտորներ ( Ն) կարելի է ավելացնել և բազմապատկել թվով, ինչպես մատրիցները։ Արդյունքը կլինի նույն հարթության վեկտորը: Թող լինեն նույն հարթության մի քանի վեկտորներ x 1 , x 2 ,...,x K և նույն թվով α α 1, α 2, ..., α թվեր Կ... Վեկտոր

y= α 1 x 1 + α 2 x 2 + ... + α Կ x Կ

կանչեց գծային համադրությունվեկտորներ x կ .

Եթե ​​կան α ոչ զրոյական թվեր կ ≠ 0, կ = 1,..., Կ, ինչ y = 0 , ապա վեկտորների նման մի շարք x կկանչեց գծային կախված... Հակառակ դեպքում, վեկտորները կոչվում են գծային անկախ: Օրինակ վեկտորները x 1 = (2, 2) տ և x 2 = (−1, −1) t են գծային կախված, քանի որ x 1 +2x 2 = 0

1.13. Մատրիցային դասակարգում

Դիտարկենք մի շարք Կվեկտորներ x 1 , x 2 ,...,x Կչափերը Ն... Վեկտորների այս համակարգի աստիճանը գծային անկախ վեկտորների առավելագույն քանակն է: Օրինակ, հավաքածուի մեջ

կան միայն երկու գծային անկախ վեկտորներ, օրինակ x 1 և x 2, ուստի նրա վարկանիշը 2 է:

Ակնհայտ է, որ եթե հավաքածուում ավելի շատ վեկտորներ կան, քան դրանց չափերը ( Կ>Ն), ապա դրանք անպայմանորեն գծային կախված են։

Ըստ մատրիցայի աստիճանի(նշվում է աստիճանով ( Ա)) կոչվում է վեկտորների համակարգի աստիճան, որից այն բաղկացած է։ Չնայած ցանկացած մատրիցա կարող է ներկայացվել երկու ձևով (սյունակի վեկտորներ կամ տողեր), դա չի ազդում դասակարգման արժեքի վրա, քանի որ

1.14. հակադարձ մատրիցա

Քառակուսի մատրիցա Ակոչվում է ոչ այլասերված, եթե ունի եզակի հակադարձմատրիցա Ա-1 պայմանավորված պայմաններով

ԱԱ −1 = Ա −1 Ա = Ի.

Հակադարձ մատրիցա գոյություն չունի բոլոր մատրիցների համար: Ոչ այլասերվածության համար անհրաժեշտ և բավարար պայման է

դետ ( Ա) ≠ 0 կամ աստիճան ( Ա) = Ն.

Matrix inversion-ը բարդ ընթացակարգ է, որի համար կան հատուկ ծրագրեր։ Օրինակ,

Բրինձ. 17 Մատրիցային ինվերսիա

Ներկայացնենք բանաձևեր ամենապարզ դեպքի համար՝ 2 × 2 մատրիցներ

Եթե ​​մատրիցներ Աև Բոչ այլասերված, ուրեմն

(ԱԲ) −1 = Բ −1 Ա −1 .

1.15. Կեղծ հակադարձ մատրիցա

Եթե ​​մատրիցը Ադեգեներատ է, և հակադարձ մատրիցը գոյություն չունի, ապա որոշ դեպքերում կարող եք օգտագործել կեղծ հակադարձմատրիցա, որը սահմանվում է որպես այդպիսի մատրիցա Ա+ դա

ԱԱ + Ա = Ա.

Կեղծ հակադարձ մատրիցը միակը չէ, և դրա տեսակը կախված է կառուցման մեթոդից: Օրինակ, ուղղանկյուն մատրիցայի համար կարող եք օգտագործել Moore-Penrose մեթոդը:

Եթե ​​սյունակների թիվը տողերի քանակից քիչ է, ապա

Ա + =(Ատ Ա) −1 Ատ

Օրինակ,

Բրինձ. 17ա Մատրիցային կեղծ ինվերսիա

Եթե ​​սյունակների թիվը տողերի քանակից մեծ է, ապա

Ա + =Ատ ( ԱԱտ) −1

1.16. Վեկտորի բազմապատկում մատրիցով

Վեկտոր xկարելի է բազմապատկել մատրիցով Ահարմար հարթություն. Այս դեպքում սյունակի վեկտորը բազմապատկվում է աջ կողմում Կացինիսկ տողի վեկտորը ձախ կողմում է xտ Ա... Եթե ​​վեկտորի չափը Ջ, և մատրիցայի չափը Ի× Ջապա արդյունքը չափման վեկտոր է Ի... Օրինակ,

Բրինձ. 18 Մատրիցային բազմապատկման վեկտոր

Եթե ​​մատրիցը Ա- քառակուսի ( Ի× Ի), ապա վեկտորը y = Կացինունի նույն չափը, ինչ x... Ակնհայտ է, որ

Ա(α 1 x 1 + α 2 x 2) = α 1 Կացին 1 + α 2 Կացին 2 .

Հետևաբար, մատրիցները կարող են դիտվել որպես վեկտորների գծային փոխակերպումներ։ Մասնավորապես Իքս = x, Եզ = 0 .

2. Լրացուցիչ տեղեկություններ

2.1. Գծային հավասարումների համակարգեր

Թող Ա- մատրիցայի չափը Ի× Ջ, ա բ- չափման վեկտոր Ջ... Դիտարկենք հավասարումը

Կացին = բ

վեկտորի նկատմամբ x, չափերը Ի... Իրականում սա համակարգ է Իհետ գծային հավասարումներ Ջանհայտ x 1 ,...,x Ջ... Լուծումը կա, եթե և միայն այն դեպքում

աստիճան ( Ա) = կոչում ( Բ) = Ռ,

որտեղ Բընդլայնված չափման մատրիցա է Ի×( J + 1) բաղկացած մատրիցից Ալիցքավորված սյունակով բ, Բ = (Ա բ): Հակառակ դեպքում, հավասարումները անհամապատասխան են:

Եթե Ռ = Ի = Ջ, ապա լուծումը եզակի է

x = Ա −1 բ.

Եթե Ռ < Ի, ապա կան բազմաթիվ տարբեր լուծումներ, որոնք կարող են արտահայտվել գծային համակցության առումով Ջ−Ռվեկտորներ. Միատարր հավասարումների համակարգ Կացին = 0 քառակուսի մատրիցա Ա (Ն× Ն) ունի ոչ տրիվիալ լուծում ( x ≠ 0 ) եթե և միայն եթե det ( Ա) = 0. Եթե Ռ= կոչում ( Ա)<Նապա գոյություն ունենալ Ն−Ռգծային անկախ լուծումներ.

2.2. Երկգծային և քառակուսի ձևեր

Եթե Աքառակուսի մատրից է, և xև yհամապատասխան չափման վեկտորներ են, ապա ձևի սկալյար արտադրյալը xտ Այկանչեց երկգծայինմատրիցով սահմանված ձևը Ա... ժամը x = yարտահայտություն xտ Կացինկանչեց քառակուսիձեւը։

2.3. Դրական որոշակի մատրիցներ

Քառակուսի մատրիցա Ականչեց դրականորեն սահմանվածեթե որևէ ոչ զրոյական վեկտորի համար x ≠ 0 ,

xտ Կացին > 0.

Նմանապես, բացասաբար (xտ Կացին < 0), ոչ բացասական (xտ Կացին≥ 0) և ոչ դրական (xտ Կացին≤ 0) որոշակի մատրիցներ.

2.4. Չոլեսկու տարրալուծում

Եթե ​​սիմետրիկ մատրիցա Ադրական որոշակի է, ապա կա եզակի եռանկյուն մատրիցա Uդրական տարրերով, որոնց համար

Ա = Uտ U.

Օրինակ,

Բրինձ. 19 Չոլեսկու տարրալուծում

2.5. Բևեռային տարրալուծում

Թող Աչափումների ոչ այլասերված քառակուսի մատրից է Ն× Ն... Այնուհետև կա մեկ առ մեկ բևեռայիններկայացուցչություն

Ա = SR,

որտեղ Սոչ բացասական սիմետրիկ մատրից է, և Ռուղղանկյուն մատրիցա է: Մատրիցներ Սև Ռկարելի է հստակորեն սահմանել.

Ս 2 = ԱԱտ կամ Ս = (ԱԱտ) ½ և Ռ = Ս −1 Ա = (ԱԱտ) −1 Ա.

Օրինակ,

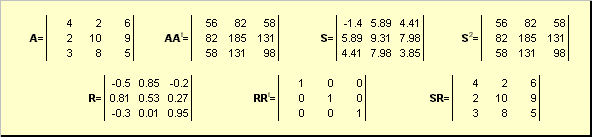
Բրինձ. 20 Բևեռային տարրալուծում

Եթե ​​մատրիցը Ադեգեներատ է, ապա ընդլայնումը եզակի չէ, մասնավորապես. Սդեռ մենակ, բայց Ռգուցե շատ. Բևեռային տարրալուծումը ներկայացնում է մատրիցը Աորպես սեղմման / ձգման համադրություն Սև շրջադարձ Ռ.

2.6. Սեփական վեկտորներ և սեփական արժեքներ

Թող Աքառակուսի մատրիցա է: Վեկտոր vկանչեց սեփական վեկտորըմատրիցներ Ա, եթե

Ավ = λ v,

որտեղ կոչվում է λ թիվը սեփական իմաստըմատրիցներ Ա... Այսպիսով, փոխակերպումը, որը կատարում է մատրիցը Ավեկտորի վրա v, վերածվում է պարզ ձգման կամ սեղմման λ գործակցով։ Սեփական վեկտորը որոշվում է մինչև α ≠ 0 հաստատունով բազմապատկելը, այսինքն. եթե vսեփական վեկտոր է, ապա α vնաև սեփական վեկտոր է:

2.7. Սեփական արժեքներ

Մատրիցա Ա, չափս ( Ն× Ն) չի կարող լինել ավելի քան Նսեփական արժեքներ. Նրանք բավարարում են բնորոշ հավասարում

դետ ( Ա − λ Ի) = 0,

որը հանրահաշվական հավասարում է Ն-րդ կարգը։ Մասնավորապես, 2 × 2 մատրիցայի համար բնորոշ հավասարումն ունի ձև

Օրինակ,

Բրինձ. 21 սեփական արժեքներ

Սեփական արժեքների բազմություն λ 1, ..., λ Նմատրիցներ Ականչեց սպեկտրը Ա.

Սպեկտրը ունի մի շարք հատկություններ. Մասնավորապես

դետ ( Ա) = λ 1 × ... × λ Ն, Սպ ( Ա) = λ 1 + ... + λ Ն.

Կամայական մատրիցայի սեփական արժեքները կարող են լինել բարդ թվեր, բայց եթե մատրիցը սիմետրիկ է ( Ա t = Ա), ապա դրա սեփական արժեքները իրական են:

2.8. Սեփական վեկտորներ

Մատրիցա Ա, չափս ( Ն× Ն) չի կարող լինել ավելի քան Նսեփական վեկտորներ, որոնցից յուրաքանչյուրը համապատասխանում է իր արժեքին: Որոշել սեփական վեկտորը v nդուք պետք է լուծեք միատարր հավասարումների համակարգ

(Ա − λ n Ի)v n = 0 .

Այն ունի ոչ տրիվիալ լուծում, քանի որ det ( Ա -λ n Ի) = 0.

Օրինակ,

Բրինձ. 22 սեփական վեկտորներ

Սիմետրիկ մատրիցայի սեփական վեկտորները ուղղանկյուն են:

ՀԱՄԱՍԵՆ ԳԾԱՅԻՆ ՀԱՎԱՍԱՐՈՒՄՆԵՐԻ ՀԱՄԱԿԱՐԳ

Միատարր գծային հավասարումների համակարգը ձևի համակարգ է

Հասկանալի է, որ այս դեպքում քանի որ Այս որակիչների սյունակներից մեկի բոլոր տարրերը հավասար են զրոյի:

Քանի որ անհայտները հայտնաբերվում են բանաձևերով , ապա այն դեպքում, երբ Δ ≠ 0, համակարգը ունի եզակի զրոյական լուծում x = y = զ= 0. Այնուամենայնիվ, շատ խնդիրներում հետաքրքրական է այն հարցը, թե արդյոք համասեռ համակարգը զրոյից տարբեր լուծումներ ունի:

Թեորեմ.Որպեսզի գծային միատարր հավասարումների համակարգն ունենա ոչ զրոյական լուծում, անհրաժեշտ և բավարար է, որ Δ ≠ 0:

Այսպիսով, եթե Δ ≠ 0 որոշիչը, ապա համակարգն ունի յուրահատուկ լուծում։ Եթե ​​Δ ≠ 0, ապա գծային միատարր հավասարումների համակարգն ունի լուծումների անսահման բազմություն։

Օրինակներ.

Մատրիցայի սեփական վեկտորները և սեփական արժեքները

Թող տրվի քառակուսի մատրիցա , X- ինչ-որ մատրից-սյունակ, որի բարձրությունը համընկնում է մատրիցայի կարգի հետ Ա. .

Շատ խնդիրների դեպքում պետք է հաշվի առնել հավասարումը X

որտեղ λ-ն ինչ-որ թիվ է: Պարզ է, որ ցանկացած λ-ի համար այս հավասարումն ունի զրոյական լուծում:

Այն λ թիվը, որի համար այս հավասարումը ունի ոչ զրոյական լուծումներ, կոչվում է սեփական իմաստըմատրիցներ Ա, ա Xնման λ-ի համար կոչվում է սեփական վեկտորըմատրիցներ Ա.

Գտե՛ք մատրիցի սեփական վեկտորը Ա... Այնքանով, որքանով Ե∙X = X, ապա մատրիցային հավասարումը կարող է վերաշարադրվել որպես կամ ... Ընդլայնված ձևով այս հավասարումը կարող է վերաշարադրվել որպես գծային հավասարումների համակարգ: Իսկապես .

Եւ, հետեւաբար

Այսպիսով, մենք ստացանք միատարր գծային հավասարումների համակարգ կոորդինատները որոշելու համար x 1, x 2, x 3վեկտոր X... Որպեսզի համակարգը ունենա ոչ զրոյական լուծումներ, անհրաժեշտ և բավարար է, որ համակարգի որոշիչը հավասար լինի զրոյի, այսինքն.

Սա 3-րդ աստիճանի հավասարում է λ-ի նկատմամբ։ Դա կոչվում է բնորոշ հավասարումմատրիցներ Աև ծառայում է սեփական արժեքները որոշելու λ.

Յուրաքանչյուր սեփական արժեք λ համապատասխանում է սեփական վեկտորի X, որոնց կոորդինատները որոշվում են համակարգից λ-ի համապատասխան արժեքով։

Օրինակներ.

ՎԵԿՏՈՐԱՅԻՆ ՀԱՇԱՀԻՐ. ՎԵԿՏՈՐԻ ՀԱՍԿԱՑՈՒԹՅՈՒՆ

Ֆիզիկայի տարբեր ճյուղեր ուսումնասիրելիս կան մեծություններ, որոնք ամբողջությամբ որոշվում են՝ նշելով դրանց թվային արժեքները, օրինակ՝ երկարությունը, մակերեսը, զանգվածը, ջերմաստիճանը և այլն։ Նման մեծությունները կոչվում են սկալյար։ Սակայն դրանցից բացի կան նաև մեծություններ, որոնց որոշման համար, բացի թվային արժեքից, անհրաժեշտ է նաև իմանալ դրանց ուղղությունը տարածության մեջ, օրինակ՝ մարմնի վրա ազդող ուժը, արագությունը և արագացումը. մարմնի, երբ այն շարժվում է տարածության մեջ, մագնիսական դաշտի ուժգնությունը տարածության տվյալ կետում և այլն: Նման մեծությունները կոչվում են վեկտոր:

Ներկայացնենք խիստ սահմանում.

Ուղղորդված հատվածանվանենք մի հատված, որի ծայրերի նկատմամբ հայտնի է, թե դրանցից որն է առաջինը, որը՝ երկրորդը։

Վեկտորկոչվում է ուղղորդված հատված, որն ունի որոշակի երկարություն, այսինքն. դա որոշակի երկարության հատված է, որի սահմանափակող կետերից մեկը վերցվում է որպես սկիզբ, իսկ մյուսը՝ վերջ։ Եթե Ա- վեկտորի սկիզբը, Բ- դրա վերջը, ապա վեկտորը նշվում է խորհրդանիշով, բացի այդ, վեկտորը հաճախ նշվում է մեկ տառով: Նկարում վեկտորը նշվում է գծի հատվածով, իսկ ուղղությունը՝ սլաքով:

Մոդուլկամ երկարությունվեկտորը այն սահմանող ուղղորդված հատվածի երկարությունն է: Նշվում է || կամ ||.

Այսպես կոչված զրոյական վեկտորը, որի սկիզբն ու վերջը համընկնում են, նույնպես կվերաբերվեն վեկտորներին: Նշված է. Զրոյական վեկտորը չունի որոշակի ուղղություն և նրա մոդուլը հավասար է զրոյի || = 0-ի:

Վեկտորները և կոչվում են համագիծեթե դրանք գտնվում են մեկ ուղիղ կամ զուգահեռ գծերի վրա։ Ավելին, եթե վեկտորները և նույն ուղղությամբ են, մենք կգրենք հակառակ ձևով.

Նույն հարթությանը զուգահեռ ուղիղ գծերի վրա գտնվող վեկտորները կոչվում են համակողմանի.

Երկու վեկտոր և կոչվում են հավասարեթե դրանք համագիծ են, հավասարապես ուղղորդված և հավասար երկարությամբ: Այս դեպքում գրեք.

Վեկտորների հավասարության սահմանումից հետևում է, որ վեկտորը կարող է փոխանցվել իրեն զուգահեռ՝ տեղադրելով իր ծագումը տարածության ցանկացած կետում։

օրինակ.

ԳԾԱՅԻՆ ԳՈՐԾՈՂՈՒԹՅՈՒՆՆԵՐ ՎԵԿՏՈՐՆԵՐԻ ՎՐԱ

1. Վեկտորը թվով բազմապատկելը.

   Վեկտորի արտադրյալը λ թվով այնպիսի նոր վեկտոր է, որ.

   Վեկտորի արտադրյալը նշվում է λ թվով:

   

   Օրինակ,վեկտոր է, որն ուղղված է վեկտորի նույն ուղղությամբ և ունի վեկտորի երկարությունը:

   Ներկայացված օպերացիան ունի հետևյալը հատկությունները:

2. Վեկտորների ավելացում.

   Թող և լինեն երկու կամայական վեկտորներ: Վերցրեք կամայական կետ Օև կառուցիր վեկտոր: Դրանից հետո, կետից Ամի կողմ դնել վեկտորը. Առաջին վեկտորի սկիզբը երկրորդի վերջի հետ կապող վեկտորը կոչվում է գումարըայս վեկտորներից և նշվում է .

   

   Վեկտորի ավելացման ձևակերպված սահմանումը կոչվում է զուգահեռագծի կանոն, քանի որ վեկտորների նույն գումարը կարելի է ստանալ հետևյալ կերպ. Մի կողմ դրեք կետից Օվեկտորներ և. Եկեք այս վեկտորների վրա կառուցենք զուգահեռագիծ OAVS... Քանի որ վեկտորները, վեկտորը, որը գագաթից գծված զուգահեռագծի անկյունագիծն է Օ, ակնհայտորեն կլինի վեկտորների գումարը։

   

   Հեշտ է ստուգել հետևյալը վեկտորի ավելացման հատկությունները.

3. Վեկտորների տարբերություն.

   Տրված վեկտորին համակողմանի վեկտորը, որը հավասար է երկարությամբ և հակառակ ուղղված, կոչվում է հակառակըվեկտորը վեկտորի համար և նշվում է. Հակառակ վեկտորը կարելի է համարել վեկտորը λ = –1: թվով բազմապատկելու արդյունք:

Անկյունագծային մատրիցներն ամենապարզն են։ Հարց է առաջանում՝ հնարավո՞ր է գտնել հիմք, որի դեպքում գծային օպերատորի մատրիցը կունենա անկյունագծային ձև։ Նման հիմք կա.
Թող տրվի R n գծային տարածություն և դրանում գործող գծային A օպերատոր; այս դեպքում A օպերատորն իր մեջ վերցնում է R n, այսինքն՝ A: R n → R n:

Սահմանում. Ոչ զրոյական վեկտորը կոչվում է A օպերատորի սեփական վեկտոր, եթե A օպերատորը վերածվում է նրան համագիծ վեկտորի, այսինքն. λ թիվը կոչվում է A օպերատորի սեփական արժեք կամ սեփական արժեք, որը համապատասխանում է սեփական վեկտորին։
Եկեք նշենք սեփական արժեքների և սեփական վեկտորների որոշ հատկություններ:
1. Սեփական վեկտորների ցանկացած գծային համակցություն նույն սեփական արժեքին համապատասխանող A օպերատորի λ նույն սեփական արժեքով սեփական վեկտորն է:
2. Սեփական վեկտորներ A օպերատորի զույգ-զույգ տարբեր սեփական արժեքներով λ 1, λ 2,…, λ m են գծային անկախ:
3. Եթե սեփական արժեքները λ 1 = λ 2 = λ m = λ, ապա λ սեփական արժեքը համապատասխանում է առավելագույնը m գծային անկախ սեփական վեկտորներին:

Այսպիսով, եթե կան n գծային անկախ սեփական վեկտորներ համապատասխանում են տարբեր սեփական արժեքներին λ 1, λ 2,…, λ n, ապա դրանք գծային անկախ են, հետևաբար, դրանք կարելի է ընդունել որպես R n տարածության հիմք: Եկեք գտնենք A գծային օպերատորի մատրիցայի ձևը նրա սեփական վեկտորների հիման վրա, որի համար մենք գործում ենք A օպերատորի կողմից հիմքի վեկտորների վրա. ապա .
Այսպիսով, գծային A օպերատորի մատրիցը իր սեփական վեկտորների հիման վրա ունի անկյունագծային ձև, իսկ A օպերատորի սեփական արժեքները գտնվում են անկյունագծի վրա:
Կա՞ մեկ այլ հիմք, որի դեպքում մատրիցը անկյունագծային է: Այս հարցի պատասխանը տրվում է հետևյալ թեորեմով.

Թեորեմ. Գծային A օպերատորի մատրիցը հիմքում (i = 1..n) ունի անկյունագծային ձև, եթե և միայն այն դեպքում, եթե հիմքի բոլոր վեկտորները A օպերատորի սեփական վեկտորներն են:

Սեփական արժեքներ և սեփական վեկտորներ գտնելու կանոն

Թող տրվի վեկտոր , որտեղ x 1, x 2, ..., x n վեկտորի կոորդինատներն են հիմքի նկատմամբ և գծային A օպերատորի սեփական վեկտորն է, որը համապատասխանում է λ սեփական արժեքին, այսինքն. Այս հարաբերությունը կարելի է գրել մատրիցային տեսքով

. (*)

Հավասարումը (*) կարելի է համարել որպես գտնելու հավասարում, ընդ որում՝ մեզ հետաքրքրում են ոչ տրիվիալ լուծումները, քանի որ սեփական վեկտորը չի կարող զրո լինել։ Հայտնի է, որ գծային հավասարումների միատարր համակարգի ոչ տրիվիալ լուծումներ գոյություն ունեն, եթե և միայն այն դեպքում, եթե det (A - λE) = 0: Այսպիսով, որպեսզի λ լինի A օպերատորի սեփական արժեքը, անհրաժեշտ և բավարար է, որ det (A - λE) = 0:
Եթե ​​(*) հավասարումը մանրամասն գրված է կոորդինատային ձևով, ապա մենք ստանում ենք գծային միատարր հավասարումների համակարգ.

(1)
որտեղ գծային օպերատորի մատրիցն է։

Համակարգը (1) ունի ոչ զրոյական լուծում, եթե նրա որոշիչը D-ն հավասար է զրոյի

Ստացել է սեփական արժեքները գտնելու հավասարում:
Այս հավասարումը կոչվում է բնորոշ հավասարում, իսկ ձախ կողմը կոչվում է A մատրիցի բնորոշ բազմանդամ (օպերատոր): Եթե բնորոշ բազմանդամը չունի իրական արմատներ, ապա A մատրիցը չունի սեփական վեկտորներ և չի կարող վերածվել անկյունագծային ձևի: .
Թող λ 1, λ 2,…, λ n լինեն բնորոշ հավասարման իրական արմատներ, և դրանց մեջ կարող են լինել բազմաթիվ արմատներ: Փոխարինելով այս արժեքներն իր հերթին (1) համակարգի՝ մենք գտնում ենք սեփական վեկտորները:

Օրինակ 12. Գծային A օպերատորը գործում է R 3-ում օրենքի համաձայն, որտեղ x 1, x 2, .., x n հիմքում ընկած վեկտորի կոորդինատներն են: , , ... Գտեք այս օպերատորի սեփական արժեքները և սեփական վեկտորները:
Լուծում. Մենք կառուցում ենք այս օպերատորի մատրիցը.
.
Մենք կազմում ենք սեփական վեկտորների կոորդինատների որոշման համակարգ.

Մենք կազմում ենք բնորոշ հավասարում և լուծում այն.

.
λ 1,2 = -1, λ 3 = 3:
Փոխարինելով λ = -1 համակարգում, մենք ունենք.
կամ
Որովհետեւ , ապա կան երկու կախյալ փոփոխականներ, և մեկ ազատ փոփոխական։
Թող x 1-ը լինի ազատ անհայտ, ուրեմն Մենք լուծում ենք այս համակարգը ցանկացած ձևով և գտնում ենք այս համակարգի ընդհանուր լուծումը. Լուծումների հիմնարար համակարգը բաղկացած է մեկ լուծումից, քանի որ n - r = 3 - 2 = 1:
λ = -1 սեփական արժեքին համապատասխանող սեփական վեկտորների բազմությունը ունի հետևյալ ձևը, որտեղ x 1-ը ցանկացած ոչ զրոյական թիվ է: Եկեք այս բազմությունից ընտրենք մեկ վեկտոր, օրինակ՝ դնելով x 1 = 1: .
Նմանապես վիճելով՝ մենք գտնում ենք սեփական վեկտորը, որը համապատասխանում է սեփական արժեքին λ = 3: .
R 3 տարածության մեջ հիմքը բաղկացած է երեք գծային անկախ վեկտորներից, բայց մենք ստացել ենք միայն երկու գծային անկախ սեփական վեկտոր, որոնցից R3-ում հիմքը չի կարող կազմվել։ Հետևաբար, գծային օպերատորի A մատրիցը չի կարող կրճատվել մինչև անկյունագծային ձև:

Օրինակ 13. Տրվում է մատրիցա .
1. Ապացուցեք, որ վեկտորը A մատրիցի սեփական վեկտորն է: Գտեք այս սեփական վեկտորին համապատասխան սեփական արժեքը:
2. Գտե՛ք հիմք, որում A մատրիցն ունի անկյունագծային ձև:
Լուծում.
1. Եթե, ապա - սեփական վեկտոր

.
Վեկտորը (1, 8, -1) սեփական վեկտոր է: Սեփական արժեք λ = -1:
Մատրիցը հիմքում ունի անկյունագծային ձև, որը բաղկացած է սեփական վեկտորներից: Նրանցից մեկը հայտնի է. Մնացածը գտնենք։
Մենք որոնում ենք սեփական վեկտորներ համակարգից.

Բնութագրական հավասարում. ;
(3 + λ) [- 2 (2-λ) (2 + λ) +3] = 0; (3 + λ) (λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1:
Եկեք գտնենք սեփական վեկտորը, որը համապատասխանում է λ = -3 սեփական արժեքին:

Այս համակարգի մատրիցայի աստիճանը հավասար է երկուսի և հավասար է անհայտների թվին, հետևաբար այս համակարգն ունի միայն զրոյական լուծում x 1 = x 3 = 0: x 2 այստեղ կարող է լինել ցանկացած ոչ զրո, օրինակ, x 2: = 1. Այսպիսով, վեկտորը (0 , 1,0) սեփական վեկտոր է, որը համապատասխանում է λ = -3: Եկեք ստուգենք.
.
Եթե ​​λ = 1, ապա մենք ստանում ենք համակարգը
Մատրիցայի աստիճանը երկու է: Մենք ջնջում ենք վերջին հավասարումը.
Թող x 3-ը լինի անվճար անհայտ: Այնուհետև x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3:
Սահմանելով x 3 = 1, մենք ունենք (-3, -9,1) - սեփական վեկտորը, որը համապատասխանում է սեփական արժեքին λ = 1. Ստուգում.

.
Քանի որ սեփական արժեքները իրական են և տարբեր, դրանց համապատասխան վեկտորները գծային անկախ են, ուստի դրանք կարող են հիմք ընդունել R 3-ում: Այսպիսով, հիմքում , , Ա մատրիցը ունի ձև.
.
Գծային A օպերատորի ոչ բոլոր մատրիցները՝ R n → R n-ը կարող են կրճատվել անկյունագծով, քանի որ որոշ գծային օպերատորների համար գծային անկախ սեփական վեկտորները կարող են փոքր լինել n-ից: Այնուամենայնիվ, եթե մատրիցը սիմետրիկ է, ապա ճշգրիտ m գծային անկախ վեկտորներ համապատասխանում են m բազմակիության բնորոշ հավասարման արմատին:

Սահմանում. Սիմետրիկ մատրիցը քառակուսի մատրից է, որի հիմնական անկյունագծով սիմետրիկ տարրերը հավասար են, այսինքն, որում:
Դիտողություններ. 1. Սիմետրիկ մատրիցայի բոլոր սեփական արժեքները իրական են:
2. Զույգ տարբեր սեփական արժեքներին համապատասխանող սիմետրիկ մատրիցայի սեփական վեկտորները ուղղանկյուն են:
Որպես ուսումնասիրված ապարատի բազմաթիվ կիրառություններից մեկը՝ դիտարկենք երկրորդ կարգի կորի ձևի որոշման խնդիրը։