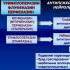
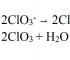مختصات نقاط کانونی بیضی. معادله متعارف یک بیضی. نیمه محورهای بیضی. ساختن بیضی در صورتی که معادله متعارف آن مشخص باشد
بیضی مکان نقاط صفحه است، مجموع فواصل هر یک از آنها تا دو نقطه داده شده F_1، و F_2 مقدار ثابتی است (2a)، بزرگتر از فاصله (2c) بین این نقاط داده شده (شکل 3.36). ، آ). این تعریف هندسی بیان می کند خاصیت بیضی کانونی.
ویژگی کانونی بیضی
نقاط F_1 و F_2 کانون بیضی نامیده می شوند، فاصله بین آنها 2c = F_1F_2 - فاصله کانونی، O وسط قطعه F_1F_2 - مرکز بیضی، عدد 2a - طول محور اصلی است. از بیضی (به ترتیب، عدد a - محور نیمه اصلی بیضی). بخش های F_1M و F_2M که نقطه دلخواه M از بیضی را با کانون های آن متصل می کنند، شعاع کانونی نقطه M نامیده می شوند. قطعه ای که دو نقطه از بیضی را به هم متصل می کند وتر بیضی نامیده می شود.
نسبت e = \ frac (c) (a) خارج از مرکز بیضی نامیده می شود. از تعریف (2a> 2c) چنین بر می آید که 0 \ leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр O совпадают, и эллипс является окружностью радиуса a (рис.3.36,6).
تعریف هندسی بیضی، که ویژگی کانونی آن را بیان می کند، معادل تعریف تحلیلی آن است - خطی که با معادله متعارف یک بیضی تعریف می شود:
در واقع، ما یک سیستم مختصات مستطیلی را معرفی می کنیم (شکل 3.36، ج). مرکز O بیضی به عنوان مبدأ سیستم مختصات در نظر گرفته می شود. خط مستقیمی که از کانون ها می گذرد (محور کانونی یا اولین محور بیضی) به عنوان محور آبسیسا (جهت مثبت روی آن از نقطه F_1 تا نقطه F_2) در نظر گرفته می شود. خط مستقیم عمود بر محور کانونی و عبور از مرکز بیضی (محور دوم بیضی) به عنوان محور ارتین در نظر گرفته می شود (جهت روی محور ارتین طوری انتخاب می شود که سیستم مختصات مستطیلی Oxy درست باشد).
بیایید با استفاده از تعریف هندسی آن که خاصیت کانونی را بیان می کند، معادله بیضی را بسازیم. در سیستم مختصات انتخاب شده، مختصات فوکوس ها را تعیین می کنیم F_1 (-c، 0)، ~ F_2 (c، 0)... برای یک نقطه دلخواه M (x,y) متعلق به یک بیضی، داریم:
\ vline \، \ overrightarrow (F_1M) \, \ vline \, + \ vline \, \ overrightarrow (F_2M) \, \ vline \, = 2a.
با نوشتن این تساوی به صورت مختصات، به دست می آوریم:
\ sqrt ((x + c) ^ 2 + y ^ 2) + \ sqrt ((x-c) ^ 2 + y ^ 2) = 2a.
رادیکال دوم را به سمت راست منتقل می کنیم، دو طرف معادله را مربع می کنیم و عبارت های مشابه را می دهیم:
(x + c) ^ 2 + y ^ 2 = 4a ^ 2-4a \ sqrt ((xc) ^ 2 + y ^ 2) + (xc) ^ 2 + y ^ 2 ~ \ فلش راست چپ ~ 4a \ sqrt ((xc ) ^ 2 + y ^ 2) = 4a ^ 2-4cx.
با تقسیم بر 4، دو طرف معادله را مربع می کنیم:
a ^ 2 (xc) ^ 2 + a ^ 2y ^ 2 = a ^ 4-2a ^ 2cx + c ^ 2x ^ 2 ~ \ فلش راست چپ ~ (a ^ 2-c ^ 2) ^ 2x ^ 2 + a ^ 2y ^ 2 = a ^ 2 (a ^ 2-c ^ 2).
با تعیین b = \ sqrt (a ^ 2-c ^ 2)> 0، ما گرفتیم b ^ 2x ^ 2 + a ^ 2y ^ 2 = a ^ 2b ^ 2... با تقسیم هر دو طرف به ^ 2b ^ 2 \ ne0 به معادله متعارف بیضی می رسیم:
\ frac (x ^ 2) (a ^ 2) + \ frac (y ^ 2) (b ^ 2) = 1.
بنابراین، سیستم مختصات انتخاب شده متعارف است.
اگر کانون های بیضی منطبق باشند، بیضی یک دایره است (شکل 3.36.6)، زیرا a = b. در این حالت، هر سیستم مختصات مستطیلی با مبدا در نقطه O \ معادل F_1 \ معادل F_2و معادله x ^ 2 + y ^ 2 = a ^ 2 معادله دایره ای با مرکز O و شعاع a است.
با انجام استدلال به ترتیب معکوس، می توانیم نشان دهیم که تمام نقاطی که مختصات آنها معادله (3.49) را برآورده می کند، و فقط آنها، متعلق به یک مکان از نقاط به نام بیضی هستند. به عبارت دیگر، تعریف تحلیلی بیضی معادل تعریف هندسی آن است که خاصیت کانونی بیضی را بیان می کند.
ویژگی فهرست بیضی
جهات بیضی دو خط مستقیم هستند که به موازات محور ارتینی سیستم مختصات متعارف در همان فاصله \ frac (a ^ 2) (c) از آن عبور می کنند. برای c = 0، وقتی بیضی یک دایره است، هیچ جهتی وجود ندارد (می توانیم فرض کنیم که جهت ها بی نهایت دور هستند).
بیضی با خروج از مرکز 0
در واقع، برای مثال، برای فوکوس F_2 و Directrix d_2 (شکل 3.37.6)، شرط \ frac (r_2) (\ rho_2) = eمی توان به صورت مختصات نوشت:
\ sqrt ((x-c) ^ 2 + y ^ 2) = e \ cdot \! \ چپ (\ frac (a ^ 2) (c) -x \ راست)
رهایی از بی منطقی و جایگزینی e = \ فراک (ج) (a)، ~ a ^ 2-c ^ 2 = b ^ 2، به معادله متعارف بیضی می رسیم (3.49). استدلال مشابهی را می توان برای فوکوس F_1 و Directrix انجام داد d_1 \ colon \ frac (r_1) (\ rho_1) = e.
معادله یک بیضی در یک سیستم مختصات قطبی
معادله بیضی در سیستم مختصات قطبی F_1r \ varphi (شکل 3.37، c و 3.37 (2)) شکل دارد.
r = \ frac (p) (1-e \ cdot \ cos \ varphi)
که در آن p = \ frac (b ^ 2) (a) پارامتر کانونی بیضی است.
در واقع، اجازه دهید کانون سمت چپ F_1 بیضی را به عنوان قطب سیستم مختصات قطبی، و پرتو F_1F_2 را به عنوان محور قطبی انتخاب کنیم (شکل 3.37، ج). سپس، برای یک نقطه دلخواه M (r، \ varphi)، با توجه به تعریف هندسی (ویژگی کانونی) یک بیضی، r + MF_2 = 2a داریم. ما فاصله بین نقاط M (r, \ varphi) و F_2 (2c, 0) را بیان می کنیم (نگاه کنید به):
\ start (تراز شده) F_2M & = \ sqrt ((2c) ^ 2 + r ^ 2-2 \ cdot (2c) \ cdot r \ cos (\ varphi-0)) = \\ & = \ sqrt (r ^ 2 - 4 \ cdot c \ cdot r \ cdot \ cos \ varphi + 4 \ cdot c ^ 2). \ پایان (تراز شده)
بنابراین، در شکل مختصات، معادله بیضی F_1M + F_2M = 2a دارای شکل است.
r + \ sqrt (r ^ 2-4 \ cdot c \ cdot r \ cdot \ cos \ varphi + 4 \ cdot c ^ 2) = 2 \ cdot a.
ما رادیکال را ترشح می کنیم، هر دو طرف معادله را مربع می کنیم، بر 4 تقسیم می کنیم و عبارت های مشابه را می دهیم:
r ^ 2-4 \ cdot c \ cdot r \ cdot \ cos \ varphi + 4 \ cdot c ^ 2 ~ \ Leftright arrow ~ a \ cdot \! \ چپ (1- \ frac (c) (a) \ cdot \ cos \ varphi \ راست) \! \ cdot r = a ^ 2-c ^ 2.
شعاع قطبی r را بیان کرده و جایگزین کنید e = \ frac (c) (a)، ~ b ^ 2 = a ^ 2-c ^ 2, ~ p = \ frac (b ^ 2) (a):
r = \ frac (a ^ 2-c ^ 2) (a \ cdot (1-e \ cdot \ cos \ varphi)) \ quad \ فلش چپ \ چهار r = \ frac (b ^ 2) (a \ cdot (1 -e \ cdot \ cos \ varphi)) \ quad \ فلش چپ \ چهار r = \ frac (p) (1-e \ cdot \ cos \ varphi)
Q.E.D.
معنی هندسی ضرایب در معادله بیضی
بیایید نقاط تقاطع بیضی (به شکل 3.37، a) را با محورهای مختصات (رأس zllipse) پیدا کنیم. با جایگزینی y = 0 در معادله، نقاط تقاطع بیضی را با محور آبسیسا (با محور کانونی) پیدا می کنیم: x = \ pm a. بنابراین، طول بخش از محور کانونی محصور در بیضی 2 a است. این قطعه همانطور که در بالا ذکر شد، محور اصلی بیضی و عدد a را محور اصلی بیضی می نامند. با جایگزینی x = 0، y = \ pm b را بدست می آوریم. بنابراین، طول قطعه از محور دوم بیضی، محصور در بیضی، برابر با 2b است. این قطعه را محور فرعی بیضی و عدد b را محور فرعی بیضی می نامند.
واقعا، b = \ sqrt (a ^ 2-c ^ 2) \ leqslant \ sqrt (a ^ 2) = aو برابری b = a فقط در حالت c = 0 به دست می آید که بیضی دایره باشد. نگرش k = \ frac (b) (a) \ leqslant1نسبت تراکم بیضی نامیده می شود.
اظهارات 3.9
1. خطوط x = \ pm a، ~ y = \ pm b در صفحه مختصات مستطیل اصلی را محدود می کنند، که داخل آن یک بیضی وجود دارد (به شکل 3.37، a مراجعه کنید).
2. بیضی را می توان به صورت تعریف کرد مکان نقاط به دست آمده از فشرده سازی یک دایره به قطر آن.
در واقع، اجازه دهید در سیستم مختصات مستطیلی Oxy معادله دایره به شکل x ^ 2 + y ^ 2 = a ^ 2 باشد. هنگامی که به محور آبسیسا با ضریب 0 فشرده می شود \ شروع (موارد) x "= x، \\ y" = k \ cdot y. \ پایان (موارد) با جایگزینی x = x "و y = \ frac (1) (k) y" در معادله دایره، معادله مختصات تصویر M "(x"، y") نقطه M (x) را به دست می آوریم. ، y): (x ") ^ 2 + (\ چپ (\ فرک (1) (k) \ cdot y" \ راست) \^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
!} از آنجایی که b = k \ cdot a. این معادله متعارف بیضی است. 3. محورهای مختصات (سیستم مختصات متعارف) محورهای تقارن بیضی هستند (که به آنها محورهای اصلی بیضی می گویند) و مرکز آن مرکز تقارن است. در واقع، اگر نقطه M (x، y) متعلق به بیضی باشد. سپس نقاط M "(x, -y) و M" "(- x, y) که با نقطه M نسبت به محورهای مختصات متقارن هستند نیز متعلق به همان بیضی هستند. 4. از معادله بیضی در سیستم مختصات قطبی r = \ frac (p) (1-e \ cos \ varphi)(شکل 3.37، ج را ببینید)، معنای هندسی پارامتر کانونی روشن شده است - این نیمی از طول وتر بیضی است که از کانون آن عمود بر محور کانونی عبور می کند (r = p در \ varphi = \ frac (\ pi) (2)). 5. خروج از مرکز e مشخص کننده شکل یک بیضی، یعنی تفاوت بین یک بیضی و یک دایره است. هرچه e بزرگتر باشد، بیضی کشیده تر است و هر چه e به صفر نزدیکتر باشد، بیضی به دایره نزدیکتر است (شکل 3.38، a). در واقع، با توجه به اینکه e = \ frac (c) (a) و c ^ 2 = a ^ 2-b ^ 2، به دست می آوریم e ^ 2 = \ frac (c ^ 2) (a ^ 2) = \ frac (a ^ 2-b ^ 2) (a ^ 2) = 1 - (\ چپ (\ frac (a) (b) \ راست ) \^2=1-k^2,
!} که در آن k نسبت فشرده سازی بیضی، 0 است 6. معادله \ فراک (x ^ 2) (a ^ 2) + \ frac (y ^ 2) (b ^ 2) = 1در یک 7. معادله \ frac ((x-x_0) ^ 2) (a ^ 2) + \ frac ((y-y_0) ^ 2) (b ^ 2) = 1, ~ a \ geqslant bیک بیضی را در مرکز نقطه O "(x_0، y_0) تعریف می کند، که محورهای آن موازی با محورهای مختصات هستند (شکل 3.38، ج). این معادله با استفاده از ترجمه موازی به معادله متعارف کاهش می یابد (3.36). برای a = b = R معادله (x-x_0) ^ 2 + (y-y_0) ^ 2 = R ^ 2دایره ای با شعاع R را که در مرکز نقطه O "(x_0، y_0) قرار دارد، توصیف می کند. معادله بیضی پارامتریکدر سیستم مختصات متعارف شکل دارد \ شروع (موارد) x = a \ cdot \ cos (t)، \\ y = b \ cdot \ sin (t)، \ پایان (موارد) 0 \ leqslant t<2\pi.
در واقع، با جایگزینی این عبارات به معادله (3.49)، به هویت مثلثاتی اصلی می رسیم. \ cos ^ 2t + \ sin ^ 2t = 1. مثال 3.20.بیضی بکش \ فراک (x ^ 2) (2 ^ 2) + \ فرک (y ^ 2) (1 ^ 2) = 1در سیستم مختصات متعارف Oxy. نیم محورها، فاصله کانونی، خروج از مرکز، نسبت تراکم، پارامتر کانونی، معادلات مستقیم را بیابید. راه حل.با مقایسه معادله داده شده با معادله متعارف، نیم محورها را تعیین می کنیم: a = 2 - محور نیمه اصلی، b = 1 - محور نیمه جزئی بیضی. ما مستطیل اصلی را با اضلاع 2a = 4، ~ 2b = 2 در مرکز مبدا می سازیم (شکل 3.39). با توجه به تقارن بیضی، آن را در مستطیل اصلی قرار می دهیم. در صورت لزوم مختصات برخی از نقاط بیضی را تعیین کنید. به عنوان مثال، با جایگزینی x = 1 در معادله بیضی، دریافت می کنیم \ frac (1 ^ 2) (2 ^ 2) + \ frac (y ^ 2) (1 ^ 2) = 1 \ quad \ Leftright arrow \ quad y ^ 2 = \ frac (3) (4) \ quad \ Leftright arrow \ quad y = \ pm \ frac (\ sqrt (3)) (2). بنابراین، نقاط با مختصات \ چپ (1; \, \ frac (\ sqrt (3)) (2) \ راست) \ !, ~ \ چپ (1; \, - \ frac (\ sqrt (3)) (2) \ راست)- متعلق به بیضی است. نسبت تراکم را محاسبه کنید k = \ فراک (ب) (a) = \ فراک (1) (2); فاصله کانونی 2c = 2 \ sqrt (a ^ 2-b ^ 2) = 2 \ sqrt (2 ^ 2-1 ^ 2) = 2 \ sqrt (3); عجیب و غریب e = \ frac (c) (a) = \ frac (\ sqrt (3)) (2); پارامتر کانونی p = \ فراک (b ^ 2) (a) = \ فرک (1 ^ 2) (2) = \ فراک (1) (2)... معادلات مستقیم را می سازیم: x = \ pm \ frac (a ^ 2) (c) ~ \ فلش راست چپ ~ x = \ pm \ frac (4) (\ sqrt (3)). معادله متعارف بیضی شکل دارد که در آن a محور نیمه اصلی است. ب - محور نیمه فرعی. نقاط F1 (c, 0) و F2 (-c, 0) - c نامیده می شوند a، b - نیم محورهای بیضی. یافتن کانون ها، خروج از مرکز، جهت بیضی، در صورتی که معادله متعارف آن مشخص باشد. تعریف هایپربولی کانون های هذلولی. تعریف. هذلولی مجموعه ای از نقاط در صفحه ای است که مدول اختلاف بین فواصل از دو نقطه داده شده، که کانون نامیده می شوند، مقدار ثابتی کمتر از فاصله بین کانون ها است. طبق تعریف، | r1 - r2 | = 2a. F1، F2 - کانون های هذلولی. F1F2 = 2c. معادله متعارف هذلولی. نیمه محورهای هذلولی. ساخت هذلولی در صورتی که معادله متعارف آن شناخته شده باشد. معادله متعارف: محور نیمه اصلی هذلولی نصف حداقل فاصله بین دو شاخه هذلولی در دو طرف مثبت و منفی محور (چپ و راست نسبت به مبدا) است. برای شاخه ای که در سمت مثبت قرار دارد، نیم محور برابر است با: اگر آن را از طریق یک مقطع مخروطی و خارج از مرکز بیان کنیم، این عبارت به شکل زیر در می آید: یافتن کانون ها، گریز از مرکز، جهت هذلولی، در صورتی که معادله متعارف آن مشخص باشد. خروج از مرکز هذلولی تعریف. این نسبت خروج از مرکز هذلولی نامیده می شود که در آن c - نیمی از فاصله بین کانون ها و نیم محور واقعی است. با توجه به اینکه c2 - a2 = b2: اگر a = b، e =، هذلولی را متساوی الساقین (متساوی الاضلاع) می نامند. جهت های هایپربولی تعریف. دو خط مستقیم عمود بر محور واقعی هذلولی که به طور متقارن در اطراف مرکز در فاصله a / e از آن قرار دارند، جهت هذلولی نامیده می شوند. معادلات آنها عبارتند از:. قضیه. اگر r فاصله از یک نقطه دلخواه M از هذلولی به هر کانونی باشد، d فاصله از همان نقطه تا جهت متناظر با این کانون است، پس نسبت r / d یک مقدار ثابت برابر با خروج از مرکز است. تعریف سهمی. تمرکز و کارگردان سهمی. سهمی. سهمی نقطه ای از نقاط است که فاصله هر کدام از یک نقطه ثابت معین و از یک خط مستقیم ثابت معین به یک اندازه است. نقطه ای که در تعریف به آن اشاره می شود کانون سهمی و خط را جهت آن می نامند. معادله سهمی متعارف. پارامتر پارابولا ساخت سهمی. معادله متعارف سهمی در یک سیستم مختصات مستطیلی: (یا اگر محورها عوض شوند). ساخت سهمی برای مقدار معینی از پارامتر p به ترتیب زیر انجام می شود: محور تقارن سهمی رسم شده و قطعه KF = p روی آن گذاشته می شود. Directrix DD1 از نقطه K عمود بر محور تقارن کشیده شده است. قطعه KF به نصف تقسیم می شود؛ راس 0 سهمی به دست می آید. تعدادی از نقاط دلخواه 1، 2، 3، 5، 6 از بالا با فاصله بین آنها به تدریج افزایش می یابد. از طریق این نقاط، خطوط مستقیم کمکی عمود بر محور سهمی ترسیم می شوند. در خطوط کمکی، سری ها با شعاع برابر با فاصله از خط تا مستقیم ساخته می شوند. نقاط به دست آمده توسط یک منحنی صاف به هم متصل می شوند. تعریف. بیضی جایگاهی از نقاط روی یک صفحه است که مجموع فواصل هر یک از دو نقطه داده شده از این صفحه که کانون نامیده می شود ثابت است (به شرطی که این مقدار از فاصله بین کانون ها بیشتر باشد). بیایید کانون ها را از طریق فاصله بین آنها - از طریق، و مقدار ثابتی برابر با مجموع فواصل هر نقطه از بیضی تا کانون ها از طریق (بر اساس شرط) نشان دهیم. بیایید یک سیستم مختصات دکارتی بسازیم به طوری که کانون ها روی محور آبسیسا قرار گیرند و مبدا مختصات با وسط قطعه مطابقت داشته باشد (شکل 44). سپس فوکوس ها مختصات زیر را خواهند داشت: فوکوس چپ و فوکوس راست. بیایید معادله بیضی را در سیستم مختصات انتخاب شده استخراج کنیم. برای این منظور یک نقطه دلخواه از بیضی را در نظر بگیرید. با تعریف بیضی، مجموع فواصل این نقطه تا کانون ها برابر است با: بنابراین با استفاده از فرمول فاصله بین دو نقطه به دست می آوریم برای ساده سازی این معادله، آن را به شکل می نویسیم پس از دو طرف معادله به دست می آوریم یا پس از ساده سازی های آشکار: حالا دوباره دو طرف معادله را مربع می کنیم و بعد از آن خواهیم داشت: یا پس از تبدیل های یکسان: از آنجایی که طبق شرط در تعریف بیضی، عدد مثبت است. اجازه دهید نماد را معرفی کنیم سپس معادله به شکل زیر در می آید: با تعریف بیضی، مختصات هر یک از نقاط آن معادله (26) را برآورده می کند. اما رابطه (29) پیامد معادله (26) است. بنابراین مختصات هر نقطه از بیضی نیز آن را برآورده می کند. می توان نشان داد که مختصات نقاطی که روی بیضی قرار ندارند معادله (29) را برآورده نمی کند. بنابراین، معادله (29) معادله یک بیضی است. به آن معادله متعارف بیضی می گویند. اجازه دهید شکل بیضی را با استفاده از معادله متعارف آن تعیین کنیم. اول از همه به این نکته توجه کنید که این معادله فقط دارای توان های زوج x و y است. این بدان معناست که اگر هر نقطه ای متعلق به یک بیضی باشد، آنگاه شامل یک نقطه متقارن با یک نقطه نسبت به محور آبسیسا و یک نقطه متقارن با یک نقطه نسبت به محور مختصات نیز می شود. بنابراین، بیضی دارای دو محور متقارن عمود بر یکدیگر است که در سیستم مختصات انتخاب شده با محورهای مختصات منطبق است. محورهای تقارن بیضی را بیشتر محورهای بیضی و نقطه تقاطع آنها را مرکز بیضی می نامیم. محوری که کانون های بیضی روی آن قرار دارند (در این مورد، محور آبسیسا) محور کانونی نامیده می شود. بیایید ابتدا شکل بیضی را در ربع اول تعریف کنیم. برای این منظور، معادله (28) را با توجه به y حل می کنیم: بدیهی است که در اینجا، از آنجایی که at ارزش های خیالی می گیرد. هنگام افزایش از 0 به a، y از b به 0 کاهش می یابد. بخشی از بیضی که در ربع I قرار دارد، کمانی است که توسط نقاط B محدود شده است (0؛ b) و روی محورهای مختصات قرار دارد (شکل 45). حال با استفاده از تقارن بیضی به این نتیجه می رسیم که بیضی شکلی را دارد که در شکل نشان داده شده است. 45. نقاط تلاقی بیضی با محورها را رئوس بیضی می گویند. از تقارن بیضی بر می آید که، علاوه بر رئوس، بیضی دو رأس دیگر نیز دارد (شکل 45 را ببینید). قطعات و اتصال رئوس مخالف بیضی و همچنین طول آنها را به ترتیب محور اصلی و فرعی بیضی می نامند. اعداد a و b به ترتیب نیم محور اصلی و فرعی بیضی نامیده می شوند. نسبت نصف فاصله بین کانون ها به محور نیمه اصلی بیضی را خروج از مرکز بیضی می نامند و معمولاً با حرف نشان داده می شود: از آنجایی که خروج از مرکز بیضی کمتر از یک است: خروج از مرکز شکل بیضی را مشخص می کند. در واقع، از فرمول (28) چنین می شود، از این نتیجه می توان دریافت که هر چه خروج از مرکز بیضی کوچکتر باشد، تفاوت محور نیمه فرعی b آن با محور نیمه اصلی a کمتر است، یعنی بیضی کمتر کشیده می شود. در امتداد محور کانونی). در حالت محدود، وقتی دایره ای به شعاع a:، یا به دست می آوریم. در این مورد، به نظر می رسد کانون های بیضی در یک نقطه - مرکز دایره - ادغام می شوند. خروج از مرکز دایره صفر است: ارتباط بین بیضی و دایره را می توان از دیدگاه دیگری برقرار کرد. اجازه دهید نشان دهیم که یک بیضی با نیم محورهای a و b را می توان به عنوان برآمدگی دایره ای به شعاع a در نظر گرفت. دو صفحه P و Q را در نظر بگیرید که چنین زاویه ای را بین خود تشکیل می دهند (شکل 46). اجازه دهید یک سیستم مختصات در صفحه P بسازیم، و در صفحه Q - سیستم Oxy با مبدأ مشترک مختصات O و یک آبسیسا مشترک که با خط تقاطع صفحات منطبق است. در صفحه P دایره را در نظر بگیرید با مرکز در مبدا و شعاع برابر با a. اجازه دهید یک نقطه انتخابی دلخواه از دایره باشد، طرح آن بر روی صفحه Q و طرح نقطه M بر روی محور Ox باشد. اجازه دهید نشان دهیم که نقطه روی یک بیضی با نیم محورهای a و b قرار دارد. منحنی های مرتبه دومدر صفحه خطوطی نامیده می شوند که با معادلاتی که در آن متغیر مختصات مشخص می شود، تعریف می شوند ایکسو yموجود در درجه دوم اینها شامل بیضی، هذلولی و سهمی است. نمای کلی معادله منحنی مرتبه دوم به شرح زیر است: جایی که الف، ب، ج، د، ای، اف- اعداد و حداقل یکی از ضرایب الف، ب، جصفر نیست هنگام حل مسائل با منحنی های مرتبه دوم، اغلب معادلات متعارف بیضی، هذلولی و سهمی در نظر گرفته می شود. عبور از معادلات کلی به آنها آسان است؛ مثال 1 از مسائل بیضی به این اختصاص داده خواهد شد. تعریف بیضیبیضی مجموعه ای از تمام نقاط صفحه است که برای آنها مجموع فواصل نقاطی که کانون نامیده می شوند مقدار ثابت و بزرگتر از فاصله بین کانون ها است. فوکوس ها مانند شکل زیر نشان داده شده اند. معادله متعارف بیضی: جایی که آو ب (آ > ب) - طول نیم محورها، یعنی نصف طول قطعات بریده شده توسط بیضی روی محورهای مختصات. خط مستقیمی که از کانون های بیضی می گذرد، محور تقارن آن است. یکی دیگر از محورهای تقارن بیضی، خط مستقیمی است که از وسط یک قطعه عمود بر این قطعه می گذرد. نقطه Oتقاطع این خطوط به عنوان مرکز تقارن بیضی یا به سادگی مرکز بیضی عمل می کند. محور آبسیسا بیضی را در نقاطی قطع می کند ( آ, O) و (- آ, O) ، و محور ترتیب در نقاط ( ب, O) و (- ب, O). این چهار نقطه را رئوس بیضی می نامند. بخش بین رئوس بیضی روی محور آبسیسا، محور اصلی آن و در محور ارتین - محور فرعی نامیده می شود. بخش های آنها از بالا تا مرکز بیضی را نیم محور می نامند. اگر آ = ب، سپس معادله بیضی شکل می گیرد. این معادله یک دایره با شعاع است آو دایره حالت خاصی از بیضی است. بیضی را می توان از دایره ای با شعاع به دست آورد آاگر آن را فشرده کنید آ/ببار در امتداد محور اوه
. مثال 1.بررسی کنید که آیا خط معادله کلی داده شده است یا خیر راه حل. ما تبدیل معادله کلی را انجام می دهیم. ما انتقال عبارت آزاد را به سمت راست اعمال می کنیم، تقسیم معادله را به تعداد یکسان و کاهش کسرها: پاسخ. معادله ای که در نتیجه تبدیل ها به دست می آید، معادله متعارف بیضی است. بنابراین، این خط یک بیضی است. مثال 2.معادله متعارف یک بیضی را بنویسید اگر نیم محورهای آن به ترتیب 5 و 4 باشد. راه حل. ما به فرمول معادله متعارف بیضی نگاه می کنیم و جایگزین می کنیم: نیم محور اصلی آ= 5، نیم محور جزئی است ب= 4. معادله متعارف بیضی را بدست می آوریم: نقاط و، با رنگ سبز در محور اصلی، که در آن مشخص شده است نامیده می شوند ترفندها. تماس گرفت عجیب و غریببیضی نگرش ب/آ"صاف شدن" بیضی را مشخص می کند. هر چه این نسبت کوچکتر باشد، بیضی بیشتر در امتداد محور اصلی کشیده می شود. با این حال، درجه ازدیاد طول بیضی بیشتر بر حسب خروج از مرکز بیان می شود که فرمول آن در بالا آورده شده است. برای بیضی های مختلف، خروج از مرکز از 0 تا 1 متغیر است و همیشه کمتر از یک باقی می ماند. مثال 3.اگر فاصله کانونها 8 و محور اصلی 10 باشد معادله متعارف بیضی را بنویسید. راه حل. ما نتیجه گیری های ساده ای می کنیم: اگر محور اصلی 10 باشد، نیمه آن، یعنی نیم محور آ = 5
, اگر فاصله بین کانون ها 8 باشد، عدد جمختصات فوکوس 4 است. جایگزین و محاسبه کنید: نتیجه معادله متعارف بیضی است: مثال 4.معادله متعارف بیضی را بنویسید اگر محور اصلی آن 26 و گریز از مرکز آن باشد. راه حل. همانطور که از اندازه محور اصلی و معادله خروج از مرکز به دست می آید، نیم محور اصلی بیضی آ= 13. از معادله خروج از مرکز عدد را بیان می کنیم جبرای محاسبه طول نیم محور فرعی لازم است: ما مجذور طول نیم محور کوچک را محاسبه می کنیم: معادله متعارف بیضی را می سازیم: مثال 5.کانون های بیضی را با معادله متعارف تعیین کنید. راه حل. شماره را پیدا کنید جتعریف اولین مختصات کانون های بیضی: ما کانون های بیضی را دریافت می کنیم: مثال 6.کانون های بیضی روی محور قرار دارند گاو نرمتقارن در مورد مبدا معادله متعارف بیضی را بنویسید اگر: 1) فاصله بین کانون ها 30 و محور اصلی 34 است 2) محور فرعی 24 است و یکی از کانون ها در نقطه (-5; 0) است. 3) خارج از مرکز، و یکی از کانون ها در نقطه (6; 0) است. اگر یک نقطه دلخواه از بیضی باشد (در نقاشی با رنگ سبز در قسمت سمت راست بالای بیضی مشخص شده است) و فاصله تا این نقطه از کانون ها باشد، فرمول فواصل به شرح زیر است: برای هر نقطه متعلق به بیضی، مجموع فواصل از کانون ها یک مقدار ثابت برابر با 2 است. آ. خطوط مستقیم که با معادلات تعریف می شوند نامیده می شوند کارگردانانبیضی (در نقاشی - خطوط قرمز در لبه ها). از دو معادله فوق نتیجه می شود که برای هر نقطه از بیضی فواصل این نقطه تا جهات و. مثال 7.بیضی داده می شود. برای مدیران آن معادله بسازید. راه حل. ما به معادله مستقیم نگاه می کنیم و متوجه می شویم که برای یافتن خروج از مرکز بیضی لازم است، یعنی. همه داده ها برای این وجود دارد. محاسبه می کنیم: معادله جهت بیضی را بدست می آوریم: مثال 8.معادله متعارف یک بیضی را در صورتی بنویسید که کانون های آن نقاط و جهت ها خطوط مستقیم باشند. 11.1. مفاهیم اساسی خطوط تعریف شده توسط معادلات درجه دوم را با توجه به مختصات فعلی در نظر بگیرید ضرایب معادله اعداد واقعی هستند، اما حداقل یکی از اعداد A، B یا C غیر صفر است. چنین خطوطی خطوط (منحنی) مرتبه دوم نامیده می شوند. در زیر مشخص خواهد شد که معادله (11.1) یک دایره، بیضی، هذلولی یا سهمی را در صفحه تعریف می کند. قبل از ادامه این بیانیه، اجازه دهید خواص منحنی های ذکر شده را مطالعه کنیم. 11.2. دایره سپس از شرط معادله را بدست می آوریم معادله (11.2) با مختصات هر نقطه از دایره مشخص می شود و مختصات هر نقطه ای که روی دایره قرار ندارد برآورده نمی شود. معادله (11.2) نامیده می شود معادله متعارف دایره به طور خاص، تنظیم و، معادله یک دایره در مرکز مبدا را به دست می آوریم معادله دایره (11.2) پس از تبدیل های ساده شکل می گیرد. هنگام مقایسه این معادله با معادله کلی (11.1) منحنی مرتبه دوم، به راحتی می توان دریافت که دو شرط برای معادله دایره برقرار است: 1) ضرایب در x 2 و y 2 با یکدیگر برابر هستند. 2) هیچ عبارتی حاوی حاصل ضرب xy مختصات فعلی وجود ندارد. مسئله معکوس را در نظر بگیرید. با قرار دادن مقادیر و در رابطه (11.1) بدست می آوریم بیایید این معادله را تبدیل کنیم: از این رو نتیجه می شود که معادله (11.3) یک دایره را تحت شرایط تعریف می کند اگر به مختصات یک نقطه بسنده می کند اگر 11.3. بیضی معادله بیضی متعارف بیضی
مجموعه تمام نقاط صفحه نامیده می شود که مجموع فواصل هر یک از آنها تا دو نقطه داده شده از این صفحه نامیده می شود. ترفندها
، یک مقدار ثابت بیشتر از فاصله بین کانون ها وجود دارد. برای استخراج معادله بیضی، یک سیستم مختصات را انتخاب می کنیم تا کانون ها F 1و F 2روی محور قرار داشت و مبدأ با نقطه میانی قطعه منطبق بود F 1 F 2... سپس کانون ها دارای مختصات زیر خواهند بود: و. اجازه دهید یک نقطه دلخواه از بیضی باشد. سپس با توجه به تعریف بیضی، یعنی. این، در اصل، معادله بیضی است. معادله (11.5) را به شکل ساده تر به صورت زیر تبدیل می کنیم: زیرا آ>با، سپس . ما گذاشتیم سپس آخرین معادله شکل یا را به خود می گیرد می توان ثابت کرد که معادله (11.7) معادل معادله اصلی است. نامیده می شود معادله بیضی متعارف
. بیضی یک منحنی مرتبه دوم است. بررسی شکل بیضی با معادله آن اجازه دهید شکل بیضی را با استفاده از معادله متعارف آن تعیین کنیم. 1. معادله (11.7) حاوی x و y فقط در توانهای زوج است، بنابراین، اگر نقطه ای متعلق به یک بیضی باشد، نقاط ,, نیز به آن تعلق دارند. نتیجه این است که بیضی نسبت به محورها و همچنین در مورد نقطه ای به نام مرکز بیضی متقارن است. 3. از معادله (11.7) چنین بر می آید که هر جمله در سمت چپ از واحد تجاوز نمی کند، یعنی. نابرابری ها و یا و رخ می دهد. بنابراین، تمام نقاط بیضی در داخل مستطیلی هستند که توسط خطوط مستقیم تشکیل شده است. 4. در رابطه (11.7) مجموع جمله های غیر منفی برابر با یک است. در نتیجه، با افزایش یک ترم، دیگری کاهش می یابد، یعنی اگر افزایش یابد، کاهش می یابد و بالعکس. از آنچه گفته شد به دست می آید که بیضی شکل نشان داده شده در شکل 1 را دارد. 50 (منحنی بسته بیضی). درباره بیضی بیشتر بدانید شکل بیضی به نسبت بستگی دارد. هنگامی که بیضی به دایره تبدیل می شود، معادله بیضی (11.7) شکل می گیرد. این نسبت اغلب به عنوان مشخصه شکل یک بیضی استفاده می شود. نسبت نصف فاصله بین کانون ها به محور نیمه اصلی بیضی را خروج از مرکز بیضی و o6o با حرف ε ("epsilon") نشان داده می شود. و 0<ε< 1, так как 0<с<а. С учетом равенства (11.6) формулу
(11.8) можно переписать в виде از این جا می توان دریافت که هر چه خارج از مرکز بیضی کمتر باشد، بیضی کمتر مسطح می شود. اگر ε = 0 قرار دهیم، بیضی به دایره تبدیل می شود. فرمول های زیر معتبر هستند خطوط مستقیم نامیده می شود برابری (11.6) دلالت بر آن دارد. اگر، پس معادله (11.7) یک بیضی را تعریف می کند که محور اصلی آن روی محور Oy و محور فرعی روی محور Ox قرار دارد (شکل 52 را ببینید). کانون چنین بیضی در نقاط و، جایی است 11.4. هذلولی معادله هایپربولای متعارف هایپربولی
مجموعه تمام نقاط صفحه نامیده می شود، مدول اختلاف بین فواصل هر یک از آنها تا دو نقطه داده شده از این صفحه، به نام ترفندها
، یک مقدار ثابت کمتر از فاصله بین کانون ها وجود دارد. برای استخراج معادله هذلولی، یک سیستم مختصات را انتخاب می کنیم تا کانون ها F 1و F 2روی محور قرار داشت و مبدا با نقطه میانی قطعه منطبق بود F 1 F 2(شکل 53 را ببینید). سپس فوکوس ها دارای مختصات و اجازه دهید یک نقطه دلخواه از هذلولی باشد. سپس با توجه به تعریف هذلولی هذلولی خطی از مرتبه دوم است. بررسی شکل هذلولی با معادله آن اجازه دهید شکل هذلولی را با استفاده از معادله کاکونی آن تعیین کنیم. 1. معادله (11.9) حاوی x و y فقط در توانهای زوج است. در نتیجه، هذلولی نسبت به محورها و همچنین در مورد نقطه ای به نام متقارن است. مرکز هذلولی
2. نقاط تقاطع هذلولی را با محورهای مختصات بیابید. با قرار دادن معادله (11.9)، دو نقطه تقاطع هذلولی با محور پیدا می کنیم: و. با قرار دادن (11.9)، آنچه را که نمی تواند باشد دریافت می کنیم. در نتیجه، هذلولی محور Oy را قطع نمی کند. امتیاز و نامیده می شوند
قله ها
هذلولی، و بخش محور واقعی
، بخش - نیم محور واقعی
هایپربولی قطعه اتصال نقاط نامیده می شود
محور خیالی
، شماره b - نیم محور خیالی
... مستطیل با اضلاع 2aو 2bتماس گرفت مستطیل اصلی هذلولی
. 3. از رابطه (11.9) چنین بر می آید که مقداری که باید کاهش یابد کمتر از یک نیست، یعنی آن یا. این بدان معناست که نقاط هذلولی در سمت راست خط مستقیم (شاخه سمت راست هذلولی) و در سمت چپ خط مستقیم (شاخه چپ هذلولی) قرار دارند. 4. از معادله (11.9) هذلولی می توان دریافت که وقتی افزایش می یابد، آنگاه نیز افزایش می یابد. این از این واقعیت ناشی می شود که تفاوت برابر با یک ثابت می ماند. از آنچه گفته شد چنین استنباط می شود که هذلولی دارای شکل نشان داده شده در شکل 54 است (منحنی متشکل از دو شاخه نامحدود). مجانب هایپربولا
خط L مجانب نامیده می شود اجازه دهید نشان دهیم که هذلولی دو مجانب دارد: از آنجایی که خطوط مستقیم (11.11) و هذلولی (11.9) با توجه به محورهای مختصات متقارن هستند، کافی است تنها نقاطی از خطوط نشان داده شده را در نظر بگیریم که در ربع اول قرار دارند. نقطه N را روی یک خط مستقیم بگیرید که همان آبسیس x با نقطه ای از هذلول را دارد همانطور که می بینید، با افزایش x، مخرج کسر افزایش می یابد. شمارنده ثابت است بنابراین، طول بخش هنگام ساخت هذلولی (11.9)، توصیه می شود ابتدا مستطیل اصلی هذلولی را بسازید (نگاه کنید به شکل 57)، خطوط مستقیمی را که از رئوس مخالف این مستطیل - مجانب هذلولی می گذرد، رسم کنید، و راس ها و راس ها را علامت گذاری کنید. هذلولی ها معادله هذلولی متساوی الاضلاع. که مجانب آن محورهای مختصات هستند مجانب هذلولی متساوی الاضلاع معادلاتی دارند و بنابراین نیمساز زوایای مختصات هستند. معادله این هذلولی را در سیستم مختصات جدید در نظر بگیرید (نگاه کنید به شکل 58)، که با چرخش محورهای مختصات با یک زاویه به دست آمده است. برای چرخش محورهای مختصات از فرمول ها استفاده می کنیم: مقادیر x و y را با معادله (11.12) جایگزین کنید: معادله هذلولی متساوی الاضلاع که محورهای Ox و Oy مجانب آن هستند، شکل خواهد داشت. درباره هایپربولی بیشتر بدانید عجیب و غریب
هذلولی (11.9) به نسبت فاصله بین کانون ها به مقدار محور واقعی هذلولی گفته می شود که با ε نشان داده می شود: از آنجایی که برای هذلولی، خروج از مرکز هذلولی بیشتر از یک است:. خروج از مرکز شکل هذلولی را مشخص می کند. در واقع، برابری (11.10) دلالت بر این دارد که و از این رو، می توان دریافت که هر چه گریز از مرکز هذلولی کوچکتر باشد، نسبت نیم محورهای آن کمتر است و از این رو مستطیل اصلی آن کشیده تر می شود. خروج از مرکز هذلولی متساوی الاضلاع است. واقعا، شعاع کانونی خطوط مستقیم را جهات هذلولی می نامند. از آنجایی که برای هذلولی ε> 1، پس. این بدان معنی است که جهت راست بین مرکز و راس راست هذلولی قرار دارد، سمت چپ بین مرکز و راس چپ. جهت های هایپربولا دارای ویژگی های مشابه جهت های بیضی هستند. منحنی تعریف شده توسط معادله نیز یک هذلولی است که محور واقعی 2b آن روی محور Oy و محور فرضی 2 قرار دارد. آ- در محور Ox. در شکل 59 با یک خط نقطه نشان داده شده است. بدیهی است که هذلولی ها و مجانب مشترکی دارند. چنین هذلولی ها مزدوج نامیده می شوند. 11.5. سهمی معادله سهمی متعارف سهمی مجموعه ای از تمام نقاط صفحه است که هر یک از آنها به یک اندازه از یک نقطه معین که کانون نامیده می شود و یک خط مستقیم معین به نام جهت دار فاصله دارند. فاصله کانونی F تا جهات را پارامتر سهمی می نامند و با p نشان داده می شود (p> 0). 1. در رابطه (11.13) متغیر y در توان زوج گنجانده شده است، به این معنی که سهمی متقارن حول محور Ox است. محور Ox، محور تقارن سهمی است. 2. از آنجایی که ρ> 0، از (11.13) نتیجه می شود که. در نتیجه سهمی در سمت راست محور Oy قرار دارد. 3. برای، ما y = 0 داریم. در نتیجه، سهمی از مبدأ عبور می کند. 4. با افزایش x به طور نامحدود، ماژول y نیز به طور نامحدود افزایش می یابد. سهمی شکل (شکل) را دارد که در شکل 61 نشان داده شده است. نقطه O (0؛ 0) راس سهمی نامیده می شود، قطعه FM = r شعاع کانونی نقطه M نامیده می شود. معادلات،، ( p> 0) همچنین سهمی ها را تعریف می کنند، آنها در شکل 62 نشان داده شده اند به راحتی می توان نشان داد که نمودار یک مثلث مربع، که در آن، B و C هر اعداد واقعی هستند، یک سهمی به معنای تعریف آن در بالا است. 11.6. معادله عمومی خطوط مرتبه دوم معادلات منحنی های مرتبه دوم با محورهای تقارن موازی با محورهای مختصات اجازه دهید ابتدا معادله بیضی را در مرکز نقطه ای پیدا کنیم که محورهای تقارن آن با محورهای مختصات Ox و Oy موازی هستند و نیم محورها به ترتیب برابر هستند. آو ب... ما در مرکز بیضی O 1 مبدا سیستم مختصات جدید را قرار می دهیم که محورهای آن و نیم محورها آو ب(شکل 64 را ببینید): در نهایت، سهمی های نشان داده شده در شکل 65 دارای معادلات متناظر هستند. معادله معادلات بیضی، هذلولی، سهمی و معادله یک دایره پس از تبدیل (پرانتزها را باز کنید، تمام عبارت های معادله را در یک جهت حرکت دهید، عبارت های مشابه را بیاورید، نامگذاری های جدیدی برای ضرایب معرفی کنید) را می توان با استفاده از یک واحد نوشت. معادله فرم که در آن ضرایب A و C همزمان با صفر برابر نیستند. این سوال مطرح می شود: آیا معادله ای از شکل (11.14) یکی از منحنی های مرتبه دوم (دایره، بیضی، هذلولی، سهمی) را تعیین می کند؟ پاسخ با قضیه زیر داده می شود. قضیه 11.2... معادله (11.14) همیشه تعیین می کند: یا یک دایره (برای A = C)، یا یک بیضی (برای A C> 0)، یا یک هذلولی (برای A C)< 0), либо
параболу (при А×С= 0). При этом возможны случаи вырождения: для эллипса (окружности)
- в точку или мнимый эллипс (окружность), для гиперболы - в пару пересекающихся
прямых, для параболы - в пару параллельных прямых. معادله مرتبه دوم عمومی اکنون یک معادله کلی درجه دوم با دو مجهول را در نظر بگیرید: با معادله (11.14) با وجود یک جمله با حاصلضرب مختصات (B10) تفاوت دارد. می توان با چرخش محورهای مختصات در زاویه a، این معادله را طوری تبدیل کرد که هیچ جمله ای با حاصلضرب مختصات در آن وجود نداشته باشد. استفاده از فرمول های چرخش محورها مختصات قدیمی را بر حسب مختصات جدید بیان می کنیم: زاویه a را طوری انتخاب می کنیم که ضریب x "· y" ناپدید شود، یعنی تساوی بنابراین، هنگامی که محورها از طریق زاویه a می چرخند و شرط (11.17) را برآورده می کنند، معادله (11.15) به معادله (11.14) کاهش می یابد. خروجی: معادله کلی مرتبه دوم (11.15) منحنی های زیر را بر روی صفحه تعریف می کند (به جز موارد انحطاط و زوال): دایره، بیضی، هذلولی، سهمی. نکته: اگر A = C باشد، معادله (11.17) معنای خود را از دست می دهد. در این مورد cos2α = 0 (نگاه کنید به (11.16))، سپس 2α = 90 درجه، یعنی α = 45 درجه. بنابراین، هنگامی که A = C، سیستم مختصات باید 45 درجه بچرخد.معادله بیضی پارامتریک
بیضی داده شده توسط معادله متعارف
، یک بیضی
.
.
ما با هم به حل مشکلات روی بیضی ادامه می دهیم
,
.
ساده ترین منحنی مرتبه دوم یک دایره است. به یاد بیاورید که دایره ای با شعاع R در مرکز یک نقطه، مجموعه تمام نقاط Μ صفحه است که شرط را برآورده می کند. بگذارید یک نقطه در یک سیستم مختصات مستطیلی دارای مختصات x 0، y 0 و - یک نقطه دلخواه از دایره باشد (شکل 48 را ببینید).
(11.2)
.
(11.4)
... مرکز آن در نقطه است 
و شعاع
.
، سپس معادله (11.3) شکل می گیرد
.
... در این مورد می گویند: "دایره به نقطه ای منحط شده است" (شعاع صفر دارد).
، سپس معادله (11.4) و از این رو معادله معادل (11.3) هیچ خطی را تعریف نمی کند، زیرا سمت راست معادله (11.4) منفی است و سمت چپ منفی نیست (مثلاً "دایره خیالی").
فوکوس ها را با علامت گذاری می کنیم F 1و F 2، فاصله بین آنها در 2 ج، و مجموع فواصل از یک نقطه دلخواه بیضی تا کانون - بعد از 2 آ(شکل 49 را ببینید). طبق تعریف 2 آ > 2ج، یعنی آ
> ج.
(11.6)
(11.7)
2. نقاط تقاطع بیضی را با محورهای مختصات بیابید. با قرار دادن، دو نقطه پیدا می کنیم که در آن محور بیضی را قطع می کند (شکل 50 را ببینید). با قرار دادن معادله (11.7)، نقاط تقاطع بیضی را با محور: و می یابیم. نکته ها آ 1 ,
الف 2 , ب 1, ب 2نامیده می شوند رئوس بیضی... بخش ها آ 1 الف 2و B 1 B 2و همچنین طول آنها 2 آو 2 ببر این اساس نامگذاری شده اند محورهای بزرگ و کوچکبیضی شماره آو ببه ترتیب بزرگ و کوچک نامیده می شوند نیمه محورهابیضی
فرض کنید M (x; y) یک نقطه دلخواه از یک بیضی با کانون های F 1 و F 2 باشد (شکل 51 را ببینید). طول قطعات F 1 M = r 1 و F 2 M = r 2 را شعاع کانونی نقطه Μ می نامند. به طور مشخص،
قضیه 11.1.اگر فاصله یک نقطه دلخواه از بیضی تا مقداری کانونی باشد، d فاصله همان نقطه تا جهت متناظر با این کانون است، آنگاه این نسبت یک مقدار ثابت برابر با خروج از مرکز بیضی است:
.
فوکوس ها را با علامت گذاری می کنیم F 1و F 2فاصله بین آنها از طریق 2cو مدول تفاوت بین فواصل هر نقطه از هذلولی تا کانون از طریق 2a... الف - مقدماتی 2a < 2c، یعنی آ < ج.
یا، یعنی پس از ساده سازی ها، همانطور که هنگام استخراج معادله بیضی انجام شد، به دست می آوریم.
معادله هذلولی متعارف
(11.9)
(11.10)
منحنی نامحدود K اگر فاصله d از یک نقطه M منحنی K تا این خط مستقیم در فاصله نامحدود یک نقطه M در امتداد منحنی K از مبدا به صفر گرایش داشته باشد. شکل 55 مفهوم مجانبی را نشان می دهد: خط L مجانبی برای منحنی K است.
(11.11)
(شکل 56 را ببینید)، و تفاوت ΜΝ بین مختصات خط و شاخه هذلولی را بیابید:
ΜΝ به صفر تمایل دارد. از آنجایی که ΜΝ بزرگتر از فاصله d از نقطه Μ تا خط مستقیم است، پس d حتی بیشتر به صفر میل می کند. بنابراین، خطوط مستقیم مجانب هذلولی هستند (11.9).
هذلولی (9/11) متساوی الاضلاع نامیده می شود که نیم محورهای آن برابر () باشد. معادله متعارف او
(11.12)
.
و 
برای نقاط شاخه سمت راست، هذلولی ها شکل و و برای شاخه چپ، 
و 
.
برای به دست آوردن معادله سهمی، سیستم مختصات Oxy را انتخاب می کنیم تا محور Ox از کانون F عمود بر جهات در جهت جهت مستقیم به F عبور کند و مبدأ مختصات O در وسط بین کانون و مرکز قرار گیرد. جهت (نگاه کنید به شکل 60). در سیستم انتخاب شده، کانون F دارای مختصاتی است و معادله مستقیم دارای شکل یا است.
