Taylor serija, kvadratinė šaknis. Maitinimo serijos, jų konvergencija, funkcijų išplėtimas galios serijose

Aukštosios matematikos studentai turėtų žinoti, kad tam tikros galios serijos, priklausančios mums pateiktos serijos konvergencijos intervalui, suma yra tęstinė ir begalinė kartų diferencijuota funkcija. Kyla klausimas: ar galima teigti, kad duota savavališka funkcija f (x) yra tam tikros galios serijos suma? Tai yra, kokiomis sąlygomis f-ija f (x) gali būti pavaizduota galios serija? Tokio klausimo svarba slypi tame, kad galima apytiksliai pakeisti f-yu f (x) kelių pirmųjų galios eilučių sumų suma, tai yra daugianariu. Šis funkcijos pakeitimas gana paprasta išraiška - daugianariu - taip pat patogu sprendžiant kai kurias problemas, būtent: sprendžiant integralus, skaičiuojant ir pan.

Įrodyta, kad kai kuriems fu ir f (x), kuriuose galima apskaičiuoti išvestines iki (n + 1) eilės, įskaitant pastarąją, kaimynystėje (α - R; x 0 + R) kai kuris taškas x = α yra teisinga formulė:

Ši formulė turi garsaus mokslininko Brooko Tayloro vardą. Serija, gauta iš ankstesnės, vadinama „Maclaurin“ serija:

Taisyklė, leidžianti išplėsti „Maclaurin“ seriją:

Nustatykite pirmosios, antrosios, trečiosios ... eilės darinius.
Apskaičiuokite, kokios išvestinės x = 0 yra lygios.
Užrašykite šiai funkcijai skirtą „Maclaurin“ seriją ir nustatykite jos suartėjimo intervalą.
Nustatykite intervalą (-R; R), kuriame yra likusi Maclaurino formulės dalis

R n (x) -> 0 kaip n -> begalybė. Jei tokia yra, funkcija f (x) turi sutapti su Maclaurin serijos suma.

Dabar apsvarstykime „Maclaurin“ seriją atskiroms funkcijoms.

1. Taigi, pirmasis bus f (x) = e x. Žinoma, pagal savo ypatybes tokia funkcija turi įvairių eilių darinius, o f (k) (x) = e x, kur k yra lygus visiems. Pakaitalas x = 0. Gauname f (k) (0) = e 0 = 1, k = 1,2 ... Remiantis tuo, kas išdėstyta, e x eilutė atrodys taip:

2. Maklaurino serija funkcijai f (x) = sin x. Iš karto paaiškinkime, kad visų nežinomųjų f -ai bus dariniai, be f "(x) = cos x = sin (x + n / 2), f" "(x) = -sin x = sin (x + 2) * n / 2) ..., f (k) (x) = sin (x + k * n / 2), kur k yra lygus bet kuriam natūraliajam skaičiui. Tai yra, atlikdami paprastus skaičiavimus, galime padaryti išvadą kad f (x) = sin x serija bus tokios formos:

3. Dabar pabandykime apsvarstyti f-yu f (x) = cos x. Visiems nežinomiesiems jis turi savavališkos eilės darinius ir | f (k) (x) | = | cos (x + k * n / 2) |<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

Taigi, mes išvardinome svarbiausias funkcijas, kurias galima išplėsti į „Maclaurin“ seriją, tačiau kai kurioms funkcijoms jas papildo „Taylor“ serija. Dabar išvardinsime ir juos. Taip pat verta paminėti, kad „Taylor“ ir „Maclaurin“ serijos yra svarbi aukštojo matematikos serijų sprendimo dirbtuvių dalis. Taigi, Taylor gretos.

1. Pirmoji bus serija f-ii f (x) = ln (1 + x). Kaip ir ankstesniuose pavyzdžiuose, tam tikram f (x) = ln (1 + x), mes galime pridėti seriją naudodami bendrą Maclaurin serijos formą. tačiau „Maclaurin“ seriją galima gauti daug paprasčiau šiai funkcijai. Integravę tam tikrą geometrinę seriją, gauname tokio pavyzdžio f (x) = ln (1 + x) seriją:

2. Ir antrasis, kuris bus galutinis mūsų straipsnyje, bus f (x) = arctan x serija. Jei intervalas [-1; 1] priklauso x, skaidymas galioja:

Tai viskas. Šiame straipsnyje buvo nagrinėjamos dažniausiai naudojamos Taylor ir Maclaurin serijos aukštojoje matematikoje, ypač ekonomikos ir technikos universitetuose.

Kaip įterpti matematines formules į svetainę?

Jei jums kada nors reikia pridėti vieną ar dvi matematines formules prie tinklalapio, paprasčiausias būdas tai padaryti yra taip, kaip aprašyta straipsnyje: matematinės formulės lengvai įterpiamos į svetainę nuotraukų pavidalu, kurias automatiškai sukuria „Wolfram Alpha“. Be paprastumo, šis universalus metodas padės pagerinti jūsų svetainės matomumą paieškos sistemose. Jis veikė ilgą laiką (ir manau, kad veiks amžinai), tačiau jau yra morališkai pasenęs.

Jei savo svetainėje reguliariai naudojate matematines formules, rekomenduoju naudoti „MathJax“ - specialią „JavaScript“ biblioteką, rodančią matematikos žymėjimą žiniatinklio naršyklėse, naudojant „MathML“, „LaTeX“ arba „ASCIIMathML“ žymėjimą.

Yra du būdai, kaip pradėti naudoti „MathJax“: (1) naudodami paprastą kodą, galite greitai prijungti „MathJax“ scenarijų prie savo svetainės, kuris bus automatiškai įkeliamas iš nuotolinio serverio tinkamu laiku (serverių sąrašas); (2) įkelkite „MathJax“ scenarijų iš nuotolinio serverio į savo serverį ir prijunkite jį prie visų savo svetainės puslapių. Antrasis metodas, kuris yra sudėtingesnis ir reikalauja daug laiko, pagreitins jūsų svetainės puslapių įkėlimą, o jei pagrindinis „MathJax“ serveris dėl kokių nors priežasčių laikinai nepasiekiamas, tai neturės jokios įtakos jūsų svetainei. Nepaisant šių privalumų, pasirinkau pirmąjį metodą, nes jis paprastesnis, greitesnis ir nereikalaujantis techninių įgūdžių. Sekite mano pavyzdžiu ir po 5 minučių galėsite naudotis visomis „MathJax“ funkcijomis savo svetainėje.

Galite prijungti „MathJax“ bibliotekos scenarijų iš nuotolinio serverio naudodami dvi kodo versijas, paimtas iš pagrindinės „MathJax“ svetainės arba iš dokumentacijos puslapio:

Vienas iš šių kodo variantų turi būti nukopijuotas ir įklijuotas į jūsų tinklalapio kodą, geriausia tarp žymų ir arba iškart po žymės ... Pagal pirmąją parinktį „MathJax“ įkeliama greičiau ir mažiau sulėtina puslapį. Tačiau antroji parinktis automatiškai seka ir įkelia naujausias „MathJax“ versijas. Jei įterpsite pirmąjį kodą, jį reikės periodiškai atnaujinti. Jei įterpsite antrąjį kodą, puslapiai bus įkeliami lėčiau, tačiau jums nereikės nuolat stebėti „MathJax“ atnaujinimų.

Lengviausias būdas prijungti „MathJax“ yra „Blogger“ arba „WordPress“: savo svetainės prietaisų skydelyje pridėkite valdiklį, skirtą įterpti trečiosios šalies „JavaScript“ kodą, nukopijuokite pirmąją ar antrąją aukščiau pateikto įkėlimo kodo versiją ir padėkite valdiklį arčiau šablono pradžią (beje, tai visai nebūtina, nes „MathJax“ scenarijus įkeliamas asinchroniškai). Tai viskas. Dabar išmokite „MathML“, „LaTeX“ ir „ASCIIMathML“ žymėjimo sintaksę ir esate pasiruošę įterpti matematines formules į savo svetainės tinklalapius.

Bet koks fraktalas yra statomas pagal tam tikrą taisyklę, kuri nuosekliai taikoma neribotą skaičių kartų. Kiekvienas toks laikas vadinamas iteracija.

Pakartotinis „Menger“ kempinės konstravimo algoritmas yra gana paprastas: originalus kubas su 1 puse yra padalintas plokštumomis, lygiagrečiomis jo veidams, į 27 vienodus kubus. Iš jo pašalinamas vienas centrinis kubas ir 6 gretimi kubeliai. Rezultatas yra rinkinys, susidedantis iš likusių 20 mažesnių kubelių. Atlikdami tą patį su kiekvienu iš šių kubelių, gauname rinkinį, kurį jau sudaro 400 mažesnių kubelių. Tęsdami šį procesą be galo, mes gauname „Menger“ kempinę.

Tarp funkcinių serijų svarbiausią vietą užima galios serijos.

Serija vadinama galios serija

kurių terminai yra galios funkcijos, išdėstytos didinant sveikųjų skaičių neneigiamas galias x, a c0 , c 1 , c 2 , c n - pastovios vertės. Numeriai c1 , c 2 , c n - serijos narių koeficientai, c0 - laisvas narys. Galių serijos nariai yra apibrėžti visoje skaičių eilutėje.

Susipažinkime su koncepcija galios serijų konvergencijos sritis. Tai kintamųjų verčių rinkinys x kuriam serija suartėja. Maitinimo serijos turi gana paprastą konvergencijos sritį. Tikrosioms kintamojo reikšmėms x konvergencijos sritis susideda iš vieno taško arba yra tam tikras intervalas (konvergencijos intervalas) arba sutampa su visa ašimi Jautis .

Pakeitus galios seriją, reikšmės x= 0 gausite skaičių seriją

c0 +0+0+...+0+... ,

kuris susilieja.

Todėl už x= 0 bet kokia galios serija susilieja, todėl jos konvergencijos sritis negali būti tuščias. Visų galios serijų konvergencijos regiono struktūra yra ta pati. Tai galima nustatyti naudojant šią teoremą.

1 teorema (Abelio teorema)... Jei galios serija susilieja dėl tam tikros vertės x = x 0 nulis, tada jis susilieja ir, be to, absoliučiai visoms vertybėms |x| < |x 0 | ... Atkreipkite dėmesį: tiek pradinė vertė „x yra nulis“, tiek bet kokia „x“ vertė, lyginama su pradine verte, yra moduliuojama - neatsižvelgiant į ženklą.

Pasekmė. Jei galios serijos skiriasi tam tikra verte x = x 1 , tada jis skiriasi dėl visų vertybių |x| > |x 1 | .

Kaip mes sužinojome anksčiau, bet kokia galios serija susilieja su verte x= 0. Yra galios serijų, kurios susilieja tik x= 0 ir skiriasi kitoms vertėms NS... Pašalinus šį atvejį, mes manome, kad galios serija susilieja dėl tam tikros vertės x = x 0 nulis. Tada pagal Abelio teoremą ji susilieja visuose intervalo taškuose] - | x0 |, |x 0 |[ (intervalas, kurio kairioji ir dešinė ribos yra x reikšmės, ties kuriomis susilieja galios eilutės, atitinkamai pažymėtos minuso ir pliuso ženklais), simetriškas kilmės atžvilgiu.

Jei galios serija skiriasi dėl tam tikros vertės x = x 1 , tada, remiantis Abelio teoremos išvadomis, ji taip pat skiriasi visais taškais, esančiais už segmento ribų [- | x1 |, |x 1 |] ... Iš to išplaukia, kad bet kuriai galios serijai yra intervalas simetriškas apie kilmę, vadinamas konvergencijos intervalas , kiekviename taške, kurio serija susilieja, ties ribomis ji gali suartėti ir gali skirtis, ir nebūtinai vienu metu, bet už segmento ribų serija skiriasi. Skaičius R vadinamas galios serijos suartėjimo spinduliu.

Ypatingais atvejais galios serijų suartėjimo intervalas gali išsigimti iki tam tikro taško (tada serija susilieja tik x= 0 ir daroma prielaida, kad R= 0) arba pavaizduoti visą skaičių eilutę (tada serija susilieja visuose skaičių tiesės taškuose ir daroma prielaida).

Taigi galios serijos konvergencijos regiono apibrėžimą sudaro jo apibrėžimas konvergencijos spindulys R ir serijos konvergencijos tyrimas dėl konvergencijos intervalo ribų (at).

2 teorema. Jei visi galios serijos koeficientai, pradedant nuo kažkokio, yra nuliniai, tai jo konvergencijos spindulys yra lygus ribai, esant bendrų sekančių bendrų terminų koeficientų absoliučių verčių santykiui, t.y.

1 pavyzdys. Raskite galios eilutės konvergencijos sritį

Sprendimas. Čia

Naudodami formulę (28), randame šios serijos suartėjimo spindulį:

Panagrinėkime serijų suartėjimą konvergencijos intervalo galuose. 13 pavyzdys rodo, kad ši serija suartėja x= 1 ir skiriasi x= -1. Vadinasi, konvergencijos sritis yra pusė intervalo.

2 pavyzdys. Raskite galios eilutės konvergencijos sritį

Sprendimas. Serijos koeficientai yra teigiami, ir

Raskime šio santykio ribą, t.y. galios serijos suartėjimo spindulys:

Panagrinėkime serijos konvergenciją intervalo pabaigoje. Vertybių pakeitimas x= -1/5 ir x= 1/5 tam tikroje eilutėje suteikia:

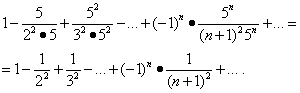
Pirmoji iš šių serijų susilieja (žr. 5 pavyzdį). Bet tada, remiantis teorema skyriuje „Absoliuti konvergencija“, antroji serija taip pat suartėja, o jos konvergencijos regionas yra segmentas

3 pavyzdys. Raskite galios eilutės konvergencijos sritį

Sprendimas. Čia

Naudodami formulę (28), randame serijos suartėjimo spindulį:

Išnagrinėkime verčių serijų konvergenciją. Pakeisdami juos šioje eilutėje, atitinkamai gauname

Abi serijos skiriasi, nes nėra įvykdyta būtina konvergencijos sąlyga (jų bendros sąlygos nėra linkusios nuliui). Taigi abiejuose konvergencijos intervalo galuose duota serija skiriasi, o jos konvergencijos sritis yra intervalas.

5 pavyzdys. Raskite galios eilutės konvergencijos sritį

Sprendimas. Raskite ryšį, kur ir :

Pagal (28) formulę šios serijos suartėjimo spindulys yra

tai serija susilieja tik dėl x= 0 ir skiriasi kitoms vertėms NS.

Pavyzdžiai rodo, kad konvergencijos intervalo pabaigoje serijos elgiasi skirtingai. 1 pavyzdyje serija susilieja viename konvergencijos intervalo gale ir skiriasi kitame; 2 pavyzdyje ji susilieja iš abiejų galų; 3 pavyzdyje skiriasi abiejuose galuose.

Galių serijos suartėjimo spindulio formulė gaunama darant prielaidą, kad visi serijos terminų koeficientai, pradedant nuo kai kurių, yra nuliniai. Todėl naudoti formulę (28) leidžiama tik šiais atvejais. Jei ši sąlyga pažeidžiama, reikia ieškoti galios serijos suartėjimo spindulio d'Alemberto ženklas, arba, pakeisdami kintamąjį, pakeiskite seriją į formą, kuria įvykdyta nurodyta sąlyga.

6 pavyzdys. Raskite galios serijos suartėjimo intervalą

Sprendimas. Šioje serijoje nėra nelyginių laipsnių narių. NS... Todėl seriją keičiame nustatydami. Tada mes gauname seriją

norint rasti (28) formulės suartėjimo spindulį. Kadangi, a, tada šios serijos suartėjimo spindulys

Taigi iš gautos lygybės ši serija susilieja su intervalu.

Galių serijos suma. Maitinimo serijų diferenciacija ir integravimas

Leiskite jėgos serijai

konvergencijos spindulys R> 0, t.y. ši serija susilieja su intervalu.

Tada kiekviena vertė NS nuo konvergencijos intervalo atitinka tam tikrą serijos sumą. Todėl galios serijos suma yra funkcija NS dėl konvergencijos intervalo. Žymėdamas jį per f(x), galime parašyti lygybę

suprasti tai ta prasme, kad serijos suma kiekviename taške NS nuo konvergencijos intervalo yra lygus funkcijos vertei f(x) Šiuo atveju. Ta pačia prasme sakysime, kad galios serija (29) susilieja su funkcija f(x) dėl konvergencijos intervalo.

Už konvergencijos intervalo ribų lygybė (30) yra beprasmė.

7 pavyzdys. Raskite galios serijos sumos sumą

Sprendimas. Tai geometrinė serija su a= 1 ir q= x... Todėl jo suma yra funkcija ... Serija susilieja, jei ir yra jos konvergencijos intervalas. Todėl lygybė

galioja tik reikšmėms, nors funkcija apibrėžta visoms vertėms NS, išskyrus NS= 1.

Galima įrodyti, kad galios serijos suma f(x) yra tęstinis ir diferencijuojamas bet kuriame segmente, esančiame konvergencijos intervalo viduje, ypač bet kuriame serijos konvergencijos intervalo taške.

Pateiksime teoremas apie galios eilučių diferenciaciją ir integraciją.

1 teorema. Galių eilutes (30) savo konvergencijos intervale galima terminiškai diferencijuoti neribotą skaičių kartų, o gautos galios eilutės turi tokį patį suartėjimo spindulį kaip ir pradinės serijos, ir jų sumos yra atitinkamai lygios.

2 teorema. Maitinimo serijas (30) galima neribotą skaičių kartų integruoti diapazone nuo 0 iki NS jei

Funkcijų išplėtimas galios serijose

Suteikta funkcija f(x), kurį reikia išplėsti galios serijoje, t.y. pavaizduoti forma (30):

Užduotis yra nustatyti koeficientus eilutė (30). Taigi, diferencijuodami lygybės (30) terminus pagal terminus, iš eilės randame:

……………………………………………….. (31)

Lygumų nustatymas (30) ir (31) NS= 0, randame

Pakeitus rastas išraiškas lygybe (30), gauname

(32)

Raskime kai kurių elementarių funkcijų išplėtimą „Maclaurin“ serijoje.

8 pavyzdys. Išplėskite „Maclaurin“ serijos funkciją

Sprendimas. Šios funkcijos dariniai yra tokie patys kaip ir pati funkcija:

Todėl, val NS= 0 mes turime

Pakeitus šias reikšmes į formulę (32), gauname reikiamą išplėtimą:

(33)

Ši serija susilieja su visa skaičių linija (jos konvergencijos spinduliu).

16.1. Elementarių funkcijų išplėtimas Taylor serijoje ir

Maklaurinas

Parodykime tai, jei rinkinyje apibrėžta savavališka funkcija
, netoli taško
turi daug išvestinių priemonių ir yra galios serijos suma:

tada galima rasti šios serijos koeficientus.

Maitinimo serijos pakaitalas
... Tada
.

Raskite pirmąjį funkcijos darinį
:

At
:
.

Antrajam dariniui gauname:

At
:
.

Tęsiant šią procedūrą n kai tik gausime:
.

Taigi, mes gavome formos galios seriją:

kuris vadinamas šalia Taylor funkcijai
taško apylinkėse
.

Ypatingas „Taylor“ serijos atvejis yra Maclaurin serija adresu
:

Likusi Taylor (Maclaurin) serijos dalis gaunama išmetant iš pagrindinių eilučių n pirmieji nariai ir žymimi kaip
... Tada funkcija
galima parašyti kaip sumą n ankstyvieji numerio nariai
ir likusi dalis
:,

Likusi dalis paprastai
išreikštas skirtingomis formulėmis.

Vienas iš jų yra „Lagrange“ pavidalu:

, kur
.
.

Atkreipkite dėmesį, kad praktiškai „Maclaurin“ serija naudojama dažniau. Taigi, norint parašyti funkciją
galios serijos sumos pavidalu būtina:

1) rasti Maclaurin (Taylor) serijos koeficientus;

2) rasti gautos galios serijos suartėjimo sritį;

3) įrodyti, kad pateikta serija susilieja su funkcija
.

Teorema1 (būtina ir pakankama „Maclaurin“ serijos konvergencijos sąlyga). Tegul serijos suartėjimo spindulys
... Kad ši serija suartėtų intervale
veikti
, būtina ir pakanka, kad būtų įvykdyta sąlyga:
nurodytu intervalu.

2 teorema. Jei bet kurios funkcijos eilės išvestiniai
tam tikru intervalu
absoliučia verte apribotas tuo pačiu skaičiumi M, tai yra
, tada per šį intervalą funkcija
galima išplėsti į „Maclaurin“ seriją.

Pavyzdys1 . Išplėskite Taylor eilutę aplink tašką
funkcija.

Sprendimas.

,
;

.......................................................................................................................................

,
;

Konvergencijos regionas
.

Pavyzdys2 . Išplėsti funkciją Taylor eilėje aplink tašką
.

Sprendimas:

Raskite funkcijos ir jos darinių vertę
.

,
;

...........……………………………

,
.

Mes pakeičiame šias vertes iš eilės. Mes gauname:

arba
.

Raskime šios serijos susiliejimo regioną. Pagal d'Alemberto bruožą serija susilieja, jei

Todėl bet kuriam ši riba yra mažesnė nei 1, todėl serijos konvergencijos sritis bus:
.

Pažvelkime į keletą pagrindinių išplėtimo pavyzdžių „Maclaurin“ pagrindinių elementų serijoje. Prisiminkite, kad „Maclaurin“ serija:

susilieja tarp intervalo
veikti
.

Atminkite, kad norint išplėsti funkciją serijoje, būtina:

a) raskite šios funkcijos Maclaurin serijos koeficientus;

b) apskaičiuoti gautos serijos suartėjimo spindulį;

c) įrodyti, kad gauta eilutė susilieja su funkcija
.

3 pavyzdys. Apsvarstykite funkciją
.

Sprendimas.

Apskaičiuokime funkcijos ir jos darinių vertę
.

Tada serijos skaitiniai koeficientai yra:

bet kam n. Pakeiskite nustatytus koeficientus į „Maclaurin“ seriją ir gaukite:

Raskite gautos serijos suartėjimo spindulį, būtent:

Todėl serija susilieja su intervalu
.

Ši serija atitinka funkciją už bet kokias vertybes nes bet koks tarpas
funkcija o jo išvestines priemones absoliučia verte riboja skaičius .

Pavyzdys4 . Apsvarstykite funkciją
.

Sprendimas.

Nesunku pastebėti, kad lygios tvarkos dariniai
, o dariniai yra nelyginės eilės. Mes pakeičiame nustatytus koeficientus į „Maclaurin“ seriją ir gauname išplėtimą:

Raskime šios serijos suartėjimo intervalą. Remiantis d'Alembertu:

bet kam ... Todėl serija susilieja su intervalu
.

Ši serija atitinka funkciją
, nes visi jo dariniai yra tik vienas.

Pavyzdys5 .
.

Sprendimas.

Raskime funkcijos ir jos darinių vertę ties
:

Taigi šios serijos koeficientai:
ir
, taigi:

Panašiai kaip ir ankstesnėje serijoje, konvergencijos regionas
... Serija susilieja su funkcija
, nes visi jo dariniai yra tik vienas.

Atkreipkite dėmesį, kad funkcija
nelyginis ir serijinis išplėtimas nelyginėmis galiomis, funkcija
- tolygus ir serijinis išplėtimas lygiomis galiomis.

Pavyzdys6 . Binominė serija:
.

Sprendimas.

Raskime funkcijos ir jos darinių vertę ties
:

Iš to aišku, kad:

Pakeiskite šias „Maclaurin“ serijos koeficientų reikšmes ir išplėskite šią funkciją galios serijoje:

Raskite šios serijos suartėjimo spindulį:

Todėl serija susilieja su intervalu
... Ribiniuose taškuose
ir
serija gali arba negali suartėti, priklausomai nuo rodiklio
.

Tiriamos serijos sutampa su intervalu
veikti
, tai yra mokesčio suma
adresu
.

Pavyzdys7 . Išplėskime funkciją „Maclaurin“ serijoje
.

Sprendimas.

Norėdami išplėsti šios funkcijos seriją, mes naudojame dvejetaines serijas
... Mes gauname:

Remdamiesi galios serijų savybėmis (galios serijas galima integruoti į jų konvergencijos sritį), randame šios serijos kairės ir dešinės pusės integralą:

Raskite šios serijos susiliejimo regioną:
,

tai šios serijos konvergencijos regionas yra intervalas
... Apibrėžkime serijos konvergenciją intervalo pabaigoje. At

... Ši eilutė yra harmoninga eilutė, tai yra, ji skiriasi. At
gauname skaičių seriją su bendru terminu
.

Leibnico serija susilieja. Taigi šios serijos konvergencijos regionas yra intervalas
.

16.2. Galios serijos taikymas apytiksliuose skaičiavimuose

Apytiksliais skaičiavimais galios serijos vaidina nepaprastai svarbų vaidmenį. Jų pagalba buvo sudarytos trigonometrinių funkcijų lentelės, logaritmų lentelės, kitų funkcijų reikšmių lentelės, kurios naudojamos įvairiose žinių srityse, pavyzdžiui, tikimybių teorijoje ir matematinėje statistikoje. Be to, funkcijų išplėtimas galios serijoje yra naudingas jų teoriniam tyrimui. Pagrindinė problema, kai apytiksliai naudojami galios serijos, yra klaidos įvertinimo problema, kai serijos suma pakeičiama jos pirmosios sumos suma n nariai.

Apsvarstykite du atvejus:

funkcija išplėsta į kintamas serijas;

funkcija išplėsta į pastovią seriją.

Skaičiavimas naudojant kintamas eilutes

Leiskite funkcijai
išsiplėtė į kintamosios galios seriją. Tada, apskaičiuojant šią funkciją konkrečiai vertei gauname skaitinę seriją, kuriai galima pritaikyti Leibnico testą. Pagal šią funkciją, jei serijos suma pakeičiama jos pirmosios suma n terminai, tada absoliuti paklaida neviršija pirmosios likusios šios serijos dalies, tai yra:
.

Pavyzdys8 . Apskaičiuoti
tikslumas iki 0,0001.

Sprendimas.

Mes naudosime „Maclaurin“ seriją
, pakeisdami kampo vertę radianais:

Jei lyginsime pirmąjį ir antrąjį serijos terminus su tam tikru tikslumu, tada :.

Trečias plėtros terminas:

mažesnis už nurodytą skaičiavimo tikslumą. Todėl apskaičiuoti
pakanka palikti du serijos narius, tai yra

Taigi
.

Pavyzdys9 . Apskaičiuoti
0,001 tikslumu.

Sprendimas.

Mes naudosime binominės serijos formulę. Norėdami tai padaryti, rašykite
kaip:
.

Šia išraiška
,

Palyginkime kiekvieną iš serijos narių nurodytu tikslumu. Aišku, kad
... Todėl apskaičiuoti
pakanka palikti tris eilės narius.

arba
.

Skaičiavimas naudojant teigiamas eilutes

Pavyzdys10 . Apskaičiuokite skaičių tikslumas iki 0,001.

Sprendimas.

Funkcijai iš eilės
pakaitalas
... Mes gauname:

Įvertinkime klaidą, kuri atsiranda, kai serijos suma pakeičiama pirmosios suma nariai. Užrašykime akivaizdžią nelygybę:

tai yra 2<<3. Используем формулу остаточного члена ряда в форме Лагранжа:
,
.

Atsižvelgiant į problemos būklę, reikia rasti n kad būtų tokia nelygybė:
arba
.

Tai nesunku patikrinti n= 6:
.

Vadinasi,
.

Pavyzdys11 . Apskaičiuoti
0,0001 tikslumu.

Sprendimas.

Atminkite, kad norint apskaičiuoti logaritmus, funkcijai galima taikyti seriją
, tačiau ši serija susilieja labai lėtai, o norint pasiekti nurodytą tikslumą, reikėtų priimti 9999 terminus! Todėl, norint apskaičiuoti logaritmus, paprastai naudojama šios funkcijos eilutė
kuris susilieja intervale
.

Paskaičiuokime
naudojant šią eilutę. Leisti būti
, tada .

Vadinasi,
,

Norėdami apskaičiuoti
su tam tikru tikslumu imame pirmųjų keturių terminų sumą:
.

Likusi eilė
išmesti. Įvertinkime klaidą. Akivaizdu, kad

arba
.

Taigi serijoje, kuri buvo naudojama skaičiavimui, funkcijai pakako paimti tik pirmuosius keturis terminus, o ne 9999.
.

Savikontrolės klausimai

1. Kas yra „Taylor“ serija?

2. Kokia buvo „Maclaurin“ serija?

3. Suformuluokite Tayloro serijos funkcijos išplėtimo teoremą.

4. Parašykite „Maclaurin“ serijos pagrindinių funkcijų išplėtimą.

5. Nurodykite nagrinėjamų serijų suartėjimo regionus.

6. Kaip įvertinti apytikslių skaičiavimų paklaidą naudojant galios serijas?

Jei funkcija f (x) turi tam tikrą intervalą, kuriame yra taškas a, visų užsakymų išvestinės priemonės, tada jam gali būti taikoma Taylor formulė:

kur r n- vadinamoji likutinė arba likusi serijos dalis, ją galima apskaičiuoti naudojant Lagranžo formulę:

, kur skaičius x yra tarp NS ir a.

Jei už tam tikrą vertę x r n®0 už n® ¥, tada riboje Taylor formulė šią vertę paverčia konvergentu Taylor serija:

Taigi funkcija f (x) galima išplėsti į „Taylor“ seriją nagrinėjamu metu NS, jei:

1) ji turi visų pavedimų išvestines priemones;

2) sukonstruota serija šioje vietoje susilieja.

At a= 0 gauname seriją pavadinimu netoli Maclaurin:

1 pavyzdys f (x) = 2x.

Sprendimas... Raskime funkcijos ir jos darinių reikšmes NS=0

f (x) = 2x, f ( 0) = 2 0 =1;

f ¢ (x) = 2x ln2, f ¢ ( 0) = 2 0 ln2 = ln2;

f ¢¢ (x) = 2x 22, f ¢¢ ( 0) = 2 0 ln 2 2 = ln 2 2;

f (n) (x) = 2x ln n 2, f (n) ( 0) = 2 0 ln n 2 = ln n 2.

Pakeitus gautas išvestinių verčių vertes į Taylor serijos formulę, gauname:

Šios serijos suartėjimo spindulys yra lygus begalybei, todėl ši plėtra galioja - ¥<x<+¥.

2 pavyzdys NS+4) funkcijai f (x) = e x.

Sprendimas... Raskite funkcijos e vedinius x ir jų vertybes NS=-4.

f (x)= e x, f (-4) = e -4 ;

f ¢ (x)= e x, f ¢ (-4) = e -4 ;

f ¢¢ (x)= e x, f ¢¢ (-4) = e -4 ;

f (n) (x)= e x, f (n) ( -4) = e -4 .

Todėl reikiama funkcijos Taylor serija yra tokios formos:

Šis išplėtimas taip pat galioja - ¥<x<+¥.

3 pavyzdys ... Išplėsti funkciją f (x)= ln x iš eilės galių ( NS- 1),

(t.y. „Taylor“ serijoje netoli taško NS=1).

Sprendimas... Raskite šios funkcijos darinius.

Pakeitus šias reikšmes į formulę, gauname reikiamą Taylor seriją:

Naudojant d'Alembert testą, galima įsitikinti, kad serija susilieja

½ NS- 1½<1. Действительно,

Serija susilieja, jei ½ NS- 1½<1, т.е. при 0<x<2. При NS= 2 gauname kintamą seriją, atitinkančią Leibnizo testo sąlygas. At NS= 0 funkcija neapibrėžta. Taigi „Taylor“ serijos konvergencijos sritis yra pusiau atviras intervalas (0; 2].

Pateiksime panašiai gautus išplėtimus Maclaurin serijoje (t. Y. Netoli taško NS= 0) kai kurioms elementarioms funkcijoms:

(2) ,

(3) ,

( vadinamas paskutinis skilimas binominė serija)

4 pavyzdys ... Išplėskite galios serijos funkciją

Sprendimas... Išplėtime (1) mes pakeičiame NSį - NS 2, gauname:

5 pavyzdys ... Išplėskite „Maclaurin“ serijos funkciją

Sprendimas... Mes turime

Naudodami formulę (4), galime parašyti:

pakeisdamas NSį formulę -NS, mes gauname:

Iš čia randame:

Išplėsdami skliaustus, pertvarkydami serijos sąlygas ir sumažindami panašius terminus, gauname

Ši serija suartėja intervale

(-1; 1), nes jis gaunamas iš dviejų eilučių, kurių kiekviena susilieja per šį intervalą.

Komentuoti .

Formulės (1) - (5) taip pat gali būti naudojamos atitinkamoms Taylor serijos funkcijoms išplėsti, t.y. funkcijų išplėtimui teigiamaisiais sveikais skaičiais ( Cha). Norėdami tai padaryti, per tam tikrą funkciją būtina atlikti tokias pačias transformacijas, kad gautumėte vieną iš funkcijų (1) - (5), kurioje vietoj funkcijos NS kainuoja k ( Cha) m, kur k yra pastovus skaičius, m yra teigiamas sveikasis skaičius. Dažnai patogu keisti kintamąjį t=Cha ir išplėsti gautą funkciją t atžvilgiu Maclaurin serijoje.

Šis metodas iliustruoja teoriją apie funkcijos išplėtimo galios serijoje unikalumą. Šios teoremos esmė yra ta, kad šalia to paties taško negalima gauti dviejų skirtingų galios eilučių, kurios susilietų su ta pačia funkcija, nesvarbu, kaip būtų vykdomas jos išplėtimas.

6 pavyzdys ... Išplėskite „Taylor“ serijos funkciją taško kaimynystėje NS=3.

Sprendimas... Šią problemą, kaip ir anksčiau, galima išspręsti naudojant „Taylor“ serijos apibrėžimą, kuriam reikia rasti funkcijos išvestines priemones ir jų reikšmes NS= 3. Tačiau bus lengviau naudoti esamą skilimą (5):

Gautos serijos sutampa su arba –3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

7 pavyzdys ... Parašykite „Taylor“ seriją galiomis ( NS-1) funkcijos .

Sprendimas.

Serija susilieja , arba 2< x£ 5.