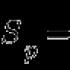Online eine Gerade aus zwei Punkten bauen. Allgemeine Geradengleichung in einer Ebene

Eigenschaften einer Geraden in der euklidischen Geometrie.

Es gibt unendlich viele Linien, die durch jeden Punkt gezogen werden können.

Durch zwei beliebige Punkte, die nicht zusammenfallen, gibt es nur eine Gerade.

Zwei nicht zusammenfallende Linien in der Ebene schneiden sich entweder in einem einzigen Punkt oder sind es

parallel (folgt aus dem vorherigen).

Im dreidimensionalen Raum gibt es drei Möglichkeiten für die relative Position zweier Linien:

Linien schneiden sich;

gerade Linien sind parallel;

Geraden schneiden sich.

Gerade Linie- algebraische Kurve erster Ordnung: im kartesischen Koordinatensystem eine Gerade

ist in der Ebene durch eine Gleichung ersten Grades (lineare Gleichung) gegeben.

Allgemeine Geradengleichung.

Definition. Jede Linie in der Ebene kann durch eine Gleichung erster Ordnung gegeben werden

Ah + Wu + C = 0,

und konstant A, B gleichzeitig nicht gleich Null. Diese Gleichung erster Ordnung wird aufgerufen Allgemeines

Gerade Gleichung. Abhängig von den Werten der Konstanten A, B und MIT Folgende Sonderfälle sind möglich:

. C = 0, A ≠ 0, B ≠ 0- Die Linie geht durch den Ursprung

. A = 0, B ≠0, C ≠0 ( By + C = 0)- Gerade parallel zur Achse Oh

. B = 0, A ≠ 0, C ≠ 0 ( Ax + C = 0)- Gerade parallel zur Achse OU

. B = C = 0, A ≠ 0- Die Linie fällt mit der Achse zusammen OU

. A = C = 0, B ≠ 0- Die Linie fällt mit der Achse zusammen Oh

Die Geradengleichung kann je nach Vorgabe in verschiedenen Formen dargestellt werden

Anfangsbedingungen.

Gleichung einer Geraden durch einen Punkt und einen Normalenvektor.

Definition. In einem kartesischen rechtwinkligen Koordinatensystem ein Vektor mit den Komponenten (A, B)

senkrecht zu der durch die Gleichung gegebenen Linie

Ah + Wu + C = 0.

Beispiel. Finden Sie die Gleichung einer geraden Linie, die durch einen Punkt geht A(1, 2) senkrecht zum Vektor (3, -1).

Lösung. Lassen Sie uns bei A \u003d 3 und B \u003d -1 die Gleichung der geraden Linie zusammenstellen: 3x - y + C \u003d 0. Um den Koeffizienten C zu finden

wir setzen die Koordinaten des gegebenen Punktes A in den resultierenden Ausdruck ein und erhalten somit: 3 - 2 + C = 0

C = -1. Gesamt: die gewünschte Gleichung: 3x - y - 1 \u003d 0.

Gleichung einer Geraden, die durch zwei Punkte geht.

Gegeben seien zwei Punkte im Raum M 1 (x 1 , y 1 , z 1) und M2 (x 2, y 2 , z 2), dann Gerade Gleichung,

diese Punkte durchlaufen:

Wenn einer der Nenner gleich Null ist, sollte der entsprechende Zähler gleich Null gesetzt werden. Auf der

Ebene wird die oben geschriebene Geradengleichung vereinfacht:

wenn x1 ≠ x2 und x = x 1, wenn x1 = x2 .

Fraktion = k namens Neigungsfaktor gerade.

Beispiel. Finden Sie die Gleichung einer geraden Linie, die durch die Punkte A(1, 2) und B(3, 4) verläuft.

Lösung. Wenden wir die obige Formel an, erhalten wir:

Gleichung einer Geraden durch einen Punkt und eine Steigung.

Wenn die allgemeine Gleichung einer geraden Linie Ah + Wu + C = 0 ins Formular bringen:

und benennen , dann wird die resultierende Gleichung aufgerufen

Gleichung einer Geraden mit Steigung k.

Die Gleichung einer Geraden auf einem Punkt und einem Richtungsvektor.

Analog zum Punkt, der die Gleichung einer Geraden durch den Normalenvektor betrachtet, können Sie die Aufgabe eingeben

eine Gerade durch einen Punkt und einen Richtungsvektor einer Geraden.

Definition. Jeder Nicht-Null-Vektor (α 1 , α 2), deren Komponenten die Bedingung erfüllen

Aα 1 + Bα 2 = 0 namens Richtungsvektor der Geraden.

Ah + Wu + C = 0.

Beispiel. Finden Sie die Gleichung einer geraden Linie mit Richtungsvektor (1, -1) und durch den Punkt A(1, 2) verlaufend.

Lösung. Wir suchen die Gleichung der gewünschten Geraden in der Form: Ax + By + C = 0. Laut Definition ist

Koeffizienten müssen die Bedingungen erfüllen:

1 * A + (-1) * B = 0, d.h. A = B.

Dann hat die Geradengleichung die Form: Ax + Ay + C = 0, oder x + y + C / A = 0.

beim x=1, y=2 wir bekommen C/A = -3, d.h. Gewünschte Gleichung:

x + y - 3 = 0

Gleichung einer Geraden in Segmenten.

Wenn in der allgemeinen Gleichung der geraden Linie Ah + Wu + C = 0 C≠0, dann erhalten wir durch Teilen durch -C:

oder wo

Die geometrische Bedeutung der Koeffizienten ist, dass der Koeffizient a die Koordinate des Schnittpunkts ist

gerade mit Achse Oh, ein B- die Koordinate des Schnittpunkts der Linie mit der Achse OU.

Beispiel. Die allgemeine Geradengleichung ist gegeben x - y + 1 = 0. Finden Sie die Gleichung dieser geraden Linie in Segmenten.

C \u003d 1, , a \u003d -1, b \u003d 1.

Normalgleichung einer Geraden.

Wenn beide Seiten der Gleichung Ah + Wu + C = 0 durch Zahl dividieren , welches heisst

normalisierender Faktor, dann bekommen wir

xcosφ + ysinφ - p = 0 -Normalgleichung einer Geraden.

Das Vorzeichen ± des Normierungsfaktors muss so gewählt werden, dass μ * C< 0.

R- die Länge der vom Ursprung zur Linie fallenden Senkrechten,

ein φ - der Winkel, den diese Senkrechte mit der positiven Richtung der Achse bildet Oh.

Beispiel. Gegeben sei die allgemeine Geradengleichung 12x - 5y - 65 = 0. Erforderlich, um verschiedene Arten von Gleichungen zu schreiben

diese Gerade.

Die Gleichung dieser Geraden in Segmenten:

Die Gleichung dieser Geraden mit Steigung: (durch 5 teilen)

Gleichung einer geraden Linie:

cos φ = 12/13; sin φ= -5/13; p=5.

Zu beachten ist, dass nicht jede Gerade durch eine Segmentgleichung dargestellt werden kann, z. B. Geraden,

parallel zu den Achsen oder durch den Ursprung gehend.

Winkel zwischen Linien in einer Ebene.

Definition. Wenn zwei Zeilen angegeben sind y \u003d k 1 x + b 1, y \u003d k 2 x + b 2, dann der spitze Winkel zwischen diesen Linien

wird definiert als

Zwei Geraden sind parallel, wenn k1 = k2. Zwei Geraden sind senkrecht

wenn k1 \u003d -1 / k2 .

Satz.

Direkte Ah + Wu + C = 0 und A 1 x + B 1 y + C 1 \u003d 0 sind parallel, wenn die Koeffizienten proportional sind

A 1 \u003d λA, B 1 \u003d λB. Wenn auch С 1 \u003d λС, dann fallen die Linien zusammen. Koordinaten des Schnittpunktes zweier Geraden

werden als Lösung des Gleichungssystems dieser Geraden gefunden.

Die Gleichung einer Geraden, die durch einen gegebenen Punkt verläuft, steht senkrecht auf einer gegebenen Geraden.

Definition. Eine Linie, die durch einen Punkt verläuft M 1 (x 1, y 1) und senkrecht zur Linie y = kx + b

dargestellt durch die Gleichung:

Der Abstand von einem Punkt zu einer Linie.

Satz. Wenn ein Punkt vergeben wird M(x 0, y 0), dann die Entfernung zur Linie Ah + Wu + C = 0 definiert als:

Nachweisen. Lassen Sie den Punkt M 1 (x 1, y 1)- Die Basis der Senkrechten fällt vom Punkt ab m für ein gegebenes

Direkte. Dann der Abstand zwischen den Punkten m und M 1:

(1)

Koordinaten x 1 und 1 kann als Lösung des Gleichungssystems gefunden werden:

Die zweite Gleichung des Systems ist die Gleichung einer geraden Linie, die senkrecht durch einen gegebenen Punkt M 0 verläuft

gegebene Zeile. Wenn wir die erste Gleichung des Systems in die Form umwandeln:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

dann erhalten wir beim Lösen:

Setzen wir diese Ausdrücke in Gleichung (1) ein, finden wir:

Der Satz ist bewiesen.

Die Linie, die durch den Punkt K(x 0; y 0) und parallel zur Linie y = kx + a verläuft, wird durch die Formel gefunden:

y - y 0 \u003d k (x - x 0) (1)

Wobei k die Steigung der Geraden ist.

Alternative Formel:
Die Linie, die durch den Punkt M 1 (x 1 ; y 1) und parallel zur Linie Ax + By + C = 0 verläuft, wird durch die Gleichung dargestellt

A(x-x 1)+B(y-y 1)=0 . (2)

Beispiel 1. Stellen Sie die Gleichung einer geraden Linie auf, die durch den Punkt M 0 (-2.1) verläuft, und gleichzeitig:
a) parallel zur Geraden 2x+3y -7 = 0;
b) senkrecht zur Linie 2x+3y -7 = 0.
Lösung . Stellen wir die Steigungsgleichung als y = kx + a dar. Dazu übertragen wir alle Werte außer y auf die rechte Seite: 3y = -2x + 7 . Dann dividieren wir die rechte Seite durch den Koeffizienten 3 . Wir erhalten: y = -2/3x + 7/3
Finden Sie die Gleichung NK, die durch den Punkt K(-2;1) parallel zur geraden Linie y = -2 / 3 x + 7 / 3 verläuft
Durch Ersetzen von x 0 \u003d -2, k \u003d -2 / 3, y 0 \u003d 1 erhalten wir:
y-1 = -2 / 3 (x-(-2))
oder
y = -2 / 3 x - 1 / 3 oder 3y + 2x +1 = 0

Beispiel #2. Schreiben Sie die Gleichung einer geraden Linie parallel zur geraden Linie 2x + 5y = 0 und bilden Sie zusammen mit den Koordinatenachsen ein Dreieck mit der Fläche 5.
Lösung . Da die Linien parallel sind, lautet die Gleichung der gewünschten Linie 2x + 5y + C = 0. Die Fläche eines rechtwinkligen Dreiecks, wobei a und b seine Beine sind. Finden Sie die Schnittpunkte der gewünschten Linie mit den Koordinatenachsen:
;
.
Also A(-C/2,0), B(0,-C/5). Ersetzen Sie in der Formel für die Fläche: . Wir erhalten zwei Lösungen: 2x + 5y + 10 = 0 und 2x + 5y - 10 = 0 .

Beispiel #3. Schreiben Sie die Gleichung der Geraden auf, die durch den Punkt (-2; 5) und die parallele Gerade 5x-7y-4=0 verläuft.
Lösung. Diese Gerade lässt sich durch die Gleichung y = 5/7 x – 4/7 (hier a = 5/7) darstellen. Die Gleichung der gewünschten Linie ist y - 5 = 5 / 7 (x - (-2)), d.h. 7(y-5)=5(x+2) oder 5x-7y+45=0 .

Beispiel Nr. 4. Beim Lösen von Beispiel 3 (A=5, B=-7) mit Formel (2) finden wir 5(x+2)-7(y-5)=0.

Beispiel Nummer 5. Schreiben Sie die Gleichung einer Geraden, die durch den Punkt (-2;5) verläuft, und einer parallelen Geraden 7x+10=0.
Lösung. Hier A=7, B=0. Formel (2) ergibt 7(x+2)=0, d.h. x+2=0. Formel (1) ist nicht anwendbar, da diese Gleichung nicht nach y gelöst werden kann (diese Gerade ist parallel zur y-Achse).

Gleichung einer Geraden, die durch zwei Punkte geht. Im Artikel" " Ich habe Ihnen versprochen, den zweiten Weg zur Lösung der vorgestellten Probleme zum Finden der Ableitung mit einem gegebenen Funktionsgraphen und einer Tangente an diesen Graphen zu analysieren. Wir werden diese Methode in untersuchen , nicht verpassen! Warum nächste?

Tatsache ist, dass dort die Formel der Gleichung einer geraden Linie verwendet wird. Natürlich könnte man diese Formel einfach zeigen und dir raten, sie zu lernen. Aber es ist besser zu erklären, woher es kommt (wie es abgeleitet wird). Es ist notwendig! Wenn Sie es vergessen haben, stellen Sie es schnell wieder herwird nicht schwierig sein. Alles ist unten detailliert. Wir haben also zwei Punkte A auf der Koordinatenebene(x 1; y 1) und B (x 2; y 2) wird eine gerade Linie durch die angegebenen Punkte gezogen:

Hier ist die direkte Formel:

*Das heißt, wenn wir die spezifischen Koordinaten der Punkte ersetzen, erhalten wir eine Gleichung der Form y=kx+b.

** Wenn diese Formel einfach „auswendig gelernt“ wird, dann besteht eine hohe Wahrscheinlichkeit, dass man sie mit Indizes verwechselt x. Darüber hinaus können Indizes auf unterschiedliche Weise bezeichnet werden, zum Beispiel:

Deshalb ist es wichtig, die Bedeutung zu verstehen.

Nun die Herleitung dieser Formel. Alles ist sehr einfach!

Die Dreiecke ABE und ACF sind ähnlich in Bezug auf einen spitzen Winkel (das erste Zeichen für die Ähnlichkeit von rechtwinkligen Dreiecken). Daraus folgt, dass die Verhältnisse der entsprechenden Elemente gleich sind, das heißt:

Jetzt drücken wir diese Segmente einfach durch die Differenz der Koordinaten der Punkte aus:

Natürlich wird es keinen Fehler geben, wenn Sie die Beziehungen der Elemente in einer anderen Reihenfolge schreiben (die Hauptsache ist, die Korrespondenz beizubehalten):

Das Ergebnis ist die gleiche Gleichung einer geraden Linie. Das ist alles!

Das heißt, egal wie die Punkte selbst (und ihre Koordinaten) bezeichnet werden, wenn Sie diese Formel verstehen, finden Sie immer die Gleichung einer geraden Linie.

Die Formel kann anhand der Eigenschaften von Vektoren abgeleitet werden, aber das Prinzip der Ableitung ist dasselbe, da wir über die Proportionalität ihrer Koordinaten sprechen werden. In diesem Fall funktioniert die gleiche Ähnlichkeit rechtwinkliger Dreiecke. Meiner Meinung nach ist die oben beschriebene Schlussfolgerung verständlicher)).

Ausgabe über Vektorkoordinaten anzeigen >>>

Es sei eine Gerade auf der Koordinatenebene konstruiert, die durch zwei gegebene Punkte A (x 1; y 1) und B (x 2; y 2) geht. Markieren wir einen beliebigen Punkt C auf der Geraden mit Koordinaten ( x; j). Wir bezeichnen auch zwei Vektoren:

Es ist bekannt, dass für Vektoren, die auf parallelen Linien (oder auf einer Linie) liegen, ihre entsprechenden Koordinaten proportional sind, das heißt:

- wir schreiben die Gleichheit der Verhältnisse der entsprechenden Koordinaten:

Betrachten Sie ein Beispiel:

Finden Sie die Gleichung einer geraden Linie, die durch zwei Punkte mit den Koordinaten (2;5) und (7:3) verläuft.

Sie können nicht einmal die Leitung selbst bauen. Wir wenden die Formel an:

Es ist wichtig, dass Sie die Korrespondenz bei der Erstellung der Quote erfassen. Sie können nichts falsch machen, wenn Sie schreiben:

Antwort: y=-2/5x+29/5 geht y=-0,4x+5,8

Um sicherzustellen, dass die resultierende Gleichung korrekt gefunden wird, überprüfen Sie sie unbedingt - ersetzen Sie die Datenkoordinaten in der Bedingung der Punkte. Sie sollten korrekte Gleichheiten erhalten.

Das ist alles. Ich hoffe, das Material war hilfreich für Sie.

Mit freundlichen Grüßen, Alexander.

P.S: Ich wäre Ihnen dankbar, wenn Sie in sozialen Netzwerken über die Website berichten.

Definition. Jede Linie in der Ebene kann durch eine Gleichung erster Ordnung gegeben werden

Ah + Wu + C = 0,

und die Konstanten A, B sind gleichzeitig ungleich Null. Diese Gleichung erster Ordnung wird aufgerufen die allgemeine Geradengleichung. Abhängig von den Werten der Konstanten A, B und C sind folgende Sonderfälle möglich:

C \u003d 0, A ≠ 0, B ≠ 0 - die Linie verläuft durch den Ursprung

A \u003d 0, B ≠ 0, C ≠ 0 (By + C \u003d 0) - die Linie verläuft parallel zur Ox-Achse

B \u003d 0, A ≠ 0, C ≠ 0 ( Ax + C \u003d 0) - die Linie ist parallel zur Oy-Achse

B \u003d C \u003d 0, A ≠ 0 - die gerade Linie fällt mit der Oy-Achse zusammen

A \u003d C \u003d 0, B ≠ 0 - die gerade Linie fällt mit der Ox-Achse zusammen

Die Geradengleichung kann je nach gegebenen Anfangsbedingungen in verschiedenen Formen dargestellt werden.

Gleichung einer Geraden durch einen Punkt und einen Normalenvektor

Definition. In einem rechtwinkligen kartesischen Koordinatensystem steht ein Vektor mit den Komponenten (A, B) senkrecht auf der Linie, die durch die Gleichung Ax + By + C = 0 gegeben ist.

Beispiel. Finden Sie die Gleichung einer geraden Linie, die durch den Punkt A (1, 2) senkrecht zu (3, -1) verläuft.

Lösung. Bei A = 3 und B = -1 stellen wir die Gleichung einer geraden Linie auf: 3x - y + C = 0. Um den Koeffizienten C zu finden, setzen wir die Koordinaten des gegebenen Punktes A in den resultierenden Ausdruck ein. Wir erhalten: 3 - 2 + C = 0, also C = -1 . Gesamt: die gewünschte Gleichung: 3x - y - 1 \u003d 0.

Gleichung einer Geraden, die durch zwei Punkte geht

Seien zwei Punkte M 1 (x 1, y 1, z 1) und M 2 (x 2, y 2, z 2) im Raum gegeben, dann ist die Gleichung einer geraden Linie, die durch diese Punkte verläuft:

Wenn einer der Nenner gleich Null ist, sollte der entsprechende Zähler gleich Null gesetzt werden.In der Ebene wird die oben geschriebene Geradengleichung vereinfacht:

wenn x 1 ≠ x 2 und x = x 1 wenn x 1 = x 2.

Bruch = k wird aufgerufen Neigungsfaktor gerade.

Beispiel. Finden Sie die Gleichung einer geraden Linie, die durch die Punkte A(1, 2) und B(3, 4) verläuft.

Lösung. Wenden wir die obige Formel an, erhalten wir:

Gleichung einer Geraden aus einem Punkt und einer Steigung

Wenn die Summe Ax + Wu + C = 0 zu der Form führt:

und benennen , dann wird die resultierende Gleichung aufgerufen Gleichung einer Geraden mit einer Steigungk.

Gleichung einer Geraden mit einem Punkt- und Richtungsvektor

Analog zum Absatz über die Gleichung einer Geraden durch den Normalenvektor können Sie die Zuordnung einer Geraden durch einen Punkt und eines Richtungsvektors einer Geraden eingeben.

Definition. Jeder Nicht-Null-Vektor (α 1, α 2), dessen Komponenten die Bedingung A α 1 + B α 2 = 0 erfüllen, wird als Richtungsvektor der Linie bezeichnet

Ah + Wu + C = 0.

Beispiel. Finden Sie die Gleichung einer geraden Linie mit Richtungsvektor (1, -1) und durch den Punkt A(1, 2) verlaufend.

Lösung. Wir suchen die Gleichung der gesuchten Geraden in der Form: Ax + By + C = 0. Gemäß der Definition müssen die Koeffizienten die Bedingungen erfüllen:

1 * A + (-1) * B = 0, d.h. A = B.

Dann hat die Geradengleichung die Form: Ax + Ay + C = 0, oder x + y + C / A = 0. Für x = 1, y = 2 erhalten wir C / A = -3, d.h. Gewünschte Gleichung:

Gleichung einer Geraden in Segmenten

Wenn in der allgemeinen Gleichung der Geraden Ah + Wu + C = 0 C≠0, dann erhalten wir durch Division durch –C: oder

Die geometrische Bedeutung der Koeffizienten ist, dass der Koeffizient ein ist die Koordinate des Schnittpunkts der Linie mit der x-Achse, und B- die Koordinate des Schnittpunkts der Geraden mit der Oy-Achse.

Beispiel. Gegeben sei die allgemeine Gleichung der Linie x - y + 1 = 0. Finde die Gleichung dieser Linie in den Segmenten.

C \u003d 1, , a \u003d -1, b \u003d 1.

Normalgleichung einer Geraden

Wenn beide Seiten der Gleichung Ax + Vy + C = 0 mit der Zahl multipliziert werden , welches heisst normalisierender Faktor, dann bekommen wir

xcosφ + ysinφ - p = 0 –

Normalgleichung einer Geraden. Das Vorzeichen ± des Normierungsfaktors muss so gewählt werden, dass μ * С< 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Beispiel. Angesichts der allgemeinen Gleichung der Linie 12x - 5y - 65 = 0. Es ist erforderlich, verschiedene Arten von Gleichungen für diese Linie zu schreiben.

die Gleichung dieser Geraden in Segmenten:

die Gleichung dieser Geraden mit der Steigung: (dividiere durch 5)

; cos φ = 12/13; sin φ= -5/13; p=5.

Es ist zu beachten, dass nicht jede Gerade durch eine Streckengleichung dargestellt werden kann, z. B. Geraden, die parallel zu den Achsen verlaufen oder durch den Ursprung gehen.

Beispiel. Die Gerade schneidet gleiche positive Segmente auf den Koordinatenachsen ab. Schreiben Sie die Gleichung einer geraden Linie, wenn die Fläche des von diesen Segmenten gebildeten Dreiecks 8 cm 2 beträgt.

Lösung. Die Geradengleichung hat die Form: , ab /2 = 8; ab=16; a=4, a=-4. a = -4< 0 не подходит по условию задачи. Итого: или х + у – 4 = 0.

Beispiel. Schreiben Sie die Gleichung einer geraden Linie, die durch den Punkt A (-2, -3) und den Ursprung geht.

Lösung. Die Geradengleichung hat die Form: , wobei x 1 \u003d y 1 \u003d 0; x 2 \u003d -2; y 2 \u003d -3.

Winkel zwischen Linien in einer Ebene

Definition. Wenn zwei Linien gegeben sind y = k 1 x + b 1 , y = k 2 x + b 2 , dann wird der spitze Winkel zwischen diesen Linien definiert als

Zwei Geraden sind parallel, wenn k 1 = k 2 . Zwei Geraden sind senkrecht, wenn k 1 = -1/ k 2 .

Satz. Die geraden Linien Ax + Vy + C \u003d 0 und A 1 x + B 1 y + C 1 \u003d 0 sind parallel, wenn die Koeffizienten A 1 \u003d λA, B 1 \u003d λB proportional sind. Wenn auch С 1 = λС, dann fallen die Geraden zusammen. Als Lösung des Gleichungssystems dieser Geraden werden die Koordinaten des Schnittpunktes zweier Geraden gefunden.

Gleichung einer Geraden, die durch einen gegebenen Punkt senkrecht zu einer gegebenen Geraden verläuft

Definition. Die Linie, die durch den Punkt M 1 (x 1, y 1) und senkrecht zur Linie y \u003d kx + b verläuft, wird durch die Gleichung dargestellt:

Abstand von Punkt zu Linie

Satz. Wenn ein Punkt M(x 0, y 0) gegeben ist, ist der Abstand zur Linie Ax + Vy + C \u003d 0 definiert als

Nachweisen. Der Punkt M 1 (x 1, y 1) sei die Basis der Senkrechten, die vom Punkt M auf die gegebene Linie fällt. Dann ist der Abstand zwischen den Punkten M und M 1:

(1)

Die Koordinaten x 1 und y 1 finden sich als Lösung des Gleichungssystems:

Die zweite Gleichung des Systems ist die Gleichung einer geraden Linie, die durch einen gegebenen Punkt M 0 senkrecht zu einer gegebenen geraden Linie verläuft. Wenn wir die erste Gleichung des Systems in die Form umwandeln:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

dann erhalten wir beim Lösen:

Setzen wir diese Ausdrücke in Gleichung (1) ein, finden wir:

Der Satz ist bewiesen.

Beispiel. Bestimmen Sie den Winkel zwischen den Linien: y = -3 x + 7; y = 2 x + 1.

k 1 \u003d -3; k2 = 2; tgφ = ; φ = π /4.

Beispiel. Zeigen Sie, dass die Geraden 3x - 5y + 7 = 0 und 10x + 6y - 3 = 0 senkrecht zueinander stehen.

Lösung. Wir finden: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 * k 2 \u003d -1, daher sind die Linien senkrecht.

Beispiel. Die Eckpunkte des Dreiecks A(0; 1), B (6; 5), C (12; -1) sind gegeben. Finden Sie die Gleichung für die vom Scheitelpunkt C gezogene Höhe.

Lösung. Wir finden die Gleichung der Seite AB: ; 4x = 6y - 6;

2x – 3y + 3 = 0;

Die gesuchte Höhengleichung lautet: Ax + By + C = 0 oder y = kx + b. k = . Dann ist y = . Denn die Höhe durch den Punkt C geht, dann erfüllen ihre Koordinaten diese Gleichung: womit b = 17. Gesamt: .

Antwort: 3x + 2y - 34 = 0.

Allgemeine Geradengleichung:

Sonderfälle der allgemeinen Geradengleichung:

und wenn C= 0, Gleichung (2) hat die Form

Axt + Durch = 0,

und die durch diese Gleichung definierte gerade Linie geht durch den Ursprung, da die Koordinaten des Ursprungs x = 0, j= 0 erfüllen diese Gleichung.

b) Wenn in der allgemeinen Gleichung der Geraden (2) B= 0, dann nimmt die Gleichung die Form an

Axt + MIT= 0 oder .

Gleichung enthält keine Variable j, und die durch diese Gleichung definierte Gerade ist parallel zur Achse Ey.

c) Wenn in der allgemeinen Gleichung der Geraden (2) EIN= 0, dann nimmt diese Gleichung die Form an

Durch + MIT= 0, oder ;

Die Gleichung enthält keine Variable x, und die durch sie definierte Gerade ist parallel zur Achse Ochse.

Es sei daran erinnert: Wenn eine gerade Linie parallel zu einer Koordinatenachse verläuft, enthält ihre Gleichung keinen Term, der eine gleichnamige Koordinate mit dieser Achse enthält.

d) Wann C= 0 und EIN= 0 Gleichung (2) nimmt die Form an Durch= 0, oder j = 0.

Dies ist die Achsengleichung Ochse.

e) Wann C= 0 und B= 0 Gleichung (2) kann in der Form geschrieben werden Axt= 0 bzw x = 0.

Dies ist die Achsengleichung Ey.

Gegenseitige Anordnung von Geraden in einer Ebene. Winkel zwischen Linien in einer Ebene. Zustand paralleler Linien. Die Bedingung der Rechtwinkligkeit von Linien.

l 1 l 2 l 1: A 1 x + B 1 y + C 1 = 0
l 2: A 2 x + B 2 y + C 2 = 0

S 2 S 1 Die Vektoren S 1 und S 2 heißen Hilfslinien für ihre Linien.

Der Winkel zwischen den Linien l 1 und l 2 wird durch den Winkel zwischen den Richtungsvektoren bestimmt.
Satz 1: cos-Winkel zwischen l 1 und l 2 \u003d cos (l 1; l 2) \u003d

Satz 2: Damit 2 Zeilen gleich sind, ist es notwendig und ausreichend:

Satz 3: damit 2 Geraden senkrecht stehen ist notwendig und ausreichend:

L 1 l 2 ó A 1 A 2 + B 1 B 2 = 0

Allgemeine Gleichung der Ebene und ihre Sonderfälle. Gleichung einer Ebene in Segmenten.

Allgemeine Ebenengleichung:

Ax + By + Cz + D = 0

Sonderfälle:

1. D=0 Ax+By+Cz = 0 - die Ebene geht durch den Ursprung

2. С=0 Ax+By+D = 0 – Ebene || oz

3. Â=0 Ax+Cz+d = 0 – Ebene || OY

4. A=0 By+Cz+D = 0 – Ebene || OCHSE

5. A=0 und D=0 By+Cz = 0 - die Ebene geht durch OX

6. B=0 und D=0 Ax+Cz = 0 - das Flugzeug passiert OY

7. C=0 und D=0 Ax+By = 0 - das Flugzeug geht durch OZ

Gegenseitige Anordnung von Ebenen und Geraden im Raum:

1. Der Winkel zwischen Linien im Raum ist der Winkel zwischen ihren Richtungsvektoren.

cos(l 1 ; l 2) = cos(S 1 ; S 2) = =

2. Der Winkel zwischen den Ebenen wird durch den Winkel zwischen ihren Normalenvektoren bestimmt.

Cos (l 1 ; l 2) = cos (N 1 ; N 2) = =

3. Der Kosinus des Winkels zwischen einer Geraden und einer Ebene ergibt sich aus dem Sinus des Winkels zwischen dem Richtungsvektor der Geraden und dem Normalenvektor der Ebene.

4. 2 Zeilen || im Raum, wenn ihre || Vektorführer

5. 2 Flugzeuge || wann || normale Vektoren

6. Die Begriffe der Rechtwinkligkeit von Linien und Ebenen werden ähnlich eingeführt.

Frage Nr. 14

Verschiedene Arten der Gleichung einer geraden Linie in einer Ebene (die Gleichung einer geraden Linie in Segmenten, mit einer Steigung usw.)

Gleichung einer Geraden in Segmenten:
Angenommen, in der allgemeinen Geradengleichung gilt:

1. C \u003d 0 Ah + Wu \u003d 0 - die gerade Linie verläuft durch den Ursprung.

2. a \u003d 0 Wu + C \u003d 0 y \u003d

3. in \u003d 0 Axt + C \u003d 0 x \u003d

4. v \u003d C \u003d 0 Axt \u003d 0 x \u003d 0

5. a \u003d C \u003d 0 Wu \u003d 0 y \u003d 0

Die Gleichung einer Geraden mit Steigung:

Jede Gerade, die ungleich der y-Achse ist (B nicht = 0), kann im Folgenden geschrieben werden. bilden:

k = tgα α ist der Winkel zwischen der Geraden und der positiv gerichteten Linie ОХ

b - Schnittpunkt der Geraden mit der OS-Achse

Doc-in:

Ax+By+C = 0

Wu \u003d -Ax-C |: B

Gleichung einer Geraden an zwei Punkten:

Frage Nr. 16

Der endliche Grenzwert einer Funktion an einem Punkt und für x→∞

Endbegrenzung am Punkt x 0:

Die Zahl A wird als Grenze der Funktion y \u003d f (x) für x → x 0 bezeichnet, wenn es für jedes E > 0 b > 0 gibt, so dass für x ≠ x 0 die Ungleichung |x - x 0 erfüllt wird |< б, выполняется условие |f(x) - A| < Е

Die Grenze wird bezeichnet: = A

Endbegrenzung bei Punkt +∞:

Die Zahl A heißt Grenzwert der Funktion y = f(x) für x → + ∞ , wenn für jedes E > 0 ein C > 0 existiert, so dass für x > C die Ungleichung |f(x) - A| gilt< Е

Die Grenze wird bezeichnet: = A

Endbegrenzung bei Punkt -∞:

Die Zahl A heißt Grenzwert der Funktion y = f(x) für x→-∞, wenn für irgendein E< 0 существует С < 0 такое, что при х < -С выполняется неравенство |f(x) - A| < Е