Varijanca u primjerima matematičke statistike. Disperzija diskretne slučajne varijable. Standardna devijacija
Međutim, sama ova karakteristika nije dovoljna za proučavanje slučajna varijabla. Zamislite dva strijelca koji pucaju u metu. Jedan precizno šutira i pogađa blizu centra, a drugi ... samo se zabavlja a ni ne cilja. Ali ono što je smiješno je to srednji rezultat će biti potpuno isti kao kod prvog strijelca! Ovu situaciju uslovno ilustruju sljedeće slučajne varijable:
"Snajper" očekivana vrijednost jednako je, međutim, za "zanimljivu osobu": - takođe je nula!
Stoga, postoji potreba da se kvantifikuje koliko daleko rasuti metke (vrijednosti slučajne varijable) u odnosu na centar mete (očekivanje). dobro i rasipanje prevedeno sa latinskog samo kao disperzija .
Hajde da vidimo kako je ovo definisano. numerička karakteristika na jednom od primjera iz 1. dijela lekcije: 
Tamo smo pronašli razočaravajuće matematičko očekivanje ove igre, a sada moramo izračunati njenu varijansu, koja označeno preko .
Hajde da saznamo koliko su pobede/gubici "razbacani" u odnosu na prosečnu vrednost. Očigledno, za ovo moramo izračunati razlike između vrijednosti slučajne varijable i ona matematičko očekivanje:
–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5
Sada se čini da je potrebno sumirati rezultate, ali ovaj način nije dobar - iz razloga što će se oscilacije lijevo poništiti jedna drugu sa oscilacijama udesno. Tako, na primjer, "amaterski" strijelac (primjer iznad) razlike će biti ![]() , a kada se dodaju dat će nulu, tako da nećemo dobiti nikakvu procjenu raspršenosti njegovog pucanja.
, a kada se dodaju dat će nulu, tako da nećemo dobiti nikakvu procjenu raspršenosti njegovog pucanja.
Da biste zaobišli ovu smetnju, razmislite moduli razlike, ali tehnički razlozi pristup se ukorijenio kada su na kvadrat. Pogodnije je rasporediti rješenje u tablicu: 
I ovdje počinje računati prosjećna težina vrijednost kvadrata odstupanja. Šta je? Njihovo je očekivana vrijednost, što je mjera raspršenja:
![]() – definicija disperzija. Iz definicije je odmah jasno da varijansa ne može biti negativna- obratite pažnju na vežbu!
– definicija disperzija. Iz definicije je odmah jasno da varijansa ne može biti negativna- obratite pažnju na vežbu!
Prisjetimo se kako pronaći očekivanje. Pomnožite kvadratne razlike sa odgovarajućim vjerovatnoćama (nastavak tabele):
- figurativno rečeno, ovo je "vlačna sila",
i sumirajte rezultate:
Ne mislite li da je na pozadini dobitaka rezultat ispao prevelik? Tako je - bili smo na kvadrat, a da bismo se vratili u dimenziju naše igre, potrebno je izvući Kvadratni korijen. Ova vrijednost se zove standardna devijacija
i označava se grčkim slovom "sigma":
Ponekad se ovo značenje naziva standardna devijacija .
Šta je njegovo značenje? Ako odstupimo od matematičkog očekivanja lijevo i desno po sredini standardna devijacija:![]()
– tada će najvjerovatnije vrijednosti slučajne varijable biti „koncentrirane“ na ovom intervalu. Šta zapravo vidimo:
Međutim, dogodilo se da se u analizi raspršenja gotovo uvijek operira konceptom disperzije. Hajde da vidimo šta to znači u vezi sa igricama. Ako u slučaju strijelaca govorimo o "preciznosti" pogodaka u odnosu na centar mete, onda ovdje disperzija karakterizira dvije stvari:
Prvo, očigledno je da kako se stope povećavaju, varijansa se takođe povećava. Dakle, na primjer, ako povećamo za 10 puta, onda će se matematičko očekivanje povećati za 10 puta, a varijansa će se povećati za 100 puta (čim je kvadratna vrijednost). Ali imajte na umu da se pravila igre nisu promijenila! Samo su se stope promijenile, grubo govoreći, prije smo se kladili na 10 rubalja, sada 100.
Druga, zanimljivija stvar je da varijansa karakteriše stil igre. Mentalno popravi stopu igre na nekom određenom nivou, i pogledajte šta je šta ovdje:
Igra niske varijance je oprezna igra. Igrač ima tendenciju da bira najpouzdanije šeme, u kojima ne gubi/pobeđuje previše u jednom trenutku. Na primjer, crveno/crni sistem u ruletu (vidi primjer 4 članka slučajne varijable) .
Igra velike varijance. Često je zovu disperzija igra. Ovo je avanturistički ili agresivni stil igre gdje igrač bira "adrenalinske" šeme. Da se barem prisjetimo "Martingale", u kojoj su sume u igri za redove veličine veće od „tihe“ igre iz prethodnog paragrafa.
Situacija u pokeru je indikativna: postoje tzv čvrsto igrači koji imaju tendenciju da budu oprezni i "drmaju" nad svojim igra znači (bankroll). Nije iznenađujuće da njihov bankroll ne fluktuira mnogo (mala varijansa). Suprotno tome, ako igrač ima veliku varijansu, onda je to agresor. Često rizikuje, pravi velike opklade i može i razbiti ogromnu banku i propasti.
Ista stvar se dešava i na Forexu, i tako dalje - ima mnogo primera.
Štaviše, u svim slučajevima nije bitno da li je igra za peni ili za hiljade dolara. Svaki nivo ima svoje igrače niske i velike varijacije. Pa za prosječnu pobjedu, koliko se sjećamo, "odgovorno" očekivana vrijednost.
Vjerovatno ste primijetili da je pronalaženje varijanse dug i mukotrpan proces. Ali matematika je velikodušna:
Formula za pronalaženje varijanse
Ova formula proizilazi direktno iz definicije varijanse i odmah je puštamo u promet. Kopiraću ploču sa našom igrom odozgo: 
i pronađeno očekivanje.
Izračunavamo varijansu na drugi način. Prvo, pronađimo matematičko očekivanje - kvadrat slučajne varijable. By definicija matematičkog očekivanja:
U ovom slučaju:
Dakle, prema formuli:
Kako kažu, osjetite razliku. A u praksi je, naravno, bolje primijeniti formulu (osim ako uvjet ne zahtijeva drugačije).
Savladavamo tehniku rešavanja i projektovanja:
Primjer 6

Pronađite njegovo matematičko očekivanje, varijansu i standardnu devijaciju.
Ovaj zadatak se nalazi svuda i, po pravilu, nema smislenog značenja.
Možete zamisliti nekoliko sijalica sa brojevima koje svijetle u ludnici sa određenim vjerovatnoćama :)
Rješenje: Pogodno je sumirati glavne proračune u tabeli. Prvo upisujemo početne podatke u gornja dva reda. Zatim izračunavamo proizvode, zatim i na kraju zbrojeve u desnoj koloni: 
Zapravo, skoro sve je spremno. U trećem redu nacrtano je gotovo matematičko očekivanje: ![]() .
.
Disperzija se izračunava po formuli:
I na kraju, standardna devijacija:
- lično, obično zaokružujem na 2 decimale.
Svi proračuni se mogu izvršiti na kalkulatoru, a još bolje - u Excelu:
Ovde je teško pogrešiti :)
Odgovori:
Oni koji žele mogu još više pojednostaviti svoj život i iskoristiti moje kalkulator (demo), što ne samo da će odmah riješiti ovaj zadatak, ali i graditi tematske grafike (dođi uskoro). Program može preuzeti u biblioteci– ako ste preuzeli barem jedan edukativni materijal ili dobiti drugi način. Hvala na podršci projektu!
Nekoliko zadataka za samostalno rješavanje:
Primjer 7
Izračunajte varijansu slučajne varijable iz prethodnog primjera po definiciji.
I sličan primjer:
Primjer 8
Diskretna slučajna varijabla je data vlastitim zakonom distribucije:

Da, vrijednosti slučajne varijable mogu biti prilično velike (primjer iz stvarnog rada), a ovdje, ako je moguće, koristite Excel. Kao, usput, u primjeru 7 - brže je, pouzdanije i ugodnije.
Rješenja i odgovori na dnu stranice.
U zaključku 2. dijela lekcije analizirat ćemo još jedan tipičan zadatak, moglo bi se reći i mali rebus:
Primjer 9
Diskretna slučajna varijabla može uzeti samo dvije vrijednosti: i , i . Vjerovatnoća, matematičko očekivanje i varijansa su poznati.
Rješenje: Počnimo s nepoznatom vjerovatnoćom. Kako slučajna varijabla može uzeti samo dvije vrijednosti, onda je zbir vjerovatnoća odgovarajućih događaja:
i od tada .
Ostaje da se pronađe..., lako je reći :) Ali dobro, počelo je. Po definiciji matematičkog očekivanja: ![]() - zamijeniti poznate vrijednosti:
- zamijeniti poznate vrijednosti:
![]() - i ništa se više ne može istisnuti iz ove jednadžbe, osim što je možete prepisati u uobičajenom smjeru:
- i ništa se više ne može istisnuti iz ove jednadžbe, osim što je možete prepisati u uobičajenom smjeru: ![]()

ili: ![]()
O daljim akcijama, mislim da možete pretpostaviti. Kreirajmo i riješimo sistem: 
Decimale- ovo je, naravno, potpuna sramota; pomnožite obje jednačine sa 10: 
i podijeli sa 2: 
To je bolje. Iz 1. jednačine izražavamo: ![]() (ovo je lakši nacin)- zamjena u 2. jednačini:
(ovo je lakši nacin)- zamjena u 2. jednačini:
![]()
Mi gradimo na kvadrat i napravi pojednostavljenja: 
Množimo sa: 
Kao rezultat, kvadratna jednačina, pronađite njegov diskriminant:
- savršeno!
i dobijamo dva rješenja:
1) ako ![]() , onda
, onda ![]() ;
;
2) ako ![]() , zatim .
, zatim .
Prvi par vrijednosti zadovoljava uslov. OD velika vjerovatnoća sve je tačno, ali, ipak, zapišimo zakon distribucije: 
i izvršite provjeru, odnosno pronađite očekivanje:
Često je u statistici, kada se analizira pojava ili proces, potrebno uzeti u obzir ne samo podatke o prosječnim nivoima proučavanih indikatora, već i raspršivanje ili varijacije u vrijednostima pojedinačnih jedinica , što je važna karakteristika proučavane populacije.
Cijene akcija, obim ponude i potražnje podložni su najvećim varijacijama. kamatne stope in različiti periodi vrijeme i na različitim mjestima.
Glavni pokazatelji koji karakterišu varijaciju , su raspon, varijansa, standardna devijacija i koeficijent varijacije.
Varijacija raspona je razlika između maksimalnog i minimalne vrijednosti znak: R = Xmax – Xmin. Nedostatak ovog indikatora je što on procjenjuje samo granice varijacije osobine i ne odražava njenu fluktuaciju unutar ovih granica.
Disperzija lišen ovog nedostatka. Izračunava se kao prosječni kvadrat odstupanja vrijednosti atributa od njihove prosječne vrijednosti:
Pojednostavljen način izračunavanja varijanse provodi se korištenjem sljedećih formula (jednostavnih i ponderiranih):
Primjeri primjene ovih formula prikazani su u zadacima 1 i 2.
Široko korišten indikator u praksi je standardna devijacija :
Standardna devijacija je definirana kao kvadratni korijen varijanse i ima istu dimenziju kao osobina koja se proučava.
Razmatrani pokazatelji omogućavaju dobijanje apsolutne vrijednosti varijacije, tj. procijeniti ga u mjernim jedinicama osobine koja se proučava. za razliku od njih, koeficijent varijacije mjeri fluktuaciju u relativnom smislu – u odnosu na prosječan nivo, što je u mnogim slučajevima poželjnije.
Formula za izračunavanje koeficijenta varijacije.
Primjeri rješavanja zadataka na temu "Indikatori varijacije u statistici"
Zadatak 1 . Prilikom proučavanja uticaja oglašavanja na veličinu prosječnog mjesečnog depozita u bankama regiona, ispitane su 2 banke. Dobijaju se sljedeći rezultati:
definirati:
1) za svaku banku: a) prosječan mjesečni depozit; b) disperzija doprinosa;
2) prosječan mjesečni depozit za dvije banke zajedno;
3) Disperzija depozita za 2 banke u zavisnosti od reklame;
4) Disperzija depozita za 2 banke, u zavisnosti od svih faktora osim reklamiranja;
5) Ukupna varijansa korišćenjem pravila sabiranja;
6) koeficijent determinacije;
7) Korelacioni odnos.
Rješenje
1) Napravimo proračunsku tabelu za banku sa oglašavanjem . Da bismo odredili prosječni mjesečni depozit, nalazimo sredine intervala. Istovremeno, vrijednost otvoreni interval(prvi) je uslovno izjednačen sa veličinom intervala koji je uz njega (drugi).
Prosječnu veličinu doprinosa nalazimo koristeći ponderiranu aritmetičku sredinu formule:
29.000/50 = 580 rubalja
Disperzija doprinosa se nalazi po formuli:
23 400/50 = 468
Izvršićemo slične radnje za banku bez oglasa :
2) Pronađite prosječan depozit za dvije banke zajedno. Xav \u003d (580 × 50 + 542,8 × 50) / 100 = 561,4 rubalja.
3) Varijancu depozita, za dvije banke, u zavisnosti od reklame, naći ćemo po formuli: σ 2 =pq (formula varijanse alternativnog atributa). Ovdje je p=0,5 udio faktora koji zavise od oglašavanja; q=1-0,5, zatim σ 2 =0,5*0,5=0,25.
4) Pošto je učešće ostalih faktora 0,5, onda je varijansa depozita za dve banke, koja zavisi od svih faktora osim reklama, takođe 0,25.
5) Definisati totalna varijansa koristeći pravilo sabiranja.
= (468*50+636,16*50)/100=552,08
= [(580-561,4)250+(542,8-561,4)250] / 100= 34 596/ 100=345,96
σ 2 = σ 2 činjenica + σ 2 ostatak = 552,08 + 345,96 = 898,04
6) Koeficijent determinacije η 2 = σ 2 činjenica / σ 2 = 345,96/898,04 = 0,39 = 39% - veličina doprinosa zavisi od oglašavanja za 39%.
7) Empirijski odnos korelacije η = √η 2 = √0,39 = 0,62 - odnos je prilično blizak.
Zadatak 2 . Postoji grupisanje preduzeća prema vrednosti tržišnih proizvoda:
Utvrditi: 1) disperziju vrednosti tržišnih proizvoda; 2) standardna devijacija; 3) koeficijent varijacije.
Rješenje
1) Predstavljen uslovom intervalne serije distribucija. Mora se izraziti diskretno, odnosno pronaći sredinu intervala (x"). U grupama zatvorenih intervala, sredinu nalazimo jednostavnom aritmetičkom sredinom. U grupama sa gornjom granicom, kao razliku između ove gornje granice i pola veličine intervala koji slijedi (200-(400 -200):2=100).
U grupama sa donjom granicom - zbir ove donje granice i polovina veličine prethodnog intervala (800+(800-600):2=900).
Obračun prosječne vrijednosti tržišnih proizvoda vrši se prema formuli:
Hsr = k×((Σ((x"-a):k)×f):Σf)+a. Ovdje je a=500 veličina varijante na najvišoj frekvenciji, k=600-400=200 je veličina intervala na najvišoj frekvenciji. Stavimo rezultat u tabelu:
dakle, prosječna vrijednost Tržišni proizvodi za promatrani period u cjelini je Xav = (-5:37) × 200 + 500 = 472,97 hiljada rubalja.
2) Pronalazimo disperziju koristeći sljedeću formulu:
σ 2 = (33/37) * 2002-(472,97-500) 2 = 35,675,67-730,62 = 34,945,05
3) standardna devijacija: σ = ±√σ 2 = ±√34 945,05 ≈ ±186,94 hiljada rubalja.
4) koeficijent varijacije: V \u003d (σ / Xav) * 100 = (186,94 / 472,97) * 100 = 39,52%
Za grupisane podatke rezidualna disperzija- prosjek unutargrupnih disperzija:Gdje je σ 2 j unutargrupna varijansa j -te grupe.
Za negrupisane podatke rezidualna disperzija je mjera tačnosti aproksimacije, tj. aproksimacija linije regresije originalnim podacima: 
gdje je y(t) prognoza prema jednadžbi trenda; y t – početni niz dinamike; n je broj bodova; p je broj koeficijenata regresione jednadžbe (broj varijabli koje objašnjavaju).
U ovom primjeru se zove nepristrasna procjena varijanse.
Primjer #1. Raspodjelu radnika tri preduzeća jednog udruženja po tarifnim kategorijama karakterišu sljedeći podaci:
| Kategorija plate radnika | Broj radnika u preduzeću | ||
| preduzeće 1 | preduzeće 2 | preduzeće 3 | |
| 1 | 50 | 20 | 40 |
| 2 | 100 | 80 | 60 |
| 3 | 150 | 150 | 200 |
| 4 | 350 | 300 | 400 |
| 5 | 200 | 150 | 250 |
| 6 | 150 | 100 | 150 |
definirati:
1. disperzija za svako preduzeće (unutargrupna disperzija);
2. prosjek unutargrupnih disperzija;
3. međugrupna disperzija;
4. ukupna varijansa.
Rješenje.
Prije nego što se pristupi rješavanju problema, potrebno je utvrditi koja je karakteristika efektivna, a koja faktorijalna. U primjeru koji se razmatra, efektivna karakteristika je "Tarifna kategorija", a faktorska karakteristika je "Broj (naziv) preduzeća".
Tada imamo tri grupe (preduzeća) za koje je potrebno izračunati grupni prosjek i unutargrupne varijanse:
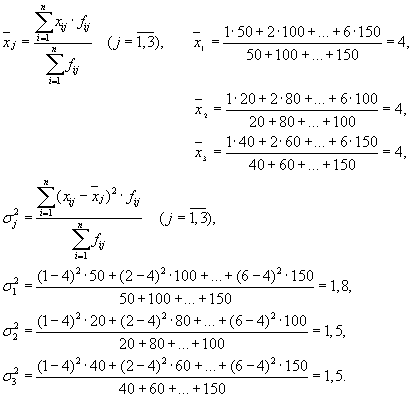
| Kompanija | prosek grupe, | varijansa unutar grupe, |
| 1 | 4 | 1,8 |
Prosek varijansi unutar grupe ( rezidualna disperzija) izračunato po formuli:

gdje možete izračunati:

ili:

onda:
Ukupna disperzija bit će jednaka: s 2 = 1,6 + 0 = 1,6.
Ukupna varijansa se također može izračunati korištenjem jedne od sljedeće dvije formule:

Prilikom rješavanja praktičnih problema često se mora suočiti sa znakom koji ima samo dvije alternativne vrijednosti. U ovom slučaju se ne govori o težini određene vrijednosti neke karakteristike, već o njenom udjelu u agregatu. Ako se udio populacijskih jedinica koje imaju osobinu koja se proučava označava sa " R", a ne posjedovanje - kroz" q“, tada se disperzija može izračunati po formuli:
s 2 = p×q
Primjer #2. Na osnovu podataka o učinku šest radnika brigade utvrditi međugrupnu varijansu i procijeniti uticaj radne smjene na njihovu produktivnost rada ako je ukupna varijansa 12,2.
| br. radne brigade | Radni učinak, kom. | |
| u prvoj smjeni | u 2. smjeni | |
| 1 | 18 | 13 |
| 2 | 19 | 14 |
| 3 | 22 | 15 |
| 4 | 20 | 17 |
| 5 | 24 | 16 |
| 6 | 23 | 15 |
Rješenje. Početni podaci
| X | f1 | f2 | f 3 | f4 | f5 | f6 | Ukupno |
| 1 | 18 | 19 | 22 | 20 | 24 | 23 | 126 |
| 2 | 13 | 14 | 15 | 17 | 16 | 15 | 90 |
| Ukupno | 31 | 33 | 37 | 37 | 40 | 38 |
Tada imamo 6 grupa za koje je potrebno izračunati grupnu srednju vrijednost i unutargrupne varijanse.
1. Pronađite prosječne vrijednosti svake grupe.
2. Pronađite srednji kvadrat svake grupe.
Rezultate proračuna sumiramo u tabeli:
| Broj grupe | Grupni prosjek | Unutargrupna varijansa |
| 1 | 1.42 | 0.24 |
| 2 | 1.42 | 0.24 |
| 3 | 1.41 | 0.24 |
| 4 | 1.46 | 0.25 |
| 5 | 1.4 | 0.24 |
| 6 | 1.39 | 0.24 |
3. Unutargrupna varijansa karakteriše promjenu (varijaciju) proučavane (rezultirajuće) osobine unutar grupe pod utjecajem svih faktora, osim faktora koji leži u osnovi grupisanja:
Izračunavamo prosjek unutargrupnih disperzija koristeći formulu:
4. Međugrupna varijansa karakteriše promjenu (varijaciju) proučavane (rezultirajuće) osobine pod utjecajem faktora (faktorske osobine) koji leži u osnovi grupisanja.
Međugrupna disperzija se definiše kao:
gdje
Onda
Ukupna varijansa karakteriše promjenu (varijaciju) proučavane (rezultirajuće) osobine pod utjecajem svih faktora (faktorskih osobina) bez izuzetka. Po uslovu zadatka jednak je 12,2.
Empirijska korelacija mjeri koliko je ukupne fluktuacije rezultirajućeg atributa uzrokovano proučavanim faktorom. Ovo je omjer faktorske varijanse i ukupne varijanse:
Određujemo empirijsku korelaciju:
Odnosi između karakteristika mogu biti slabe ili jake (bliske). Njihovi kriterijumi se vrednuju na Chaddock skali:
0,1 0,3 0,5 0,7 0,9 U našem primjeru, odnos između faktora Y karakteristike X je slab
Koeficijent determinacije.
Definirajmo koeficijent determinacije:
Dakle, 0,67% varijacije je zbog razlika između osobina, a 99,37% zbog drugih faktora.
Izlaz: u ovom slučaju učinak radnika ne zavisi od rada u određenoj smjeni, tj. uticaj radne smjene na njihovu produktivnost rada nije značajan i uzrokovan je drugim faktorima.
Primjer #3. Na osnovu prosjeka plate i kvadrata odstupanja od njegove vrijednosti za dvije grupe radnika, pronađite ukupnu varijansu primjenom pravila za sabiranje varijansi:
Rješenje:Prosjek varijansi unutar grupe
Međugrupna disperzija se definiše kao:
Ukupna varijansa će biti: 480 + 13824 = 14304
Matematičko očekivanje (prosječna vrijednost) slučajne varijable X, dato na diskretnom prostoru vjerovatnoće, je broj m =M[X]=∑x i p i, ako se niz apsolutno konvergira.
Servisni zadatak. Uz pomoć servisa online modu izračunata su matematička očekivanja, varijansa i standardna devijacija(vidi primjer). Dodatno, iscrtan je graf funkcije distribucije F(X).
Svojstva matematičkog očekivanja slučajne varijable
- Matematičko očekivanje konstantne vrijednosti je jednako samoj sebi: M[C]=C , C je konstanta;
- M=C M[X]
- Matematičko očekivanje zbira slučajnih varijabli jednako je zbiru njihovih matematičkih očekivanja: M=M[X]+M[Y]
- Matematičko očekivanje proizvoda nezavisnih slučajnih varijabli jednako je proizvodu njihovih matematičkih očekivanja: M=M[X] M[Y] ako su X i Y nezavisni.
Svojstva disperzije
- Disperzija konstantne vrijednosti je jednaka nuli: D(c)=0.
- Konstantni faktor se može izvaditi ispod znaka disperzije kvadriranjem: D(k*X)= k 2 D(X).
- Ako su slučajne varijable X i Y nezavisne, tada je varijansa sume jednaka zbroju varijansi: D(X+Y)=D(X)+D(Y).
- Ako su slučajne varijable X i Y zavisne: D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- Za varijansu je važeća formula za izračunavanje:
D(X)=M(X 2)-(M(X)) 2
Primjer. Poznata su matematička očekivanja i varijanse dvije nezavisne slučajne varijable X i Y: M(x)=8, M(Y)=7, D(X)=9, D(Y)=6. Naći matematičko očekivanje i varijansu slučajne varijable Z=9X-8Y+7 .
Rješenje. Na osnovu svojstava matematičkog očekivanja: M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23 .
Na osnovu svojstava disperzije: D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345
Algoritam za izračunavanje matematičkog očekivanja
Svojstva diskretnih slučajnih varijabli: sve njihove vrijednosti mogu se prenumerisati prirodnim brojevima; Dodijelite svakoj vrijednosti vjerovatnoću različitu od nule.- Pomnožite parove jedan po jedan: x i sa p i .
- Dodajemo proizvod svakog para x i p i .
Na primjer, za n = 4: m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
Primjer #1.
| x i | 1 | 3 | 4 | 7 | 9 |
| pi | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
Matematičko očekivanje se nalazi po formuli m = ∑x i p i .
Matematičko očekivanje M[X].
M[x] = 1*0,1 + 3*0,2 + 4*0,1 + 7*0,3 + 9*0,3 = 5,9
Disperzija se nalazi po formuli d = ∑x 2 i p i - M[x] 2 .
disperzija D[X].
D[X] = 1 2 *0,1 + 3 2 *0,2 + 4 2 *0,1 + 7 2 *0,3 + 9 2 *0,3 - 5,9 2 = 7,69
Standardna devijacija σ(x).
σ = sqrt(D[X]) = sqrt(7,69) = 2,78
Primjer #2. Diskretna slučajna varijabla ima sljedeću seriju distribucije:
| X | -10 | -5 | 0 | 5 | 10 |
| R | ali | 0,32 | 2a | 0,41 | 0,03 |
Rješenje. Vrijednost a se nalazi iz relacije: Σp i = 1
Σp i = a + 0,32 + 2 a + 0,41 + 0,03 = 0,76 + 3 a = 1
0,76 + 3 a = 1 ili 0,24=3 a , odakle je a = 0,08
Primjer #3. Odrediti zakon raspodjele diskretne slučajne varijable ako je poznata njena varijansa i x 1
p 1 =0,3; p2=0,3; p3=0,1; p 4 \u003d 0,3
d(x)=12,96
Rješenje.
Ovdje trebate napraviti formulu za pronalaženje varijanse d (x):
d(x) = x 1 2 p 1 +x 2 2 p 2 +x 3 2 p 3 +x 4 2 p 4 -m(x) 2
gdje je očekivanje m(x)=x 1 p 1 +x 2 p 2 +x 3 p 3 +x 4 p 4
Za naše podatke
m(x)=6*0.3+9*0.3+x 3 *0.1+15*0.3=9+0.1x 3
12,96 = 6 2 0,3+9 2 0,3+x 3 2 0,1+15 2 0,3-(9+0,1x 3) 2
ili -9/100 (x 2 -20x+96)=0
Shodno tome, potrebno je pronaći korijene jednačine, a bit će ih dva.
x 3 = 8, x 3 = 12
Biramo onaj koji zadovoljava uslov x 1
Zakon distribucije diskretne slučajne varijable
x 1 =6; x2=9; x 3 \u003d 12; x4=15
p 1 =0,3; p2=0,3; p3=0,1; p 4 \u003d 0,3









