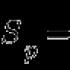Логарифмыг өргөжүүлэх. Логарифмын тодорхойлолт ба түүний шинж чанарууд: онол ба асуудал шийдвэрлэх

Энэ нийтлэлийн гол зүйл бол логарифм. Энд бид логарифмын тодорхойлолтыг өгч, хүлээн зөвшөөрөгдсөн тэмдэглэгээг үзүүлж, логарифмын жишээг өгч, натурал болон аравтын логарифмын талаар ярих болно. Үүний дараа үндсэн логарифмын таних тэмдгийг анхаарч үзээрэй.

Хуудасны навигаци.

Логарифмын тодорхойлолт

Логарифмын тухай ойлголт нь асуудлыг тодорхой утгаар урвуу утгаар шийдвэрлэх үед, зэрэг болон мэдэгдэж буй суурийн мэдэгдэж буй утгаас илтгэгчийг олох шаардлагатай үед үүсдэг.

Гэхдээ хангалттай оршил, "логарифм гэж юу вэ" гэсэн асуултанд хариулах цаг нь болсон уу? Тохиромжтой тодорхойлолтыг өгье.

Тодорхойлолт.

b-ийн логарифм нь a суурь, энд a>0 , a≠1 ба b>0 нь үр дүнд нь b авахын тулд a тоог өсгөх шаардлагатай илтгэгч юм.

Энэ үе шатанд "логарифм" гэсэн үг нь "ямар тоо" ба "ямар үндэслэлээр" гэсэн хоёр асуултыг нэн даруй гаргах ёстой гэдгийг бид тэмдэглэж байна. Өөрөөр хэлбэл, зүгээр л логарифм гэж байдаггүй, харин зарим суурь дээр зөвхөн тооны логарифм байдаг.

Бид даруй танилцуулах болно логарифмын тэмдэглэгээ: b тооны а суурийн логарифмыг ихэвчлэн log a b гэж тэмдэглэдэг. b тооны суурь e ба 10 суурьтай логарифм нь lnb ба lgb гэсэн тусгай тэмдэглэгээтэй, өөрөөр хэлбэл log e b биш, харин lnb, log 10 b биш, харин lgb гэж бичдэг.

Одоо та авчрах боломжтой: .
Мөн бичлэгүүд утгагүй, учир нь тэдгээрийн эхнийх нь логарифмын тэмдгийн дор сөрөг тоо, хоёрдугаарт - суурь дахь сөрөг тоо, гурав дахь нь - логарифмын тэмдгийн дор сөрөг тоо ба суурь дахь нэгж.

Одоо ярилцъя логарифм унших дүрэм. a b оруулгын бүртгэлийг "а суурьтай b-ийн логарифм" гэж уншина. Жишээлбэл, log 2 3 нь гурваас 2 суурьтай байх логарифм бөгөөд тавын квадрат язгуурын гуравны хоёр суурийн хоёр бүхэл тооны логарифм юм. e суурийн логарифм гэж нэрлэдэг байгалийн логарифм, мөн lnb тэмдэглэгээг "b-ийн натурал логарифм" гэж уншина. Жишээлбэл, ln7 нь долоогийн натурал логарифм бөгөөд бид үүнийг pi-ийн натурал логарифм гэж унших болно. 10-р суурийн логарифм нь мөн тусгай нэртэй байдаг - аравтын логарифм, мөн lgb тэмдэглэгээг "аравтын логарифм b" гэж уншина. Жишээлбэл, lg1 нь нэгийн аравтын логарифм, lg2.75 нь хоёр цэгийн далан таван зуутын аравтын логарифм юм.

Логарифмын тодорхойлолтыг өгсөн a>0, a≠1 ба b>0 нөхцлүүдийг тусад нь авч үзэх нь зүйтэй. Эдгээр хязгаарлалтууд хаанаас ирснийг тайлбарлая. Үүнийг хийхийн тулд дээр өгөгдсөн логарифмын тодорхойлолтоос шууд гарах хэлбэрийн тэгш байдал бидэнд туслах болно.

a≠1 -ээр эхэлцгээе. Аль ч хүчинд нэг нь нэгтэй тэнцүү тул тэгш байдал нь зөвхөн b=1-д үнэн байх боловч log 1 1 нь ямар ч бодит тоо байж болно. Энэ хоёрдмол байдлаас зайлсхийхийн тулд a≠1-ийг хүлээн зөвшөөрнө.

a>0 нөхцлийн тохиромжтойг үндэслэл болгоцгооё. a=0 байхад логарифмын тодорхойлолтоор бид тэгш эрхтэй байх ба энэ нь зөвхөн b=0 байхад л боломжтой. Харин тэгээс тэгээс өөр ямар ч хүчин чадал нь тэг байх тул log 0 0 нь ямар ч тэгээс өөр бодит тоо байж болно. a≠0 нөхцөлөөр энэ хоёрдмол байдлаас зайлсхийж болно. Мөн а<0 нам бы пришлось отказаться от рассмотрения рациональных и иррациональных значений логарифма, так как степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Поэтому и принимается условие a>0 .

Эцэст нь b>0 нөхцөл нь a>0 , учир нь тэгш бус байдлаас гарах ба эерэг суурьтай зэрэглэлийн утга үргэлж эерэг байна.

Энэ догол мөрийн төгсгөлд бид логарифмын дуут тодорхойлолт нь логарифмын тэмдгийн доорх тоо нь тодорхой хэмжээний суурь байх үед логарифмын утгыг шууд зааж өгөх боломжийг олгодог гэж бид хэлж байна. Үнэн хэрэгтээ, логарифмын тодорхойлолт нь b=a p бол b тооны а суурийн логарифм нь p-тэй тэнцүү гэдгийг батлах боломжийг бидэнд олгодог. Өөрөөр хэлбэл log a a p =p тэгш байдал үнэн байна. Жишээлбэл, бид 2 3 =8, дараа нь log 2 8=3 гэдгийг мэднэ. Энэ талаар бид нийтлэлд илүү дэлгэрэнгүй ярих болно.

Заавар

Өгөгдсөн логарифм илэрхийллийг бич. Хэрэв илэрхийлэл нь 10-ын логарифмыг ашигладаг бол түүний тэмдэглэгээг богиносгож, дараах байдлаар харагдана: lg b нь аравтын логарифм юм. Хэрэв логарифмын суурь нь e тоотой бол илэрхийлэл бичигдэнэ: ln b нь натурал логарифм юм. Ямар ч гэсэн үр дүн нь b тоог авахын тулд суурь тоог өсгөх ёстой хүчин чадал гэж ойлгогддог.

Хоёр функцийн нийлбэрийг олохдоо та тэдгээрийг нэг нэгээр нь ялгаж, үр дүнг нэмэх хэрэгтэй: (u+v)" = u"+v";

Хоёр функцийн үржвэрийн уламжлалыг олохдоо эхний функцийн деривативыг хоёр дахь функцээр үржүүлж, хоёрдугаар функцийн деривативыг эхний функцээр үржүүлэх шаардлагатай: (u*v)" = u"* v+v"*u;

Хоёр функцийн үржвэрийн деривативыг олохын тулд хуваагч функцээр үржүүлсэн ногдол ашгийн деривативын үржвэрээс хуваагч функцээр үржүүлсэн үржвэрийг хасаж, хуваах шаардлагатай. энэ бүгдийг хуваагч функцээр квадрат. (u/v)" = (u"*v-v"*u)/v^2;

Хэрэв нарийн төвөгтэй функц өгөгдсөн бол дотоод функцийн дериватив ба гаднах функцийн деривативыг үржүүлэх шаардлагатай. y=u(v(x)), дараа нь y"(x)=y"(u)*v"(x) гэе.

Дээр дурдсан зүйлсийг ашиглан та бараг бүх функцийг ялгаж чадна. Тиймээс хэд хэдэн жишээг харцгаая:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^xx^2+6), y"=2*(3*x^2*(e^xx^2+6)+x^3*(e^x-2) *x));
Мөн нэг цэгт деривативыг тооцоолох даалгавар байдаг. y=e^(x^2+6x+5) функцийг өгье, та x=1 цэг дээрх функцийн утгыг олох хэрэгтэй.
1) Функцийн деривативыг ол: y"=e^(x^2-6x+5)*(2*x +6).

2) Өгөгдсөн y"(1)=8*e^0=8 цэг дээрх функцийн утгыг тооцоол.

Холбоотой видеонууд

Хэрэгтэй зөвлөгөө

Анхан шатны деривативын хүснэгтийг сур. Энэ нь маш их цаг хэмнэх болно.

Эх сурвалжууд:

• тогтмол дериватив

Тэгэхээр иррационал тэгшитгэл ба рационал тэгшитгэлийн хооронд ямар ялгаа байдаг вэ? Хэрэв үл мэдэгдэх хувьсагч квадрат язгуур тэмдгийн доор байвал тэгшитгэлийг иррациональ гэж үзнэ.

Заавар

Ийм тэгшитгэлийг шийдвэрлэх гол арга бол хоёр хэсгийг өсгөх арга юм тэгшитгэлдөрвөлжин болгон. Гэсэн хэдий ч. Энэ бол байгалийн зүйл, эхний алхам бол тэмдгийг арилгах явдал юм. Техникийн хувьд энэ арга нь хэцүү биш боловч заримдаа асуудалд хүргэж болзошгүй юм. Жишээ нь v(2x-5)=v(4x-7) тэгшитгэл. Хоёр талыг квадрат болгосноор 2x-5=4x-7 болно. Ийм тэгшитгэлийг шийдвэрлэхэд хэцүү биш; x=1. Гэхдээ 1-ийн тоог өгөхгүй тэгшитгэл. Яагаад? Тэгшитгэлд x утгын оронд нэгжийг орлуулна.Мөн баруун, зүүн тал нь утгагүй илэрхийллийг агуулсан болно, өөрөөр хэлбэл. Ийм утга нь квадрат язгуурт тохирохгүй. Тиймээс 1 нь гадны язгуур тул энэ тэгшитгэлд үндэс байхгүй.

Тиймээс иррационал тэгшитгэлийг түүний хоёр хэсгийг квадрат болгох аргыг ашиглан шийддэг. Тэгшитгэлийг шийдсэний дараа гаднах үндсийг таслах шаардлагатай. Үүнийг хийхийн тулд олсон үндсийг анхны тэгшитгэлд орлуулна.

Өөр нэгийг авч үзье.
2x+vx-3=0
Мэдээжийн хэрэг, энэ тэгшитгэлийг өмнөхтэй ижил тэгшитгэл ашиглан шийдэж болно. Дамжуулах нэгдлүүд тэгшитгэл, квадрат язгуургүй, баруун талд, дараа нь квадратын аргыг хэрэглэнэ. гарсан рационал тэгшитгэл ба язгуурыг шийд. Гэхдээ өөр нэг нь илүү гоёмсог. Шинэ хувьсагч оруулах; vx=y. Үүний дагуу та 2y2+y-3=0 гэсэн тэгшитгэлийг авах болно. Энэ бол ердийн квадрат тэгшитгэл юм. Түүний үндсийг олох; y1=1 ба y2=-3/2. Дараа нь хоёрыг шийд тэгшитгэл vx=1; vx \u003d -3/2. Хоёр дахь тэгшитгэл нь үндэсгүй бөгөөд эхнийхээс бид x=1 гэдгийг олж мэдэв. Үндэсийг шалгах шаардлагатайг бүү мартаарай.

Тодорхойлолтыг шийдвэрлэх нь маш хялбар юм. Энэ нь зорилгодоо хүрэх хүртэл ижил төстэй өөрчлөлтүүдийг хийхийг шаарддаг. Тиймээс хамгийн энгийн арифметик үйлдлүүдийн тусламжтайгаар даалгавар шийдэгдэх болно.

Танд хэрэгтэй болно

• - цаас;
• - үзэг.

Заавар

Ийм хувиргалтуудын хамгийн энгийн нь алгебрийн товчилсон үржүүлэх (нийлбэрийн квадрат (ялгаа), квадратуудын зөрүү, нийлбэр (ялгаа), нийлбэрийн куб (ялгаа) гэх мэт) юм. Үүнээс гадна үндсэндээ ижил төстэй олон тригонометрийн томъёо байдаг.

Үнэн хэрэгтээ хоёр гишүүний нийлбэрийн квадрат нь эхний болон хоёр дахь гишүүний үржвэрийг хоёр дахин нэмсэн хоёр гишүүний квадратыг нэмсэнтэй тэнцүү, өөрөөр хэлбэл (a+b)^2= (a+b) )(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

Хоёуланг нь хялбарчлах

Шийдлийн ерөнхий зарчим

Тодорхой интеграл болох математик анализ эсвэл дээд математикийн сурах бичгээс давт. Таны мэдэж байгаагаар тодорхой интегралын шийдэл нь дериватив нь интеграл өгөх функц юм. Энэ функцийг антидериватив гэж нэрлэдэг. Энэ зарчмын дагуу үндсэн интегралуудыг байгуулна.
Энэ тохиолдолд хүснэгтийн интегралуудын аль нь тохирохыг интеграл хэлбэрээр тодорхойлно. Үүнийг шууд тодорхойлох нь үргэлж боломжгүй байдаг. Ихэнхдээ интегралыг хялбарчлахын тулд хэд хэдэн хувиргалт хийсний дараа хүснэгт хэлбэр нь мэдэгдэхүйц болдог.

Хувьсах орлуулалтын арга

Хэрэв интеграл нь аргумент нь хэд хэдэн олон гишүүнт тригонометрийн функц байвал хувьсагчийн өөрчлөлтийн аргыг ашиглаж үзнэ үү. Үүнийг хийхийн тулд интегралын аргумент дахь олон гишүүнтийг шинэ хувьсагчаар солино. Шинэ болон хуучин хувьсагчийн харьцаанд үндэслэн интеграцийн шинэ хязгаарыг тодорхойлно. Энэ илэрхийлэлийг ялгаснаар -д шинэ дифференциал ол. Тиймээс та хуучин интегралын шинэ хэлбэрийг авах болно, аль ч хүснэгттэй ойрхон эсвэл бүр харгалзах болно.

Хоёр дахь төрлийн интегралуудын шийдэл

Хэрэв интеграл нь хоёр дахь төрлийн интеграл, интегралын вектор хэлбэр бол эдгээр интегралаас скаляр руу шилжих дүрмийг ашиглах шаардлагатай болно. Ийм дүрмийн нэг бол Остроградский-Гаусын харьцаа юм. Энэ хууль нь зарим вектор функцийн роторын урсгалаас өгөгдсөн вектор талбарын дивергенцийг давсан гурвалсан интеграл руу шилжих боломжийг олгодог.

Интеграцийн хязгаарыг орлуулах

Эсрэг деривативыг олсны дараа интеграцийн хязгаарыг орлуулах шаардлагатай. Нэгдүгээрт, дээд хязгаарын утгыг эсрэг деривативын илэрхийлэлд орлуулна. Та хэд хэдэн дугаар хүлээн авах болно. Дараа нь үүссэн тооноос өөр тоог хасч, доод хязгаарыг эсрэг дериватив руу оруулна. Хэрэв интеграцийн хязгаарын нэг нь хязгааргүй бол түүнийг эсрэг дериватив функцэд орлуулахдаа хязгаарт очиж, илэрхийлэл нь юунд чиглэж байгааг олох шаардлагатай.
Хэрэв интеграл нь хоёр хэмжээст эсвэл гурван хэмжээст бол интегралыг хэрхэн тооцоолохыг ойлгохын тулд интегралын геометрийн хязгаарыг илэрхийлэх шаардлагатай болно. Эцсийн эцэст, жишээ нь гурван хэмжээст интегралын хувьд интегралын хязгаар нь нэгтгэх эзлэхүүнийг хязгаарлах бүхэл бүтэн хавтгай байж болно.

Анхан шатны алгебрийн элементүүдийн нэг нь логарифм юм. Энэ нэр нь Грек хэлнээс "тоо" эсвэл "зэрэг" гэсэн үгнээс гаралтай бөгөөд эцсийн тоог олохын тулд тоог үндсэн дээр нь нэмэгдүүлэх шаардлагатай гэсэн утгатай.

Логарифмын төрлүүд

• log a b нь b тооны a суурийн логарифм (a > 0, a ≠ 1, b > 0);
• lg b - аравтын логарифм (логарифмын суурь 10, a = 10);
• ln b - натурал логарифм (логарифмын суурь e, a = e).

Логарифмыг хэрхэн шийдэх вэ?

b тооны а суурийн логарифм нь илтгэгч бөгөөд энэ нь а суурийг b тоо хүртэл өсгөхийг шаарддаг. Үр дүн нь "b-ийн логарифм нь a-ийн суурь" гэсэн үг юм. Логарифмын асуудлын шийдэл бол өгөгдсөн зэрэглэлийг заасан тоонуудын тоогоор тодорхойлох явдал юм. Логарифмыг тодорхойлох, шийдвэрлэх, мөн тэмдэглэгээг өөрөө өөрчлөх үндсэн дүрмүүд байдаг. Тэдгээрийг ашиглан логарифмын тэгшитгэлийг шийдэж, деривативыг олох, интегралыг шийдвэрлэх, бусад олон үйлдлийг гүйцэтгэдэг. Үндсэндээ логарифмын шийдэл нь түүний хялбаршуулсан тэмдэглэгээ юм. Үндсэн томъёо, шинж чанаруудыг доор харуулав.

Ямар ч a ; a > 0; a ≠ 1 ба дурын x хувьд; y > 0.

• a log a b = b нь үндсэн логарифмын таних тэмдэг юм
• log a 1 = 0
• log a a = 1
• log a (x y ) = log a x + log a y
• log a x/ y = log a x – log a y
• log a 1/x = -log a x
• log a x p = p log a x
• log a k x = 1/k log a x , k ≠ 0-ийн хувьд
• log a x = log a c x c
• log a x \u003d log b x / log b a - шинэ суурь руу шилжих томъёо
• log a x = 1/log x a

Логарифмыг хэрхэн шийдвэрлэх вэ - алхам алхмаар шийдвэрлэх заавар

• Эхлээд шаардлагатай тэгшитгэлийг бичнэ үү.

Анхаарна уу: хэрэв суурь логарифм нь 10 бол бичлэгийг богиносгож, аравтын логарифмийг авна. Хэрэв натурал e тоо байгаа бол натурал логарифм болгон бууруулж бичнэ. Энэ нь бүх логарифмын үр дүн нь b тоог олж авахын тулд суурь тоог өсгөх хүч юм гэсэн үг юм.

Шууд шийдэл нь энэ зэргийн тооцоонд оршдог. Логарифм бүхий илэрхийлэлийг шийдэхийн өмнө үүнийг дүрмийн дагуу, өөрөөр хэлбэл томъёо ашиглан хялбарчлах ёстой. Өгүүлэлд бага зэрэг буцаж орсноор та үндсэн шинж чанаруудыг олж болно.

Хоёр өөр тоотой боловч ижил суурьтай логарифмуудыг нэмэх, хасахдаа b ба c тоонуудын үржвэр буюу хуваалтаар нэг логарифмээр солино. Энэ тохиолдолд та шилжилтийн томъёог өөр суурь дээр хэрэглэж болно (дээрхийг үзнэ үү).

Хэрэв та логарифмыг хялбарчлахын тулд илэрхийлэл ашиглаж байгаа бол зарим хязгаарлалтыг анхаарах хэрэгтэй. Энэ нь: a логарифмын суурь нь зөвхөн эерэг тоо боловч нэгтэй тэнцүү биш юм. b тоо нь а шиг тэгээс их байх ёстой.

Илэрхийллийг хялбаршуулсаны дараа та логарифмыг тоон хэлбэрээр тооцоолох боломжгүй байх тохиолдол байдаг. Ийм илэрхийлэл нь утгагүй байдаг, учир нь олон градус нь иррационал тоо юм. Энэ нөхцөлд тооны хүчийг логарифм хэлбэрээр үлдээнэ.

Нийгэм хөгжихийн хэрээр үйлдвэрлэлийн нарийн төвөгтэй байдал, математик хөгжсөн. Энгийнээс нарийн төвөгтэй рүү шилжих хөдөлгөөн. Нягтлан бодох бүртгэлийн ердийн нэмэх, хасах аргаас олон дахин давтагдсанаар тэд үржүүлэх, хуваах тухай ойлголттой болсон. Үржүүлэх давталтын үйлдлийг багасгах нь экспоненциалийн ойлголт болсон. Тоонуудын суурь ба экспонентацийн тооноос хамаарах анхны хүснэгтүүдийг Энэтхэгийн математикч Варасена 8-р зуунд эмхэтгэсэн. Тэдгээрээс та логарифм үүсэх цагийг тоолж болно.

Түүхэн тойм

16-р зуунд Европ дахин сэргэсэн нь механикийн хөгжилд түлхэц өгсөн. Т их хэмжээний тооцоолол шаарддаголон оронтой тоог үржүүлэх, хуваахтай холбоотой. Эртний ширээ нь маш сайн үйлчилгээ үзүүлсэн. Тэд нарийн төвөгтэй үйлдлүүдийг илүү энгийн зүйлээр солих боломжтой болсон - нэмэх, хасах. Математикч Майкл Стифелийн 1544 онд хэвлэгдсэн олон математикчдын санааг хэрэгжүүлсэн ажил нь урагшлах том алхам байв. Энэ нь хүснэгтийг зөвхөн анхны тоо хэлбэрээр градусын хувьд төдийгүй дур зоргоороо оновчтой тоонуудын хувьд ашиглах боломжтой болгосон.

1614 онд шотланд хүн Жон Непьер эдгээр санааг хөгжүүлж байхдаа "тооны логарифм" гэсэн шинэ нэр томъёог анх нэвтрүүлсэн. Синус ба косинусын логарифм, шүргэгчийг тооцоолох шинэ цогц хүснэгтүүдийг эмхэтгэсэн. Энэ нь одон орон судлаачдын ажлыг ихээхэн бууруулсан.

Гурван зууны турш эрдэмтэд амжилттай ашиглаж байсан шинэ хүснэгтүүд гарч ирэв. Алгебрийн шинэ үйл ажиллагаа дууссан хэлбэрээ олж авахаас өмнө маш их цаг хугацаа өнгөрчээ. Логарифмыг тодорхойлж, шинж чанарыг нь судалсан.

Зөвхөн 20-р зуунд тооны машин, компьютер гарч ирснээр хүн төрөлхтөн 13-р зууны турш амжилттай ажиллаж байсан эртний хүснэгтүүдийг орхисон.

Өнөөдөр бид b тоог гаргахын тулд a-ийн хүчин чадал болох x тоог b-ийн логарифм гэж нэрлэдэг. Үүнийг томъёогоор бичнэ: x = log a(b).

Жишээлбэл, log 3(9) нь 2-той тэнцүү байх болно. Хэрэв та тодорхойлолтыг дагаж мөрдвөл энэ нь тодорхой болно. Хэрэв бид 3-ыг 2-ын зэрэглэлд өсгөвөл бид 9-ийг авна.

Тиймээс томъёолсон тодорхойлолт нь зөвхөн нэг хязгаарлалт тавьдаг бөгөөд a ба b тоонууд бодит байх ёстой.

Логарифмын төрөл зүйл

Сонгодог тодорхойлолтыг бодит логарифм гэж нэрлэдэг бөгөөд үнэндээ a x = b тэгшитгэлийн шийдэл юм. a = 1 сонголт нь хил хязгаар бөгөөд сонирхолгүй. Тайлбар: 1-д ямар ч хүч 1 байна.

Логарифмын бодит утгазөвхөн суурь ба аргумент нь 0-ээс их, суурь нь 1-тэй тэнцүү байж болохгүй тохиолдолд л тодорхойлогддог.

Математикийн салбарт онцгой байр суурь эзэлдэглогарифмуудыг тоглуулж, тэдгээрийн суурийн утгаас хамааран нэрлэнэ:

Дүрэм ба хязгаарлалт

Логарифмын үндсэн шинж чанар нь дүрэм юм: бүтээгдэхүүний логарифм нь логарифмын нийлбэртэй тэнцүү байна. log abp = log a(b) + log a(p).

Энэ мэдэгдлийн нэг хувилбар болох нь: log c (b / p) \u003d log c (b) - log c (p), quotient функц нь функцүүдийн зөрүүтэй тэнцүү байна.

Өмнөх хоёр дүрмээс log a(b p) = p * log a(b) гэдгийг хялбархан харж болно.

Бусад шинж чанарууд нь:

Сэтгэгдэл. Нийтлэг алдаа гаргаж болохгүй - нийлбэрийн логарифм нь логарифмын нийлбэртэй тэнцүү биш байна.

Олон зууны турш логарифм олох ажиллагаа нь нэлээд цаг хугацаа шаардсан ажил байв. Математикчид олон гишүүнт тэлэлтийн логарифмын онолын сайн мэддэг томьёог ашигласан:

ln (1 + x) = x - (x^2)/2 + (x^3)/3 - (x^4)/4 + ... + ((-1)^(n + 1))* (( x^n)/n), энд n нь 1-ээс их натурал тоо бөгөөд энэ нь тооцооллын нарийвчлалыг тодорхойлдог.

Бусад сууриудтай логарифмыг нэг баазаас нөгөөд шилжих теорем болон үржвэрийн логарифмын шинж чанарыг ашиглан тооцоолсон.

Энэ арга нь маш их хөдөлмөр, учир нь практик асуудлыг шийдвэрлэх үедхэрэгжүүлэхэд хэцүү байсан тул тэд урьдчилан эмхэтгэсэн логарифмын хүснэгтүүдийг ашигласан нь бүх ажлыг ихээхэн хурдасгасан.

Зарим тохиолдолд логарифмын тусгайлан эмхэтгэсэн графикуудыг ашигласан бөгөөд энэ нь нарийвчлал багатай боловч хүссэн утгыг хайх ажлыг ихээхэн хурдасгасан. Хэд хэдэн цэг дээр суурилагдсан y = log a(x) функцийн муруй нь ердийн захирагчийг ашиглан өөр аль ч цэгээс функцийн утгыг олох боломжийг олгодог. Удаан хугацааны туршид инженерүүд эдгээр зорилгоор график цаас гэж нэрлэгддэг цаасыг ашигладаг байсан.

17-р зуунд анхны туслах аналог тооцооллын нөхцөлүүд гарч ирсэн бөгөөд 19-р зуун гэхэд дууссан хэлбэрийг олж авсан. Хамгийн амжилттай төхөөрөмжийг слайд дүрэм гэж нэрлэдэг. Төхөөрөмжийн энгийн байдлыг үл харгалзан түүний гадаад төрх байдал нь бүх инженерийн тооцооллын үйл явцыг ихээхэн хурдасгасан бөгөөд үүнийг хэт үнэлэхэд хэцүү байдаг. Одоогийн байдлаар цөөхөн хүн энэ төхөөрөмжийг мэддэг.

Тооны машин, компьютер бий болсноор өөр ямар ч төхөөрөмжийг ашиглах нь утгагүй болсон.

Тэгшитгэл ба тэгш бус байдал

Логарифм ашиглан янз бүрийн тэгшитгэл, тэгш бус байдлыг шийдвэрлэхийн тулд дараах томъёог ашигладаг.

• Нэг баазаас нөгөөд шилжих: log a(b) = log c(b) / log c(a);
• Өмнөх хувилбарын үр дүнд: log a(b) = 1 / log b(a).

Тэгш бус байдлыг шийдвэрлэхийн тулд дараахь зүйлийг мэдэх нь зүйтэй.

• Суурь болон аргумент хоёулаа нэгээс их эсвэл бага байвал логарифмын утга эерэг байх болно; хэрэв дор хаяж нэг нөхцөл зөрчвөл логарифмын утга сөрөг байна.
• Хэрэв логарифмын функцийг тэгш бус байдлын баруун ба зүүн талд хэрэглэж, логарифмын суурь нь нэгээс их байвал тэгш бус байдлын тэмдэг хадгалагдана; өөрөөр хэлбэл өөрчлөгдөнө.

Даалгаврын жишээ

Логарифм болон тэдгээрийн шинж чанарыг ашиглах хэд хэдэн сонголтыг авч үзье. Тэгшитгэл шийдвэрлэх жишээ:

Логарифмыг зэрэгт байрлуулах сонголтыг авч үзье.

• Даалгавар 3. 25^log 5(3)-ыг тооцоол. Шийдэл: асуудлын нөхцөлд тэмдэглэгээ нь дараах (5^2)^log5(3) эсвэл 5^(2 * log 5(3))-тай төстэй байна. Үүнийг өөрөөр бичье: 5^log 5(3*2), эсвэл функцын аргумент болох тооны квадратыг функцийн өөрийнх нь квадрат (5^log 5(3))^2 гэж бичиж болно. Логарифмын шинж чанарыг ашиглан энэ илэрхийлэл 3^2 байна. Хариулт: Тооцооллын үр дүнд бид 9-ийг авна.

Практик хэрэглээ

Цэвэр математикийн хэрэгсэл учраас логарифм нь бодит ертөнц дэх объектуудыг дүрслэхдээ гэнэт маш их ач холбогдолтой болсон нь бодит амьдралаас хол хөндий юм шиг санагддаг. Ашиглагдаагүй шинжлэх ухааныг олоход хэцүү байдаг. Энэ нь зөвхөн байгалийн төдийгүй хүмүүнлэгийн мэдлэгийн салбаруудад бүрэн хамаатай.

Логарифмын хамаарал

Тоон хамаарлын зарим жишээ энд байна:

Механик ба физик

Түүхээс харахад механик, физик нь үргэлж математикийн судалгааны аргуудыг ашиглан хөгжиж ирсэн бөгөөд нэгэн зэрэг математик, түүний дотор логарифмийг хөгжүүлэх хөшүүрэг болж байв. Физикийн ихэнх хуулиудын онолыг математикийн хэлээр бичдэг. Логарифм ашиглан физик хуулиудыг тайлбарлах хоёрхон жишээг бид өгсөн.

Сансар судлалын онолын үндэс суурийг тавьсан Циолковскийн томъёог ашиглан пуужингийн хурд гэх мэт нарийн төвөгтэй хэмжигдэхүүнийг тооцоолох асуудлыг шийдвэрлэх боломжтой.

V = I * ln(M1/M2), хаана

• V нь онгоцны эцсийн хурд юм.
• I бол хөдөлгүүрийн тодорхой импульс юм.
• M 1 нь пуужингийн анхны масс юм.
• M 2 - эцсийн масс.

Өөр нэг чухал жишээ- энэ бол термодинамик дахь тэнцвэрийн төлөвийг үнэлэх өөр нэг агуу эрдэмтэн Макс Планкийн томъёонд ашиглах явдал юм.

S = k * ln (Ω), хаана

• S нь термодинамик шинж чанар юм.
• k нь Больцманы тогтмол юм.
• Ω нь янз бүрийн мужуудын статистик жин юм.

Хими

Химийн шинжлэх ухаанд логарифмын харьцааг агуулсан томъёог ашиглах нь тийм ч ойлгомжтой биш юм. Энд зөвхөн хоёр жишээ байна:

• Нернстийн тэгшитгэл, бодисын идэвхжилтэй холбоотой орчны исэлдэлтийн потенциалын нөхцөл, тэнцвэрийн тогтмол.
• Автопролизийн индекс ба уусмалын хүчиллэг зэрэг тогтмол үзүүлэлтүүдийг тооцоолох нь бидний үйл ажиллагаагүйгээр бүрэн гүйцэд биш юм.

Сэтгэл судлал, биологи

Мөн сэтгэл судлал үүнтэй ямар холбоотой вэ гэдэг нь бүрэн ойлгомжгүй юм. Мэдрэхүйн хүчийг энэ функцээр өдөөлтийн эрчмийн утгыг доод эрчимтэй урвуу харьцаа гэж сайн тодорхойлсон нь харагдаж байна.

Дээрх жишээнүүдийн дараа логарифмын сэдвийг биологид өргөнөөр ашиглах болсон нь гайхах зүйлгүй болсон. Логарифмын спиральд тохирох биологийн хэлбэрүүдийн талаар бүхэл бүтэн боть бичиж болно.

Бусад бүс нутаг

Энэ функцтэй холбоогүй бол ертөнц оршин тогтнох боломжгүй юм шиг санагдаж, бүх хуулийг захирдаг. Ялангуяа байгалийн хуулиуд нь геометрийн прогресстой холбоотой байх үед. MatProfi вэбсайтад хандах нь зүйтэй бөгөөд дараах үйл ажиллагааны чиглэлээр ийм олон жишээ байдаг.

Жагсаалт эцэс төгсгөлгүй байж болно. Энэ функцийн үндсэн хуулиудыг эзэмшсэний дараа та хязгааргүй мэргэн ухааны ертөнцөд орох боломжтой.

274. Тайлбар.

а)Хэрэв үнэлэх илэрхийлэл нь агуулна нийлбэрэсвэл ялгаатоонууд, дараа нь тэдгээрийг энгийн нэмэх, хасах замаар хүснэгтийн тусламжгүйгээр олох ёстой. Жишээлбэл:

бүртгэл (35 + 7.24) 5 = 5 бүртгэл (35 + 7.24) = 5 бүртгэл 42.24.

б)Хэрхэн логарифмын илэрхийллийг мэдэхийн тулд бид логарифмын өгөгдсөн үр дүнгээс урвуу байдлаар энэ үр дүнг олж авсан илэрхийллийг олох боломжтой; тийм бол

бүртгэл X= бүртгэл а+лог б- 3 лог -тай,

үүнийг төсөөлөхөд амархан

v)Логарифмын хүснэгтийн бүтцийг авч үзэхийн өмнө бид аравтын бутархай логарифмын зарим шинж чанарыг зааж өгөх болно. 10-ын тоог үндэс болгон авсан хүмүүс (тооцоолдолд зөвхөн ийм логарифмуудыг ашигладаг).

Хоёрдугаар бүлэг.

Аравтын логарифмын шинж чанарууд.

275 . а) 10 1 = 10, 10 2 = 100, 10 3 = 1000, 10 4 = 10000 гэх мэт тул лог 10 = 1, лог 100 = 2, лог 1000 = 3, лог 10000 = 4 гэх мэт.

гэсэн үг, Тэгтэй нэгээр илэрхийлэгдсэн бүхэл тооны логарифм нь тухайн тооны зурагт тэг байгаатай адил олон нэгийг агуулсан эерэг бүхэл тоо юм.

Энэ замаар: бүртгэл 100,000 = 5, бүртгэл 1000 000 = 6 , гэх мэт.

б) Учир нь

log 0.1 = -l; бүртгэл 0.01 = - 2; бүртгэл 0.001 == -3; бүртгэл 0.0001 = - 4,гэх мэт.

гэсэн үг, Аравтын бутархайн логарифм, тэргүүлэгч тэгтэй нэгжээр илэрхийлэгдэх бутархайн логарифм нь бутархайн зурганд 0 бүхэл тоо зэрэг олон сөрөг нэгж агуулсан сөрөг бүхэл тоо юм.

Энэ замаар: log 0.00001= - 5, log 0.000001 = -6,гэх мэт.

v)Жишээлбэл, тэгтэй нэгжээр илэрхийлэгдээгүй бүхэл тоог ав. 35, эсвэл бутархай бүхэл тоо, жишээ нь. 10.7. Ийм тооны логарифм нь бүхэл тоо байж болохгүй, учир нь 10-ыг бүхэл тоон үзүүлэлттэй (эерэг эсвэл сөрөг) зэрэглэлд хүргэх замаар бид тэгтэй 1-ийг (1-ийн араас эсвэл өмнөх) авна. Ийм тооны логарифм нь зарим бутархай байна гэж бодъё а / б . Тэгвэл бид тэгш эрхтэй болно

Гэхдээ эдгээр тэгш байдал нь боломжгүй юм 10а нь тэгтэй 1, харин хүч 35б болон 10,7б үзүүлэлт байхгүй б тэгтэй 1-ийг өгөх боломжгүй. Тиймээс үүнийг зөвшөөрөх боломжгүй бүртгэл 35болон бүртгэл 10.7бутархайтай тэнцүү байв. Гэхдээ логарифмын функцийн шинж чанаруудаас бид () эерэг тоо бүр логарифмтай гэдгийг мэднэ; тиймээс 35 ба 10.7 тоо тус бүр өөрийн гэсэн логарифмтай бөгөөд энэ нь бүхэл тоо, бутархай тоо ч байж чадахгүй тул иррационал тоо тул тоогоор яг илэрхийлэх боломжгүй. Ихэвчлэн иррационал логарифмуудыг ойролцоогоор аравтын бутархайгаар хэд хэдэн аравтын бутархайгаар илэрхийлдэг. Энэ бутархайн бүхэл тоо (хэдийгээр "0 бүхэл тоо" байсан ч гэсэн) дуудагдана онцлог, ба бутархай хэсэг нь логарифмын мантис юм. Жишээлбэл, логарифм бол 1,5441 , дараа нь түүний шинж чанар юм 1 , мөн мантисса байна 0,5441 .

G)Жишээлбэл, бүхэл тоо эсвэл холимог тоог авч үзье. 623 эсвэл 623,57 . Ийм тооны логарифм нь шинж чанар ба мантиасаас бүрдэнэ. Аравтын бутархай логарифмууд ийм тохь тухтай байдаг нь харагдаж байна Бид тэдгээрийн шинж чанарыг нэг төрлийн тоогоор үргэлж олж чадна . Үүнийг хийхийн тулд бид өгөгдсөн бүхэл тоонд эсвэл холимог тооны бүхэл хэсэгт хэдэн цифр байгааг тоолно.Эдгээр тоонуудын жишээн дээр бид 3 . Тиймээс тоо тус бүр 623 болон 623,57 100-аас дээш боловч 1000-аас бага; Энэ нь тус бүрийн логарифм нь их байна гэсэн үг бүртгэл 100, өөрөөр хэлбэл илүү 2 , гэхдээ бага бүртгэл 1000, өөрөөр хэлбэл бага 3 (илүү их тоо нь том логарифмтай байдаг гэдгийг санаарай). Тиймээс, бүртгэл 623 = 2,..., ба бүртгэл 623.57 = 2,... (цэг нь үл мэдэгдэх мантисуудыг орлоно).

Үүнтэй адилаар бид олдог:

10 < 56,7 < 100 1 < log56,7 < 2 бүртгэл 56,7 = 1,...

1000 < 8634 < 10 000 3 < log8634 < 4 бүртгэл 8634 = 3,...

Өгөгдсөн бүхэл тоо буюу холимог тооны бүхэл хэсгийг ерөнхийд нь агуулна м цифрүүд. Хамгийн бага бүхэл тоо агуулсан тул м тоонууд, тэнд 1 -тай м - 1 дараа нь тэг, дараа нь (өгөгдсөн тоог тэмдэглэнэ Н) бид тэгш бус байдлыг бичиж болно:

мөн иймээс

м - 1 < log N < м ,

log N = ( м- 1) + эерэг бутархай.

Тиймээс шинж чанар logN = м - 1 .

Үүнийг бид ийм байдлаар харж байна бүхэл тоо эсвэл холимог тооны логарифмын шинж чанар нь тухайн тооны бүхэл хэсэгт нэггүй цифр байгаатай адил олон эерэг тоог агуулна.

Үүнийг харгалзан бид шууд бичиж болно:

бүртгэл 7,205 = 0,...; log83 = 1,...; бүртгэл 720.4 = 2,...гэх мэт.

д)-аас бага аравтын бутархайг авч үзье 1 (жишээ нь байх 0 бүхэл тоо): 0,35; 0,07; 0,0056; 0,0008, гэх мэт.

Иймд эдгээр логарифм тус бүр нь нэгээр ялгаатай хоёр сөрөг бүхэл тоонуудын хооронд байрладаг; тиймээс тэдгээр нь тус бүр нь эерэг бутархайгаар нэмэгдсэн эдгээр сөрөг тоонуудын багатай тэнцүү байна. Жишээлбэл, log0.0056= -3 + эерэг бутархай. Энэ бутархай 0.7482 байна гэж бодъё. Дараа нь энэ нь:

бүртгэл 0,0056 = - 3 + 0,7482 (= - 2,2518).

зэрэг дүн - 3 + 0,7482 , сөрөг бүхэл тоо ба эерэг аравтын бутархайгаас бүрдэх ба логарифмын тооцоололд дараах байдлаар товчилсон бичихээр тохиролцов. 3 ,7482 (Ийм тоо нь: 3-ыг хасахтай, 7482 арван мянганы нэг). Тиймээс дээрх хүснэгтээс үүнийг харж болно

бүртгэл 0.35 == 1 ,.....; бүртгэл 0.07 = 2 ,.....; бүртгэл 0.0008 = 4 ,....

Ер нь болъё . эхний чухал оронтой аравтын бутархай байдаг α зардал м тэг, түүний дотор 0 бүхэл тоо. Тэгвэл энэ нь ойлгомжтой

- м < log A < - (м- 1).

Хоёр бүхэл тооноос:- м ба - (м- 1) бага байна м , дараа нь

log A = - м+ эерэг бутархай,

улмаар шинж чанар log A = - м (эерэг мантисатай).

Энэ замаар, 1-ээс бага аравтын бутархайн логарифмын шинж чанар нь эхний чухал цифрийн урд байрлах аравтын бутархайн зурганд тэгтэй тэнцэх хэмжээний сөрөг тоо, түүний дотор тэг бүхэл тоог агуулна; ийм логарифмын мантис эерэг байна.

д)Зарим тоог үржүүл Н(бүхэл эсвэл бутархай - хамаагүй) 10-аар, 100-аар 1000-аар..., ерөнхийдөө 1-ээр тэгтэй. Энэ хэрхэн өөрчлөгдөхийг харцгаая бүртгэл Н. Бүтээгдэхүүний логарифм нь хүчин зүйлийн логарифмын нийлбэртэй тэнцүү тул

log(N 10) = log N + log 10 = log N + 1;

log(N 100) = log N + log 100 = log N + 2;

log(N 1000) = log N + log 1000 = log N + 3;гэх мэт.

Хэзээ бүртгэл НБид бүхэл тоог нэмбэл, энэ тоог мантисад биш харин шинж чанарт нэмж болно.

Тэгэхээр, хэрэв log N = 2.7804 бол 2.7804 + 1 = 3.7804; 2.7804 + 2 = 4.7801 гэх мэт;

эсвэл log N = 3.5649 бол 3.5649 + 1 = 2.5649; 3.5649 + 2 = 1.5649 гэх мэт.

Тоог 10, 100, 1000, .., ерөнхийдөө 1-ээр тэгээр үржүүлэхэд логарифмын мантис өөрчлөгдөхгүй бөгөөд үржүүлэгчид тэг байх тусам шинж чанар нь олон нэгжээр нэмэгддэг. .

Үүний нэгэн адил, хуваагчийн логарифмгүйгээр хуваагчийн логарифм нь ногдол ашгийн логарифмтай тэнцүү болохыг харгалзан бид дараахь зүйлийг авна.

log N / 10 = log N - log 10 = log N -1;

log N / 100 = log N - log 100 = log N -2;

log N / 1000 = log N - log 1000 = log N -3;гэх мэт.

Хэрэв бид логарифмаас бүхэл тоог хасахдаа энэ бүхэл тоог шинж чанараас үргэлж хасаж, мантисыг өөрчлөхгүй байхыг зөвшөөрвөл бид дараахь зүйлийг хэлж болно.

Тоог 1-ээр тэгээр хуваахад логарифмын мантис өөрчлөгддөггүй бөгөөд хуваагч дахь тэг байгаа тоогоор шинж чанар нь хэдэн нэгжээр буурдаг.

276. Үр дагавар.өмчөөс ( д) бид дараах хоёр дүгнэлтийг гаргаж болно.

а) Аравтын бутархай тооны логарифмын мантис нь тоон дотор таслалаар зөөгдөхөөс өөрчлөгддөггүй. , учир нь таслалыг зөөх нь 10, 100, 1000 гэх мэтийг үржүүлэх эсвэл хуваахтай тэнцүү юм. Иймээс тооны логарифмууд:

0,00423, 0,0423, 4,23, 423

Зөвхөн шинж чанараараа ялгаатай боловч мантисаар ялгаатай (бүх мантис эерэг байвал).

б) Ижил чухал хэсэгтэй, гэхдээ төгсгөлд нь зөвхөн тэгээр ялгаатай тоонуудын мантис нь ижил байна. 23, 230, 2300, 23000 гэсэн тоонуудын логарифмууд нь зөвхөн шинж чанараараа ялгаатай.

Сэтгэгдэл. Аравтын бутархай логарифмын эдгээр шинж чанаруудаас харахад бүхэл тоо ба аравтын бутархайн логарифмын шинж чанарыг хүснэгтийн тусламжгүйгээр олж болно (энэ нь аравтын бутархай логарифмын хамгийн тохиромжтой тал юм); үр дүнд нь логарифмын хүснэгтэд зөвхөн нэг мантиса байрлуулсан; Үүнээс гадна бутархайн логарифмийг олох нь бүхэл тооны логарифмийг олох хүртэл буурдаг тул (бутархайн логарифм = хуваарийн логарифмгүй тоологчийн логарифм) зөвхөн бүхэл тоонуудын логарифмуудын мантисуудыг дараах хэсэгт байрлуулна. хүснэгтүүд.

Гуравдугаар бүлэг.

Дөрвөн оронтой хүснэгтийн төхөөрөмж ба хэрэглээ.

277. Логарифмын системүүд.Логарифмын систем гэдэг нь нэг суурь дахь дараалсан бүхэл тоонуудын цуваагаар тооцсон логарифмын багц юм. Хоёр системийг ашигладаг: энгийн эсвэл аравтын бутархай логарифмын систем бөгөөд үүнд тоог үндэс болгон авдаг 10 , мөн иррационал тоог үндэс болгон авдаг натурал логарифмын систем (зарим шалтгааны улмаас математикийн бусад салбаруудад ойлгогддог) 2,7182818 ... Тооцооллын хувьд аравтын бутархай логарифмийг ашигладаг бөгөөд энэ нь бид ийм логарифмын шинж чанарыг жагсаахдаа заасан тав тухтай байдлын улмаас юм.

Байгалийн логарифмыг логарифмыг зохион бүтээгч Шотландын математикчийн нэрээр Нэпиерийн логарифм гэж бас нэрлэдэг. Непера(1550-1617), аравтын логарифмууд - профессорын нэрэмжит Бригг бригагаЭдгээр логарифмын хүснэгтүүдийг анх эмхэтгэсэн хүн (Напиерын орчин үеийн, найз).

278. Сөрөг логарифмыг эерэг мантистай нэг болгон хувиргах, урвуу хувиргалт. 1-ээс бага тооны логарифмууд сөрөг байдгийг бид харсан. Тиймээс тэдгээр нь сөрөг шинж чанар ба сөрөг мантиасаас бүрдэнэ. Ийм логарифмыг үргэлж хувиргах боломжтой бөгөөд ингэснээр мантиса нь эерэг, шинж чанар нь сөрөг хэвээр байна. Үүнийг хийхийн тулд мантисад эерэг нэгж, шинж чанарт сөрөг нэгж нэмэхэд хангалттай (мэдээжийн хэрэг, үүнээс логарифмын утга өөрчлөгдөхгүй).

Жишээлбэл, бид логарифмтай бол - 2,0873 , дараа нь та бичиж болно:

- 2,0873 = - 2 - 1 + 1 - 0,0873 = - (2 + 1) + (1 - 0,0873) = - 3 + 0,9127,

эсвэл товчилсон:

Эсрэгээр сөрөг шинж чанар, эерэг мантис бүхий аливаа логарифмыг сөрөг болгон хувиргаж болно. Үүнийг хийхийн тулд сөрөг нэгжийг эерэг мантисад, эерэгийг сөрөг шинж чанарт хавсаргахад хангалттай: иймээс та дараахь зүйлийг бичиж болно.

279. Дөрвөн оронтой хүснэгтийн тодорхойлолт.Ихэнх практик асуудлыг шийдвэрлэхийн тулд дөрвөн оронтой хүснэгтүүд хангалттай бөгөөд тэдгээрийг зохицуулах нь маш энгийн. Эдгээр хүснэгтүүдийг (дээд талд нь "логарифмууд"-тай) энэ номын төгсгөлд байрлуулсан бөгөөд тэдгээрийн багахан хэсгийг (байршлыг тайлбарлахын тулд) энэ хуудсан дээр хэвлэсэн болно. Тэд мантисуудыг агуулдаг.

Логарифм.

-аас бүх бүхэл тооны логарифмууд 1 өмнө 9999 багтаасан, дөрвөн аравтын орон хүртэл тооцоолсон, эдгээр аравтын бутархайн сүүлийнх нь нэмэгдэж байна 1 5-р бутархай нь 5 буюу 5-аас дээш байх ёстой бүх тохиолдолд; Тиймээс 4 оронтой хүснэгтүүд нь ойролцоогоор мантисыг өгдөг 1 / 2 арван мянганы хэсэг (дутагдалтай эсвэл илүүдэлтэй).

Бид аравтын бутархайн логарифмын шинж чанарт үндэслэн бүхэл тоо эсвэл аравтын бутархайн логарифмийг шууд тодорхойлж чаддаг тул хүснэгтээс зөвхөн мантисыг авах ёстой; Үүний зэрэгцээ аравтын бутархай дахь таслалын байрлал, мөн тооны төгсгөл дэх тэгийн тоо нь мантисын утгад нөлөөлөхгүй гэдгийг санах нь зүйтэй. Тиймээс өгөгдсөн тооны мантисыг олохдоо бид энэ тооны таслалыг, хэрэв байгаа бол төгсгөлд байгаа тэгүүдийг хасч, үүний дараа үүссэн бүхэл тооны мантисыг олно. Энэ тохиолдолд дараах тохиолдлууд үүсч болно.

1) Бүхэл тоо нь 3 цифрээс бүрдэнэ.Жишээлбэл, 536 тооны логарифмын мантисыг олъё. Энэ тооны эхний хоёр орон, өөрөөр хэлбэл 53 нь зүүн талын эхний босоо баганын хүснэгтүүдээс олддог (хүснэгтийг үз). 53 дугаарыг олсны дараа бид түүнээс хэвтээ шугамын дагуу баруун тийш хөдөлж, дээд талд байрлуулсан 0, 1, 2, 3, ... 9 тоонуудын аль нэгээр нь дамждаг босоо баганатай огтлолцох хүртэл (болон) Хүснэгтийн доод талд байгаа бөгөөд энэ нь энэ тооны 3-р цифрийг төлөөлдөг, өөрөөр хэлбэл бидний жишээн дээр 6 дугаар байна. Уулзвар дээр бид 536 тооны логарифмд хамаарах мантиса 7292 (өөрөөр хэлбэл 0.7292) авна. Үүний нэгэн адил, 508 тооны хувьд бид мантисыг 0.7059, 500 тооны хувьд 0.6990 гэх мэтийг олно.

2) Бүхэл тоо нь 2 эсвэл 1 цифрээс бүрдэнэ.Дараа нь бид оюун ухаанаараа энэ тоонд нэг эсвэл хоёр тэг оноож, үүссэн гурван оронтой тооны мантиссыг олдог. Жишээлбэл, бид 51-ийн тоонд нэг тэг оноож, үүнээс 510-ыг авч, мантиса 7070-ыг олно; бид 5-ын тоонд 2 тэг оноож, мантиса 6990 гэх мэтийг олдог.

3) Бүхэл тоог 4 оронтой тоогоор илэрхийлнэ.Жишээлбэл, та 5436 логоны мантисыг олох хэрэгтэй. Дараа нь бид эхлээд хүснэгтээс энэ тооны эхний 3 оронтой тоонд, өөрөөр хэлбэл 543 (энэ мантиса нь 7348 байх болно) заасан тооны мантиссыг олж болно. ); дараа нь бид олсон мантиасаас хэвтээ шугамын дагуу баруун тийш (хүснэгтийн баруун талд, зузаан босоо шугамын ард байрладаг) босоо баганатай огтлолцох хүртэл тоонуудын аль нэгээр нь шилжинэ: 1, 2 3, . .. 9, хүснэгтийн энэ хэсгийн дээд талд (болон доод талд) зогсож байгаа бөгөөд энэ нь өгөгдсөн тооны 4-р цифрийг төлөөлдөг, өөрөөр хэлбэл, бидний жишээн дээр 6-р тоо. Уулзвар дээр бид залруулга (тоо) олдог. 5), 5436 дугаартай мантисыг авахын тулд 7348 мантисад хэрэглэх ёстой; Ингэснээр бид 0.7353 мантиса авах болно.

4) Бүхэл тоог 5 ба түүнээс дээш цифрээр илэрхийлнэ.Дараа нь бид эхний 4-өөс бусад бүх цифрүүдийг хаяж, ойролцоогоор дөрвөн оронтой тоог авч, энэ тооны сүүлийн оронг 1-ээр нэмэгдүүлнэ. тухайн тооны хаясан 5-р орон 5 ба 5-аас дээш байх тохиолдол. Тэгэхээр 57842-ын оронд 5784, 30257-ын оронд 3026, 583263-ын оронд 5833 гэх мэтийг авна. Энэхүү дугуйрсан дөрвөн оронтой тооны хувьд бид одоо тайлбарласны дагуу мантиссыг олдог.

Эдгээр зааврын дагуу бид жишээ нь дараах тоонуудын логарифмуудыг олох болно.

36,5; 804,7; 0,26; 0,00345; 7,2634; 3456,06.

Юуны өмнө, одоохондоо хүснэгтүүдийг дурдаагүй байж, дараа нь бичсэн мантисуудад зай үлдээж, зарим шинж чанаруудыг бичье.

бүртгэл 36.5 = 1,.... бүртгэл 0.00345 = 3 ,....

log 804.7 = 2,.... log 7.2634 = 0,....

бүртгэл 0.26 = 1 ,.... бүртгэл 3456.86 = 3,....

бүртгэл 36.5 = 1.5623; бүртгэл 0.00345 = 3.5378;

бүртгэл 804.7 = 2.9057; бүртгэл 7.2634 = 0.8611;

бүртгэл 0.26 = 1.4150; бүртгэл 3456.86 = 3.5387.

280. Тайлбар. Зарим дөрвөн оронтой хүснэгтэд (жишээлбэл, хүснэгтэд В.Лорченко ба Н.Оглоблин, С.Глазенап, Н.Каменщикова) энэ тооны 4-р оронгийн засварыг оруулаагүй болно. Ийм хүснэгттэй ажиллахдаа эдгээр залруулгыг энгийн тооцоолол ашиглан олох хэрэгтэй бөгөөд үүнийг дараах үнэнд үндэслэн хийж болно: хэрэв тоо нь 100-аас их, тэдгээрийн хоорондох ялгаа нь 1-ээс бага бол мэдрэмжгүй болно. алдаа гэж үзэж болно логарифмын зөрүү нь харгалзах тоонуудын зөрүүтэй пропорциональ байна . Жишээлбэл, бид 5367 тоотой тохирох мантиса олох хэрэгтэй. Энэ мантиса нь мэдээжийн хэрэг 536.7 тоотой ижил байна. Бид 7292 мантисыг 536 тооны хүснэгтээс олдог. Энэ мантисыг баруун талд байгаа 537 тоотой харгалзах 7300 мантистай харьцуулбал 536 тоо 1-ээр нэмэгдэхэд мантиса нь 8 араваар нэмэгдэх болно. -мянган (8 гэж нэрлэгддэг хүснэгтийн ялгаахоёр зэргэлдээ мантисын хооронд); хэрэв 536 тоо 0.7-оор нэмэгдвэл мантис нь 8 арван мянгаар биш харин бага тоогоор нэмэгдэх болно. X Зөвшөөрөгдсөн пропорциональ байдлын дагуу дараахь пропорцийг хангах ёстой арван мянга.

X :8=0,7:1; хаана X = 8 07 = 5,6,

энэ нь 6 арван мянга болж бөөрөнхийлсөн. Энэ нь 536.7 тооны мантиса (тиймээс 5367 тоо) нь: 7292 + 6 = 7298 болно гэсэн үг юм.

Хүснэгт дэх хоёр зэргэлдээ тоогоор завсрын тоог олохыг дууддаг болохыг анхаарна уу интерполяци.Энд тайлбарласан интерполяц гэж нэрлэдэг пропорциональ, учир нь энэ нь логарифмын өөрчлөлт нь тооны өөрчлөлттэй пропорциональ байна гэсэн таамаглал дээр суурилдаг. Логарифмын функцийн өөрчлөлтийг графикаар шулуун шугамаар илэрхийлдэг гэж үздэг тул үүнийг шугаман гэж нэрлэдэг.

281. Ойролцоо логарифмын алдааны хязгаар.Хэрэв логарифмыг нь хайж байгаа тоо нь яг нарийн тоо бол 4 оронтой хүснэгтээс олох логарифмын алдааны хязгаарын хувьд бид дээр хэлсэнчлэн авч болно. 1 / 2 арван мянга дахь хувьцаа. Хэрэв өгөгдсөн тоо үнэн зөв биш бол энэ алдааны зөрүү дээр тухайн тооны буруугаас үүссэн өөр алдааны хязгаарыг нэмэх шаардлагатай. Ийм хязгаарт зориулж бүтээгдэхүүнийг авч болно гэдэг нь батлагдсан (бид энэ нотолгоог орхигдуулсан).

а(г +1) арван мянган.,

аль нь а гэж үзвэл хамгийн буруу тооны алдааны хязгаар юм Бүхэл тоон хэсэгт 3 цифрийг авна, a г Хоёр дараалсан гурван оронтой тоонд тохирох мантисын хүснэгтийн зөрүү. Тиймээс логарифмын эцсийн алдааны хязгаарыг дараах томъёогоор илэрхийлнэ.

1 / 2 + а(г +1) арван мянга дахь

Жишээ. Бүртгэлийг олох π , авах π ойролцоогоор тоо 3.14, нарийвчлал 1 / 2 зуу дахь.

3.14 дугаарын 3-р оронгийн ард таслалыг зүүн гар талаас нь тоолсноор бид гурван оронтой 314 тоог авна. 1 / 2 нэгж; Энэ нь алдааны зөрүү, өөрөөр хэлбэл бидний үсгээр тэмдэглэсэн тоо гэсэн үг юм. а , хэрэв 1 / 2 Хүснэгтүүдээс бид олж мэдсэн:

бүртгэл 3.14 = 0.4969.

Хүснэгтийн ялгаа г 314 ба 315 тоонуудын мантисын хооронд 14 байх тул олсон логарифмын алдаа бага байх болно.

1 / 2 + 1 / 2 (14 +1) = 8 арван мянга.

Бид 0.4969-ийн логарифмыг доогуур эсвэл түүнээс дээш эсэхийг мэдэхгүй тул яг логарифм гэдгийг л баталж чадна. π 0.4969 - 0.0008 ба 0.4969 + 0.0008, өөрөөр хэлбэл 0.4961 хооронд байна.< log π < 0,4977.

282. Өгөгдсөн логарифмаас тоог ол. Өгөгдсөн логарифмын дагуу тоог олохын тулд ижил хүснэгтүүдийг ашиглаж болно, үүний дагуу эдгээр тоонуудын мантисууд олддог; гэхдээ антилогарифм гэж нэрлэгддэг бусад хүснэгтүүдийг, өөрөөр хэлбэл өгөгдсөн мантисад тохирох тоог ашиглах нь илүү тохиромжтой. Дээд талд нь "антилогарифм" гэсэн шошготой эдгээр хүснэгтүүдийг логарифмын хүснэгтийн дагуу энэ номын төгсгөлд байрлуулсан бөгөөд тэдгээрийн багахан хэсгийг энэ хуудсанд (тайлбар болгон) байрлуулсан болно.

4 оронтой мантиса 2863-ыг өгье (бид шинж чанарыг анхаарч үздэггүй) харгалзах бүхэл тоог олох шаардлагатай. Дараа нь антилогарифмын хүснэгтүүдтэй бол бид тэдгээрийг өгөгдсөн тооны мантиссыг олоход тайлбарласантай яг ижил аргаар ашиглах ёстой, тухайлбал: бид зүүн эхний баганад мантисын эхний 2 цифрийг олно. Дараа нь бид эдгээр тоонуудаас дээд мөрөнд (эсвэл доод) хайх ёстой mantissa-ийн 3-р цифрээс гарч буй босоо баганатай огтлолцох хүртэл хэвтээ шугамын дагуу баруун тийш шилжинэ. Уулзвар дээр бид дөрвөн оронтой тоог олох 1932, харгалзах мантиса 286. Дараа нь энэ тооноос бид баруун тийш хэвтээ шугамын дагуу цааш цааш дамждаг мантисын 4-р цифрээс босоо баганатай огтлолцох хүртэл. 1, 2, 3,... гэсэн тоонуудын дээд талд (эсвэл доод талд) олдох болно 9. Уулзвар дээр бид өмнө нь олдсон 1032 тоонд (сэтгэлд) хэрэглэх ёстой залруулга 1-ийг олно. 2863-ын мантисад тохирох дугаарыг авахын тулд.

Ингээд 1933 гэсэн тоо гарна. Үүний дараа шинж чанарт анхаарлаа хандуулж, 1933 тоонд эзлэгдсэн нэгийг зохих байранд нь оруулах шаардлагатай. Жишээ нь:

хэрэв бүртгэл х = 3.2863, тэгвэл X = 1933,

„ бүртгэл x= 1,2863, „ X = 19,33,

, бүртгэл х = 0,2&63, „ X = 1,933,

„ бүртгэл х = 2 ,2863, „ X = 0,01933

Энд илүү олон жишээ байна:

бүртгэл х = 0,2287, X = 1,693,

бүртгэл х = 1 ,7635, X = 0,5801,

бүртгэл х = 3,5029, X = 3184,

бүртгэл х = 2 ,0436, X = 0,01106.

Хэрэв мантиса нь 5 ба түүнээс дээш оронтой бол бид зөвхөн эхний 4 цифрийг авч, үлдсэнийг нь хаяна (мөн 5 дахь орон нь тав ба түүнээс дээш бол 4-р цифрийг 1-ээр нэмэгдүүлнэ). Жишээлбэл, мантиса 35478-ийн оронд 3548, 47562-ын оронд 4756-г авна.

283. Тайлбар.Мантисын 4 ба дараагийн цифрүүдийн засварыг мөн интерполяци хийх замаар олж болно. Хэрэв мантис нь 84357 бол мантиса 843-тай тохирох 6966 тоог олсны дараа бид дараах байдлаар тайлбарлаж болно: хэрэв мантис 1 (мянгадахь) -аар нэмэгдвэл, өөрөөр хэлбэл 844 болсон бол тоо нь боломжтой болно. хүснэгтээс харахад 16 нэгжээр нэмэгдэх болно; хэрэв мантиса нь 1 (мянга) биш харин 0.57 (мянга) -аар нэмэгдвэл тоо нь нэмэгдэнэ. X нэгж, ба X харьцааг хангасан байх ёстой:

X : 16 = 0.57: 1, хаанаас x = 16 0,57 = 9,12.

Энэ нь хүссэн тоо нь 6966 + 9.12 = 6975.12 эсвэл (зөвхөн дөрвөн оронтой хязгаарлагдмал) 6975 болно гэсэн үг юм.

284. Олдсон тооны алдааны хязгаар.Олдсон тоонд зүүнээс 3-р оронгийн ард таслал байгаа тохиолдолд, өөрөөр хэлбэл логарифмын шинж чанар нь 2 байвал нийлбэрийг алдааны зөрүү болгон авч болох нь батлагдсан.

хаана а Энэ нь тухайн тоог олсон логарифмын (арван мянганы нэгээр илэрхийлсэн) алдааны хязгаар бөгөөд г - олсон тоог хавсаргасан гурван оронтой дараалсан хоёр тооны мантисын хоорондох зөрүү (зүүн талын 3-р цифрийн дараа таслалтай). Шинж чанар нь 2 биш, харин өөр байх үед олсон тоон дахь таслалыг зүүн эсвэл баруун тийш шилжүүлэх шаардлагатай болно, өөрөөр хэлбэл тоог 10-ын тодорхой хүчээр хуваах эсвэл үржүүлэх. Энэ тохиолдолд алдаа гарна. үр дүн нь 10-ын ижил хүчээр хуваагдах эсвэл үржих болно.

Жишээлбэл, бид логарифмын дагуу тоог олъё 1,5950 , энэ нь арван мянганы 3 хүртэлх нарийвчлалтай гэдгийг мэддэг; тэгвэл а = 3 . Антилогарифмын хүснэгтээс олдсон энэ логарифмд тохирох тоо нь байна 39,36 . Зүүн талд байгаа 3-р оронгийн араас таслалыг хөдөлгөвөл бид тоотой болно 393,6 хооронд 393 болон 394 . Логарифмын хүснэгтээс бид эдгээр хоёр тоонд тохирох мантисын ялгааг харж байна. 11 арван мянга; гэсэн үг г = 11 . 393.6 дугаарын алдаа бага байх болно

Тиймээс тооны алдаа 39,36 бага байх болно 0,05 .

285. Сөрөг шинж чанартай логарифмын үйлдэл.Дараах жишээнүүдээс харахад логарифм нэмэх, хасах нь ямар ч хүндрэл учруулахгүй.

Логарифмыг эерэг тоогоор үржүүлэхэд ямар ч бэрхшээл гарахгүй, жишээлбэл:

Сүүлийн жишээнд эерэг мантисыг тусад нь 34-өөр үржүүлж, сөрөг шинж чанарыг 34-өөр үржүүлнэ.

Хэрэв сөрөг шинж чанар ба эерэг мантисын логарифмыг сөрөг тоогоор үржүүлбэл тэдгээр нь хоёр янзаар үйлчилнэ: өмнө нь өгөгдсөн логарифмыг хасах, эсвэл мантис ба шинж чанарыг тусад нь үржүүлж үр дүнг нэгтгэнэ. жишээ:

3 ,5632 (- 4) = - 2,4368 (- 4) = 9,7472;

3 ,5632 (- 4) = + 12 - 2,2528 = 9,7472.

Хуваахдаа хоёр тохиолдол байдаг: 1) сөрөг шинж чанар нь хуваагдсан ба 2) хуваагчаар хуваагддаггүй. Эхний тохиолдолд шинж чанар ба мантиса нь тусад нь тусгаарлагдана.

10 ,3784: 5 = 2 ,0757.

Хоёрдахь тохиолдолд шинж чанарт маш олон сөрөг нэгжийг нэмсэн тул үр дүнгийн тоо нь хуваагчаар хуваагдах болно; Мантисад ижил тооны эерэг нэгжийг нэмсэн:

3 ,7608: 8 = (- 8 + 5,7608) : 8 = 1 ,7201.

Энэ өөрчлөлтийг оюун ухаанд хийх ёстой тул үйлдлийг дараах байдлаар зохион байгуулна.

286. Хасах логарифмуудыг нөхцлөөр солих.Логарифм ашиглан зарим нарийн төвөгтэй илэрхийллийг тооцоолохдоо зарим логарифмуудыг нэмж, заримыг нь хасах хэрэгтэй; Энэ тохиолдолд үйлдлүүдийг гүйцэтгэх ердийн аргаар тэд логарифмын нөхцлийн нийлбэрийг, дараа нь хасагдсан нийлбэрийг тус тусад нь олж, эхний нийлбэрээс хоёр дахь нь хасагдана. Жишээлбэл, хэрэв бидэнд байгаа бол:

бүртгэл X = 2,7305 - 2 ,0740 + 3 ,5464 - 8,3589 ,

Дараа нь үйлдлүүдийн ердийн гүйцэтгэл дараах байдлаар байрлана.

Гэхдээ хасахыг нэмэхээр сольж болно. Тэгэхээр:

Одоо та тооцооллыг дараах байдлаар зохион байгуулж болно.

287. Тооцооллын жишээ.

Жишээ 1. Илэрхийлэлийг үнэлэх:

хэрэв A \u003d 0.8216, B \u003d 0.04826, C \u003d 0.005127болон D = 7.246.

Бид энэ илэрхийллийг логарифм болгоно:

бүртгэл X= 1/3 лог A + 4 log B - 3 log C - 1/3 log D

Одоо, шаардлагагүй цаг хугацаа алдахаас зайлсхийх, алдаа гарах магадлалыг багасгахын тулд бид юуны өмнө бүх тооцоог хараахан хийлгүйгээр, хүснэгтэд ишлэлгүйгээр зохион байгуулдаг.

Үүний дараа бид хүснэгтүүдийг аваад зүүн хоосон газруудад логарифмуудыг байрлуулна.

Алдааны хязгаар.Эхлээд дугаарын алдааны хязгаарыг олъё х 1 = 194,5 , тэнцүү:

Тиймээс, юуны өмнө та олох хэрэгтэй а , өөрөөр хэлбэл, ойролцоогоор логарифмын алдааны хязгаарыг арван мянганы нэгээр илэрхийлнэ. Эдгээр тоонууд байна гэж бодъё A, B, Cболон Дбүгд үнэн зөв. Дараа нь бие даасан логарифмын алдаа дараах байдалтай байна (арван мянгад):

v logA.......... 1 / 2

v 1/3 лог А......... 1 / 6 + 1 / 2 = 2 / 3

( 1 / 2 нэмсэн, учир нь бид 1.9146-ийн 3 логарифмд хуваахдаа 5-р цифрийг хаях замаар хуваалтыг бөөрөнхийлсөн тул өөр алдаа гаргасан, бага 1 / 2 арван мянга дахь).

Одоо бид логарифмын алдааны хязгаарыг олно.

а = 2 / 3 + 2 + 3 / 2 + 1 / 6 = 4 1 / 3 (арван мянганы нэг).

Цаашид тодорхойлъё г . Учир нь х 1 = 194,5 , дараа нь 2 дараалсан бүхэл тоо байна х 1 болно 194 болон 195 . Хүснэгтийн ялгаа г эдгээр тоонуудад харгалзах мантисын хооронд тэнцүү байна 22 . Тиймээс тооны алдааны зөрүү х 1 байдаг:

Учир нь х = х 1 : 10, дараа нь тоон дахь алдааны зөрүү х тэнцүү байна 0,3:10 = 0,03 . Тиймээс бидний олсон тоо 19,45 -аас бага тоогоор тодорхой тооноос ялгаатай 0,03 . Ойролцоогоор дутагдалтай эсвэл илүүдэлтэй байгаа эсэхийг бид мэдэхгүй байгаа тул бид зөвхөн үүнийг л баталж чадна.

19,45 + 0,03 > X > 19,45 - 0,03 , өөрөөр хэлбэл

19,48 > X > 19,42 ,

тиймээс, хэрэв бид хүлээн зөвшөөрвөл X =19,4 , тэгвэл бид 0.1 хүртэлх сул талтай ойролцоо утгатай болно.

Жишээ 2Тооцоолох:

X = (- 2,31) 3 5 √72 = - (2,31) 3 5 √72 .

Сөрөг тоонуудад логарифм байдаггүй тул эхлээд дараах зүйлийг олно.

X" = (2,31) 3 5 √72

задралаар:

бүртгэл X"= 3 log 2.31 + 1/5 log72.

Тооцооллын дараа:

X" = 28,99 ;

тиймээс,

х = - 28,99 .

Жишээ 3. Тооцоолох:

Үргэлжилсэн логарифмыг энд хэрэглэх боломжгүй, учир нь язгуурын тэмдгийн дор y m m a тэмдэгт байрладаг. Ийм тохиолдолд томъёог хэсэг хэсгээр нь тооцоолно.

Эхлээд бид олдог Н = 5 √8 , Дараа нь Н 1 = 4 √3 ; Дараа нь энгийн нэмэлтээр бид тодорхойлно Н+ Н 1 , эцэст нь тооцоол 3 √Н+ Н 1 ; гарч ирэх болно:

N = 1.514, Н 1 = 1,316 ; Н+ Н 1 = 2,830 .

бүртгэл х= бүртгэл 3 √ 2,830 = 1 / 3 бүртгэл 2,830 = 0,1506 ;

х = 1,415 .

Дөрөвдүгээр бүлэг.

Экспоненциал ба логарифм тэгшитгэл.

288. Экспоненциал тэгшитгэл нь үл мэдэгдэх нь экспонентт багтсан тэгшитгэл юм логарифм- тэмдгийн дор үл мэдэгдэх зүйл ордог хүмүүс бүртгэл. Ийм тэгшитгэлийг зөвхөн онцгой тохиолдлуудад шийдэж болох бөгөөд логарифмын шинж чанар, хэрэв тоонууд нь тэнцүү бол тэдгээрийн логарифмууд нь тэнцүү, харин эсрэгээр, логарифмууд нь тэнцүү бол харгалзах зарчимд найдах хэрэгтэй. тоо тэнцүү байна.

Жишээ 1Тэгшитгэлийг шийд: 2 х = 1024 .

Бид тэгшитгэлийн хоёр талыг логарифм болгоно.

Жишээ 2Тэгшитгэлийг шийд: а 2x - а х = 1 . Оруулах а х = цагт , бид квадрат тэгшитгэлийг олж авна:

y 2 - цагт - 1 = 0 ,

Учир нь 1-√5 < 0 , тэгвэл сүүлчийн тэгшитгэл боломжгүй (функц а х үргэлж эерэг тоо байдаг), эхнийх нь:

Жишээ 3Тэгшитгэлийг шийд:

бүртгэл( a + x) + бүртгэл ( b + x) = бүртгэл ( c + x) .

Тэгшитгэлийг дараах байдлаар бичиж болно.

бүртгэл[( a + x) (b + x)] = бүртгэл ( c + x) .

Логарифмын тэгшитгэлээс бид тоонуудын тэгш байдлын тухай дүгнэж байна.

(a + x) (b + x) = c + x .

Энэ бол квадрат тэгшитгэл бөгөөд шийдэл нь тийм ч хэцүү биш юм.

Тавдугаар бүлэг.

Нийлмэл хүү, хугацааны төлбөр, яаралтай шимтгэл.

289. Нийлмэл хүүгийн гол асуудал.Хөрөнгийн хэмжээ хэд вэ а рубль, өсөлтөөр өгсөн Р дараа нийлмэл хүү т жил ( т бүхэл тоо)?

“Хүүгийн хүү” гэгчийг тооцож үзвэл, өөрөөр хэлбэл, капиталд төлөх ёстой хүүгийн мөнгийг жил бүрийн эцэст дарааллаар нь нэмж тооцвол нийлмэл хүүгээр хөрөнгө өгдөг гэдэг. дараагийн жилүүдэд хүүтэй нэмэгдүүлэх.

Капитал бүрийг рубль болгон өгөв Р %, нэг жилийн дотор ашиг авчрах болно х / 100 рубль болж, улмаар 1 жилийн дотор капиталын рубль бүр болж хувирна 1 + х / 100 рубль (жишээлбэл, капиталыг өгсөн бол 5 %, дараа нь нэг жилийн дотор рубль бүр болж хувирна 1 + 5 / 100 , өөрөөр хэлбэл in 1,05 рубль).

Товчхондоо бутархайг тэмдэглэж байна х / 100 жишээ нь нэг үсэг r , бид нэг жилийн хугацаанд капиталын рубль бүр болж хувирна гэж хэлж болно 1 + r рубль; тиймээс, а рубль 1 жилийн дараа болж хувирна а (1 + r ) үрэх. Жилийн дараа, өөрөөр хэлбэл, өсөлт эхэлснээс хойш 2 жилийн дараа эдгээрийн рубль бүр а (1 + r ) үрэх. руу буцах болно 1 + r үрэх; Энэ нь бүх капиталыг хөрвүүлнэ гэсэн үг а (1 + r ) 2 үрэх. Үүнтэй адилаар бид гурван жилийн дараа нийслэл болно гэдгийг олж мэдсэн а (1 + r ) 3 , дөрвөн жилийн дараа болно а (1 + r ) 4 ,... ерөнхийдөө дамжуулан т жил бол т бүхэл тоо, энэ нь болж хувирна а (1 + r ) түрэх. Тиймээс, тэмдэглэж байна Аэцсийн хөрөнгийн хувьд бид дараах нийлмэл хүүгийн томъёог авна.

А = а (1 + r ) тхаана r = х / 100 .

Жишээ.Болъё а =2300 рубль, х = 4, т=20 жил; Дараа нь томъёо нь:

r = 4 / 100 = 0,04 ; A \u003d 2 300 (1.04) 20.

Тооцоолохын тулд А, бид логарифм ашигладаг:

бүртгэл а = бүртгэл 2 300 + 20 бүртгэл 1.04 = 3.3617 + 20 0.0170 = 3.3617+0.3400 = 3.7017.

A=5031рубль.

Сэтгэгдэл.Энэ жишээнд бид байсан бүртгэл 1.04-ээр үржүүлнэ 20 . Тооноос хойш 0,0170 ойролцоогоор байна бүртгэл 1.04Шалтгаална, хамаарна 1 / 2 арван мянганы хэсэг, дараа нь энэ тооны үржвэр 20 хүртэл л байх болно 1 / 2 20, өөрөөр хэлбэл 10 хүртэл аравны мянга \u003d 1 мянга. Тиймээс нийтдээ 3,7017 бид зөвхөн арван мянгатын тоог төдийгүй мянгатын тоог ч баталж чадахгүй. Ийм тохиолдолд илүү нарийвчлалтай байхын тулд тоо нь илүү дээр юм 1 + r Жишээлбэл, логарифмуудыг 4 оронтой биш, харин олон тооны оронтой тоогоор ав. 7 оронтой. Энэ зорилгоор бид энд хамгийн түгээмэл хэрэглэгддэг утгуудын хувьд 7 оронтой логарифмуудыг бичсэн жижиг хүснэгтийг толилуулж байна. Р .

290. Яаралтай төлбөрийн үндсэн үүрэг.Хэн нэгэн авсан а рубль Р % нь өрийг төлөх нөхцөлтэй, түүнд төлөх ёстой хүүгийн хамт, in т жил бүрийн эцэст ижил хэмжээний төлбөр төлдөг. Энэ хэмжээ ямар байх ёстой вэ?

нийлбэр х Ийм нөхцөлд жил бүр төлдөг төлбөрийг яаралтай төлбөр гэж нэрлэдэг. Дахин тэмдэглэе r 1 рубльээс жилийн хүүгийн мөнгө, өөрөөр хэлбэл тоо х / 100 . Дараа нь эхний жилийн эцэс гэхэд өр а хүртэл өсдөг а (1 + r ), төлбөрийн дараа X рубль хийх болно а (1 + r )-X .

Хоёр дахь жилийн эцэс гэхэд энэ хэмжээний рубль бүр дахин болж хувирна 1 + r рубль, тиймээс өр нь [ а (1 + r )-X ](1 + r ) = а (1 + r ) 2 - х (1 + r ), мөн төлбөрийн хувьд х рубль байх болно: а (1 + r ) 2 - х (1 + r ) - X . Яг үүнтэй адил 3-р жилийн эцэс гэхэд өртэй болно гэдгийг анхаарна

а (1 + r ) 3 - х (1 + r ) 2 - х (1 + r ) - х ,

мөн ерөнхийдөө ба төгсгөл т -дахь жил нь:

а (1 + r ) т - х (1 + r ) t-1 - х (1 + r ) t-2 ... - х (1 + r ) - х , эсвэл

а (1 + r ) т - х [ 1 + (1 + r ) + (1 + r ) 2 + ...+ (1 + r ) t-2 + (1 + r ) t-1 ]

Хаалт доторх олон гишүүнт нь геометр прогрессийн гишүүний нийлбэрийг илэрхийлнэ; анхны гишүүнтэй 1 , сүүлчийн ( 1 + r ) t-1, ба хуваагч ( 1 + r ). Геометр прогрессийн гишүүдийн нийлбэрийн томъёоны дагуу (10-р хэсэг 3-р бүлэг § 249) бид дараахь зүйлийг олно.

ба түүнээс хойшхи өрийн хэмжээ т -дахь төлбөр нь:

Асуудлын нөхцөл байдлын дагуу эцсийн эцэст өр т -р жилтэй тэнцүү байх ёстой 0 ; Тийм учраас:

хаана

Үүнийг тооцоолохдоо яаралтай төлбөрийн томъёологарифм ашиглан бид эхлээд туслах тоог олох ёстой Н = (1 + r ) тлогарифмоор: logN = тбүртгэл (1 + r) ; олох Н, үүнээс 1-ийг хасаад бид томъёоны хуваагчийг авна X, Үүний дараа хоёрдогч логарифмын дагуу бид дараахь зүйлийг олно.

бүртгэл X= бүртгэл а+ log N + log r - бүртгэл (N - 1).

291. Яаралтай хандив өгөх үндсэн ажил.Жил бүрийн эхэнд хэн нэгэн банкинд ижил хэмжээний мөнгө байршуулдаг а үрэх. Дараа нь эдгээр шимтгэлээс ямар хөрөнгө бий болохыг тодорхойл т банк төлсөн бол жил Р нийлмэл хүү.

Дамжуулан тэмдэглэнэ r 1 рубльээс жилийн хүүгийн мөнгө, өөрөөр хэлбэл. х / 100 , бид дараах байдлаар маргаж байна: эхний жилийн эцэс гэхэд нийслэл болно а (1 + r );

2-р жилийн эхэнд энэ хэмжээ нэмэгдэнэ а рубль; Энэ нь энэ үед нийслэл болно гэсэн үг юм а (1 + r ) + а . 2 оны эцэс гэхэд тэр болно а (1 + r ) 2 + a (1 + r );

3-р жилийн эхэнд дахин танилцуулж байна а рубль; Энэ нь энэ үед нийслэл болно гэсэн үг юм а (1 + r ) 2 + a (1 + r ) + а ; 3-р сарын эцэс гэхэд тэр байх болно а (1 + r ) 3 + a (1 + r ) 2 + a (1 + r ) Эдгээр бодол санааг цааш үргэлжлүүлбэл эцэст нь бид үүнийг олж мэднэ т жилд шаардлагатай хөрөнгө Аболно:

Энэ нь жил бүрийн эхэнд тогтмол хугацааны шимтгэл төлөх томъёо юм.

Үүнтэй ижил томъёог дараахь үндэслэлээр гаргаж болно. эхний ээлжинд а рубль банкинд байхдаа т жил, нийлмэл хүүгийн томъёоны дагуу болж хувирна а (1 + r ) түрэх. Хоёр дахь хэсэг нь банкинд нэг жил бага байх, өөрөөр хэлбэл. т - 1 жил, холбоо барих а (1 + r ) t-1үрэх. Үүний нэгэн адил гурав дахь хэсэг нь өгөх болно а (1 + r ) t-2гэх мэт, эцэст нь банкинд ердөө 1 жилийн хугацаатай байх хамгийн сүүлийн хэсэг рүү шилжих болно а (1 + r ) үрэх. Тиймээс эцсийн нийслэл Аүрэх. болно:

А= а (1 + r ) т + а (1 + r ) t-1 + а (1 + r ) t-2 + . . . + а (1 + r ),

хялбаршуулсаны дараа дээрх томъёог өгдөг.

Энэ томьёоны логарифмуудыг ашиглан тооцоолохдоо та яаралтай төлбөрийн томъёог тооцоолохтой ижил зүйлийг хийх ёстой, өөрөөр хэлбэл эхлээд N = ( тоог олох хэрэгтэй. 1 + r ) тлогарифмын дагуу: logN = тбүртгэл(1 + r ), дараа нь тоо N-1Дараа нь томъёоны логарифмыг авна уу:

бүртгэл A = бүртгэл а+ бүртгэл (1 + r) + лог (N - 1) - 1огr

Сэтгэгдэл.Яаралтай хувь нэмэр оруулах бол а үрэх. Жил бүрийн эхэнд биш, харин эцэст нь хийсэн (жишээлбэл, яаралтай төлбөр хийх гэх мэт). X өрийг төлөх), дараа нь өмнөх шигээ маргаж, эцэст нь бид үүнийг олж мэднэ т жилд шаардлагатай хөрөнгө А"үрэх. байх болно (сүүлийн хэсгийг оруулаад а үрэх., хүү тооцохгүй):

А"= а (1 + r ) t-1 + а (1 + r ) t-2 + . . . + а (1 + r ) + а

тэнцүү байна:

өөрөөр хэлбэл А"гарч ирдэг ( 1 + r ) дахин бага А, капиталын рубль бүрээс хойш хүлээгдэж буй байсан А"банкинд нэг жилийн хугацаанд харгалзах рублийн хөрөнгийн хэмжээнээс бага хугацаагаар оршино А.