Matricos radimo metodai. Atvirkštinė matrica. Matricinių lygčių sprendimas

Daugeliu savybių panašus į atvirkštinį.

Kolegialus „YouTube“.

1 / 5

✪ Kaip rasti atvirkštinę matricos vertę - bezbotvy

✪ Atvirkštinė matrica (2 būdai rasti)

✪ Atvirkštinė matrica Nr. 1

✪ 2015-01-28. Atvirkštinė 3x3 matrica

✪ 2015-01-27. Atvirkštinė 2x2 matrica

Subtitrai

Atvirkštinės matricos savybės

det A - 1 = 1 det A (\ displaystyle \ det A ^ (- 1) = (\ frac (1) (\ det A))), kur det (\ displaystyle \ \ det)žymi determinantą.
(A B) - 1 = B - 1 A - 1 (\ displaystyle \ (AB) ^ (- 1) = B ^ (- 1) A ^ (- 1)) dviem kvadratinėms apverčiamoms matricoms A (\ rodymo stilius A) ir B (\ ekrano stilius B).
(A T) - 1 = (A - 1) T (\ ekrano stilius \ (A ^ (T)) ^ (- 1) = (A ^ (- 1)) ^ (T)), kur (...) T (\ ekrano stilius (...) ^ (T))žymi transponuotą matricą.
(k A) - 1 = k - 1 A - 1 (\ rodymo stilius \ (kA) ^ (- 1) = k ^ (- 1) A ^ (- 1)) bet kokiam koeficientui k ≠ 0 (\ rodymo stilius k \ ne = 0).
E - 1 = E (\ ekrano stilius \ E ^ (- 1) = E).
Jei reikia išspręsti tiesinių lygčių sistemą, (b yra nulinis vektorius) kur x (\ displaystyle x) yra reikalingas vektorius, o jei A - 1 (\ ekrano stilius A ^ (- 1)) tada egzistuoja x = A – 1 b (\ displaystyle x = A ^ (- 1) b)... Priešingu atveju arba sprendinių erdvės matmenys yra didesni už nulį, arba jų visai nėra.

Atvirkštinės matricos radimo metodai

Jei matrica yra apverčiama, galite naudoti vieną iš šių metodų, kad surastumėte atvirkštinę matricos vertę:

Tikslieji (tiesioginiai) metodai

Gauss-Jordan metodas

Paimkime dvi matricas: pati A ir viena E... Pateikime matricą A tapatumo matricai Gauss-Jordan metodu, taikant transformacijas eilutėmis (galite taikyti ir transformacijas stulpeliais, bet ne maišyti). Pritaikę kiekvieną operaciją pirmajai matricai, taikykite tą pačią operaciją antrajai. Kai bus baigtas pirmosios matricos redukavimas į vieneto formą, antroji matrica bus lygi A –1.

Naudojant Gauso metodą, pirmoji matrica bus padauginta iš kairės iš vienos iš elementariųjų matricų Λ i (\ displaystyle \ lambda _ (i))(transvekcinė arba įstrižainė matrica su pagrindinėmis įstrižainėmis, išskyrus vieną padėtį):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A - 1 (\ displaystyle \ Lambda _ (1) \ cdot \ dots \ cdot \ Lambda _ (n) \ cdot A = \ Lambda A = E \ rodyklė dešinėn \ lambda = A ^ (- 1)). Λ m = [1… 0 – a 1 m / amm 0… 0… 0… 1 - am - 1 m / amm 0… 0 0… 0 1 / amm 0… 0 0… 0 - am + 1 m / amm 1 … 0… 0… 0 - anm / amm 0… 1] (\ displaystyle \ Lambda _ (m) = (\ start (bmatrica) 1 & \ dots & 0 & -a_ (1m) / a_ (mm) & 0 & \ taškai & 0 \\ &&& \ taškai &&& \\ 0 & \ taškai & 1 & -a_ (m-1m) / a_ (mm) & 0 & \ taškai & 0 \\ 0 & \ taškai & 0 ir 1 / a_ (mm) & 0 & \ taškai & 0 \\ 0 & \ taškai & 0 & -a_ ( m + 1 m) / a_ (mm) & 1 & \ taškai & 0 \\ &&& \ taškai &&& \\ 0 & \ taškai & 0 & -a_ (nm) / a_ (mm) & 0 & \ taškai & 1 \ pabaiga (bmatrica))).

Antroji matrica pritaikius visas operacijas bus lygi Λ (\ displaystyle \ lambda), tai yra, jis bus norimas. Algoritmo sudėtingumas - O (n 3) (\ displaystyle O (n ^ (3))).

Naudojant algebrinių komplementų matricą

Matrica atvirkštinė matrica A (\ rodymo stilius A), gali būti pavaizduotas kaip

A - 1 = adj (A) det (A) (\ displaystyle (A) ^ (- 1) = (((\ mbox (adj)) (A)) \ over (\ det (A))))

kur adj (A) (\ displaystyle (\ mbox (adj)) (A))- pritvirtinta matrica;

Algoritmo sudėtingumas priklauso nuo determinanto O det skaičiavimo algoritmo sudėtingumo ir yra lygus O (n²) · O det.

Naudojant LU / LUP skaidymą

Matricos lygtis A X = I n (\ displaystyle AX = I_ (n)) atvirkštinei matricai X (\ displaystyle X) Galima žiūrėti kaip į kolekciją n (\ displaystyle n) formos sistemos A x = b (\ displaystyle Ax = b)... Mes pažymime i (\ displaystyle i) matricos stulpelis X (\ displaystyle X) skersai X i (\ displaystyle X_ (i)); tada A X i = e i (\ rodymo stilius AX_ (i) = e_ (i)), i = 1,…, n (\ displaystyle i = 1, \ ldots, n), kiek i (\ displaystyle i) matricos stulpelis I n (\ rodymo stilius I_ (n)) yra vieneto vektorius e i (\ displaystyle e_ (i))... kitaip tariant, atvirkštinės matricos radimas sumažinamas iki n lygčių su viena matrica ir skirtingomis dešiniosiomis pusėmis išsprendimo. Atlikus LUP skaidymą (laikas O (n³)), kiekvienai iš n lygčių išspręsti reikia laiko O (n²), taigi ir šiai darbo daliai reikia laiko O (n³).

Jei matrica A yra neišsigimusi, tada jai galima apskaičiuoti LUP skaidymą P A = L U (\ displaystyle PA = LU)... Leisti būti P A = B (\ ekrano stilius PA = B), B – 1 = D (\ rodymo stilius B ^ (- 1) = D)... Tada iš atvirkštinės matricos savybių galime parašyti: D = U - 1 L - 1 (\ displaystyle D = U ^ (- 1) L ^ (- 1))... Jei šią lygybę padauginsime iš U ir L, tai gausime dvi formos lygybes U D = L - 1 (\ displaystyle UD = L ^ (- 1)) ir D L = U - 1 (\ displaystyle DL = U ^ (- 1))... Pirmoji iš šių lygčių yra n² tiesinių lygčių sistema n (n + 1) 2 (\ displaystyle (\ frac (n (n + 1)) (2))) kurių dešiniosios pusės žinomos (iš trikampių matricų savybių). Antrasis taip pat reiškia n² tiesinių lygčių sistemą n (n - 1) 2 (\ displaystyle (\ frac (n (n-1)) (2))) kurių dešiniosios pusės žinomos (taip pat iš trikampių matricų savybių). Kartu jie sudaro n² lygybių sistemą. Naudodami šias lygybes galime rekursyviai nustatyti visus n² matricos D elementus. Tada iš lygybės (PA) −1 = A −1 P −1 = B −1 = D. gauname lygybę A – 1 = D P (\ rodymo stilius A ^ (- 1) = DP).

Naudojant LU skaidymą, matricos D stulpelių permutacija nereikalinga, tačiau sprendimas gali skirtis, net jei matrica A yra neišsigimusi.

Algoritmo sudėtingumas yra O (n³).

Iteraciniai metodai

Schultzo metodai

(Ψ k = E - AU k, U k + 1 = U k ∑ i = 0 n Ψ ki (\ rodymo stilius (\ pradžia (atvejai) \ Psi _ (k) = E-AU_ (k), k), \\ U_) k + 1) = U_ (k) \ suma _ (i = 0) ^ (n) \ Psi _ (k) ^ (i) \ pabaiga (atvejai)))

Klaidos įvertinimas

Pradinio spėjimo pasirinkimas

Pradinės aproksimacijos pasirinkimo problema čia nagrinėjamuose iteracinės matricos inversijos procesuose neleidžia jų traktuoti kaip nepriklausomų universalių metodų, konkuruojančių su tiesioginiais inversijos metodais, pagrįstais, pavyzdžiui, matricų LU skaidymu. Yra keletas rekomendacijų, kaip pasirinkti U 0 (\ displaystyle U_ (0)) sąlygos įvykdymo užtikrinimas ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (matricos spektrinis spindulys yra mažesnis nei vienas), kuris yra būtinas ir pakankamas proceso konvergencijai. Tačiau šiuo atveju pirmiausia reikia žinoti viršutinę apverstos matricos A arba matricos spektro ribą A A T (\ ekrano stilius AA ^ (T))(būtent jei A yra simetriška teigiama apibrėžtoji matrica ir ρ (A) ≤ β (\ displaystyle \ rho (A) \ leq \ beta), tada galite pasiimti U 0 = α E (\ ekrano stilius U_ (0) = (\ alfa) E), kur; jei A yra savavališka neišsigimusi matrica ir ρ (A A T) ≤ β (\ displaystyle \ rho (AA ^ (T)) \ leq \ beta) tada tikima U 0 = α A T (\ rodymo stilius U_ (0) = (\ alfa) A ^ (T)) kur taip pat α ∈ (0, 2 β) (\ displaystyle \ alfa \ in \ left (0, (\ frac (2) (\ beta)) \ right)); Žinoma, galite supaprastinti situaciją ir pasinaudoti tuo ρ (A A T) ≤ k A A T k (\ ekrano stilius \ rho (AA ^ (T)) \ leq (\ mathcal (k)) AA ^ (T) (\ mathcal (k))), įdėti U 0 = A T ‖ A A T ‖ (\ rodymo stilius U_ (0) = (\ frac (A ^ (T)) (\ | AA ^ (T) \ |)))). Antra, su tokiu pradinės matricos apibrėžimu nėra jokios garantijos ‖ Ψ 0 ‖ (\ displaystyle \ | \ Psi _ (0) \ |) bus mažas (gali net būti ‖ Ψ 0 ‖> 1 (\ displaystyle \ | \ Psi _ (0) \ |> 1)), o aukštas konvergencijos rodiklis nebus atskleistas iš karto.

Pavyzdžiai

Matrica 2x2

A - 1 = [a b c d] - 1 = 1 det (A) [d - b - c a] = 1 a d - b c [d - b - c a]. (\ displaystyle \ mathbf (A) ^ (- 1) = (\ pradžia (bmatrica) a & b \\ c & d \\\ pabaiga (bmatrica)) ^ (- 1) = (\ frac (1) (\ det (\ mathbf (A)))) (\ pradžia (bmatrica) \, \, \, d & \! \! - b \\ - c & \, a \\\ pabaiga (bmatrica)) = (\ frac (1) (ad- bc)) (\ pradžia (bmatrica) \, \, \, d & \! \! - b \\ - c & \, a \\\ pabaiga (bmatrica)).)

2x2 matricos inversija galima tik tuo atveju, jei a d - b c = det A ≠ 0 (\ displaystyle ad-bc = \ det A \ neq 0).

Atvirkštinės matricos radimas- užduotis, kuri dažnai išsprendžiama dviem būdais:

algebrinių komplementų metodas, kuriame reikia rasti determinantus ir transponuoti matricas;
nežinomųjų Gauso pašalinimo metodu, kuriame reikia atlikti elementariąsias matricos transformacijas (sudėti eilutes, eilutes padauginti iš to paties skaičiaus ir pan.).

Tiems, kuriems ypač įdomu, yra ir kitų metodų, pavyzdžiui, tiesinių transformacijų metodas. Šioje pamokoje išanalizuosime tris minėtus metodus ir algoritmus, kaip šiais metodais rasti atvirkštinę matricą.

Atvirkštinė matrica A, tokia matrica vadinama

A
. (1)

Atvirkštinė matrica , kurią reikia rasti tam tikrai kvadratinei matricai A, tokia matrica vadinama

sandauga, pagal kurią matricos A dešinėje yra tapatybės matrica, ty
. (1)

Tapatybės matrica yra įstrižainė, kurioje visi įstrižainės elementai yra lygūs vienetui.

Teorema.Kiekvienai nevienskaitinei (neišsigimusiai, ne vienaskaitinei) kvadratinei matricai galite rasti atvirkštinę matricą, be to, tik vieną. Specialiai (išsigimusiai, vienaskaitei) kvadratinei matricai atvirkštinė neegzistuoja.

Kvadratinė matrica vadinama neypatingas(arba neišsigimęs, ne vienaskaita) jei jo determinantas nėra nulis, ir ypatingas(arba išsigimęs, vienaskaita), jei jo determinantas lygus nuliui.

Atvirkštinę matricą galima rasti tik kvadratinei matricai. Natūralu, kad atvirkštinė matrica taip pat bus kvadratinė ir tokios pat eilės kaip ir duotoji matrica. Matrica, kuriai galima rasti atvirkštinę matricą, vadinama apverčiamąja matrica.

Dėl atvirkštinė matrica yra tinkama analogija su abipuse. Už kiekvieną skaičių a, nelygus nuliui, yra toks skaičius b kad darbas a ir b lygus vienam: ab= 1. Skaičius b vadinamas atvirkštine skaičiaus b... Pavyzdžiui, skaičiui 7 atvirkštinė vertė yra 1/7, nes 7 * 1/7 = 1.

Atvirkštinės matricos radimas taikant algebrinių komplementų metodą (sąjunginė matrica)

Ne vienaskaitos kvadratinei matricai A atvirkštinė yra matrica

kur yra matricos determinantas A, a yra matrica, susieta su matrica A.

Sąjunga su kvadratine matrica A vadinama tos pačios eilės matrica, kurios elementai yra atitinkamų matricos determinanto elementų, perkeltų matricos A atžvilgiu, algebriniai papildiniai.

tada

Atvirkštinės matricos radimo algoritmas algebrinių komplementų metodu

1. Raskite duotosios matricos determinantą A... Jei determinantas yra nulis, atvirkštinės matricos paieška sustabdoma, nes matrica yra išsigimusi ir jos atvirkštinės nėra.

2. Raskite matricą, transponuotą atžvilgiu A.

3. Apskaičiuokite adjungtinės matricos elementus kaip 2 veiksme rastos Maritsa algebrinius papildinius.

4. Taikykite (2) formulę: padauginkite atvirkštinę matricos determinanto vertę A, į adjungtinę matricą, rastą 4 veiksme.

5. Patikrinkite 4 veiksme gautą rezultatą, padaugindami šią matricą Aį atvirkštinę matricą. Jei šių matricų sandauga yra lygi tapatybės matricai, tada atvirkštinė matrica buvo rasta teisingai. Priešingu atveju iš naujo pradėkite sprendimo procesą.

1 pavyzdys. Dėl matricos

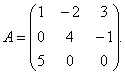
rasti atvirkštinę matricos vertę.

Sprendimas. Norint rasti atvirkštinę matricą, reikia rasti matricos determinantą A... Pagal trikampių taisyklę randame:

Taigi matrica A- ne vienaskaita (neišsigimęs, ne vienaskaita) ir jam yra atvirkštinė.

Raskite matricą, besiribojančią su duota matrica A.

Raskite matricos atžvilgiu transponuotą matricą A:

Apskaičiuokite adjungtinės matricos elementus kaip matricos, perkeltos matricos atžvilgiu, algebrinius papildinius A:

Todėl matrica, besiribojanti su matrica A, turi formą

komentuoti. Elementų skaičiavimo ir matricos perkėlimo tvarka gali būti skirtinga. Pirmiausia galima apskaičiuoti matricos algebrinius papildinius A ir tada transponuokite komplemento matricą. Rezultatas turėtų būti tie patys sąjungos matricos elementai.

Taikydami formulę (2), randame matricą atvirkštinę matricai A:

Atvirkštinės matricos radimas pagal Gauso eliminaciją

Pirmasis žingsnis ieškant atvirkštinės matricos Gauso eliminavimo metodu yra priskirti matricą A tos pačios eilės tapatybės matricą, atskiriant jas vertikalia juosta. Gauname dvigubą matricą. Abi šios matricos puses padauginame iš, tada gauname

Algoritmas atvirkštinei matricai rasti pagal Gauso nežinomųjų pašalinimą

1. Į matricą A priskirti tos pačios eilės tapatybės matricą.

2. Transformuokite gautą dvigubą matricą taip, kad tapatybės matrica būtų gauta kairėje jos pusėje, tada atvirkštinė matrica automatiškai atsiras dešinėje esančios tapatybės matricos vietoje. Matrica A kairėje pusėje elementarios matricos transformacijomis paverčiama tapatumo matrica.

2. Jei matricos transformacijos metu Aį tapatybės matricą bet kurioje eilutėje ar bet kuriame stulpelyje bus tik nuliai, tada matricos determinantas yra lygus nuliui, taigi ir matrica A bus išsigimęs ir neturi atvirkštinės matricos. Tokiu atveju tolesnis atvirkštinės matricos radimas nutraukiamas.

2 pavyzdys. Dėl matricos

rasti atvirkštinę matricos vertę.

ir transformuosime taip, kad kairėje pusėje gautume tapatybės matricą. Pradedame transformacijas.

Pirmąją kairiosios ir dešiniosios matricos eilutę padauginkite iš (-3) ir pridėkite prie antros eilės, o tada padauginkite pirmąją eilutę iš (-4) ir pridėkite prie trečios eilės, tada gausime

Kad, jei įmanoma, vėlesnių transformacijų metu nebūtų trupmeninių skaičių, pirmiausia sukuriame vienetą antroje eilutėje kairėje padvigubintos matricos pusėje. Norėdami tai padaryti, padauginkite antrą eilutę iš 2 ir iš jos atimkite trečią eilutę, tada gausime

Pirmąją eilutę pridėkite prie antrosios, o antrąją eilutę padauginkite iš (-9) ir pridėkite prie trečios eilutės. Tada gauname

Tada padalykite trečią eilutę iš 8

Trečią eilutę padauginkime iš 2 ir pridėkime prie antros eilės. Paaiškėja:

Sukeiskime antrąją ir trečiąją eilutes, tada galiausiai gausime:

Matome, kad vieneto matrica gaunama kairėje pusėje, todėl atvirkštinė matrica gaunama dešinėje. Taigi:

Skaičiavimų teisingumą galite patikrinti padauginę pradinę matricą iš rastos atvirkštinės matricos:

Rezultatas turėtų būti atvirkštinė matrica.

3 pavyzdys. Dėl matricos

rasti atvirkštinę matricos vertę.

Sprendimas. Dvigubos matricos sudarymas

ir mes jį pakeisime.

Pirmą eilutę padauginame iš 3, o antrąją iš 2 ir atimame iš antrosios, tada padauginame pirmą eilutę iš 5, o trečią iš 2 ir atimame iš trečios eilės, tada gauname

Pirmą eilutę padauginame iš 2 ir pridedame prie antrosios, o tada iš trečios eilutės atimame antrąją, tada gauname

Matome, kad trečioje eilutėje kairėje visi elementai pasirodė lygūs nuliui. Vadinasi, matrica yra išsigimusi ir neturi atvirkštinės matricos. Mes nustojame toliau ieškoti atvirkštinės maritza.

Matrica $ A ^ (- 1) $ vadinama atvirkštine kvadratinės matricos $ A $ atžvilgiu, jei tenkinama sąlyga $ A ^ (- 1) \ cdot A = A \ cdot A ^ (- 1) = E $ , kur $ E $ Yra tapatumo matrica, kurios tvarka lygi matricos $ A $ tvarkai.

Neišsigimusi matrica – matrica, kurios determinantas nėra lygus nuliui. Atitinkamai, išsigimusi matrica yra ta, kurios determinantas yra lygus nuliui.

Atvirkštinė matrica $ A ^ (- 1) $ egzistuoja tada ir tik tada, jei matrica $ A $ yra neišsigimusi. Jei atvirkštinė matrica $ A ^ (- 1) $ egzistuoja, tada ji yra unikali.

Yra keletas būdų, kaip rasti atvirkštinę matricos vertę, ir mes pažvelgsime į du iš jų. Šiame puslapyje bus aptariamas adjungtinės matricos metodas, kuris laikomas standartiniu daugumoje aukštųjų matematikos kursų. Antroje dalyje aptariamas antrasis atvirkštinės matricos radimo būdas (elementariųjų transformacijų metodas), kuris apima Gauso metodo arba Gauso-Jordano metodo naudojimą.

Adjungtinės (adjungtinės) matricos metodas

Tegu duota matrica $ A_ (n \ kartus n) $. Norint rasti atvirkštinę vertę $ A ^ (- 1) $, reikia atlikti tris veiksmus:

Raskite matricos $ A $ determinantą ir įsitikinkite, kad $ \ Delta A \ neq 0 $, t.y. kad matrica A yra neišsigimusi.
Sudarykite kiekvieno matricos elemento $ A $ algebrinius papildymus $ A_ (ij) $ ir parašykite matricą $ A_ (n \ kartus n) ^ (*) = \ kairėje (A_ (ij) \ dešinėje) $ iš rasti algebriniai papildiniai.
Parašykite atvirkštinę matricą atsižvelgdami į formulę $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $.

Matrica $ (A ^ (*)) ^ T $ dažnai vadinama adjoinuota (reciprokine, adjointine) su matrica $ A $.

Jei sprendimas atliekamas rankiniu būdu, pirmasis metodas tinka tik santykinai mažų užsakymų matricoms: antrasis (), trečiasis (), ketvirtasis (). Kiti metodai naudojami norint rasti aukštesnės eilės matricos atvirkštinę vertę. Pavyzdžiui, Gauso metodas, apie kurį kalbama antroje dalyje.

1 pavyzdys

Raskite atvirkštinę vertę $ A = \ left (\ begin (masyvas) (cccc) 5 & -4 & 1 & 0 \\ 12 & -11 & 4 & 0 \\ -5 & 58 & 4 & 0 \\ 3 & - 1 & -9 & 0 \ pabaiga (masyvas) \ dešinė) $.

Kadangi visi ketvirtojo stulpelio elementai yra lygūs nuliui, tada $ \ Delta A = 0 $ (tai yra, matrica $ A $ yra išsigimusi). Kadangi $ \ Delta A = 0 $, atvirkštinė matrica $ A $ neegzistuoja.

2 pavyzdys

Raskite atvirkštinę matricos $ A = \ left (\ pradžia (masyvas) (cc) -5 & 7 \\ 9 & 8 \ pabaiga (masyvas) \ dešinė) $.

Mes naudojame adjungtinės matricos metodą. Pirmiausia randame nurodytos matricos $ A $ determinantą:

$$ \ Delta A = \ kairėje | \ pradžia (masyvas) (cc) -5 ir 7 \\ 9 ir 8 \ pabaiga (masyvas) \ dešinė | = -5 \ cdot 8-7 \ cdot 9 = -103. $$

Kadangi $ \ Delta A \ neq 0 $, tada atvirkštinė matrica egzistuoja, todėl tęsime sprendimą. Algebrinių komplementų paieška

\ pradėti (sulygiuoti) & A_ (11) = (- 1) ^ 2 \ cdot 8 = 8; \; A_ (12) = (- 1) ^ 3 \ cdot 9 = -9; \\ & A_ (21) = (- 1) ^ 3 \ cdot 7 = -7; \; A_ (22) = (- 1) ^ 4 \ cdot (-5) = - 5. \\ \ pabaiga (sulygiuota)

Sudarome matricą iš algebrinių komplementų: $ A ^ (*) = \ left (\ start (masyvas) (cc) 8 & -9 \\ -7 & -5 \ end (masyvas) \ dešinėn) $.

Perkelkite gautą matricą: $ (A ^ (*)) ^ T = \ left (\ start (masyvas) (cc) 8 & -7 \\ -9 & -5 \ end (masyvas) \ dešinėn) $ (gautas matrica dažnai vadinama jungtine arba jungtine matrica $ A $). Naudodami formulę $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, turime:

$$ A ^ (- 1) = \ frac (1) (- 103) \ cdot \ left (\ pradžia (masyvas) (cc) 8 & -7 \\ -9 & -5 \ pabaiga (masyvas) \ dešinė) = \ kairė (\ pradžia (masyvas) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ pabaiga (masyvas) \ dešinė) $$

Taigi randama atvirkštinė: $ A ^ (- 1) = \ left (\ pradžia (masyvas) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ pabaiga (masyvas) \ dešinė) $. Norint patikrinti rezultato teisingumą, pakanka patikrinti vienos iš lygybių teisingumą: $ A ^ (- 1) \ cdot A = E $ arba $ A \ cdot A ^ (- 1) = E $. Patikrinkime lygybę $ A ^ (- 1) \ cdot A = E $. Kad mažiau dirbtume su trupmenomis, matricą $ A ^ (- 1) $ pakeisime ne forma $ \ left (\ begin (masyvas) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ pabaiga (masyvas) \ dešinė) $ ir kaip $ - \ frac (1) (103) \ cdot \ left (\ pradžia (masyvas) (cc) 8 & -7 \\ -9 & -5 \ pabaiga (masyvas ) \ dešinė) $:

Atsakymas: $ A ^ (- 1) = \ left (\ pradžia (masyvas) (cc) -8/103 & 7/103 \\ 9/103 & 5/103 \ pabaiga (masyvas) \ dešinė) $.

3 pavyzdys

Raskite atvirkštinę matricos $ A = \ left (\ pradžia (masyvas) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (masyvas) \ dešinė) $.

Pradėkime nuo matricos $ A $ determinanto apskaičiavimo. Taigi, matricos $ A $ determinantas yra toks:

$$ \ Delta A = \ kairėje | \ pradžia (masyvas) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2 \ end (masyvas) \ dešinė | = 18-36 + 56-12 = 26. $$

Kadangi $ \ Delta A \ neq 0 $, tada atvirkštinė matrica egzistuoja, todėl tęsime sprendimą. Mes randame kiekvieno duotosios matricos elemento algebrinius papildinius:

Sudarome algebrinių komplementų matricą ir ją transponuojame:

$$ A ^ * = \ left (\ pradžia (masyvas) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37 \ end (masyvas) \ dešinė); \; (A ^ *) ^ T = \ kairė (\ pradžia (masyvas) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ pabaiga (masyvas) \ dešinė) $$

Naudodami formulę $ A ^ (- 1) = \ frac (1) (\ Delta A) \ cdot (A ^ (*)) ^ T $, gauname:

$$ A ^ (- 1) = \ frac (1) (26) \ cdot \ left (\ begin (masyvas) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 ir 37 \ pabaiga (masyvas) \ dešinė) = \ kairė (\ pradžia (masyvas) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \ pabaiga (masyvas) \ dešinė) $$

Taigi $ A ^ (- 1) = \ left (\ start (masyvas) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \ pabaiga (masyvas) \ dešinė) $. Norint patikrinti rezultato teisingumą, pakanka patikrinti vienos iš lygybių teisingumą: $ A ^ (- 1) \ cdot A = E $ arba $ A \ cdot A ^ (- 1) = E $. Patikrinkime lygybę $ A \ cdot A ^ (- 1) = E $. Kad mažiau dirbtume su trupmenomis, matricą $ A ^ (- 1) $ pakeisime ne forma $ \ left (\ begin (masyvas) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \ pabaiga (masyvas) \ dešinėn) $ ir kaip $ \ frac (1) (26) \ cdot \ left ( \ pradžia (masyvas) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37 \ pabaiga (masyvas) \ dešinė) $:

Patikrinimas buvo sėkmingas, atvirkštinis $ A ^ (- 1) $ rastas teisingai.

Atsakymas: $ A ^ (- 1) = \ left (\ start (masyvas) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 / 13 & -3/26 & 37/26 \ pabaiga (masyvas) \ dešinė) $.

4 pavyzdys

Raskite atvirkštinę vertę $ A = \ left (\ begin (masyvas) (cccc) 6 & -5 & 8 & 4 \\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7 \\ -4 & 8 & -8 & -3 \ pabaiga (masyvas) \ dešinė) $.

Ketvirtosios eilės matricai rasti atvirkštinę matricą naudojant algebrinius papildinius yra šiek tiek sunku. Tačiau tokių pavyzdžių galima rasti bandomuosiuose darbuose.

Norėdami rasti atvirkštinę matricos vertę, pirmiausia turite apskaičiuoti matricos determinantą $ A $. Geriausias būdas tai padaryti šioje situacijoje yra išplėsti determinantą pagal eilutę (stulpelį). Parenkame bet kurią eilutę ar stulpelį ir randame kiekvieno pasirinktos eilutės ar stulpelio elemento algebrinius papildinius.

Matricinė algebra – atvirkštinė matrica

atvirkštinė matrica

Atvirkštinė matrica vadinama matrica, kurią dešinėje ir kairėje padauginus iš nurodytos matricos, gaunama tapatumo matrica.
Pažymime matricą atvirkštine matrica A tada pagal apibrėžimą gauname:

kur E Ar tapatybės matrica.
Kvadratinė matrica paskambino neypatingas (neišsigimęs), jei jo determinantas nėra nulis. Priešingu atveju jis vadinamas ypatingas (išsigimęs) arba vienaskaita.

Galioja ši teorema: kiekviena nevienskaita matrica turi atvirkštinę.

Vadinama atvirkštinės matricos radimo operacija apeliacija matricos. Apsvarstykite matricos inversijos algoritmą. Tebūna pateikta nevienskaita matrica n- užsakymas:

kur Δ = det A ≠ 0.

Algebrinis elemento papildymas matricos n– įsakymas A matricos determinantas ( n–1) eilė, gauta išbraukus i-toji eilutė ir j matricos stulpelis A:

Sudarykime vadinamąją pridedamas matrica:

kur yra atitinkamų matricos elementų algebriniai papildiniai A.
Atkreipkite dėmesį, kad matricos eilučių elementų algebriniai papildiniai A dedami į atitinkamus matricos stulpelius Ã ty matrica perkeliama tuo pačiu metu.
Padalijus visus matricos elementus Ã pagal Δ – matricos determinanto reikšmė A, gauname atvirkštinę matricą:

Atkreipiame dėmesį į keletą specialių atvirkštinės matricos savybių:
1) duotai matricai A jo atvirkštinė matrica yra vienintelis;
2) jei yra atvirkštinė matrica, tai dešinė atvirkštinė ir kairėje pusėje matricos sutampa su juo;
3) speciali (išsigimusi) kvadratinė matrica neturi atvirkštinės matricos.

Pagrindinės atvirkštinės matricos savybės:
1) atvirkštinės matricos determinantas ir pradinės matricos determinantas yra abipusės reikšmės;
2) kvadratinių matricų sandaugos atvirkštinė matrica yra lygi atvirkštinių veiksnių matricų sandaugai, paimtai atvirkštine tvarka:

3) matricos perkelta atvirkštinė vertė yra lygi nurodytos perkeltos matricos atvirkštinei:

PAVYZDYS Apskaičiuokite pateiktos matricos atvirkštinę vertę.

Tebūnie n-osios eilės kvadratinė matrica

Matrica A -1 vadinama atvirkštinė matrica matricos A atžvilgiu, jei A * A -1 = E, kur E yra n-osios eilės vienetinė matrica.

Vieneto matrica- tokia kvadratinė matrica, kurioje visi pagrindinės įstrižainės elementai, einantys iš viršutinio kairiojo kampo į apatinį dešinįjį kampą, yra vienetai, o likusieji yra nuliai, pavyzdžiui:

atvirkštinė matrica gali egzistuoti tik kvadratinėms matricoms tie. toms matricoms, kuriose yra tiek pat eilučių ir stulpelių.

Teorema apie atvirkštinės matricos egzistavimo sąlygą

Kad matrica turėtų atvirkštinę matricą, būtina ir pakanka, kad ji nebūtų išsigimusi.

Vadinama matrica A = (A1, A2, ... A n). neišsigimęs jei stulpelių vektoriai yra tiesiškai nepriklausomi. Tiesiškai nepriklausomų matricos stulpelių vektorių skaičius vadinamas matricos rangu. Todėl galime teigti, kad atvirkštinei matricai egzistuoti būtina ir pakanka, kad matricos rangas būtų lygus jos matmeniui, t.y. r = n.

Atvirkštinės matricos radimo algoritmas

Lentelėje užrašykite matricą A lygčių sistemų sprendimui Gauso metodu ir dešinėje (vietoj dešiniųjų lygčių pusių) priskirkite matricą E.
Naudodami Jordano transformaciją, sumažinkite matricą A į matricą, susidedančią iš vienetinių stulpelių; šiuo atveju būtina tuo pačiu metu transformuoti matricą E.
Jei reikia, pertvarkykite paskutinės lentelės eilutes (lygtis), kad po pradinės lentelės matrica A gautume vienetinę matricą E.
Užrašykite atvirkštinę matricą A -1, kuri yra paskutinėje lentelėje po pradinės lentelės matrica E.

1 pavyzdys

Matricai A raskite atvirkštinę matricą A -1

Sprendimas: Užrašome matricą A ir dešinėje priskiriame tapatybės matricą E. Naudodami Jordano transformacijas, matricą A sumažiname iki tapatybės matricos E. Skaičiavimai pateikti 31.1 lentelėje.

Skaičiavimų teisingumą patikrinkime pradinę matricą A ir atvirkštinę matricą A padauginę -1.

Dėl matricos daugybos gaunama vienetinė matrica. Todėl skaičiavimai yra teisingi.

Atsakymas:

Matricinių lygčių sprendimas

Matricos lygtys gali būti tokios formos:

AX = B, XA = B, AXB = C,

kur A, B, C yra nurodytos matricos, X yra reikalinga matrica.

Matricinės lygtys išsprendžiamos lygtį padauginus iš atvirkštinių matricų.

Pavyzdžiui, norėdami rasti matricą iš lygties, padauginkite tą lygtį iš kairės.

Todėl norėdami rasti lygties sprendimą, turite rasti atvirkštinę matricą ir padauginti ją iš matricos, esančios dešinėje lygties pusėje.

Kitos lygtys sprendžiamos panašiai.

2 pavyzdys

Išspręskite lygtį AX = B, jei

Sprendimas: Kadangi atvirkštinė matrica yra (žr. 1 pavyzdį)

Matricos metodas ekonominėje analizėje

Kartu su kitais jie taip pat randa pritaikymą matricos metodai... Šie metodai yra pagrįsti tiesine ir vektorine matrica algebra. Tokie metodai naudojami sudėtingiems ir daugiamačiams ekonomikos reiškiniams analizuoti. Dažniausiai šie metodai taikomi, kai reikia atlikti lyginamąjį organizacijų ir jų struktūrinių padalinių funkcionavimo vertinimą.

Matricinių analizės metodų taikymo procese galima išskirti keletą etapų.

Pirmajame etape sudaroma ekonominių rodiklių sistema ir jos pagrindu sudaroma pradinių duomenų matrica, kuri yra lentelė, kurios atskirose eilutėse rodomi sistemos numeriai (i = 1,2, ...., n), o išilgai vertikalių stulpelių – rodiklių skaičiai (j = 1,2, ...., m).

Antrame etape kiekvienam vertikaliam stulpeliui atskleidžiama didžiausia iš turimų rodiklių verčių, kuri laikoma vienetu.

Po to visos šioje skiltyje atsispindinčios sumos dalijamos iš didžiausios reikšmės ir susidaro standartizuotų koeficientų matrica.

Trečiajame etape visos matricos sudedamosios dalys yra kvadratinės. Jei jie turi skirtingą reikšmę, kiekvienam matricos rodikliui priskiriamas tam tikras svorio koeficientas k... Pastarosios vertė nustatoma eksperto sprendimu.

Paskutiniame, ketvirtasis etapas rastos reitingų reikšmės R j yra sugrupuoti didėjimo arba mažėjimo tvarka.

Nurodytus matricinius metodus reikėtų naudoti, pavyzdžiui, atliekant įvairių investicinių projektų lyginamąją analizę, taip pat vertinant kitus organizacijų veiklos ekonominius rodiklius.