Išplėskite Furjė eilutę ir sukurkite grafikus. Aukštoji matematika

Kuriems jau atsibodo tvarka. Ir jaučiu, kad atėjo momentas, kai laikas iš strateginių teorijos rezervų išgauti naujus konservus. Ar yra koks nors kitas būdas išplėsti funkciją serijoje? Pavyzdžiui, išreikšti tiesios linijos atkarpą sinusais ir kosinusais? Atrodo neįtikėtina, bet tokios iš pažiūros nutolusios funkcijos tinka
„Susijungimas“. Be žinomų teorijos ir praktikos laipsnių, yra ir kitų požiūrių į funkcijos išplėtimą serijoje.

Šioje pamokoje susipažinsime su trigonometrine Furjė eilute, paliesime jos konvergencijos ir sumos klausimą ir, žinoma, išanalizuosime daugybę Furjė eilučių funkcijų išplėtimo pavyzdžių. Straipsnį nuoširdžiai norėjau pavadinti „Fourier Series for Dummies“, bet tai būtų gudrus dalykas, nes sprendžiant uždavinius reikėtų kitų matematinės analizės šakų žinių ir šiek tiek praktinės patirties. Todėl preambulė primins astronautų mokymą =)

Pirma, puslapyje esančios medžiagos tyrimas turėtų būti atliktas puikia forma. Miegas, pailsėjęs ir blaivus. Be stiprių emocijų apie lūžusią žiurkėno leteną ir įkyrių minčių apie akvariumo žuvų gyvenimo sunkumus. Furjė serija nėra sudėtinga supratimo požiūriu, tačiau praktinės užduotys tiesiog reikalauja didesnės dėmesio koncentracijos - idealiu atveju reikėtų visiškai atsisakyti išorinių dirgiklių. Situaciją apsunkina tai, kad nėra lengvo būdo patikrinti sprendimą ir atsakyti. Taigi, jei jaučiatės žemiau nei vidutinis, geriau daryti ką nors paprastesnio. Tiesa.

Antra, prieš skrendant į kosmosą būtina apžiūrėti erdvėlaivio prietaisų skydelį. Pradėkime nuo funkcijų, kurias reikia spustelėti ant automato, verčių:

Dėl bet kokios gamtos vertės:

1) . Iš tiesų, sinusoidas „susiuva“ abscisę per kiekvieną „pi“:
... Esant neigiamoms argumento reikšmėms, rezultatas, žinoma, bus toks pat:.

2). Tačiau ne visi tai žinojo. Kosinusas „pi en“ yra „blyksnio“ atitikmuo:

Neigiamas argumentas nesikeičia: .

Galbūt to užtenka.

Ir, trečia, gerbiamas kosmonautų korpusas, jūs turite sugebėti ... integruoti.
Ypač užtikrintai priskirti funkciją po diferencialiniu ženklu, integruoti gabalas po gabalo ir būti su jais gerais santykiais pagal Niutono-Leibnizo formulę... Pradėkime nuo kai kurių svarbių pratimų prieš skrydį. Kategoriškai nerekomenduoju jo praleisti, kad vėliau jis nesuplotų esant nulinei gravitacijai:

1 pavyzdys

Apskaičiuokite apibrėžtuosius integralus

kur paima gamtos vertybes.

Sprendimas: integravimas atliekamas per kintamąjį "x" ir šiame etape diskretinis kintamasis "en" laikomas pastoviu. Visuose integraluose funkciją perkeliame po diferencialiniu ženklu:

Trumpa sprendimo versija, kurią būtų naudinga taikyti, atrodo taip:

Priprasti prie:

Likę keturi daiktai priklauso jums. Stenkitės sąžiningai atlikti užduotį ir trumpai sudaryti integralus. Pamokos pabaigoje sprendimų pavyzdžiai.

Atlikę KOKYBINIUS pratimus, apsivilkame skafandrus
ir ruošiamės pradėti!

Funkcijos išplėtimas Furjė serijoje intervale

Apsvarstykite kai kurias funkcijas apibrėžta bent jau intervale (ir, galbūt, didesniame intervale). Jei ši funkcija yra integruota į segmentą, ji gali būti išplėsta į trigonometrinę Furjė serija:
, kur yra vadinamieji Furjė koeficientai.

Tokiu atveju skambinama numeriu skilimo laikotarpis o skaičius yra pusinės eliminacijos laikas.

Akivaizdu, kad bendruoju atveju Furjė seriją sudaro sinusai ir kosinusai:

Iš tiesų, mes tai išsamiai apibūdinsime:

Formoje įprasta rašyti nulinį serijos terminą.

Furjė koeficientai apskaičiuojami naudojant šias formules:

Puikiai suprantu, kad nauji terminai vis dar menkai suprantami pradedantiesiems studijuoti temą: skilimo laikotarpis, pusės laikotarpis, Furjė koeficientai Ir tt Jokios panikos, tai nepalyginama su jauduliu prieš išeinant į kosmosą. Viską išsiaiškinsime kitame pavyzdyje, prieš jį vykdant logiška užduoti aktualius praktinius klausimus:

Kas turėtų būti padaryta atliekant šias užduotis?

Išplėskite funkciją Furjė serijoje. Be to, dažnai reikalaujama pavaizduoti funkcijos grafiką, serijos sumos grafiką, dalinę sumą, o esant įmantrioms profesoriaus fantazijoms – dar ką nors padaryti.

Kaip išplėsti Furjė serijos funkciją?

Iš esmės reikia rasti Furjė koeficientai, tai yra, sudarykite ir apskaičiuokite tris apibrėžtasis integralas.

Prašome perrašyti bendrą Furjė serijos vaizdą ir tris darbo formules savo bloknote. Labai džiaugiuosi, kad kai kurių svetainės lankytojų akyse išsipildo vaikystės svajonė tapti astronautu =)

2 pavyzdys

Išplėskite funkciją Furjė serijoje intervale. Sukurkite grafiką, serijų sumos ir dalinės sumos grafiką.

Sprendimas: Pirmoji užduoties dalis yra išplėsti Furjė serijos funkciją.

Pradžia yra standartinė, būtinai užsirašykite, kad:

Šioje užduotyje skilimo laikotarpis yra pusė periodo.

Išplečiame funkciją Furjė serijoje intervale:

Naudodami atitinkamas formules randame Furjė koeficientai... Dabar reikia sudaryti ir apskaičiuoti tris apibrėžtasis integralas... Patogumui sunumeruosiu prekes:

1) Pirmasis integralas yra paprasčiausias, tačiau jam jau reikia akies ir akių:

2) Mes naudojame antrąją formulę:

Šis integralas yra gerai žinomas ir jis paimamas dalimis:

Kai rasta, panaudota funkcijos perkėlimo po diferencialiniu ženklu metodas.

Nagrinėjamoje užduotyje patogiau iš karto naudoti integravimo dalimis į apibrėžtąjį integralą formulė :

Pora techninių pastabų. Pirma, pritaikius formulę visa išraiška turi būti įterpta į didelius skliaustus, nes prieš pradinį integralą yra konstanta. Mes to neprarandame! Skliaustus galima atidaryti bet kuriame tolesniame žingsnyje, aš tai padariau paskutinį kartą. Pirmame "gabale" Keisdami esame labai atsargūs, kaip matote, konstanta neveikia, o integracijos ribos yra pakeistos į produktą. Šis veiksmas paryškintas laužtiniuose skliaustuose. Na, antrojo formulės „gabalo“ integralas jums pažįstamas iš treniruočių užduoties ;-)

O svarbiausia – didžiausia dėmesio koncentracija!

3) Ieškome trečiojo Furjė koeficiento:

Gaunamas ankstesnio integralo giminaitis, kuris taip pat yra integruojasi dalimis:

Šis atvejis yra šiek tiek sudėtingesnis, žingsnis po žingsnio pakomentuosiu tolesnius veiksmus:

(1) Išraiška yra visiškai uždaryta dideliuose skliaustuose.... Nenorėjau skambėti kaip nuobodu, per dažnai jie praranda konstantą.

(2) Šiuo atveju aš iš karto atidariau tuos didelius skliaustus. Ypatingas dėmesys skiriame pirmajam „gabalui“: nuolatinis rūko nuošalyje ir nedalyvauja integravimo (ir) į gaminį ribų pakeitime. Dėl netvarkingo įrašo vėlgi patartina šį veiksmą pažymėti laužtiniais skliaustais. Su antruoju "gabalu" viskas paprasčiau: čia trupmena atsirado po didelių skliaustų išplėtimo, o konstanta - kaip pažįstamo integralo integravimo rezultatas ;-)

(3) Atliekame transformacijas laužtiniuose skliaustuose ir integravimo ribų pakeitimą dešiniuoju integralu.

(4) Išimame „mirksinčią lemputę“ iš laužtinių skliaustų:, po to atidarome vidinius skliaustus:.

(5) Sumažinkite 1 ir –1 skliausteliuose, atlikite galutinius supaprastinimus.

Galiausiai buvo rasti visi trys Furjė koeficientai:

Pakeiskime juos formulėje :

Tuo pačiu metu nepamirškite padalyti per pusę. Paskutiniame žingsnyje konstanta („minus du“), kuri nepriklauso nuo „en“, perkeliama už sumos ribų.

Taigi, mes gavome funkcijos išplėtimą Furjė serijoje intervale:

Panagrinėkime Furjė eilučių konvergencijos klausimą. Konkrečiai paaiškinsiu teoriją Dirichlet teorema, pažodžiui „ant pirštų“, taigi, jei reikia griežtos formuluotės, skaitykite matematinės analizės vadovėlį (pavyzdžiui, 2-asis Bohano tomas; arba 3-asis Fichtengolzo tomas, bet jame sunkiau).

Antroje uždavinio dalyje turite parodyti grafiką, serijos sumos grafiką ir dalinės sumos grafiką.

Funkcijų grafikas yra įprastas tiesi linija, kuris nubrėžtas juoda punktyrine linija:

Mes kalbame apie serijos sumą. Kaip žinote, eilės funkcijų susilieja su funkcijomis. Mūsų atveju sukonstruota Furjė serija bet kuriai "x" reikšmei susilieja su raudonai pavaizduota funkcija. Ši funkcija toleruoja 1 tipo pertraukos taškuose, bet ir juose apibrėžtas (raudoni taškai brėžinyje)

Taigi: ... Nesunku pastebėti, kas pastebimai skiriasi nuo pradinės funkcijos, todėl žymėjime naudojama tildė, o ne lygybės ženklas.

Panagrinėkime algoritmą, pagal kurį patogu sudaryti serijų sumą.

Centriniame intervale Furjė serija susilieja su pačia funkcija (centrinis raudonas segmentas sutampa su juoda punktyrine tiesinės funkcijos linija).

Dabar šiek tiek spėliokime apie nagrinėjamo trigonometrinio skilimo pobūdį. Furjė serijoje įtraukiamos tik periodinės funkcijos (konstanta, sinusai ir kosinusai), todėl eilutės suma taip pat yra periodinė funkcija.

Ką tai reiškia mūsų konkrečiame pavyzdyje? Ir tai reiškia, kad serijos suma –tikrai periodiškai o raudonasis intervalo segmentas turi be galo kartotis kairėje ir dešinėje.

Manau, dabar pagaliau paaiškėjo posakio „irimo laikotarpis“ prasmė. Paprasčiau tariant, kiekviena situacija kartojasi vėl ir vėl.

Praktikoje dažniausiai pakanka pavaizduoti tris skilimo laikotarpius, kaip tai daroma brėžinyje. Na, ir dar kaimyninių laikotarpių „kelmai“ – kad būtų aišku, kad diagrama tęsiasi.

Ypatingą susidomėjimą kelia 1-osios rūšies lūžio taškai... Tokiuose taškuose Furjė serija susilieja į izoliuotas vertes, kurios yra tiksliai pertraukos „šuolio“ viduryje (raudoni taškai brėžinyje). Kaip žinote šių taškų ordinatę? Pirmiausia randame „viršutinio aukšto“ ordinates: tam apskaičiuojame funkcijos reikšmę kraštutiniame dešiniajame centrinio išsiplėtimo laikotarpio taške:. Norint apskaičiuoti „apatinio aukšto“ ordinates, paprasčiausias būdas yra paimti to paties laikotarpio kairiausią reikšmę: ... Vidurkio ordinatė yra „viršaus ir apačios“ sumos aritmetinis vidurkis:. Smagu tai, kad statant piešinį iškart pamatysite, ar vidurys paskaičiuotas teisingai, ar neteisingai.

Sukonstruokime dalinę eilutės sumą ir tuo pačiu pakartokime termino „konvergencija“ reikšmę. Motyvas taip pat žinomas iš pamokos apie skaičių serijos suma... Išsamiai apibūdinkime savo turtus:

Norint sudaryti dalinę sumą, reikia užrašyti nulį + dar du serijos narius. Tai yra,

Brėžinyje funkcijų grafikas pavaizduotas žaliai ir, kaip matote, gana tvirtai apgaubia visą sumą. Jei atsižvelgsime į dalinę penkių serijos narių sumą, tai šios funkcijos grafikas dar tiksliau apytiksliai apytikslės raudonas linijas, jei yra šimtas narių, tada „žalia gyvatė“ iš tikrųjų visiškai susilies su raudonais segmentais, ir tt Taigi Furjė eilutė suartėja su jos suma.

Įdomu pastebėti, kad bet kokia dalinė suma yra nuolatinė funkcija, tačiau bendra serijų suma vis dar nenutrūksta.

Praktikoje neretai nubraižoma ir dalinė suma. Kaip tai padaryti? Mūsų atveju reikia atsižvelgti į atkarpos funkciją, apskaičiuoti jos reikšmes atkarpos galuose ir tarpiniuose taškuose (kuo daugiau taškų atsižvelgsite, tuo tikslesnis bus grafikas). Tada turėtumėte pažymėti šiuos taškus brėžinyje ir tiksliai pavaizduoti laikotarpio grafiką, o tada „atkartoti“ jį gretimuose intervaluose. Kaip kitaip? Juk aproksimacija taip pat yra periodinė funkcija ... ... jos grafikas man kažkaip primena tolygų širdies ritmą medicinos prietaiso ekrane.

Žinoma, tai nėra labai patogu atlikti konstrukciją, nes jūs turite būti ypač tikslus, išlaikant ne mažesnį nei pusės milimetro tikslumą. Tačiau nudžiuginsiu skaitytojus, kurie nesiderina su piešimu - atliekant „tikrą“ užduotį, piešti ne visada reikia, kažkur 50% atvejų reikia išplėsti funkciją Furjė serijoje ir tiek.

Užbaigę piešinį, atliekame užduotį:

Atsakymas:

Daugelyje užduočių nukenčia funkcija 1-osios rūšies pertrauka tiesiai skilimo laikotarpiu:

3 pavyzdys

Furjė serijoje išplėskite segmente nurodytą funkciją. Nubraižykite funkciją ir bendrą serijų sumą.

Siūloma funkcija pateikiama dalimis (be to, atminkite, tik segmente) ir ištveria 1-osios rūšies pertrauka taške. Ar galima apskaičiuoti Furjė koeficientus? Jokiu problemu. Tiek kairioji, tiek dešinė funkcijos pusės yra integruojamos savo intervalais, todėl kiekvienoje iš trijų formulių integralai turi būti pavaizduoti kaip dviejų integralų suma. Pavyzdžiui, pažiūrėkime, kaip tai daroma su nuliniu koeficientu:

Antrasis integralas pasirodė lygus nuliui, o tai sumažino darbą, tačiau taip būna ne visada.

Kiti du Furjė koeficientai rašomi taip pat.

Kaip pavaizduoti serijos sumą? Kairiajame intervale nubrėžiame tiesios linijos atkarpą, o intervale - tiesiosios linijos atkarpą (ašies atkarpą pasirinkite paryškintu ir paryškintu). Tai yra, išplėtimo intervale serijų suma sutampa su funkcija visur, išskyrus tris „blogus“ taškus. Funkcijos nepertraukiamumo taške Furjė serija susilieja į izoliuotą reikšmę, kuri yra tiksliai pertraukos „šuolio“ viduryje. Tai nesunku pamatyti žodžiu: kairės pusės riba:, dešinės pusės riba: ir, aišku, vidurio taško ordinatė yra 0,5.

Dėl sumos periodiškumo paveikslas turi būti „padaugintas“ iš gretimų laikotarpių, ypač norint pavaizduoti tą patį intervaluose ir. Šiuo atveju Furjė eilutės taškuose suartėja su medianinėmis reikšmėmis.

Tiesą sakant, čia nieko naujo.

Pabandykite patys susidoroti su šia užduotimi. Apytikslis apdailos projekto pavyzdys ir brėžinys pamokos pabaigoje.

Funkcijos išplėtimas Furjė serijoje savavališkame periode

Savavališkam išplėtimo laikotarpiui, kur "el" yra bet koks teigiamas skaičius, Furjė eilučių ir Furjė koeficientų formulės skiriasi šiek tiek sudėtingu sinuso ir kosinuso argumentu:

Jei, tada gauname spragų formules, nuo kurių pradėjome.

Problemos sprendimo algoritmas ir principai yra visiškai išsaugoti, tačiau techninis skaičiavimų sudėtingumas didėja:

4 pavyzdys

Išplėskite funkciją Furjė eilutėje ir nubraižykite sumą.

Sprendimas: iš tikrųjų 3 pavyzdžio analogas su 1-osios rūšies pertrauka taške. Šioje užduotyje skilimo laikotarpis yra pusė periodo. Funkcija apibrėžiama tik per pusę intervalo, tačiau tai nekeičia reikalo – svarbu, kad abi funkcijos dalys būtų integruojamos.

Išplėskime funkciją Furjė serijoje:

Kadangi funkcija pradžioje yra nepertraukiama, kiekvienas Furjė koeficientas turėtų būti parašytas kaip dviejų integralų suma:

1) Pirmąjį integralą parašysiu kuo išsamiau:

2) Atidžiai žiūrime į Mėnulio paviršių:

Antrasis integralas paimti dalimis:

Į ką turėtumėte atkreipti ypatingą dėmesį, kai sprendimo tęsinį atidarome žvaigždute?

Pirma, mes neprarandame pirmojo integralo , kur iš karto vykdome diferencialinis ženklas... Antra, nepamirškite nelemtos konstantos prieš didžiuosius skliaustus ir nesipainiokite ženkluose kai naudojate formulę ... Tačiau didelius laikiklius patogiau atidaryti iškart kitame žingsnyje.

Likusi dalis yra technologijos reikalas, sunkumų gali kilti tik dėl nepakankamos integralų sprendimo patirties.

Taip, ne veltui garsūs prancūzų matematiko Furjė kolegos piktinosi - kaip jis išdrįso išskaidyti funkcijas į trigonometrines eilutes ?! =) Beje, turbūt visus domina praktinė nagrinėjamos užduoties prasmė. Pats Furjė kūrė matematinį šilumos laidumo modelį, o vėliau jo vardu pavadinta serija imta tirti daugybę periodinių procesų, kurie aplinkiniame pasaulyje, matyt, nematomi. Dabar, beje, pagavau save galvojant, kad neatsitiktinai antrojo pavyzdžio grafiką palyginau su periodiniu pulso dažniu. Norintieji gali susipažinti su praktiniu pritaikymu Furjė transformacija trečiųjų šalių šaltiniuose. ... Nors geriau ne - tai bus prisiminta kaip Pirmoji meilė =)

3) Atsižvelgdami į ne kartą minėtas silpnąsias grandis, nagrinėjame trečiąjį koeficientą:

Integruojame gabalas po gabalo:

Rastus Furjė koeficientus pakeiskite į formulę , nepamirštant nulinio koeficiento padalyti per pusę:

Nubraižykime serijos sumą. Trumpai pakartokime procedūrą: ties intervale pastatykite tiesę, o intervale – tiesią. Jei x reikšmė lygi nuliui, tarpo viduryje dedame tašką „peršokti“ ir „atkartoti“ gretimų laikotarpių diagramą:

Periodų „susijungimo vietose“ suma taip pat bus lygi tarpo „šuolio“ vidurio taškams.

Paruošta. Leiskite jums priminti, kad pati funkcija, remiantis hipoteze, yra apibrėžta tik per pusę intervalo ir, žinoma, sutampa su intervalų serijų suma

Atsakymas:

Kartais dalimis duota funkcija taip pat yra nenutrūkstama per išplėtimo laikotarpį. Paprasčiausias pavyzdys: ... Sprendimas (žr. 2-ąjį Bohano tomą) yra toks pat kaip dviejuose ankstesniuose pavyzdžiuose: nepaisant funkcijos tęstinumas taške kiekvienas Furjė koeficientas išreiškiamas kaip dviejų integralų suma.

Skilimo intervale 1-osios rūšies lūžio taškai ir (arba) grafiko „sankryžos“ taškų gali būti daugiau (du, trys ir paprastai bet kurie galutinis skaičius). Jei funkcija yra integruota kiekvienoje dalyje, tada ją taip pat galima išplėsti Furjė serijoje. Bet iš praktinės patirties neprisimenu tokio sunkaus dalyko. Nepaisant to, yra ir sunkesnių užduočių nei ką tik svarstyta, o straipsnio pabaigoje visiems yra nuorodos į padidinto sudėtingumo Furjė serijas.

Tuo tarpu atsipalaiduokime, atsilošdami į kėdes ir apmąstykime nesibaigiančias žvaigždėtas platybes:

5 pavyzdys

Išplėskite funkciją Furjė eilutėje intervale ir nubraižykite serijos sumą.

Šioje problemoje funkcija tęstinis dėl skilimo pusės intervalo, kuris supaprastina sprendimą. Viskas labai panašu į 2 pavyzdį. Nuo erdvėlaivio nepabėgsi – turi apsispręsti =) Pamokos pabaigoje projekto pavyzdys, grafikas pridedamas.

Furjė serijos lyginių ir nelyginių funkcijų išplėtimas

Naudojant lygines ir nelygines funkcijas, problemos sprendimo procesas pastebimai supaprastėja. Ir todėl. Grįžkime prie Furjė serijos funkcijos išplėtimo periode "du pi" ir savavališkas laikotarpis "du ale" .

Tarkime, kad mūsų funkcija yra lygi. Bendrame serijos termine, kaip matote, yra lyginiai kosinusai ir nelyginiai sinusai. O jei išplečiame LYGinę funkciją, kam tada reikia nelyginių sinusų?! Išmeskime nereikalingą koeficientą:.

Taigi, lygi funkcija gali būti išplėsta į Furjė eilutę tik kosinusais:

Tiek, kiek lyginių funkcijų integralai per integravimo segmentą, simetrišką nulio atžvilgiu, galima padvigubinti, tada supaprastinami ir likę Furjė koeficientai.

Dėl tarpo:

Savavališkam intervalui:

Vadovėlių pavyzdžiai, kuriuos galima rasti beveik bet kuriame skaičiavimo vadovėlyje, apima lyginių funkcijų skaidymus ... Be to, jie ne kartą susitiko mano asmeninėje praktikoje:

6 pavyzdys

Pateikta funkcija. Reikalinga:

1) Furjė serijos funkciją išplėskite tašku, kur yra savavališkas teigiamas skaičius;

2) Užrašykite intervalo išplėtimą, sukurkite visos eilučių sumos funkciją ir grafiką.

Sprendimas: pirmoje pastraipoje siūloma problemą spręsti bendra forma, ir tai labai patogu! Atsiras poreikis – tiesiog pakeiskite savo vertę.

1) Šioje užduotyje plėtimosi laikotarpis yra pusės periodas. Atliekant tolesnius veiksmus, ypač integracijos metu, „el“ laikomas konstanta

Funkcija yra lygi, o tai reiškia, kad ją galima išplėsti į Furjė seriją tik kosinusais: .

Furjė koeficientų ieškome pagal formules ... Atkreipkite dėmesį į jų besąlyginę naudą. Pirma, integracija vykdoma per teigiamą išplėtimo segmentą, o tai reiškia, kad mes saugiai atsikratome modulio , atsižvelgiant tik į "X" iš dviejų dalių. Ir, antra, integracija pastebimai supaprastinta.

Du:

Integruojame gabalas po gabalo:

Taigi:
, šiuo atveju iš sumos išimama konstanta, kuri nepriklauso nuo „en“.

Atsakymas:

2) Rašome intervalo išplėtimą, tam bendrojoje formulėje pakeičiame reikiamą pusės periodo reikšmę:

Bendrojo ir profesinio švietimo ministerija

Sočio valstybinis turizmo universitetas

ir kurorto verslas

Pedagoginis institutas

Matematikos fakultetas

Bendrosios matematikos katedra

BAIGIAMOSIOS DARBOS

Furjė serijos ir jų taikymas

Matematinės fizikos srityje.

Baigė: 5 kurso studentas

etatinio parašo

Specialybė 010100

"Matematika"

Kasperova N.S.

Mokinio pažymėjimo numeris 95471

Mokslinis patarėjas: docentas, Cand.

techninis parašas mokslai

Pozin P.A.

Sočis, 2000 m

1. Įvadas.

2. Furjė serijos samprata.

2.1. Furjė eilutės koeficientų nustatymas.

2.2. Periodinių funkcijų integralai.

3. Furjė eilučių konvergencijos kriterijai.

3.1. Funkcijų išplėtimo Furjė serijose pavyzdžiai.

4. Pastaba apie periodinės funkcijos išplėtimą Furjė eilutėje

5. Furjė serijos lyginėms ir nelyginėms funkcijoms.

6. Furjė serija funkcijoms su 2 periodu l .

7. Neperiodinės funkcijos Furjė eilutės išplėtimas.

Įvadas.

Jean Baptiste Joseph Fourier – prancūzų matematikas, Paryžiaus mokslų akademijos narys (1817).

Pirmieji Furjė darbai buvo susiję su algebra. Jau 1796 m. paskaitose jis išdėstė teoremą apie jo vardu pavadintos algebrinės lygties, esančios tarp duotų ribų, realiųjų šaknų skaičiaus (publ. 1820); Išsamų algebrinės lygties realiųjų šaknų skaičiaus sprendimą 1829 m. gavo Zh.Sh.F. Per audrą. 1818 metais Furjė nagrinėjo Niutono sukurto lygčių skaitinio sprendimo metodo pritaikymo sąlygų klausimą, nežinodamas apie panašius rezultatus, 1768 metais gautus prancūzų matematiko J.R. Murailem. Furjė darbo, susijusio su skaitiniais lygčių sprendimo metodais, rezultatas yra „Tam tikrų lygčių analizė“, paskelbta po mirties 1831 m.

Pagrindinė Furjė studijų sritis buvo matematinė fizika. 1807 ir 1811 metais jis Paryžiaus mokslų akademijai pristatė savo pirmuosius šilumos sklidimo kietuosiuose kūne teorijos atradimus, o 1822 metais paskelbė garsųjį veikalą „Analitinė šilumos teorija“, suvaidinusį svarbų vaidmenį vėlesnėje matematikos istorijoje. Tai matematinė šilumos laidumo teorija. Dėl metodo bendrumo ši knyga tapo visų šiuolaikinių matematinės fizikos metodų šaltiniu. Šiame darbe Furjė išvedė diferencialinę šilumos laidumo lygtį ir išplėtojo anksčiau D. Bernoulli išdėstytas idėjas, sukūrė kintamųjų atskyrimo metodą (Fourier metodas), sprendžiant šilumos lygtį tam tikromis ribinėmis sąlygomis, kurią pritaikė ypatingų atvejų skaičius (kubas, cilindras ir kt.). Šis metodas pagrįstas funkcijų atvaizdavimu trigonometrinėmis Furjė eilutėmis.

Furjė serijos dabar tapo gerai išvystyta dalinių diferencialinių lygčių teorijos priemone ribinėms reikšmėms spręsti.

1. Furjė serijos samprata.(p. 94, Uvarenkovas)

Furjė serijos vaidina svarbų vaidmenį matematinės fizikos, elastingumo teorijos, elektrotechnikos, o ypač jų ypatingas atvejis - trigonometrinės Furjė serijos.

Trigonometrinė serija yra formos serija

arba simboliškai:

(1)

kur ω, a 0, a 1,…, a n,…, b 0, b 1,…, b n,… yra pastovūs skaičiai (ω> 0).

Istoriškai kai kurios fizikos problemos paskatino tokias eilutes tirti, pavyzdžiui, stygų virpesių problema (XVIII a.), šilumos laidumo reiškinių dėsningumų problema ir kt. Taikymuose atsižvelgiama į trigonometrines eilutes. , pirmiausia yra susijęs su tam tikro judesio vaizdavimo problema, aprašyta lygtimi y = ƒ (x),

paprasčiausių harmoninių virpesių sumos forma, dažnai imama be galo dideliu skaičiumi, t.y. kaip (1) formos serijos suma.

Taigi pasiekiame tokią problemą: išsiaiškinkite, ar duotai funkcijai ƒ (x) tam tikrame intervale egzistuoja eilutė (1), kuri konverguotų šiame intervale į šią funkciją. Jei tai įmanoma, sakoma, kad funkcija ƒ (x) yra išplėsta trigonometrine seka šiame intervale.

Serija (1) konverguoja tam tikru tašku x 0 dėl funkcijų periodiškumo

(n = 1,2, ..), jis pasirodo konvergencinis visuose formos taškuose (m yra bet koks sveikas skaičius), taigi jo suma S (x) bus (eilės konvergencijos srityje) periodinė funkcija: jei S n ( x) yra n-oji šios serijos dalinė suma, tada turime

ir todėl

, tai yra, S (x 0 + T) = S (x 0). Todėl, kalbėdami apie kokios nors funkcijos ƒ (x) išplėtimą (1) formos eilutėje, laikysime, kad ƒ (x) yra periodinė funkcija.

2. Eilučių koeficientų nustatymas Furjė formulėmis.

Tegul periodinė funkcija ƒ (x) su periodu 2π yra tokia, kad ją pavaizduotų trigonometrinė eilutė, konverguojanti į nurodytą funkciją intervale (-π, π), tai yra, tai yra šios eilutės suma:

. (2)

Tarkime, kad funkcijos integralas kairėje šios lygybės pusėje yra lygus šios eilutės narių integralų sumai. Tai bus atlikta, jei darysime prielaidą, kad skaitinės eilutės, sudarytos iš duotų trigonometrinių eilučių koeficientų, konverguoja absoliučiai, ty teigiamų skaičių eilutės konverguoja

(3)

Serija (1) yra suskirstyta į didžiąją dalį ir gali būti integruojama po termino intervale (-π, π). Mes integruojame abi lygybės puses (2):

Skaičiuojame atskirai kiekvieną integralą dešinėje:

, .

Taigi,

, kur

. (4)

Furjė koeficientų įvertinimas.(Bugrov)

1 teorema. Tegul 2π periodo funkcija ƒ (x) turi nuolatinę išvestinę ƒ ( s) (x) įsakymo s, tenkinant nelygybę visoje realioje ašyje:

│ ƒ (s) (x) │≤ M s; (5)

tada funkcijos Furjė koeficientai ƒ patenkinti nelygybę

(6)

Įrodymas. Integravimas dalimis ir atsižvelgiant į tai

ƒ (-π) = ƒ (π), turime

Integruojant (7) dešinę pusę paeiliui, atsižvelgiant į tai, kad išvestinės ƒ ΄, ..., ƒ (s-1) yra ištisinės ir taškuose t = -π ir t = turi tokias pačias reikšmes. π, taip pat įvertį (5), gauname pirmąjį įvertį (6).

Antrasis įvertinimas (6) gaunamas panašiu būdu.

2 teorema. Furjė koeficientai ƒ (x) tenkina nelygybę

(8)

Įrodymas. Mes turime

Furjė serija yra savavališkos funkcijos su tam tikru periodu atvaizdavimas serijos pavidalu. Apskritai šis sprendimas vadinamas elemento išplėtimu stačiakampiu pagrindu. Funkcijų išplėtimas Furjė serijoje yra gana galingas įrankių rinkinys sprendžiant įvairias problemas dėl šios transformacijos savybių integravimo, diferenciacijos metu, taip pat išraiškos poslinkio argumentu ir konvoliucija.

Žmogus, kuris nėra susipažinęs su aukštąja matematika, taip pat su prancūzų mokslininko Furjė darbais, greičiausiai nesupras, kas yra „gretai“ ir kam jie skirti. Tuo tarpu ši transformacija tapo gana tankia mūsų gyvenimo dalimi. Jį naudoja ne tik matematikai, bet ir fizikai, chemikai, medikai, astronomai, seismologai, okeanografai ir daugelis kitų. Pažvelkime atidžiau į didžiojo prancūzų mokslininko, kuris atrado anksčiau laiko, darbus.

Žmogaus ir Furjė transformacija

Furjė serija yra vienas iš metodų (kartu su analize ir kitais) Šis procesas vyksta kiekvieną kartą, kai žmogus girdi garsą. Mūsų ausis automatiškai transformuoja elementarias daleles į elastingą terpę, kurios suskaidomos į eiles (išilgai spektro) nuoseklių garsumo lygio verčių, skirtų skirtingo aukščio tonams. Be to, smegenys šiuos duomenis paverčia mums žinomais garsais. Visa tai vyksta atskirai nuo mūsų noro ar sąmonės, savaime, tačiau norint suprasti šiuos procesus, prireiks kelerių metų studijuoti aukštąją matematiką.

Daugiau apie Furjė transformaciją

Furjė transformaciją galima atlikti naudojant analitinius, skaitinius ir kitus metodus. Furjė serija reiškia bet kokio svyravimo proceso skaitinį skaidymą – nuo vandenyno potvynių ir šviesos bangų iki saulės (ir kitų astronominių objektų) veiklos ciklų. Naudodami šiuos matematinius metodus galite išanalizuoti funkcijas, vaizduojančias bet kokius svyruojančius procesus kaip sinusoidinių komponentų seriją, kuri pereina nuo minimumo iki maksimumo ir atgal. Furjė transformacija yra funkcija, apibūdinanti sinusoidų fazę ir amplitudę tam tikru dažniu. Šis procesas gali būti naudojamas sprendžiant labai sudėtingas lygtis, apibūdinančias dinaminius procesus, vykstančius šiluminės, šviesos ar elektros energijos įtakoje. Taip pat Furjė serija leidžia išskirti pastovius komponentus sudėtinguose virpesių signaluose, dėl kurių atsirado galimybė teisingai interpretuoti gautus eksperimentinius stebėjimus medicinoje, chemijoje ir astronomijoje.

Istorinė nuoroda

Šios teorijos įkūrėjas yra prancūzų matematikas Jeanas Baptiste'as Josephas Fourier. Vėliau ši transformacija buvo pavadinta jo vardu. Iš pradžių mokslininkas savo metodą taikė tirdamas ir aiškindamas šilumos laidumo – šilumos sklidimo kietose medžiagose – mechanizmus. Furjė pasiūlė, kad pradinis netaisyklingas pasiskirstymas gali būti išskaidytas į paprasčiausias sinusoidus, kurių kiekviena turės savo temperatūros minimumą ir maksimumą, taip pat savo fazę. Be to, kiekvienas toks komponentas bus matuojamas nuo minimumo iki maksimumo ir atgal. Matematinė funkcija, apibūdinanti kreivės viršutinę ir apatinę smailes, taip pat kiekvienos harmonikos fazę, vadinama temperatūros pasiskirstymo išraiškos Furjė transformacija. Teorijos autorius sumažino matematiškai sunkiai nusakomą bendrąją skirstinio funkciją iki labai patogios kosinuso ir sinuso eilės, kurios kartu duoda pirminį skirstinį.

Transformacijos principas ir amžininkų pažiūros

Mokslininko amžininkai – žymiausi XIX amžiaus pradžios matematikai – šios teorijos nepriėmė. Pagrindinis prieštaravimas buvo Furjė tvirtinimas, kad nenutrūkstamą funkciją, apibūdinančią tiesią liniją arba nepertraukiamą kreivę, galima pavaizduoti kaip sinusoidinių išraiškų, kurios yra tolydžios, sumą. Kaip pavyzdį apsvarstykite Heaviside „žingsnį“: jo reikšmė lygi nuliui kairėje nuo tarpo ir vienai dešinėje. Ši funkcija apibūdina elektros srovės priklausomybę nuo laiko kintamojo, kai grandinė uždaryta. To meto teorijos amžininkai niekada nebuvo susidūrę su panašia situacija, kai nepertraukiama išraiška būtų apibūdinta nuolatinių, įprastų funkcijų, tokių kaip eksponentinė, sinusoidė, tiesinė ar kvadratinė, deriniu.

Kas supainiojo prancūzų matematikus apie Furjė teoriją?

Galų gale, jei matematikas buvo teisus savo teiginiuose, tai susumavus begalinę trigonometrinę Furjė eilutę, galima gauti tikslų laipsniškos išraiškos vaizdą, net jei joje yra daug tokių žingsnių. Devynioliktojo amžiaus pradžioje toks teiginys atrodė absurdiškas. Tačiau nepaisant visų abejonių, daugelis matematikų išplėtė šio reiškinio tyrimo apimtį, perkeldami jį už šilumos laidumo tyrimų ribų. Tačiau daugumą mokslininkų ir toliau kankino klausimas: „Ar sinusoidinės eilutės suma gali susilyginti su tikslia nenutrūkstamos funkcijos verte?

Furjė eilučių konvergencija: pavyzdys

Konvergencijos klausimas iškeliamas kaskart, kai reikia susumuoti begalines skaičių eilutes. Norėdami suprasti šį reiškinį, apsvarstykite klasikinį pavyzdį. Ar kada nors pavyks pasiekti sieną, jei kiekvienas tolesnis žingsnis bus perpus mažesnis už ankstesnį? Tarkime, kad esate du metrai nuo tikslo, pirmas žingsnis priartina jus prie pusiaukelės, kitas - prie trijų ketvirčių atžymos, o po penktojo įveiksite beveik 97 procentus kelio. Tačiau kad ir kiek žingsnių žengtumėte, užsibrėžto tikslo griežtąja matematine prasme nepasieksite. Naudodamiesi skaitiniais skaičiavimais, galite įrodyti, kad galų gale galite priartėti prie savavališkai mažo nustatyto atstumo. Šis įrodymas prilygsta parodymui, kad bendra pusės, ketvirtadalio ir tt vertė bus linkusi į vienybę.

Konvergencijos klausimas: antrasis atėjimas arba lordo Kelvino aparatas

Šis klausimas vėl buvo iškeltas XIX amžiaus pabaigoje, kai Furjė serija buvo bandoma numatyti atoslūgių ir atoslūgių intensyvumą. Per tą laiką lordas Kelvinas išrado įrenginį – analoginį skaičiavimo įrenginį, kuris leido kariuomenės ir prekybinio laivyno jūreiviams sekti šį gamtos reiškinį. Šis mechanizmas nustatė fazių ir amplitudių rinkinius iš potvynių aukščių lentelės ir atitinkamų laiko momentų, kruopščiai išmatuotų tam tikrame uoste ištisus metus. Kiekvienas parametras buvo sinusoidinis potvynio aukščio išraiškos komponentas ir buvo vienas iš reguliarių komponentų. Matavimų rezultatai buvo įvesti į lordo Kelvino skaičiuotuvą, kuris susintetino kreivę, numatančią vandens aukštį kaip laiko funkciją kitiems metams. Labai greitai panašios kreivės buvo nubrėžtos visuose pasaulio uostuose.

Ką daryti, jei procesą nutraukia nepertraukiama funkcija?

Tuo metu atrodė akivaizdu, kad potvynio bangos prognozuotojas su daugybe skaičiavimų gali apskaičiuoti daug fazių ir amplitudių ir taip pateikti tikslesnes prognozes. Nepaisant to, paaiškėjo, kad šis modelis nepastebėtas tais atvejais, kai potvynio išraiška, kurią reikėtų susintetinti, turėjo staigų šuolį, tai yra, jis buvo nenutrūkstamas. Tuo atveju, kai į įrenginį įvedami duomenys iš laiko momentų lentelės, jis apskaičiuoja kelis Furjė koeficientus. Sinusoidinių komponentų dėka (pagal rastus koeficientus) atkuriama pirminė funkcija. Neatitikimas tarp originalo ir atkurtos išraiškos gali būti išmatuotas bet kuriame taške. Atliekant pakartotinius skaičiavimus ir palyginimus, matyti, kad didžiausios paklaidos reikšmė nemažėja. Tačiau jie yra lokalizuoti regione, atitinkančiame nutrūkimo tašką, o bet kuriame kitame taške jie linkę į nulį. 1899 metais šį rezultatą teoriškai patvirtino Joshua Willardas Gibbsas iš Jeilio universiteto.

Furjė eilučių konvergencija ir matematikos raida apskritai

Furjė analizė netaikoma išraiškoms, turinčioms begalinį skaičių serijų tam tikru intervalu. Apskritai Furjė eilutės, jei pradinė funkcija pavaizduota realaus fizinio matavimo rezultatu, visada suartėja. Šio proceso konvergencijos konkrečioms funkcijų klasėms klausimai lėmė naujų matematikos šakų, pavyzdžiui, apibendrintų funkcijų teorijos, atsiradimą. Jis siejamas su tokiais vardais kaip L. Schwartz, J. Mikusinsky ir J. Temple. Šios teorijos rėmuose buvo sukurtas aiškus ir tikslus teorinis pagrindas tokioms išraiškoms kaip Dirako delta funkcija (ji apibūdina vienos srities plotą, sutelktą be galo mažoje taško kaimynystėje) ir Heaviside „žingsnis“. . Šio darbo dėka Furjė serija tapo pritaikyta sprendžiant lygtis ir uždavinius, kuriuose atsiranda intuityvios sąvokos: taškinis krūvis, taškinė masė, magnetiniai dipoliai, taip pat koncentruota spindulio apkrova.

Furjė metodas

Furjė serija, vadovaujantis trukdžių principais, prasideda sudėtingų formų skaidymu į paprastesnes. Pavyzdžiui, šilumos srauto pasikeitimas paaiškinamas jo praėjimu per įvairias netaisyklingos formos šilumą izoliuojančios medžiagos kliūtis arba žemės paviršiaus pasikeitimu – žemės drebėjimu, dangaus kūno orbitos pasikeitimu planetų įtaka. Paprastai tokias paprastas klasikines sistemas apibūdinančias lygtis galima nesunkiai išspręsti kiekvienai atskirai bangai. Furjė parodė, kad paprasti sprendimai taip pat gali būti apibendrinti, kad būtų galima išspręsti sudėtingesnes problemas. Matematikos kalba Furjė serija yra būdas pateikti išraišką kaip harmonikų - kosinuso ir sinusoidų - sumą. Todėl ši analizė taip pat žinoma kaip „harmoninė analizė“.

Furjė serija – ideali technika prieš „kompiuterių amžių“

Prieš kuriant kompiuterines technologijas, Furjė technika buvo geriausias ginklas mokslininkų arsenale dirbant su mūsų pasaulio bangine prigimtimi. Sudėtinga Furjė serija leidžia išspręsti ne tik paprastas problemas, kurias galima tiesiogiai pritaikyti Niutono mechanikos dėsniams, bet ir pagrindines lygtis. Dauguma Niutono mokslo atradimų XIX amžiuje buvo įmanomi tik Furjė metodu.

Furjė serija šiandien

Tobulėjant kompiuteriams Furjė transformacijos pakilo į kokybiškai naują lygį. Ši technika yra tvirtai įsitvirtinusi beveik visose mokslo ir technologijų srityse. Pavyzdžiui, skaitmeninis garso ir vaizdo įrašas. Ją įgyvendinti tapo įmanoma tik XIX amžiaus pradžioje prancūzų matematiko sukurtos teorijos dėka. Taigi Furjė serija sudėtinga forma leido padaryti proveržį kosminės erdvės tyrime. Be to, tai turėjo įtakos puslaidininkinių medžiagų ir plazmos fizikos, mikrobangų akustikos, okeanografijos, radaro, seismologijos studijoms.

Trigonometrinė Furjė serija

Matematikoje Furjė serija yra būdas pavaizduoti savavališkas sudėtingas funkcijas kaip paprastesnių funkcijų sumą. Paprastai tokių išraiškų skaičius gali būti begalinis. Be to, kuo daugiau skaičiuojant atsižvelgiama į jų skaičių, tuo tiksliau gaunamas galutinis rezultatas. Dažniausiai trigonometrinės kosinuso arba sinuso funkcijos naudojamos kaip paprasčiausios. Šiuo atveju Furjė eilutė vadinama trigonometrine, o tokių išraiškų sprendimas vadinamas harmonine plėtra. Šis metodas vaidina svarbų vaidmenį matematikoje. Visų pirma, trigonometrinė serija yra priemonė vaizdui, taip pat funkcijoms tirti, tai yra pagrindinis teorijos aparatas. Be to, tai leidžia išspręsti daugybę matematinės fizikos problemų. Galiausiai ši teorija prisidėjo prie raidos ir davė pradžią kelioms labai svarbioms matematikos mokslo šakoms (integralų teorijai, periodinių funkcijų teorijai). Be to, tai buvo atspirties taškas kuriant šias realaus kintamojo funkcijas, taip pat padėjo pagrindą harmoninei analizei.

Veikia suskaidydamas jas į komponentus. Kintamosios srovės ir įtampa, poslinkiai, švaistiklio greitis ir pagreitis bei akustinės bangos yra tipiški praktiniai periodinių funkcijų naudojimo inžineriniuose skaičiavimuose pavyzdžiai.

Furjė eilutės išplėtimas grindžiamas prielaida, kad visos praktinės reikšmės funkcijos intervale -π ≤x≤ π gali būti išreikštos konverguojančių trigonometrinių eilučių forma (eilutė laikoma konvergentine, jei dalinių sumų seka susideda iš jos narių susilieja):

Standartinis (= normalus) žymėjimas per sinx ir cosx sumą

f (x) = a o + a 1 cosx + a 2 cos2x + a 3 cos3x + ... + b 1 sinx + b 2 sin2x + b 3 sin3x + ...,

kur a o, a 1, a 2, ..., b 1, b 2, .. yra tikrosios konstantos, t.y.

Kur diapazone nuo -π iki π Furjė eilutės koeficientai apskaičiuojami pagal formules:

Vadinami koeficientai a o, a n ir b n Furjė koeficientai, o jei juos galima rasti, vadinasi serija (1). šalia Furjė, atitinkančią funkciją f (x). Serijai (1) terminas (a 1 cosx + b 1 sinx) vadinamas pirmuoju arba pagrindinė harmonika,

Kitas būdas rašyti seriją yra naudoti santykį acosx + bsinx = csin (x + α)

f (x) = a o + c 1 sin (x + α 1) + c 2 sin (2x + α 2) + ... + c n sin (nx + α n)

Kur ao yra konstanta, kai 1 = (a 1 2 + b 1 2) 1/2, kai n = (an 2 + bn 2) 1/2 yra įvairių komponentų amplitudės ir yra lygi an = arctan an / b n.

Serijoje (1) terminas (a 1 cosx + b 1 sinx) arba c 1 sin (x + α 1) vadinamas pirmuoju arba pagrindinė harmonika,(a 2 cos2x + b 2 sin2x) arba c 2 sin (2x + α 2) vadinamas antroji harmonika ir tt

Norint tiksliai pavaizduoti sudėtingą signalą, paprastai reikia begalinio skaičiaus terminų. Tačiau daugelyje praktinių problemų pakanka atsižvelgti tik į keletą pirmųjų terminų.

Furjė neperiodinių funkcijų serija su periodu 2π.

Neperiodinių funkcijų išplėtimas Furjė serijoje.

Jei funkcija f (x) yra neperiodinė, ji negali būti išplėsta Furjė serijoje visoms x reikšmėms. Tačiau galite apibrėžti Furjė eilutę, vaizduojančią funkciją bet kuriame 2π pločio diapazone.

Jei nurodyta neperiodinė funkcija, galite sukurti naują funkciją, paimdami f (x) reikšmes tam tikrame diapazone ir pakartodami jas už šio diapazono ribų 2π intervalais. Kadangi naujoji funkcija yra periodinė su 2π periodu, ją galima išplėsti Furjė serijoje visoms x reikšmėms. Pavyzdžiui, funkcija f (x) = x nėra periodinė. Tačiau, jei reikia ją išplėsti Furjė eilutėje intervale nuo o iki 2π, tada už šio intervalo ribų sudaroma periodinė funkcija, kurios periodas yra 2π (kaip parodyta paveikslėlyje žemiau).

Neperiodinėms funkcijoms, tokioms kaip f (x) = x, Furjė eilutės suma yra lygi f (x) reikšmei visuose nurodyto diapazono taškuose, tačiau ji nėra lygi f (x) taškams. už diapazono ribų. Norint rasti neperiodinės funkcijos Furjė eilutes 2π diapazone, naudojama ta pati Furjė koeficientų formulė.

Lyginės ir nelyginės funkcijos.

Jie sako, kad funkcija y = f (x) net jei f (-x) = f (x) visoms x reikšmėms. Lyginių funkcijų grafikai visada yra simetriški y ašiai (t. y. jie yra veidrodiniai). Du lyginių funkcijų pavyzdžiai: y = x 2 ir y = cosx.

Sakoma, kad funkcija y = f (x). keista, jei f (-x) = - f (x) visoms x reikšmėms. Nelyginių funkcijų diagramos visada yra simetriškos kilmės atžvilgiu.

Daugelis funkcijų nėra nei lyginės, nei nelyginės.

Furjė plėtimasis kosinusais.

Lyginės periodinės funkcijos f (x) Furjė eilutėje, kurios periodas yra 2π, yra tik terminai su kosinusais (t. y. joje nėra terminų su sinusais) ir gali būti pastovus narys. Vadinasi,

kur Furjė eilutės koeficientai,

Nelyginės periodinės funkcijos f (x), kurios periodas yra 2π, Furjė eilutėje yra tik terminai su sinusais (t. y. joje nėra terminų su kosinusais).

Vadinasi,

kur Furjė eilutės koeficientai,

Pusės ciklo Furjė serija.

Jei funkcija apibrėžta diapazonui, tarkime, nuo 0 iki π, o ne tik nuo 0 iki 2π, ji gali būti išplėsta serijoje tik sinusais arba tik kosinusais. Gauta Furjė serija vadinama šalia Furjė pusės periodo metu.

Jei norite gauti skaidymą Furjė pusciklas kosinusais funkcija f (x) diapazone nuo 0 iki π, tada reikia sudaryti lyginę periodinę funkciją. Fig. funkcija f (x) = x parodyta žemiau, pavaizduota intervale nuo x = 0 iki x = π. Kadangi lyginė funkcija yra simetriška f (x) ašiai, brėžiame liniją AB, kaip parodyta Fig. žemiau. Jei darysime prielaidą, kad už nagrinėjamo intervalo ribų gauta trikampio forma yra periodinė su 2π periodu, tada galutinis grafikas turi formą, rodančią. pav. žemiau. Kadangi Furjė plėtimąsi reikia gauti kosinusais, kaip ir anksčiau, apskaičiuojame Furjė koeficientus a o ir a n

Jei reikia gauti funkcijas f (x) intervale nuo 0 iki π, tada reikia sudaryti nelyginę periodinę funkciją. Fig. funkcija f (x) = x parodyta žemiau, pavaizduota intervale nuo x = 0 iki x = π. Kadangi nelyginė funkcija yra simetriška kilmei, nubrėžiame liniją CD, kaip parodyta Fig. Jei darysime prielaidą, kad už nagrinėjamo intervalo ribų gautas pjūklo signalas yra periodinis su 2π periodu, tada galutinis grafikas turi tokią formą, kaip parodyta Fig. Kadangi Furjė skilimą reikia gauti per pusę periodo sinusais, kaip ir anksčiau, apskaičiuojame Furjė koeficientą. b

Furjė serija savavališkam intervalui.

Periodinės funkcijos išplėtimas su L periodu.

Periodinė funkcija f (x) kartojama x didėjant L, t.y. f (x + L) = f (x). Perėjimas nuo anksčiau svarstytų funkcijų su periodu 2π prie funkcijų su periodu L yra gana paprastas, nes tai galima padaryti keičiant kintamąjį.

Norėdami rasti funkcijos f (x) Furjė eilutę diapazone -L / 2≤x≤L / 2, įvedame naują kintamąjį u, kad funkcijos f (x) periodas u atžvilgiu būtų 2π. Jei u = 2πx / L, tai x = -L / 2, kai u = -π ir x = L / 2, kai u = π. Taip pat tegul f (x) = f (Lu / 2π) = F (u). Furjė serija F (u) turi formą

Kur yra Furjė serijos koeficientai,

Tačiau dažniau aukščiau pateikta formulė lemia priklausomybę nuo x. Kadangi u = 2πх / L, tai reiškia, kad du = (2π / L) dx, o integravimo ribos yra nuo -L / 2 iki L / 2, o ne nuo - π iki π. Vadinasi, Furjė eilutė priklausomybei nuo x turi formą

kur diapazone nuo -L / 2 iki L / 2 Furjė serijos koeficientai,

(Integravimo ribas galima pakeisti į bet kurį L ilgio intervalą, pavyzdžiui, nuo 0 iki L)

Pusės periodo Furjė eilutė funkcijoms, apibrėžtoms intervale L ≠ 2π.

Pakeitimui u = πх / L intervalas nuo x = 0 iki x = L atitinka intervalą nuo u = 0 iki u = π. Todėl funkcija eilute gali būti išplėsta tik kosinusais arba tik sinusais, t.y. v pusės ciklo Furjė serija.

Išplėtimas kosinusais diapazone nuo 0 iki L turi formą

Furjė periodinių funkcijų serija su periodu 2π.

Furjė serija leidžia tirti periodines funkcijas, jas skaidant į komponentus. Kintamosios srovės ir įtampa, poslinkiai, švaistiklio greitis ir pagreitis bei akustinės bangos yra tipiški praktiniai periodinių funkcijų naudojimo inžineriniuose skaičiavimuose pavyzdžiai.

Standartinis (= normalus) žymėjimas per sinx ir cosx sumą

f (x) = a o + a 1 cosx + a 2 cos2x + a 3 cos3x + ... + b 1 sinx + b 2 sin2x + b 3 sin3x + ...,

kur a o, a 1, a 2, ..., b 1, b 2, .. yra tikrosios konstantos, t.y.

Kur diapazone nuo -π iki π Furjė eilutės koeficientai apskaičiuojami pagal formules:

Kitas būdas rašyti seriją yra naudoti santykį acosx + bsinx = csin (x + α)

f (x) = a o + c 1 sin (x + α 1) + c 2 sin (2x + α 2) + ... + c n sin (nx + α n)

Kur ao yra konstanta, kai 1 = (a 1 2 + b 1 2) 1/2, kai n = (an 2 + bn 2) 1/2 yra įvairių komponentų amplitudės ir yra lygi an = arctan an / b n.

Norint tiksliai pavaizduoti sudėtingą signalą, paprastai reikia begalinio skaičiaus terminų. Tačiau daugelyje praktinių problemų pakanka atsižvelgti tik į keletą pirmųjų terminų.

Furjė neperiodinių funkcijų serija su periodu 2π.

Neperiodinių funkcijų skaidymas.

Lyginės ir nelyginės funkcijos.

Sakoma, kad funkcija y = f (x). keista, jei f (-x) = - f (x) visoms x reikšmėms. Nelyginių funkcijų diagramos visada yra simetriškos kilmės atžvilgiu.

Daugelis funkcijų nėra nei lyginės, nei nelyginės.

Furjė plėtimasis kosinusais.

Lyginės periodinės funkcijos f (x) Furjė eilutėje, kurios periodas yra 2π, yra tik terminai su kosinusais (t. y. joje nėra terminų su sinusais) ir gali būti pastovus narys. Vadinasi,

kur Furjė eilutės koeficientai,

Nelyginės periodinės funkcijos f (x), kurios periodas yra 2π, Furjė eilutėje yra tik terminai su sinusais (t. y. joje nėra terminų su kosinusais).

Vadinasi,

kur Furjė eilutės koeficientai,

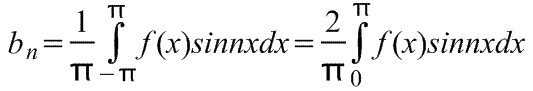
Pusės ciklo Furjė serija.

Jei nori gauti pusės ciklo Furjė skilimas sinusais funkcija f (x) diapazone nuo 0 iki π, tada reikia sudaryti nelyginę periodinę funkciją. Fig. funkcija f (x) = x parodyta žemiau, pavaizduota intervale nuo x = 0 iki x = π. Kadangi nelyginė funkcija yra simetriška kilmei, nubrėžiame liniją CD, kaip parodyta Fig. Jei darysime prielaidą, kad už nagrinėjamo intervalo ribų gautas pjūklo signalas yra periodinis su 2π periodu, tada galutinis grafikas turi tokią formą, kaip parodyta Fig. Kadangi Furjė skilimą reikia gauti per pusę periodo sinusais, kaip ir anksčiau, apskaičiuojame Furjė koeficientą. b

Furjė serija savavališkam intervalui.

Periodinės funkcijos išplėtimas su L periodu.

(Integravimo ribas galima pakeisti į bet kurį L ilgio intervalą, pavyzdžiui, nuo 0 iki L)

Pusės periodo Furjė eilutė funkcijoms, apibrėžtoms intervale L ≠ 2π.

Išplėtimas kosinusais diapazone nuo 0 iki L turi formą