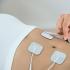
Ką reiškia vietinis maksimumas ir minimumas. Etiketė: vietinis ekstremumas
$ E \ poaibis \ mathbb (R) ^ (n) $. Teigiama, kad $ F $ turi vietinis maksimumas taške $ x_ (0) \ E $, jei yra taško $ x_ (0) $ kaimynystė $ U $ taip, kad visiems $ x \ U $ nelygybė $ f \ kairėje (x \ dešinėje ) \ leqslant f \ left (x_ (0) \ right) $.
Vietinis maksimumas vadinamas griežtas jei kaimynystę $ U $ galima pasirinkti taip, kad visiems $ x \ U $, išskyrus $ x_ (0) $, būtų $ f \ left (x \ right)< f\left(x_{0}\right)$.
Apibrėžimas
Tegul $ f $ yra reali funkcija atvirojoje aibėje $ E \ poaibis \ mathbb (R) ^ (n) $. Teigiama, kad $ F $ turi vietinis minimumas taške $ x_ (0) \ E $, jei yra taško $ x_ (0) $ kaimynystė $ U $ taip, kad visiems $ x \ U $ nelygybė $ f \ kairėje (x \ dešinėje ) \ geqslant f \ left (x_ (0) \ right) $.
Vietinis minimumas vadinamas griežtu, jei kaimynystę $ U $ galima pasirinkti taip, kad visiems $ x \ U $, išskyrus $ x_ (0) $, $ f \ left (x \ right)> f \ left (x_ () 0) \ dešinėje) $.
Vietinis ekstremumas jungia vietinio minimumo ir vietinio maksimumo sąvokas.
Teorema (būtina diferencijuojamos funkcijos ekstremumo sąlyga)
Tegul $ f $ yra reali funkcija atvirojoje aibėje $ E \ poaibis \ mathbb (R) ^ (n) $. Jei taške $ x_ (0) \ E $ funkcija $ f $ turi vietinį ekstremumą, tai $$ \ text (d) f \ left (x_ (0) \ right) = 0. $$ Lygybė nuliui skirtumui prilygsta tam, kad visi lygūs nuliui, t.y. $$ \ displaystyle \ frac (\ partial f) (\ partial x_ (i)) \ left (x_ (0) \ right) = 0. $$
Vienmačiu atveju tai yra. Žymime $ \ phi \ left (t \ right) = f \ left (x_ (0) + th \ right) $, kur $ h $ yra savavališkas vektorius. Funkcija $ \ phi $ yra apibrėžta pakankamai mažoms $ t $ reikšmėms absoliučia verte. Be to, pagal, jis skiriasi ir $ (\ phi) '\ left (t \ right) = \ text (d) f \ left (x_ (0) + th \ right) h $.
Tegul $ f $ turi vietinį maksimumą taške x $ 0 $. Vadinasi, funkcija $ \ phi $, kai $ t = 0 $, turi vietinį maksimumą ir, pagal Fermato teoremą, $ (\ phi) '\ left (0 \ right) = 0 $.
Taigi, gavome, kad $ df \ left (x_ (0) \ right) = 0 $, t.y. funkcijos $ f $ taške $ x_ (0) $ yra lygus nuliui bet kuriame vektoriuje $ h $.
Apibrėžimas
Taškai, kuriuose skirtumas lygus nuliui, t.y. tos, kuriose visos dalinės išvestinės lygios nuliui, vadinamos stacionariais. Kritiniai taškai funkcija $ f $ vadinami taškais, kuriuose $ f $ nėra diferencijuojamas arba yra lygus nuliui. Jei taškas yra nejudantis, tai dar nereiškia, kad funkcija šiame taške turi ekstremumą.
1 pavyzdys.
Tegul $ f \ left (x, y \ right) = x ^ (3) + y ^ (3) $. Tada $ \ displaystyle \ frac (\ dalinis f) (\ dalinis x) = 3 \ cdot x ^ (2) $, $ \ displaystyle \ frac (\ dalinis f) (\ dalinis y) = 3 \ cdot y ^ (2 ) $, taigi $ \ left (0,0 \ right) $ yra stacionarus taškas, tačiau šiuo metu funkcija neturi ekstremumo. Iš tiesų, $ f \ left (0,0 \ right) = 0 $, tačiau nesunku pastebėti, kad bet kurioje taško $ \ left (0,0 \ right) $ kaimynystėje funkcija įgauna ir teigiamas, ir neigiamas reikšmes.
2 pavyzdys.
Funkcijos $ f \ left (x, y \ right) = x ^ (2) - y ^ (2) $ kilmė yra stacionarus taškas, tačiau aišku, kad šiame taške nėra ekstremumo.
Teorema (pakankama sąlyga ekstremumui).
Tegul funkcija $ f $ yra du kartus nuolat diferencijuojama atvirojoje aibėje $ E \ poaibis \ mathbb (R) ^ (n) $. Tegu $ x_ (0) \ E $ yra stacionarus taškas, o $$ \ ekrano stilius Q_ (x_ (0)) \ left (h \ right) \ equiv \ sum_ (i = 1) ^ n \ sum_ (j = 1) ) ^ n \ frac (\ dalinis ^ (2) f) (\ dalinis x_ (i) \ dalinis x_ (j)) \ kairėje (x_ (0) \ dešinėje) h ^ (i) h ^ (j). $ $ Tada
- jei $ Q_ (x_ (0)) $ -, tai funkcija $ f $ taške $ x_ (0) $ turi vietinį ekstremumą, ty minimumą, jei forma yra teigiama apibrėžtoji, ir maksimumą, jei forma yra neigiamas apibrėžtasis;
- jei kvadratinė forma $ Q_ (x_ (0)) $ neapibrėžta, tai funkcija $ f $ taške $ x_ (0) $ neturi ekstremumo.
Naudokime plėtimą pagal Teiloro formulę (12.7 p. 292). Atsižvelgiant į tai, kad pirmosios eilės dalinės išvestinės taške $ x_ (0) $ yra lygios nuliui, gauname $$ \ displaystyle f \ left (x_ (0) + h \ right) −f \ left (x_ (0) \ dešinė) = \ frac (1) (2) \ suma_ (i = 1) ^ n \ suma_ (j = 1) ^ n \ frakcija (\ dalinė ^ (2) f) (\ dalinė x_ (i) ) \ dalinė x_ (j)) \ kairė (x_ (0) + \ teta h \ dešinė) h ^ (i) h ^ (j), $$ kur $ 0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0 $ ir $ \ epsilon \ kairė (h \ dešinė) \ rodyklė dešinėn 0 $ $ h \ rodyklė dešinėn 0 $, tada dešinė pusė bus teigiama bet kuriam pakankamai mažo ilgio vektoriui $ h $.
Taigi, padarėme išvadą, kad tam tikroje taško $ x_ (0) $ kaimynystėje galioja nelygybė $ f \ left (x \ right)> f \ left (x_ (0) \ right) $, jei tik $ x \ neq x_ (0) $ (įdedame $ x = x_ (0) + h $ \ dešinėje). Tai reiškia, kad taške $ x_ (0) $ funkcija turi griežtą lokalinį minimumą, taigi įrodoma pirmoji mūsų teoremos dalis.
Tarkime, kad $ Q_ (x_ (0)) $ yra neapibrėžta forma. Tada yra vektoriai $ h_ (1) $, $ h_ (2) $, kad $ Q_ (x_ (0)) \ kairėje (h_ (1) \ dešinėje) = \ lambda_ (1)> 0 $, $ Q_ ( x_ (0)) \ kairė (h_ (2) \ dešinė) = \ lambda_ (2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0 $. Tada gauname $$ f \ left (x_ (0) + th_ (1) \ right) −f \ left (x_ (0) \ right) = \ frac (1) (2) \ left [t ^ (2) \ lambda_ (1) + t ^ (2) | h_ (1) | ^ (2) \ epsilonas \ kairė (th_ (1) \ dešinė) \ dešinė] = \ frac (1) (2) t ^ (2) \ kairysis [\ lambda_ (1) + | h_ (1) | ^ (2) \ epsilonas \ kairė (th_ (1) \ dešinė) \ dešinė]. $$ Už pakankamai mažą $ t> 0 $ dešinė pusė yra teigiamas. Tai reiškia, kad bet kurioje taško $ x_ (0) $ kaimynystėje funkcija $ f $ įgyja reikšmes $ f \ left (x \ right) $, kurios yra didesnės nei $ f \ left (x_ (0) \ right) $.
Panašiai gauname, kad bet kurioje taško $ x_ (0) $ kaimynystėje funkcija $ f $ įgyja reikšmes, mažesnes nei $ f \ left (x_ (0) \ right) $. Tai kartu su ankstesniu reiškia, kad taške $ x_ (0) $ funkcija $ f $ neturi ekstremumo.
Apsvarstykite ypatinga bylašios teoremos funkcijai $ f \ left (x, y \ right) $ dviejų kintamųjų, apibrėžtų tam tikroje taško $ \ left (x_ (0), y_ (0) \ right) $ kaimynystėje ir turinčių ištisinę dalinę pirmosios ir antrosios eilės vediniai. Tarkime, $ \ left (x_ (0), y_ (0) \ right) $ yra stacionarus taškas ir žymi $$ \ displaystyle a_ (11) = \ frac (\ partial ^ (2) f) (\ dalinis x ^ (2)) \ kairė (x_ (0), y_ (0) \ dešinė), a_ (12) = \ frac (\ dalinis ^ (2) f) (\ dalinis x \ dalinis y) \ kairysis (x_ ( 0) ), y_ (0) \ dešinė), a_ (22) = \ frac (\ dalinis ^ (2) f) (\ dalinis y ^ (2)) \ kairėn (x_ (0), y_ (0) \ dešinėje ) $$ Tada ankstesnė teorema įgauna tokią formą.
Teorema
Tegul $ \ Delta = a_ (11) \ cdot a_ (22) - a_ (12) ^ 2 $. Tada:
- jei $ \ Delta> 0 $, tada funkcija $ f $ turi vietinį ekstremumą taške $ \ left (x_ (0), y_ (0) \ right) $, ty minimumą, jei $ a_ (11)> 0 $ , o didžiausia, jei $ a_ (11)<0$;
- jei $ \ Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.
Problemų sprendimo pavyzdžiai
Daugelio kintamųjų funkcijos ekstremumo radimo algoritmas:
- Rasti stacionarius taškus;
- Raskite 2 eilės skirtumą visuose stacionariuose taškuose
- Naudodami pakankamą kelių kintamųjų funkcijos ekstremumo sąlygą, atsižvelgiame į antros eilės skirtumą kiekviename stacionariame taške
- Išnagrinėkite ekstremumo funkciją $ f \ left (x, y \ right) = x ^ (3) + 8 \ cdot y ^ (3) + 18 \ cdot x - 30 \ cdot y $.
SprendimasRaskite 1-osios eilės dalines išvestis: $$ \ displaystyle \ frac (\ partial f) (\ partial x) = 3 \ cdot x ^ (2) - 6 \ cdot y; $$ $$ \ displaystyle \ frac (\ partial f ) (\ partial y) = 24 \ cdot y ^ (2) - 6 \ cdot x. $$ Sudarykime ir išspręskime sistemą: $$ \ displaystyle \ begin (cases) \ frac (\ partial f) (\ partial x ) = 0 \\\ frac (\ dalinis f) (\ dalinis y) = 0 \ pabaiga (didžiosios ir mažosios raidės) \ rodyklė dešinėn \ pradžia (didieji atvejai) 3 \ cdot x ^ (2) - 6 \ cdot y = 0 \\ 24 \ cdot y ^ (2) - 6 \ cdot x = 0 \ pabaiga (didžiosios ir mažosios raidės) \ rodyklė dešinėn \ pradžia (atvesta) x ^ (2) - 2 \ cdot y = 0 \\ 4 \ cdot y ^ (2) - x = 0 \ pabaiga (atvejai) $$ Iš 2-osios lygties išreikškite $ x = 4 \ cdot y ^ (2) $ - pakaitalas 1-oje lygtyje: $$ \ displaystyle \ left (4 \ cdot y ^ (2) \ dešinė ) ^ (2) -2 \ cdot y = 0 $$ $$ 16 \ cdot y ^ (4) - 2 \ cdot y = 0 $$ $$ 8 \ cdot y ^ (4) - y = 0 $$ $ $ y \ kairėje (8 \ cdot y ^ (3) -1 \ dešinėje) = 0 $ $ Dėl to gaunami 2 stacionarūs taškai:
1) $ y = 0 \ rodyklė dešinėn x = 0, M_ (1) = \ kairė (0, 0 \ dešinė) $;
2) $ \ displaystyle 8 \ cdot y ^ (3) -1 = 0 \ Rodyklė dešinėn y ^ (3) = \ frac (1) (8) \ rodyklė dešinėn y = \ frac (1) (2) \ rodyklė dešinėn x = 1 , M_ (2) = \ kairė (\ frac (1) (2), 1 \ dešinė) $
Patikrinkime, ar įvykdyta pakankama ekstremumo sąlyga:
$$ \ displaystyle \ frac (\ dalinis ^ (2) f) (\ dalinis x ^ (2)) = 6 \ cdot x; \ frac (\ dalinis ^ (2) f) (\ dalinis x \ dalinis y) = - 6; \ frac (\ dalinis ^ (2) f) (\ dalinis y ^ (2)) = 48 \ cdot y $$
1) Taškui $ M_ (1) = \ kairė (0,0 \ dešinė) $:
$$ \ displaystyle A_ (1) = \ frac (\ dalinis ^ (2) f) (\ dalinis x ^ (2)) \ kairysis (0,0 \ dešinėn) = 0; B_ (1) = \ frac (\ dalinis ^ (2) f) (\ dalinis x \ dalinis y) \ kairė (0,0 \ dešinė) = - 6; C_ (1) = \ frac (\ dalinis ^ (2) f) (\ dalinis y ^ (2)) \ kairė (0,0 \ dešinė) = 0; $$
$ A_ (1) \ cdot B_ (1) - C_ (1) ^ (2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) Taškui $ M_ (2) $:
$$ \ displaystyle A_ (2) = \ frac (\ dalinis ^ (2) f) (\ dalinis x ^ (2)) \ left (1, \ frac (1) (2) \ right) = 6; B_ (2) = \ frac (\ dalinis ^ (2) f) (\ dalinis x \ dalinis y) \ kairė (1, \ frac (1) (2) \ dešinė) = - 6; C_ (2) = \ frac (\ dalinis ^ (2) f) (\ dalinis y ^ (2)) \ kairė (1, \ frac (1) (2) \ dešinė) = 24; $$
$ A_ (2) \ cdot B_ (2) - C_ (2) ^ (2) = 108> 0 $, taigi taške $ M_ (2) $ yra ekstremumas, o kadangi $ A_ (2)> 0 $, tada tai yra minimumas.
Atsakymas: Taškas $ \ displaystyle M_ (2) \ left (1, \ frac (1) (2) \ right) $ yra mažiausias funkcijos $ f $ taškas. - Išnagrinėkite ekstremumo funkciją $ f = y ^ (2) + 2 \ cdot x \ cdot y - 4 \ cdot x - 2 \ cdot y - 3 $.
SprendimasRaskite stacionarius taškus: $$ \ displaystyle \ frac (\ dalinis f) (\ dalinis x) = 2 \ cdot y - 4; $$ $$ \ displaystyle \ frac (\ dalinis f) (\ dalinis y) = 2 \ cdot y + 2 \ cdot x - 2. $$
Sudarykime ir išspręskime sistemą: $$ \ displaystyle \ begin (atvejai) \ frac (\ partial f) (\ partial x) = 0 \\\ frac (\ partial f) (\ partial y) = 0 \ end (atvejai) ) \ Rodyklė dešinėn \ pradžia (didžiosios ir mažosios raidės) 2 \ cdot y - 4 = 0 \\ 2 \ cdot y + 2 \ cdot x - 2 = 0 \ end (didieji atvejai) \ Rodyklė dešinėn \ pradžia (didieji atvejai) y = 2 \\ y + x = 1 \ pabaiga (dydžiai) \ Rodyklė dešinėn x = -1 $$
$ M_ (0) \ kairėje (-1, 2 \ dešinėje) $ yra stacionarus taškas.
Patikrinkime, ar įvykdyta pakankama ekstremumo sąlyga: $$ \ displaystyle A = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (-1,2 \ right) = 0; B = \ frac (\ dalinis ^ (2) f) (\ dalinis x \ dalinis y) \ kairė (-1,2 \ dešinė) = 2; C = \ frac (\ dalinė ^ (2) f) (\ dalinė y ^ (2)) \ kairė (-1,2 \ dešinė) = 2; $$
$ A \ cdot B - C ^ (2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Atsakymas: nėra kraštutinumų.
Laiko limitas: 0
Navigacija (tik darbo numeriai)
Užpildyta 0 iš 4 klausimų
Informacija
Atlikite šį testą, kad patikrintumėte savo žinias ką tik perskaityta tema „Daugelio kintamųjų funkcijų vietinis kraštutinumas“.
Jūs jau atlikote testą anksčiau. Negalite to pradėti iš naujo.
Bandymas įkeliamas...
Norėdami pradėti testą, turite prisijungti arba užsiregistruoti.
Norėdami pradėti, turite atlikti šiuos testus:
rezultatus
Teisingi atsakymai: 0 iš 4
Tavo laikas:
Laikas baigėsi
Jūs surinkote 0 taškų iš 0 (0)
Jūsų rezultatas buvo įrašytas į lyderių lentelę
- Su atsakymu
- Pažymėta kaip peržiūrėta
2 klausimas iš 4
2 .
Taškai: 1Ar funkcija $ f = 4 + \ sqrt ((x ^ (2) + y ^ (2)) ^ (2)) $
1 užduotis iš 4
1 .
Taškai: 1Išnagrinėkite ekstremalių funkciją $ f $: $ f = e ^ (x + y) (x ^ (2) -2 \ cdot y ^ (2)) $
Teisingai
Neteisus
Funkcijos pokytis tam tikrame taške apibrėžiamas kaip funkcijos padidėjimo iki argumento prieaugio riba, kuri linkusi į nulį. Norėdami jį rasti, naudokite išvestinių lentelę. Pavyzdžiui, funkcijos y = x3 išvestinė bus lygi y ’= x2.
Nustatykite šią išvestinę į nulį (šiuo atveju x2 = 0).
Raskite duoto kintamojo reikšmę. Tai bus reikšmės, kai duota išvestinė yra lygi 0. Norėdami tai padaryti, reiškinyje vietoj x pakeiskite savavališkus skaitmenis, kuriems esant visa išraiška tampa nuliu. Pavyzdžiui:
2-2x2 = 0
(1-x) (1 + x) = 0
x1 = 1, x2 = -1
Nubraižykite gautas reikšmes koordinačių tiesėje ir apskaičiuokite kiekvienos gautos išvestinės ženklą. Koordinačių tiesėje pažymėti taškai, kurie laikomi pradine taškais. Norėdami apskaičiuoti intervalų vertę, pakeiskite savavališkas vertes, kurios atitinka kriterijus. Pavyzdžiui, ankstesnei funkcijai iki -1 galite pasirinkti reikšmę -2. Nuo -1 iki 1 galite pasirinkti 0, o jei reikšmės yra didesnės nei 1, pasirinkite 2. Pakeiskite šiuos skaičius išvestinėje ir sužinokite išvestinės ženklą. Šiuo atveju išvestinė su x = -2 bus -0,24, t.y. neigiamas ir šiame intervale bus minuso ženklas. Jei x = 0, tada reikšmė bus lygi 2, o šiame intervale dedamas ženklas. Jei x = 1, tada išvestinė taip pat bus -0,24 ir dedamas minusas.
Jei, eidama per tašką koordinačių tiesėje, išvestinė pakeičia ženklą iš minuso į pliusą, tai yra mažiausias taškas, o jei iš pliuso į minusą, tai yra didžiausias taškas.
Susiję vaizdo įrašai
Naudingas patarimas
Norint rasti išvestinę priemonę, yra internetinių paslaugų, kurios apskaičiuoja reikiamas reikšmes ir parodo rezultatą. Tokiose svetainėse galite rasti išvestinį produktą iki 5 eilės.
Šaltiniai:
- Viena iš išvestinių finansinių priemonių skaičiavimo paslaugų
- maksimalus funkcijos taškas
Maksimalūs funkcijos taškai kartu su minimaliais taškais vadinami ekstremumais. Šiuose taškuose funkcija keičia savo elgesį. Ekstrema nustatomi ribotais skaitiniais intervalais ir visada yra vietinė.
Instrukcijos
Vietinių ekstremalių radimo procesas vadinamas funkcija ir atliekamas analizuojant pirmąjį ir antrąjį funkcijos darinius. Prieš tirdami įsitikinkite, kad nurodytas argumentų reikšmių diapazonas yra tinkamos reikšmės. Pavyzdžiui, funkcijai F = 1 / x argumento x = 0 reikšmė neteisinga. Arba, kai funkcija Y = tg (x), argumentas negali turėti reikšmės x = 90 °.
Įsitikinkite, kad Y funkcija yra diferencijuojama visame duotame segmente. Raskite pirmąją išvestinę Y ". Akivaizdu, kad prieš pasiekiant lokalaus maksimumo tašką, funkcija didėja, o pereinant per maksimumą, funkcija tampa mažėjančia. Pirmoji išvestinė savo fizine prasme apibūdina funkcijos kitimo greitį Funkcijai didėjant, šio proceso greitis yra teigiamas. funkcija pradeda mažėti per lokalų maksimumą, o funkcijos pokyčio greitis tampa neigiamas. Įvyksta funkcijos kitimo greičio perėjimas per nulį vietinio maksimumo taške.
>> kraštutinumai
Ekstremali funkcija
Ekstremo nustatymas
Funkcija y = f (x) vadinamas didėja (mažėja) tam tikru intervalu, jei x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f (x 2)).
Jei diferencijuojama funkcija y = f (x) didėja (mažėja) intervale, tai jos išvestinė šiame intervale f " (x)> 0
(f "(x)< 0).
Taškas x O paskambino vietinio maksimumo taškas (minimumas) funkcijos f (x), jei yra taško kaimynystė x apie, visiems taškams, kurių nelygybė f (x)≤ f (x o) (f (x)≥ f (x o)).
Vadinami didžiausi ir mažiausi taškai ekstremalūs taškai, o funkcijos reikšmės šiuose taškuose yra jos ekstremalumas.
Ekstremalūs taškai
Būtinos sąlygos ekstremumas ... Jei taškas x O yra funkcijos f (x) ekstremumo taškas, tada arba f " (x о) = 0 arba f(x o) neegzistuoja. Tokie taškai vadinami kritiškas, be to, pati funkcija apibrėžiama kritiniame taške. Funkcijos kraštutinumo reikia ieškoti tarp jos kritinių taškų.
Pirma pakankama sąlyga. Leisti būti x O - kritinis taškas. Jei f " (x) einant per tašką x O pakeičia pliuso ženklą į minusą, tada taške x apie funkcija turi maksimumą, kitu atveju turi minimumą. Jei išvestinė nekeičia ženklo, eidama per kritinį tašką, tai taške x O ekstremalaus nera.
Antra pakankama sąlyga.
Tegu turi funkciją f (x).
f " (x) šalia taško x
O
o antrasis darinys pačiame taške x apie... Jei f "(x apie) = 0, >0 ( <0), то точка x apie yra funkcijos f (x) lokalaus minimumo (maksimalaus) taškas. Jei = 0, tada reikia naudoti pirmąją pakankamą sąlygą arba įtraukti aukštesnes.
Atkarpoje funkcija y = f (x) gali pasiekti mažiausią arba didžiausią reikšmę kritiniuose taškuose arba atkarpos galuose.
3.22 pavyzdys.
Sprendimas. Nes f " (
Funkcijos ekstremumo radimo problemos
3.23 pavyzdys. a
Sprendimas. x ir y y
0
≤ x≤
> 0 ir už x> a / 4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
funkcijas kv..
vienetų).
3.24 pavyzdys. p ≈
Sprendimas. p p
S "
R = 2, H = 16/4 = 4.
3.22 pavyzdys.Raskite funkcijos f (x) = 2x 3 - 15x 2 + 36x - 14 ekstremalumą.
Sprendimas. Nes f " (x) = 6x 2 - 30x +36 = 6 (x -2) (x - 3), tada funkcijos kritiniai taškai x 1 = 2 ir x 2 = 3. Ekstrema gali būti tik šiuose taškuose. Kadangi, eidama per tašką x 1 = 2, išvestinė ženklą pliusą pakeičia į minusą, tai šioje vietoje funkcija turi maksimumą. Eidama per tašką x 2 = 3, išvestinė savo minuso ženklą pakeičia į pliusą, todėl taške x 2 = 3 funkcija turi minimumą. Funkcijos reikšmių skaičiavimas taškais
x 1 = 2 ir x 2 = 3, randame funkcijos kraštutinumus: maksimalus f (2) = 14 ir minimalus f (3) = 13.
3.23 pavyzdys.Prie akmeninės sienos reikia pastatyti stačiakampį plotą, kad iš trijų pusių ji būtų aptverta vielos tinklu, o iš ketvirtos pusės – greta sienos. Tam yra a bėgimo metrų tinklelio. Kokiu formatu svetainė turės didžiausią plotą?
Sprendimas.Svetainės puses žymime x ir y... Svetainės plotas S = xy. Leisti būti y yra kraštinės, esančios greta sienos, ilgis. Tada pagal sąlygą turi būti įvykdyta lygybė 2x + y = a. Todėl y = a - 2x ir S = x (a - 2x), kur
0
≤ x≤ a / 2 (trinkelės ilgis ir plotis negali būti neigiami). S "= a - 4x, a - 4x = 0, jei x = a / 4, iš kur
y = a - 2 × a / 4 = a / 2. Tiek, kiek x = a / 4 yra vienintelis kritinis taškas, patikrinkime, ar pereinant per šį tašką keičiasi išvestinės ženklas. Skirta x a / 4 S "> 0 ir už x> a / 4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
funkcijas S (a / 4) = a / 4 (a - a / 2) = a 2/8 (kv..
vienetų).
Kadangi S yra nuolatinis, o jo reikšmės galuose S (0) ir S (a / 2) yra lygios nuliui, rasta reikšmė bus didžiausia funkcijos reikšmė. Taigi naudingiausias svetainės kraštinių santykis nurodytomis uždavinio sąlygomis yra y = 2x.
3.24 pavyzdys.Būtina pagaminti uždarą cilindrinį baką, kurio talpa V = 16 p ≈ 50 m 3. Kokie yra bako matmenys (spindulys R ir aukštis H), kad jo gamybai būtų sunaudota mažiausiai medžiagos?
Sprendimas.Bendras cilindro paviršiaus plotas yra S = 2 p R (R + H). Mes žinome cilindro tūrį V = p R 2 H Þ H = V / p R 2 = 16 p / p R 2 = 16 / R 2. Vadinasi, S (R) = 2 p (R 2 + 16 / R). Raskite šios funkcijos išvestinę:
S "(R) = 2 p (2R- 16 / R 2) = 4 p (R- 8 / R 2). S " (R) = 0, kai R3 = 8, todėl
R = 2, H = 16/4 = 4.
Kelių kintamųjų funkcijos f (x) taškas x yra vektorius, f '(x) yra funkcijos f (x) pirmųjų išvestinių (gradiento) vektorius, f ′ ′ (x) yra simetriškas. antrųjų dalinių išvestinių (Heso matrica yra Heseno) funkcijos f (x) matrica.
Kelių kintamųjų funkcijai optimalumo sąlygos formuluojamos taip.
Būtina sąlyga vietiniam optimalumui. Tegu f (x) yra diferencijuotas taške x * R n. Jei x * yra vietinis ekstremumo taškas, tada f '(x *) = 0.
Kaip ir anksčiau, taškai, kurie yra lygčių sistemos sprendiniai, vadinami stacionariais. Stacionaraus taško x * pobūdis yra susijęs su Heseno matricos f ′ ′ (x) apibrėžtumu.
Matricos A apibrėžtumas priklauso nuo kvadratinės formos Q (α) = ženklų< α A, α >visiems nuliniams α∈R n.
Čia ir toliau
Matrica A yra teigiama (neneigiama) apibrėžta, jei Q (α)> 0 (Q (α) ≥0) visoms nulinėms α∈R n; neigiamai (neteigiamai) apibrėžtas, jei Q (α)<0 (Q(α)≤0) при всех ненулевых α∈R n ; неопределенной, если Q(α)>0 kai kuriems nuliniams α∈R n ir Q (α)<0 для остальных ненулевых α∈R n .
Pakankama sąlyga vietiniam optimalumui. Tegul f (x) yra du kartus diferencijuojamas taške x * R n, o f ’(x *) = 0, tai yra, x * - stacionarus taškas. Tada, jei matrica f ′ ′ (x *) yra teigiama (neigiama) apibrėžtoji, tai x * yra vietinio minimumo (maksimalaus) taškas; jei matrica f ′ ′ (x *) yra neapibrėžta, tai x * yra balno taškas.
Jei matrica f ′ ′ (x *) yra neneigiama (ne teigiama) apibrėžtoji, tai norint nustatyti stacionaraus taško x * charakterį, reikalingas aukštesnės eilės išvestinių tyrimas.
Silvesterio kriterijus dažniausiai naudojamas matricos apibrėžtumui patikrinti. Pagal šį kriterijų simetrinė matrica A yra teigiama apibrėžtoji tada ir tik tada, kai visi jos kampiniai mažumai yra teigiami. Šiuo atveju matricos A kampinis minoras yra determinantas matricos, sudarytos iš matricos A elementų, stovinčios vienodais (ir pirmaisiais) skaičiais turinčių eilučių ir stulpelių sankirtoje. Norint patikrinti simetrinės matricos A neigiamą apibrėžtumą, būtina patikrinti matricos (−A) teigiamą apibrėžtumą.
Taigi daugelio kintamųjų funkcijos lokalių ekstremalių taškų nustatymo algoritmas yra toks.
1. Raskite f ′ (x).
2. Sistema išspręsta 
Dėl to apskaičiuojami stacionarūs taškai x i.
3. Raskite f ′ ′ (x), nustatykite i = 1.
4. Raskite f ′ ′ (x i)
5. Apskaičiuojami matricos f ′ ′ (x i) kampiniai mažumai. Jei ne visi kampiniai minorai yra nuliniai, tai norint nustatyti stacionaraus taško x i prigimtį, reikalingas aukštesnės eilės išvestinių tyrimas. Tokiu atveju pereinama prie 8 punkto.
Kitu atveju pereikite prie 6 veiksmo.
6. Nagrinėjami kampinių nepilnamečių f ′ ′ (x i) požymiai. Jei f ′ ′ (x i) yra teigiamas apibrėžtasis, tai x i yra vietinis minimumas. Tokiu atveju pereinama prie 8 punkto.
Kitu atveju pereikite prie 7 veiksmo.
7. Apskaičiuojami matricos -f ′ ′ (x i) kampiniai minorai ir analizuojami jų ženklai.
Jei -f ′ ′ (x i) – yra teigiamas apibrėžtasis, tai f ′ ′ (x i) yra neigiamas apibrėžtasis, o x i yra vietinis maksimalus taškas.
Kitu atveju f ′ ′ (x i) yra neapibrėžtas, o x i yra balno taškas.
8. Patikrinta visų stacionarių taškų i = N prigimties nustatymo sąlyga.
Jei jis įvykdomas, tada skaičiavimai baigti.
Jei sąlyga neįvykdyta, nustatome i = i + 1 ir pereiname prie 4 veiksmo.
1 pavyzdys. Raskite funkcijos f (x) = x 1 3 - 2x 1 x 2 + x 2 2 - 3x 1 - 2x 2 lokalinių ekstremalių taškus 



Kadangi visos kampinės mažosios reikšmės nėra nulio, simbolis x 2 apibrėžiamas naudojant f ′ ′ (x).
Kadangi matrica f ′ ′ (x 2) yra teigiama apibrėžtoji, tai x 2 yra vietinis minimumas.
Atsakymas: funkcija f (x) = x 1 3 - 2x 1 x 2 + x 2 2 - 3x 1 - 2x 2 turi vietinį minimumą taške x = (5/3; 8/3).
Funkcijos ekstremalus taškas yra funkcijos srities taškas, kuriame funkcijos reikšmė įgyja mažiausią arba didžiausią reikšmę. Funkcijos reikšmės šiuose taškuose vadinamos funkcijos kraštutinumais (minimalus ir didžiausias)..
Apibrėžimas... Taškas x1 funkcijų domenas f(x) vadinamas maksimalus funkcijos taškas , jei funkcijos reikšmė šiame taške yra didesnė už funkcijos reikšmes pakankamai arti jos taškuose, esančiuose jos dešinėje ir kairėje (ty nelygybė f(x0 ) > f(x 0 + Δ x) x1 maksimalus.
Apibrėžimas... Taškas x2 funkcijų domenas f(x) vadinamas mažiausias funkcijos taškas, jei funkcijos reikšmė šiame taške yra mažesnė už funkcijos reikšmes pakankamai arti jos taškuose, esančiuose jos dešinėje ir kairėje (ty nelygybė f(x0 ) < f(x 0 + Δ x) ). Šiuo atveju sakoma, kad funkcija turi tašką x2 minimumas.
Tarkime, taškas x1 yra maksimalus funkcijos taškas f(x). Tada intervale iki x1 funkcija didėja, todėl funkcijos išvestinė yra didesnė už nulį ( f "(x)> 0), o intervale po x1 funkcija mažėja, todėl ir funkcijos išvestinė mažiau nei nulis (f "(x) < 0 ). Тогда в точке x1
Taip pat manykime, kad taškas x2 yra mažiausias funkcijos taškas f(x). Tada intervale iki x2 funkcija mažėja, o funkcijos išvestinė yra mažesnė už nulį ( f "(x) < 0 ), а в интервале после x2 funkcija didėja, o funkcijos išvestinė yra didesnė už nulį ( f "(x)> 0). Šiuo atveju taip pat taške x2 funkcijos išvestinė lygi nuliui arba neegzistuoja.
Ferma teorema (būtinas funkcijos ekstremumo egzistavimo kriterijus)... Jei taškas x0 yra funkcijos kraštutinis taškas f(x), tada šioje vietoje funkcijos išvestinė lygi nuliui ( f "(x) = 0) arba neegzistuoja.
Apibrėžimas... Vadinami taškai, kuriuose funkcijos išvestinė lygi nuliui arba neegzistuoja kritiniai taškai .

1 pavyzdys. Panagrinėkime funkciją.
Taške x= 0, funkcijos išvestinė lygi nuliui, todėl taškas x= 0 yra kritinis taškas. Tačiau, kaip matyti iš funkcijos grafiko, ji didėja visoje apibrėžimo srityje, todėl taškas x= 0 nėra šios funkcijos ekstremumo taškas.
Taigi sąlygos, kad funkcijos išvestinė taške yra lygi nuliui arba neegzistuoja, yra būtinos sąlygos ekstremumui, bet nepakankamos, nes kiti funkcijų pavyzdžiai, kurioms šios sąlygos tenkinamos, bet funkcija neturi atitinkamame taške gali būti pateiktas ekstremumas. Štai kodėl reikia turėti pakankamai ženklų, leidžianti spręsti, ar tam tikrame kritiniame taške yra ekstremumas ir kuris iš jų yra maksimalus ar minimumas.
Teorema (pirmasis pakankamas funkcijos ekstremumo egzistavimo kriterijus). Kritinis taškas x0 f(x), jei funkcijos išvestinė einant per šį tašką keičia ženklą, o jei ženklas keičiasi iš "pliuso" į "minusą", tada maksimalus taškas, o jei iš "minuso" į "pliusas", tada minimalus taškas. .
Jei netoli taško x0 , kairėje ir dešinėje išvestinė išsaugo ženklą, tai reiškia, kad funkcija arba tik mažėja, arba tik didėja tam tikroje taško kaimynystėje x0 ... Šiuo atveju taške x0 ekstremalaus nera.
Taigi, norėdami nustatyti funkcijos kraštutinius taškus, turite atlikti šiuos veiksmus :
- Raskite funkcijos išvestinę.
- Išvestinę nustatykite į nulį ir nustatykite kritinius taškus.
- Mintyse arba popieriuje skaitinėje ašyje pažymėkite kritinius taškus ir gautuose intervaluose nustatykite funkcijos išvestinės požymius. Jei išvestinės ženklas pasikeičia iš „pliuso“ į „minusą“, tai kritinis taškas yra maksimalus taškas, o jei iš „minuso“ į „pliusas“, tai minimalus taškas.
- Apskaičiuokite funkcijos reikšmę ekstremaliuose taškuose.

2 pavyzdys. Raskite funkcijos kraštutinumus ![]() .
.
Sprendimas. Raskime funkcijos išvestinę:
Nustatykime išvestinę į nulį, kad surastume kritinius taškus:
![]() .
.
Kadangi bet kuriai „x“ vertei vardiklis nėra lygus nuliui, tada skaitiklį prilyginame nuliui:
Gavau vieną lūžio tašką x= 3. Nustatykime išvestinės ženklą intervaluose, kuriuos riboja šis taškas:
diapazone nuo minus begalybės iki 3 - minuso ženklas, tai yra, funkcija mažėja,
diapazone nuo 3 iki pliuso begalybės - pliuso ženklas, tai yra, funkcija didėja.
Tai yra taškas x= 3 yra mažiausias taškas.
Raskime funkcijos reikšmę minimaliame taške:
Taigi randamas funkcijos ekstremumo taškas: (3; 0), ir tai yra minimalus taškas.
Teorema (antrasis pakankamas funkcijos ekstremumo egzistavimo kriterijus). Kritinis taškas x0 yra funkcijos kraštutinis taškas f(x) jei antroji funkcijos išvestinė šiame taške nėra lygi nuliui ( f ""(x) ≠ 0), o jei antroji išvestinė didesnė už nulį ( f ""(x)> 0), tada maksimalus taškas, o jei antroji išvestinė mažesnė už nulį ( f ""(x) < 0 ), то точкой минимума.
Pastaba 1. Jei taške x0 išnyksta ir pirmasis, ir antrasis vediniai, tada šiuo metu neįmanoma spręsti apie ekstremumo buvimą pagal antrąjį pakankamą kriterijų. Tokiu atveju būtina naudoti pirmąjį pakankamą funkcijos ekstremumo rodiklį.
2 pastaba. Antrasis pakankamas funkcijos ekstremumo kriterijus taip pat netaikomas, jei stacionariame taške nėra pirmosios išvestinės (tada neegzistuoja ir antroji išvestinė). Šiuo atveju taip pat būtina naudoti pirmąjį pakankamą funkcijos ekstremumo rodiklį.
Funkcijos ekstremumo vietinis pobūdis
Iš aukščiau pateiktų apibrėžimų matyti, kad funkcijos ekstremumas turi vietinį pobūdį – tai didžiausia ir mažiausia funkcijos reikšmė, palyginti su artimiausiomis reikšmėmis.
Tarkime, kad žiūrite į savo pajamas per vienerius metus. Jei gegužę uždirbote 45 000 rublių, balandį - 42 000 rublių ir birželį 39 000 rublių, tada gegužės mėn. uždarbis yra uždarbio funkcijos maksimumas, palyginti su artimiausiomis reikšmėmis. Bet spalį uždirbote 71 000 rublių, rugsėjį 75 000, lapkritį 74 000 rublių, taigi spalio mėnesio uždarbis yra uždarbio funkcijos minimumas, palyginti su šalia esančiomis vertėmis. Ir jūs galite lengvai pamatyti, kad didžiausias tarp balandžio–gegužės–birželio mėn. verčių yra mažesnis nei rugsėjo–spalio–lapkričio mėn.
Paprastai tariant, intervale funkcija gali turėti kelis kraštutinumus ir gali pasirodyti, kad bet kuris funkcijos minimumas yra didesnis už bet kurį maksimumą. Taigi, aukščiau esančiame paveikslėlyje parodytai funkcijai.
Tai reiškia, kad nereikėtų manyti, kad funkcijos maksimumas ir minimumas yra atitinkamai didžiausios ir mažiausiosios vertės per visą nagrinėjamą intervalą. Didžiausiame taške funkcija turi didžiausią reikšmę tik lyginant su reikšmėmis, kurias ji turi visuose taškuose pakankamai arti maksimalaus taško, o minimaliame taške – mažiausią reikšmę tik lyginant su reikšmėmis ji visuose taškuose yra pakankamai arti minimalaus taško.
Todėl galima patikslinti aukščiau pateiktą funkcijos ekstremalių taškų sampratą ir minimalius taškus vadinti lokaliniais minimaliais taškais, o maksimalius – vietiniais maksimaliais taškais.
Ieškau funkcijos ekstremalumo kartu

3 pavyzdys.
Sprendimas: Funkcija apibrėžta ir tęstinė visoje skaičių eilutėje. Jo darinys ![]() taip pat egzistuoja sveikoje skaičių eilutėje. Todėl šiuo atveju kritiniais taškais laikomi tik tie, kuriuose, t.y. , iš kur ir. Kritiniai taškai ir padalinkite visą funkcijos sritį į tris monotoniškumo intervalus:. Kiekviename iš jų pasirinkkime po vieną kontrolinį tašką ir šiame taške raskime išvestinės ženklą.
taip pat egzistuoja sveikoje skaičių eilutėje. Todėl šiuo atveju kritiniais taškais laikomi tik tie, kuriuose, t.y. , iš kur ir. Kritiniai taškai ir padalinkite visą funkcijos sritį į tris monotoniškumo intervalus:. Kiekviename iš jų pasirinkkime po vieną kontrolinį tašką ir šiame taške raskime išvestinės ženklą.
Intervalui kontrolinis taškas gali būti: rasti. Paėmę tašką intervale, gauname, o paėmę tašką intervale, turime. Taigi, intervaluose ir, ir intervale. Pagal pirmąjį pakankamą ekstremumo kriterijų, taške ekstremumo nėra (nes išvestinė intervale išlaiko savo ženklą), o taške funkcija turi minimumą (nes išvestinė pereinant pakeičia ženklą iš minuso į pliusą per šį tašką). Raskime atitinkamas funkcijos reikšmes:, a. Intervale funkcija mažėja, kaip ir šiame intervale, o intervale – didėja, kaip ir šiame intervale.
Norėdami patikslinti grafiko konstrukciją, rasime jo susikirtimo su koordinačių ašimis taškus. Mat gauname lygtį, kurios šaknys ir, t.y., randami du funkcijos grafiko taškai (0; 0) ir (4; 0). Naudodami visą gautą informaciją sudarome grafiką (žr. pavyzdžio pradžioje).

4 pavyzdys. Raskite funkcijos ekstremalumą ir sukurkite jos grafiką.
Funkcijos sritis yra sveikoji skaičiaus eilutė, išskyrus tašką, t.y. ...
Norėdami sutrumpinti tyrimą, galite pasinaudoti tuo, kad ši funkcija yra lygi, nes  ... Todėl jo grafikas yra simetriškas ašies atžvilgiu Oy o tyrinėjimas gali būti atliekamas tik tam tikrą intervalą.
... Todėl jo grafikas yra simetriškas ašies atžvilgiu Oy o tyrinėjimas gali būti atliekamas tik tam tikrą intervalą.
Raskite išvestinę ![]() ir kritinius funkcijos taškus:
ir kritinius funkcijos taškus:
1)  ;
;
2) ![]() ,
,
tačiau funkcija šiuo metu nutrūksta, todėl tai negali būti ekstremumo taškas.
Taigi, iš anksto nustatyta funkcija turi du kritinius taškus: ir. Atsižvelgdami į funkcijos paritetą, patikrinkime tik tašką antruoju pakankamu ekstremumo kriterijumi. Norėdami tai padaryti, randame antrąją išvestinę ![]() ir apibrėžkite jo ženklą: gauname. Kadangi ir, tada yra mažiausias funkcijos taškas, while
ir apibrėžkite jo ženklą: gauname. Kadangi ir, tada yra mažiausias funkcijos taškas, while ![]() .
.
Norėdami gauti išsamesnį funkcijos grafiko vaizdą, išsiaiškinkime jos elgesį apibrėžimo srities ribose:

(čia simbolis reiškia norą x iki nulio dešinėje ir x išlieka teigiamas; taip pat reiškia siekį x iki nulio kairėje ir x išlieka neigiamas). Taigi, jei, tada. Be to, randame
 ,
,
tie. jei tada.
Funkcijos grafikas neturi susikirtimo su ašimis taškų. Paveikslėlis yra pavyzdžio pradžioje.
Mes ir toliau kartu ieškome funkcijos kraštutinumų
8 pavyzdys. Raskite funkcijos kraštutinumą.

Sprendimas. Raskime funkcijos sritį. Kadangi nelygybė turi galioti, gauname iš.
Raskime pirmąją funkcijos išvestinę:

Raskime kritinius funkcijos taškus.