تعریف 9.3.بردار NS تماس گرفت بردار خودماتریس ها آاگر چنین عددی وجود داشته باشد λ, که برابری وجود دارد: آ NS= λ NS, یعنی نتیجه اعمال به NS تبدیل خطی داده شده توسط ماتریس آ، ضرب این بردار در عدد است λ ... خود شماره λ تماس گرفت شماره خودماتریس ها آ.

جایگزینی به فرمول (9.3) x` j = λx j،ما سیستمی از معادلات را برای تعیین مختصات بردار ویژه به دست می آوریم:

. (9.5)

این سیستم همگن خطی تنها در صورتی یک راه حل غیر ضروری خواهد داشت که تعیین کننده اصلی آن 0 باشد (قانون کرامر). نوشتن این شرط به شکل:

معادله تعیین مقادیر ویژه را بدست می آوریم λ تماس گرفت معادله مشخصه... به طور خلاصه می توان آن را به شرح زیر ارائه کرد:

| A - λE | = 0, (9.6)

از آنجایی که سمت چپ آن دارای تعیین کننده ماتریس است A-λE... چند جمله ای با توجه به λ | A - λE| تماس گرفت چند جمله ای مشخصهماتریس های A.

ویژگی های چند جمله ای مشخص:

1) چند جمله ای مشخصه تبدیل خطی به انتخاب مبنا بستگی ندارد. اثبات (نگاه کنید به (9.4))، اما از این رو، . بنابراین، به انتخاب پایه بستگی ندارد. از این رو، و | A-λE| هنگام تغییر به یک پایه جدید تغییر نمی کند.

2) اگر ماتریس آتبدیل خطی است متقارن(آنها و ij = یک جی، پس تمام ریشه های معادله مشخصه (9.6) اعداد واقعی هستند.

ویژگی های مقادیر ویژه و بردارهای ویژه:

1) اگر مبنایی از بردارهای ویژه انتخاب کنیم x 1، x 2، x 3 مربوط به مقادیر ویژه λ 1، λ 2، λ 3ماتریس ها آ، پس بر این اساس تبدیل خطی A دارای ماتریسی به شکل مورب است:

(9.7) اثبات این ویژگی از تعریف بردارهای ویژه حاصل می شود.

2) اگر مقادیر ویژه تبدیل آمتفاوت هستند، سپس بردارهای ویژه مربوطه به صورت خطی مستقل هستند.

3) اگر چند جمله ای مشخصه ماتریس آدارای سه ریشه متفاوت است، سپس در برخی موارد ماتریس آفرم مورب دارد.

اجازه دهید مقادیر ویژه و بردارهای ویژه ماتریس را پیدا کنیم بیایید معادله مشخصه را بسازیم: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0، λ 1 = -2, λ 2 = 3, λ 3 = 6.

اجازه دهید مختصات بردارهای ویژه مربوط به هر مقدار یافت شده را پیدا کنیم λ. از (9.5) بر می آید که اگر NS (1) ={x 1، x 2، x 3) آیا بردار ویژه مربوط است λ 1 = -2، سپس

- یک سیستم مشارکتی اما تعریف نشده. راه حل آن را می توان به صورت NS (1) ={آ,0,-آ) که در آن a هر عددی است. به ویژه، اگر ما به آن نیاز داشته باشیم | ایکس (1) |=1, NS (1) =

جایگزینی در سیستم (9.5) λ 2 = 3، سیستمی برای تعیین مختصات بردار ویژه دوم به دست می آوریم - ایکس (2) ={y 1، y 2، y 3}:

، جایی که NS (2) ={ب، -ب، ب) یا، موضوع | ایکس (2) |=1, ایکس (2) =

برای λ 3 = 6 بردار ویژه را پیدا کنید ایکس (3) ={z 1، z 2، z 3}:

, ایکس (3) ={ج,2c، c) یا در نسخه عادی

x (3) = شما می توانید آن را ببینید NS (1) NS (2) = ab - ab= 0, ایکس (1) ایکس (3) = ac - ac= 0, ایکس (2) ایکس (3) = قبل از میلاد مسیح- 2قبل از میلاد + قبل از میلاد= 0. بنابراین، بردارهای ویژه این ماتریس متعامد به صورت زوجی هستند.

سخنرانی 10.

فرم های درجه دوم و رابطه آنها با ماتریس های متقارن. ویژگی های بردارهای ویژه و مقادیر ویژه یک ماتریس متقارن. تقلیل شکل درجه دوم به شکل متعارف.

تعریف 10.1.فرم درجه دوممتغیرهای واقعی x 1، x 2، ...، x nیک چند جمله ای درجه دوم نسبت به این متغیرها است که شامل یک عبارت آزاد و عبارت درجه اول نیست.

نمونه هایی از فرم های درجه دوم:

(n = 2),

(n = 3). (10.1)

بیایید تعریف یک ماتریس متقارن را که در آخرین سخنرانی ارائه شد را به یاد بیاوریم:

تعریف 10.2.ماتریس مربع نامیده می شود متقارن، اگر، یعنی اگر عناصر ماتریس متقارن نسبت به قطر اصلی برابر باشند.

ویژگی های مقادیر ویژه و بردارهای ویژه یک ماتریس متقارن:

1) تمام مقادیر ویژه یک ماتریس متقارن واقعی هستند.

اثبات (برای n = 2).

اجازه دهید ماتریس آبه نظر می رسد: ... بیایید معادله مشخصه را بسازیم:

(10.2) ممیز را بیابید:

بنابراین، معادله فقط ریشه واقعی دارد.

2) بردارهای ویژه ماتریس متقارن متعامد هستند.

اثبات (برای n= 2).

مختصات بردارهای ویژه و باید معادلات را برآورده کند.

مقادیر ویژه (اعداد) و بردارهای ویژه.
نمونه هایی از راه حل ها

خودت باش

از هر دو معادله بر می آید که.

پس فرض کنید: .

در نتیجه: بردار ویژه دوم است.

نکات مهم راه حل را تکرار می کنیم:

- سیستم حاصل مطمئناً یک راه حل کلی دارد (معادلات به صورت خطی وابسته هستند).

- "بازی" را به گونه ای انتخاب می کنیم که کل باشد و مختصات "x" اول کل، مثبت و تا حد امکان کوچک باشد.

- بررسی کنید که راه حل خاص هر معادله سیستم را برآورده کند.

پاسخ .

"نقاط کنترل" متوسط ​​​​به اندازه کافی وجود داشت، بنابراین، بررسی برابری، در اصل، یک موضوع غیر ضروری است.

در منابع مختلف اطلاعات، مختصات بردارهای ویژه اغلب نه در ستون ها، بلکه در ردیف ها نوشته می شود، به عنوان مثال: (و صادقانه بگویم، من خودم عادت دارم آنها را در خطوط بنویسم)... این گزینه قابل قبول است، اما با توجه به موضوع تبدیلات خطیاستفاده از نظر فنی راحت تر است بردارهای ستونی.

شاید راه حل برای شما بسیار طولانی به نظر می رسید، اما این تنها به این دلیل است که من در مورد مثال اول با جزئیات بسیار توضیح دادم.

مثال 2

ماتریس ها

ما خودمان را آموزش می دهیم! یک مثال تقریبی از اتمام کار در پایان درس.

گاهی اوقات لازم است یک کار اضافی انجام شود، یعنی:

تجزیه ماتریس متعارف را بنویسید

چیست؟

اگر بردارهای ویژه ماتریس تشکیل شود اساس، سپس می توان آن را به صورت زیر نشان داد:

کجا ماتریس متشکل از مختصات بردارهای ویژه است، - موربماتریس با مقادیر ویژه مربوطه

چنین تجزیه ماتریسی نامیده می شود ابتدایییا مورب.

ماتریس مثال اول را در نظر بگیرید. بردارهای خودش مستقل خطی(غیر خطی) و پایه را تشکیل می دهند. بیایید یک ماتریس از مختصات آنها بسازیم:

بر مورب اصلیماتریس ها به ترتیب مناسبمقادیر ویژه قرار دارند و بقیه عناصر برابر با صفر هستند:
- یک بار دیگر بر اهمیت ترتیب تأکید می کنم: "دو" با بردار 1 مطابقت دارد و بنابراین در ستون 1 قرار دارد، "سه" - به بردار 2.

طبق الگوریتم معمول یافتن ماتریس معکوسیا روش گاوس-اردنپیدا کردن ... نه این اشتباه تایپی نیست! - قبل از شما یک رویداد نادر، مانند خورشید گرفتگی، زمانی که معکوس با ماتریس اصلی منطبق است.

باقی مانده است که تجزیه متعارف ماتریس را بنویسیم:

سیستم را می توان با استفاده از تبدیل های ابتدایی حل کرد و در مثال های زیر از این روش استفاده خواهیم کرد. اما در اینجا روش "مدرسه" بسیار سریعتر عمل می کند. از معادله 3 بیان خواهیم کرد: - در معادله دوم جایگزین خواهیم کرد:

از آنجایی که مختصات اول صفر است، سیستمی به دست می آید که از هر معادله آن نتیجه می شود.

و دوباره به وجود اجباری یک وابستگی خطی توجه کنید... اگر فقط یک راه حل بی اهمیت دریافت کنید ، سپس یا مقدار ویژه اشتباه پیدا شد یا سیستم با یک خطا کامپایل / حل شد.

مختصات فشرده معنی می دهد

بردار ویژه:

و یک بار دیگر - ما بررسی می کنیم که راه حل پیدا شده است هر معادله سیستم را برآورده می کند... در پاراگراف های بعدی و در کارهای بعدی، توصیه می کنم این آرزو را به عنوان یک قانون اجباری در نظر بگیرید.

2) برای مقدار ویژه، طبق همان اصل، سیستم زیر را بدست می آوریم:

از معادله 2 سیستم بیان می کنیم: - جایگزین در معادله سوم:

از آنجایی که مختصات "زتا" برابر با صفر است، سیستمی به دست می آید که از هر معادله آن یک وابستگی خطی به دست می آید.

بگذار باشد

ما بررسی می کنیم که راه حل هر معادله در سیستم را برآورده می کند.

بنابراین، بردار ویژه عبارت است از:.

3) و در نهایت، سیستم با مقدار ویژه مطابقت دارد:

معادله دوم ساده ترین به نظر می رسد، بنابراین ما از آن بیان می کنیم و آن را با معادلات 1 و 3 جایگزین می کنیم:

همه چیز خوب است - یک رابطه خطی پدید آمده است که ما آن را به عبارت جایگزین می کنیم:

در نتیجه، "x" و "igrek" از طریق "z" بیان شد:. در عمل، دستیابی به چنین روابطی ضروری نیست؛ در برخی موارد، بیان هم از طریق و هم از طریق راحت تر است. یا حتی یک "قطار" - برای مثال، "X" از طریق "igrek"، و "igrek" از طریق "z"

پس فرض کنید:

ما بررسی می کنیم که راه حل پیدا شده است هر معادله سیستم را برآورده می کند و بردار ویژه سوم را یادداشت می کند

پاسخ: بردارهای ویژه:

از نظر هندسی، این بردارها سه جهت فضایی مختلف را تعریف می کنند. ("آنجا و دوباره بازگشت")که توسط آن تبدیل خطیبردارهای غیر صفر (بردارهای ویژه) را به بردارهایی هم خط با آنها تبدیل می کند.

اگر شرط لازم برای یافتن یک تجزیه متعارف باشد، در اینجا این امکان وجود دارد، زیرا مقادیر ویژه مختلف با بردارهای ویژه مستقل خطی متفاوت مطابقت دارند. ترکیب ماتریس از مختصات آنها، ماتریس مورب از جانب مربوطهمقادیر ویژه و پیدا کردن ماتریس معکوس .

اگر بنا به شرط لازم است بنویسید ماتریس تبدیل خطی بر اساس بردارهای ویژه، سپس پاسخ را در فرم می دهیم. تفاوت وجود دارد و تفاوت قابل توجه است!برای این ماتریس ماتریس "de" است.

یک مسئله با محاسبات ساده تر برای یک راه حل مستقل:

مثال 5

بردارهای ویژه یک تبدیل خطی که توسط یک ماتریس به دست می آید را پیدا کنید

هنگام یافتن مقادیر ویژه، سعی کنید موضوع را به چند جمله ای درجه 3 نرسانید. علاوه بر این، راه حل های سیستم شما ممکن است با راه حل های من متفاوت باشد - هیچ ابهامی در اینجا وجود ندارد. و بردارهایی که پیدا می کنید ممکن است با بردارهای نمونه تا تناسب مختصات مربوطه آنها متفاوت باشد. به عنوان مثال، و. ارائه پاسخ در فرم زیباتر است، اما اگر روی گزینه دوم متوقف شوید اشکالی ندارد. با این حال، محدودیت های معقولی برای همه چیز وجود دارد، نسخه دیگر خیلی خوب به نظر نمی رسد.

نمونه نهایی تقریبی تکلیف در پایان درس.

چگونه مشکل را در مورد مقادیر ویژه چندگانه حل کنیم؟

الگوریتم کلی یکسان است، اما ویژگی های خاص خود را دارد و توصیه می شود برخی از بخش های راه حل را به سبک آکادمیک دقیق تری حفظ کنید:

مثال 6

مقادیر ویژه و بردارهای ویژه را پیدا کنید

راه حل

البته، ستون اول افسانه‌ای را با حروف بزرگ می‌نویسیم:

و پس از فاکتورگیری مثلث مربع:

در نتیجه مقادیر ویژه به دست می آید که دو عدد از آنها مضرب هستند.

بیایید بردارهای ویژه را پیدا کنیم:

1) طبق طرح "ساده شده" با سرباز تنها برخورد خواهیم کرد:

از دو معادله آخر، تساوی به وضوح قابل مشاهده است، که بدیهی است که باید به معادله 1 سیستم جایگزین شود:

ترکیب بهتری وجود ندارد:
بردار ویژه:

2-3) حالا به چند نگهبان شلیک کنید. در این مورد، ممکن است معلوم شود یا دو یا یکبردار ویژه صرف نظر از تعدد ریشه ها، مقدار را به جای تعیین کننده قرار می دهیم که موارد زیر را برای ما به ارمغان می آورد سیستم همگن معادلات خطی:

بردارهای ویژه دقیقاً بردار هستند
سیستم تصمیم گیری اساسی

در واقع، در کل درس، ما فقط درگیر یافتن بردارهای سیستم بنیادی بودیم. فقط در حال حاضر، این اصطلاح به ویژه مورد نیاز نبود. ضمناً آن دانش آموزان باهوشی که با مانتوهای استتاری موضوع را لغزش کردند معادلات همگناکنون مجبور به خوردن آن خواهد شد.

تنها اقدام حذف خطوط اضافی بود. نتیجه یک ماتریس یک به سه با یک "پله" رسمی در وسط است.
- متغیر پایه، - متغیرهای آزاد. دو متغیر رایگان وجود دارد، بنابراین، بردارهای سیستم بنیادی نیز دو هستند.

بیایید متغیر پایه را بر حسب متغیرهای آزاد بیان کنیم:. ضریب صفر در مقابل "x" به آن اجازه می دهد مطلقاً هر مقداری را بگیرد (که به وضوح از سیستم معادلات دیده می شود).

در زمینه این مشکل، راحت تر است که راه حل کلی را نه در یک ردیف، بلکه در یک ستون بنویسید:

بردار ویژه با جفت مطابقت دارد:
بردار ویژه با جفت مطابقت دارد:

توجه داشته باشید : خوانندگان پیچیده می توانند این بردارها را انتخاب کنند و به صورت شفاهی - فقط با تجزیه و تحلیل سیستم ، اما در اینجا به مقداری دانش نیاز است: سه متغیر وجود دارد، رتبه ماتریس سیستم- واحد که به معنی سیستم تصمیم گیری اساسیشامل 3 - 1 = 2 بردار است. با این حال، بردارهای یافت شده، حتی بدون این دانش، کاملاً در سطح شهودی قابل مشاهده هستند. در این صورت، بردار سوم حتی "زیباتر" نوشته می شود:. با این حال، من به شما هشدار می دهم که در مثال دیگری، انتخاب ساده ممکن است ظاهر نشود، به همین دلیل است که سلب مسئولیت برای افراد با تجربه در نظر گرفته شده است. علاوه بر این، چرا مثلاً بردار سوم را در نظر نگیریم؟ از این گذشته، مختصات آن نیز هر معادله سیستم و بردارها را برآورده می کند مستقل خطی این گزینه، در اصل، مناسب است، اما "کم"، زیرا بردار "دیگر" ترکیبی خطی از بردارهای سیستم اساسی است.

پاسخ: مقادیر ویژه:، بردارهای ویژه:

یک مثال مشابه برای یک راه حل مستقل:

مثال 7

مقادیر ویژه و بردارهای ویژه را پیدا کنید

یک مثال تقریبی از اتمام در پایان درس.

لازم به ذکر است که در هر دو مثال ششم و هفتم، سه بردار ویژه خطی مستقل به دست می آید و بنابراین ماتریس اصلی در تجزیه متعارف قابل نمایش است. اما چنین تمشک در همه موارد اتفاق نمی افتد:

مثال 8

راه حل: معادله مشخصه را بسازید و حل کنید:

ما تعیین کننده را با ستون اول باز می کنیم:

ساده سازی های بیشتر با توجه به روش در نظر گرفته شده انجام می شود و از چند جمله ای درجه 3 اجتناب می شود:

- مقادیر ویژه

بیایید بردارهای ویژه را پیدا کنیم:

1) هیچ مشکلی با ریشه وجود ندارد:

تعجب نکنید، علاوه بر کیت، از متغیرها نیز استفاده می شود - در اینجا تفاوتی وجود ندارد.

از معادله 3 بیان خواهیم کرد - در معادلات 1 و 2 جایگزین خواهیم کرد:

از هر دو معادله به دست می آید:

پس بگذار:

2-3) برای مقادیر متعدد، سیستم را بدست می آوریم .

اجازه دهید ماتریس سیستم را بنویسیم و با استفاده از تبدیل های ابتدایی، آن را به شکل گام به گام در آوریم:

بخش اول حداقل مقررات را برای درک شیمی سنجی ارائه می کند و بخش دوم حاوی حقایقی است که برای درک عمیق تر از روش های تجزیه و تحلیل چند متغیره باید بدانید. Matrix.xlsکه همراه این سند است.

ارجاع به مثال ها به عنوان اشیاء اکسل در متن قرار می گیرند. این مثال ها ماهیت انتزاعی دارند و به هیچ وجه به مسائل شیمی تجزیه گره نمی خورند. نمونه های واقعی استفاده از جبر ماتریسی در شیمی سنجی در سایر متون اختصاص داده شده به کاربردهای مختلف شیمی سنجی در نظر گرفته شده است.

اکثر اندازه گیری های انجام شده در شیمی تجزیه مستقیم نیستند، اما غیر مستقیم... یعنی در آزمایش به جای مقدار آنالیت مورد نظر C (غلظت)، مقدار دیگری به دست می آید. ایکس(سیگنال) مرتبط اما برابر با C نیست، یعنی. ایکس(C) ≠ C. به عنوان یک قاعده، نوع وابستگی ایکس(C) شناخته شده نیست، با این حال، خوشبختانه در شیمی تجزیه، اکثر اندازه گیری ها متناسب هستند. این بدان معنی است که با افزایش غلظت C در آبار، سیگنال X به همان مقدار افزایش می یابد. ایکس(آج) = تبر(C). علاوه بر این، سیگنال ها نیز افزودنی هستند، به طوری که سیگنال از یک نمونه حاوی دو ماده با غلظت های C 1 و C 2 برابر با مجموع سیگنال های هر جزء خواهد بود، یعنی. ایکس(C 1 + C 2) = ایکس(C 1) + ایکس(ج 2). تناسب و افزایش با هم می دهد خطی بودن... مثال های زیادی برای نشان دادن اصل خطی بودن وجود دارد، اما کافی است به دو نمونه از بارزترین نمونه ها اشاره کنیم - کروماتوگرافی و طیف سنجی. دومین ویژگی آزمایش در شیمی تجزیه است چند کاناله... تجهیزات تحلیلی مدرن به طور همزمان سیگنال های بسیاری از کانال ها را اندازه گیری می کنند. به عنوان مثال، شدت عبور نور برای چندین طول موج به طور همزمان اندازه گیری می شود، یعنی. طیف بنابراین در آزمایش با سیگنال های زیادی سروکار داریم ایکس 1 , ایکس 2 ,...., ایکس n، مشخص کننده مجموعه ای از غلظت های C 1، C 2، ...، C m از مواد موجود در سیستم مورد مطالعه.

برنج. 1 طیف

بنابراین، یک آزمایش تحلیلی با خطی بودن و چند بعدی بودن مشخص می شود. بنابراین، راحت است که داده های تجربی را به عنوان بردار و ماتریس در نظر بگیریم و آنها را با استفاده از دستگاه جبر ماتریسی دستکاری کنیم. ثمربخشی این رویکرد با مثال نشان داده شده در نشان داده شده است، که سه طیف ثبت شده برای 200 طول موج از 4000 تا 4796 سانتی متر – 1 را نشان می دهد. اولین ( ایکس 1) و دومی ( ایکس 2) طیف برای نمونه های استاندارد به دست آمد که در آنها غلظت دو ماده A و B مشخص است: در نمونه اول [A] = 0.5، [B] = 0.1، و در نمونه دوم [A] = 0.2، [B] ] = 0.6. در مورد یک نمونه جدید و ناشناخته که طیف آن مشخص شده است، چه می توان گفت ایکس 3 ?

سه طیف تجربی را در نظر بگیرید ایکس 1 , ایکس 2 و ایکس 3 به عنوان سه بردار بعد 200. با استفاده از جبر خطی می توان به راحتی نشان داد که ایکس 3 = 0.1 ایکس 1 +0.3 ایکس 2؛ بنابراین، نمونه سوم بدیهی است که تنها حاوی مواد A و B در غلظت های [A] = 0.5 × 0.1 + 0.2 × 0.3 = 0.11 و [B] = 0.1 × 0.1 + 0.6 × 0.3 = 0.19 است.

1. اطلاعات اولیه

1.1 ماتریس

ماتریسبه عنوان مثال یک جدول مستطیلی از اعداد نامیده می شود

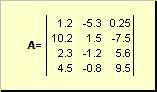
برنج. 2 ماتریس

ماتریس ها با حروف بزرگ درشت مشخص شده اند ( آ، و عناصر آنها - حروف کوچک مربوطه با شاخص ها، یعنی. آ ij. شاخص اول ردیف ها را شماره گذاری می کند و دومی ستون ها را شماره گذاری می کند. در شیمی سنجی، مرسوم است که حداکثر مقدار شاخص را با همان حرف خود شاخص، اما با حروف بزرگ نشان می دهند. بنابراین ماتریس آهمچنین می توان به صورت ( آ ij , من = 1,..., من; j = 1,..., جی). برای ماتریس نشان داده شده در مثال من = 4, جی= 3 و آ 23 = −7.5.

جفت اعداد منو جیبعد ماتریس نامیده می شود و به عنوان نشان داده می شود من× جی... نمونه ای از یک ماتریس در شیمی سنجی مجموعه ای از طیف های به دست آمده برای مننمونه بر روی جیطول موج

1.2. عملیات ماتریس ساده

ماتریس ها می توانند ضرب در اعداد... در این حالت هر عنصر در این عدد ضرب می شود. مثلا -

برنج. 3 ضرب ماتریس در عدد

دو ماتریس از یک بعد می توانند از نظر عنصر باشند تا کردنو کم کردن... مثلا،

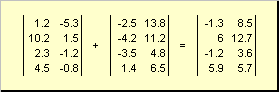
برنج. 4 اضافه کردن ماتریس

در نتیجه ضرب در عدد و جمع، ماتریسی با همان ابعاد به دست می آید.

ماتریس صفر ماتریسی متشکل از صفر است. نشان داده شده است O... بدیهی است که آ+O = آ, آ−آ = Oو 0 آ = O.

ماتریس می تواند باشد جابجا کردن... در طی این عملیات، ماتریس برگردانده می شود، یعنی. سطرها و ستون ها با هم عوض می شوند. انتقال با سکته مغزی نشان داده می شود، آ"یا شاخص آتی بنابراین اگر آ = {آ ij , من = 1,..., من; j = 1,...,جی)، سپس آ t = ( آ جی , j = 1,...,جی; i = 1، ...، من). مثلا

برنج. 5 ماتریس را جابجا کنید

واضح است که ( آ t) t = آ, (آ+ب) t = A t + بتی

1.3. ضرب ماتریس

ماتریس ها می توانند تکثیر کردن، اما به شرطی که دارای ابعاد مناسب باشند. چرایی این چنین است از تعریف مشخص خواهد شد. حاصل ضرب ماتریس آ، بعد، ابعاد، اندازه من× کو ماتریس ها ب، بعد، ابعاد، اندازه ک× جیماتریس نامیده می شود سی، بعد، ابعاد، اندازه من× جیکه عناصر آن اعداد هستند

بنابراین، برای تولید ABلازم است که تعداد ستون ها در ماتریس سمت چپ آبرابر تعداد سطرهای ماتریس سمت راست بود ب... نمونه ای از محصول ماتریس -

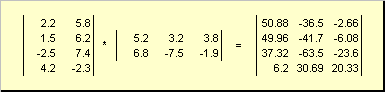
شکل 6 محصول ماتریس

قانون ضرب ماتریس را می توان به صورت زیر فرموله کرد. برای پیدا کردن یک عنصر از یک ماتریس سیایستاده در تقاطع من-خط و jستون -ام ( ج ij) باید عنصر به عنصر ضرب شود منسطر اول ماتریس آبر jستون هفتم ماتریس دوم بو تمام نتایج را جمع کنید. بنابراین در مثال نشان داده شده، یک عنصر از ردیف سوم و ستون دوم به عنوان مجموع حاصلضرب های عنصری ردیف سوم به دست می آید. آو ستون دوم ب

شکل 7 عنصر محصول ماتریس

حاصل ضرب ماتریس ها به ترتیب بستگی دارد، یعنی. AB ≠ BA، اگر فقط به دلایل بعد. می گویند غیر قابل تعویض است. با این حال، محصولات ماتریسی انجمنی هستند. معنیش اینه که ABC = (AB)سی = آ(قبل از میلاد مسیح). علاوه بر این، توزیعی نیز هست، یعنی. آ(ب+سی) = AB+AC... بدیهی است که AO = O.

1.4. ماتریس های مربعی

اگر تعداد ستون های ماتریس برابر با تعداد سطرهای آن باشد ( من = J = N، پس چنین ماتریسی مربع نامیده می شود. در این بخش، ما فقط چنین ماتریس هایی را در نظر خواهیم گرفت. از بین این ماتریس ها می توان ماتریس هایی با ویژگی های خاص را مشخص کرد.

تنهاماتریس (نشان داده شده است من،و گاهی اوقات E) ماتریسی است که در آن همه عناصر برابر با صفر هستند، به جز عناصر مورب که برابر با 1 هستند، یعنی.

به طور مشخص Ai = IA = آ.

ماتریس نامیده می شود مورباگر همه عناصر آن، به جز عناصر مورب ( آ ii) برابر با صفر هستند. مثلا

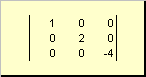
برنج. 8 ماتریس مورب

ماتریس آبالا نامیده می شود مثلثیاگر تمام عناصر آن زیر قطر برابر با صفر باشد، یعنی. آ ij= 0، برای من>j... مثلا

برنج. 9 ماتریس مثلثی بالا

ماتریس مثلثی پایین به طور مشابه تعریف شده است.

ماتریس آتماس گرفت متقارن، اگر آ t = آ... به عبارت دیگر آ ij = آ جی... مثلا

برنج. 10 ماتریس متقارن

ماتریس آتماس گرفت ارتودنسی، اگر

آتی آ = AA t = من.

ماتریس نامیده می شود طبیعیاگر

1.5. ردیابی و تعیین کننده

ذیلماتریس مربع آ(با Tr ( آ) یا Sp ( آ)) مجموع عناصر مورب آن است،

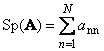
مثلا،

برنج. 11 ردیابی ماتریسی

بدیهی است که

Sp (α آ) = α Sp ( آ) و

Sp ( آ+ب) = Sp ( آ) + Sp ( ب).

می توان نشان داد که

Sp ( آ) = Sp ( آ t)، Sp ( من) = ن,

و همچنین آن

Sp ( AB) = Sp ( BA).

یکی دیگر از ویژگی های مهم ماتریس مربعی بودن آن است تعیین کننده(نشان داده شده با det ( آ)). تعیین تعیین کننده در حالت کلی نسبتاً دشوار است ، بنابراین ما با ساده ترین نسخه - ماتریس شروع می کنیم. آابعاد (2×2). سپس

برای یک ماتریس (3×3)، تعیین کننده خواهد بود

در مورد ماتریس ( ن× ن) تعیین کننده به صورت مجموع 1 2 3 محاسبه می شود ... ن= ن! شرایط، که هر یک برابر است

شاخص ها ک 1 , ک 2 ,..., k Nبه عنوان همه جایگشت های مرتب شده ممکن تعریف می شوند rاعداد در مجموعه (1، 2، ...، ن). محاسبه تعیین کننده یک ماتریس یک روش پیچیده است که در عمل با استفاده از برنامه های خاص انجام می شود. مثلا،

برنج. 12 تعیین کننده ماتریس

ما فقط به ویژگی های آشکار توجه می کنیم:

دت ( من) = 1، دت ( آ) = دت ( آت)

دت ( AB) = دت ( آ) دت ( ب).

1.6. بردارها

اگر ماتریس فقط از یک ستون تشکیل شده باشد ( جی= 1)، سپس چنین شیئی فراخوانی می شود بردار... به طور دقیق تر، یک بردار ستونی. مثلا

به عنوان مثال می توان ماتریس هایی متشکل از یک ردیف را نیز در نظر گرفت

این شی نیز بردار است، اما وکتور ردیف... هنگام تجزیه و تحلیل داده ها، مهم است که بفهمیم با کدام بردارها سروکار داریم - ستون ها یا ردیف ها. بنابراین طیف گرفته شده برای یک نمونه را می توان به عنوان بردار ردیف در نظر گرفت. سپس مجموعه شدت های طیفی در یک طول موج معین برای همه نمونه ها باید به عنوان بردار ستون در نظر گرفته شود.

بعد یک بردار تعداد عناصر آن است.

واضح است که هر بردار ستونی را می توان با جابجایی به بردار ردیفی تبدیل کرد، یعنی.

در مواردی که شکل یک بردار به طور خاص مشخص نشده است، بلکه صرفاً یک بردار گفته می شود، منظور آنها بردار ستونی است. ما نیز به این قانون پایبند خواهیم بود. یک بردار با یک حروف پررنگ مستقیم و کوچک نشان داده می شود. بردار صفر برداری است که همه عناصر آن صفر هستند. تعیین شده است 0 .

1.7. عملیات اساسی با بردارها

بردارها را می توان مانند ماتریس ها با اعداد اضافه و ضرب کرد. مثلا،

برنج. 13 عملیات بردار

دو بردار ایکسو yنامیده می شوند خط خطیاگر عدد α وجود داشته باشد به طوری که

1.8. محصولات بردارها

دو بردار با ابعاد یکسان نقابل ضرب است. بگذارید دو بردار وجود داشته باشد ایکس = (ایکس 1 , ایکس 2 ,...,ایکسن) t و y = (y 1 , y 2 ,...,yن) تی. با هدایت قاعده ضرب "ردیف به ستون"، می توانیم دو محصول از آنها بسازیم: ایکستی yو xyتی قطعه اول

تماس گرفت اسکالریا درونی؛ داخلی... نتیجه آن یک عدد است. همچنین از علامت گذاری ( ایکس,y)= ایکستی y... مثلا،

برنج. 14 محصول داخلی (محصول نقطه ای)

قطعه دوم

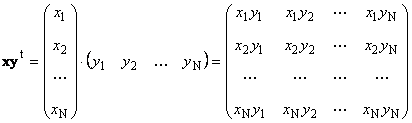
تماس گرفت خارجی... نتیجه آن یک ماتریس بعد است ( ن× ن). مثلا،

برنج. 15 کار خارجی

بردارهایی که حاصل ضرب اسکالر آنها برابر با صفر است نامیده می شوند ارتودنسی.

1.9. هنجار برداری

حاصل ضرب اسکالر یک بردار به خودی خود مربع اسکالر نامیده می شود. این مقدار

مربع را تعریف می کند طولبردار ایکس... برای نشان دادن طول (همچنین نامیده می شود عرفبردار)، از نماد استفاده می شود

مثلا،

برنج. 16 هنجار برداری

بردار واحد طول (|| ایکس|| = 1) نرمال شده نامیده می شود. یک بردار غیر صفر ( ایکس ≠ 0 ) را می توان با تقسیم آن بر طول نرمال کرد، یعنی. ایکس = ||ایکس|| (ایکس /||ایکس||) = ||ایکس|| ه... اینجا ه = ایکس /||ایکس|| بردار نرمال شده است.

بردارها را در صورتی متعامد می نامند که همگی نرمال شده و متعامد به صورت زوجی باشند.

1.10. زاویه بین بردارها

محصول نقطه ای و تزریقφ بین دو بردار ایکسو y

اگر بردارها متعامد باشند، cosφ = 0 و φ = π / 2، و اگر آنها خطی باشند، cosφ = 1 و φ = 0.

1.11. نمایش برداری از یک ماتریس

هر ماتریس آاندازه من× جیرا می توان به صورت مجموعه ای از بردارها نشان داد

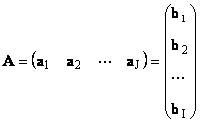
در اینجا هر بردار آ jهست یک jستون و بردار سطر ب منهست یک منردیف -امین ماتریس آ

1.12. بردارهای وابسته خطی

بردارهای یک بعد ( ن) را می توان مانند ماتریس ها در یک عدد اضافه و ضرب کرد. نتیجه یک بردار با همان ابعاد خواهد بود. بگذارید چندین بردار با یک بعد وجود داشته باشد ایکس 1 , ایکس 2 ,...,ایکس K و همان تعداد اعداد α α 1، α 2، ...، α ک... بردار

y= α 1 ایکس 1 + α 2 ایکس 2 + ... + α ک ایکس ک

تماس گرفت ترکیب خطیبردارها ایکس ک .

اگر اعداد غیرصفر α وجود داشته باشد ک ≠ 0, ک = 1,..., ک، چی y = 0 ، سپس چنین مجموعه ای از بردارها ایکس کتماس گرفت وابسته به خط... در غیر این صورت، بردارها مستقل خطی نامیده می شوند. به عنوان مثال بردارها ایکس 1 = (2، 2) t و ایکس 2 = (-1، -1) t به صورت خطی وابسته هستند، زیرا ایکس 1 +2ایکس 2 = 0

1.13. رتبه ماتریسی

مجموعه ای را در نظر بگیرید کبردارها ایکس 1 , ایکس 2 ,...,ایکس کابعاد ن... رتبه این سیستم از بردارها حداکثر تعداد بردارهای مستقل خطی است. مثلا در مجموعه

برای مثال فقط دو بردار مستقل خطی وجود دارد ایکس 1 و ایکس 2، پس رتبه آن 2 است.

بدیهی است که اگر تعداد بردارها در مجموعه بیشتر از ابعاد آنها باشد ( ک>ن، پس آنها لزوماً به طور خطی وابسته هستند.

با رتبه ماتریس(نشان داده شده با رتبه ( آ)) به رتبه سیستم بردارهایی گفته می شود که از آن تشکیل شده است. اگرچه هر ماتریس را می توان به دو صورت (بردارهای ستونی یا ردیف) نشان داد، این بر مقدار رتبه تأثیر نمی گذارد، زیرا

1.14. ماتریس معکوس

ماتریس مربع آدر صورتی که منحصر به فرد باشد، غیر منحط نامیده می شود معکوسماتریس آ-1 با شرایط تعیین می شود

AA −1 = آ −1 آ = من.

ماتریس معکوس برای همه ماتریس ها وجود ندارد. شرط لازم و کافی برای عدم انحطاط است

دت ( آ) ≠ 0 یا رتبه ( آ) = ن.

وارونگی ماتریس یک روش پیچیده است که برنامه های خاصی برای آن وجود دارد. مثلا،

برنج. 17 وارونگی ماتریس

اجازه دهید فرمول هایی را برای ساده ترین حالت - ماتریس های 2×2 ارائه کنیم

اگر ماتریس ها آو بپس غیر منحط

(AB) −1 = ب −1 آ −1 .

1.15. ماتریس شبه معکوس

اگر ماتریس آمنحط است و ماتریس معکوس وجود ندارد، پس در برخی موارد می توانید استفاده کنید شبه معکوسماتریسی که به عنوان چنین ماتریسی تعریف می شود آ+ اون

AA + آ = آ.

ماتریس شبه معکوس تنها نیست و نوع آن به روش ساخت بستگی دارد. به عنوان مثال، برای یک ماتریس مستطیلی، می توانید از روش مور-پنروز استفاده کنید.

اگر تعداد ستون ها کمتر از تعداد ردیف ها باشد، پس

آ + =(آتی آ) −1 آتی

مثلا،

برنج. 17a شبه وارونگی ماتریس

اگر تعداد ستون ها از تعداد سطرها بیشتر باشد، پس

آ + =آتی ( AAت) −1

1.16. ضرب یک بردار در یک ماتریس

بردار ایکسرا می توان در یک ماتریس ضرب کرد آبعد مناسب در این حالت بردار ستون در سمت راست ضرب می شود تبرو بردار ردیف در سمت چپ است ایکستی آ... اگر بعد بردار جی، و بعد ماتریس من× جیسپس نتیجه یک بردار بعد است من... مثلا،

برنج. 18 بردار با ضرب ماتریس

اگر ماتریس آ- مربع ( من× من، سپس بردار y = تبرهمان ابعاد را دارد ایکس... بدیهی است که

آ(α 1 ایکس 1 + α 2 ایکس 2) = α 1 تبر 1 + α 2 تبر 2 .

بنابراین، ماتریس ها را می توان به عنوان تبدیل خطی بردارها مشاهده کرد. به خصوص IX = ایکس, گاو نر = 0 .

2. اطلاعات تکمیلی

2.1. سیستم های معادلات خطی

بگذار باشد آ- اندازه ماتریس من× جی، آ ب- بردار بعد جی... معادله را در نظر بگیرید

تبر = ب

با توجه به بردار ایکس، ابعاد من... در واقع، این یک سیستم از منمعادلات خطی با جیناشناس ایکس 1 ,...,ایکس جی... راه حل وجود دارد اگر و فقط اگر

رتبه ( آ) = رتبه ( ب) = آر,

جایی که بیک ماتریس بعد توسعه یافته است من×( J + 1) متشکل از ماتریس آپر شده با ستون ب, ب = (آ ب). در غیر این صورت، معادلات ناسازگار هستند.

اگر آر = من = جی، سپس راه حل منحصر به فرد است

ایکس = آ −1 ب.

اگر آر < من، سپس راه حل های مختلفی وجود دارد که می توان آنها را بر حسب ترکیب خطی بیان کرد جی−آربردارها سیستم معادلات همگن تبر = 0 ماتریس مربع آ (ن× ن) یک راه حل غیر ضروری دارد ( ایکس ≠ 0 ) اگر و فقط اگر det ( آ) = 0. اگر آر= رتبه ( آ)<نسپس وجود داشته باشد ن−آرراه حل های مستقل خطی

2.2. اشکال دو خطی و درجه دوم

اگر آیک ماتریس مربع است و ایکسو yبردارهای بعد مربوطه، سپس حاصل ضرب اسکالر فرم هستند ایکستی آیتماس گرفت دو خطیشکل تعریف شده توسط ماتریس آ... در ایکس = yاصطلاح ایکستی تبرتماس گرفت درجه دومفرم.

2.3. ماتریس های قطعی مثبت

ماتریس مربع آتماس گرفت مثبت تعریف شده استاگر برای هر بردار غیر صفر ایکس ≠ 0 ,

ایکستی تبر > 0.

به همین ترتیب، منفی (ایکستی تبر < 0), غیر منفی (ایکستی تبر≥ 0) و مثبت نیست (ایکستی تبر≤ 0) ماتریس های خاص.

2.4. تجزیه کولسکی

اگر یک ماتریس متقارن آمثبت قطعی است، پس یک ماتریس مثلثی منحصر به فرد وجود دارد Uبا عناصر مثبت، که برای آن

آ = Uتی U.

مثلا،

برنج. 19 تجزیه کولسکی

2.5. تجزیه قطبی

بگذار باشد آیک ماتریس مربع غیر منحط ابعاد است ن× ن... سپس یک به یک وجود دارد قطبیکارایی

آ = SR،

جایی که اسیک ماتریس متقارن غیر منفی است و آریک ماتریس متعامد است. ماتریس ها اسو آررا می توان به صراحت تعریف کرد:

اس 2 = AA t یا اس = (AAت) ½ و آر = اس −1 آ = (AAت) -1 آ.

مثلا،

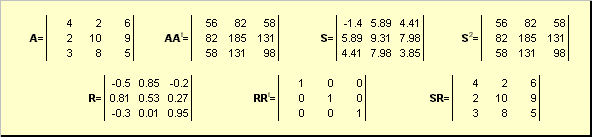
برنج. 20 تجزیه قطبی

اگر ماتریس آمنحط است، پس گسترش منحصر به فرد نیست - یعنی: اسهنوز تنهاست اما آرشاید خیلی تجزیه قطبی نشان دهنده ماتریس است آبه عنوان ترکیبی از فشرده سازی / کشش اسو چرخش آر.

2.6. بردارهای ویژه و مقادیر ویژه

بگذار باشد آیک ماتریس مربع است. بردار vتماس گرفت بردار خودماتریس ها آ، اگر

Av = λ v,

جایی که عدد λ نامیده می شود معنی خودماتریس ها آ... بنابراین، تبدیلی که ماتریس انجام می دهد آبیش از بردار v، به کشش یا فشرده سازی ساده با ضریب λ کاهش می یابد. بردار ویژه تا ضرب در ثابت α ≠ 0 تعیین می شود، یعنی. اگر vیک بردار ویژه است، سپس α vهمچنین یک بردار ویژه است.

2.7. مقادیر ویژه

ماتریس آ، بعد، ابعاد، اندازه ( ن× ن) نمی تواند بیشتر از نمقادیر ویژه راضی می کنند معادله مشخصه

دت ( آ − λ من) = 0,

که یک معادله جبری است نمرتبه به طور خاص، برای یک ماتریس 2 × 2، معادله مشخصه شکل دارد

مثلا،

برنج. 21 مقادیر ویژه

مجموعه مقادیر ویژه λ 1، ...، λ نماتریس ها آتماس گرفت طیف آ.

طیف دارای خواص مختلفی است. به خصوص

دت ( آ) = λ 1 × ... × λ ن, Sp ( آ) = λ 1 + ... + λ ن.

مقادیر ویژه یک ماتریس دلخواه می تواند اعداد مختلط باشد، اما اگر ماتریس متقارن باشد ( آ t = آ، سپس مقادیر ویژه آن واقعی هستند.

2.8. بردارهای خود

ماتریس آ، بعد، ابعاد، اندازه ( ن× ن) نمی تواند بیشتر از نبردارهای ویژه که هر کدام با مقدار خود مطابقت دارد. برای تعیین بردار ویژه v nشما باید یک سیستم معادلات همگن را حل کنید

(آ − λ n من)v n = 0 .

این یک راه حل غیر ضروری دارد، زیرا آ -λ n من) = 0.

مثلا،

برنج. 22 بردار ویژه

بردارهای ویژه یک ماتریس متقارن متعامد هستند.

سیستم معادلات خطی همگن

سیستم معادلات خطی همگن سیستمی از فرم است

واضح است که در این مورد از آنجا که تمام عناصر یکی از ستون ها در این واجد شرایط برابر با صفر هستند.

از آنجایی که مجهولات با فرمول ها پیدا می شوند ، در صورتی که Δ ≠ 0 باشد، سیستم یک راه حل صفر منحصر به فرد دارد ایکس = y = z= 0. با این حال، در بسیاری از مسائل این سوال که آیا یک سیستم همگن راه حل هایی غیر از صفر دارد یا خیر جالب است.

قضیه.برای اینکه یک سیستم معادلات همگن خطی جواب غیر صفر داشته باشد، کافی و لازم است که Δ ≠ 0 باشد.

بنابراین، اگر دترمینال Δ ≠ 0 باشد، سیستم یک راه حل منحصر به فرد دارد. اگر Δ ≠ 0 باشد، سیستم معادلات همگن خطی دارای مجموعه ای بی نهایت از راه حل ها است.

مثال ها.

بردارهای ویژه و مقادیر ویژه ماتریس

اجازه دهید یک ماتریس مربع داده شود , ایکس- تعدادی ماتریس-ستون که ارتفاع آن با ترتیب ماتریس مطابقت دارد آ. .

در بسیاری از مسائل باید معادله را در نظر گرفت ایکس

جایی که λ مقداری است. واضح است که برای هر λ این معادله یک جواب صفر دارد.

عدد λ را که این معادله برای آن جواب های غیر صفر دارد نامیده می شود معنی خودماتریس ها آ، آ ایکسبرای چنین λ نامیده می شود بردار خودماتریس ها آ.

بردار ویژه ماتریس را پیدا کنید آ... تا جایی که E∙X = X، سپس معادله ماتریس را می توان به صورت بازنویسی کرد یا ... در شکل بسط یافته، این معادله را می توان به صورت سیستمی از معادلات خطی بازنویسی کرد. واقعا .

و بنابراین

بنابراین، سیستمی از معادلات خطی همگن برای تعیین مختصات به دست آوردیم x 1, x 2, x 3بردار ایکس... برای اینکه سیستم جواب های غیر صفر داشته باشد، کافی و لازم است که تعیین کننده سیستم برابر با صفر باشد، یعنی.

این یک معادله درجه 3 با توجه به λ است. نامیده می شود معادله مشخصهماتریس ها آو برای تعیین مقادیر ویژه λ خدمت می کند.

هر مقدار ویژه λ مربوط به یک بردار ویژه است ایکسکه مختصات آن از سیستم در مقدار متناظر λ تعیین می شود.

مثال ها.

جبر برداری. مفهوم وکتور

هنگام مطالعه شاخه های مختلف فیزیک، کمیت هایی وجود دارد که با تعیین مقادیر عددی آنها به طور کامل تعیین می شوند، مثلاً طول، مساحت، جرم، دما و غیره. به چنین مقادیری اسکالر می گویند. اما علاوه بر آنها، کمیت هایی نیز وجود دارد که برای تعیین آنها علاوه بر مقدار عددی، باید جهت آنها را در فضا نیز دانست، مثلاً نیروی وارد بر بدن، سرعت و شتاب. وقتی جسم در فضا حرکت می کند، قدرت میدان مغناطیسی در یک نقطه معین از فضا و غیره. به چنین کمیت هایی بردار می گویند.

بیایید یک تعریف دقیق ارائه کنیم.

بخش جهت داربیایید یک قطعه را نام ببریم که نسبت به انتهای آن مشخص است که کدام یک از آنها اول و کدام دوم است.

بردارقطعه جهت دار نامیده می شود که طول معینی دارد، یعنی. قطعه ای به طول معین است که در آن یکی از نقاط محدود کننده آن به عنوان ابتدا و دیگری به عنوان پایان در نظر گرفته می شود. اگر آ- ابتدای بردار، ب- انتهای آن، سپس بردار با یک نماد مشخص می شود، علاوه بر این، بردار اغلب با یک حرف نشان داده می شود. در شکل یک بردار با یک پاره خط و جهت آن با یک فلش نشان داده شده است.

مدولیا طولبردار طول بخش جهتی است که آن را تعریف می کند. با || نشان داده می شود یا ||.

به اصطلاح بردار صفر که در آن ابتدا و انتها منطبق است به بردارها نیز اطلاق خواهد شد. اشاره شده است. بردار صفر جهت مشخصی ندارد و مدول آن برابر با صفر || = 0 است.

بردارها و نامیده می شوند خطیاگر روی یک خط مستقیم یا روی خطوط موازی قرار گیرند. علاوه بر این، اگر بردارها و در یک جهت باشند، برعکس خواهیم نوشت.

بردارهایی که روی خطوط مستقیم موازی با همان صفحه قرار دارند نامیده می شوند هم صفحه.

دو بردار و نامیده می شوند برابراگر آنها خطی، به یک اندازه جهت و طول مساوی باشند. در این صورت بنویسید.

از تعریف برابری بردارها، چنین استنباط می شود که یک بردار را می توان به موازات خود منتقل کرد و مبدا خود را در هر نقطه ای از فضا قرار داد.

مثلا.

عملیات خطی روی بردارها

1. ضرب بردار در عدد.

   حاصل ضرب یک بردار با عدد λ بردار جدیدی است که:

   حاصل ضرب یک بردار با عدد λ نشان داده می شود.

   

   مثلا،بردار است که در همان جهت بردار است و طول آن نصف بردار است.

   عملیات معرفی شده دارای موارد زیر است خواص:

2. جمع بردارها

   اجازه دهید و دو بردار دلخواه باشد. یک نکته دلخواه را در نظر بگیرید Oو یک بردار بسازید. پس از آن، از نقطه آبردار را کنار بگذارید بردار اتصال ابتدای بردار اول به انتهای بردار دوم نامیده می شود مجموعاز این بردارها و نشان داده می شود .

   

   تعریف فرمول بندی شده جمع بردار نامیده می شود قانون متوازی الاضلاع، از آنجایی که همان مجموع بردارها را می توان به صورت زیر بدست آورد. نقطه را کنار بگذارید Oبردارها و. اجازه دهید یک متوازی الاضلاع روی این بردارها بسازیم OAVS... از آنجایی که بردارها، برداری است که مورب متوازی الاضلاع است که از راس کشیده شده است O، بدیهی است که مجموع بردارها خواهد بود.

   

   بررسی موارد زیر آسان است خواص افزودن بردار.

3. تفاوت بردارها

   یک بردار هم خط به یک بردار معین، از نظر طول مساوی و جهت مخالف، نامیده می شود مقابلبردار برای بردار و با نشان داده می شود. بردار مقابل را می توان حاصل ضرب بردار در عدد λ = –1: دانست.

ماتریس های مورب ساده ترین هستند. این سوال مطرح می شود که آیا می توان مبنایی را پیدا کرد که در آن ماتریس یک عملگر خطی شکل مورب داشته باشد؟ چنین مبنایی وجود دارد.
اجازه دهید یک فضای خطی R n و یک عملگر خطی A در آن داده شود. در این حالت عملگر A R n را در خود می گیرد، یعنی A: R n → R n.

تعریف. یک بردار غیرصفر بردار ویژه عملگر A نامیده می شود که عملگر A به بردار هم خط با آن تبدیل شود، یعنی. عدد λ را مقدار ویژه یا مقدار ویژه عملگر A می نامند که مربوط به بردار ویژه است.
اجازه دهید به برخی از ویژگی های مقادیر ویژه و بردارهای ویژه توجه کنیم.
1. هر ترکیب خطی از بردارهای ویژه از عملگر A مربوط به مقدار ویژه λ یک بردار ویژه با مقدار ویژه یکسان است.
2. بردارهای ویژه از عملگر A با مقادیر ویژه جفتی مختلف λ 1، λ 2،…، λ m به صورت خطی مستقل هستند.
3. اگر مقادیر ویژه λ 1 = λ 2 = λ m = λ، آنگاه مقدار ویژه λ با حداکثر m بردارهای ویژه مستقل خطی مطابقت دارد.

بنابراین، اگر n بردار ویژه مستقل خطی وجود داشته باشد مربوط به مقادیر ویژه مختلف λ 1، λ 2، ...، λ n، سپس آنها به صورت خطی مستقل هستند، بنابراین، می توان آنها را به عنوان مبنای فضای R n در نظر گرفت. اجازه دهید شکل ماتریس عملگر خطی A را بر اساس بردارهای ویژه آن پیدا کنیم، که برای آن توسط عملگر A بر اساس بردارهای پایه عمل می کنیم: سپس .
بنابراین، ماتریس عملگر خطی A بر اساس بردارهای ویژه آن شکل مورب دارد و مقادیر ویژه عملگر A بر روی قطر قرار دارند.
آیا مبنای دیگری وجود دارد که در آن ماتریس مورب باشد؟ پاسخ این سوال با قضیه زیر داده می شود.

قضیه. ماتریس یک عملگر خطی A در پایه (i = 1..n) شکل مورب دارد اگر و فقط اگر همه بردارهای پایه بردارهای ویژه عملگر A باشند.

قانون برای یافتن مقادیر ویژه و بردارهای ویژه

بگذارید یک بردار داده شود ، که در آن x 1، x 2، ...، x n مختصات بردار نسبت به پایه هستند. و بردار ویژه عملگر خطی A مربوط به مقدار ویژه λ است، یعنی. این رابطه را می توان به صورت ماتریسی نوشت

. (*)

معادله (*) را می توان به عنوان معادله ای برای یافتن در نظر گرفت، علاوه بر این، ما به راه حل های غیر پیش پا افتاده علاقه مند هستیم، زیرا بردار ویژه نمی تواند صفر باشد. مشخص است که راه حل های غیر ضروری یک سیستم همگن معادلات خطی وجود دارند اگر و فقط اگر det (A - λE) = 0 باشد. بنابراین، برای اینکه λ یک مقدار ویژه عملگر A باشد، لازم و کافی است که det (A - λE) = 0.
اگر معادله (*) با جزئیات به صورت مختصات نوشته شده باشد، سیستم معادلات همگن خطی به دست می آید:

(1)
جایی که ماتریس عملگر خطی است.

اگر سیستم (1) تعیین کننده D برابر با صفر باشد، جواب غیر صفر دارد

معادله ای برای یافتن مقادیر ویژه دریافت کرد.
این معادله را معادله مشخصه و سمت چپ آن را چند جمله ای مشخصه ماتریس (عملگر) A می نامند. اگر چند جمله ای مشخصه ریشه واقعی نداشته باشد، ماتریس A فاقد بردار ویژه است و نمی توان آن را به صورت مورب تقلیل داد. .
فرض کنید λ 1، λ 2،...، λ n ریشه های واقعی معادله مشخصه باشند و در بین آنها ممکن است چندین ریشه وجود داشته باشد. با جایگزینی این مقادیر به نوبه خود با سیستم (1)، بردارهای ویژه را پیدا می کنیم.

مثال 12. عملگر خطی A در R 3 طبق قانون عمل می کند، که در آن x 1، x 2، ..، x n مختصات بردار در پایه هستند. , , ... مقادیر ویژه و بردارهای ویژه این عملگر را پیدا کنید.
راه حل. ماتریس این عملگر را می سازیم:
.
ما یک سیستم برای تعیین مختصات بردارهای ویژه می سازیم:

یک معادله مشخصه ترسیم می کنیم و آن را حل می کنیم:

.
λ 1،2 = -1، λ 3 = 3.
با جایگزینی λ = -1 در سیستم، داریم:
یا
زیرا ، سپس دو متغیر وابسته و یک متغیر آزاد وجود دارد.
پس اجازه دهید x 1 یک مجهول رایگان باشد ما این سیستم را به هر طریقی حل می کنیم و یک راه حل کلی برای این سیستم پیدا می کنیم: سیستم اساسی راه حل ها از یک راه حل تشکیل شده است، زیرا n - r = 3 - 2 = 1.
مجموعه بردارهای ویژه متناظر با مقدار ویژه λ = -1 به شکل: است، که در آن x 1 هر عدد غیر صفر است. اجازه دهید از این مجموعه یک بردار را انتخاب کنیم، برای مثال x 1 = 1 را قرار دهیم: .
با استدلال مشابه، بردار ویژه مربوط به مقدار ویژه λ = 3 را می یابیم: .
در فضای R 3 اساس از سه بردار مستقل خطی تشکیل شده است، اما ما فقط دو بردار ویژه خطی مستقل دریافت کرده‌ایم که اساس R3 را نمی‌توان از آنها تشکیل داد. در نتیجه، ماتریس A عملگر خطی را نمی توان به شکل مورب کاهش داد.

مثال 13. با توجه به یک ماتریس .
1. ثابت کنید که بردار یک بردار ویژه از ماتریس A است. مقدار ویژه مربوط به این بردار ویژه را پیدا کنید.
2. مبنایی را پیدا کنید که در آن ماتریس A شکل مورب داشته باشد.
راه حل.
1. اگر، پس - بردار ویژه

.
بردار (1, 8, -1) یک بردار ویژه است. مقدار ویژه λ = -1.
ماتریس دارای یک فرم مورب در پایه است که از بردارهای ویژه تشکیل شده است. یکی از آنها معروف است. بیا بقیه رو پیدا کنیم
ما بردارهای ویژه را از سیستم جستجو می کنیم:

معادله مشخصه: ;
(3 + λ) [- 2 (2-λ) (2 + λ) +3] = 0; (3 + λ) (λ 2 - 1) = 0
λ 1 = -3، λ 2 = 1، λ 3 = -1.
اجازه دهید بردار ویژه مربوط به مقدار ویژه λ = -3 را پیدا کنیم:

رتبه ماتریس این سیستم برابر با دو و برابر با تعداد مجهولات است، بنابراین این سیستم فقط یک جواب صفر دارد x 1 = x 3 = 0. x 2 در اینجا می تواند هر غیر صفر باشد، به عنوان مثال، x 2 = 1. بنابراین، بردار (0، 1،0) یک بردار ویژه مربوط به λ = -3 است. بیایید بررسی کنیم:
.
اگر λ = 1، سیستم را بدست می آوریم
رتبه ماتریس دو است. معادله آخر را حذف می کنیم.
اجازه دهید x 3 یک مجهول رایگان باشد. سپس x 1 = -3x 3، 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3، x 2 = -9x 3.
با تنظیم x 3 = 1، (-3، -9،1) داریم - بردار ویژه مربوط به مقدار ویژه λ = 1. تأیید:

.
از آنجایی که مقادیر ویژه واقعی و متفاوت هستند، بردارهای مربوط به آنها به صورت خطی مستقل هستند، بنابراین می توان آنها را به عنوان پایه در R3 در نظر گرفت. بنابراین، در اساس , , ماتریس A به شکل زیر است:
.
همه ماتریس های یک عملگر خطی A: Rn → Rn را نمی توان به شکل مورب کاهش داد، زیرا برای برخی از عملگرهای خطی بردارهای ویژه مستقل خطی می توانند کمتر از n باشند. با این حال، اگر ماتریس متقارن باشد، دقیقاً m بردار مستقل خطی با ریشه معادله مشخصه تعدد m مطابقت دارد.

تعریف. ماتریس متقارن یک ماتریس مربعی است که در آن عناصر متقارن نسبت به قطر اصلی برابر هستند، یعنی در آن.
ملاحظات. 1. تمام مقادیر ویژه یک ماتریس متقارن واقعی هستند.
2. بردارهای ویژه یک ماتریس متقارن متناظر با مقادیر ویژه مختلف جفتی متعامد هستند.
به عنوان یکی از کاربردهای فراوان دستگاه مورد مطالعه، اجازه دهید مسئله تعیین شکل یک منحنی مرتبه دوم را در نظر بگیریم.