وظایف با مشتق در امتحان. کلاس کارشناسی ارشد "مشتق یک تابع در وظایف امتحان. معنای هندسی و فیزیکی مشتق، معادله مماس بر نمودار تابع، مطالعه تابع با استفاده از مشتق

مشتق تابع یکی از دشوارترین مباحث در برنامه درسی مدرسه است. هر فارغ التحصیل به این سؤال پاسخ نمی دهد که مشتق چیست.

این مقاله به سادگی و به وضوح توضیح می دهد که مشتق چیست و چرا به آن نیاز است.. ما اکنون برای دقت ریاضی ارائه تلاش نخواهیم کرد. مهمترین چیز این است که معنی را درک کنید.

بیایید تعریف را به خاطر بسپاریم:

مشتق نرخ تغییر تابع است.

شکل نمودارهای سه تابع را نشان می دهد. به نظر شما کدام یک سریعتر رشد می کند؟

پاسخ واضح است - سوم. بالاترین نرخ تغییر یعنی بزرگترین مشتق را دارد.

در اینجا یک مثال دیگر وجود دارد.

کوستیا، گریشا و ماتوی در همان زمان شغل پیدا کردند. بیایید ببینیم درآمد آنها در طول سال چگونه تغییر کرده است:

شما می توانید بلافاصله همه چیز را در نمودار ببینید، درست است؟ درآمد Kostya در شش ماه بیش از دو برابر شده است. و درآمد گریشا نیز افزایش یافت، اما فقط کمی. و درآمد متیو به صفر کاهش یافت. شرایط شروع یکسان است، اما نرخ تغییر تابع، یعنی. مشتق، - ناهمسان. در مورد ماتوی، مشتق درآمد او به طور کلی منفی است.

به طور شهودی، ما به راحتی می توانیم نرخ تغییر یک تابع را تخمین بزنیم. اما چگونه این کار را انجام دهیم؟

آنچه ما واقعاً به آن نگاه می کنیم این است که نمودار تابع با چه شدتی بالا (یا پایین) می رود. به عبارت دیگر، سرعت y با x چقدر تغییر می کند. بدیهی است که یک تابع در نقاط مختلف می تواند مقدار متفاوتی از مشتق داشته باشد - یعنی می تواند سریعتر یا کندتر تغییر کند.

مشتق تابع با نشان داده می شود.

بیایید نحوه پیدا کردن را با استفاده از نمودار نشان دهیم.

نمودار برخی از تابع ها رسم می شود. یک نقطه روی آن را با آبسیسا بگیرید. در این نقطه مماس بر نمودار تابع رسم کنید. ما می خواهیم ارزیابی کنیم که نمودار تابع با چه شدتی بالا می رود. یک ارزش مفید برای این است مماس شیب مماس.

مشتق تابع در یک نقطه برابر است با مماس شیب مماس رسم شده بر نمودار تابع در آن نقطه.

لطفا توجه داشته باشید - به عنوان زاویه تمایل مماس، زاویه بین مماس و جهت مثبت محور را در نظر می گیریم.

گاهی اوقات دانش آموزان می پرسند که مماس بر نمودار یک تابع چقدر است؟ این یک خط مستقیم است که تنها نقطه مشترک آن با نمودار در این بخش است، علاوه بر این، همانطور که در شکل ما نشان داده شده است. به نظر مماس بر دایره است.

بیایید پیدا کنیم. به یاد داریم که مماس یک زاویه تند در یک مثلث قائم الزاویه برابر است با نسبت پای مقابل به مجاور. از مثلث:

ما مشتق را با استفاده از نمودار حتی بدون دانستن فرمول تابع پیدا کردیم. چنین وظایفی اغلب در امتحان ریاضیات زیر عدد یافت می شود.

همبستگی مهم دیگری وجود دارد. به یاد بیاورید که خط مستقیم با معادله داده می شود

کمیت در این معادله نامیده می شود شیب یک خط مستقیم. برابر است با مماس زاویه میل خط مستقیم به محور.

.

ما آن را دریافت می کنیم

بیایید این فرمول را به خاطر بسپاریم. معنای هندسی مشتق را بیان می کند.

مشتق تابع در یک نقطه برابر است با شیب مماس رسم شده به نمودار تابع در آن نقطه.

به عبارت دیگر مشتق برابر است با مماس شیب مماس.

قبلاً گفتیم که یک تابع می تواند مشتقات مختلفی در نقاط مختلف داشته باشد. بیایید ببینیم مشتق چگونه با رفتار تابع مرتبط است.

بیایید یک نمودار از یک تابع رسم کنیم. اجازه دهید این تابع در برخی مناطق افزایش یابد و در برخی دیگر و با نرخ های متفاوت کاهش یابد. و اجازه دهید این تابع حداکثر و حداقل امتیاز داشته باشد.

در یک نقطه، تابع در حال افزایش است. مماس بر نمودار، که در نقطه رسم شده است، یک زاویه تند با جهت مثبت محور تشکیل می دهد. بنابراین مشتق در نقطه مثبت است.

در این نقطه، عملکرد ما در حال کاهش است. مماس در این نقطه با جهت مثبت محور یک زاویه منفرد تشکیل می دهد. از آنجایی که مماس یک زاویه کج منفی است، مشتق در نقطه منفی است.

این چیزی است که اتفاق می افتد:

اگر تابعی در حال افزایش باشد، مشتق آن مثبت است.

اگر کاهش یابد، مشتق آن منفی است.

و در نقاط حداکثر و حداقل چه اتفاقی خواهد افتاد؟ می بینیم که در (حداکثر نقطه) و (نقطه حداقل) مماس افقی است. بنابراین مماس شیب مماس در این نقاط صفر است و مشتق نیز صفر است.

نقطه حداکثر نقطه است. در این مرحله، افزایش تابع با کاهش جایگزین می شود. در نتیجه، علامت مشتق در نقطه از "بعلاوه" به "منهای" تغییر می کند.

در نقطه - حداقل نقطه - مشتق نیز برابر با صفر است، اما علامت آن از "منهای" به "بعلاوه" تغییر می کند.

نتیجه گیری: با کمک مشتق، می توانید هر چیزی را که در مورد رفتار تابع مورد علاقه ما است، پیدا کنید.

اگر مشتق مثبت باشد، تابع در حال افزایش است.

اگر مشتق منفی باشد، تابع در حال کاهش است.

در حداکثر نقطه، مشتق صفر است و علامت مثبت به منفی را تغییر می دهد.

در نقطه حداقل، مشتق نیز صفر است و علامت را از منفی به مثبت تغییر می دهد.

این یافته ها را در قالب یک جدول می نویسیم:

	افزایش	حداکثر امتیاز	کاهش می دهد	حداقل امتیاز	افزایش
+	0	-	0	+

اجازه دهید دو توضیح کوچک ارائه دهیم. هنگام حل مشکلات امتحانی به یکی از آنها نیاز خواهید داشت. دیگری - در سال اول، با مطالعه جدی تر از توابع و مشتقات.

یک مورد زمانی ممکن است که مشتق یک تابع در نقطه‌ای برابر با صفر باشد، اما تابع در این نقطه نه ماکزیمم داشته باشد و نه حداقل. این به اصطلاح :

در یک نقطه مماس بر نمودار افقی و مشتق آن صفر است. با این حال، قبل از نقطه، تابع افزایش یافته است - و بعد از نقطه به افزایش ادامه می دهد. علامت مشتق تغییر نمی کند - همانطور که بود مثبت باقی مانده است.

همچنین اتفاق می افتد که در نقطه حداکثر یا حداقل، مشتق وجود ندارد. در نمودار، این مربوط به یک شکست شدید است، زمانی که کشیدن مماس در یک نقطه مشخص غیرممکن است.

اما اگر تابع نه با نمودار، بلکه با فرمول داده شود، چگونه مشتق را پیدا کنیم؟ در این مورد اعمال می شود

مشتق تابع $y = f(x)$ در یک نقطه معین $x_0$ حد نسبت افزایش تابع به افزایش متناظر آرگومان آن است، مشروط بر اینکه دومی به سمت صفر گرایش داشته باشد:

$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$

تمایز عملیات یافتن مشتق است.

جدول مشتقات برخی از توابع ابتدایی

تابع	مشتق
$c$	$0$
x$	$1$
$x^n$	$nx^(n-1)$
$(1)/(x)$	$-(1)/(x^2)$
$√x$	$(1)/(2√x)$
$e^x$	$e^x$
$lnx$	$(1)/(x)$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	$(1)/(cos^2x)$
$ctgx$	$-(1)/(sin^2x)$

قوانین اساسی تمایز

1. مشتق جمع (تفاوت) برابر است با مجموع (تفاوت) مشتقات.

$(f(x) ± g(x))"= f"(x)±g"(x)$

مشتق تابع $f(x)=3x^5-cosx+(1)/(x)$ را بیابید

مشتق جمع (تفاوت) برابر است با مجموع (تفاوت) مشتقات.

$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + sinx - (1)/(x^2)$

2. مشتق از یک محصول

$(f(x) g(x))"= f"(x) g(x)+ f(x) g(x)"$

مشتق $f(x)=4x cosx$ را بیابید

$f"(x)=(4x)" cosx+4x (cosx)"=4 cosx-4x sinx$

3. مشتق از ضریب

$((f(x))/(g(x)))"=(f"(x) g(x)-f(x) g(x)")/(g^2(x)) $

مشتق $f(x)=(5x^5)/(e^x)$ را بیابید

$f"(x)=((5x^5)" e^x-5x^5 (e^x)")/((e^x)^2)=(25x^4 e^x- 5x^5 e^x)/((e^x)^2)$

4. مشتق تابع مختلط برابر است با حاصلضرب مشتق تابع خارجی و مشتق تابع داخلی.

$f(g(x))"=f"(g(x)) g"(x)$

$f"(x)=cos"(5x) (5x)"=-sin(5x) 5= -5sin(5x)$

معنای فیزیکی مشتق

اگر یک نقطه مادی در یک خط مستقیم حرکت کند و مختصات آن بسته به زمان بر اساس قانون $x(t)$ تغییر کند، سرعت آنی این نقطه برابر با مشتق تابع است.

نقطه مطابق با قانون $x(t)= 1.5t^2-3t + 7$ در امتداد خط مختصات حرکت می کند، که در آن $x(t)$ مختصات در زمان $t$ است. در چه نقطه ای از زمان سرعت نقطه برابر با 12 دلار خواهد بود؟

1. Speed ​​مشتق $x(t)$ است، پس بیایید مشتق تابع داده شده را پیدا کنیم.

$v(t) = x"(t) = 1.5 2t -3 = 3t -3$

2. برای اینکه بفهمیم در چه زمانی سرعت $t$ برابر با $12 بوده است، معادله را می سازیم و حل می کنیم:

معنای هندسی مشتق

به یاد بیاورید که معادله یک خط مستقیم که با محورهای مختصات موازی نیست را می توان به صورت $y = kx + b$ نوشت، که $k$ شیب خط مستقیم است. ضریب $k$ برابر است با مماس شیب بین خط مستقیم و جهت مثبت محور $Ox$.

مشتق تابع $f(x)$ در نقطه $x_0$ برابر است با شیب $k$ مماس بر نمودار در نقطه داده شده:

بنابراین، می توانیم یک برابری کلی ایجاد کنیم:

$f"(x_0) = k = tgα$

در شکل، مماس بر تابع $f(x)$ در حال افزایش است، بنابراین ضریب $k > 0$ است. از آنجایی که $k > 0$، پس $f"(x_0) = tgα > 0$. زاویه $α$ بین مماس و جهت مثبت $Ox$ حاد است.

در شکل، مماس بر تابع $f(x)$ کاهش می یابد، بنابراین ضریب $k است.< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

در شکل، مماس تابع $f(x)$ موازی با محور $Ох$ است، بنابراین ضریب $k = 0$، بنابراین $f"(x_0) = tg α = 0$. نقطه $. x_0$ که در آن $f "(x_0) = 0$، فراخوانی شد نقاط بحرانی.

شکل، نمودار تابع $y=f(x)$ و مماس بر این نمودار را نشان می دهد که در نقطه ای با ابسیسا $x_0$ ترسیم شده است. مقدار مشتق تابع $f(x)$ را در نقطه $x_0$ پیدا کنید.

مماس بر نمودار افزایش می یابد، بنابراین، $f"(x_0) = tg α > 0$

برای یافتن $f"(x_0)$، مماس شیب بین مماس و جهت مثبت محور $Ox$ را پیدا می کنیم. برای این کار مماس بر مثلث $ABC$ را تکمیل می کنیم.

مماس زاویه $BAC$ را پیدا کنید. (مماس یک زاویه تند در مثلث قائم الزاویه، نسبت پای مقابل به ساقه مجاور است.)

$tg BAC = (BC)/(AC) = (3)/(12)= (1)/(4)=0.25$

$f"(x_0) = tg شما = 0.25 دلار

پاسخ: 0.25 دلار

مشتق همچنین برای یافتن فواصل توابع افزایش و کاهش استفاده می شود:

اگر $f"(x) > 0$ در یک بازه، تابع $f(x)$ در این بازه افزایش می یابد.

اگر $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

شکل، نمودار تابع $y = f(x)$ را نشان می دهد. در بین نقاط $х_1,х_2,х_3…х_7$ نقاطی را پیدا کنید که مشتق تابع منفی است.

در پاسخ، تعداد نقاط داده را یادداشت کنید.

کار عملی فوق برنامه 2

تبدیل نمودار توابع.

هدف

نمودارهای تابع را با استفاده از تبدیل های مختلف رسم کنید، به سوال مسئله پاسخ دهید.

تکمیل کار

رهنمودها

این کار برای 10 گزینه طراحی شده است، شماره گزینه با آخرین رقم شماره سریال موجود در لیست مطابقت دارد. به عنوان مثال، 1، 11، 21، 31 ... انجام 1 گزینه، 2،12، 22 ... - 2 گزینه، و غیره.

این کار از دو قسمت تشکیل شده است: قسمت اول وظایف 1 - 5، اینها کارهایی هستند که برای گرفتن اعتبار باید تکمیل شوند، اگر این کارها با خطا تکمیل شدند، باید آنها را اصلاح کنید و دوباره کار را برای تأیید ارسال کنید. . قسمت دوم شامل وظایفی است که با تکمیل آنها می توانید نمره اضافی کسب کنید: قسمت اصلی +2 کار - "4" ، قسمت اصلی +3 کار - "5".

وظیفه 1. نمودار یک تابع خطی یک خط مستقیم است، دو نقطه برای ساخت آن کافی است. (مقادیر آرگومان x را به دلخواه می گیریم و مقدار تابع y را در فرمول جایگزین می کنیم).

برای بررسی اینکه آیا نمودار تابع از نقطه مشخص شده عبور می کند یا خیر، باید مختصات نقطه را به جای x و y جایگزین کنید، اگر برابری صحیح را به دست آورید، خط از نقطه مشخص شده عبور می کند، در غیر این صورت نمی گذرد. .

وظیفه 2، 3، 4. نمودارهای توابع نشان داده شده از نمودارهای توابع به دست می آیند. , با استفاده از یک تغییر در امتداد محور x یا y.

، ابتدا تابع را رسم کنید یا ، سپس آن را با واحدهای "a" به راست یا چپ (+ a - به چپ، - a به راست) منتقل می کنیم، سپس آن را با واحدهای "b" به بالا یا پایین (+ در - بالا، - در) تغییر می دهیم. - پایین)

به طور مشابه با سایر توابع:

وظیفه 5 رسم نمودار تابع: ، شما باید: 1) یک نمودار از تابع بسازید ، 2) بخشی از نمودار که بالای محور x است بدون تغییر باقی می ماند، 3) بخشی از نمودار که زیر محور x قرار دارد آینه می شود.

وظایف برای راه حل مستقل.

قسمت اجباری

وظیفه 1. نمودار یک تابع خطی را رسم کنید، تعیین کنید که آیا نمودار تابع از نقطه مشخص شده عبور می کند یا خیر:

وظیفه 2. نمودار یک تابع درجه دوم را رسم کنید، مجموعه مقادیر را برای این تابع نشان دهید.

وظیفه 3. یک نمودار از یک تابع بسازید، تعیین کنید که آیا تابع مشخص شده در حال افزایش یا کاهش است.

وظیفه 4. یک نمودار از تابع بسازید، به سوال کار پاسخ دهید.

وظیفه 5. یک نمودار از یک تابع حاوی علامت مدول بسازید.

وظایف برای ارزیابی اضافی

وظیفه 6. نموداری از یک تابع را به صورت تکه ای رسم کنید، مشخص کنید که آیا این تابع نقطه شکست دارد یا خیر:

وظیفه 7. تعیین کنید که سیستم معادلات چند راه حل دارد، پاسخ را توجیه کنید. با پاسخ دادن به سوالات نتیجه گیری کنید.

نمودارهای توابعی را در این کار ساختید؟

نام نمودار یک تابع خطی چیست؟

نام نمودار یک تابع درجه دوم چیست؟

چه تغییرات نموداری را می دانید؟

نمودار یک تابع زوج چگونه در دستگاه مختصات قرار دارد؟ نمودار یک تابع فرد؟

در کار شماره 13 آزمون یکپارچه دولتی در ریاضیات سطح پایه، باید مهارت و دانش یکی از مفاهیم رفتار یک تابع را نشان دهید: مشتقات در یک نقطه یا نرخ های افزایش یا کاهش. تئوری این کار کمی بعد اضافه خواهد شد، اما این مانع از آن نمی شود که چندین گزینه معمولی را با جزئیات تجزیه و تحلیل کنیم.

تجزیه و تحلیل گزینه های معمولی برای وظایف شماره 14 استفاده در ریاضیات سطح پایه

گزینه 14MB1

نمودار وابستگی دما به زمان در فرآیند گرم کردن موتور یک ماشین را نشان می دهد. محور افقی زمان را بر حسب دقیقه نشان می دهد که از راه اندازی موتور گذشته است. در محور عمودی دمای موتور بر حسب درجه سانتیگراد است.

با استفاده از نمودار، هر بازه زمانی را با ویژگی های فرآیند گرم کردن موتور در این بازه مطابقت دهید.

در جدول زیر هر حرف عدد مربوطه را مشخص کنید.

الگوریتم اجرا:

1. بازه زمانی کاهش دما را انتخاب کنید.
2. یک خط کش را روی 30 درجه سانتیگراد وصل کنید و فاصله زمانی را که در آن دما زیر 30 درجه سانتیگراد بود تعیین کنید.

راه حل:

اجازه دهید فاصله زمانی کاهش دما را انتخاب کنیم. این بخش با چشم غیر مسلح قابل مشاهده است، 8 دقیقه از لحظه روشن شدن موتور شروع می شود.

یک خط کش را روی دمای 30 درجه سانتیگراد اعمال کنید و فاصله زمانی را که در آن دما زیر 30 درجه سانتیگراد بود تعیین کنید.

در زیر خط کش یک بخش مربوط به فاصله زمانی 0 - 1 دقیقه وجود دارد.

با کمک یک مداد و یک خط کش متوجه می شویم که دما در چه بازه زمانی در محدوده 40 درجه سانتیگراد تا 80 درجه سانتیگراد بوده است.

از نقاط مربوط به 40 درجه سانتیگراد و 80 درجه سانتیگراد عمودها را روی نمودار و از نقاط به دست آمده عمودها را روی محور زمان رها می کنیم.

می بینیم که این فاصله دمایی با فاصله زمانی 3 تا 6.5 دقیقه مطابقت دارد. یعنی از موارد داده شده در شرایط 3 - 6 دقیقه.

پاسخ گم شده را با استفاده از روش حذف انتخاب کنید.

گزینه 14MB2

راه حل:

بیایید نمودار تابع A را تجزیه و تحلیل کنیم. اگر تابع افزایش یابد، مشتق مثبت است و بالعکس. مشتق تابع در نقاط انتهایی برابر با صفر است.

اول، تابع A افزایش می یابد، یعنی. مشتق مثبت است این مربوط به نمودارهای مشتقات 2 و 3 است. در حداکثر نقطه تابع x = -2، یعنی در این نقطه، مشتق باید برابر با صفر باشد. این شرط با نمودار شماره 3 مطابقت دارد.

اول، تابع B کاهش می یابد، یعنی. مشتق منفی است. این مربوط به نمودارهای مشتقات 1 و 4 است. حداکثر نقطه تابع x \u003d -2، یعنی در این نقطه مشتق باید برابر با صفر باشد. این شرط با نمودار شماره 4 مطابقت دارد.

اول، تابع B افزایش می یابد، یعنی. مشتق مثبت است این مربوط به نمودارهای مشتقات 2 و 3 است. حداکثر نقطه تابع x = 1، یعنی در این نقطه، مشتق باید برابر با صفر باشد. این شرط با نمودار شماره 2 مطابقت دارد.

با روش حذف می توان تعیین کرد که نمودار تابع Г با نمودار مشتق شماره 1 مطابقت دارد.

جواب: 3421.

گزینه 14MB3

الگوریتم اجرای هر یک از توابع:

1. فواصل توابع افزایش و کاهش را تعیین کنید.
2. حداکثر و حداقل نقاط توابع را تعیین کنید.
3. نتیجه گیری کنید، برنامه های پیشنهادی را مطابقت دهید.

راه حل:

بیایید نمودار تابع A را تجزیه و تحلیل کنیم.

اگر تابع در حال افزایش باشد، مشتق مثبت است و بالعکس. مشتق تابع در نقاط انتهایی برابر با صفر است.

نقطه افراطی نقطه ای است که در آن مقدار حداکثر یا حداقل تابع به دست می آید.

اول، تابع A افزایش می یابد، یعنی. مشتق مثبت است این مربوط به نمودارهای مشتقات 3 و 4 است. در نقطه حداکثر تابع x=0، یعنی در این نقطه، مشتق باید برابر با صفر باشد. این شرط با نمودار شماره 4 مطابقت دارد.

بیایید نمودار تابع B را تجزیه و تحلیل کنیم.

اول، تابع B کاهش می یابد، یعنی. مشتق منفی است. این مربوط به نمودارهای مشتقات 1 و 2 است. حداقل نقطه تابع x=-1، یعنی در این نقطه مشتق باید برابر با صفر باشد. این شرط با نمودار شماره 2 مطابقت دارد.

بیایید نمودار تابع B را تجزیه و تحلیل کنیم.

اول، تابع B کاهش می یابد، یعنی. مشتق منفی است. این مربوط به نمودارهای مشتقات 1 و 2 است. حداقل نقطه تابع x \u003d 0 است، یعنی در این نقطه مشتق باید برابر با صفر باشد. این شرط با نمودار شماره 1 مطابقت دارد.

با روش حذف می توان تعیین کرد که نمودار تابع Г با نمودار مشتق شماره 3 مطابقت دارد.

جواب: 4213.

گزینه 14MB4

شکل نموداری از یک تابع و مماس های کشیده شده روی آن را در نقاطی با ابسیساهای A، B، C و D نشان می دهد.ستون سمت راست مقادیر مشتق را در نقاط A، B، C و D نشان می دهد. با استفاده از نمودار، هر نقطه را با مقدار مشتق تابع در آن مطابقت دهید.

نکته ها
ولی
که در
از جانب
دی

ارزش های مشتق
1) –4
2) 3
3) 2/3
4) -1/2

به یاد بیاورید که مشتق به چه معناست، یعنی مقدار آن در نقطه - مقدار تابع مشتق در یک نقطه برابر است با مماس شیب (ضریب) مماس.

در پاسخ ها دو گزینه مثبت و دو گزینه منفی داریم. همانطور که به یاد داریم، اگر ضریب مستقیم باشد (گرافیک y = kx + b) مثبت است، پس خط در حال افزایش است، اگر منفی باشد، خط در حال کاهش است.

ما دو خط صعودی داریم - در نقطه A و D. حالا بیایید به یاد بیاوریم که مقدار ضریب k به چه معناست؟

ضریب k نشان می دهد که تابع با چه سرعتی افزایش یا کاهش می یابد (در واقع ضریب k خود مشتق تابع y = kx + b است).

بنابراین، k \u003d 2/3 مربوط به یک خط مستقیم ملایم تر - D و k \u003d 3 - A است.

به طور مشابه، در مورد مقادیر منفی: نقطه B مربوط به یک خط مستقیم تندتر با k = -4، و نقطه C - -1/2 است.

گزینه 14MB5

در شکل، نقاط، حجم فروش ماهانه بخاری در یک فروشگاه لوازم خانگی را نشان می دهد. ماه ها به صورت افقی نشان داده شده است، تعداد بخاری های فروخته شده به صورت عمودی نشان داده شده است. برای وضوح، نقاط با یک خط به هم متصل می شوند.

با استفاده از شکل، هر یک از دوره های زمانی مشخص شده را با ویژگی های فروش بخاری مطابقت دهید.

الگوریتم اجرا

بخش های نمودار مربوط به فصول مختلف را تجزیه و تحلیل می کنیم. ما موقعیت های نمایش داده شده در نمودار را فرمول بندی می کنیم. ما مناسب ترین پاسخ ها را برای آنها پیدا می کنیم.

راه حل:

در زمستان، تعداد فروش بیش از 120 قطعه در ماه بود و همیشه در حال افزایش است. این وضعیت با پاسخ 3 مطابقت دارد. آن ها ما گرفتیم: الف-3.

در بهار، فروش به تدریج از 120 بخاری در ماه به 50 کاهش یافت. گزینه شماره 2 به این فرمول نزدیکتر است. ما داریم: B-2.

در تابستان تعداد فروش تغییری نکرد و حداقل بود. قسمت 2 این عبارت در پاسخ ها منعکس نشده است و فقط شماره 4 برای اولی مناسب است. از این رو داریم: در ساعت 4.

در پاییز، فروش افزایش یافت، اما تعداد آنها در هیچ یک از ماه ها از 100 قطعه تجاوز نکرد. این وضعیت در گزینه شماره 1 توضیح داده شده است. ما گرفتیم: G–1.

گزینه 14MB6

نمودار وابستگی سرعت یک اتوبوس معمولی به زمان را نشان می دهد. محور عمودی سرعت اتوبوس را بر حسب کیلومتر در ساعت نشان می دهد، محور افقی زمان را بر حسب دقیقه از شروع اتوبوس نشان می دهد.

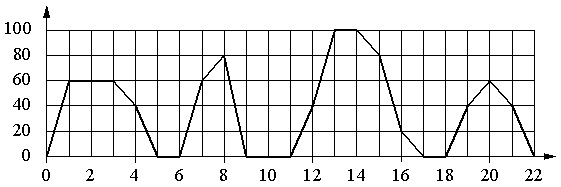
با استفاده از نمودار، هر بازه زمانی را با مشخصه حرکت اتوبوس در این بازه مطابقت دهید.

الگوریتم اجرا

1. ما قیمت تقسیم را در مقیاس افقی و عمودی تعیین می کنیم.
2. ما به نوبه خود عبارات پیشنهادی 1-4 را از ستون سمت راست ("ویژگی ها") تجزیه و تحلیل می کنیم. ما آنها را با فواصل زمانی از ستون سمت چپ جدول مقایسه می کنیم، جفت "حرف-عدد" را برای پاسخ پیدا می کنیم.

راه حل:

مقدار تقسیم مقیاس افقی 1 ثانیه، مقیاس عمودی 20 کیلومتر در ساعت است.

1. وقتی اتوبوس می ایستد سرعتش 0 است. 2 دقیقه پشت سر هم اتوبوس فقط از دقیقه 9 تا 11 صفر بود. این زمان در فاصله 8 تا 12 دقیقه قرار می گیرد. بنابراین ما یک زوج برای پاسخ داریم: B-1.
2. سرعت اتوبوس برای چندین دوره زمانی 20 کیلومتر در ساعت یا بیشتر بود. علاوه بر این، گزینه A در اینجا مناسب نیست، زیرا به عنوان مثال، در دقیقه 7 سرعت 60 کیلومتر در ساعت بود، گزینه B - زیرا قبلا اعمال شده است، گزینه D - زیرا در ابتدا و انتهای فاصله اتوبوس سرعت صفر داشت در این مورد، گزینه B مناسب است (12-16 دقیقه). در این فاصله، اتوبوس با سرعت 40 کیلومتر در ساعت شروع به حرکت می کند، سپس به سرعت 100 کیلومتر بر متر می رسد و به تدریج سرعت را به 20 کیلومتر در ساعت کاهش می دهد. بنابراین ما داریم: در 2.
3. اینجاست که محدودیت سرعت تعیین می شود. ما گزینه های B و C را در نظر نمی گیریم. بازه های باقی مانده A و G هر دو مناسب هستند. بنابراین، درست است که ابتدا گزینه 4 را در نظر بگیرید و دوباره به گزینه 3 برگردید.
4. از دو بازه باقیمانده، تنها 4 تا 8 دقیقه برای مشخصه شماره 4 مناسب است، زیرا در این فاصله (در دقیقه 6) توقف وجود داشت. در فاصله 18 تا 22 دقیقه هیچ توقفی وجود نداشت. ما گرفتیم: الف-4. از این نتیجه می شود که برای مشخصه شماره 3 لازم است که فاصله Г، یعنی. معلوم می شود یک زوج G–3.

گزینه 14MB7

شکل نقطه چین رشد جمعیت چین را از سال 2004 تا 2013 نشان می دهد. سال به صورت افقی نشان داده شده است، رشد جمعیت به عنوان درصد (افزایش جمعیت نسبت به سال قبل) به صورت عمودی نشان داده شده است. برای وضوح، نقاط با یک خط به هم متصل می شوند.

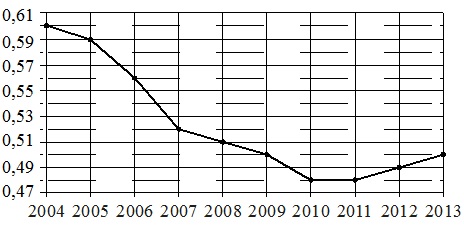
با استفاده از نمودار، هر یک از دوره های زمانی مشخص شده را با ویژگی رشد جمعیت چین در این دوره مطابقت دهید..

الگوریتم اجرا

1. مقدار تقسیم مقیاس عمودی تصویر را تعیین کنید. به عنوان تفاوت بین یک جفت مقادیر مقیاس مجاور تقسیم بر 2 یافت می شود (زیرا بین دو مقدار مجاور 2 تقسیم وجود دارد).
2. ما ویژگی های 1-4 را به صورت متوالی در شرایط (ستون جدول سمت چپ) ارائه می کنیم. ما هر یک از آنها را با یک دوره زمانی خاص (ستون جدول سمت راست) مقایسه می کنیم.

راه حل:

مقدار تقسیم مقیاس عمودی 0.01٪ است.

1. کاهش رشد به طور مداوم از سال 2004 تا 2010 ادامه یافت. در سال 2010-2011، این افزایش به طور مداوم حداقل بود و از سال 2012 شروع به افزایش کرد. آن ها رشد در سال 2010 متوقف شد. امسال در دوره 2009-2011 است. بر این اساس داریم: در 1.
2. بزرگترین افت در رشد را باید "تند"ترین خط سقوط نمودار در نظر گرفت. مربوط به دوره 2006-2007 است. و 0.04% در سال است (0.59–0.56=0.04% در سال 2006 و 0.56–0.52=0.04% در سال 2007). از اینجا دریافت می کنیم: الف-2.
3. رشد نشان داده شده در مشخصه شماره 3 در سال 2007 آغاز شد، در سال 2008 ادامه یافت و در سال 2009 به پایان رسید. این مربوط به دوره زمانی B است، یعنی. ما داریم: B-3.
4. رشد جمعیت پس از سال 2011 شروع به افزایش کرد، یعنی. در سال 2012-2013 بنابراین دریافت می کنیم: G-4.

گزینه 14MB8

شکل یک نمودار تابع و مماس های کشیده شده روی آن را در نقاطی با ابسیساهای A، B، C و D نشان می دهد.

ستون سمت راست مقادیر مشتق تابع را در نقاط A، B، C و D نشان می دهد. با استفاده از نمودار، هر نقطه را با مقدار مشتق تابع در آن مطابقت دهید.

الگوریتم اجرا

1. ما یک جفت مماس را در نظر می گیریم که زاویه تند با جهت مثبت محور x دارند. ما آنها را مقایسه می کنیم، بین جفت مقادیر متناظر مشتقات مطابقت پیدا می کنیم.
2. ما یک جفت مماس را در نظر می گیریم که یک زاویه منفرد را با جهت مثبت محور x تشکیل می دهند. ما آنها را با مدول مقایسه می کنیم، مطابقت را با مقادیر مشتقات آنها در بین دو باقی مانده در ستون سمت راست تعیین می کنیم.

راه حل:

یک زاویه حاد با جهت مثبت محور x توسط مشتقات در t.B و t.C تشکیل می شود. این مشتقات دارای مقادیر مثبت هستند. بنابراین، در اینجا باید بین مقادیر شماره 1 و 3 انتخاب شود. با استفاده از این قانون که اگر زاویه کمتر از 45 0 باشد، مشتق کمتر از 1 است و اگر بیشتر باشد، بیشتر از 1 است. نتیجه می گیریم: در tB، مشتق مدول بزرگتر از 1 در t.C - کمتر از 1 است. این بدان معنی است که می توانید برای پاسخ جفت ایجاد کنید: در 3و S-1.

مشتقات در t.A و t.D یک زاویه منفرد با جهت مثبت محور x تشکیل می دهند. و در اینجا ما همان قانون را اعمال می کنیم و کمی آن را بازنویسی می کنیم: هرچه مماس در نقطه به خط محور آبسیسا (به جهت منفی آن) "فشار" شود، قدر مطلق آن بیشتر است. سپس دریافت می کنیم: مشتق در نقطه A از نظر قدر مطلق کمتر از مشتق در نقطه D است. از اینجا ما جفت هایی برای پاسخ داریم: الف-2و D-4.

گزینه 14MB9

نقاط در شکل میانگین دمای هوای روزانه مسکو را در ژانویه 2011 نشان می دهد. تاریخ های ماه به صورت افقی نشان داده شده است، درجه حرارت بر حسب درجه سانتیگراد به صورت عمودی نشان داده شده است. برای وضوح، نقاط با یک خط به هم متصل می شوند.

با استفاده از شکل، هر یک از دوره های زمانی مشخص شده را با یک مشخصه تغییر دما مطابقت دهید.

الگوریتم اجرا

ما به طور متوالی ویژگی های 1-4 (ستون سمت راست) را با استفاده از نمودار در شکل تجزیه و تحلیل می کنیم. هر کدام را در یک بازه زمانی خاص قرار می دهیم (ستون سمت چپ).

راه حل:

1. افزایش دما تنها در پایان دوره در 22 تا 28 ژانویه مشاهده شد. اینجا در 27 و 28 به ترتیب 1 و 2 درجه افزایش یافت. در پایان دوره در 1-7 ژانویه، دما پایدار بود (10- درجه)، در پایان 8-14 ژانویه و 15-21 ژانویه کاهش یافت (از 1- به -2 و از -11 به -12-). به ترتیب). بنابراین دریافت می کنیم: G–1.
2. از آنجایی که هر دوره زمانی 7 روز را شامل می شود، دما باید از روز چهارم هر دوره تجزیه و تحلیل شود. دما فقط از 4 تا 7 ژانویه به مدت 3-4 روز بدون تغییر باقی ماند. پس جواب میگیریم: الف-2.
3. حداقل دمای ماهانه در 17 ژانویه مشاهده شد. این عدد در بازه زمانی 15 تا 21 ژانویه قرار دارد. از اینجا ما یک زوج داریم: در 3.
4. حداکثر دما در 10 ژانویه کاهش یافت و به +1 درجه رسید. این تاریخ در بازه زمانی 8 تا 14 ژانویه قرار دارد. بنابراین ما داریم: ب-4.

گزینه 14MB10

الگوریتم اجرا

1. اگر این نقطه بالای محور Ox قرار گیرد، مقدار تابع در یک نقطه مثبت است.
2. مشتق در یک نقطه بزرگتر از صفر است اگر مماس به آن نقطه یک زاویه تند با جهت مثبت محور x تشکیل دهد.

راه حل:

نقطه A. زیر محور Ox است، یعنی مقدار تابع در آن منفی است. اگر یک مماس در آن رسم کنیم، زاویه بین آن و جهت مثبت Ox حدود 90 0 خواهد بود، یعنی. یک زاویه حاد تشکیل می دهد. بنابراین، در این مورد، مشخصه شماره 3 مناسب است. آن ها ما داریم: الف-3.

نقطه B. در بالای محور Ox قرار دارد، i.e. نقطه دارای مقدار تابع مثبت است. مماس در این نقطه کاملاً نزدیک به محور آبسیسا خواهد بود و زاویه ای مبهم (کمی کمتر از 180 0) با جهت مثبت آن تشکیل می دهد. بر این اساس، مشتق در این نقطه منفی است. بنابراین، مشخصه 1 در اینجا مناسب است. پاسخ را دریافت می کنیم: در 1.

نقطه C. نقطه در زیر محور Ox قرار دارد، مماس در آن یک زاویه منفرد بزرگ با جهت مثبت محور آبسیسا تشکیل می دهد. آن ها در t.C مقدار تابع و مشتق هر دو منفی است که با مشخصه شماره 2 مطابقت دارد. پاسخ: S-2.

نقطه D. نقطه بالای محور Ox قرار دارد و مماس موجود در آن یک زاویه تند با جهت مثبت محور تشکیل می دهد. این نشان می دهد که هم مقدار تابع و هم مقدار مشتق در اینجا بزرگتر از صفر هستند. پاسخ: D-4.

گزینه 14MB11

در شکل نقطه ها حجم فروش ماهیانه یخچال در یک فروشگاه لوازم خانگی را نشان می دهد. ماه ها به صورت افقی نشان داده شده است، تعداد یخچال های فروخته شده به صورت عمودی نشان داده شده است. برای وضوح، نقاط با یک خط به هم متصل می شوند.

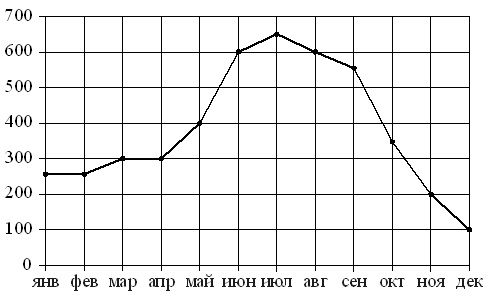
با استفاده از شکل، هر یک از بازه های زمانی مشخص شده را با ویژگی های فروش یخچال مطابقت دهید.

ابتدا سعی کنید محدوده تابع را پیدا کنید:

توانستی مدیریت کنی؟ بیایید پاسخ ها را با هم مقایسه کنیم:

خیلی خوب؟ آفرین!

حالا بیایید سعی کنیم محدوده تابع را پیدا کنیم:

پیدا شد؟ مقایسه کنید:

موافق بود؟ آفرین!

بیایید دوباره با نمودارها کار کنیم، فقط اکنون کمی دشوارتر است - یافتن دامنه تابع و محدوده تابع.

چگونه دامنه و محدوده یک تابع را پیدا کنیم (پیشرفته)

این چیزی است که اتفاق افتاد:

با گرافیک فکر کنم متوجه شدید. حالا بیایید سعی کنیم دامنه تابع را مطابق با فرمول ها پیدا کنیم (اگر نمی دانید چگونه این کار را انجام دهید، بخش مربوط به آن را بخوانید):

توانستی مدیریت کنی؟ چک کردن پاسخ می دهد:

1. ، زیرا عبارت ریشه باید بزرگتر یا مساوی صفر باشد.
2. ، از آنجایی که تقسیم بر صفر غیرممکن است و عبارت رادیکال نمی تواند منفی باشد.
3. ، از آنجا که، به ترتیب، برای همه.
4. چون نمیشه بر صفر تقسیم کرد

با این حال، هنوز یک لحظه دیگر داریم که مرتب نشده است ...

اجازه دهید تعریف را تکرار کنم و روی آن تمرکز کنم:

متوجه شدید؟ کلمه "فقط" یک عنصر بسیار بسیار مهم در تعریف ما است. من سعی خواهم کرد به شما در انگشتان دست توضیح دهم.

فرض کنید تابعی داریم که با خط مستقیم داده می شود. . وقتی، این مقدار را با "قاعده" خود جایگزین می کنیم و آن را دریافت می کنیم. یک مقدار با یک مقدار مطابقت دارد. ما حتی می‌توانیم جدولی از مقادیر مختلف بسازیم و یک تابع مشخص را برای تأیید آن رسم کنیم.

"نگاه کن! - شما می گویید، - "" دو بار ملاقات می کند!" پس شاید سهمی تابع نیست؟ نه، این است!

اینکه "" دو بار اتفاق بیفتد دلیلی برای متهم کردن سهمی به ابهام نیست!

واقعیت این است که هنگام محاسبه برای، ما یک بازی دریافت کردیم. و هنگام محاسبه با، یک بازی گرفتیم. پس درست است، سهمی یک تابع است. به نمودار نگاه کن:

فهمیدم؟ اگر نه، در اینجا یک مثال واقعی برای شما وجود دارد، به دور از ریاضیات!

فرض کنید ما گروهی از متقاضیان داریم که هنگام ارائه مدارک با یکدیگر ملاقات کردند و هر یک از آنها در گفتگویی به محل زندگی خود گفتند:

موافقم، کاملاً واقع بینانه است که چندین پسر در یک شهر زندگی می کنند، اما غیرممکن است که یک نفر همزمان در چندین شهر زندگی کند. این، همانطور که بود، یک نمایش منطقی از "پارابولا" ما است - چندین x مختلف با y یکسان مطابقت دارند.

حالا بیایید مثالی بیاوریم که در آن وابستگی یک تابع نیست. فرض کنید همین بچه ها گفتند برای چه تخصص هایی درخواست داده اند:

در اینجا وضعیت کاملاً متفاوتی داریم: یک نفر به راحتی می تواند برای یک یا چند جهت درخواست دهد. یعنی یک عنصرمجموعه ها در مکاتبات قرار می گیرند عناصر متعددمجموعه ها به ترتیب، این یک تابع نیست.

بیایید دانش خود را در عمل آزمایش کنیم.

از روی تصاویر مشخص کنید که یک تابع چیست و چه چیزی نیست:

فهمیدم؟ و اینجاست پاسخ می دهد:

• تابع - B، E است.
• تابع نیست - A، B، D، D.

می پرسی چرا؟ بله، این دلیل است:

در تمام ارقام به جز که در)و E)چندین برای یک وجود دارد!

من مطمئن هستم که اکنون می توانید به راحتی یک تابع را از یک غیر تابع تشخیص دهید، بگویید آرگومان چیست و متغیر وابسته چیست و همچنین محدوده آرگومان و محدوده تابع را تعیین کنید. بیایید به بخش بعدی برویم - چگونه یک تابع را تعریف کنیم؟

راه های تنظیم یک تابع

به نظر شما معنی کلمات چیست؟ "تنظیم تابع"? درست است، یعنی برای همه توضیح دهید که در این مورد از چه عملکردی صحبت می کنیم. ضمناً طوری توضیح دهید که همه شما را به درستی درک کنند و نمودار توابع ترسیم شده توسط افراد طبق توضیحات شما یکسان بود.

چطور می توانم آن را انجام بدهم؟ چگونه یک تابع تنظیم کنیم؟ساده ترین راه، که قبلاً بیش از یک بار در این مقاله استفاده شده است - با استفاده از یک فرمولیک فرمول می نویسیم و با جایگزین کردن یک مقدار در آن مقدار را محاسبه می کنیم. و همانطور که به یاد دارید، فرمول یک قانون است، قاعده ای که طبق آن برای ما و شخص دیگری روشن می شود که چگونه X به Y تبدیل می شود.

معمولاً این دقیقاً همان کاری است که آنها انجام می دهند - در وظایف ما توابع آماده را می بینیم که با فرمول ها تعریف شده اند ، با این حال ، راه های دیگری برای تنظیم یک تابع وجود دارد که همه آن را فراموش می کنند و بنابراین سؤال "چگونه می توانید یک تابع را تنظیم کنید؟" گیج می کند. بیایید همه چیز را به ترتیب بررسی کنیم و با روش تحلیلی شروع کنیم.

روش تحلیلی برای تعریف یک تابع

روش تحلیلی وظیفه یک تابع با استفاده از فرمول است. این جهانی ترین و جامع ترین و بی ابهام ترین راه است. اگر یک فرمول دارید، پس کاملاً همه چیز را در مورد تابع می دانید - می توانید جدولی از مقادیر روی آن درست کنید، می توانید یک نمودار بسازید، تعیین کنید که در کجا تابع افزایش می یابد و کجا کاهش می یابد، به طور کلی، آن را بررسی کنید. تمام و کمال.

بیایید یک تابع را در نظر بگیریم. چه اهمیتی دارد؟

"چه مفهومی داره؟" - تو پرسیدی. الان توضیح میدم

یادآوری می کنم که در علامت گذاری به عبارت داخل پرانتز آرگومان می گویند. و این استدلال می تواند هر بیانی باشد، نه لزوما ساده. بر این اساس، آرگومان هر چه باشد (بیان داخل پرانتز)، به جای آن در عبارت می نویسیم.

در مثال ما، به این صورت خواهد بود:

وظیفه دیگری را در رابطه با روش تحلیلی تعیین تابعی که در امتحان خواهید داشت در نظر بگیرید.

مقدار عبارت را در پیدا کنید.

مطمئنم که اولش با دیدن چنین تعبیری ترسیدی، اما مطلقاً هیچ چیز ترسناکی در آن نیست!

همه چیز مانند مثال قبلی است: هر آرگومان (بیان در پرانتز)، به جای آن در عبارت می نویسیم. به عنوان مثال، برای یک تابع.

در مثال ما چه باید کرد؟ در عوض، باید بنویسید و به جای -:

عبارت حاصل را کوتاه کنید:

همین!

کار مستقل

حال سعی کنید معنی عبارات زیر را خودتان پیدا کنید:

1. ، اگر
2. ، اگر

توانستی مدیریت کنی؟ بیایید پاسخ های خود را با هم مقایسه کنیم: ما به این واقعیت عادت کرده ایم که تابع دارای فرم باشد

حتی در مثال های خود ما تابع را به این صورت تعریف می کنیم، اما از نظر تحلیلی می توان مثلاً تابع را به صورت ضمنی تعریف کرد.

سعی کنید خودتان این تابع را بسازید.

توانستی مدیریت کنی؟

در اینجا نحوه ساخت من است.

به چه معادله ای رسیدیم؟

درست! خطی، به این معنی که نمودار یک خط مستقیم خواهد بود. بیایید جدولی درست کنیم تا مشخص کنیم کدام نقاط متعلق به خط ما هستند:

این فقط همان چیزی است که ما در مورد آن صحبت می کردیم ... یکی با چندین مطابقت دارد.

بیایید سعی کنیم آنچه را که اتفاق افتاد ترسیم کنیم:

آیا چیزی که به دست آوردیم تابعی است؟

درست است، نه! چرا؟ سعی کنید با تصویر به این سوال پاسخ دهید. چی به دست آوردی؟

"زیرا یک مقدار با چندین مقدار مطابقت دارد!"

از این چه نتیجه ای می توانیم بگیریم؟

درست است، یک تابع همیشه نمی تواند به صراحت بیان شود، و چیزی که به عنوان یک تابع "تبدیل" می شود همیشه یک تابع نیست!

روش جدولی برای تعریف یک تابع

همانطور که از نام آن پیداست، این روش یک بشقاب ساده است. بله بله. مثل اونی که قبلا درست کردیم مثلا:

در اینجا بلافاصله متوجه یک الگو شدید - Y سه برابر بزرگتر از X است. و اکنون وظیفه "خیلی خوب فکر کن": آیا به نظر شما تابعی که به شکل جدول داده می شود معادل یک تابع است؟

بیایید زیاد حرف نزنیم، اما بکشیم!

بنابراین. تابعی را که به هر دو صورت داده شده رسم می کنیم:

آیا تفاوت را میبینید؟ در مورد نقاط مشخص شده نیست! نگاه دقیقتری بینداز:

الان دیدی؟ وقتی تابع را به صورت جدولی تنظیم می کنیم، فقط نقاطی را که در جدول داریم در نمودار منعکس می کنیم و خط (مانند مورد ما) فقط از آنها عبور می کند. وقتی یک تابع را به صورت تحلیلی تعریف می کنیم، می توانیم هر نقطه ای را بگیریم و عملکرد ما محدود به آنها نیست. در اینجا چنین ویژگی وجود دارد. یاد آوردن!

روش گرافیکی برای ساخت یک تابع

روش گرافیکی ساخت یک تابع کمتر راحت نیست. ما تابع خود را رسم می کنیم و شخص دیگری که علاقه مند است می تواند معادل y در x معینی را پیدا کند و غیره. روش های گرافیکی و تحلیلی از رایج ترین روش ها هستند.

با این حال، در اینجا باید آنچه را که در همان ابتدا در مورد آن صحبت کردیم به خاطر بسپارید - هر "squiggle" کشیده شده در سیستم مختصات یک تابع نیست! به یاد آورد؟ در هر صورت، من تعریف تابع چیست را اینجا کپی می کنم:

به عنوان یک قاعده، مردم معمولاً دقیقاً آن سه روش را برای تعیین یک تابع که تجزیه و تحلیل کرده‌ایم نام می‌برند - تحلیلی (با استفاده از فرمول)، جدولی و گرافیکی، کاملاً فراموش می‌کنند که یک تابع را می‌توان به صورت شفاهی توصیف کرد. مثل این؟ بله، خیلی راحت!

شرح شفاهی عملکرد

چگونه عملکرد را به صورت شفاهی توصیف کنیم؟ بیایید مثال اخیر خود را در نظر بگیریم - . این تابع را می توان به صورت "هر مقدار واقعی x با مقدار سه گانه آن مطابقت دارد" توصیف کرد. همین. هیچ چیز پیچیده ای نیست. البته، شما اعتراض خواهید کرد - "چنین توابع پیچیده ای وجود دارد که تنظیم شفاهی آنها به سادگی غیرممکن است!" بله، تعدادی وجود دارد، اما توابعی وجود دارد که توصیف شفاهی آنها آسان تر از تنظیم کردن با یک فرمول است. به عنوان مثال: "هر مقدار طبیعی x مربوط به تفاوت بین ارقامی است که از آن تشکیل شده است، در حالی که بزرگترین رقم موجود در ورودی عدد به عنوان minuend در نظر گرفته می شود." حال در نظر بگیرید که چگونه توصیف شفاهی ما از تابع در عمل پیاده سازی می شود:

بزرگترین رقم در یک عدد معین - به ترتیب - کاهش می یابد، سپس:

انواع اصلی توابع

حالا بیایید به جالب ترین ها برویم - انواع اصلی توابعی را که با آنها کار کردید / کار می کنید و در دوره مدرسه و ریاضیات مؤسسه کار خواهید کرد را در نظر خواهیم گرفت ، یعنی به اصطلاح با آنها آشنا خواهیم شد و به آنها توضیح مختصری بدهید در مورد هر تابع در بخش مربوطه بیشتر بخوانید.

تابع خطی

تابعی از فرم، که در آن، اعداد واقعی هستند.

نمودار این تابع یک خط مستقیم است، بنابراین ساخت یک تابع خطی به یافتن مختصات دو نقطه کاهش می یابد.

موقعیت خط مستقیم در صفحه مختصات به شیب بستگی دارد.

محدوده تابع (معروف به محدوده آرگومان) - .

محدوده مقادیر است.

تابع درجه دوم

تابع فرم، جایی که

نمودار تابع یک سهمی است، زمانی که شاخه های سهمی به سمت پایین، زمانی که - به سمت بالا هستند.

بسیاری از ویژگی های یک تابع درجه دوم به مقدار تفکیک کننده بستگی دارد. تفکیک کننده با فرمول محاسبه می شود

موقعیت سهمی در صفحه مختصات نسبت به مقدار و ضریب در شکل نشان داده شده است:

دامنه

محدوده مقادیر به حداکثر تابع داده شده (راس سهمی) و ضریب (جهت شاخه های سهمی) بستگی دارد.

نسبت معکوس

تابعی که با فرمول، Where

به این عدد ضریب تناسب معکوس می گویند. بسته به مقدار، شاخه های هذلولی در مربع های مختلفی قرار دارند:

دامنه - .

محدوده مقادیر است.

خلاصه و فرمول اساسی

1. تابع قاعده ای است که بر اساس آن به هر عنصر از مجموعه یک عنصر منحصر به فرد از مجموعه اختصاص می یابد.

• - این فرمولی است که یک تابع را نشان می دهد، یعنی وابستگی یک متغیر به متغیر دیگر.
• - متغیر یا آرگومان؛
• - مقدار وابسته - با تغییر آرگومان تغییر می کند، یعنی طبق فرمول خاصی که وابستگی یک مقدار به مقدار دیگر را منعکس می کند.

2. مقادیر آرگومان معتبر، یا محدوده یک تابع، چیزی است که به امکانی مربوط می شود که تابع تحت آن معنا پیدا می کند.

3. محدوده مقادیر تابع- این همان مقادیری است که می گیرد، با مقادیر معتبر.

4. 4 راه برای تنظیم تابع وجود دارد:

• تحلیلی (با استفاده از فرمول ها)؛
• جدولی
• گرافیکی
• توصیف شفاهی

5. انواع اصلی توابع:

• : ، جایی که، اعداد واقعی هستند.
• : ، جایی که؛
• : ، جایی که.