Online-Rechner Limit-Lösung. Online-Limitlösung

Die Regel von L'Hôpital (S. L.) erleichtert die Berechnung der Funktionsgrenzen. Sie müssen beispielsweise den Grenzwert einer Funktion finden, der das Verhältnis von Funktionen gegen Null ist. Jene. die Funktionsbeziehung ist 0/0 Unsicherheit. Es wird helfen, es aufzudecken. Im Grenzfall kann das Verhältnis der Funktionen durch das Verhältnis der Ableitungen dieser Funktionen ersetzt werden. Jene. es ist notwendig, die Ableitung des Zählers durch die Ableitung des Nenners zu dividieren und den Grenzwert von diesem Bruch zu nehmen.

1. Unsicherheit 0/0. Erster Artikel L.

Wenn = 0, dann wenn letzteres vorhanden ist.

2. Unsicherheit der Form ∞ / ∞ Zweiter Sek. L.

Das Auffinden von Grenzen dieser Art wird als Offenlegung von Unsicherheiten bezeichnet.

Wenn = ∞, dann wenn letzteres existiert.

3. Die Unsicherheiten 0⋅∞, ∞- ∞, 1 ∞ und 0 0 werden durch Transformationen auf die Unsicherheiten 0/0 und ∞ / ∞ reduziert. Dieser Eintrag dient als kurzer Hinweis auf den Fall beim Finden des Limits. Jede Unsicherheit offenbart sich auf ihre Weise. Die Regel von L'Hôpital kann mehrmals angewendet werden, bis wir die Unsicherheit loswerden. Die Anwendung der Regel von L'Hôpital ist sinnvoll, wenn das Verhältnis der Ableitungen leichter in eine bequemere Form umgewandelt werden kann als das Verhältnis der Funktionen.

0⋅∞ ist das Produkt zweier Funktionen, die erste geht gegen Null, die zweite gegen Unendlich;
∞- ∞ ist die Differenz von Funktionen, die ins Unendliche tendiert;
1 ∞ Grad, seine Basis geht gegen eins und der Exponent geht gegen unendlich;
∞ 0 Grad, seine Basis geht gegen Unendlich und der Grad gegen Null;
0 0 Grad, seine Basis geht gegen 0 und der Exponent geht ebenfalls gegen null.

Beispiel 1. In diesem Beispiel beträgt die Unsicherheit 0/0

Beispiel 2. Hier ∞ / ∞

In diesen Beispielen dividieren wir die Ableitungen des Zählers durch die Ableitungen des Nenners und setzen den Grenzwert für x ein.

Beispiel 3. Art der Unsicherheit 0⋅∞ .

Wir transformieren die Unsicherheit 0⋅∞ in ∞ / ∞, übertragen dazu x als Bruch 1 / x auf den Nenner, schreiben die Ableitung des Zählers in den Zähler und die Ableitung des Nenners in den Nenner.

Beispiel 4 Berechnen Sie den Grenzwert einer Funktion

Hier ist die Unsicherheit der Form ∞ 0 Zuerst logarithmieren wir die Funktion, dann finden wir den Grenzwert daraus

Um die Antwort zu erhalten, müssen Sie e mit -1 potenzieren, wir erhalten e -1.

Beispiel 5. Berechnen Sie den Grenzwert von, wenn x → 0

Lösung. Unsicherheitstyp ∞ -∞ Wenn wir den Bruch auf einen gemeinsamen Nenner reduzieren, gehen wir von ∞-∞ zu 0/0 über. Wir wenden die Regel von L'Hôpital an, erhalten aber wieder eine Unsicherheit von 0/0, sodass L. ein zweites Mal angewendet werden muss. Die Lösung sieht so aus:

= = = =
= =

Beispiel 6 Lösen

Lösung. Die Art der Unsicherheit ist ∞ / ∞, beim Öffnen erhalten wir

In den Fällen 3), 4), 5) wird zunächst die Funktion logarithmiert und der Grenzwert des Logarithmus gefunden und dann der gesuchte Grenzwert e potenziert.

Beispiel 7. Berechnen Sie den Grenzwert

Lösung. Hier beträgt die Unsicherheit 1 ∞. Wir bezeichnen A =

Dann ist lnA = = = = 2.

Die Basis des Logarithmus ist e. Um also die Antwort zum Quadrat von e zu erhalten, erhalten wir e 2.

Manchmal gibt es Fälle, in denen das Verhältnis von Funktionen eine Grenze hat, im Gegensatz zum Verhältnis von Ableitungen, die dies nicht tut.

Betrachten wir ein Beispiel:

Weil sinx ist beschränkt und x wächst unbegrenzt, der zweite Term ist 0.

Diese Funktion ist unbegrenzt, da er schwankt ständig zwischen 0 und 2, p.L. ist auf dieses Beispiel nicht anwendbar.

Angabe von Unsicherheiten der Form 0/0 oder ∞ / ∞ und einiger anderer Unsicherheiten, die sich bei der Berechnung ergeben Grenze die Beziehung zweier infinitesimaler oder unendlich großer Funktionen wird mit Hilfe der Regel von L'Hôpital (eigentlich zwei Regeln und Bemerkungen dazu) stark vereinfacht.

Die Essenz Die Regeln von L'Hôpital ist, dass für den Fall, dass die Berechnung des Grenzwertes der Verhältnisse zweier infinitesimaler oder unendlich großer Funktionen Unsicherheiten der Form 0/0 oder ∞ / ergibt, der Grenzwert des Verhältnisses zweier Funktionen durch den Grenzwert ihrer Verhältnis Derivate und erhalten so ein bestimmtes Ergebnis.

Kommen wir zur Formulierung der Regeln von L'Hôpital.

Regel von L'Hôpital für den Grenzfall zweier infinitesimaler Größen... Wenn Funktionen F(x) und g(x einein, und in dieser Nachbarschaft g"(x ein gleich zueinander und gleich null

().

Regel von L'Hôpital für den Grenzfall zweier unendlich großer Größen... Wenn Funktionen F(x) und g(x) sind in einer Umgebung des Punktes differenzierbar ein, mit Ausnahme des Punktes selbst ein, und in dieser Nachbarschaft g"(x) ≠ 0 und wenn und falls die Grenzen dieser Funktionen als x gegen den Wert der Funktion im Punkt ein gleich zueinander und gleich unendlich

(),

dann ist der Grenzwert des Verhältnisses dieser Funktionen gleich dem Grenzwert des Verhältnisses ihrer Ableitungen

().

Mit anderen Worten, für Unsicherheiten der Form 0/0 oder ∞ / ist die Grenze des Verhältnisses zweier Funktionen gleich der Grenze des Verhältnisses ihrer Ableitungen, falls diese existiert (endlich oder unendlich).

Bemerkungen.

1. Die Regeln von L'Hôpital gelten auch, wenn die Funktionen F(x) und g(x) sind nicht definiert für x = ein.

2. Wenn bei der Berechnung der Grenze des Verhältnisses der Ableitungen von Funktionen F(x) und g(x) kommen wir wieder zu einer Unsicherheit der Form 0/0 oder ∞ / ∞, dann sollten die Regeln von L'Hôpital mehrfach (mindestens zweimal) angewendet werden.

3. Die Regeln von L'Hôpital sind auch anwendbar, wenn das Argument der Funktionen (x) nicht gegen eine endliche Zahl strebt ein, und bis unendlich ( x → ∞).

Unsicherheiten anderer Typen können auch auf Unsicherheiten von 0/0- und ∞ / ∞-Typen reduziert werden.

Offenlegung von Unsicherheiten der Typen "Null geteilt durch Null" und "Unendlich geteilt durch Unendlich"

Beispiel 1.

x= 2 ergibt eine Unsicherheit der Form 0/0. Daher ist die Ableitung jeder Funktion und wir erhalten

Die Ableitung des Polynoms wurde im Zähler berechnet und im Nenner - Ableitung einer komplexen logarithmischen Funktion... Vor dem letzten Gleichheitszeichen das übliche Grenze, ersetzt zwei statt x.

Beispiel 2. Berechnen Sie die Grenze des Verhältnisses zweier Funktionen mit der Regel von L'Hôpital:

Lösung. Einsetzen eines Wertes in eine gegebene Funktion x

Beispiel 3. Berechnen Sie die Grenze des Verhältnisses zweier Funktionen mit der Regel von L'Hôpital:

Lösung. Einsetzen eines Wertes in eine gegebene Funktion x= 0 ergibt eine Unsicherheit der Form 0/0. Daher berechnen wir die Ableitungen der Funktionen im Zähler und Nenner und erhalten:

Beispiel 4. Berechnung

Lösung. Einsetzen des x-Wertes gleich plus unendlich in die gegebene Funktion führt zu einer Unsicherheit der Form ∞ / ∞. Daher wenden wir die Regel von L'Hôpital an:

Kommentar. Wenden wir uns Beispielen zu, in denen die Regel von L'Hôpital zweimal angewendet werden muss, d. h. um die Grenze der Verhältnisse der zweiten Ableitungen zu erreichen, da die Grenze des Verhältnisses der ersten Ableitungen eine Unsicherheit der Form /0 oder ∞ / ∞.

Wenden Sie die Regel von L'Hôpital selbst an und sehen Sie dann die Lösung

Offenlegung von Unsicherheiten der Form "Null mal Unendlich"

Beispiel 12. Berechnung

Lösung. Wir bekommen

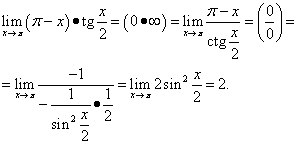
Dieses Beispiel verwendet trigonometrische Identität.

Offenlegung von Unsicherheiten der Typen „Null hoch Null“, „Unendlich hoch Null“ und „Eins hoch Unendlich“

Unsicherheiten der Form, oder werden in der Regel mit dem Logarithmus einer Funktion der Form auf die Form 0/0 oder ∞ / ∞ reduziert

Um den Grenzwert eines Ausdrucks zu berechnen, sollte man die logarithmische Identität verwenden, deren Sonderfall die Eigenschaft des Logarithmus ist .

Unter Verwendung der logarithmischen Identität und der Stetigkeitseigenschaft der Funktion (um das Grenzzeichen zu überschreiten) sollte der Grenzwert wie folgt berechnet werden:

Separat sollten Sie die Ausdrucksgrenze im Exponenten finden und aufbauen e bis zum gefundenen Grad.

Beispiel 13.

Lösung. Wir bekommen

Beispiel 14. Berechnen Sie mit der Regel von L'Hôpital

Lösung. Wir bekommen

Wir berechnen die Ausdrucksgrenze im Exponenten

Beispiel 15. Berechnen Sie mit der Regel von L'Hôpital

Regel von L'Hôpital und Offenlegung von Unsicherheiten
Offenlegung von Unsicherheiten der Typen "Null geteilt durch Null" und "Unendlich geteilt durch Unendlich"
Offenlegung von Unsicherheiten der Form "Null mal Unendlich"
Offenlegung von Unsicherheiten der Typen „Null hoch Null“, „Unendlich hoch Null“ und „Eins hoch Unendlich“
Offenlegung von Unsicherheiten der Form "unendlich minus unendlich"

Regel von L'Hôpital und Offenlegung von Unsicherheiten

Die Angabe von Unsicherheiten der Form 0/0 oder ∞ / ∞ und einiger anderer Unsicherheiten wird mit der L'Hôpital-Regel stark vereinfacht.

Die Essenz Die Regeln von L'Hôpital ist, dass für den Fall, dass die Berechnung des Grenzwertes der Verhältnisse zweier Funktionen Unsicherheiten der Form 0/0 oder ∞ / ergibt, der Grenzwert des Verhältnisses zweier Funktionen durch den Grenzwert des Verhältnisses ihrer Ableitungen ersetzt werden kann und somit kann ein eindeutiges Ergebnis erzielt werden.

Im Allgemeinen bedeuten die L'Hôpital-Regeln mehrere Sätze, die in der nächsten Formulierung vermittelt werden können.

Die Regel von L'Hôpital... Wenn Funktionen F(x) und g(x) sind in einer Umgebung des Punktes differenzierbar, mit Ausnahme vielleicht des Punktes selbst, und in dieser Umgebung

(1)

Bei Gleichheit (1) kann der Wert, zu dem die Variable tendiert, entweder eine endliche Zahl oder unendlich oder minus unendlich sein.

Unsicherheiten anderer Typen können auch auf Unsicherheiten von 0/0- und ∞ / ∞-Typen reduziert werden.

Offenlegung von Unsicherheiten der Typen "Null geteilt durch Null" und "Unendlich geteilt durch Unendlich"

Beispiel 1. Berechnung

x= 2 ergibt eine Unsicherheit der Form 0/0. Daher wenden wir die Regel von L'Hôpital an:

Beispiel 2. Berechnung

Lösung. Einsetzen eines Wertes in eine gegebene Funktion x

Beispiel 3. Berechnung

Lösung. Einsetzen eines Wertes in eine gegebene Funktion x= 0 ergibt eine Unsicherheit der Form 0/0. Daher wenden wir die Regel von L'Hôpital an:

Beispiel 4. Berechnung

Lösung. Einsetzen des x-Wertes gleich plus unendlich in die gegebene Funktion führt zu einer Unsicherheit der Form ∞ / ∞. Daher wenden wir die Regel von L'Hôpital an:

Kommentar. Ist der Grenzwert des Ableitungsverhältnisses eine Unsicherheit der Form 0/0 oder ∞ / ∞, dann kann wieder die L'Hôpital-Regel angewendet werden, d.h. gehen Sie an die Grenze des Verhältnisses der zweiten Ableitungen usw.

Beispiel 5. Berechnung

Lösung. Wir finden

Hier wird die Regel von L'Hôpital zweimal angewendet, da sowohl der Grenzwert des Verhältnisses von Funktionen als auch der Grenzwert des Verhältnisses von Ableitungen eine Unsicherheit der Form ∞ / ergeben.

Beispiel 6. Berechnung

Stellen Sie sich einen Schwarm Spatzen mit hervortretenden Augen vor. Nein, das ist kein Donner, kein Hurrikan oder auch nur ein kleiner Junge mit einer Steinschleuder in der Hand. Es ist nur so, dass eine riesige, riesige Kanonenkugel mitten in die Küken fliegt. Genau so Die Regeln von L'Hôpital mit den Grenzen umgehen, in denen Unsicherheit besteht bzw.

Die Regeln von L'Hôpital sind eine sehr leistungsfähige Methode, mit der Sie die angegebenen Unsicherheiten schnell und effizient beseitigen können. die Regel von L'Hôpital nicht verwenden". Die fett markierte Anforderung kann guten Gewissens auf jede Unterrichtsgrenze zurückgeführt werden. Grenzen. Lösungsbeispiele, Wunderbare Grenzen. Limit-Lösungsmethoden, Bemerkenswerte Äquivalenzen, wo die Unsicherheit "Null bis Null" oder "Unendlich bis Unendlich" angetroffen wird. Auch wenn die Aufgabe kurz formuliert ist – „Berechnen Sie die Grenzen“, wird implizit impliziert, dass Sie alles, alles, aber nicht die Regeln von L'Hôpital verwenden werden.

Es gibt insgesamt zwei Regeln, die sich sowohl im Wesentlichen als auch in der Anwendungsweise sehr ähneln. Neben direkten Beispielen zum Thema werden wir auch zusätzliches Material studieren, das für das weitere Studium der mathematischen Analysis nützlich sein wird.

Ich werde sofort reservieren, dass die Regeln in einer prägnanten "praktischen" Form gegeben werden, und wenn Sie die Theorie bestehen müssen, empfehle ich Ihnen, für genauere Berechnungen das Lehrbuch zu Rate zu ziehen.

Die erste Regel von L'Hôpital

Betrachten Sie die Funktionen, die unendlich klein irgendwann. Wenn es eine Grenze für ihre Beziehung gibt, können Sie, um Unsicherheit zu beseitigen, nehmen zwei Derivate- vom Zähler und vom Nenner. Dabei: , also .

Notiz : die Grenze muss auch vorhanden sein, sonst gilt die Regel nicht.

Was folgt aus obigem?

Zuerst müssen Sie in der Lage sein, zu finden Ableitungen von Funktionen, und je besser - desto besser =)

Zweitens werden Ableitungen SEPARAT vom Zähler und SEPARATE vom Nenner genommen. Bitte nicht mit der Quotientendifferenzierungsregel verwechseln !!!

Und drittens kann "X" überall hinstreben, auch bis ins Unendliche - wenn nur Ungewissheit herrscht.

Gehen wir zurück zu Beispiel 5 des ersten Artikels über die Grenzen, bei dem folgendes Ergebnis erhalten wurde:

Für die 0:0-Unsicherheit gilt die erste L'Hôpital-Regel:

Wie Sie sehen, führte uns die Differenzierung von Zähler und Nenner zu einer halbrunden Antwort: Wir fanden zwei einfache Ableitungen, ersetzten sie durch eine „Zwei“ und es stellte sich heraus, dass die Unsicherheit spurlos verschwand!

Es ist nicht ungewöhnlich, dass die Regeln von L'Hôpital zwei- oder mehrmals hintereinander angewendet werden müssen (dies gilt auch für die zweite Regel). Ziehen wir es für einen Retro-Abend heraus Beispiel 2 Lektion über wunderbare Grenzen:

Auf dem Etagenbett chillen wieder zwei Bagels. Wenden wir die Regel von L'Hôpital an:

Bitte beachten Sie, dass im ersten Schritt der Nenner genommen wird Ableitung einer zusammengesetzten Funktion... Danach führen wir eine Reihe von Vereinfachungen durch, insbesondere entfernen wir den Kosinus, was darauf hindeutet, dass er zur Einheit neigt. Die Unsicherheit wurde nicht beseitigt, daher wenden wir die Regel von L'Hôpital erneut an (zweite Zeile).

Ich habe bewusst nicht das einfachste Beispiel gewählt, damit Sie einen kleinen Selbsttest durchführen können. Wenn nicht ganz klar ist, wie sie gefunden wurden Derivate, sollten Sie Ihre Differenzierungstechnik stärken, wenn der Fokus mit dem Kosinus nicht klar ist, gehen Sie bitte zurück zu wunderbare grenzen... Ich sehe nicht viel Sinn in Schritt-für-Schritt-Kommentaren, da ich bereits ausführlich genug über Derivate und Limits gesprochen habe. Die Neuheit des Artikels liegt in den Regeln selbst und einigen technischen Lösungen.

Wie bereits erwähnt, müssen die Regeln von L'Hôpital in den meisten Fällen nicht verwendet werden, es ist jedoch oft ratsam, sie für eine grobe Überprüfung der Lösung zu verwenden. Oft, aber nicht immer. So ist zum Beispiel das gerade betrachtete Beispiel viel rentabler zu überprüfen wunderbare Äquivalenzen.

Die zweite Regel von L'Hôpital

Bruder 2 kämpft gegen zwei schlafende Achter. Gleichfalls:

Wenn es eine Grenze für die Beziehung gibt unendlich groß am Punkt der Funktionen: Um Unsicherheit zu beseitigen, können Sie zwei Ableitungen- SEPARATE vom Zähler und SEPARATE vom Nenner. Dabei: , also bei Differenzierung von Zähler und Nenner ändert sich der Wert der Grenze nicht.

Notiz : die Grenze muss existieren

Auch hier in verschiedenen Praxisbeispielen die bedeutung kann unterschiedlich sein, einschließlich endlos. Wichtig ist, dass Unsicherheit herrscht.

Schauen wir uns Beispiel Nr. 3 der ersten Lektion an: ... Wir verwenden die zweite Regel von L'Hôpital:

Sobald wir über Riesen sprechen, werden wir zwei kanonische Grenzen analysieren:

Beispiel 1

Limit berechnen

Es ist nicht einfach, mit "üblichen" Methoden eine Antwort zu erhalten, daher verwenden wir zur Offenlegung der Unbestimmtheit "Unendlich zu Unendlich" die Regel von L'Hôpital:

Auf diese Weise, lineare Funktion höherer Wachstumsordnung als Logarithmus mit Basis größer als eins( usw.). Natürlich wird „x“ in höheren Graden auch solche Logarithmen „ziehen“. Tatsächlich wächst die Funktion eher langsam und ihre zeitlicher Ablauf ist im Vergleich zum gleichen "x" flacher.

Beispiel 2

Limit berechnen

Eine weitere bekannte Aufnahme. Um Mehrdeutigkeiten zu beseitigen, verwenden wir außerdem zweimal hintereinander die Regel von L'Hôpital:

Exponentialfunktion mit einer Basis größer als eins( usw.) einer höheren Wachstumsordnung als eine Potenzfunktion mit positivem Grad.

Ähnliche Grenzen werden während Vollfunktionsstudie, nämlich beim Finden Asymptoten von Graphen... Sie fallen auch bei einigen Aufgaben auf Wahrscheinlichkeitstheorie... Ich rate Ihnen, die beiden betrachteten Beispiele zur Kenntnis zu nehmen, dies ist einer der wenigen Fälle, in denen es nichts Besseres gibt, als Zähler und Nenner zu unterscheiden.

Im weiteren Text werde ich nicht zwischen der ersten und der zweiten Regel von L'Hôpital unterscheiden, dies diente nur der Strukturierung des Artikels. Im Allgemeinen ist es aus meiner Sicht etwas schädlich, mathematische Axiome, Theoreme, Regeln, Eigenschaften unnötig zu nummerieren, da Formulierungen wie „nach Korollar 3 bis Theorem 19 ...“ nur im Rahmen eines bestimmten Lehrbuchs informativ sind . In einer anderen Informationsquelle wäre das gleiche "Korollar 2 und Theorem 3". Solche Aussagen sind nur für die Autoren selbst formell und bequem. Im Idealfall ist es am besten, sich auf die Essenz einer mathematischen Tatsache zu beziehen. Ausgenommen sind historisch gewachsene Begriffe, z. erste wunderbare Grenze oder zweite wunderbare grenze.

Wir entwickeln ein Thema weiter, das uns von einem Mitglied der Pariser Akademie der Wissenschaften, Marquis Guillaume François de L'Hôpital, vorgeschlagen wurde. Der Artikel hat eine ausgeprägte praktische Konnotation und wird in einer recht häufigen Aufgabe gefordert:

Zum Aufwärmen beschäftigen wir uns mit ein paar kleinen Spatzen:

Beispiel 3

Die Grenze lässt sich vorab vereinfachen, indem man den Kosinus weglässt, aber Respekt vor der Bedingung und sofort Zähler und Nenner unterscheiden:

Bei der Suche nach Derivaten gibt es nichts Ungewöhnliches, daher im Nenner das Übliche Differenzierungsregel funktioniert .

Das betrachtete Beispiel ist erledigt und danach wunderbare grenzen, ein ähnlicher Fall wird am Ende des Artikels "Schwierige Grenzen" behandelt.

Beispiel 4

Berechnen Sie den Grenzwert nach der Regel von L'Hôpital

Dies ist ein Beispiel für eine Do-it-yourself-Lösung. Witzig gemacht =)

Eine typische Situation ist, wenn nach Differenzierung drei- oder vierstöckige Fraktionen erhalten werden:

Beispiel 5

Berechnen Sie das Limit mit der Regel von L'Hôpital

Die Anwendung liegt nahe bemerkenswerte Gleichwertigkeit, aber der Pfad ist durch die Bedingung fest vorgegeben:

Nach der Differenzierung empfehle ich dringend, den mehrstöckigen Anteil loszuwerden und die maximalen Vereinfachungen vorzunehmen.... Fortgeschrittene können natürlich den letzten Schritt überspringen und gleich schreiben: , aber in gewissen Grenzen werden selbst exzellente Studenten verwirrt.

Beispiel 6

Berechnen Sie das Limit mit der Regel von L'Hôpital

Beispiel 7

Berechnen Sie das Limit mit der Regel von L'Hôpital

Dies sind Beispiele für eine Do-it-yourself-Lösung. In Beispiel 7 lässt sich nichts vereinfachen, der Bruch ist nach der Differenzierung zu einfach. In Beispiel 8 ist es jedoch nach Anwendung der L'Hôpital-Regel sehr wünschenswert, die dreistöckige Struktur loszuwerden, da die Berechnungen nicht die bequemsten sind. Komplette Lösung und Antwort am Ende des Tutorials. Wenn Sie Schwierigkeiten haben - trigonometrische Tabelle helfen.

Und Vereinfachungen sind unbedingt erforderlich, wenn nach der Differenzierung die Unsicherheit nicht beseitigt.

Beispiel 8

Berechnen Sie das Limit mit der Regel von L'Hôpital

Gehen:

Interessanterweise wurde aus der anfänglichen Unsicherheit nach der ersten Differenzierung eine Unsicherheit, und die Regel von L'Hôpital wird ruhig weiter angewendet. Beachten Sie auch, wie nach jedem "Annähern" der vierstöckige Bruch eliminiert wird und die Konstanten außerhalb des Grenzzeichens verschoben werden. In einfacheren Beispielen ist es bequemer, keine Konstanten zu ertragen, aber wenn die Grenze komplex ist, vereinfachen wir alles, alles, alles. Die Heimtücke des gelösten Beispiels liegt auch darin, dass für , a, daher ist es nicht verwunderlich, bei der Beseitigung der Nebenhöhlen in den Zeichen verwirrt zu werden. In der vorletzten Zeile könnten die Nebenhöhlen nicht getötet worden sein, aber das Beispiel ist ziemlich schwierig, verzeihlich.

Neulich bin ich auf eine interessante Aufgabe gestoßen:

Beispiel 9

Um ehrlich zu sein, bezweifelte ich ein wenig, was diese Grenze bedeuten würde. Wie oben gezeigt, hat das „x“ eine höhere Wachstumsordnung als der Logarithmus, aber wird es den Kubus des Logarithmus „ziehen“? Versuchen Sie selbst herauszufinden, wer gewinnen wird.

Ja, die Regeln von L'Hôpital sind nicht nur das Abfeuern von Spatzen aus einer Kanone, sondern auch akribische Arbeit….

Um die Regeln von L'Hôpital anzuwenden, werden die Unsicherheiten der Art auf Bagels oder müde Acht reduziert.

Die Repressalien mit Unsicherheit werden in den Beispielen Nr. 9-13 der Lektion ausführlich besprochen Limit-Lösungsmethoden... Nehmen wir der Form halber noch einen:

Beispiel 10

Berechnen Sie den Grenzwert einer Funktion mit der Regel von L'Hôpital

Im ersten Schritt bringen wir den Ausdruck auf einen gemeinsamen Nenner und verwandeln so Unsicherheit in Unsicherheit. Und dann laden wir die Regel von L'Hôpital:

Hier ist übrigens der Fall, wenn es sinnlos ist, den vierstöckigen Ausdruck zu berühren.

Unsicherheit widersetzt sich auch nicht, in oder:

Beispiel 11

Berechnen Sie den Grenzwert einer Funktion mit der Regel von L'Hôpital

Die Grenze hier ist einseitig, und solche Grenzen wurden bereits im Handbuch besprochen Funktionsgraphen und Eigenschaften... Wie Sie sich erinnern, existiert der Graph des "klassischen" Logarithmus nicht links von der Achse, daher können wir uns nur von rechts an Null annähern.

Die Regeln von L'Hôpital für einseitige Limits funktionieren, aber Sie müssen zuerst mit der Unsicherheit umgehen. Im ersten Schritt machen wir einen dreistöckigen Bruch, erhalten Unsicherheit, dann folgt die Lösung einem Musterschema:

Nach der Differenzierung von Zähler und Nenner entfernen wir zur Vereinfachung den vierstöckigen Bruch. Als Ergebnis wurde Unsicherheit gezogen. Wir wiederholen den Trick: wieder machen wir den Bruch dreistöckig und wenden die L'Hôpital-Regel wieder auf die resultierende Unsicherheit an:

Bereit.

Das ursprüngliche Limit könnte auf zwei Bagels reduziert werden:

Aber erstens ist die Ableitung im Nenner schwieriger und zweitens wird nichts Gutes dabei herauskommen.

Auf diese Weise, Bevor Sie ähnliche Beispiele lösen, müssen Sie analysieren(mündlich oder auf Entwurf) WELCHE Unsicherheit zu reduzieren ist lohnender - auf "Null auf Null" oder auf "Unendlich auf Unendlich".

Im Gegenzug werden Trinkgefährten und exotischere Kameraden ans Licht gezogen. Die Transformationsmethode ist einfach und Standard.