Definition 9.3. Vektor NS namens eigener Vektor Matrizen EIN wenn es so eine nummer gibt λ, diese Gleichheit gilt: EIN NS= λ NS, das heißt, das Ergebnis der Anwendung bei NS lineare Transformation gegeben durch die Matrix EIN, ist die Multiplikation dieses Vektors mit der Zahl λ ... Die Nummer selbst λ namens eigene Nummer Matrizen EIN.

Einsetzen in Formeln (9.3) x`j = λxj, erhalten wir ein Gleichungssystem zur Bestimmung der Koordinaten des Eigenvektors:

. (9.5)

Dieses lineare homogene System hat nur dann eine nichttriviale Lösung, wenn seine Hauptdeterminante 0 ist (Cramersche Regel). Schreiben Sie diese Bedingung in das Formular:

erhalten wir die Gleichung zur Bestimmung der Eigenwerte λ namens charakteristische Gleichung... Es lässt sich kurz wie folgt darstellen:

| A - λE | = 0, (9.6)

da seine linke Seite die Determinante der Matrix enthält A-λE... Polynom bezüglich | A - λE| namens charakteristisches Polynom Matrizen A.

Charakteristische Polynomeigenschaften:

1) Das charakteristische Polynom einer linearen Transformation hängt nicht von der Wahl der Basis ab. Nachweisen. (siehe (9.4)), aber somit, . Es kommt also nicht auf die Wahl der Basis an. Daher und | A-λE| ändert sich beim Wechsel auf eine neue Basis nicht.

2) Wenn die Matrix EIN lineare Transformation ist symmetrisch(jene. und ij = a ji), dann sind alle Wurzeln der charakteristischen Gleichung (9.6) reelle Zahlen.

Eigenschaften von Eigenwerten und Eigenvektoren:

1) Wählen wir eine Basis von Eigenvektoren x 1, x 2, x 3 entsprechend den Eigenwerten 1, 2, 3 Matrizen EIN, dann hat in dieser Basis die lineare Transformation A eine Matrix der Diagonalform:

(9.7) Der Beweis dieser Eigenschaft folgt aus der Definition der Eigenvektoren.

2) Wenn die Eigenwerte der Transformation EIN unterschiedlich sind, dann sind die entsprechenden Eigenvektoren linear unabhängig.

3) Wenn das charakteristische Polynom der Matrix EIN hat drei verschiedene Wurzeln, dann ist in gewisser Weise die Matrix EIN hat eine diagonale Form.

Finden wir die Eigenwerte und Eigenvektoren der Matrix Stellen wir die charakteristische Gleichung zusammen: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Lassen Sie uns die Koordinaten der Eigenvektoren finden, die jedem gefundenen Wert entsprechen λ. Aus (9.5) folgt, dass wenn NS (1) ={x 1, x 2, x 3) Entspricht der Eigenvektor λ 1 = -2, dann

- ein kollaboratives, aber undefiniertes System. Seine Lösung kann geschrieben werden als NS (1) ={ein,0,-ein), wobei a eine beliebige Zahl ist. Insbesondere wenn wir verlangen, dass | x (1) |=1, NS (1) =

Einsetzen in das System (9.5) λ 2 = 3 erhalten wir ein System zur Bestimmung der Koordinaten des zweiten Eigenvektors - x (2) ={y 1, y 2, y 3}:

, wo NS (2) ={b, -b, b) oder, vorbehaltlich | x (2) |=1, x (2) =

Zum λ 3 = 6 Finde den Eigenvektor x (3) ={z 1, z 2, z 3}:

, x (3) ={C,2c, c) oder in der normalisierten Version

x (3) = Sie können sehen, dass NS (1) NS (2) = ab - ab= 0, x (1) x (3) = ac - ac= 0, x (2) x (3) = bc- 2bc + bc= 0. Somit sind die Eigenvektoren dieser Matrix paarweise orthogonal.

Vorlesung 10.

Quadratische Formen und ihre Beziehung zu symmetrischen Matrizen. Eigenschaften von Eigenvektoren und Eigenwerten einer symmetrischen Matrix. Reduktion der quadratischen Form auf die kanonische Form.

Definition 10.1.Quadratische Form reelle Variablen x 1, x 2, ..., x n ist bezüglich dieser Variablen ein Polynom zweiten Grades, das keinen freien Term und Terme ersten Grades enthält.

Beispiele für quadratische Formen:

(n = 2),

(n = 3). (10.1)

Erinnern wir uns an die Definition einer symmetrischen Matrix aus der letzten Vorlesung:

Definition 10.2. Die quadratische Matrix heißt symmetrisch, wenn, das heißt, wenn die um die Hauptdiagonalen symmetrischen Matrixelemente gleich sind.

Eigenschaften von Eigenwerten und Eigenvektoren einer symmetrischen Matrix:

1) Alle Eigenwerte einer symmetrischen Matrix sind reell.

Beweis (für n = 2).

Lassen Sie die Matrix EIN sieht aus wie: ... Stellen wir die charakteristische Gleichung zusammen:

(10.2) Finden Sie die Diskriminante:

Daher hat die Gleichung nur reelle Wurzeln.

2) Die Eigenvektoren der symmetrischen Matrix sind orthogonal.

Beweis (für n= 2).

Die Koordinaten der Eigenvektoren und müssen die Gleichungen erfüllen.

Eigenwerte (Zahlen) und Eigenvektoren.
Lösungsbeispiele

Sei du selbst

Aus beiden Gleichungen folgt, dass.

Angenommen, dann: .

Ergebend: Ist der zweite Eigenvektor.

Wiederholen wir die wichtigen Punkte der Lösung:

- das resultierende System hat sicherlich eine allgemeine Lösung (Gleichungen sind linear abhängig);

- Wir wählen das "Spiel" so aus, dass es ganz ist und die erste "x"-Koordinate ganz, positiv und so klein wie möglich ist.

- Überprüfen Sie, ob die jeweilige Lösung jede Gleichung des Systems erfüllt.

Antworten .

Es gab genügend Zwischen-"Kontrollpunkte", daher ist eine Gleichheitsprüfung im Prinzip überflüssig.

In verschiedenen Informationsquellen werden die Koordinaten von Eigenvektoren oft nicht in Spalten, sondern in Zeilen geschrieben, zum Beispiel: (und um ehrlich zu sein, ich bin es gewohnt, sie selbst in Zeilen zu schreiben)... Diese Option ist akzeptabel, aber angesichts des Themas lineare Transformationen technisch bequemer zu bedienen Spaltenvektoren.

Vielleicht erschien Ihnen die Lösung sehr lang, aber das liegt nur daran, dass ich das erste Beispiel sehr ausführlich kommentiert habe.

Beispiel 2

Matrizen

Wir bilden uns aus! Ein ungefähres Beispiel für das Beenden der Aufgabe am Ende der Lektion.

Manchmal ist es erforderlich, eine zusätzliche Aufgabe zu erledigen, nämlich:

schreibe die kanonische Matrixzerlegung

Was ist das?

Wenn die Eigenvektoren der Matrix Basis, dann lässt es sich darstellen als:

Wo setzt sich die Matrix aus den Koordinaten der Eigenvektoren zusammen, - Diagonale Matrix mit entsprechenden Eigenwerten.

Eine solche Matrixzerlegung heißt kanonisch oder Diagonale.

Betrachten Sie die Matrix des ersten Beispiels. Seine eigenen Vektoren linear unabhängig(nicht kollinear) und bilden eine Basis. Stellen wir eine Matrix aus ihren Koordinaten zusammen:

Auf Hauptdiagonale Matrizen in der richtigen Reihenfolge die Eigenwerte liegen und der Rest der Elemente ist gleich Null:
- Ich betone noch einmal die Bedeutung der Reihenfolge: "zwei" entspricht dem 1. Vektor und steht daher in der 1. Spalte, "drei" - dem 2. Vektor.

Nach dem üblichen Findungsalgorithmus inverse Matrix oder Gauß-Jordan-Methode finden ... Nein, das ist kein Tippfehler! - vor Ihnen ein seltenes Ereignis, wie eine Sonnenfinsternis, wenn die Umkehrung mit der ursprünglichen Matrix zusammenfiel.

Es bleibt noch die kanonische Zerlegung der Matrix aufzuschreiben:

Das System kann mit elementaren Transformationen gelöst werden und in den folgenden Beispielen werden wir diese Methode verwenden. Aber hier funktioniert die Methode "Schule" viel schneller. Aus der 3. Gleichung werden wir ausdrücken: - Wir werden in die zweite Gleichung einsetzen:

Da die erste Koordinate null ist, erhalten wir ein System, aus dem aus jeder Gleichung folgt.

Und wieder auf das obligatorische Vorhandensein einer linearen Abhängigkeit achten... Wenn Sie nur eine triviale Lösung erhalten , dann wurde entweder der Eigenwert falsch gefunden, oder das System wurde mit einem Fehler kompiliert / gelöst.

Kompakte Koordinaten geben Bedeutung

Eigenvektor:

Und noch einmal - wir überprüfen, ob die gefundene Lösung erfüllt jede Gleichung des Systems... In den folgenden Absätzen und in nachfolgenden Aufgaben empfehle ich, diesen Wunsch als zwingende Regel zu nehmen.

2) Für den Eigenwert erhalten wir nach dem gleichen Prinzip folgendes System:

Aus der 2. Gleichung des Systems drücken wir aus: - Ersetzen Sie in der dritten Gleichung:

Da die "Zeta"-Koordinate gleich Null ist, erhalten wir ein System, von dem aus jeder Gleichung eine lineare Abhängigkeit folgt.

Lassen

Wir prüfen, ob die Lösung erfüllt jede Gleichung des Systems.

Der Eigenvektor ist also:.

3) Und schließlich entspricht das System dem Eigenwert:

Die zweite Gleichung sieht am einfachsten aus, also drücken wir sie aus und setzen sie in die erste und dritte Gleichung ein:

Alles ist gut - es ist ein linearer Zusammenhang entstanden, den wir in den Ausdruck einsetzen:

Als Ergebnis wurden "x" und "igrek" durch "z" ausgedrückt:. In der Praxis ist es nicht notwendig, solche Beziehungen zu erreichen, in einigen Fällen ist es bequemer, beides durch oder durch auszudrücken. Oder sogar ein "Zug" - zum Beispiel "X" bis "igrek" und "igrek" bis "z"

Angenommen, dann:

Wir prüfen, ob die gefundene Lösung jede Gleichung des Systems erfüllt und notieren Sie den dritten Eigenvektor

Antworten: Eigenvektoren:

Geometrisch definieren diese Vektoren drei verschiedene Raumrichtungen. ("Dorthin und wieder zurück") wodurch lineare Transformation wandelt Vektoren ungleich Null (Eigenvektoren) in zu ihnen kollineare Vektoren um.

Wenn die Bedingung erforderlich ist, um eine kanonische Zerlegung zu finden, dann ist dies hier möglich, da verschiedene Eigenwerte entsprechen verschiedenen linear unabhängigen Eigenvektoren. Zusammensetzen der Matrix aus ihren Koordinaten die Diagonalmatrix von die jeweilige Eigenwerte und finden inverse Matrix .

Wenn Sie je nach Bedingung schreiben müssen Matrix der linearen Transformation in der Basis von Eigenvektoren, dann geben wir die Antwort im Formular ein. Es gibt einen Unterschied, und der Unterschied ist signifikant! Für diese Matrix ist die „de“-Matrix.

Ein Problem mit einfacheren Berechnungen für eine unabhängige Lösung:

Beispiel 5

Finden Sie die Eigenvektoren einer linearen Transformation gegeben durch eine Matrix

Versuchen Sie beim Finden der Eigenwerte, die Sache nicht auf das Polynom 3. Grades zu bringen. Außerdem können Ihre Systemlösungen von meinen Lösungen abweichen - hier gibt es keine Eindeutigkeit; und die gefundenen Vektoren können von den Beispielvektoren bis hin zur Proportionalität ihrer jeweiligen Koordinaten abweichen. Zum Beispiel und. Es ist ästhetischer, die Antwort im Formular darzustellen, aber es ist in Ordnung, wenn Sie bei der zweiten Option aufhören. Allerdings gibt es für alles vernünftige Grenzen, die Version sieht nicht mehr sehr gut aus.

Eine ungefähre Abschlussprobe der Aufgabe am Ende der Lektion.

Wie löst man das Problem bei mehreren Eigenwerten?

Der allgemeine Algorithmus bleibt derselbe, hat jedoch seine eigenen Besonderheiten, und es ist ratsam, einige Teile der Lösung in einem strengeren akademischen Stil zu pflegen:

Beispiel 6

Eigenwerte und Eigenvektoren finden

Lösung

Natürlich schreiben wir die fabelhafte erste Spalte groß:

Und nach Faktorisieren des quadratischen Trinoms:

Als Ergebnis erhält man Eigenwerte, von denen zwei Vielfache sind.

Finden wir Eigenvektoren:

1) Wir werden den einsamen Soldaten nach dem "vereinfachten" Schema behandeln:

Aus den letzten beiden Gleichungen ist die Gleichheit deutlich erkennbar, die natürlich in die 1. Gleichung des Systems eingesetzt werden sollte:

Es gibt keine bessere Kombination:
Eigenvektor:

2-3) Erschieße nun ein paar Wachen. In diesem Fall kann es sich herausstellen entweder zwei oder eins Eigenvektor. Unabhängig von der Multiplizität der Wurzeln setzen wir den Wert in die Determinante ein was uns folgendes bringt homogenes lineares Gleichungssystem:

Eigenvektoren sind genau Vektoren
grundlegendes Entscheidungssystem

Tatsächlich waren wir während der gesamten Lektion nur damit beschäftigt, die Vektoren des Fundamentalsystems zu finden. Dieser Begriff war vorerst nicht unbedingt erforderlich. Übrigens, diese schlauen Schüler, die das Thema in Tarnmäntel geschlüpft haben homogene Gleichungen wird gezwungen, es jetzt zu essen.

Die einzige Aktion bestand darin, die zusätzlichen Zeilen zu löschen. Das Ergebnis ist eine eins-mal-drei-Matrix mit einer formalen „Sprung“ in der Mitte.
- Basisvariable, - freie Variablen. Es gibt also zwei freie Variablen: Vektoren des Fundamentalsystems sind auch zwei.

Lassen Sie uns die Basisvariable in Form von freien Variablen ausdrücken:. Der Nullfaktor vor dem "x" erlaubt es, absolut beliebige Werte anzunehmen (was aus dem Gleichungssystem deutlich zu erkennen ist).

Im Kontext dieses Problems ist es bequemer, die allgemeine Lösung nicht in eine Zeile, sondern in eine Spalte zu schreiben:

Der Eigenvektor entspricht dem Paar:
Der Eigenvektor entspricht dem Paar:

Notiz : Erfahrene Leser können diese Vektoren und mündlich auswählen - einfach durch Analyse des Systems , aber hier sind einige Kenntnisse erforderlich: Es gibt drei Variablen, Systemmatrixrang- Einheit, was bedeutet grundlegendes Entscheidungssystem besteht aus 3 - 1 = 2 Vektoren. Die gefundenen Vektoren sind jedoch auch ohne dieses Wissen auf rein intuitiver Ebene perfekt sichtbar. In diesem Fall wird der dritte Vektor noch "schöner" geschrieben:. Ich warne Sie jedoch, dass in einem anderen Beispiel die einfache Auswahl möglicherweise nicht erscheint, weshalb der Haftungsausschluss für erfahrene Personen gedacht ist. Außerdem, warum nicht beispielsweise als dritten Vektor nehmen? Schließlich erfüllen seine Koordinaten auch jede Gleichung des Systems, und die Vektoren linear unabhängig. Diese Option ist im Prinzip geeignet, aber "schief", da der "andere" Vektor eine Linearkombination von Vektoren des Fundamentalsystems ist.

Antworten: Eigenwerte:, Eigenvektoren:

Ein ähnliches Beispiel für eine Stand-alone-Lösung:

Beispiel 7

Eigenwerte und Eigenvektoren finden

Ein grobes Beispiel für den Abschluss am Ende der Lektion.

Es ist zu beachten, dass sowohl im 6. als auch im 7. Beispiel ein Tripel von linear unabhängigen Eigenvektoren erhalten wird und daher die ursprüngliche Matrix in der kanonischen Zerlegung darstellbar ist. Aber solche Himbeeren kommen nicht in allen Fällen vor:

Beispiel 8

Lösung: Zusammenstellung und Lösung der charakteristischen Gleichung:

Wir öffnen die Determinante durch die erste Spalte:

Weitere Vereinfachungen erfolgen nach der betrachteten Methode unter Vermeidung des Polynoms 3. Grades:

- Eigenwerte.

Finden wir Eigenvektoren:

1) Es gibt keine Schwierigkeiten mit der Wurzel:

Wundern Sie sich nicht, neben dem Kit werden auch Variablen verwendet – hier gibt es keinen Unterschied.

Aus der 3. Gleichung werden wir ausdrücken - wir ersetzen die 1. und 2. Gleichung:

Aus beiden Gleichungen folgt:

Lass dann:

2-3) Für mehrere Werte erhalten wir das System .

Schreiben wir die Matrix des Systems auf und bringen sie mit elementaren Transformationen in eine schrittweise Form:

". Der erste Teil stellt die Mindestvoraussetzungen für das Verständnis der Chemometrie dar, und der zweite Teil enthält Fakten, die Sie für ein tieferes Verständnis der Methoden der multivariaten Analyse wissen müssen. Die Präsentation wird durch Beispiele in einem Excel-Arbeitsbuch illustriert Matrix.xls die diesem Dokument beiliegt.

Verweise auf Beispiele werden als Excel-Objekte im Text platziert. Diese Beispiele sind abstrakter Natur, sie sind in keiner Weise an die Probleme der analytischen Chemie gebunden. Reale Beispiele für die Verwendung der Matrixalgebra in der Chemometrie werden in anderen Texten betrachtet, die sich verschiedenen chemometrischen Anwendungen widmen.

Die meisten Messungen in der analytischen Chemie sind nicht direkt, aber indirekt... Dies bedeutet, dass im Experiment anstelle des Wertes des gewünschten Analyten C (Konzentration) ein anderer Wert erhalten wird x(Signal) verwandt aber nicht gleich C, d.h. x(C) ≠ C. In der Regel die Art der Abhängigkeit x(C) nicht bekannt, aber glücklicherweise sind in der analytischen Chemie die meisten Messungen proportional. Dies bedeutet, dass mit einer Erhöhung der Konzentration von C in ein Mal erhöht sich das Signal X um den gleichen Betrag. x(ein C) = ein x(C). Darüber hinaus sind die Signale auch additiv, so dass das Signal einer Probe, die zwei Substanzen mit Konzentrationen von C 1 und C 2 enthält, gleich der Summe der Signale von jeder Komponente ist, d. x(C1 + C2) = x(C1) + x(C2). Verhältnismäßigkeit und Additivität zusammen ergeben Linearität... Es gibt viele Beispiele, um das Linearitätsprinzip zu veranschaulichen, aber es genügt, zwei der auffälligsten Beispiele zu nennen - Chromatographie und Spektroskopie. Das zweite Merkmal eines Experiments in der analytischen Chemie ist Mehrkanal... Moderne Analysegeräte messen gleichzeitig Signale für viele Kanäle. Beispielsweise wird die Intensität der Lichttransmission für mehrere Wellenlängen gleichzeitig gemessen, d.h. Spektrum. Daher beschäftigen wir uns im Experiment mit vielen Signalen x 1 , x 2 ,...., x n, charakterisiert den Satz von Konzentrationen C 1, C 2, ..., C m von Substanzen, die im untersuchten System vorhanden sind.

Reis. 1 Spektren

Ein analytisches Experiment zeichnet sich also durch Linearität und Mehrdimensionalität aus. Daher ist es praktisch, experimentelle Daten als Vektoren und Matrizen zu betrachten und sie unter Verwendung der Vorrichtung der Matrixalgebra zu manipulieren. Die Fruchtbarkeit dieses Ansatzes wird durch das auf gezeigte Beispiel veranschaulicht, das drei Spektren zeigt, die für 200 Wellenlängen von 4000 bis 4796 cm – 1 aufgenommen wurden. Zuerst ( x 1) und der zweite ( x 2) Spektren wurden von Standardproben erhalten, bei denen die Konzentration von zwei Substanzen A und B bekannt ist: in der ersten Probe [A] = 0,5, [B] = 0,1, und in der zweiten Probe [A] = 0,2, [B ] = 0,6. Was kann man über eine neue, unbekannte Probe sagen, deren Spektrum bezeichnet wird x 3 ?

Betrachten Sie drei experimentelle Spektren x 1 , x 2 und x 3 als drei Vektoren der Dimension 200. Mittels linearer Algebra kann man leicht zeigen, dass x 3 = 0.1 x 1 +0.3 x 2, daher enthält die dritte Probe offensichtlich nur die Stoffe A und B in den Konzentrationen [A] = 0,5 × 0,1 + 0,2 × 0,3 = 0,11 und [B] = 0,1 × 0,1 + 0,6 × 0,3 = 0,19.

1. Grundlegende Informationen

1.1 Matrizen

Matrix nennt man zum Beispiel eine rechteckige Zahlentabelle

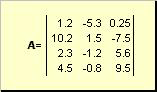
Reis. 2 Matrix

Matrizen werden in fetten Großbuchstaben ( EIN) und deren Elemente - entsprechende Kleinbuchstaben mit Indizes, d.h. ein ij. Der erste Index nummeriert die Zeilen und der zweite die Spalten. In der Chemometrie ist es üblich, den Höchstwert des Index mit dem gleichen Buchstaben wie der Index selbst zu bezeichnen, jedoch großgeschrieben. Daher ist die Matrix EIN kann auch geschrieben werden als ( ein ij , ich = 1,..., ich; J = 1,..., J). Für die im Beispiel gezeigte Matrix ich = 4, J= 3 und ein 23 = −7.5.

Zahlenpaar ich und J heißt Dimension der Matrix und wird bezeichnet als ich× J... Ein Beispiel für eine Matrix in der Chemometrie ist die Menge von Spektren, die für ich Proben auf J Wellenlängen.

1.2. Einfache Matrixoperationen

Matrizen können mit Zahlen multiplizieren... In diesem Fall wird jedes Element mit dieser Zahl multipliziert. Zum Beispiel -

Reis. 3 Matrixmultiplikation mit Zahl

Zwei Matrizen der gleichen Dimension können elementweise sein falten und subtrahieren... Zum Beispiel,

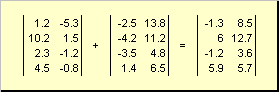
Reis. 4 Matrixaddition

Durch Multiplikation mit einer Zahl und Addition erhält man eine Matrix gleicher Dimension.

Eine Nullmatrix ist eine Matrix, die aus Nullen besteht. Es wird bezeichnet Ö... Es ist klar, dass EIN+Ö = EIN, EIN−EIN = Ö und 0 EIN = Ö.

Die Matrix kann sein transponieren... Während dieser Operation wird die Matrix umgedreht, d.h. Zeilen und Spalten werden vertauscht. Transponieren wird durch einen Strich angezeigt, EIN"oder index EIN T. Also wenn EIN = {ein ij , ich = 1,..., ich; J = 1,...,J), dann EIN t = ( ein ji , J = 1,...,J; ich = 1, ..., ich). Zum Beispiel

Reis. 5 Transponierungsmatrix

Es ist klar, dass ( EIN t) t = EIN, (EIN+B) T = A t + B T.

1.3. Matrix-Multiplikation

Matrizen können multiplizieren, aber nur, wenn sie die entsprechenden Abmessungen haben. Warum das so ist, geht aus der Definition hervor. Das Produkt der Matrix EIN, Abmessungen ich× K und Matrizen B, Abmessungen K× J heißt die Matrix C, Abmessungen ich× J deren Elemente Zahlen sind

So produzieren AB es ist notwendig, dass die Anzahl der Spalten in der linken Matrix EIN war gleich der Anzahl der Zeilen in der rechten Matrix B... Ein Beispiel für ein Matrixprodukt -

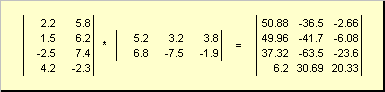
Abb. 6 Matrixprodukt

Die Matrixmultiplikationsregel kann wie folgt formuliert werden. Um ein Element einer Matrix zu finden C an der Kreuzung stehen ich-te Zeile und J-te Spalte ( C ij) muss Element mit Element multipliziert werden ich Zeile der ersten Matrix EIN An J Spalte der zweiten Matrix B und addiere alle Ergebnisse. Im gezeigten Beispiel ergibt sich also ein Element aus der dritten Zeile und der zweiten Spalte als Summe der elementweisen Produkte der dritten Zeile EIN und die zweite Spalte B

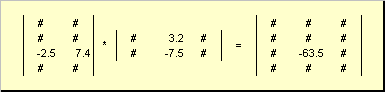
Abb. 7 Matrixproduktelement

Das Produkt von Matrizen hängt von der Ordnung ab, d.h. AB ≠ BA, schon allein aus Dimensionsgründen. Es wird als nicht kommutativ bezeichnet. Matrixprodukte sind jedoch assoziativ. Es bedeutet, dass ABC = (AB)C = EIN(BC). Darüber hinaus ist es auch distributiv, d.h. EIN(B+C) = AB+AC... Es ist klar, dass AO = Ö.

1.4. Quadratische Matrizen

Wenn die Anzahl der Spalten der Matrix der Anzahl ihrer Zeilen entspricht ( ich = J = N), dann wird eine solche Matrix als Quadrat bezeichnet. In diesem Abschnitt betrachten wir nur solche Matrizen. Unter diesen Matrizen kann man Matrizen mit besonderen Eigenschaften herausgreifen.

Einzel Matrix (bezeichnet ICH, und manchmal E) ist eine Matrix, in der alle Elemente gleich Null sind, mit Ausnahme der Diagonalen, die gleich 1 sind, d.h.

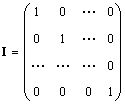
Offensichtlich Ai = NS = EIN.

Die Matrix heißt Diagonale wenn alle seine Elemente außer den diagonalen ( ein ii) sind gleich Null. Zum Beispiel

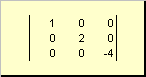
Reis. 8 Diagonalmatrix

Matrix EIN die Spitze genannt dreieckig wenn alle seine Elemente unterhalb der Diagonale gleich Null sind, d.h. ein ij= 0, für ich>J... Zum Beispiel

Reis. 9 Obere Dreiecksmatrix

Die untere Dreiecksmatrix ist ähnlich definiert.

Matrix EIN namens symmetrisch, wenn EIN t = EIN... Mit anderen Worten ein ij = ein ji... Zum Beispiel

Reis. 10 Symmetrische Matrix

Matrix EIN namens senkrecht, wenn

EIN T EIN = AA t = ich.

Die Matrix heißt normal wenn

1.5. Spur und Determinante

Folge quadratische Matrix EIN(bezeichnet mit Tr ( EIN) oder Sp ( EIN)) ist die Summe seiner diagonalen Elemente,

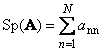
Zum Beispiel,

Reis. 11 Matrixspur

Es ist klar, dass

Sp (α EIN) = αSp ( EIN) und

Sp ( EIN+B) = Sp ( EIN) + Sp ( B).

Es kann gezeigt werden, dass

Sp ( EIN) = Sp ( EIN t), Sp ( ich) = n,

und auch das

Sp ( AB) = Sp ( BA).

Ein weiteres wichtiges Merkmal einer quadratischen Matrix ist ihre bestimmend(gekennzeichnet mit det ( EIN)). Die Bestimmung der Determinante im allgemeinen Fall ist ziemlich schwierig, daher beginnen wir mit der einfachsten Version - der Matrix EIN Abmessung (2 × 2). Dann

Für eine (3 × 3)-Matrix ist die Determinante

Bei der Matrix ( n× n) berechnet sich die Determinante als Summe von 1 2 3 ... n= n! Terme, von denen jeder gleich ist

Indizes k 1 , k 2 ,..., k N sind definiert als alle möglichen geordneten Permutationen R Zahlen im Satz (1, 2, ..., n). Die Berechnung der Determinante einer Matrix ist ein komplexes Verfahren, das in der Praxis mit speziellen Programmen durchgeführt wird. Zum Beispiel,

Reis. 12 Matrixdeterminante

Wir beachten nur die offensichtlichen Eigenschaften:

det ( ich) = 1, det ( EIN) = det ( EIN T),

det ( AB) = det ( EIN) det ( B).

1.6. Vektoren

Besteht die Matrix nur aus einer Spalte ( J= 1), dann heißt ein solches Objekt Vektor... Genauer gesagt ein Spaltenvektor. Zum Beispiel

Man kann sich beispielsweise auch Matrizen vorstellen, die aus einer Reihe bestehen

Dieses Objekt ist auch ein Vektor, aber Zeilenvektor... Bei der Datenanalyse ist es wichtig zu verstehen, mit welchen Vektoren wir es zu tun haben – Spalten oder Zeilen. Das Spektrum, das für eine Probe aufgenommen wurde, kann also als Zeilenvektor betrachtet werden. Dann muss der Satz spektraler Intensitäten bei einer bestimmten Wellenlänge für alle Proben als Spaltenvektor behandelt werden.

Die Dimension eines Vektors ist die Anzahl seiner Elemente.

Es ist klar, dass jeder Spaltenvektor durch Transposition in einen Zeilenvektor umgewandelt werden kann, d.h.

In den Fällen, in denen die Form eines Vektors nicht speziell angegeben wird, sondern lediglich ein Vektor gesagt wird, handelt es sich um einen Spaltenvektor. Auch wir werden uns an diese Regel halten. Ein Vektor wird durch einen geraden fetten Kleinbuchstaben gekennzeichnet. Ein Nullvektor ist ein Vektor, dessen Elemente alle Null sind. Es ist bezeichnet 0 .

1.7. Grundoperationen mit Vektoren

Vektoren können wie Matrizen addiert und mit Zahlen multipliziert werden. Zum Beispiel,

Reis. 13 Vektoroperationen

Zwei Vektoren x und ja werden genannt kolinear wenn es eine Zahl α gibt, so dass

1.8. Produkte von Vektoren

Zwei Vektoren der gleichen Dimension n multipliziert werden kann. Es gebe zwei Vektoren x = (x 1 , x 2 ,...,x N) t und ja = (ja 1 , ja 2 ,...,ja N) t. Geleitet von der Multiplikationsregel "Zeile für Spalte" können wir daraus zwei Produkte zusammensetzen: x T ja und xy T. Erstes Stück

namens Skalar oder intern... Das Ergebnis ist eine Zahl. Es verwendet auch die Notation ( x,ja)= x T ja... Zum Beispiel,

Reis. 14 Inneres Produkt (Punktprodukt)

Zweites Stück

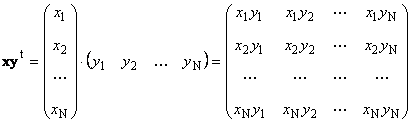
namens extern... Das Ergebnis ist eine Dimensionsmatrix ( n× n). Zum Beispiel,

Reis. 15 Externe Arbeiten

Vektoren, deren Skalarprodukt gleich Null ist, heißen senkrecht.

1.9. Vektornorm

Das Skalarprodukt eines Vektors selbst heißt Skalarquadrat. Dieser Wert

definiert ein Quadrat Länge Vektor x... Länge bezeichnen (auch genannt Die Norm Vektor), wird die Notation verwendet

Zum Beispiel,

Reis. 16 Vektornorm

Ein Vektor der Einheitslänge (|| x|| = 1) heißt normalisiert. Ein Vektor ungleich Null ( x ≠ 0 ) kann durch Division durch die Länge normalisiert werden, d.h. x = ||x|| (x /||x||) = ||x|| e... Hier e = x /||x|| ist der normierte Vektor.

Vektoren heißen orthonormal, wenn sie alle normalisiert und paarweise orthogonal sind.

1.10. Winkel zwischen Vektoren

Das Punktprodukt definiert und Injektionφ zwischen zwei Vektoren x und ja

Sind die Vektoren orthogonal, dann ist cosφ = 0 und φ = π / 2, und wenn sie kollinear sind, dann cosφ = 1 und φ = 0.

1.11. Vektordarstellung einer Matrix

Jede Matrix EIN Größe ich× J kann als eine Menge von Vektoren dargestellt werden

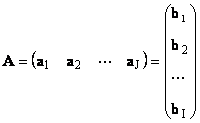
Hier jeder Vektor ein J ist ein J Spalte und der Zeilenvektor B ich ist ein ich-te Zeile der Matrix EIN

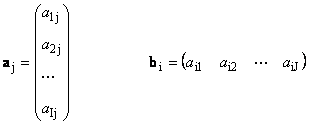
1.12. Linear abhängige Vektoren

Vektoren der gleichen Dimension ( n) können wie Matrizen addiert und mit einer Zahl multipliziert werden. Das Ergebnis ist ein Vektor der gleichen Dimension. Seien mehrere Vektoren der gleichen Dimension x 1 , x 2 ,...,x K und gleich viele Zahlen α α 1, α 2, ..., α K... Vektor

ja= α 1 x 1 + α2 x 2 + ... + α K x K

namens lineare Kombination Vektoren x k .

Wenn es Zahlen ungleich null gibt, α k ≠ 0, k = 1,..., K, was ja = 0 , dann ist eine solche Menge von Vektoren x k namens linear abhängig... Ansonsten heißen die Vektoren linear unabhängig. Zum Beispiel Vektoren x 1 = (2, 2) t und x 2 = (−1, −1) t sind linear abhängig, da x 1 +2x 2 = 0

1.13. Matrixrang

Betrachten Sie eine Reihe von K Vektoren x 1 , x 2 ,...,x K Maße n... Der Rang dieses Vektorsystems ist die maximale Anzahl von linear unabhängigen Vektoren. Zum Beispiel im Set

es gibt nur zwei linear unabhängige Vektoren, zum Beispiel x 1 und x 2, also ist sein Rang 2.

Wenn es mehr Vektoren in der Menge gibt als ihre Dimension ( K>n), dann sind sie notwendigerweise linear abhängig.

Nach dem Rang der Matrix(bezeichnet durch Rang ( EIN)) heißt der Rang des Vektorsystems, aus dem es besteht. Obwohl jede Matrix auf zwei Arten dargestellt werden kann (Spaltenvektoren oder Zeilen), hat dies keinen Einfluss auf den Rangwert, da

1.14. inverse Matrix

Quadratische Matrix EIN heißt nicht entartet, wenn es eine eindeutige umkehren Matrix EIN-1 durch Bedingungen bestimmt

AA −1 = EIN −1 EIN = ich.

Eine inverse Matrix existiert nicht für alle Matrizen. Eine notwendige und hinreichende Bedingung für Nichtentartung ist

det ( EIN) ≠ 0 oder Rang ( EIN) = n.

Die Matrixinversion ist ein komplexes Verfahren, für das es spezielle Programme gibt. Zum Beispiel,

Reis. 17 Matrixinversion

Lassen Sie uns Formeln für den einfachsten Fall präsentieren - 2 × 2 Matrizen

Wenn Matrizen EIN und B nicht entartet, dann

(AB) −1 = B −1 EIN −1 .

1.15. Pseudoinverse Matrix

Wenn die Matrix EIN entartet ist und die inverse Matrix nicht existiert, dann können Sie in einigen Fällen verwenden pseudo-invers eine Matrix, die als eine solche Matrix definiert ist EIN+ das

AA + EIN = EIN.

Die pseudoinverse Matrix ist nicht die einzige und ihr Typ hängt von der Konstruktionsmethode ab. Für eine rechteckige Matrix können Sie beispielsweise die Moore-Penrose-Methode verwenden.

Wenn die Anzahl der Spalten kleiner als die Anzahl der Zeilen ist, dann

EIN + =(EIN T EIN) −1 EIN T

Zum Beispiel,

Reis. 17a Matrix-Pseudo-Inversion

Wenn die Anzahl der Spalten größer als die Anzahl der Zeilen ist, dann

EIN + =EIN T ( AA T) −1

1.16. Multiplizieren eines Vektors mit einer Matrix

Vektor x kann mit einer Matrix multipliziert werden EIN passendes Maß. In diesem Fall wird der Spaltenvektor rechts multipliziert Axt und der Zeilenvektor ist links x T EIN... Wenn die Dimension des Vektors J, und die Dimension der Matrix ich× J dann ist das Ergebnis ein Vektor der Dimension ich... Zum Beispiel,

Reis. 18 Vektor-durch-Matrix-Multiplikation

Wenn die Matrix EIN- Quadrat ( ich× ich), dann ist der Vektor ja = Axt hat die gleiche Dimension wie x... Es ist klar, dass

EIN(α 1 x 1 + α2 x 2) = α 1 Axt 1 + α2 Axt 2 .

Daher können Matrizen als lineare Transformationen von Vektoren angesehen werden. Insbesondere Ix = x, Ochse = 0 .

2. Zusätzliche Informationen

2.1. Lineare Gleichungssysteme

Lassen EIN- Matrixgröße ich× J, ein B- Maßvektor J... Betrachten Sie die Gleichung

Axt = B

bezüglich des Vektors x, Maße ich... Tatsächlich ist dies ein System von ich lineare Gleichungen mit J Unbekannt x 1 ,...,x J... Die Lösung existiert genau dann, wenn

Rang ( EIN) = Rang ( B) = R,

wo B ist eine erweiterte Dimensionsmatrix ich×( J + 1) bestehend aus der Matrix EIN gepolstert mit Spalte B, B = (EIN B). Ansonsten sind die Gleichungen inkonsistent.

Wenn R = ich = J, dann ist die Lösung eindeutig

x = EIN −1 B.

Wenn R < ich, dann gibt es viele verschiedene Lösungen, die durch die Linearkombination ausgedrückt werden können J−R Vektoren. System homogener Gleichungen Axt = 0 quadratische Matrix EIN (n× n) hat eine nichttriviale Lösung ( x ≠ 0 ) genau dann, wenn det ( EIN) = 0. Wenn R= Rang ( EIN)<n dann existiert n−R linear unabhängige Lösungen.

2.2. Bilineare und quadratische Formen

Wenn EIN eine quadratische Matrix ist und x und ja Vektoren der entsprechenden Dimension sind, dann ist das Skalarprodukt der Form x T Ja namens bilinear die durch die Matrix definierte Form EIN... Bei x = ja Ausdruck x T Axt namens quadratisch Form.

2.3. Positiv bestimmte Matrizen

Quadratische Matrix EIN namens positiv definiert falls für einen Vektor ungleich null x ≠ 0 ,

x T Axt > 0.

Ähnlich, negativ (x T Axt < 0), nicht negativ (x T Axt≥ 0) und nicht positiv (x T Axt≤ 0) bestimmte Matrizen.

2.4. Cholesky-Zerlegung

Wenn eine symmetrische Matrix EIN positiv definit ist, dann gibt es eine eindeutige Dreiecksmatrix U mit positiven Elementen, für die

EIN = U T U.

Zum Beispiel,

Reis. 19 Cholesky-Zerlegung

2.5. Polare Zersetzung

Lassen EIN ist eine nicht entartete quadratische Matrix der Dimension n× n... Dann gibt es eins zu eins Polar- Leistung

EIN = SR,

wo S eine nichtnegative symmetrische Matrix ist und R ist eine orthogonale Matrix. Matrizen S und R kann explizit definiert werden:

S 2 = AA t oder S = (AA t) ½ und R = S −1 EIN = (AA t) -1 EIN.

Zum Beispiel,

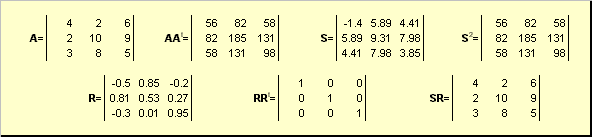
Reis. 20 Polare Zersetzung

Wenn die Matrix EIN entartet ist, dann ist die Erweiterung nicht eindeutig - nämlich: S immer noch allein, aber R vielleicht viel. Die polare Zerlegung repräsentiert die Matrix EIN als Kombination aus Kompression / Dehnung S und drehen R.

2.6. Eigenvektoren und Eigenwerte

Lassen EIN ist eine quadratische Matrix. Vektor v namens eigener Vektor Matrizen EIN, wenn

Ein V = λ v,

wo die Zahl λ heißt eigene Bedeutung Matrizen EIN... Somit ist die Transformation, die die Matrix durchführt EINüber Vektor v, wird mit einem Koeffizienten λ auf eine einfache Dehnung oder Kompression reduziert. Der Eigenvektor wird bis zur Multiplikation mit der Konstanten α ≠ 0 bestimmt, d.h. wenn v ein Eigenvektor ist, dann ist α v ist auch ein Eigenvektor.

2.7. Eigenwerte

Matrix EIN, Abmessungen ( n× n) kann nicht mehr sein als n Eigenwerte. Sie befriedigen charakteristische Gleichung

det ( EIN − λ ich) = 0,

das ist eine algebraische Gleichung n te Bestellung. Insbesondere für eine 2 × 2-Matrix hat die charakteristische Gleichung die Form

Zum Beispiel,

Reis. 21 Eigenwerte

Die Menge der Eigenwerte 1, ..., λ n Matrizen EIN namens Spektrum EIN.

Das Spektrum hat eine Vielzahl von Eigenschaften. Insbesondere

det ( EIN) = λ 1 × ... × λ n, Sp ( EIN) = λ 1 + ... + λ n.

Die Eigenwerte einer beliebigen Matrix können komplexe Zahlen sein, aber wenn die Matrix symmetrisch ist ( EIN t = EIN), dann sind seine Eigenwerte reell.

2.8. Eigene Vektoren

Matrix EIN, Abmessungen ( n× n) kann nicht mehr sein als n Eigenvektoren, von denen jeder seinem eigenen Wert entspricht. Zur Bestimmung des Eigenvektors v n Sie müssen ein homogenes Gleichungssystem lösen

(EIN − λ n ich)v n = 0 .

Es hat eine nichttriviale Lösung, da det ( EIN -λ n ich) = 0.

Zum Beispiel,

Reis. 22 Eigenvektoren

Die Eigenvektoren einer symmetrischen Matrix sind orthogonal.

SYSTEM HOMOGENER LINEARER GLEICHUNGEN

Ein homogenes lineares Gleichungssystem ist ein System der Form

Es ist klar, dass in diesem Fall schon seit alle Elemente einer der Spalten in diesen Qualifizierern sind gleich Null.

Da die Unbekannten durch die Formeln gefunden werden , dann hat das System im Fall Δ ≠ 0 eine eindeutige Nulllösung x = ja = z= 0. Bei vielen Problemen ist jedoch die Frage interessant, ob ein homogenes System andere Lösungen als Null hat.

Satz. Damit ein lineares homogenes Gleichungssystem eine von Null verschiedene Lösung hat, ist es notwendig und ausreichend, dass Δ ≠ 0 ist.

Ist also die Determinante Δ ≠ 0, dann hat das System eine eindeutige Lösung. Wenn Δ ≠ 0, dann hat das lineare homogene Gleichungssystem eine unendliche Menge von Lösungen.

Beispiele.

Eigenvektoren und Eigenwerte der Matrix

Gegeben sei eine quadratische Matrix , x- eine Matrixspalte, deren Höhe mit der Ordnung der Matrix übereinstimmt EIN. .

Bei vielen Problemen muss man die Gleichung bezüglich x

wobei λ eine Zahl ist. Es ist klar, dass diese Gleichung für jedes λ eine Nulllösung hat.

Die Zahl λ, für die diese Gleichung Lösungen ungleich Null hat, heißt eigene Bedeutung Matrizen EIN, ein x für solches λ heißt eigener Vektor Matrizen EIN.

Finden Sie den Eigenvektor der Matrix EIN... Soweit E∙X = X, dann kann die Matrixgleichung umgeschrieben werden als oder ... In erweiterter Form lässt sich diese Gleichung in ein lineares Gleichungssystem umschreiben. Wirklich .

Und deshalb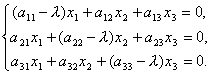

Wir haben also ein System homogener linearer Gleichungen zur Bestimmung der Koordinaten x 1, x 2, x 3 Vektor x... Damit das System Lösungen ungleich null hat, ist es notwendig und ausreichend, dass die Determinante des Systems gleich null ist, d.h.

Dies ist eine Gleichung 3. Grades bezüglich λ. Es heißt charakteristische Gleichung Matrizen EIN und dient zur Ermittlung der Eigenwerte λ.

Jeder Eigenwert λ entspricht einem Eigenvektor x, deren Koordinaten aus dem System beim entsprechenden Wert von λ bestimmt werden.

Beispiele.

VEKTORALGEBRA. KONZEPT VON VEKTOR

Beim Studium verschiedener Zweige der Physik gibt es Größen, die vollständig durch die Angabe ihrer Zahlenwerte bestimmt werden, zum Beispiel Länge, Fläche, Masse, Temperatur usw. Solche Größen nennt man skalar. Daneben gibt es aber auch Größen, zu deren Bestimmung neben dem Zahlenwert auch deren Richtung im Raum bekannt sein muss, zum Beispiel die auf den Körper wirkende Kraft, die Geschwindigkeit und Beschleunigung des Körpers, wenn er sich im Raum bewegt, die Stärke des Magnetfelds an einem bestimmten Punkt im Raum usw. Solche Größen werden Vektoren genannt.

Führen wir eine strenge Definition ein.

Richtungssegment nennen wir ein Segment, von dessen Enden man weiß, welches das erste und welches das zweite ist.

Vektor wird als gerichtetes Segment bezeichnet, das eine bestimmte Länge hat, d.h. es ist ein Abschnitt bestimmter Länge, bei dem einer seiner Grenzpunkte als Anfang und der andere als Ende genommen wird. Wenn EIN- der Anfang des Vektors, B- sein Ende, dann wird der Vektor mit einem Symbol bezeichnet, außerdem wird der Vektor oft mit einem Buchstaben bezeichnet. In der Abbildung wird ein Vektor durch ein Liniensegment und seine Richtung durch einen Pfeil angezeigt.

Modul oder die Länge vector ist die Länge des Richtungssegments, das ihn definiert. Es wird mit || . bezeichnet oder ||.

Der sogenannte Nullvektor, bei dem Anfang und Ende zusammenfallen, wird auch als Vektor bezeichnet. Es ist angegeben. Der Nullvektor hat keine eindeutige Richtung und sein Modul ist gleich Null || = 0.

Die Vektoren und heißen kollinear wenn sie sich auf einer Geraden oder auf Parallelen befinden. Wenn die Vektoren und in die gleiche Richtung weisen, schreiben wir außerdem umgekehrt.

Vektoren, die auf Geraden parallel zur gleichen Ebene liegen, heißen koplanar.

Zwei Vektoren und heißen gleich wenn sie kollinear, gleichgerichtet und gleich lang sind. Schreiben Sie in diesem Fall.

Aus der Definition der Gleichheit von Vektoren folgt, dass ein Vektor parallel zu sich selbst übertragen werden kann, wobei sein Ursprung an einem beliebigen Punkt im Raum liegt.

Zum Beispiel.

LINEARE OPERATIONEN AUF VEKTOREN

1. Multiplizieren eines Vektors mit einer Zahl.

   Das Produkt eines Vektors mit der Zahl λ ist ein neuer Vektor mit:

   Das Produkt eines Vektors mit der Zahl wird bezeichnet.

   

   Zum Beispiel, ist ein Vektor, der in die gleiche Richtung wie der Vektor gerichtet ist und eine Länge hat, die halb so lang ist wie die des Vektors.

   Die eingeführte Operation hat folgendes Eigenschaften:

2. Hinzufügen von Vektoren.

   Seien und zwei beliebige Vektoren. Nehmen Sie einen beliebigen Punkt Ö und konstruiere einen Vektor. Danach von dem Punkt EIN den Vektor beiseite legen. Der Vektor, der den Anfang des ersten Vektors mit dem Ende des zweiten verbindet, heißt Summe dieser Vektoren und heißt .

   

   Die formulierte Definition der Vektoraddition heißt Parallelogrammregel, da die gleiche Vektorsumme wie folgt erhalten werden kann. Setzen Sie sich von dem Punkt ab Ö Vektoren und. Konstruieren wir ein Parallelogramm auf diesen Vektoren OAVS... Da Vektoren, der Vektor, der die Diagonale des vom Scheitelpunkt gezogenen Parallelogramms ist, Ö, ist offensichtlich die Summe der Vektoren.

   

   Es ist einfach, Folgendes zu überprüfen Vektoradditionseigenschaften.

3. Unterschied der Vektoren.

   Ein Vektor, der zu einem gegebenen Vektor kollinear ist, gleich lang und entgegengesetzt gerichtet ist, heißt Gegenteil Vektor für Vektor und wird mit bezeichnet. Der entgegengesetzte Vektor kann als Ergebnis der Multiplikation des Vektors mit der Zahl λ = –1: angesehen werden.

Die Diagonalmatrizen sind die einfachsten. Es stellt sich die Frage, ob es möglich ist, eine Basis zu finden, in der die Matrix eines linearen Operators eine Diagonalform hätte. Eine solche Grundlage ist vorhanden.
Es sei ein linearer Raum R n und ein darin wirkender linearer Operator A gegeben; in diesem Fall nimmt der Operator A R n in sich auf, dh A: R n → R n.

Definition. Ein Vektor ungleich Null heißt Eigenvektor des Operators A, wenn sich der Operator A in einen dazu kollinearen Vektor transformiert, d. h. Die Zahl λ heißt Eigenwert oder Eigenwert des Operators A, entsprechend dem Eigenvektor.
Beachten wir einige Eigenschaften der Eigenwerte und Eigenvektoren.
1. Beliebige Linearkombination von Eigenvektoren des Operators A, der demselben Eigenwert λ entspricht, ist ein Eigenvektor mit demselben Eigenwert.
2. Eigenvektoren des Operators A mit paarweise unterschiedlichen Eigenwerten λ 1, λ 2,…, λ m sind linear unabhängig.
3. Sind die Eigenwerte 1 = λ 2 = λ m = λ, dann entspricht der Eigenwert λ höchstens m linear unabhängigen Eigenvektoren.

Gibt es also n linear unabhängige Eigenvektoren entsprechen verschiedenen Eigenwerten λ 1, λ 2,…, λ n, dann sind sie linear unabhängig und können daher dem Raum R n zugrunde gelegt werden. Finden wir die Form der Matrix des linearen Operators A in der Basis seiner Eigenvektoren, für die wir mit dem Operator A auf den Basisvektoren agieren: dann .
Somit hat die Matrix des linearen Operators A in der Basis seiner Eigenvektoren eine Diagonalform und die Eigenwerte des Operators A befinden sich auf der Diagonalen.
Gibt es eine andere Basis, in der die Matrix diagonal ist? Die Antwort auf diese Frage gibt der folgende Satz.

Satz. Die Matrix eines linearen Operators A in der Basis (i = 1..n) hat genau dann eine Diagonalform, wenn alle Vektoren der Basis Eigenvektoren des Operators A sind.

Die Regel zum Finden von Eigenwerten und Eigenvektoren

Sei ein Vektor gegeben , wobei x 1, x 2, ..., x n die Koordinaten des Vektors relativ zur Basis sind und ist der Eigenvektor des linearen Operators A entsprechend dem Eigenwert λ, d.h. Diese Beziehung kann in Matrixform geschrieben werden

. (*)

Gleichung (*) kann als Gleichung zum Finden betrachtet werden, das heißt, wir interessieren uns für nicht-triviale Lösungen, da der Eigenvektor nicht Null sein kann. Es ist bekannt, dass nichttriviale Lösungen eines homogenen linearen Gleichungssystems genau dann existieren, wenn det (A - λE) = 0. Damit λ ein Eigenwert des Operators A ist, ist es also notwendig und ausreichend, dass det (A - E) = 0.
Wird die Gleichung (*) detailliert in Koordinatenform geschrieben, erhalten wir ein lineares homogenes Gleichungssystem:

(1)
wo ist die Matrix des linearen Operators.

System (1) hat eine von Null verschiedene Lösung, wenn seine Determinante D gleich Null ist

Habe eine Gleichung zum Finden der Eigenwerte erhalten.
Diese Gleichung heißt charakteristische Gleichung und ihre linke Seite heißt charakteristisches Polynom der Matrix (Operator) A. Wenn das charakteristische Polynom keine reellen Wurzeln hat, dann hat die Matrix A keine Eigenvektoren und kann nicht auf die Diagonalform reduziert werden .
Seien λ 1, λ 2,…, λ n reelle Nullstellen der charakteristischen Gleichung, und unter diesen können mehrere Nullstellen sein. Setzen wir diese Werte wiederum in das System (1) ein, finden wir die Eigenvektoren.

Beispiel 12. Der Linearoperator A wirkt in R 3 nach dem Gesetz, wobei x 1, x 2, .., x n die Koordinaten des Vektors in der Basis sind , , ... Finden Sie die Eigenwerte und Eigenvektoren dieses Operators.
Lösung. Wir bauen die Matrix dieses Operators:
.
Wir stellen ein System zur Bestimmung der Koordinaten von Eigenvektoren zusammen:

Wir stellen eine charakteristische Gleichung auf und lösen sie:

.
1,2 = -1, λ 3 = 3.
Setzen wir λ = -1 in das System ein, erhalten wir:
oder
Als , dann gibt es zwei abhängige Variablen und eine freie Variable.
Sei x 1 eine freie Unbekannte, dann Wir lösen dieses System auf beliebige Weise und finden eine allgemeine Lösung für dieses System: Das fundamentale Lösungssystem besteht aus einer Lösung, da n - r = 3 - 2 = 1.
Die dem Eigenwert λ = -1 entsprechende Menge von Eigenvektoren hat die Form:, wobei x 1 eine beliebige Zahl ungleich Null ist. Wählen wir einen Vektor aus dieser Menge aus, zum Beispiel setzen wir x 1 = 1: .
Ähnlich argumentieren wir den Eigenvektor zum Eigenwert λ = 3: .
Im Raum R 3 besteht die Basis aus drei linear unabhängigen Vektoren, wir haben aber nur zwei linear unabhängige Eigenvektoren erhalten, aus denen sich die Basis in R 3 nicht zusammensetzen lässt. Folglich kann die Matrix A des linearen Operators nicht auf eine Diagonalform reduziert werden.

Beispiel 13. Gegeben eine Matrix .
1. Beweisen Sie, dass der Vektor ist ein Eigenvektor der Matrix A. Finden Sie den Eigenwert, der diesem Eigenvektor entspricht.
2. Finden Sie eine Basis, in der die Matrix A eine Diagonalform hat.
Lösung.
1. Wenn, dann - Eigenvektor

.
Vektor (1, 8, -1) ist ein Eigenvektor. Eigenwert λ = -1.
Die Matrix hat eine Diagonalform in der Basis bestehend aus Eigenvektoren. Einer von ihnen ist berühmt. Lass uns den Rest finden.
Wir suchen nach Eigenvektoren aus dem System:

Charakteristische Gleichung: ;
(3 + ) [- 2 (2-λ) (2 + λ) +3] = 0; (3 + λ) (λ 2 - 1) = 0
1 = -3, 2 = 1, λ 3 = -1.
Finden wir den Eigenvektor zum Eigenwert λ = -3:

Der Rang der Matrix dieses Systems ist gleich zwei und ist gleich der Anzahl der Unbekannten, daher hat dieses System nur eine Nulllösung x 1 = x 3 = 0. x 2 kann hier jede beliebige Nicht-Null sein, zum Beispiel x 2 = 1. Somit ist der Vektor (0 , 1,0) ein Eigenvektor entsprechend λ = -3. Lass uns das Prüfen:
.
Ist λ = 1, dann erhalten wir das System
Der Rang der Matrix ist zwei. Wir löschen die letzte Gleichung.
Sei x 3 eine freie Unbekannte. Dann x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Bei x 3 = 1 haben wir (-3, -9,1) - den Eigenvektor entsprechend dem Eigenwert λ = 1. Nachweis:

.
Da die Eigenwerte reell und verschieden sind, sind die ihnen entsprechenden Vektoren linear unabhängig, können also in R 3 zugrunde gelegt werden. Also in der Basis , , Matrix A hat die Form:
.
Nicht jede Matrix eines linearen Operators A: R n → R n lässt sich auf die Diagonalform reduzieren, da für einige lineare Operatoren linear unabhängige Eigenvektoren kleiner als n sein können. Wenn die Matrix jedoch symmetrisch ist, entsprechen genau m linear unabhängige Vektoren der Wurzel der charakteristischen Multiplizitätsgleichung m.

Definition. Eine symmetrische Matrix ist eine quadratische Matrix, in der die in Bezug auf die Hauptdiagonale symmetrischen Elemente gleich sind, dh in der.
Bemerkungen. 1. Alle Eigenwerte einer symmetrischen Matrix sind reell.
2. Die Eigenvektoren einer symmetrischen Matrix, die paarweise unterschiedlichen Eigenwerten entsprechen, sind orthogonal.
Betrachten wir als eine der vielen Anwendungen der untersuchten Apparatur das Problem der Bestimmung der Form einer Kurve zweiter Ordnung.