Разширете серия на Фурие и изградете графики. Висша математика

На които вече им е писнало от поръчката. И чувствам, че е настъпил моментът, когато е време да се извлекат нови консерви от стратегическите резерви на теорията. Има ли някакъв друг начин за разширяване на функцията в серия? Например, изразете сегмент от права линия по отношение на синуси и косинуси? Изглежда невероятно, но такива привидно далечни функции са подходящи
„Обединение“. В допълнение към познатите степени в теорията и практиката, има и други подходи за разширяване на функция в серия.

В този урок ще се запознаем с тригонометричния ред на Фурие, ще засегнем въпроса за неговата конвергенция и сума и, разбира се, ще анализираме многобройни примери за разширяване на функциите в ред на Фурие. Искрено исках да нарека статията „Серия на Фурие за манекени“, но това би било лукаво, тъй като решаването на задачи изисква познаване на други клонове на математическия анализ и известен практически опит. Следователно преамбюлът ще прилича на обучението на астронавти =)

Първо, изучаването на материалите на страницата трябва да се подхожда в отлична форма. Спи, отпочинало и трезво. Без силни емоции за счупена лапа на хамстер и натрапчиви мисли за трудностите на живота на аквариумните рибки. Серията на Фурие не е трудна от гледна точка на разбирането, но практическите задачи просто изискват повишена концентрация на внимание - в идеалния случай човек трябва напълно да изостави външните стимули. Ситуацията се влошава от факта, че няма лесен начин за проверка на решението и отговор. По този начин, ако се чувствате под средното, тогава е по-добре да направите нещо по-просто. Истина.

Второ, преди да полетите в космоса, е необходимо да разгледате арматурното табло на космическия кораб. Нека започнем със стойностите на функциите, върху които трябва да щракнете върху автомата:

За всяка естествена стойност:

1) . Всъщност синусоидата "зашива" абсцисата през всяко "пи":
... В случай на отрицателни стойности на аргумента, резултатът, разбира се, ще бъде същият:.

2). Но не всички знаеха това. Косинусът "pi en" е еквивалент на "мигач":

Отрицателен аргумент не се променя: .

Може би това е достатъчно.

И трето, уважаван корпус на космонавтите, трябва да можете да ... интегрирайте.
По-специално, уверено приведете функция под диференциалния знак, интегрирайте парче по парчеи бъдете в добри отношения с по формулата на Нютон-Лайбниц... Нека започнем с някои важни упражнения преди полета. Категорично не препоръчвам да го пропускате, за да не се сплеска по-късно при нулева гравитация:

Пример 1

Изчисляване на определени интеграли

където приема природни стойности.

Решение: интегрирането се извършва върху променливата "x" и на този етап дискретната променлива "en" се счита за постоянна. Във всички интеграли привеждаме функцията под диференциалния знак:

Кратка версия на решението, която би било добре да се насочи, изглежда така:

Свиквам с:

Останалите четири елемента са ваши. Опитайте се да бъдете съвестни по отношение на задачата и начертайте интегралите по кратък начин. Примерни решения в края на урока.

След КАЧЕСТВЕНО изпълнение на упражненията обличаме скафандри
и се готви да започнем!

Разширяване на функция в ред на Фурие на интервал

Помислете за някаква функция, която дефиниранпоне в интервала (и евентуално в по-голям интервал). Ако тази функция е интегрируема в сегмент, тогава тя може да бъде разширена в тригонометрична Ред на Фурие:
, където са т.нар Коефициенти на Фурие.

В този случай номерът се извиква период на разлаганеи числото е разлагане на полуразпад.

Очевидно в общия случай редът на Фурие се състои от синуси и косинуси:

Всъщност, ние ще го опишем подробно:

Обичайно е да се записва нулевият член на поредицата във формата.

Коефициентите на Фурие се изчисляват по следните формули:

Напълно разбирам, че новите термини все още са слабо разбрани за начинаещи да изучават темата: период на разлагане, полупериод, Коефициенти на Фуриеи т.н. Без паника, това не е сравнимо с вълнението преди излизане в космоса. Ще разберем всичко в следващия пример, преди да изпълним който е логично да зададем належащи практически въпроси:

Какво трябва да се направи в следните задачи?

Разширете функцията в серия на Фурие. Освен това често се изисква да се изобрази графика на функция, графика на сумата от поредица, частична сума, а в случай на сложни професорски фантазии - да се направи нещо друго.

Как да разширим функция в ред на Фурие?

По същество трябва да намерите Коефициенти на Фурие, тоест съставете и изчислите три определен интеграл.

Моля, пренапишете общия изглед на серията на Фурие и трите работни формули в бележника си. Много се радвам, че някои от посетителите на сайта имат детска мечта да стана космонавт, която се сбъдва точно пред очите ми =)

Пример 2

Разширете функцията в серия на Фурие на интервала. Изградете графика, графика на сумата на редовете и частичната сума.

Решение: Първата част от задачата е да се разшири функцията в ред на Фурие.

Началото е стандартно, не забравяйте да запишете това:

В този проблем периодът на разлагане е полупериод.

Разширяваме функцията в ред на Фурие на интервала:

Използвайки съответните формули, намираме Коефициенти на Фурие... Сега трябва да съставите и изчислите три определен интеграл... За улеснение ще номерирам артикулите:

1) Първият интеграл е най-простият, но той вече изисква око и око:

2) Използваме втората формула:

Този интеграл е добре известен и взема се на части:

Когато бъде намерен, използван метод за подвеждане на функция под диференциалния знак.

В разглежданата задача е по-удобно да се използва незабавно формулата за интегриране по части в определен интеграл :

Няколко технически бележки. Първо, след прилагане на формулата целият израз трябва да бъде затворен в големи скоби, тъй като има константа пред оригиналния интеграл. Ние не го губим! Скобите могат да се отварят на всяка следваща стъпка, направих това последно. В първото "парче" ние сме изключително внимателни при заместването, както виждате, константата не работи, а границите на интегриране са заместени в продукта. Това действие е подчертано в квадратни скоби. Е, интегралът на второто "парче" от формулата ви е познат от тренировъчната задача ;-)

И най-важното е максималната концентрация на внимание!

3) Търсим третия коефициент на Фурие:

Получава се относителен на предишния интеграл, който също е интегрира на парче:

Този случай е малко по-сложен, ще коментирам следващите стъпки стъпка по стъпка:

(1) Изразът е изцяло затворен в големи скоби.... Не исках да звуча като скука, твърде често губят константа.

(2) В този случай веднага отворих тези големи скоби. Специално вниманиепосвещаваме на първото „парче“: постоянното пуши встрани и не участва в подмяната на границите на интеграция (и) в продукта. Поради претрупания запис отново е препоръчително да отбележите това действие с квадратни скоби. С второто "парче" всичко е по-просто: тук дробът се появи след разширяването на големи скоби, а константата - в резултат на интегриране на познатия интеграл ;-)

(3) Извършваме трансформации в квадратни скоби и заместване на границите на интегриране в десния интеграл.

(4) Изваждаме "мигащата светлина" от квадратните скоби:, след което отваряме вътрешните скоби:.

(5) Намалете 1 и –1 в скоби, направете окончателни опростявания.

Накрая са намерени и трите коефициента на Фурие:

Нека ги заменим във формулата :

В същото време не забравяйте да разделите наполовина. На последната стъпка константата ("минус две"), която не зависи от "en", се премества извън сумата.

Така получихме разширението на функцията в ред на Фурие на интервала:

Нека проучим въпроса за сходимостта на редовете на Фурие. Ще обясня по-специално теорията Теорема на Дирихле, буквално "на пръсти", така че ако имате нужда от строги формулировки, моля, вижте учебника по математически анализ (например 2-ри том на Бохан; или 3-ти том на Фихтенголц, но в него е по-трудно).

Във втората част на задачата трябва да покажете графика, графика за поредица и графика за частична сума.

Графиката на функциите е обикновена права, който е начертан с черна пунктирана линия:

Занимаваме се със сбора на поредицата. Както знаете, сериите от функции се сближават с функции. В нашия случай, конструираният ред на Фурие за всяка стойност на "x"се доближава до функцията, показана в червено. Тази функция толерира прекъсвания от 1-ви видв точки, но и дефинирани в тях (червени точки на чертежа)

Поради това: ... Лесно е да се види какво е забележимо различно от оригиналната функция, поради което в нотацията използва се тилда, а не знак за равенство.

Нека проучим алгоритъма, по който е удобно да се построи сумата от редицата.

На централния интервал редът на Фурие се сближава до самата функция (централният червен сегмент съвпада с черната пунктирана линия на линейната функция).

Сега нека спекулираме малко за естеството на разглежданото тригонометрично разлагане. В серия на Фурие Включени са само периодични функции (константа, синуси и косинуси), следователно сумата от редовете също е периодична функция.

Какво означава това в нашия конкретен пример? А това означава, че сумата на серията –със сигурност периодичнои червеният сегмент на интервала трябва да се повтаря безкрайно отляво и отдясно.

Мисля, че сега най-накрая стана ясно значението на израза "период на разпад". Казано по-просто, всяка ситуация се повтаря отново и отново.

На практика обикновено е достатъчно да се изобразят три периода на разлагане, както е направено на чертежа. Е, а също и "пънове" от съседни периоди - за да стане ясно, че графиката продължава.

Особен интерес представляват точки на прекъсване от 1-ви вид... В такива точки редът на Фурие се сближава до изолирани стойности, които се намират точно в средата на "скока" на прекъсването (червени точки на чертежа). Откъде знаете ординатата на тези точки? Първо намираме ординатата на "горния етаж": за това изчисляваме стойността на функцията в крайната дясна точка на централния период на разширение:. За да изчислите ординатата на "долния етаж", най-лесният начин е да вземете най-лявата стойност на същия период: ... Ординатата на средната е средноаритметичната на сумата "отгоре и отдолу":. Хубавото е, че при изграждането на чертеж веднага ще видите дали средата е правилно или неправилно изчислена.

Нека построим частичен сбор от редицата и в същото време да повторим значението на термина "конвергенция". Мотивът е известен и от урока за сумата на числов ред... Нека опишем подробно нашето богатство:

За да съставите частична сума, е необходимо да запишете нула + още два члена от поредицата. Това е,

На чертежа функционалната графика е показана в зелено и, както можете да видите, тя обвива цялата сума доста плътно. Ако разгледаме частичния сбор от пет члена на серията, тогава графиката на тази функция ще приближи червените линии още по-точно, ако има сто члена, тогава "зелената змия" всъщност ще се слее напълно с червените сегменти, и т.н. Така редът на Фурие се сближава до своя сбор.

Интересно е да се отбележи, че всяка частична сума е непрекъсната функция, обаче, общият сбор на серията все още е прекъснат.

На практика не е необичайно да се начертае и частична сума. Как да го направим? В нашия случай е необходимо да разгледаме функция на сегмент, да изчислим нейните стойности в краищата на сегмента и в междинните точки (колкото повече точки разглеждате, толкова по-точна ще бъде графиката). След това трябва да маркирате тези точки на чертежа и точно да изобразите графиката върху периода и след това да я "репликирате" на съседни интервали. Как иначе? Все пак приближението също е периодична функция ... ... графиката му някак ми напомня за равномерен пулс на дисплея на медицинско устройство.

Разбира се, не е много удобно да се извършва конструкцията, тъй като трябва да сте супер точни, поддържайки точност не по-малко от половин милиметър. Все пак ще зарадвам читателите, които не са в тон с рисуването - при "реална" задача рисуването не винаги е необходимо, някъде в 50% от случаите се изисква разширяване на функцията в серия на Фурие и това е всичко.

След като завършим чертежа, изпълняваме задачата:

Отговор:

При много задачи функцията страда прекъсване от 1-ви видточно в периода на разлагане:

Пример 3

Разширете в серия на Фурие функцията, посочена в сегмента. Начертайте функцията и общата сума на серията.

Предложената функция е дадена на части (при това, имайте предвид, само в сегмента)и издържа прекъсване от 1-ви видв точката. Могат ли да се изчислят коефициентите на Фурие? Няма проблем. И лявата, и дясната част на функцията са интегрируеми на своите интервали, следователно интегралите във всяка от трите формули трябва да бъдат представени като сума от два интеграла. Нека видим например как се прави това с нулев коефициент:

Вторият интеграл се оказа равен на нула, което намали работата, но това не винаги е така.

Другите два коефициента на Фурие се записват по същия начин.

Как да представим сумата от серия? На левия интервал начертаваме сегмент от права линия, а на интервала - сегмент от права линия (изберете секцията на оста с удебелен и удебелен шрифт). Тоест на интервала на разширение сумата от серията съвпада с функцията навсякъде, с изключение на три "лоши" точки. В точката на прекъсване на функцията редът на Фурие се сближава до изолирана стойност, която се намира точно в средата на „скока“ на прекъсването. Не е трудно да го видите устно: ляво ограничение:, дясно ограничение: и очевидно ординатата на средната точка е 0,5.

Поради периодичността на сумата, картината трябва да бъде "умножена" по съседни периоди, по-специално, за да се изобрази същото на интервалите и. В този случай в точките редът на Фурие се сближава до средните стойности.

Всъщност тук няма нищо ново.

Опитайте се сами да се справите с тази задача. Приблизителна извадка от довършителния дизайн и чертеж в края на урока.

Разширяване на функция в ред на Фурие върху произволен период

За произволен период на разширение, където "el" е всяко положително число, формулите за редовете на Фурие и коефициентите на Фурие се различават по малко сложен аргумент на синус и косинус:

Ако, тогава получаваме формулите за пропуски, с които започнахме.

Алгоритъмът и принципите за решаване на проблема са напълно запазени, но техническата сложност на изчисленията се увеличава:

Пример 4

Разширете функцията в ред на Фурие и начертайте сумата.

Решение: всъщност аналог на Пример № 3 с прекъсване от 1-ви видв точката. В този проблем периодът на разлагане е полупериод. Функцията се дефинира само на полуинтервал, но това не променя въпроса - важно е и двете части на функцията да са интегрируеми.

Нека разширим функцията в ред на Фурие:

Тъй като функцията е прекъсната в началото, всеки коефициент на Фурие очевидно трябва да бъде записан като сума от два интеграла:

1) Ще напиша първия интеграл възможно най-подробно:

2) Внимателно се вглеждаме в повърхността на Луната:

Втори интеграл вземете на части:

На какво трябва да обърнете специално внимание, след като отворим продължението на решението със звездичка?

Първо, не губим първия интеграл , където незабавно изпълняваме диференциален знак... Второ, не забравяйте злощастната константа пред големите скоби и не се бъркайте в знацитекогато използвате формулата ... Големите скоби обаче е по-удобно да ги отворите веднага на следващата стъпка.

Останалото е въпрос на технология, трудности могат да бъдат причинени само от недостатъчен опит в решаването на интеграли.

Да, не напразно видните колеги на френския математик Фурие бяха възмутени - как се осмели да разложи функциите на тригонометрични редове ?! =) Между другото, сигурно всеки се интересува от практическия смисъл на въпросната задача. Самият Фурие работи върху математически модел на топлопроводимост, а по-късно серията, наречена на негово име, започва да се използва за изследване на много периодични процеси, които очевидно са невидими в околния свят. Сега, между другото, се хванах на мисълта, че неслучайно сравних графиката на втория пример с периодичен пулс. Желаещите могат да се запознаят с практическото приложение Преобразуване на Фуриев източници на трети страни. ... Въпреки че е по-добре не - ще бъде запомнено като Първата любов =)

3) Като се вземат предвид многократно споменаваните слаби връзки, ние се занимаваме с третия коефициент:

Интегрираме парче по парче:

Заместете намерените коефициенти на Фурие във формулата , като не забравяме да разделим нулевия коефициент наполовина:

Нека начертаем сбора на поредицата. Нека повторим накратко процедурата: построете права линия върху интервал и права линия върху интервал. Ако стойността на x е нула, поставяме точка в средата на празнината „скок“ и „възпроизвеждане“ на диаграмата за съседни периоди:

В „пресичанията“ на периодите сумата също ще бъде равна на средните точки на „скока“ на пропастта.

Готов. Нека ви напомня, че самата функция по хипотеза е дефинирана само на полуинтервал и, очевидно, съвпада със сумата от редица на интервалите

Отговор:

Понякога дадена функция на парчета също е непрекъсната през периода на разширяване. Най-простият пример: ... Решение (вижте 2-ри том на Бохан)е същото като в двата предишни примера: въпреки непрекъснатост на функциятав точка всеки коефициент на Фурие се изразява като сума от два интеграла.

В интервала на разлагане точки на прекъсване от 1-ви види/или точките на "свързочни точки" на графиката могат да бъдат повече (две, три и обикновено всякакви финалътномер). Ако функцията е интегрируема за всяка част, тогава тя също може да бъде разширена в ред на Фурие. Но от практически опит не помня толкова трудно нещо. Въпреки това има по-трудни задачи от току-що разгледаната и в края на статията за всички има връзки към серия на Фурие с повишена сложност.

Междувременно нека се отпуснем, облегнати се на столове и съзерцавайки безкрайните звездни простори:

Пример 5

Разширете функцията в серия на Фурие върху интервала и начертайте сумата на серията.

В този проблем функцията непрекъснатовърху полуинтервала на разлагане, което опростява решението. Всичко е много подобно на Пример №2. Няма бягство от космическия кораб - трябва да решите =) Примерен дизайн в края на урока, графикът е приложен.

Разлагане в ред на Фурие на четни и нечетни функции

С четни и нечетни функции процесът на решаване на проблем е забележимо опростен. И ето защо. Нека се върнем към разширяването на функцията в ред на Фурие за периода "два пи" и произволна точка "два ейла" .

Да приемем, че нашата функция е четна. Общият термин на серията, както можете да видите, съдържа четни косинуси и нечетни синуси. И ако разширим функция EVEN, тогава защо имаме нужда от нечетни синуси ?! Нека нулираме ненужния коефициент:.

Поради това, четна функция може да бъде разширена в ред на Фурие само в косинуси:

Дотолкова доколкото интеграли от четни функциивърху сегмент от интегриране, симетричен спрямо нула, може да се удвои, тогава останалите коефициенти на Фурие също се опростяват.

За празнината:

За произволен интервал:

Примерите от учебници, които могат да бъдат намерени в почти всеки учебник по смятане, включват разлагане на четни функции ... Освен това те многократно са се срещали в моята лична практика:

Пример 6

Дадена е функция. Задължително:

1) разширяване на функцията в ред на Фурие с период, където е произволно положително число;

2) запишете разширението на интервала, изградете функция и графика на общата сума на редицата.

Решение: в първия параграф се предлага да се реши проблемът в общ вид и е много удобно! Ще се появи нуждата - просто заменете стойността си.

1) В този проблем периодът на разширяване е полупериод. В хода на по-нататъшни действия, по-специално по време на интеграция, "el" се счита за константа

Функцията е четна, което означава, че може да бъде разширена в ред на Фурие само в косинуси: .

Търсим коефициентите на Фурие по формулите ... Обърнете внимание на безусловните им ползи. Първо, интеграцията се извършва върху положителния сегмент на разширението, което означава, че безопасно се отърваваме от модула , като се има предвид само "X" от две парчета. И, второ, интеграцията е забележимо опростена.

две:

Интегрираме парче по парче:

Поради това:
, в този случай от сумата се изважда константата, която не зависи от "en".

Отговор:

2) Записваме разширението на интервала, за това заместваме необходимата стойност на полупериода в общата формула:

Министерство на общото и професионалното образование

Сочи държавен университет по туризъм

и курортен бизнес

Педагогически институт

Факултет по математика

Катедра Обща математика

ДИПЛОМНА РАБОТА

Редове на Фурие и техните приложения

В математическата физика.

Изпълнено от: студент 5 курс

подпис на пълен работен ден

Специалност 010100

"математика"

Касперова Н.С.

Номер на студентска карта 95471

Научен ръководител: доцент, канд.

технически подпис науки

Позин П.А.

Сочи, 2000 г

1. Въведение.

2. Концепцията за ред на Фурие.

2.1. Определяне на коефициентите на реда на Фурие.

2.2. Интеграли от периодични функции.

3. Критерии за сходимост на редовете на Фурие.

3.1. Примери за разширяване на функции в ред на Фурие.

4. Забележка относно разширяването на периодична функция в ред на Фурие

5. Ред на Фурие за четни и нечетни функции.

6. Ред на Фурие за функции с период 2 л .

7. Разлагане в ред на Фурие на непериодична функция.

Въведение.

Жан Батист Жозеф Фурие - френски математик, член на Парижката академия на науките (1817).

Първите произведения на Фурие са свързани с алгебрата. Още в лекции през 1796 г. той излага теорема за броя на реалните корени на алгебрично уравнение, лежащи между дадените граници (публ. 1820 г.), наречена на негово име; пълно решение за броя на реалните корени на алгебрично уравнение е получено през 1829 г. от Ж.Ш.Ф. Чрез буря. През 1818 г. Фурие изследва въпроса за условията за приложимост на метода за числено решение на уравнения, разработен от Нютон, без да знае за подобни резултати, получени през 1768 г. от френския математик Дж.Р. Мураилем. Резултатът от работата на Фурие върху числените методи за решаване на уравнения е "Анализ на някои уравнения", публикуван посмъртно през 1831г.

Основната област на обучение на Фурие е математическата физика. През 1807 и 1811 г. той представя първите си открития относно теорията за разпространението на топлината в твърди тела на Парижката академия на науките, а през 1822 г. публикува известната си работа „Аналитична теория на топлината“, която изиграва важна роля в последващата история на математиката. Това е математическата теория на топлопроводимостта. По силата на общостта на метода, тази книга се превърна в източник на всички съвременни методи на математическата физика. В тази работа Фурие извежда диференциалното уравнение на топлопроводимостта и развива идеите, очертани по-рано от Д. Бернули, разработва метод за разделяне на променливите (метод на Фурие) за решаване на топлинното уравнение при определени зададени гранични условия, който прилага към брой специални случаи (куб, цилиндър и др.). Този метод се основава на представянето на функциите чрез тригонометричен ред на Фурие.

Редовете на Фурие вече се превърнаха в добре развит инструмент в теорията на частните диференциални уравнения за решаване на гранични задачи.

1. Концепцията за ред на Фурие.(стр. 94, Уваренков)

Редовете на Фурие играят важна роля в математическата физика, теорията на еластичността, електротехниката и особено техния специален случай - тригонометричен ред на Фурие.

Тригонометричен ред е поредица от формата

или символично:

(1)

където ω, a 0, a 1,…, a n,…, b 0, b 1,…, b n,… са постоянни числа (ω> 0).

Исторически някои проблеми във физиката са довели до изучаването на такива серии, например проблемът за вибрациите на струните (18 век), проблемът за закономерностите в явленията на топлопроводимост и др. В приложенията, разглеждането на тригонометрични редове , се свързва предимно с проблема за представяне на дадено движение, описано с уравнението y = ƒ (x), в

формата на сбора от най-простите хармонични вибрации, често взети в безкрайно голям брой, т.е. като сума от поредица от вида (1).

Така стигаме до следния проблем: разберете дали за дадена функция ƒ (x) на даден интервал съществува серия (1), която би се сближила на този интервал към тази функция. Ако това е възможно, тогава функцията ƒ (x) се казва, че е разширена в тригонометричен ред на този интервал.

Ред (1) се сближава в някаква точка x 0, поради периодичността на функциите

(n = 1,2, ..), то се оказва сходящо във всички точки от формата (m е всяко цяло число) и по този начин сумата му S (x) ще бъде (в областта на сходимост на реда) периодична функция: ако S n ( x) е n-тата частична сума от тази серия, тогава имаме

и следователно

, тоест S (x 0 + T) = S (x 0). Следователно, като говорим за разширяване на някаква функция ƒ (x) в поредица от вида (1), ще приемем, че ƒ (x) е периодична функция.

2. Определяне на коефициентите на реда по формулите на Фурие.

Нека периодична функция ƒ (x) с период 2π е такава, че да е представена от тригонометричен ред, сближаващ се към дадена функция в интервала (-π, π), т.е. е сумата от тази серия:

. (2)

Да предположим, че интегралът от функцията от лявата страна на това равенство е равен на сумата от интегралите на членовете на тази серия. Това ще стане, ако приемем, че числовият ред, съставен от коефициентите на даден тригонометричен ред, се сближава абсолютно, т.е.

(3)

Редът (1) е мажоризиран и може да бъде интегриран член по член в интервала (-π, π). Интегрираме двете страни на равенството (2):

Изчисляваме отделно всеки интеграл от дясната страна:

, .

Поради това,

, където

. (4)

Оценка на коефициентите на Фурие.(Бугров)

Теорема 1. Нека функцията ƒ (x) от период 2π има непрекъсната производна ƒ ( s) (x) от порядъка s, удовлетворяващо неравенството по цялата реална ос:

│ ƒ (s) (x) │≤ M s; (5)

след това коефициентите на Фурие на функцията ƒ удовлетворява неравенството

(6)

Доказателство. Интегриране по части и отчитане на това

ƒ (-π) = ƒ (π), имаме

Интегриране на дясната страна на (7) последователно, като се има предвид, че производните ƒ ΄, ..., ƒ (s-1) са непрекъснати и приемат едни и същи стойности в точките t = -π и t = π, както и оценка (5), получаваме първата оценка ( 6).

Втората оценка (6) се получава по подобен начин.

Теорема 2. Коефициентите на Фурие ƒ (x) удовлетворяват неравенството

(8)

Доказателство. Ние имаме

Редът на Фурие е представяне на произволна функция с определен период под формата на серия. Най-общо това решение се нарича разширяване на елемент в ортогонална основа. Разширяването на функциите в серия на Фурие е доста мощен инструментариум за решаване на различни проблеми поради свойствата на тази трансформация по време на интегриране, диференциране, както и изместване на израз чрез аргумент и конволюция.

Човек, който не е запознат с висшата математика, както и с трудовете на френския учен Фурие, най-вероятно няма да разбере какви са "ранговете" и за какво са те. Междувременно тази трансформация се превърна в доста плътна част от нашия живот. Използва се не само от математици, но и от физици, химици, лекари, астрономи, сеизмолози, океанографи и много други. Нека разгледаме по-отблизо трудовете на великия френски учен, който направи откритие, изпреварващо времето си.

Човек и трансформация на Фурие

Редът на Фурие е един от методите (заедно с анализа и други) Този процес се случва всеки път, когато човек чуе звук. Нашето ухо автоматично трансформира елементарни частици в еластична среда, които се разлагат на редове (по протежение на спектъра) от последователни стойности на нивото на силата на звука за тонове с различна височина. Освен това мозъкът превръща тези данни в познати за нас звуци. Всичко това се случва отделно от нашето желание или съзнание, от само себе си, но за да разберем тези процеси, ще са необходими няколко години, за да изучаваме висшата математика.

Повече за преобразуването на Фурие

Преобразуването на Фурие може да се извърши с помощта на аналитични, числови и други методи. Редът на Фурие се отнася до числовото разлагане на всеки осцилаторен процес - от океанските приливи и светлинни вълни до циклите на слънчева (и други астрономически обекти) активност. Използвайки тези математически техники, можете да анализирате функции, представящи всякакви осцилаторни процеси като серия от синусоидални компоненти, които преминават от минимум към максимум и обратно. Преобразуването на Фурие е функция, която описва фазата и амплитудата на синусоидите при определена честота. Този процес може да се използва за решаване на много сложни уравнения, които описват динамични процеси, възникващи под въздействието на топлинна, светлинна или електрическа енергия. Също така, сериите на Фурие позволяват да се отделят постоянните компоненти в сложни осцилаторни сигнали, поради което стана възможно правилно да се интерпретират получените експериментални наблюдения в медицината, химията и астрономията.

Историческа справка

Основателят на тази теория е френският математик Жан Батист Жозеф Фурие. По-късно тази трансформация е кръстена на него. Първоначално ученият прилага своя метод за изследване и обяснение на механизмите на топлопроводимост – разпространението на топлината в твърдите тела. Фурие предполага, че първоначалното неправилно разпределение може да бъде разложено на най-простите синусоиди, всяка от които ще има свой температурен минимум и максимум, както и своя собствена фаза. Освен това всеки такъв компонент ще бъде измерен от минимум до максимум и обратно. Математическата функция, която описва горния и долния пик на кривата, както и фазата на всеки от хармониците, се нарича преобразуване на Фурие на израза за разпределение на температурата. Авторът на теорията свежда общата функция на разпределение, която е трудно да се опише математически, до много удобен ред от косинус и синус, които заедно дават оригиналното разпределение.

Принципът на трансформацията и възгледите на съвременниците

Съвременниците на учения - водещите математици от началото на деветнадесети век - не приемат тази теория. Основното възражение беше твърдението на Фурие, че прекъсната функция, описваща права линия или прекъсната крива, може да бъде представена като сбор от синусоидални изрази, които са непрекъснати. Като пример, разгледайте "стъпката" на Хевисайд: нейната стойност е равна на нула вляво от празнината и една вдясно. Тази функция описва зависимостта на електрическия ток от времевата променлива, когато веригата е затворена. Съвременниците на теорията по това време никога не са се сблъсквали с подобна ситуация, когато прекъснат израз ще бъде описан чрез комбинация от непрекъснати, обикновени функции като експоненциална, синусоидна, линейна или квадратична.

Какво обърка френските математици относно теорията на Фурие?

В крайна сметка, ако математикът е бил прав в своите твърдения, тогава чрез сумиране на безкрайния тригонометричен ред на Фурие може да се получи точно представяне на стъпаловидно израз, дори ако има много такива стъпки. В началото на деветнадесети век подобно твърдение изглеждаше абсурдно. Но въпреки всички съмнения, много математици разшириха обхвата на изследването на това явление, извеждайки го извън обхвата на изследванията на топлопроводимостта. Повечето учени обаче продължиха да се измъчват от въпроса: „Може ли сумата от синусоидален ред да се сближи с точната стойност на прекъснатата функция?“

Сходимост на редовете на Фурие: пример

Въпросът за конвергенцията се повдига винаги, когато е необходимо да се сумират безкрайни серии от числа. За да разберете това явление, разгледайте класически пример. Ще успеете ли някога да стигнете до стената, ако всяка следваща стъпка е наполовина по-малка от предишната? Да предположим, че сте на два метра от целта, първата стъпка ви доближава до средата, следващата до три четвърти, а след петата ще покриете почти 97 процента от пътя. Въпреки това, колкото и стъпки да предприемете, няма да постигнете набелязаната цел в стриктния математически смисъл. Използвайки числени изчисления, можете да докажете, че в крайна сметка можете да се доближите до произволно малко зададено разстояние. Това доказателство е еквивалентно на демонстриране, че общата стойност на една половина, една четвърт и т.н. ще клони към единица.

Въпрос на сближаване: Второто пришествие, или апаратът на лорд Келвин

Този въпрос беше повдигнат отново в края на деветнадесети век, когато редът на Фурие се опита да се използва за прогнозиране на интензивността на приливите и отливите. През това време лорд Келвин изобретява устройство, аналогово изчислително устройство, което позволява на моряците от военния и търговския флот да проследяват този природен феномен. Този механизъм определя наборите от фази и амплитуди от таблица на височините на приливите и съответните им времеви моменти, внимателно измерени в дадено пристанище през цялата година. Всеки параметър беше синусоидален компонент на израза на височината на прилива и беше един от редовните компоненти. Резултатите от измерванията бяха въведени в калкулатора на лорд Келвин, който синтезира крива, която предсказва височината на водата като функция от времето за следващата година. Много скоро подобни криви бяха начертани за всички пристанища по света.

Ами ако процесът е нарушен от прекъсната функция?

По това време изглеждаше очевидно, че предикторът на приливните вълни с голям брой отброявания може да изчисли голям брой фази и амплитуди и така да осигури по-точни прогнози. Въпреки това се оказа, че този модел не се наблюдава в случаите, когато приливният израз, който трябва да бъде синтезиран, съдържа рязък скок, тоест беше прекъснат. В случай, че в устройството се въвеждат данни от таблицата с времеви моменти, то изчислява няколко коефициента на Фурие. Оригиналната функция се възстановява благодарение на синусоидалните компоненти (в съответствие с намерените коефициенти). Несъответствието между оригиналния и реконструирания израз може да бъде измерено във всяка точка. При извършване на многократни изчисления и сравнения се вижда, че стойността на най-голямата грешка не намалява. Въпреки това, те са локализирани в областта, съответстваща на точката на прекъсване, а във всяка друга точка те клонят към нула. През 1899 г. този резултат е теоретично потвърден от Джошуа Уилард Гибс от Йейлския университет.

Сближаване на редовете на Фурие и развитието на математиката като цяло

Анализът на Фурие не е приложим за изрази, съдържащи безкраен брой пакети на определен интервал. Като цяло, редовете на Фурие, ако първоначалната функция е представена от резултата от реално физическо измерване, винаги се сближават. Въпросите за конвергенцията на този процес за конкретни класове функции доведоха до появата на нови клонове в математиката, например теорията на обобщените функции. Свързва се с имена като Л. Шварц, Дж. Микусински и Дж. Темпъл. В рамките на тази теория беше създадена ясна и точна теоретична основа за такива изрази като делта функцията на Дирак (тоя описва област от една област, концентрирана в безкрайно малка околност на точка) и "стъпката" на Хевисайд . Благодарение на тази работа, редът на Фурие стана приложим за решаване на уравнения и задачи, в които се появяват интуитивни понятия: точков заряд, точкова маса, магнитни диполи, както и концентрирано натоварване върху лъч.

Метод на Фурие

Редът на Фурие, в съответствие с принципите на интерференцията, започва с разлагането на сложни форми в по-прости. Например промяната в топлинния поток се обяснява с преминаването му през различни препятствия, изработени от топлоизолационен материал с неправилна форма или с промяна в земната повърхност - земетресение, промяна в орбитата на небесно тяло - с влияние на планетите. По правило такива уравнения, описващи прости класически системи, могат лесно да бъдат решени за всяка отделна вълна. Фурие показа, че простите решения също могат да бъдат сумирани, за да се получат решения на по-сложни проблеми. На езика на математиката редът на Фурие е техника за представяне на израз като сума от хармоници - косинус и синусоиди. Следователно този анализ е известен още като "хармоничен анализ".

Серията на Фурие - идеалната техника преди "компютърната ера"

Преди създаването на компютърните технологии, техниката на Фурие беше най-доброто оръжие в арсенала на учените при работа с вълновата природа на нашия свят. Редът на Фурие в сложна форма дава възможност да се решават не само прости задачи, които се поддават на директно прилагане на законите на механиката на Нютон, но и фундаментални уравнения. Повечето от откритията на Нютоновата наука през деветнадесети век стават възможни само чрез метода на Фурие.

Серията на Фурие днес

С развитието на компютрите трансформациите на Фурие се издигнаха на качествено ново ниво. Тази техника е здраво закрепена в почти всички области на науката и технологиите. Примерите включват цифрово аудио и видео. Неговото изпълнение става възможно само благодарение на теория, разработена от френски математик в началото на деветнадесети век. По този начин редът на Фурие в сложна форма позволи да се направи пробив в изследването на космическото пространство. Освен това той повлия на изучаването на физиката на полупроводниковите материали и плазмата, микровълновата акустика, океанографията, радара, сеизмологията.

Тригонометричен ред на Фурие

В математиката редът на Фурие е начин за представяне на произволни сложни функции като сбор от по-прости. В общи случаи броят на такива изрази може да бъде безкраен. Освен това, колкото повече се вземе предвид техният брой при изчислението, толкова по-точно се получава крайният резултат. Най-често тригонометричните косинусови или синусови функции се използват като най-прости. В този случай редът на Фурие се нарича тригонометричен, а решението на такива изрази се нарича хармонично разширение. Този метод играе важна роля в математиката. На първо място, тригонометричният ред осигурява средство за изображение, както и за изследване на функциите, той е основният апарат на теорията. Освен това ви позволява да решавате редица проблеми по математическа физика. И накрая, тази теория допринесе за развитието и породи редица много важни клонове на математическата наука (теория на интегралите, теория на периодичните функции). В допълнение, той послужи като отправна точка за развитието на следните функции на реална променлива, а също така положи основата на хармоничния анализ.

Функционира, като ги разделя на компоненти. Променливи токове и напрежения, премествания, скорост и ускорение на манивелата и акустични вълни са типични практически примери за използването на периодични функции в инженерните изчисления.

Разширението на редовете на Фурие се основава на предположението, че всички функции с практическо значение в интервала -π ≤x≤ π могат да бъдат изразени под формата на сближаващи се тригонометрични редове (ред се счита за сближаващ се, ако поредица от частични суми, съставена от нейните членове сближава):

Стандартна (= нормална) нотация чрез сбора от sinx и cosx

f (x) = a o + a 1 cosx + a 2 cos2x + a 3 cos3x + ... + b 1 sinx + b 2 sin2x + b 3 sin3x + ...,

където a o, a 1, a 2, ..., b 1, b 2, .. са реални константи, т.е.

Където, за диапазона от -π до π, коефициентите на реда на Фурие се изчисляват по формулите:

Коефициентите a o, a n и b n се наричат Коефициенти на Фурие, и ако те могат да бъдат намерени, тогава се нарича серия (1). до Фурие,съответстваща на функцията f (x). За серия (1) членът (a 1 cosx + b 1 sinx) се нарича първи или основна хармоника,

Друг начин да напишете серията е да използвате съотношението acosx + bsinx = csin (x + α)

f (x) = a o + c 1 sin (x + α 1) + c 2 sin (2x + α 2) + ... + c n sin (nx + α n)

Където ao е константа, с 1 = (a 1 2 + b 1 2) 1/2, с n = (an 2 + bn 2) 1/2 са амплитудите на различни компоненти и е равно на an = arctan an / b n.

За серия (1) терминът (a 1 cosx + b 1 sinx) или c 1 sin (x + α 1) се нарича първия или основна хармоника,(a 2 cos2x + b 2 sin2x) или c 2 sin (2x + α 2) се нарича втори хармоники т.н.

Обикновено са необходими безкраен брой термини, за да се представи точно сложен сигнал. Въпреки това, в много практически задачи е достатъчно да се разгледат само първите няколко термина.

Ред на Фурие от непериодични функции с период 2π.

Разширяване на непериодични функции в ред на Фурие.

Ако функцията f (x) е непериодична, тогава тя не може да бъде разширена в ред на Фурие за всички стойности на x. Въпреки това, можете да дефинирате серия на Фурие, представляваща функция във всеки 2π-широк диапазон.

Ако е посочена непериодична функция, можете да създадете нова функция, като вземете f (x) стойности в определен диапазон и ги повторите извън този диапазон на интервали от 2π. Тъй като новата функция е периодична с период от 2π, тя може да бъде разширена в ред на Фурие за всички стойности на x. Например, функцията f (x) = x не е периодична. Ако обаче е необходимо да се разшири в ред на Фурие в интервала от o до 2π, тогава извън този интервал се изгражда периодична функция с период 2π (както е показано на фигурата по-долу).

За непериодични функции като f (x) = x, сумата от редицата на Фурие е равна на стойността на f (x) във всички точки в дадения диапазон, но не е равна на f (x) за точки извън обхвата. За да се намери редът на Фурие на непериодична функция в диапазона 2π, се използва същата формула за коефициентите на Фурие.

Четни и нечетни функции.

Казват, че функцията y = f (x) дориако f (-x) = f (x) за всички стойности на x. Графиките на четните функции винаги са симетрични спрямо оста y (т.е. те са огледални). Два примера за четни функции: y = x 2 и y = cosx.

За функцията y = f (x) се казва, че е странно,ако f (-x) = - f (x) за всички стойности на x. Графиките на нечетните функции винаги са симетрични спрямо началото.

Много функции не са нито четни, нито нечетни.

Разлагане на Фурие в косинуси.

Редът на Фурие на четна периодична функция f (x) с период от 2π съдържа само членове с косинуси (т.е. не съдържа членове със синуси) и може да включва постоянен член. следователно,

където коефициентите на реда на Фурие,

Редът на Фурие на нечетна периодична функция f (x) с период от 2π съдържа само членове със синуси (т.е. не съдържа членове с косинуси).

следователно,

където коефициентите на реда на Фурие,

Полупериодна серия на Фурие.

Ако функция е дефинирана за диапазон, да речем от 0 до π, а не само от 0 до 2π, тя може да бъде разширена в серия само в синуси или само в косинуси. Полученият ред на Фурие се нарича до Фурие на полупериода.

Ако искате да получите разлагане Полупериод на Фурие в косинусифункция f (x) в диапазона от 0 до π, тогава е необходимо да се състави четна периодична функция. На фиг. функцията f (x) = x е показана по-долу, нанесена върху интервала от x = 0 до x = π. Тъй като четната функция е симетрична спрямо оста f (x), начертаваме линия AB, както е показано на фиг. По-долу. Ако приемем, че извън разглеждания интервал, получената триъгълна форма е периодична с период 2π, тогава крайната графика има вида, показващ. на фиг. По-долу. Тъй като е необходимо да се получи разширението на Фурие в косинуси, както преди, ние изчисляваме коефициентите на Фурие a o и a n

Ако е необходимо да се получат функции f (x) в диапазона от 0 до π, тогава е необходимо да се състави нечетна периодична функция. На фиг. функцията f (x) = x е показана по-долу, нанесена върху интервала от x = 0 до x = π. Тъй като нечетната функция е симетрична спрямо началото, ние начертаваме линията CD, както е показано на фиг. Ако приемем, че извън разглеждания интервал полученият трионообразен сигнал е периодичен с период 2π, тогава крайната графика има вида, показан на фиг. Тъй като е необходимо да се получи разлагането на Фурие в полупериод по синуси, както преди, ние изчисляваме коефициента на Фурие. б

Ред на Фурие за произволен интервал.

Разширяване на периодична функция с период L.

Периодичната функция f (x) се повтаря, когато x се увеличава с L, т.е. f (x + L) = f (x). Преходът от разгледаните по-рано функции с период 2π към функции с период L е доста прост, тъй като може да се извърши чрез промяна на променливата.

За да намерим редицата на Фурие на функцията f (x) в диапазона -L / 2≤x≤L / 2, въвеждаме нова променлива u, така че функцията f (x) да има период от 2π спрямо u. Ако u = 2πx / L, тогава x = -L / 2 за u = -π и x = L / 2 за u = π. Също така нека f (x) = f (Lu / 2π) = F (u). Редът на Фурие F (u) има формата

Къде са коефициентите на реда на Фурие,

По-често обаче горната формула води до зависимост от x. Тъй като u = 2πх / L, това означава, че du = (2π / L) dx, а границите на интегриране са от -L / 2 до L / 2 вместо - π до π. Следователно редът на Фурие за зависимостта от x има формата

където в диапазона от -L / 2 до L / 2 коефициентите на реда на Фурие,

(Границите на интегриране могат да бъдат променени на всеки интервал с дължина L, например от 0 до L)

Полупериодични редове на Фурие за функции, определени в интервала L ≠ 2π.

За заместването u = πх / L интервалът от x = 0 до x = L съответства на интервала от u = 0 до u = π. Следователно функцията може да се разшири в редица само в косинуси или само в синуси, т.е. v полупериодна серия на Фурие.

Разширението в косинуси в диапазона от 0 до L има формата

Ред на Фурие от периодични функции с период 2π.

Серията на Фурие ви позволява да изучавате периодични функции, като ги разлагате на компоненти. Променливи токове и напрежения, премествания, скорост и ускорение на манивелата и акустични вълни са типични практически примери за използването на периодични функции в инженерните изчисления.

Стандартна (= нормална) нотация чрез сбора от sinx и cosx

f (x) = a o + a 1 cosx + a 2 cos2x + a 3 cos3x + ... + b 1 sinx + b 2 sin2x + b 3 sin3x + ...,

където a o, a 1, a 2, ..., b 1, b 2, .. са реални константи, т.е.

Където, за диапазона от -π до π, коефициентите на реда на Фурие се изчисляват по формулите:

Друг начин да напишете серията е да използвате съотношението acosx + bsinx = csin (x + α)

f (x) = a o + c 1 sin (x + α 1) + c 2 sin (2x + α 2) + ... + c n sin (nx + α n)

Ред на Фурие от непериодични функции с период 2π.

Разлагане на непериодични функции.

Четни и нечетни функции.

Много функции не са нито четни, нито нечетни.

Разлагане на Фурие в косинуси.

където коефициентите на реда на Фурие,

следователно,

където коефициентите на реда на Фурие,

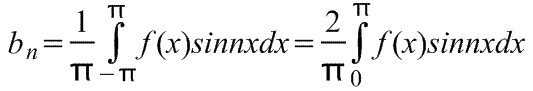
Полупериодна серия на Фурие.

Ако искате да получите полупериодно разлагане на Фурие в синусифункция f (x) в диапазона от 0 до π, тогава е необходимо да се състави нечетна периодична функция. На фиг. функцията f (x) = x е показана по-долу, нанесена върху интервала от x = 0 до x = π. Тъй като нечетната функция е симетрична спрямо началото, ние начертаваме линията CD, както е показано на фиг. Ако приемем, че извън разглеждания интервал полученият трионообразен сигнал е периодичен с период 2π, тогава крайната графика има вида, показан на фиг. Тъй като е необходимо да се получи разлагането на Фурие в полупериод по синуси, както преди, ние изчисляваме коефициента на Фурие. б

Ред на Фурие за произволен интервал.

Разширяване на периодична функция с период L.

(Границите на интегриране могат да бъдат променени на всеки интервал с дължина L, например от 0 до L)

Полупериодични редове на Фурие за функции, определени в интервала L ≠ 2π.

Разширението в косинуси в диапазона от 0 до L има формата