Тодорхойлолт 9.3.Вектор NS дуудсан өөрийн векторматрицууд Аийм тоо байгаа бол λ, Энэ тэгш байдал нь: А NS= λ NS, гэж өргөдөл гаргасны үр дүн NS матрицаар өгөгдсөн шугаман хувиргалт А, нь энэ векторыг тоогоор үржүүлэх явдал юм λ ... Тоо нь өөрөө λ дуудсан өөрийн дугаарматрицууд А.

Томьёонд орлуулах (9.3) x` j = λx j,Бид хувийн векторын координатыг тодорхойлох тэгшитгэлийн системийг олж авна.

. (9.5)

Энэхүү шугаман нэгэн төрлийн систем нь үндсэн тодорхойлогч нь 0 (Крамерын дүрэм) байвал л чухал бус шийдэлтэй байх болно. Энэ нөхцлийг дараах хэлбэрээр бичнэ үү.

бид хувийн утгыг тодорхойлох тэгшитгэлийг олж авна λ дуудсан шинж чанарын тэгшитгэл... Үүнийг дараах байдлаар товч танилцуулж болно.

| A - λE | = 0, (9.6)

Учир нь түүний зүүн тал нь матрицын тодорхойлогчийг агуулдаг A-λE... -тай холбоотой олон гишүүнт λ | A - λE| дуудсан онцлог олон гишүүнтматрицууд А.

Онцлог олон гишүүнт шинж чанарууд:

1) Шугаман хувиргалтын шинж чанарын олон гишүүнт нь суурийн сонголтоос хамаардаггүй. Баталгаа. (9.4-ийг үзнэ үү), гэхдээ иймээс, . Тиймээс энэ нь суурийн сонголтоос хамаардаггүй. Тиймээс, мөн | A-λE| шинэ суурь руу шилжихэд өөрчлөгдөхгүй.

2) Хэрэв матриц Ашугаман хувиргалт юм тэгш хэмтэй(тэдгээр. ба ij = a ji), тэгвэл (9.6) шинж чанарын тэгшитгэлийн бүх үндэс нь бодит тоо байна.

Хувийн утга ба хувийн векторын шинж чанарууд:

1) Хэрэв бид хувийн векторуудын суурийг сонговол x 1, x 2, x 3 хувийн утгатай харгалзах λ 1, λ 2, λ 3матрицууд А, тэгвэл энэ үндсэн дээр шугаман хувиргалт А нь диагональ хэлбэрийн матрицтай байна:

(9.7) Энэ өмчийн баталгаа нь хувийн векторуудын тодорхойлолтоос үүдэлтэй.

2) Хэрэв өөрчлөлтийн хувийн утга Аялгаатай бол харгалзах хувийн векторууд нь шугаман бие даасан байна.

3) Хэрэв матрицын шинж чанарын олон гишүүнт Агурван өөр үндэстэй, дараа нь ямар нэг үндэслэлээр матриц Адиагональ хэлбэртэй байна.

Матрицын хувийн утга ба хувийн векторуудыг олцгооё. Онцлогийн тэгшитгэлийг байгуулъя. (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Олдсон утга бүрт тохирох хувийн векторуудын координатыг олъё λ. (9.5)-аас үзвэл хэрэв NS (1) ={x 1, x 2, x 3) Хувийн вектор харгалзах уу λ 1 = -2, тэгвэл

- хамтын ажиллагаатай боловч тодорхойгүй систем. Үүний шийдлийг дараах байдлаар бичиж болно NS (1) ={а,0,-а), энд a нь дурын тоо юм. Ялангуяа, хэрэв бид үүнийг шаарддаг бол | х (1) |=1, NS (1) =

Системд орлуулах (9.5) λ 2 = 3, бид хоёр дахь хувийн векторын координатыг тодорхойлох системийг олж авна. х (2) ={y 1, y 2, y 3}:

, хаана NS (2) ={б, -б, б) эсвэл |-д хамаарна х (2) |=1, х (2) =

Учир нь λ 3 = 6 хувийн векторыг ол х (3) ={z 1, z 2, z 3}:

, х (3) ={в,2c, c) эсвэл хэвийн хувилбарт

x (3) = Та үүнийг харж болно NS (1) NS (2) = ab - ab= 0, х (1) х (3) = ac - ac= 0, х (2) х (3) = МЭӨ- 2МЭӨ + МЭӨ= 0. Иймд энэ матрицын хувийн векторууд хос ортогональ байна.

Лекц 10.

Квадрат хэлбэр ба тэдгээрийн тэгш хэмтэй матрицтай хамаарал. Тэгш хэмт матрицын хувийн вектор ба хувийн утгуудын шинж чанарууд. Квадрат хэлбэрийг каноник хэлбэрт оруулах.

Тодорхойлолт 10.1.Квадрат хэлбэрбодит хувьсагч x 1, x 2, ..., x nнь эдгээр хувьсагчдад хамаарах хоёрдугаар зэргийн олон гишүүнт бөгөөд нэгдүгээр зэргийн чөлөөт гишүүн, гишүүнчлэл агуулаагүй.

Квадрат хэлбэрийн жишээ:

(n = 2),

(n = 3). (10.1)

Сүүлийн лекцэд өгсөн тэгш хэмтэй матрицын тодорхойлолтыг эргэн санацгаая.

Тодорхойлолт 10.2.Квадрат матриц гэж нэрлэдэг тэгш хэмтэй, хэрэв, өөрөөр хэлбэл, үндсэн диагональтай харьцуулахад тэгш хэмтэй матрицын элементүүд тэнцүү байвал.

Симметрик матрицын хувийн утга ба хувийн векторын шинж чанарууд:

1) Тэгш хэмт матрицын бүх хувийн утга бодит байна.

Нотолгоо (for n = 2).

Матрицыг үзье Ахарагдаж байна: ... Онцлогийн тэгшитгэлийг байгуулъя:

(10.2) Ялгаварлагчийг ол:

Тиймээс тэгшитгэл нь зөвхөн бодит үндэстэй.

2) Симметрик матрицын хувийн векторууд нь ортогональ байна.

Нотолгоо (for n= 2).

Өвөрмөц векторуудын координат ба тэгшитгэлийг хангах ёстой.

Хувийн утга (тоо) ба хувийн векторууд.
Шийдлийн жишээ

Өөрийнхөөрөө бай

Энэ нь хоёр тэгшитгэлээс гарч байна.

Дараа нь гэж бодъё: .

Үр дүнд нь: Хоёр дахь хувийн вектор.

Шийдлийн чухал цэгүүдийг давтан хэлье:

- үүссэн систем нь ерөнхий шийдэлтэй байх нь гарцаагүй (тэгшитгэлүүд нь шугаман хамааралтай);

- бид "тоглоом" -ыг бүхэлд нь, эхний "х" координат нь бүхэл, эерэг, аль болох бага байхаар сонгоно.

- тодорхой шийдэл нь системийн тэгшитгэл бүрийг хангаж байгаа эсэхийг шалгана.

Хариулах .

Завсрын "хяналтын цэгүүд" хангалттай байсан тул тэгш байдлыг шалгах нь зарчмын хувьд шаардлагагүй асуудал юм.

Төрөл бүрийн мэдээллийн эх сурвалжид хувийн векторуудын координатыг ихэвчлэн багана биш, харин мөрөнд бичдэг, жишээлбэл: (Үнэнийг хэлэхэд би өөрөө тэдгээрийг мөр болгон бичдэг байсан)... Энэ сонголтыг хүлээн зөвшөөрөх боломжтой, гэхдээ сэдвийн хүрээнд шугаман хувиргалттехникийн хувьд ашиглахад илүү тохиромжтой баганын векторууд.

Магадгүй шийдэл нь танд маш урт мэт санагдаж магадгүй, гэхдээ энэ нь зөвхөн эхний жишээн дээр би маш дэлгэрэнгүй тайлбар хийсэн учраас л ийм байна.

Жишээ 2

Матрицууд

Бид өөрсдийгөө сургадаг! Хичээлийн төгсгөлд даалгавраа дуусгах ойролцоо жишээ.

Заримдаа нэмэлт ажлыг гүйцэтгэх шаардлагатай байдаг, тухайлбал:

каноник матрицын задралыг бичнэ

Энэ юу вэ?

Хэрэв матрицын хувийн векторууд үүссэн бол суурь, дараа нь үүнийг дараах байдлаар илэрхийлж болно.

Хувийн векторуудын координатаас бүрдэх матриц хаана байна, - диагональхаргалзах хувийн утга бүхий матриц.

Ийм матрицын задралыг нэрлэдэг каноникэсвэл диагональ.

Эхний жишээний матрицыг авч үзье. Өөрийн гэсэн векторууд шугаман бие даасан(конлинеар бус) ба суурь болдог. Тэдний координатаас матриц зохиоё.

Асаалттай үндсэн диагональматрицууд зохих дарааллаархувийн утгууд байрладаг бөгөөд бусад элементүүд нь тэгтэй тэнцүү байна:
- Би дарааллын ач холбогдлыг дахин нэг удаа онцолж байна: "хоёр" нь 1-р вектортой тохирч байгаа тул 1-р баганад, "гурав" нь 2-р векторт байрлана.

Ердийн олох алгоритмын дагуу урвуу матрицэсвэл Гаусс-Жорданы аргаолох ... Үгүй ээ, энэ бол үсгийн алдаа биш! - Урвуу нь анхны матрицтай давхцах нарны хиртэлт шиг ховор үйл явдал таны өмнө.

Матрицын каноник задралыг бичихэд л үлддэг.

Системийг энгийн хувиргалтуудыг ашиглан шийдэж болох бөгөөд дараах жишээн дээр бид энэ аргыг ашиглах болно. Гэхдээ энд "сургуулийн" арга илүү хурдан ажилладаг. 3-р тэгшитгэлээс бид дараахыг илэрхийлнэ: - бид хоёр дахь тэгшитгэлд орлуулна:

Эхний координат нь тэг учраас бид тэгшитгэл бүрээс дараах системийг олж авдаг.

Бас дахин шугаман хамаарал заавал байх ёстойг анхаар... Хэрэв та зөвхөн өчүүхэн шийдэлд хүрвэл , дараа нь хувийн утгыг буруу олсон эсвэл системийг алдаатай эмхэтгэсэн / шийдсэн.

Компакт координатууд нь утгыг өгдөг

Өвөрмөц вектор:

Дахин нэг удаа бид шийдлийг олсон эсэхийг шалгана системийн тэгшитгэл бүрийг хангана... Дараах догол мөрүүд болон дараагийн даалгаваруудад би энэ хүслийг заавал дагаж мөрдөх дүрэм болгон авахыг зөвлөж байна.

2) Хувийн утгын хувьд ижил зарчмын дагуу бид дараах системийг олж авна.

Системийн 2-р тэгшитгэлээс бид дараахыг илэрхийлнэ: - гурав дахь тэгшитгэлд орлуулна:

"Зета" координат нь тэгтэй тэнцүү тул тэгшитгэл бүрээс шугаман хамаарал бүхий системийг олж авна.

Байцгаая

Бид шийдлийг шалгана систем дэх тэгшитгэл бүрийг хангана.

Тиймээс хувийн вектор нь:.

3) Эцэст нь систем нь хувийн утгатай тохирч байна:

Хоёр дахь тэгшитгэл нь хамгийн энгийн мэт харагддаг тул бид үүнээс илэрхийлж, 1, 3-р тэгшитгэлд орлуулна.

Бүх зүйл сайн байна - шугаман харилцаа үүссэн бөгөөд бид үүнийг илэрхийлэл болгон орлуулж байна:

Үүний үр дүнд "x" болон "igrek" нь "z"-ээр илэрхийлэгдсэн:. Практикт ийм харилцааг бий болгох шаардлагагүй бөгөөд зарим тохиолдолд дамжуулан эсвэл дамжуулан илэрхийлэх нь илүү тохиромжтой байдаг. Эсвэл бүр "галт тэрэг" - жишээлбэл "Игрек" -ээр "X", "z" -ээр дамжуулан "игрек"

Дараа нь гэж бодъё:

Олдсон шийдэл байгаа эсэхийг шалгана системийн тэгшитгэл бүрийг хангаж, гурав дахь хувийн векторыг бичнэ

Хариулах: хувийн векторууд:

Геометрийн хувьд эдгээр векторууд нь орон зайн гурван өөр чиглэлийг тодорхойлдог. ("Тэнд, дахиад буцаж")ямар замаар шугаман хувиргалттэгээс өөр векторуудыг (өөрийн векторууд) тэдгээртэй коллинеар вектор болгон хувиргадаг.

Хэрэв каноник задралыг олох нөхцөл шаардлагатай бол энэ нь энд боломжтой, учир нь Янз бүрийн хувийн утгууд нь өөр өөр шугаман бие даасан хувийн векторуудтай тохирдог. Матриц зохиох тэдгээрийн координатаас диагональ матриц -аас тус тусхувийн утгууд ба олох урвуу матриц .

Хэрэв нөхцөл байдлын дагуу та бичих хэрэгтэй хувийн векторуудын суурь дахь шугаман хувиргалтын матриц, дараа нь бид хариултыг хэлбэрээр өгнө. Ялгаатай, ялгаа нь мэдэгдэхүйц юм!Энэ матрицын хувьд "de" матриц юм.

Бие даасан шийдлийн энгийн тооцоолол бүхий асуудал:

Жишээ 5

Матрицаар өгөгдсөн шугаман хувиргалтын хувийн векторуудыг ол

Хувийн утгуудыг олохдоо асуудлыг 3-р зэргийн олон гишүүнт рүү оруулахгүй байхыг хичээгээрэй. Нэмж дурдахад, таны системийн шийдлүүд миний шийдлүүдээс ялгаатай байж магадгүй - энд хоёрдмол утга байхгүй; мөн таны олсон векторууд нь түүврийн векторуудаас тус тусын координатын пропорциональ хүртэл ялгаатай байж болно. Жишээлбэл, ба. Хариултыг маягтаар танилцуулах нь илүү гоо зүйн шинж чанартай боловч хоёр дахь хувилбар дээр зогсвол зүгээр юм. Гэсэн хэдий ч бүх зүйлд боломжийн хязгаарлалт байдаг, хувилбар нь тийм ч сайн харагдахгүй байна.

Хичээлийн төгсгөлд даалгаврын ойролцоо эцсийн түүвэр.

Олон тооны хувийн утгатай тохиолдолд асуудлыг хэрхэн шийдвэрлэх вэ?

Ерөнхий алгоритм нь ижил хэвээр байгаа боловч энэ нь өөрийн гэсэн онцлогтой бөгөөд шийдлийн зарим хэсгийг илүү хатуу эрдэм шинжилгээний хэв маягаар хадгалахыг зөвлөж байна.

Жишээ 6

Хувийн утга ба хувийн векторыг ол

Шийдэл

Мэдээжийн хэрэг, бид гайхалтай эхний баганыг томоор бичнэ:

Мөн дөрвөлжин гурвалсан тоог үржүүлсний дараа:

Үүний үр дүнд хувийн утгуудыг олж авдаг бөгөөд тэдгээрийн хоёр нь үржвэр юм.

Хувийн векторуудыг олцгооё:

1) Бид "хялбаршуулсан" схемийн дагуу ганцаардсан цэрэгтэй харьцах болно.

Сүүлийн хоёр тэгшитгэлээс тэгшитгэл нь тодорхой харагдаж байгаа бөгөөд үүнийг системийн 1-р тэгшитгэлд орлуулах нь ойлгомжтой.

Илүү сайн хослол байхгүй:
Өвөрмөц вектор:

2-3) Одоо хэд хэдэн харуулуудыг бууд. Энэ тохиолдолд энэ нь гарч ирж магадгүй юм хоёр эсвэл нэгөөрийн вектор. Үндэсийн олон төрлөөс үл хамааран бид утгыг тодорхойлогч болгон орлуулна Энэ нь бидэнд дараахь зүйлийг авчирдаг шугаман тэгшитгэлийн нэгэн төрлийн систем:

Өвөрмөц векторууд нь яг векторууд юм
үндсэн шийдвэрийн систем

Үнэндээ бид бүхэл бүтэн хичээлийн туршид зөвхөн үндсэн системийн векторуудыг хайж байсан. Яг одоохондоо энэ нэр томъёо тийм ч их шаардлагагүй байсан. Дашрамд хэлэхэд өнгөлөн далдалсан цувтай сэдвийг хальтирсан тэдгээр ухаалаг оюутнууд нэгэн төрлийн тэгшитгэлодоо идэхээс өөр аргагүй болно.

Цорын ганц үйлдэл нь нэмэлт мөрүүдийг устгах явдал байв. Үр дүн нь дунд нь албан ёсны "шат" бүхий нэгээс гурав матриц юм.
- үндсэн хувьсагч, - чөлөөт хувьсагч. Хоёр чөлөөт хувьсагч байдаг тул, үндсэн системийн векторууд бас хоёр байна.

Үндсэн хувьсагчийг чөлөөт хувьсагчаар илэрхийлье:. "X"-ийн өмнөх тэг хүчин зүйл нь ямар ч утгыг авах боломжийг олгодог (энэ нь тэгшитгэлийн системээс тодорхой харагдаж байна).

Энэ асуудлын хүрээнд ерөнхий шийдлийг мөрөнд биш, харин баганад бичих нь илүү тохиромжтой.

Хувийн вектор нь хостой тохирч байна:
Хувийн вектор нь хостой тохирч байна:

Анхаарна уу : Нарийвчилсан уншигчид эдгээр векторуудыг сонгож, системд дүн шинжилгээ хийснээр л амаар авах боломжтой , гэхдээ энд тодорхой мэдлэг хэрэгтэй: гурван хувьсагч байдаг, системийн матрицын зэрэглэл- нэгж гэсэн үг үндсэн шийдвэрийн систем 3 - 1 = 2 вектороос бүрдэнэ. Гэсэн хэдий ч олсон векторууд нь энэ мэдлэггүй байсан ч гэсэн зөвхөн зөн совингийн түвшинд төгс харагдаж байна. Энэ тохиолдолд гурав дахь векторыг "илүү сайхан" бичих болно:. Гэсэн хэдий ч, өөр жишээн дээр энгийн сонголт харагдахгүй байж магадгүй тул татгалзсан мэдэгдэл нь туршлагатай хүмүүст зориулагдсан болохыг би танд анхааруулж байна. Түүнээс гадна яагаад гурав дахь вектор гэж авч болохгүй гэж? Эцсийн эцэст түүний координатууд нь системийн тэгшитгэл, вектор бүрийг хангадаг шугаман бие даасан. "Бусад" вектор нь үндсэн системийн векторуудын шугаман хослол тул зарчмын хувьд энэ сонголт тохиромжтой, гэхдээ "тахир".

Хариулах: хувийн утга:, хувийн вектор:

Бие даасан шийдлийн ижил төстэй жишээ:

Жишээ 7

Хувийн утга ба хувийн векторыг ол

Хичээлийн төгсгөлд дуусгах бүдүүлэг жишээ.

6 ба 7-р жишээн дээр гурвалсан шугаман бие даасан хувийн векторуудыг олж авсан тул анхны матрицыг каноник задралд төлөөлөх боломжтой гэдгийг тэмдэглэх нь зүйтэй. Гэхдээ ийм бөөрөлзгөнө бүх тохиолдолд тохиолддоггүй:

Жишээ 8

Шийдэл: шинж чанарын тэгшитгэлийг зохиож, шийдвэрлэх:

Бид тодорхойлогчийг эхний баганаар нээнэ.

3-р зэргийн олон гишүүнтээс зайлсхийж авч үзсэн аргын дагуу нэмэлт хялбарчлах ажлыг гүйцэтгэнэ.

- хувийн үнэ цэнэ.

Хувийн векторуудыг олцгооё:

1) Үндэстэй холбоотой ямар ч бэрхшээл байхгүй:

Гайхах хэрэггүй, иж бүрдэлээс гадна хувьсагчдыг бас ашигладаг - энд ямар ч ялгаа байхгүй.

3-р тэгшитгэлээс бид илэрхийлэх болно - бид 1 ба 2-р тэгшитгэлд орлуулах болно.

Хоёр тэгшитгэлээс дараах байдалтай байна.

За тэгвэл:

2-3) Олон утгын хувьд бид системийг олж авдаг .

Системийн матрицыг бичиж, энгийн хувиргалтуудыг ашиглан алхам алхмаар хэлбэрт оруулъя.

". Эхний хэсэг нь химометрийг ойлгоход шаардагдах хамгийн бага заалтуудыг тусгасан бөгөөд хоёр дахь хэсэгт олон хувьсагчийн шинжилгээний аргуудын талаар илүү гүнзгий ойлголттой болохын тулд мэдэх шаардлагатай баримтуудыг багтаасан болно. Илтгэлийг Excel-ийн ажлын дэвтэрт гүйцэтгэсэн жишээн дээр харуулсан болно. Matrix.xlsЭнэ баримт бичигт дагалддаг.

Жишээнүүдийн эшлэлийг текстэнд Excel объект хэлбэрээр байрлуулсан болно. Эдгээр жишээнүүд нь хийсвэр шинж чанартай бөгөөд тэдгээр нь аналитик химийн асуудалтай ямар ч холбоогүй юм. Хемометрийн салбарт матрицын алгебр ашиглах бодит жишээг янз бүрийн химометрийн хэрэглээнд зориулагдсан бусад бичвэрүүдэд авч үзсэн болно.

Аналитик химийн чиглэлээр хийсэн ихэнх хэмжилтүүд нь шууд биш, харин шууд бус... Энэ нь туршилтын явцад хүссэн аналитийн С (концентраци) утгын оронд өөр утгыг олж авна гэсэн үг юм. х(дохио) холбоотой боловч C-тэй тэнцүү биш, i.e. х(C) ≠ C. Дүрмээр бол хамаарлын төрөл х(C) тодорхойгүй боловч аналитик химийн хувьд азаар ихэнх хэмжилтүүд пропорциональ байдаг. Энэ нь C-ийн концентраци ихсэх тусам гэсэн үг юм аудаад X дохио ижил хэмжээгээр нэмэгдэх болно. х(а C) = а х(C). Нэмж дурдахад дохионууд нь нэмэлт шинж чанартай байдаг тул C 1 ба C 2 концентрацитай хоёр бодис агуулсан дээжийн дохио нь бүрэлдэхүүн хэсэг бүрийн дохионы нийлбэртэй тэнцүү байх болно. х(C 1 + C 2) = х(C 1) + х(C 2). Пропорциональ байдал ба нэмэлт нь хамтдаа өгдөг шугаман байдал... Шугаман байдлын зарчмыг харуулах олон жишээ байдаг боловч хамгийн гайхалтай хоёр жишээ болох хроматографи ба спектроскопиыг дурдахад хангалттай. Аналитик химийн туршилтын хоёр дахь шинж чанар олон суваг... Орчин үеийн аналитик төхөөрөмж нь олон сувгийн дохиог нэгэн зэрэг хэмждэг. Жишээлбэл, гэрлийн дамжуулалтын эрчмийг нэг дор хэд хэдэн долгионы уртаар хэмждэг, i.e. спектр. Тиймээс туршилтын явцад бид олон дохиотой харьцдаг х 1 , х 2 ,...., х n, судалж буй системд агуулагдах бодисын C 1, C 2, ..., C m агууламжийн багцыг тодорхойлдог.

Цагаан будаа. 1 спектр

Тиймээс аналитик туршилт нь шугаман болон олон хэмжээст шинж чанартай байдаг. Иймд туршилтын өгөгдлийг вектор, матриц гэж үзэж, матрицын алгебрын аппаратыг ашиглан тэдгээрийг удирдах нь тохиромжтой. Энэхүү аргын үр өгөөжийг 4000-аас 4796 см-1 хүртэлх 200 долгионы уртад бүртгэсэн гурван спектрийг харуулсан жишээн дээр харуулав. Эхлээд ( х 1) ба хоёр дахь ( х 2) А ба В хоёр бодисын концентрацийг мэддэг стандарт дээжийн спектрийг авсан: эхний дээжинд [A] = 0.5, [B] = 0.1, хоёр дахь дээжинд [A] = 0.2, [B байна. ] = 0.6. Спектр нь тодорхойлогдсон шинэ, үл мэдэгдэх дээжийн талаар юу хэлж болох вэ х 3 ?

Гурван туршилтын спектрийг авч үзье х 1 , х 2 ба х 3-ыг 200 хэмжигдэхүүнтэй гурван вектор. Шугаман алгебрын тусламжтайгаар үүнийг хялбархан харуулж чадна х 3 = 0.1 х 1 +0.3 х 2; тиймээс гурав дахь дээжинд [A] = 0.5 × 0.1 + 0.2 × 0.3 = 0.11 ба [B] = 0.1 × 0.1 + 0.6 × 0.3 = 0.19 концентрацид зөвхөн А ба В бодис агуулагдах нь ойлгомжтой.

1. Үндсэн мэдээлэл

1.1 Матрицууд

Матрицжишээлбэл тэгш өнцөгт тооны хүснэгт гэж нэрлэдэг

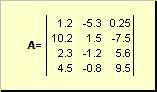
Цагаан будаа. 2 матриц

Матрицуудыг тод том үсгээр тэмдэглэв ( А), тэдгээрийн элементүүд - индекс бүхий харгалзах жижиг үсгүүд, i.e. а ij. Эхний индекс нь мөрүүдийг дугаарлаж, хоёр дахь нь баганыг дугаарлана. Хемометрийн хувьд индексийн хамгийн их утгыг индекстэй ижил үсгээр тэмдэглэх нь заншилтай байдаг, гэхдээ том үсгээр бичсэн байдаг. Тиймээс матриц Агэж бас бичиж болно ( а ij , би = 1,..., I; ж = 1,..., Ж). Жишээнд үзүүлсэн матрицын хувьд I = 4, Ж= 3 ба а 23 = −7.5.

Хос тоо Iболон Жматрицын хэмжээс гэж нэрлэгддэг ба гэж тэмдэглэнэ I× Ж... Хемометрийн матрицын жишээ бол олж авсан спектрийн багц юм Iдээжүүд дээр Ждолгионы урт.

1.2. Энгийн матрицын үйлдлүүд

Матрицууд боломжтой тоогоор үржүүлнэ... Энэ тохиолдолд элемент бүрийг энэ тоогоор үржүүлнэ. Жишээлбэл -

Цагаан будаа. 3 Матрицыг тоогоор үржүүлэх

Ижил хэмжээтэй хоёр матриц нь элементийн хувьд байж болно нугалахболон хасах... Жишээлбэл,

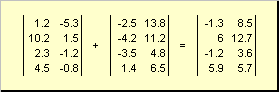
Цагаан будаа. 4 Матриц нэмэх

Тоогоор үржүүлж, нэмсний үр дүнд ижил хэмжээтэй матрицыг олж авна.

Тэг матриц нь тэгээс бүрдэх матриц юм. Үүнийг тэмдэглэсэн байна О... Энэ нь ойлгомжтой А+О = А, А−А = Оба 0 А = О.

Матриц байж болно шилжүүлэн суулгах... Энэ үйлдлийн явцад матрицыг эргүүлнэ, өөрөөр хэлбэл. мөр, баганыг сольсон. Transpose нь цус харвалтаар тодорхойлогддог. А"эсвэл индекс Ат. Тэгэхээр хэрэв А = {а ij , би = 1,..., I; ж = 1,...,Ж), дараа нь А t = ( а жи , ж = 1,...,Ж; i = 1, ..., I). Жишээлбэл

Цагаан будаа. 5 Матрицыг шилжүүлэх

Энэ нь ойлгомжтой ( А t) t = А, (А+Б) т = А t + Бт.

1.3. Матрицын үржүүлэх

Матрицууд боломжтой үржүүлэх, гэхдээ тэдгээр нь зохих хэмжээстэй байвал л. Яагаад ийм байгаа нь тодорхойлолтоос тодорхой болно. Матрицын бүтээгдэхүүн А, хэмжээс I× К, болон матрицууд Б, хэмжээс К× Жматриц гэж нэрлэдэг C, хэмжээс I× Жэлементүүд нь тоо юм

Тиймээс үйлдвэрлэх ABзүүн матриц дахь баганын тоо байх шаардлагатай Абаруун матрицын мөрүүдийн тоотой тэнцүү байв Б... Матрицын бүтээгдэхүүний жишээ -

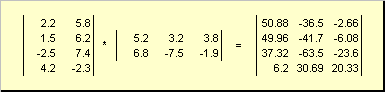
Зураг 6 Матрицын бүтээгдэхүүн

Матрицыг үржүүлэх дүрмийг дараах байдлаар томъёолж болно. Матрицын элементийг олох Cуулзвар дээр зогсож байна би-р мөр ба ж-р багана ( в ij) элементээр үржүүлсэн байх ёстой биэхний матрицын 3-р эгнээ Адээр жхоёр дахь матрицын th багана Бмөн бүх үр дүнг нэгтгэ. Тиймээс үзүүлсэн жишээн дээр гурав дахь эгнээ ба хоёр дахь баганын элементийг гурав дахь эгнээний элементийн бүтээгдэхүүний нийлбэрээр олж авна. Аба хоёр дахь багана Б

Зураг 7 Матрицын бүтээгдэхүүний элемент

Матрицын бүтээгдэхүүн нь дарааллаас хамаарна, өөрөөр хэлбэл. AB ≠ БА, хэрэв зөвхөн хэмжээсийн шалтгаанаар бол. Үүнийг солигддоггүй гэдэг. Гэсэн хэдий ч матрицын бүтээгдэхүүнүүд ассоциатив байдаг. Энэ нь тийм гэсэн үг ABC = (AB)C = А(МЭӨ). Үүнээс гадна, энэ нь бас түгээх, i.e. А(Б+C) = AB+АС... Энэ нь ойлгомжтой А.О = О.

1.4. Квадрат матрицууд

Хэрэв матрицын баганын тоо нь түүний мөрүүдийн тоотой тэнцүү бол ( I = J = N), ийм матрицыг квадрат гэж нэрлэдэг. Энэ хэсэгт бид зөвхөн ийм матрицуудыг авч үзэх болно. Эдгээр матрицуудаас онцгой шинж чанартай матрицуудыг ялгаж салгаж болно.

Ганц биематриц (тэмдэглэсэн би,мөн заримдаа Э) нь диагональ элементүүдээс бусад бүх элементүүд нь тэгтэй тэнцүү байх матриц бөгөөд 1-тэй тэнцүү, i.e.

Мэдээжийн хэрэг Ай = IA = А.

Матриц гэж нэрлэдэг диагональХэрэв диагональ элементүүдээс бусад бүх элементүүд ( а ii) тэгтэй тэнцүү байна. Жишээлбэл

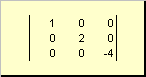
Цагаан будаа. 8 Диагональ матриц

Матриц Адээд гэж нэрлэдэг гурвалжинхэрэв диагональ доорх бүх элементүүд нь тэгтэй тэнцүү бол, өөрөөр хэлбэл. а ij= 0, хувьд би>ж... Жишээлбэл

Цагаан будаа. 9 Дээд гурвалжин матриц

Доод гурвалжин матрицыг ижил төстэй байдлаар тодорхойлно.

Матриц Адуудсан тэгш хэмтэй, хэрэв А t = А... Өөрөөр хэлбэл а ij = а жи... Жишээлбэл

Цагаан будаа. 10 Симметрик матриц

Матриц Адуудсан ортогональ, хэрэв

Ат А = АА t = I.

Матриц гэж нэрлэдэг хэвийнхэрэв

1.5. Мөр ба тодорхойлогч

Дагаж байнаквадрат матриц А(Tr гэж тэмдэглэсэн ( А) эсвэл Sp ( А)) нь диагональ элементүүдийн нийлбэр,

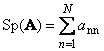
Жишээлбэл,

Цагаан будаа. 11 Матрицын ул мөр

Энэ нь ойлгомжтой

Sp (α А) = α Sp ( А) ба

Sp ( А+Б) = Sp ( А) + Sp ( Б).

Үүнийг харуулж болно

Sp ( А) = Sp ( А t), Sp ( I) = Н,

бас тэр

Sp ( AB) = Sp ( БА).

Квадрат матрицын өөр нэг чухал шинж чанар нь түүний хэмжээ юм тодорхойлогч(детээр тэмдэглэсэн ( А)). Ерөнхий тохиолдолд тодорхойлогчийг тодорхойлох нь нэлээд хэцүү тул бид хамгийн энгийн хувилбар болох матрицаас эхэлнэ. Ахэмжээс (2 × 2). Дараа нь

(3 × 3) матрицын хувьд тодорхойлогч нь байх болно

матрицын хувьд ( Н× Н) тодорхойлогчийг 1 2 3 ... нийлбэрээр тооцно. Н= Н! нэр томъёо тус бүр нь тэнцүү байна

Индексүүд к 1 , к 2 ,..., к Нбүх боломжит эрэмбэлэгдсэн орлуулалтууд гэж тодорхойлогддог rбагц дахь тоонууд (1, 2, ..., Н). Матрицын тодорхойлогчийг тооцоолох нь практикт тусгай програм ашиглан хийгддэг нарийн төвөгтэй процедур юм. Жишээлбэл,

Цагаан будаа. 12 Матрицын тодорхойлогч

Бид зөвхөн тодорхой шинж чанаруудыг тэмдэглэж байна:

det ( I) = 1, det ( А) = det ( А t),

det ( AB) = det ( А) det ( Б).

1.6. Векторууд

Хэрэв матриц нь зөвхөн нэг баганаас бүрдэх бол ( Ж= 1), тэгвэл ийм объектыг дуудна вектор... Илүү нарийн, баганын вектор. Жишээлбэл

Жишээлбэл, нэг мөрөөс бүрдэх матрицуудыг авч үзэж болно

Энэ объект нь мөн вектор боловч эгнээ вектор... Өгөгдөлд дүн шинжилгээ хийхдээ бид аль вектортой харьцаж байгааг ойлгох нь чухал юм - багана эсвэл мөр. Тиймээс нэг дээжинд авсан спектрийг эгнээний вектор гэж үзэж болно. Дараа нь бүх дээжийн хувьд тодорхой долгионы урттай спектрийн эрчмийн багцыг баганын вектор гэж үзэх ёстой.

Векторын хэмжээс нь түүний элементүүдийн тоо юм.

Аливаа баганын векторыг шилжүүлэн суулгах замаар эгнээний вектор болгон хувиргах нь ойлгомжтой.

Векторын хэлбэрийг тусгайлан заагаагүй, зүгээр л вектор гэж хэлсэн тохиолдолд тэдгээр нь баганын вектор гэсэн үг юм. Бид ч гэсэн энэ дүрмийг баримтална. Векторыг жижиг шулуун тод үсгээр тэмдэглэнэ. Тэг вектор нь бүх элементүүд нь тэг байх вектор юм. Энэ нь томилогдсон 0 .

1.7. Векторуудтай хийх үндсэн үйлдлүүд

Векторуудыг матрицтай адил тоогоор нэмж, үржүүлж болно. Жишээлбэл,

Цагаан будаа. 13 Вектор үйлдлүүд

Хоёр вектор хболон yгэж нэрлэдэг колинеарийм α тоо байвал

1.8. Векторуудын бүтээгдэхүүн

Ижил хэмжээтэй хоёр вектор Нүржүүлж болно. Хоёр вектор байг х = (х 1 , х 2 ,...,х N) t ба y = (y 1 , y 2 ,...,y N) т. "Мөр багана" үржүүлэх дүрмийг удирдан бид тэдгээрээс хоёр бүтээгдэхүүнийг бүрдүүлж болно. хт yболон xyт. Эхний хэсэг

дуудсан скалярэсвэл дотоод... Үүний үр дүн нь тоо юм. Энэ нь мөн тэмдэглэгээг ашигладаг ( х,y)= хт y... Жишээлбэл,

Цагаан будаа. 14 Дотоод бүтээгдэхүүн (цэг бүтээгдэхүүн)

Хоёр дахь хэсэг

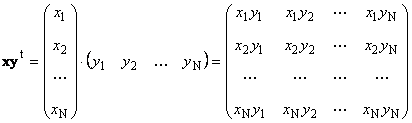
дуудсан гадна... Үүний үр дүн нь хэмжээсийн матриц юм ( Н× Н). Жишээлбэл,

Цагаан будаа. 15 Гадаад ажил

Скаляр үржвэр нь тэгтэй тэнцүү векторуудыг дууддаг ортогональ.

1.9. Вектор норм

Векторын скаляр үржвэрийг скаляр квадрат гэнэ. Энэ үнэ цэнэ

квадратыг тодорхойлдог уртвектор х... Уртыг илэрхийлэхийн тулд (мөн гэж нэрлэдэг нормвектор), тэмдэглэгээг ашиглана

Жишээлбэл,

Цагаан будаа. 16 Вектор норм

Нэгж урттай вектор (|| х|| = 1) нормчлогдсон гэж нэрлэдэг. Тэг биш вектор ( х ≠ 0 ) уртаар хуваах замаар хэвийн болгож болно, i.e. х = ||х|| (x /||х||) = ||х|| д... Энд д = x /||х|| нь нормчлогдсон вектор юм.

Хэрэв векторууд бүгд нормчлогдсон, хосоороо ортогональ байвал ортонормаль гэж нэрлэдэг.

1.10. Векторуудын хоорондох өнцөг

Цэгийн бүтээгдэхүүн нь ба тарилгаХоёр векторын хоорондох φ хболон y

Хэрэв векторууд ортогональ бол cosφ = 0 ба φ = π / 2, хэрэв тэдгээр нь коллинеар байвал cosφ = 1 ба φ = 0 болно.

1.11. Матрицын вектор дүрслэл

Матриц бүр Ахэмжээ I× Жвекторуудын багц хэлбэрээр төлөөлүүлж болно

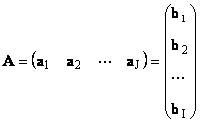
Энд вектор бүр а жнь жбагана, мөрийн вектор б бинь би- матрицын 1-р эгнээ А

1.12. Шугаман хамааралтай векторууд

Ижил хэмжээтэй векторууд ( Н)-ийг матрицтай адил тоогоор нэмж, үржүүлж болно. Үр дүн нь ижил хэмжээтэй вектор байх болно. Ижил хэмжээтэй хэд хэдэн вектор байг х 1 , х 2 ,...,х K ба ижил тооны α α ​​1, α 2, ..., α К... Вектор

y= α 1 х 1 + α 2 х 2 + ... + α К х К

дуудсан шугаман хослолвекторууд х к .

Хэрэв тэгээс өөр тоо байвал α к ≠ 0, к = 1,..., К, юу y = 0 , дараа нь ийм векторуудын багц х кдуудсан шугаман хамааралтай... Үгүй бол векторуудыг шугаман бие даасан гэж нэрлэдэг. Жишээлбэл, векторууд х 1 = (2, 2) t ба х 2 = (−1, −1) t нь шугаман хамааралтай, учир нь х 1 +2х 2 = 0

1.13. Матрицын зэрэглэл

багцыг авч үзье Квекторууд х 1 , х 2 ,...,х Кхэмжээсүүд Н... Энэ векторын системийн зэрэглэл нь шугаман бие даасан векторуудын хамгийн их тоо юм. Жишээлбэл, багцад

жишээ нь зөвхөн хоёр шугаман бие даасан вектор байдаг х 1 ба х 2, тиймээс түүний зэрэглэл 2 байна.

Мэдээжийн хэрэг, хэрэв олонлогт тэдгээрийн хэмжээсээс олон вектор байгаа бол ( К>Н), тэгвэл тэдгээр нь заавал шугаман хамааралтай байна.

Матрицын зэрэглэлээр(зэрэглэлээр тэмдэглэсэн ( А)) нь түүний бүрдэх векторуудын системийн зэрэг юм. Хэдийгээр аливаа матрицыг хоёр аргаар (баганын вектор эсвэл мөр) төлөөлж болох боловч энэ нь зэрэглэлийн утгад нөлөөлөхгүй.

1.14. урвуу матриц

Квадрат матриц Аөвөрмөц шинж чанартай бол доройтдоггүй гэж нэрлэдэг урвууматриц А-1 нөхцөлөөр тодорхойлогддог

АА −1 = А −1 А = I.

Урвуу матриц бүх матрицад байдаггүй. Ядардаггүй байх зайлшгүй бөгөөд хангалттай нөхцөл

det ( А) ≠ 0 эсвэл зэрэглэл ( А) = Н.

Матрицын урвуулалт нь тусгай програмууд байдаг нарийн төвөгтэй процедур юм. Жишээлбэл,

Цагаан будаа. 17 Матрицын урвуу

Хамгийн энгийн тохиолдлын томьёог танилцуулъя - 2 × 2 матриц

Хэрэв матрицууд Аболон Бтэгвэл доройтдоггүй

(AB) −1 = Б −1 А −1 .

1.15. Псевдоурвуу матриц

Хэрэв матриц Адоройтсон бөгөөд урвуу матриц байхгүй бол зарим тохиолдолд та ашиглаж болно псевдо-урвууийм матриц гэж тодорхойлсон матриц А+ тэр

АА + А = А.

Псевдо урвуу матриц нь цорын ганц биш бөгөөд түүний төрөл нь барилгын аргаас хамаарна. Жишээлбэл, тэгш өнцөгт матрицын хувьд та Мур-Пенроузын аргыг ашиглаж болно.

Хэрэв баганын тоо мөрийн тооноос бага байвал

А + =(Ат А) −1 Ат

Жишээлбэл,

Цагаан будаа. 17a Матрицын псевдо-инверси

Хэрэв баганын тоо мөрийн тооноос их байвал

А + =А t ( ААт) −1

1.16. Векторыг матрицаар үржүүлэх

Вектор хматрицаар үржүүлж болно Атохиромжтой хэмжээс. Энэ тохиолдолд баганын векторыг баруун талд үржүүлнэ Сүхмөн эгнээний вектор зүүн талд байна хт А... Хэрэв векторын хэмжээс Ж, мөн матрицын хэмжээс I× Жтэгвэл үр дүн нь хэмжээсийн вектор болно I... Жишээлбэл,

Цагаан будаа. 18 Матрицын үржүүлэх замаар вектор

Хэрэв матриц А- дөрвөлжин ( I× I), дараа нь вектор y = Сүххэмжээтэй ижил хэмжээтэй байна х... Энэ нь ойлгомжтой

А(α 1 х 1 + α 2 х 2) = α 1 Сүх 1 + α 2 Сүх 2 .

Тиймээс матрицуудыг векторуудын шугаман хувиргалт гэж үзэж болно. Тухайлбал Ix = х, Үхэр = 0 .

2. Нэмэлт мэдээлэл

2.1. Шугаман тэгшитгэлийн системүүд

Байцгаая А- матрицын хэмжээ I× Ж, a б- хэмжээсийн вектор Ж... Тэгшитгэлийг авч үзье

Сүх = б

векторын хувьд х, хэмжээс I... Үнэндээ энэ бол систем юм Iшугаман тэгшитгэлүүд Жүл мэдэгдэх х 1 ,...,х Ж... Шийдэл нь зөвхөн хэрэв байгаа бол л бий

зэрэглэл ( А) = зэрэглэл ( Б) = Р,

хаана Бнь өргөтгөсөн хэмжээсийн матриц юм I×( J + 1) матрицаас бүрдэнэ Абаганаар бүрхэгдсэн б, Б = (А б). Үгүй бол тэгшитгэлүүд хоорондоо зөрчилддөг.

Хэрэв Р = I = Ж, тэгвэл шийдэл нь өвөрмөц юм

х = А −1 б.

Хэрэв Р < I, тэгвэл шугаман хослолоор илэрхийлэгдэх олон янзын шийдлүүд байдаг Ж−Рвекторууд. Нэг төрлийн тэгшитгэлийн систем Сүх = 0 квадрат матриц А (Н× Н) чухал биш шийдэлтэй ( х ≠ 0 ) хэрэв зөвхөн хэрэв det ( А) = 0. Хэрэв Р= зэрэглэл ( А)<Ндараа нь оршино Н−Ршугаман бие даасан шийдлүүд.

2.2. Хоёр шугаман ба квадрат хэлбэрүүд

Хэрэв Ань квадрат матриц бөгөөд хболон yнь харгалзах хэмжээсийн векторууд, дараа нь хэлбэрийн скаляр үржвэр юм хт Айдуудсан хоёр шугаманматрицаар тодорхойлсон хэлбэр А... At х = yилэрхийлэл хт Сүхдуудсан квадратхэлбэр.

2.3. Эерэг тодорхой матрицууд

Квадрат матриц Адуудсан эерэгээр тодорхойлсонхэрэв тэгээс өөр векторын хувьд х ≠ 0 ,

хт Сүх > 0.

Үүний нэгэн адил, сөрөг (хт Сүх < 0), сөрөг бус (хт Сүх≥ 0) ба эерэг биш (хт Сүх≤ 0) тодорхой матрицууд.

2.4. Холескийн задрал

Хэрэв тэгш хэмтэй матриц Аэерэг тодорхой бол өвөрмөц гурвалжин матриц байна Уэерэг элементүүдтэй, үүний тулд

А = Ут У.

Жишээлбэл,

Цагаан будаа. 19 Холескийн задрал

2.5. Туйлын задрал

Байцгаая Ахэмжээс нь доройтдоггүй квадрат матриц юм Н× Н... Дараа нь нэгийг харьцах гэж байна туйлгүйцэтгэл

А = SR,

хаана Снь сөрөг бус тэгш хэмтэй матриц бөгөөд Рнь ортогональ матриц юм. Матрицууд Сболон Ртодорхой тодорхойлж болно:

С 2 = ААт эсвэл С = (АА t) ½ ба Р = С −1 А = (АА t) −1 А.

Жишээлбэл,

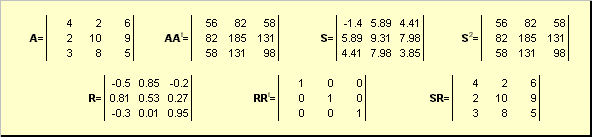
Цагаан будаа. 20 Туйлын задрал

Хэрэв матриц Адоройтсон бол өргөтгөл нь өвөрмөц биш юм - тухайлбал: Сганцаараа, гэхдээ Рмагадгүй маш их. Туйлын задрал нь матрицыг илэрхийлдэг Ашахалт / сунгалтын хослол хэлбэрээр Сболон эргэх Р.

2.6. Хувийн вектор ба хувийн утга

Байцгаая Аквадрат матриц юм. Вектор vдуудсан өөрийн векторматрицууд А, хэрэв

Av = λ v,

λ тоог хаана дууддаг өөрийн гэсэн утгатайматрицууд А... Тиймээс матрицын гүйцэтгэдэг хувиргалт Агаруй вектор v, λ коэффициенттэй энгийн суналт эсвэл шахалтаар багасдаг. Өвөрмөц векторыг α ≠ 0 тогтмолоор үржүүлэх хүртэл тодорхойлно, өөрөөр хэлбэл. хэрэв vнь хувийн вектор, дараа нь α vнь мөн хувийн вектор юм.

2.7. Хувийн үнэ цэнэ

Матриц А, хэмжээс ( Н× Н) илүү байж болохгүй Нхувийн үнэ цэнэ. Тэд сэтгэл хангалуун байдаг шинж чанарын тэгшитгэл

det ( А − λ I) = 0,

Энэ нь алгебрийн тэгшитгэл юм Нр захиалга. Ялангуяа 2х2 матрицын хувьд шинж чанарын тэгшитгэл нь хэлбэртэй байна

Жишээлбэл,

Цагаан будаа. 21 Хувийн утга

Хувийн утгуудын багц λ 1, ..., λ Нматрицууд Адуудсан спектр А.

Спектр нь янз бүрийн шинж чанартай байдаг. Тухайлбал

det ( А) = λ 1 × ... × λ Н, Sp ( А) = λ 1 + ... + λ Н.

Дурын матрицын хувийн утга нь нарийн төвөгтэй тоо байж болно, гэхдээ матриц нь тэгш хэмтэй бол ( А t = А), тэгвэл түүний хувийн утга бодит байна.

2.8. Өөрийн векторууд

Матриц А, хэмжээс ( Н× Н) илүү байж болохгүй Нөөрийн векторууд тус бүр өөрийн гэсэн утгатай тохирч байна. Өвөрмөц векторыг тодорхойлох v nТа нэгэн төрлийн тэгшитгэлийн системийг шийдэх хэрэгтэй

(А − λ n I)v n = 0 .

Энэ нь энгийн шийдэлтэй, учир нь det ( А -λ n I) = 0.

Жишээлбэл,

Цагаан будаа. 22 хувийн векторууд

Тэгш хэмт матрицын хувийн векторууд нь ортогональ байна.

Нэг төрлийн шугаман тэгшитгэлийн СИСТЕМ

Нэг төрлийн шугаман тэгшитгэлийн систем нь хэлбэрийн систем юм

Энэ тохиолдолд энэ нь тодорхой байна оноос хойш эдгээр шалгуур үзүүлэлтийн аль нэг баганын бүх элементүүд тэгтэй тэнцүү байна.

Үл мэдэгдэхийг томъёогоор олдог тул , дараа нь Δ ≠ 0 тохиолдолд систем нь өвөрмөц тэг шийдэлтэй байна х = y = z= 0. Гэсэн хэдий ч олон асуудалд нэгэн төрлийн систем тэгээс өөр шийдэлтэй эсэх нь сонирхолтой байдаг.

Теорем.Шугаман нэгэн төрлийн тэгшитгэлийн систем тэгээс өөр шийдэлтэй байхын тулд Δ ≠ 0 байх шаардлагатай бөгөөд хангалттай.

Тэгэхээр тодорхойлогч Δ ≠ 0 бол систем нь өвөрмөц шийдэлтэй байна. Хэрэв Δ ≠ 0 бол шугаман нэгэн төрлийн тэгшитгэлийн систем хязгааргүй олон шийдтэй байна.

Жишээ.

Матрицын хувийн вектор ба хувийн утга

Квадрат матрицыг өгье , X- өндөр нь матрицын дараалалтай давхцдаг зарим матриц-багана А. .

Олон асуудалд тэгшитгэлийг харгалзан үзэх шаардлагатай X

Энд λ нь зарим тоо юм. Аливаа λ-ийн хувьд энэ тэгшитгэл нь тэг шийдэлтэй байх нь ойлгомжтой.

Энэ тэгшитгэл нь тэгээс өөр шийдэлтэй байх λ тоог нэрлэнэ өөрийн гэсэн утгатайматрицууд А, a XУчир нь ийм λ гэж нэрлэгддэг өөрийн векторматрицууд А.

Матрицын хувийн векторыг ол А... Үүний хэрээр Э∙X = X, дараа нь матрицын тэгшитгэлийг дахин бичиж болно эсвэл ... Өргөтгөсөн хэлбэрээр энэ тэгшитгэлийг шугаман тэгшитгэлийн систем болгон дахин бичиж болно. Үнэхээр .

Тиймээс

Тиймээс бид координатыг тодорхойлох нэгэн төрлийн шугаман тэгшитгэлийн системийг олж авлаа x 1, x 2, x 3вектор X... Систем нь тэгээс өөр шийдлүүдтэй байхын тулд системийн тодорхойлогч нь тэгтэй тэнцүү байх шаардлагатай бөгөөд хангалттай юм.

Энэ нь λ-тэй холбоотой 3-р зэргийн тэгшитгэл юм. Энэ нь гэж нэрлэгддэг шинж чанарын тэгшитгэлматрицууд Амөн хувийн утгуудыг λ тодорхойлоход үйлчилдэг.

Хувийн утга бүр λ нь хувийн вектортой тохирч байна X, тэдгээрийн координатууд нь системээс λ-ийн харгалзах утгаар тодорхойлогддог.

Жишээ.

ВЕКТОР АЛГЕБР. ВЕКТОРЫН ОЙЛГОЛТ

Физикийн янз бүрийн салбарыг судлахдаа урт, талбай, масс, температур гэх мэт тоон утгыг зааж өгөх замаар бүрэн тодорхойлогддог хэмжигдэхүүнүүд байдаг. Ийм хэмжигдэхүүнийг скаляр гэж нэрлэдэг. Гэсэн хэдий ч тэдгээрээс гадна хэмжигдэхүүнүүд байдаг бөгөөд тэдгээрийг тодорхойлохын тулд тоон утгаас гадна орон зай дахь чиглэлийг, жишээлбэл, биед үйлчлэх хүч, хурд, хурдатгал зэргийг мэдэх шаардлагатай. орон зайд хөдөлж байх үеийн бие, орон зайн өгөгдсөн цэг дэх соронзон орны хүч гэх мэт. Ийм хэмжигдэхүүнийг вектор гэж нэрлэдэг.

Нэг хатуу тодорхойлолтыг танилцуулъя.

Чиглэлийн сегментТөгсгөлд нь аль нь эхний, аль нь хоёрдугаарт байгаа нь тодорхой болох сегментийг дуудъя.

Вектортодорхой урттай чиглэсэн сегмент гэж нэрлэгддэг, i.e. энэ нь тодорхой урттай сегмент бөгөөд түүний хязгаарлах цэгүүдийн нэгийг эхлэл, нөгөөг нь төгсгөл болгон авдаг. Хэрэв А- векторын эхлэл, Б- түүний төгсгөл, дараа нь векторыг тэмдэгээр тэмдэглэдэг, үүнээс гадна векторыг ихэвчлэн нэг үсгээр тэмдэглэдэг. Зураг дээр векторыг шугамын сегментээр, түүний чиглэлийг сумаар зааж өгсөн болно.

Модульэсвэл уртвектор нь түүнийг тодорхойлсон чиглэлийн сегментийн урт юм. Үүнийг || гэж тэмдэглэнэ эсвэл ||.

Эхлэл ба төгсгөл нь давхцдаг тэг вектор гэж нэрлэгддэг векторыг мөн вектор гэж нэрлэнэ. Үүнийг зааж өгсөн. Тэг вектор нь тодорхой чиглэлгүй бөгөөд модуль нь тэгтэй тэнцүү || = 0.

векторуудыг ба гэж нэрлэдэг collinearхэрэв тэдгээр нь нэг шулуун эсвэл зэрэгцээ шугам дээр байрласан бол. Түүнээс гадна, хэрэв ба векторууд нэг чиглэлд байвал бид эсрэгээр бичих болно.

Нэг хавтгайд параллель шулуун дээр байрлах векторуудыг нэрлэдэг хавтгай.

Хоёр вектор ба гэж нэрлэдэг тэнцүүхэрэв тэдгээр нь хоорондоо уялдаатай, ижил чиглэлтэй, уртаараа тэнцүү бол. Энэ тохиолдолд бичнэ үү.

Векторуудын тэгш байдлын тодорхойлолтоос үзэхэд векторыг сансар огторгуйн аль ч цэгт гарал үүслийг нь байрлуулж өөртэйгөө параллель шилжүүлж болно.

Жишээлбэл.

ВЕКТОР ДЭЭР ШУГААН ҮЙЛ АЖИЛЛАГАА

1. Векторыг тоогоор үржүүлэх.

   Векторын λ тооны үржвэр нь шинэ вектор бөгөөд дараах байдлаар:

   λ тоогоор векторын үржвэрийг тэмдэглэнэ.

   

   Жишээлбэл,нь вектортой ижил чиглэлд чиглэсэн, векторын уртын хагасын урттай вектор юм.

   Оруулсан үйл ажиллагаа нь дараах байдалтай байна шинж чанарууд:

2. Вектор нэмэх.

   Дурын хоёр вектор ба байг. Дурын цэгийг ав Оба вектор барих. Үүний дараа, цэгээс Авекторыг хойш тавь. Эхний векторын эхлэлийг хоёр дахь векторын төгсгөлтэй холбосон векторыг нэрлэнэ нийлбэрЭдгээр векторуудын ба тэмдэглэсэн байна .

   

   Вектор нэмэхийн томъёолсон тодорхойлолтыг нэрлэдэг параллелограммын дүрэм, учир нь ижил векторуудын нийлбэрийг дараах байдлаар авч болно. Гол цэгээс хойш тавь Овекторууд ба. Эдгээр векторууд дээр параллелограмм байгуулъя OAVS... Векторуудаас хойш оройноос татсан параллелограммын диагональ болох вектор О, векторуудын нийлбэр байх нь ойлгомжтой.

   

   Дараахь зүйлийг шалгахад хялбар байдаг вектор нэмэх шинж чанарууд.

3. Векторуудын ялгаа.

   Өгөгдсөн вектортой ижил урттай, эсрэг чиглэлтэй коллинеар векторыг гэнэ эсрэгвекторын хувьд вектор бөгөөд үүгээр тэмдэглэнэ. Эсрэг векторыг векторыг λ = –1: тоогоор үржүүлсний үр дүн гэж үзэж болно.

Диагональ матрицууд нь хамгийн энгийн. Шугаман операторын матриц диагональ хэлбэртэй байх үндэслэлийг олох боломжтой юу гэсэн асуулт гарч ирнэ. Ийм суурь бий.
Шугаман орон зай R n ба түүн дээр ажиллаж байгаа шугаман оператор А өгөгдсөн байг; энэ тохиолдолд A оператор R n-ийг өөртөө авна, өөрөөр хэлбэл A: R n → R n.

Тодорхойлолт. Хэрэв А оператор өөрт нь коллинеар вектор болж хувирвал тэгээс өөр векторыг А операторын хувийн вектор гэнэ, өөрөөр хэлбэл. λ тоог хувийн векторт харгалзах А операторын хувийн утга буюу хувийн утга гэнэ.
Хувийн утга ба хувийн векторуудын зарим шинж чанарыг тэмдэглэе.
1. Хувийн векторуудын дурын шугаман хослол ижил хувийн утгатай λ харгалзах операторын А нь ижил хувийн утгатай хувийн вектор байна.
2. Хувийн векторууд λ 1, λ 2,..., λ m хосоор өөр өөр хувийн утгатай A операторын шугаман хамааралгүй.
3. Хэрэв хувийн утгууд λ 1 = λ 2 = λ m = λ бол хувийн утга λ нь хамгийн ихдээ m шугаман бие даасан хувийн векторуудтай тохирно.

Тэгэхээр шугаман бие даасан n хувийн вектор байвал λ 1, λ 2,…, λ n өөр өөр хувийн утгатай тохирч байвал тэдгээр нь шугаман хамааралгүй тул R n орон зайн үндэс болгон авч болно. Шугаман A операторын матрицын хэлбэрийг түүний хувийн векторуудын үндсэн дээр олъё, үүний тулд бид А операторын үндсэн векторууд дээр ажилладаг. тэгээд .
Тиймээс шугаман оператор А матриц нь өөрийн векторуудын үндсэн дээр диагональ хэлбэртэй бөгөөд A операторын хувийн утгууд диагональ дээр байрладаг.
Матриц диагональ байх өөр үндэслэл бий юу? Энэ асуултын хариултыг дараах теоремоор өгнө.

Теорем. Суурийн (i = 1..n) шугаман операторын матриц нь суурийн бүх векторууд нь А операторын хувийн векторууд байх тохиолдолд диагональ хэлбэртэй байна.

Хувийн утга ба хувийн векторыг олох дүрэм

Вектор өгье , энд x 1, x 2, ..., x n нь суурьтай харьцуулахад векторын координатууд юм. ба λ хувийн утгад харгалзах шугаман операторын хувийн вектор, өөрөөр хэлбэл. Энэ хамаарлыг матриц хэлбэрээр бичиж болно

. (*)

(*) тэгшитгэлийг олох тэгшитгэл гэж үзэж болно, өөрөөр хэлбэл, хувийн вектор нь тэг байх боломжгүй тул бид өчүүхэн бус шийдлүүдийг сонирхож байна. Нэг төрлийн шугаман тэгшитгэлийн системийн ач холбогдолгүй шийдлүүд нь зөвхөн det (A - λE) = 0 тохиолдолд л байдаг гэдгийг мэддэг. Тиймээс λ нь A операторын хувийн утга байхын тулд det (A -) байх шаардлагатай бөгөөд хангалттай. λE) = 0.
Хэрэв (*) тэгшитгэлийг координат хэлбэрээр нарийвчлан бичсэн бол шугаман нэгэн төрлийн тэгшитгэлийн системийг авна.

(1)
хаана шугаман операторын матриц юм.

Хэрэв тодорхойлогч D нь тэгтэй тэнцүү бол систем (1) нь тэгээс өөр шийдэлтэй байна

Хувийн утгыг олох тэгшитгэлийг хүлээн авлаа.
Энэ тэгшитгэлийг шинж чанарын тэгшитгэл гэж нэрлэдэг ба түүний зүүн талыг А матрицын (оператор) шинж чанарын олон гишүүнт гэж нэрлэдэг. Хэрэв шинж чанарын олон гишүүнт бодит үндэсгүй бол А матриц нь хувийн векторгүй бөгөөд диагональ хэлбэрт оруулах боломжгүй. .
λ 1, λ 2,…, λ n нь шинж чанарын тэгшитгэлийн бодит язгуур байх ба тэдгээрийн дунд олон үндэс байж болно. Эдгээр утгыг систем (1) болгон орлуулснаар бид хувийн векторуудыг олно.

Жишээ 12. Шугаман оператор A нь хуулийн дагуу R 3-т үйлчилдэг ба энд x 1, x 2, .., x n нь суурь дээрх векторын координатууд юм. , , ... Энэ операторын хувийн утга ба хувийн векторыг ол.
Шийдэл. Бид энэ операторын матрицыг бүтээдэг:
.
Бид хувийн векторуудын координатыг тодорхойлох системийг бүрдүүлдэг.

Бид шинж чанарын тэгшитгэлийг гаргаж, үүнийг шийднэ.

.
λ 1,2 = -1, λ 3 = 3.
Системд λ = -1-ийг орлуулбал бид:
эсвэл
Учир нь , дараа нь хоёр хамааралтай хувьсагч, нэг чөлөөт хувьсагч байна.
Тэгвэл x 1 нь чөлөөт үл мэдэгдэх болно Бид энэ системийг ямар ч аргаар шийдэж, энэ системийн ерөнхий шийдлийг олдог: n - r = 3 - 2 = 1 тул шийдлийн үндсэн систем нь нэг шийдлээс бүрдэнэ.
Хувийн утга λ = -1-д харгалзах хувийн векторуудын багц нь: хэлбэртэй байна, энд x 1 нь ямар ч тэгээс өөр тоо юм. Энэ олонлогоос нэг векторыг сонгоод, жишээ нь x 1 = 1-ийг тавиад: .
Үүнтэй адилаар бид хувийн утга λ = 3-д тохирох хувийн векторыг олно. .
R 3 орон зайд суурь нь шугаман бие даасан гурван вектороос бүрдэх боловч бид зөвхөн хоёр шугаман бие даасан хувийн векторыг хүлээн авсан бөгөөд үүнээс R 3-ийн суурийг бүрдүүлэх боломжгүй юм. Иймээс шугаман операторын А матрицыг диагональ хэлбэрт оруулах боломжгүй.

Жишээ 13. Матриц өгөгдсөн .
1. Вектор гэдгийг батал нь А матрицын хувийн вектор. Энэ хувийн векторт тохирох хувийн утгыг ол.
2. А матриц диагональ хэлбэртэй байх суурийг ол.
Шийдэл.
1. Хэрэв, тэгвэл - хувийн вектор

.
Вектор (1, 8, -1) нь хувийн вектор юм. Хувийн утга λ = -1.
Матриц нь хувийн векторуудаас бүрдэх суурь нь диагональ хэлбэртэй байна. Тэдний нэг нь алдартай. Үлдсэнийг нь олъё.
Бид системээс өөрийн векторуудыг хайдаг:

Онцлог тэгшитгэл: ;
(3 + λ) [- 2 (2-λ) (2 + λ) +3] = 0; (3 + λ) (λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Хувийн утга λ = -3-д тохирох хувийн векторыг олъё.

Энэ системийн матрицын зэрэглэл нь хоёртой тэнцүү ба үл мэдэгдэх тоотой тэнцүү тул энэ систем нь зөвхөн тэг шийдэлтэй байна x 1 = x 3 = 0. Энд x 2 нь тэгээс өөр ямар ч байж болно, жишээлбэл, x 2 = 1. Тиймээс (0 , 1,0) вектор нь λ = -3-д харгалзах хувийн вектор байна. Шалгацгаая:
.
Хэрэв λ = 1 бол бид системийг олж авна
Матрицын зэрэглэл нь хоёр байна. Бид сүүлчийн тэгшитгэлийг устгана.
x 3 нь чөлөөт үл мэдэгдэх зүйл байг. Дараа нь x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Тохиргоо x 3 = 1, бид (-3, -9,1) - хувийн утга λ = 1-д тохирох хувийн вектор байна. Баталгаажуулалт:

.
Хувийн утгууд нь бодит бөгөөд өөр байдаг тул тэдгээрт харгалзах векторууд нь шугаман бие даасан байдаг тул тэдгээрийг R 3-д үндэс болгон авч болно. Тиймээс, үндсэн дээр , , А матриц нь дараах хэлбэртэй байна.
.
Зарим шугаман операторуудын хувьд шугаман хамааралгүй хувийн векторууд нь n-ээс бага байж болох тул A: R n → R n шугаман операторын матриц бүрийг диагональ хэлбэрт оруулж болохгүй. Гэсэн хэдий ч матриц нь тэгш хэмтэй бол яг m шугаман бие даасан векторууд m үржвэрийн шинж чанарын тэгшитгэлийн үндэстэй тохирно.

Тодорхойлолт. Тэгш хэмтэй матриц гэдэг нь үндсэн диагональтай харьцуулахад тэгш хэмтэй элементүүд нь тэнцүү байх дөрвөлжин матриц юм.
Тайлбар. 1. Тэгш хэмт матрицын бүх хувийн утга бодит байна.
2. Хосоор ялгаатай хувийн утгуудад харгалзах тэгш хэмт матрицын хувийн векторууд нь ортогональ байна.
Судлагдсан аппаратын олон хэрэглээний нэг болохын хувьд хоёр дахь эрэмбийн муруйн хэлбэрийг тодорхойлох асуудлыг авч үзье.