Քառակուսի մատրիցայի սեփական վեկտորն այն մեկն է, որը, երբ բազմապատկվում է տրված մատրիցով, ստացվում է համագիծ վեկտոր: Պարզ բառերով ասած, երբ մատրիցը բազմապատկվում է սեփական վեկտորով, վերջինս մնում է նույնը, բայց բազմապատկվում է ինչ-որ թվով:

Սահմանում

Սեփական վեկտորը ոչ զրոյական V վեկտորն է, որը M քառակուսի մատրիցով բազմապատկելիս վերածվում է ինքն իրեն՝ մեծանալով որոշակի թվով λ։ Հանրահաշվական նշումներում այն ​​նման է.

M × V = λ × V,

որտեղ λ-ն M մատրիցայի սեփական արժեքն է:

Դիտարկենք թվային օրինակ: Հարմարության համար մատրիցայի թվերը կբաժանվեն ստորակետով: Եկեք ունենանք մատրիցա.

• M = 0; 4;
• 6; 10.

Եկեք այն բազմապատկենք սյունակի վեկտորով.

• V = -2;

Երբ մատրիցը բազմապատկում ենք սյունակի վեկտորով, ստանում ենք նաև սյունակի վեկտոր: Խիստ մաթեմատիկական առումով, 2 × 2 մատրիցը սյունակով վեկտորով բազմապատկելու բանաձևը կունենա հետևյալ տեսքը.

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 նշանակում է M մատրիցայի տարր, որը գտնվում է առաջին շարքում և առաջին սյունակում, իսկ M22՝ երկրորդ շարքում և երկրորդ սյունակում գտնվող տարրը: Մեր մատրիցայի համար այս տարրերը հավասար են M11 = 0, M12 = 4, M21 = 6, M22 10: Սյունակի վեկտորի համար այս արժեքներն են V11 = –2, V21 = 1: Այս բանաձևի համաձայն մենք ստանում ենք. քառակուսի մատրիցայի արտադրյալի վեկտորի հետևյալ արդյունքը.

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2:

Հարմարության համար գրենք սյունակի վեկտորը տողով։ Այսպիսով, մենք քառակուսի մատրիցը բազմապատկեցինք վեկտորով (-2; 1) և ստացանք վեկտորը (4; -2): Ակնհայտ է, որ սա նույն վեկտորն է, որը բազմապատկվում է λ = -2-ով: Lambda-ն այս դեպքում նշանակում է մատրիցայի սեփական արժեքը:

Մատրիցայի սեփական վեկտորը համագիծ վեկտոր է, այսինքն՝ առարկա, որը չի փոխում իր դիրքը տարածության մեջ, երբ բազմապատկվում է մատրիցով: Վեկտորային հանրահաշիվում համաչափությունը նման է երկրաչափության զուգահեռությանը: Երկրաչափական մեկնաբանության մեջ կոլգծային վեկտորները տարբեր երկարությունների զուգահեռ ուղղորդված գծերի հատվածներ են։ Էվկլիդեսի ժամանակներից մենք գիտենք, որ մեկ ուղիղն ունի անսահման թվով զուգահեռ ուղիղներ, ուստի տրամաբանական է ենթադրել, որ յուրաքանչյուր մատրիցա ունի անսահման թվով սեփական վեկտորներ։

Նախորդ օրինակից դուք կարող եք տեսնել, որ սեփական վեկտորները կարող են լինել (-8; 4), և (16; -8), և (32, -16): Սրանք բոլորը համագիծ վեկտորներ են, որոնք համապատասխանում են λ = -2 սեփական արժեքին: Բնօրինակ մատրիցը այս վեկտորներով բազմապատկելիս մենք դեռ կստանանք մի վեկտոր, որը բնօրինակից տարբերվում է 2 անգամ։ Այդ իսկ պատճառով սեփական վեկտոր գտնելու խնդիրներ լուծելիս պահանջվում է գտնել միայն գծային անկախ վեկտորային օբյեկտներ։ Ամենից հաճախ, n × n մատրիցի համար կան սեփական վեկտորների n-րդ թիվը: Մեր հաշվիչը հարմարեցված է երկրորդ կարգի քառակուսի մատրիցների վերլուծության համար, հետևաբար, գրեթե միշտ արդյունքում կգտնվեն երկու սեփական վեկտորներ, բացառությամբ այն դեպքերի, երբ դրանք համընկնում են։

Վերոնշյալ օրինակում մենք նախապես գիտեինք սկզբնական մատրիցայի սեփական վեկտորը և հստակ որոշեցինք լամբդայի թիվը: Այնուամենայնիվ, գործնականում ամեն ինչ հակառակն է լինում. սկզբում հայտնաբերվում են սեփական արժեքները, և միայն դրանից հետո են սեփական վեկտորները:

Ալգորիթմ լուծելու համար

Եկեք վերանայենք սկզբնական M մատրիցը և փորձենք գտնել դրա երկու սեփական վեկտորները: Այսպիսով, մատրիցը նման է.

• M = 0; 4;
• 6; 10.

Նախ, մենք պետք է որոշենք λ սեփական արժեքը, որի համար պետք է հաշվարկենք հետևյալ մատրիցայի որոշիչը.

• (0 - λ); 4;
• 6; (10 - λ).

Այս մատրիցը ստացվում է հիմնական անկյունագծի տարրերից անհայտ λ-ն հանելով: Որոշիչը որոշվում է ստանդարտ բանաձևով.

• detA = M11 × M21 - M12 × M22
• detA = (0 - λ) × (10 - λ) - 24

Քանի որ մեր վեկտորը չպետք է զրո լինի, մենք ստացված հավասարումը վերցնում ենք որպես գծային կախված և մեր detA որոշիչին հավասարեցնում ենք զրոյի:

(0 - λ) × (10 - λ) - 24 = 0

Եկեք բացենք փակագծերը և ստանանք մատրիցայի բնորոշ հավասարումը.

λ 2 - 10λ - 24 = 0

Սա ստանդարտ քառակուսի հավասարումն է, որը պետք է լուծվի դիսկրիմինանտի միջոցով:

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

Տարբերիչի արմատը sqrt (D) = 14 է, հետևաբար, λ1 = -2, λ2 = 12: Այժմ յուրաքանչյուր լամբդա արժեքի համար պետք է գտնել սեփական վեկտոր: Եկեք արտահայտենք համակարգի գործակիցները λ = -2-ի համար:

• M - λ × E = 2; 4;
• 6; 12.

Այս բանաձևում E-ն ինքնության մատրիցն է: Ելնելով ստացված մատրիցից՝ մենք կազմում ենք գծային հավասարումների համակարգ.

2x + 4y = 6x + 12y,

որտեղ x և y սեփական վեկտորի տարրերն են:

Հավաքեք բոլոր X-երը ձախ կողմում, իսկ բոլոր խաղացողներին՝ աջ: Ակնհայտ է - 4x = 8y: Արտահայտությունը բաժանեք - 4-ի և ստացեք x = –2y: Այժմ մենք կարող ենք որոշել մատրիցայի առաջին սեփական վեկտորը՝ վերցնելով անհայտների ցանկացած արժեք (հիշեք գծային կախված սեփական վեկտորների անսահմանությունը): Վերցնենք y = 1, ապա x = –2: Հետևաբար, առաջին սեփական վեկտորը նման է V1 = (–2; 1): Վերադարձեք հոդվածի սկզբին։ Հենց այս վեկտորային օբյեկտի վրա մենք բազմապատկեցինք մատրիցը՝ սեփական վեկտորի հասկացությունը ցուցադրելու համար:

Այժմ մենք կգտնենք սեփական վեկտորը λ = 12-ի համար:

• M - λ × E = -12; 4
• 6; -2.

Կազմենք գծային հավասարումների նույն համակարգը.

• -12x + 4y = 6x - 2y
• -18x = -6y
• 3x = y.

Այժմ վերցնենք x = 1, հետևաբար y = 3: Այսպիսով, երկրորդ սեփական վեկտորը նման է V2 = (1; 3): Երբ սկզբնական մատրիցը բազմապատկվում է այս վեկտորով, արդյունքը միշտ կլինի նույն վեկտորը, որը բազմապատկվում է 12-ով: Սա եզրափակում է լուծման ալգորիթմը: Այժմ դուք գիտեք, թե ինչպես կարելի է ձեռքով սահմանել մատրիցայի սեփական վեկտորը:

• որոշիչ;
• հետք, այսինքն՝ հիմնական անկյունագծի վրա գտնվող տարրերի գումարը.
• դասակարգում, այսինքն, գծային անկախ տողերի / սյունակների առավելագույն քանակը:

Ծրագիրը գործում է վերը նշված ալգորիթմի համաձայն՝ նվազագույնի հասցնելով լուծման գործընթացը։ Կարևոր է նշել, որ ծրագրում լամբդան նշվում է «c» տառով: Բերենք թվային օրինակ.

Ծրագրի օրինակ

Փորձենք սահմանել սեփական վեկտորներ հետևյալ մատրիցայի համար.

• M = 5; 13;
• 4; 14.

Եկեք այս արժեքները մուտքագրենք հաշվիչի բջիջներում և ստանանք պատասխանը հետևյալ ձևով.

• Մատրիցային դասակարգում: 2
• Մատրիցայի որոշիչ՝ 18;
• Մատրիցային հետք՝ 19;
• Սեփական վեկտորի հաշվարկ՝ c 2 - 19.00c + 18.00 (բնութագրական հավասարում);
• Սեփական վեկտորի հաշվարկ՝ 18 (առաջին լամբդա արժեք);
• Սեփական վեկտորի հաշվարկ՝ 1 (երկրորդ լամբդայի արժեքը);
• Վեկտորի 1-ի հավասարումների համակարգը՝ -13x1 + 13y1 = 4x1 - 4y1;
• Վեկտորի 2-ի հավասարումների համակարգը՝ 4x1 + 13y1 = 4x1 + 13y1;
• Eigenvector 1: (1; 1);
• Eigenvector 2: (-3.25; 1):

Այսպիսով, մենք ստացել ենք երկու գծային անկախ սեփական վեկտոր:

Եզրակացություն

Գծային հանրահաշիվը և վերլուծական երկրաչափությունը ստանդարտ առարկաներ են ճարտարագիտության առաջին կուրսեցիների համար: Վեկտորների և մատրիցների մեծ թիվը սարսափելի է, և հեշտ է սխալվել նման ծանրաբեռնված հաշվարկներում: Մեր ծրագիրը հնարավորություն կտա ուսանողներին ստուգել իրենց հաշվարկները կամ ինքնաբերաբար կլուծի սեփական վեկտորը գտնելու խնդիրը։ Մեր կատալոգում կան գծային հանրահաշվի այլ հաշվիչներ, օգտագործեք դրանք ձեր ուսումնասիրության կամ աշխատանքի մեջ:

Առաջին մասը սահմանում է նվազագույն դրույթները քիմիոմետրիկայի հասկանալու համար, իսկ երկրորդ մասը պարունակում է փաստեր, որոնք դուք պետք է իմանաք բազմաչափ վերլուծության մեթոդները ավելի խորը հասկանալու համար: Ներկայացումը պատկերված է Excel-ի աշխատանքային գրքում կատարված օրինակներով: Matrix.xlsորը ուղեկցում է այս փաստաթղթին:

Օրինակների հղումները տեքստում տեղադրվում են որպես Excel օբյեկտներ: Այս օրինակներն իրենց բնույթով վերացական են, դրանք ոչ մի կերպ կապված չեն անալիտիկ քիմիայի խնդիրների հետ։ Քիմիոմետրիկության մեջ մատրիցային հանրահաշվի կիրառման իրական օրինակները դիտարկված են քիմիաչափական տարբեր կիրառություններին նվիրված այլ տեքստերում:

Անալիտիկ քիմիայում կատարված չափումների մեծ մասը ուղղակի չեն, այլ անուղղակի... Սա նշանակում է, որ փորձի ժամանակ ցանկալի անալիտի C արժեքի փոխարեն (կոնցենտրացիան) ստացվում է մեկ այլ արժեք. x(ազդանշան) կապված, բայց ոչ հավասար C-ին, այսինքն. x(C) ≠ C. Որպես կանոն, կախվածության տեսակը x(C) հայտնի չէ, սակայն, բարեբախտաբար, անալիտիկ քիմիայում չափումների մեծ մասը համաչափ են: Սա նշանակում է, որ C-ի կոնցենտրացիայի աճով աանգամ, X ազդանշանը կաճի նույնքանով: x(աԳ) = կացին(C). Բացի այդ, ազդանշանները նաև հավելում են, այնպես որ C 1 և C 2 կոնցենտրացիաներով երկու նյութեր պարունակող նմուշից ազդանշանը հավասար կլինի յուրաքանչյուր բաղադրիչի ազդանշանների գումարին, այսինքն. x(C 1 + C 2) = x(C 1) + x(C 2): Համաչափությունն ու հավելյալությունը միասին տալիս են գծայինություն... Գծայինության սկզբունքը լուսաբանելու համար կան բազմաթիվ օրինակներ, սակայն բավական է նշել ամենաակնառու օրինակներից երկուսը` քրոմատագրությունը և սպեկտրոսկոպիան: Անալիտիկ քիմիայի փորձի երկրորդ հատկանիշն է բազմալիքային... Ժամանակակից վերլուծական սարքավորումները միաժամանակ չափում են ազդանշանները բազմաթիվ ալիքների համար: Օրինակ, լույսի հաղորդման ինտենսիվությունը չափվում է միանգամից մի քանի ալիքի երկարության համար, այսինքն. սպեկտրը. Հետևաբար, փորձի ժամանակ մենք գործ ունենք բազմաթիվ ազդանշանների հետ x 1 , x 2 ,...., x n, որը բնութագրում է ուսումնասիրվող համակարգում առկա նյութերի C 1, C 2, ..., C m կոնցենտրացիաների հավաքածուն:

Բրինձ. 1 Սպեկտրա

Այսպիսով, վերլուծական փորձը բնութագրվում է գծայինությամբ և բազմաչափությամբ: Հետևաբար, հարմար է փորձարարական տվյալները դիտարկել որպես վեկտորներ և մատրիցներ և շահարկել դրանք՝ օգտագործելով մատրիցային հանրահաշվի ապարատը։ Այս մոտեցման արդյունավետությունը ցույց է տրված օրինակով, որը ցույց է տալիս երեք սպեկտրներ, որոնք գրանցված են 200 ալիքի երկարությունների համար 4000-ից 4796 սմ – 1: Առաջին ( x 1) և երկրորդը ( x 2) սպեկտրներ են ստացվել ստանդարտ նմուշների համար, որոնցում հայտնի է երկու նյութերի A և B կոնցենտրացիան՝ առաջին նմուշում [A] = 0,5, [B] = 0,1, իսկ երկրորդ նմուշում [A] = 0,2, [B. ] = 0,6: Ինչ կարելի է ասել նոր, անհայտ նմուշի մասին, որի սպեկտրը նշանակված է x 3 ?

Դիտարկենք երեք փորձարարական սպեկտր x 1 , x 2 և x 3-ը որպես 200 չափման երեք վեկտոր: Գծային հանրահաշվի միջոցով կարելի է հեշտությամբ ցույց տալ, որ x 3 = 0.1 x 1 +0.3 x 2; հետևաբար, երրորդ նմուշն ակնհայտորեն պարունակում է միայն A և B նյութեր [A] = 0,5 × 0,1 + 0,2 × 0,3 = 0,11 և [B] = 0,1 × 0,1 + 0,6 × 0,3 = 0,19 կոնցենտրացիաներում:

1. Հիմնական տեղեկատվություն

1.1 Մատրիցներ

Մատրիցակոչվում է թվերի ուղղանկյուն աղյուսակ, օրինակ

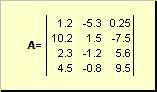
Բրինձ. 2 Մատրիցա

Մատրիցները նշված են թավ մեծատառերով ( Ա), իսկ դրանց տարրերը՝ համապատասխան փոքրատառերը՝ ինդեքսներով, այսինքն. ա ij. Առաջին ինդեքսը համարակալում է տողերը, իսկ երկրորդը՝ սյունակները։ Քիմիոմետրիկայի մեջ ընդունված է ինդեքսի առավելագույն արժեքը նշել նույն տառով, ինչ ինդեքսը, բայց մեծատառով։ Հետևաբար մատրիցը Ակարելի է գրել նաև որպես ( ա ij , ես = 1,..., Ի; ժ = 1,..., Ջ). Օրինակում ներկայացված մատրիցայի համար Ի = 4, Ջ= 3 և ա 23 = −7.5.

Զույգ թվեր Իև Ջկոչվում է մատրիցայի չափ և նշվում է որպես Ի× Ջ... Քիմիոմետրիկության մեջ մատրիցայի օրինակ է ստացված սպեկտրների բազմությունը Ինմուշների վրա Ջալիքի երկարություններ.

1.2. Պարզ մատրիցային գործողություններ

Մատրիցները կարող են բազմապատկել թվերով... Այս դեպքում յուրաքանչյուր տարր բազմապատկվում է այս թվով: Օրինակ -

Բրինձ. 3 Մատրիցային բազմապատկում թվով

Նույն չափման երկու մատրիցա կարող է լինել տարրական առումով ծալելև հանել... Օրինակ,

Բրինձ. 4 Մատրիցայի ավելացում

Թվով բազմապատկելու և գումարման արդյունքում ստացվում է նույն չափի մատրիցա։

Զրոյական մատրիցը զրոյից բաղկացած մատրից է: Նշվում է Օ... Ակնհայտ է, որ Ա+Օ = Ա, Ա−Ա = Օև 0 Ա = Օ.

Մատրիցը կարող է լինել փոխադրել... Այս գործողության ընթացքում մատրիցը շրջվում է, այսինքն. տողերն ու սյունակները փոխանակվում են: Տրանսպոզիցիան նշվում է կաթվածով, Ա«կամ ինդեքս Ատ. Այսպիսով, եթե Ա = {ա ij , ես = 1,..., Ի; ժ = 1,...,Ջ), ապա Ա t = ( ա ջի , ժ = 1,...,Ջ; i = 1, ..., Ի). Օրինակ

Բրինձ. 5 Փոխադրել մատրիցը

Ակնհայտ է, որ ( Ատ) տ = Ա, (Ա+Բ) տ = Ա t + Բտ.

1.3. Մատրիցային բազմապատկում

Մատրիցները կարող են բազմապատկել, բայց միայն այն դեպքում, եթե դրանք ունենան համապատասխան չափսեր։ Թե ինչու է դա այդպես, պարզ կլինի սահմանումից: Մատրիցայի արտադրյալը Ա, չափս Ի× Կ, և մատրիցներ Բ, չափս Կ× Ջկոչվում է մատրիցա Գ, չափս Ի× Ջորի տարրերը թվերն են

Այսպիսով, արտադրել ԱԲանհրաժեշտ է, որ ձախ մատրիցայի սյունակների քանակը Ահավասար էր աջ մատրիցի տողերի թվին Բ... Մատրիցային արտադրանքի օրինակ.

Նկ. 6 Մատրիցային արտադրանք

Մատրիցային բազմապատկման կանոնը կարելի է ձևակերպել հետևյալ կերպ. Մատրիցայի տարր գտնելու համար Գկանգնած խաչմերուկում ես-րդ գիծը և ժ-րդ սյունակ ( գ ij) պետք է բազմապատկել տարր առ տարր եսառաջին մատրիցայի րդ շարքը Ավրա ժերկրորդ մատրիցայի սյունակ Բև ավելացրեք բոլոր արդյունքները: Այսպիսով, ցույց տրված օրինակում երրորդ տողից և երկրորդ սյունակից տարրը ստացվում է որպես երրորդ շարքի տարրական արտադրյալների գումար։ Աև երկրորդ սյունակը Բ

Նկ. 7 Մատրիցային արտադրանքի տարր

Մատրիցների արտադրյալը կախված է հերթականությունից, այսինքն. ԱԲ ≠ ԲԱ, եթե միայն չափման նկատառումներով։ Ասվում է, որ այն ոչ փոխադարձ է: Այնուամենայնիվ, մատրիցային արտադրանքները ասոցիատիվ են: Դա նշանակում է որ ABC = (ԱԲ)Գ = Ա(մ.թ.ա). Բացի այդ, այն նաև բաշխիչ է, այսինքն. Ա(Բ+Գ) = ԱԲ+AC... Ակնհայտ է, որ ԱՕ = Օ.

1.4. Քառակուսի մատրիցներ

Եթե ​​մատրիցայի սյունակների թիվը հավասար է նրա տողերի թվին ( Ի = J = N), ապա նման մատրիցը կոչվում է քառակուսի: Այս բաժնում մենք կքննարկենք միայն այդպիսի մատրիցները: Այս մատրիցներից կարելի է առանձնացնել հատուկ հատկություններով մատրիցներ։

Միայնակմատրիցա (նշված է ես,և երբեմն Ե) մատրից է, որտեղ բոլոր տարրերը հավասար են զրոյի, բացառությամբ անկյունագծերի, որոնք հավասար են 1-ի, այսինքն.

Ակնհայտորեն Աի = ԻԱ = Ա.

Մատրիցը կոչվում է անկյունագծայինեթե նրա բոլոր տարրերը, բացառությամբ շեղանկյունների ( ա ii) հավասար են զրոյի։ Օրինակ

Բրինձ. 8 Անկյունագծային մատրիցա

Մատրիցա Ակոչվում է գագաթ եռանկյունաձեւեթե շեղանկյունից ներքեւ նրա բոլոր տարրերը հավասար են զրոյի, այսինքն. ա ij= 0, համար ես>ժ... Օրինակ

Բրինձ. 9 Վերին եռանկյունաձև մատրիցա

Ստորին եռանկյուն մատրիցը սահմանվում է նույն կերպ:

Մատրիցա Ականչեց սիմետրիկ, եթե Ա t = Ա... Այլ կերպ ասած ա ij = ա ջի... Օրինակ

Բրինձ. 10 Սիմետրիկ մատրիցա

Մատրիցա Ականչեց ուղղանկյուն, եթե

Ատ Ա = ԱԱ t = Ի.

Մատրիցը կոչվում է նորմալեթե

1.5. Հետք և որոշիչ

Հետևելովքառակուսի մատրիցա Ա(նշվում է Tr-ով Ա) կամ Sp ( Ա)) նրա անկյունագծային տարրերի գումարն է,

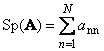
Օրինակ,

Բրինձ. 11 Մատրիցային հետք

Ակնհայտ է, որ

Sp (α Ա) = α Sp ( Ա) և

Սպ ( Ա+Բ) = Սպ ( Ա) + Սպ ( Բ).

Կարելի է ցույց տալ, որ

Սպ ( Ա) = Սպ ( Ա t), Sp ( Ի) = Ն,

և նաև այն

Սպ ( ԱԲ) = Սպ ( ԲԱ).

Քառակուսի մատրիցայի մեկ այլ կարևոր բնութագիր այն է որոշիչ(նշվում է det-ով ( Ա)): Ընդհանուր դեպքում որոշիչի որոշումը բավականին դժվար է, ուստի մենք կսկսենք ամենապարզ տարբերակից՝ մատրիցով Աչափս (2 × 2): Հետո

(3 × 3) մատրիցայի համար որոշիչը կլինի

Մատրիցայի դեպքում ( Ն× Ն) որոշիչը հաշվարկվում է որպես 1 2 3 ... Ն= Ն! պայմաններ, որոնցից յուրաքանչյուրը հավասար է

Ցուցանիշներ կ 1 , կ 2 ,..., կ Նսահմանվում են որպես բոլոր հնարավոր պատվիրված փոխարկումներ rթվեր հավաքածուում (1, 2, ..., Ն). Մատրիցայի որոշիչի հաշվարկը բարդ ընթացակարգ է, որը գործնականում իրականացվում է հատուկ ծրագրերի միջոցով: Օրինակ,

Բրինձ. 12 Մատրիցային որոշիչ

Մենք միայն նշում ենք ակնհայտ հատկությունները.

դետ ( Ի) = 1, det ( Ա) = դետ ( Ատ),

դետ ( ԱԲ) = դետ ( Ա) դետ ( Բ).

1.6. Վեկտորներ

Եթե ​​մատրիցը բաղկացած է միայն մեկ սյունակից ( Ջ= 1), ապա կոչվում է այդպիսի օբյեկտ վեկտոր... Ավելի ճիշտ՝ սյունակի վեկտոր։ Օրինակ

Կարելի է նաև դիտարկել, օրինակ, մեկ տողից բաղկացած մատրիցներ

Այս օբյեկտը նույնպես վեկտոր է, բայց շարքի վեկտոր... Տվյալները վերլուծելիս կարևոր է հասկանալ, թե որ վեկտորների հետ գործ ունենք՝ սյունակների, թե տողերի: Այսպիսով, մեկ նմուշի համար վերցված սպեկտրը կարելի է համարել որպես տող վեկտոր: Այնուհետև բոլոր նմուշների համար որոշակի ալիքի երկարության սպեկտրային ինտենսիվությունների բազմությունը պետք է դիտարկվի որպես սյունակի վեկտոր:

Վեկտորի չափը նրա տարրերի քանակն է։

Հասկանալի է, որ ցանկացած սյունակային վեկտոր կարող է փոխակերպվել տողի վեկտորի փոխադրման միջոցով, այսինքն.

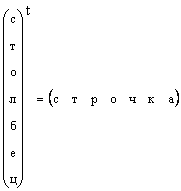
Այն դեպքերում, երբ վեկտորի ձևը հատուկ չի նշվում, այլ ուղղակի վեկտոր է ասվում, ապա դրանք նշանակում են սյունակային վեկտոր։ Մենք նույնպես կպահպանենք այս կանոնը. Վեկտորը նշվում է փոքրատառ ուղիղ թավ տառով: Զրոյական վեկտորը վեկտոր է, որի բոլոր տարրերը զրո են: Նշանակված է 0 .

1.7. Հիմնական գործողություններ վեկտորների հետ

Վեկտորները կարելի է ավելացնել և բազմապատկել թվերով այնպես, ինչպես մատրիցները: Օրինակ,

Բրինձ. 13 Վեկտորային գործողություններ

Երկու վեկտոր xև yկոչվում են համաչափեթե կա α այնպիսի թիվ, որ

1.8. Վեկտորների արտադրանք

Նույն հարթության երկու վեկտոր Նկարելի է բազմապատկել։ Թող լինի երկու վեկտոր x = (x 1 , x 2 ,...,xՆ) տ և y = (y 1 , y 2 ,...,yՆ) տ. Ղեկավարվելով «տող առ սյունակ» բազմապատկման կանոնով՝ մենք կարող ենք դրանցից կազմել երկու արտադրյալ. xտ yև xyտ. Առաջին կտոր

կանչեց սկալյարկամ ներքին... Դրա արդյունքը մի թիվ է: Այն նաև օգտագործում է նշումը ( x,y)= xտ y... Օրինակ,

Բրինձ. 14 Ներքին արտադրանք (կետային արտադրանք)

Երկրորդ կտոր

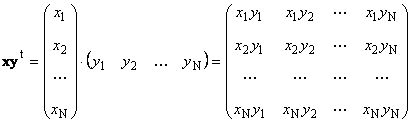
կանչեց արտաքին... Դրա արդյունքը չափումների մատրիցն է ( Ն× Ն). Օրինակ,

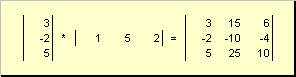
Բրինձ. 15 Արտաքին աշխատանք

Վեկտորները, որոնց սկալյար արտադրյալը հավասար է զրոյի, կոչվում են ուղղանկյուն.

1.9. Վեկտորի նորմ

Վեկտորի սկալյար արտադրյալն ինքնին կոչվում է սկալյար քառակուսի: Այս արժեքը

սահմանում է քառակուսի երկարությունըվեկտոր x... Երկարությունը նշելու համար (նաև կոչվում է նորմըվեկտոր), օգտագործվում է նշումը

Օրինակ,

Բրինձ. 16 Վեկտորային նորմ

Միավոր երկարության վեկտոր (|| x|| = 1) կոչվում է նորմալացված: Ոչ զրոյական վեկտոր ( x ≠ 0 ) կարելի է նորմալացնել՝ բաժանելով երկարության վրա, այսինքն. x = ||x|| (x /||x||) = ||x|| ե... Այստեղ ե = x /||x|| նորմալացված վեկտորն է:

Վեկտորները կոչվում են օրթոնորմալ, եթե դրանք բոլորը նորմալացված են և զույգերով ուղղանկյուն:

1.10. Անկյուն վեկտորների միջև

Կետային արտադրանքը սահմանում է և ներարկումφ երկու վեկտորների միջև xև y

Եթե ​​վեկտորները ուղղանկյուն են, ապա cosφ = 0 և φ = π / 2, իսկ եթե դրանք համագիծ են, ապա cosφ = 1 և φ = 0:

1.11. Մատրիցայի վեկտորային ներկայացում

Յուրաքանչյուր մատրիցա Աչափը Ի× Ջկարող է ներկայացվել որպես վեկտորների մի շարք

Այստեղ յուրաքանչյուր վեկտոր ա ժէ ժ-րդ սյունակը և տողի վեկտորը բ եսէ ես- մատրիցայի-րդ շարքը Ա

1.12. Գծային կախված վեկտորներ

Նույն չափի վեկտորներ ( Ն) կարելի է ավելացնել և բազմապատկել թվով, ինչպես մատրիցները։ Արդյունքը կլինի նույն հարթության վեկտորը: Թող լինեն նույն հարթության մի քանի վեկտորներ x 1 , x 2 ,...,x K և նույն թվով α α 1, α 2, ..., α թվեր Կ... Վեկտոր

y= α 1 x 1 + α 2 x 2 + ... + α Կ x Կ

կանչեց գծային համադրությունվեկտորներ x կ .

Եթե ​​կան α ոչ զրոյական թվեր կ ≠ 0, կ = 1,..., Կ, ինչ y = 0 , ապա վեկտորների նման մի շարք x կկանչեց գծային կախված... Հակառակ դեպքում, վեկտորները կոչվում են գծային անկախ: Օրինակ վեկտորները x 1 = (2, 2) տ և x 2 = (−1, −1) t են գծային կախված, քանի որ x 1 +2x 2 = 0

1.13. Մատրիցային դասակարգում

Դիտարկենք մի շարք Կվեկտորներ x 1 , x 2 ,...,x Կչափերը Ն... Վեկտորների այս համակարգի աստիճանը գծային անկախ վեկտորների առավելագույն քանակն է: Օրինակ, հավաքածուի մեջ

կան միայն երկու գծային անկախ վեկտորներ, օրինակ x 1 և x 2, ուստի նրա վարկանիշը 2 է:

Ակնհայտ է, որ եթե հավաքածուում ավելի շատ վեկտորներ կան, քան դրանց չափերը ( Կ>Ն), ապա դրանք անպայմանորեն գծային կախված են։

Ըստ մատրիցայի աստիճանի(նշվում է աստիճանով ( Ա)) այն վեկտորների համակարգի աստիճանն է, որից այն բաղկացած է։ Չնայած ցանկացած մատրիցա կարող է ներկայացվել երկու ձևով (սյունակի վեկտորներ կամ տողեր), դա չի ազդում դասակարգման արժեքի վրա, քանի որ

1.14. հակադարձ մատրիցա

Քառակուսի մատրիցա Ակոչվում է ոչ այլասերված, եթե ունի եզակի հակադարձմատրիցա Ա-1 պայմանավորված պայմաններով

ԱԱ −1 = Ա −1 Ա = Ի.

Հակադարձ մատրիցա գոյություն չունի բոլոր մատրիցների համար: Ոչ այլասերվածության համար անհրաժեշտ և բավարար պայման է

դետ ( Ա) ≠ 0 կամ աստիճան ( Ա) = Ն.

Matrix inversion-ը բարդ ընթացակարգ է, որի համար կան հատուկ ծրագրեր։ Օրինակ,

Բրինձ. 17 Մատրիցային ինվերսիա

Ներկայացնենք բանաձևեր ամենապարզ դեպքի համար՝ 2 × 2 մատրիցներ

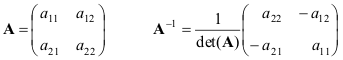
Եթե ​​մատրիցներ Աև Բոչ այլասերված, ուրեմն

(ԱԲ) −1 = Բ −1 Ա −1 .

1.15. Կեղծ հակադարձ մատրիցա

Եթե ​​մատրիցը Ադեգեներատ է, և հակադարձ մատրիցը գոյություն չունի, ապա որոշ դեպքերում կարող եք օգտագործել կեղծ հակադարձմատրիցա, որը սահմանվում է որպես այդպիսի մատրիցա Ա+ դա

ԱԱ + Ա = Ա.

Կեղծ հակադարձ մատրիցը միակը չէ, և դրա տեսակը կախված է կառուցման մեթոդից: Օրինակ, ուղղանկյուն մատրիցայի համար կարող եք օգտագործել Moore-Penrose մեթոդը:

Եթե ​​սյունակների թիվը տողերի քանակից քիչ է, ապա

Ա + =(Ատ Ա) −1 Ատ

Օրինակ,

Բրինձ. 17ա Մատրիցային կեղծ ինվերսիա

Եթե ​​սյունակների թիվը տողերի քանակից մեծ է, ապա

Ա + =Ատ ( ԱԱտ) −1

1.16. Վեկտորի բազմապատկում մատրիցով

Վեկտոր xկարելի է բազմապատկել մատրիցով Ահարմար հարթություն. Այս դեպքում սյունակի վեկտորը բազմապատկվում է աջ կողմում Կացինիսկ տողի վեկտորը ձախ կողմում է xտ Ա... Եթե ​​վեկտորի չափը Ջ, և մատրիցայի չափը Ի× Ջապա արդյունքը չափման վեկտոր է Ի... Օրինակ,

Բրինձ. 18 Մատրիցային բազմապատկման վեկտոր

Եթե ​​մատրիցը Ա- քառակուսի ( Ի× Ի), ապա վեկտորը y = Կացինունի նույն չափը, ինչ x... Ակնհայտ է, որ

Ա(α 1 x 1 + α 2 x 2) = α 1 Կացին 1 + α 2 Կացին 2 .

Հետևաբար, մատրիցները կարող են դիտվել որպես վեկտորների գծային փոխակերպումներ։ Մասնավորապես Իքս = x, Եզ = 0 .

2. Լրացուցիչ տեղեկություններ

2.1. Գծային հավասարումների համակարգեր

Թող լինի Ա- մատրիցայի չափը Ի× Ջ, ա բ- չափման վեկտոր Ջ... Դիտարկենք հավասարումը

Կացին = բ

վեկտորի նկատմամբ x, չափերը Ի... Իրականում սա համակարգ է Իհետ գծային հավասարումներ Ջանհայտ x 1 ,...,x Ջ... Լուծումը կա, եթե և միայն այն դեպքում

աստիճան ( Ա) = կոչում ( Բ) = Ռ,

որտեղ Բընդլայնված չափման մատրիցա է Ի×( J + 1) բաղկացած մատրիցից Ալիցքավորված սյունակով բ, Բ = (Ա բ). Հակառակ դեպքում, հավասարումները անհամապատասխան են:

Եթե Ռ = Ի = Ջ, ապա լուծումը եզակի է

x = Ա −1 բ.

Եթե Ռ < Ի, ապա կան բազմաթիվ տարբեր լուծումներ, որոնք կարող են արտահայտվել գծային համակցության առումով Ջ−Ռվեկտորներ. Միատարր հավասարումների համակարգ Կացին = 0 քառակուսի մատրիցա Ա (Ն× Ն) ունի ոչ տրիվիալ լուծում ( x ≠ 0 ) եթե և միայն եթե det ( Ա) = 0. Եթե Ռ= կոչում ( Ա)<Նապա գոյություն ունենալ Ն−Ռգծային անկախ լուծումներ.

2.2. Երկգծային և քառակուսի ձևեր

Եթե Աքառակուսի մատրից է, և xև yհամապատասխան չափման վեկտորներ են, ապա ձևի սկալյար արտադրյալը xտ Այկանչեց երկգծայինմատրիցով սահմանված ձևը Ա... ժամը x = yարտահայտություն xտ Կացինկանչեց քառակուսիձեւը։

2.3. Դրական որոշակի մատրիցներ

Քառակուսի մատրիցա Ականչեց դրականորեն սահմանվածեթե որևէ ոչ զրոյական վեկտորի համար x ≠ 0 ,

xտ Կացին > 0.

Նմանապես, բացասաբար (xտ Կացին < 0), ոչ բացասական (xտ Կացին≥ 0) և ոչ դրական (xտ Կացին≤ 0) որոշակի մատրիցներ.

2.4. Չոլեսկու տարրալուծում

Եթե ​​սիմետրիկ մատրիցա Ադրական որոշակի է, ապա կա եզակի եռանկյուն մատրիցա Uդրական տարրերով, որոնց համար

Ա = Uտ U.

Օրինակ,

Բրինձ. 19 Չոլեսկու տարրալուծում

2.5. Բևեռային տարրալուծում

Թող լինի Աչափումների ոչ այլասերված քառակուսի մատրից է Ն× Ն... Այնուհետև կա մեկ առ մեկ բևեռայինկատարումը

Ա = SR,

որտեղ Սոչ բացասական սիմետրիկ մատրից է, և Ռուղղանկյուն մատրիցա է: Մատրիցներ Սև Ռկարելի է հստակորեն սահմանել.

Ս 2 = ԱԱտ կամ Ս = (ԱԱտ) ½ և Ռ = Ս −1 Ա = (ԱԱտ) −1 Ա.

Օրինակ,

Բրինձ. 20 Բևեռային տարրալուծում

Եթե ​​մատրիցը Ադեգեներատ է, ապա ընդլայնումը եզակի չէ, մասնավորապես. Սդեռ մենակ, բայց Ռգուցե շատ. Բևեռային տարրալուծումը ներկայացնում է մատրիցը Աորպես սեղմման / ձգման համադրություն Սև շրջադարձ Ռ.

2.6. Սեփական վեկտորներ և սեփական արժեքներ

Թող լինի Աքառակուսի մատրիցա է: Վեկտոր vկանչեց սեփական վեկտորըմատրիցներ Ա, եթե

Ավ = λ v,

որտեղ կոչվում է λ թիվը սեփական իմաստըմատրիցներ Ա... Այսպիսով, փոխակերպումը, որը կատարում է մատրիցը Ավեկտորի վրա v, վերածվում է պարզ ձգման կամ սեղմման λ գործակցով։ Սեփական վեկտորը որոշվում է մինչև α ≠ 0 հաստատունով բազմապատկելը, այսինքն. եթե vսեփական վեկտոր է, ապա α vնաև սեփական վեկտոր է:

2.7. Սեփական արժեքներ

Մատրիցա Ա, չափս ( Ն× Ն) չի կարող լինել ավելի քան Նսեփական արժեքներ. Նրանք բավարարում են բնորոշ հավասարում

դետ ( Ա − λ Ի) = 0,

որը հանրահաշվական հավասարում է Ն-րդ կարգը։ Մասնավորապես, 2 × 2 մատրիցայի համար բնորոշ հավասարումն ունի ձև

Օրինակ,

Բրինձ. 21 սեփական արժեքներ

Սեփական արժեքների բազմություն λ 1, ..., λ Նմատրիցներ Ականչեց սպեկտրը Ա.

Սպեկտրը ունի մի շարք հատկություններ. Մասնավորապես

դետ ( Ա) = λ 1 × ... × λ Ն, Սպ ( Ա) = λ 1 + ... + λ Ն.

Կամայական մատրիցայի սեփական արժեքները կարող են լինել բարդ թվեր, բայց եթե մատրիցը սիմետրիկ է ( Ա t = Ա), ապա դրա սեփական արժեքները իրական են:

2.8. Սեփական վեկտորներ

Մատրիցա Ա, չափս ( Ն× Ն) չի կարող լինել ավելի քան Նսեփական վեկտորներ, որոնցից յուրաքանչյուրը համապատասխանում է իր արժեքին: Որոշել սեփական վեկտորը v nդուք պետք է լուծեք միատարր հավասարումների համակարգ

(Ա − λ n Ի)v n = 0 .

Այն ունի ոչ տրիվիալ լուծում, քանի որ det ( Ա -λ n Ի) = 0.

Օրինակ,

Բրինձ. 22 սեփական վեկտորներ

Սիմետրիկ մատրիցայի սեփական վեկտորները ուղղանկյուն են:

Սահմանում 9.3.Վեկտոր Ն.Ս կանչեց սեփական վեկտորըմատրիցներ Աեթե այդպիսի թիվ կա λ, այդ հավասարությունը գործում է. Ա Ն.Ս= λ Ն.Ս, այսինքն՝ դիմելու արդյունքը Ն.Ս գծային փոխակերպում, որը տրված է մատրիցով Ա, այս վեկտորի բազմապատկումն է թվով λ ... Թիվն ինքնին λ կանչեց սեփական համարըմատրիցներ Ա.

Փոխարինելով բանաձևերով (9.3) x` j = λx j,մենք ստանում ենք հավասարումների համակարգ սեփական վեկտորի կոորդինատները որոշելու համար.

. (9.5)

Այս գծային միատարր համակարգը կունենա ոչ տրիվիալ լուծում միայն այն դեպքում, եթե նրա հիմնական որոշիչը 0-ն է (Կրամերի կանոն): Այս պայմանը գրելով հետևյալ ձևով.

մենք ստանում ենք սեփական արժեքները որոշելու հավասարումը λ կանչեց բնորոշ հավասարում... Այն հակիրճ կարելի է ներկայացնել հետևյալ կերպ.

| A - λE | = 0, (9.6)

քանի որ նրա ձախ կողմը պարունակում է մատրիցայի որոշիչը A-λE... Բազմանդամի նկատմամբ λ | A - λE| կանչեց բնորոշ բազմանդամմատրիցներ Ա.

Բնութագրական բազմանդամ հատկություններ.

1) Գծային փոխակերպման բնորոշ բազմանդամը կախված չէ հիմքի ընտրությունից. Ապացույց. (տես (9.4)), բայց հետևաբար, . Այսպիսով, դա կախված չէ հիմքի ընտրությունից: Հետևաբար, և | A-λE| չի փոխվում նոր հիմքի անցնելիս:

2) Եթե մատրիցը Ագծային փոխակերպումն է սիմետրիկ(դրանք. եւ ij = a ji), ապա բնորոշ հավասարման (9.6) բոլոր արմատները իրական թվեր են։

Սեփական արժեքների և սեփական վեկտորների հատկությունները.

1) Եթե ընտրենք սեփական վեկտորների հիմքը x 1, x 2, x 3 սեփական արժեքներին համապատասխան λ 1, λ 2, λ 3մատրիցներ Ա, ապա այս հիմքում A գծային փոխակերպումն ունի անկյունագծային ձևի մատրիցա.

(9.7) Այս հատկության ապացույցը բխում է սեփական վեկտորների սահմանումից:

2) Եթե վերափոխման սեփական արժեքները Ատարբեր են, ապա համապատասխան սեփական վեկտորները գծային անկախ են:

3) Եթե մատրիցի բնորոշ բազմանդամը Աունի երեք տարբեր արմատներ, ապա որոշ հիմքերով մատրիցա Աունի անկյունագծային ձև.

Եկեք գտնենք մատրիցայի սեփական արժեքները և սեփական վեկտորները. Կազմենք բնորոշ հավասարումը. (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Եկեք գտնենք յուրաքանչյուր գտած արժեքին համապատասխան սեփական վեկտորների կոորդինատները λ. (9.5)-ից հետևում է, որ եթե Ն.Ս (1) ={x 1, x 2, x 3) Արդյո՞ք սեփական վեկտորը համապատասխանում է λ 1 = -2, ապա

- համագործակցային, բայց չսահմանված համակարգ: Դրա լուծումը կարելի է գրել այսպես Ն.Ս (1) ={ա,0,-ա), որտեղ a-ն ցանկացած թիվ է: Մասնավորապես, եթե մենք պահանջում ենք, որ | x (1) |=1, Ն.Ս (1) =

Համակարգում փոխարինում (9.5) λ 2 = 3, մենք ստանում ենք համակարգ երկրորդ սեփական վեկտորի կոորդինատները որոշելու համար. x (2) ={y 1, y 2, y 3}:

, որտեղ Ն.Ս (2) ={բ, -բ, բ) կամ, ենթակա | x (2) |=1, x (2) =

Համար λ 3 = 6 գտնել սեփական վեկտորը x (3) ={z 1, z 2, z 3}:

, x (3) ={գ,2c, c) կամ նորմալացված տարբերակով

x (3) = Դուք կարող եք դա տեսնել Ն.Ս (1) Ն.Ս (2) = աբ - աբ= 0, x (1) x (3) = ac - ac= 0, x (2) x (3) = մ.թ.ա- 2մ.թ.ա. + մ.թ.ա= 0. Այսպիսով, այս մատրիցայի սեփական վեկտորները զույգերով ուղղանկյուն են:

Դասախոսություն 10.

Քառակուսային ձևերը և դրանց կապը սիմետրիկ մատրիցների հետ: Սիմետրիկ մատրիցայի սեփական վեկտորների և սեփական արժեքների հատկությունները: Քառակուսի ձևի կրճատում մինչև կանոնական ձև:

Սահմանում 10.1.Քառակուսի ձևիրական փոփոխականներ x 1, x 2, ..., x nայս փոփոխականների նկատմամբ երկրորդ աստիճանի բազմանդամ է, որը չի պարունակում առաջին աստիճանի ազատ անդամ և անդամներ։

Քառակուսի ձևերի օրինակներ.

(n = 2),

(n = 3). (10.1)

Եկեք հիշենք վերջին դասախոսության մեջ տրված սիմետրիկ մատրիցայի սահմանումը.

Սահմանում 10.2.Քառակուսի մատրիցը կոչվում է սիմետրիկ, եթե, այսինքն, եթե հիմնական անկյունագծի նկատմամբ սիմետրիկ մատրիցային տարրերը հավասար են։

Սիմետրիկ մատրիցայի սեփական արժեքների և սեփական վեկտորների հատկությունները.

1) Սիմետրիկ մատրիցայի բոլոր սեփական արժեքները իրական են:

Ապացույց (համար n = 2).

Թող մատրիցը Անման է: ... Կազմենք բնորոշ հավասարումը.

(10.2) Գտեք տարբերակիչ.

Հետևաբար, հավասարումը միայն իրական արմատներ ունի:

2) Սիմետրիկ մատրիցայի սեփական վեկտորները ուղղանկյուն են.

Ապացույց (համար n= 2).

Սեփական վեկտորների կոորդինատները և պետք է բավարարեն հավասարումները:

A մատրիցով, եթե կա l այնպիսի թիվ, որ AX = lX:

Ընդ որում, կոչվում է l թիվը սեփական իմաստը X վեկտորին համապատասխան օպերատոր (մատրիցան A):

Այլ կերպ ասած, սեփական վեկտորը այն վեկտորն է, որը գծային օպերատորի գործողության ներքո վերածվում է համագիծ վեկտորի, այսինքն. պարզապես բազմապատկվում է ինչ-որ թվով: Ի հակադրություն, ոչ պատշաճ վեկտորներն ավելի դժվար են փոխակերպվում:

Եկեք գրենք սեփական վեկտորի սահմանումը հավասարումների համակարգի տեսքով.

Տեղափոխեք բոլոր պայմանները ձախ կողմում.

Վերջին համակարգը մատրիցային ձևով կարելի է գրել հետևյալ կերպ.

(A - lE) X = O

Ստացված համակարգը միշտ ունի զրոյական լուծում X = O: Այն համակարգերը, որոնցում բոլոր ազատ անդամները հավասար են զրոյի, կոչվում են. միատարր... Եթե ​​նման համակարգի մատրիցը քառակուսի է, և դրա որոշիչը հավասար չէ զրոյի, ապա օգտագործելով Կրամերի բանաձևերը միշտ ստանում ենք եզակի լուծում՝ զրո։ Կարելի է ապացուցել, որ համակարգն ունի ոչ զրոյական լուծումներ, եթե և միայն այն դեպքում, եթե այս մատրիցայի որոշիչը հավասար է զրոյի, այսինքն.

|Ա - ԼԵ | = = 0

Անհայտ l-ով այս հավասարումը կոչվում է բնորոշ հավասարում (բնորոշ բազմանդամ) A մատրիցի (գծային օպերատոր):

Կարելի է ցույց տալ, որ գծային օպերատորի բնորոշ բազմանդամը կախված չէ հիմքի ընտրությունից։

Օրինակ, եկեք գտնենք A = մատրիցով տրված գծային օպերատորի սեփական արժեքները և սեփական վեկտորները:

Դրա համար մենք կազմում ենք բնորոշ հավասարումը | A - lЕ | = = (1 - լ) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0; D = 4 + 140 = 144; սեփական արժեքներ l 1 = (2 - 12) / 2 = -5; լ 2 = (2 + 12) / 2 = 7:

Սեփական վեկտորները գտնելու համար լուծում ենք հավասարումների երկու համակարգ

(A + 5E) X = O

(A - 7E) X = O

Դրանցից առաջինի համար ընդլայնված մատրիցը ձև է ընդունում

,

որտեղից x 2 = c, x 1 + (2/3) c = 0; x 1 = - (2/3) s, այսինքն. X (1) = (- (2/3) s; s).

Դրանցից երկրորդի համար ընդլայնված մատրիցը ձև է ընդունում

,

որտեղից x 2 = c 1, x 1 - (2/3) c 1 = 0; x 1 = (2/3) s 1, այսինքն. X (2) = ((2/3) s 1; s 1):

Այսպիսով, այս գծային օպերատորի սեփական վեկտորները (- (2/3) с; с) սեփական արժեքով (-5) ձևի բոլոր վեկտորներն են և ((2/3) с 1; с 1) ձևի բոլոր վեկտորները: 7 սեփական արժեքով ...

Կարելի է ապացուցել, որ A օպերատորի մատրիցը իր սեփական վեկտորներից բաղկացած հիմքում անկյունագծային է և ունի ձև.

,

որտեղ l i-ն այս մատրիցայի սեփական արժեքներն են:

Ճիշտ է նաև հակառակը. եթե որոշ հիմքում A մատրիցը անկյունագծային է, ապա այս հիմքի բոլոր վեկտորները կլինեն այս մատրիցի սեփական վեկտորները:

Կարելի է նաև ապացուցել, որ եթե գծային օպերատորն ունի n զույգ-զույգ տարբեր սեփական արժեքներ, ապա համապատասխան սեփական վեկտորները գծային անկախ են, և համապատասխան հիմքում այս օպերատորի մատրիցն ունի անկյունագծային ձև։

Սա բացատրենք նախորդ օրինակով։ Մենք վերցնում ենք կամայական ոչ զրոյական արժեքներ с և с 1, բայց այնպիսին, որ X (1) և X (2) վեկտորները գծային անկախ են, այսինքն. հիմք կհանդիսանա։ Օրինակ, թող c = c 1 = 3, ապա X (1) = (-2; 3), X (2) = (2; 3):

Եկեք ստուգենք այս վեկտորների գծային անկախությունը.

12 ≠ 0. Այս նոր հիմքում A մատրիցը կունենա A * = ձև:

Սա ստուգելու համար մենք օգտագործում ենք A * = C -1 AC բանաձևը: Նախ, մենք գտնում ենք C -1:

С -1 = ;

Քառակուսի ձևեր

Քառակուսի ձև n փոփոխականների f (x 1, x 2, xn) կոչվում է գումար, որի յուրաքանչյուր անդամ կամ փոփոխականներից մեկի քառակուսին է, կամ երկու տարբեր փոփոխականների արտադրյալը՝ վերցված որոշակի գործակցով՝ f (x 1): , x 2, xn) = (a ij = a ji):

Այս գործակիցներից կազմված A մատրիցը կոչվում է մատրիցաքառակուսի ձև. Դա միշտ սիմետրիկմատրիցա (այսինքն մատրիցա, որը սիմետրիկ է հիմնական անկյունագծի նկատմամբ, a ij = a ji):

Մատրիցային նշումներում քառակուսի ձևը f (X) = X T AX է, որտեղ

Իսկապես

Օրինակ, եկեք գրենք քառակուսի ձևը մատրիցային տեսքով:

Դա անելու համար մենք գտնում ենք քառակուսի ձևի մատրիցա: Նրա անկյունագծային տարրերը հավասար են փոփոխականների քառակուսիների գործակիցներին, իսկ մնացած տարրերը հավասար են քառակուսի ձևի համապատասխան գործակիցների կեսին։ Ահա թե ինչու

Թող X փոփոխականների մատրից-սյունակը ստացվի Y մատրից-սյունակի ոչ այլասերված գծային փոխակերպմամբ, այսինքն. X = CY, որտեղ С-ն n կարգի ոչ դեգեներատիվ մատրից է: Այնուհետև քառակուսի ձևը f (X) = X T AX = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y:

Այսպիսով, C ոչ այլասերված գծային փոխակերպմամբ քառակուսի ձևի մատրիցը ստանում է ձև՝ A * = C T AC:

Օրինակ՝ գտնենք f (y 1, y 2) քառակուսի ձևը, որը ստացվել է f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 քառակուսի ձևից գծային փոխակերպմամբ։

Քառակուսի ձևը կոչվում է կանոնական(Այն ունի կանոնական տեսակետ) եթե նրա բոլոր գործակիցները a ij = 0 i ≠ j-ի համար, այսինքն.
f (x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Դրա մատրիցը անկյունագծային է:

Թեորեմ(այստեղ ապացույց չկա): Ցանկացած քառակուսի ձև կարող է վերածվել կանոնական ձևի՝ օգտագործելով ոչ այլասերված գծային փոխակերպումը:

Օրինակ, մենք կարող ենք կրճատել քառակուսի ձևը մինչև կանոնական
f (x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3:

Դա անելու համար նախ ընտրեք ամբողջական քառակուսի x 1 փոփոխականով:

f (x 1, x 2, x 3) = 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2 (x 1 + x 2) 2 - 5x 2 2 - x 2 x 3:

Այժմ մենք ընտրում ենք ամբողջական քառակուսի x 2 փոփոխականով.

f (x 1, x 2, x 3) = 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 =
= 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2:

Այնուհետև ոչ այլասերված գծային փոխակերպումը y 1 = x 1 + x 2, y 2 = x 2 + (1/10) x 3 և y 3 = x 3 նվազեցնում է այս քառակուսի ձևը մինչև f (y 1, y 2) կանոնական ձևը: , y 3) = 2y 1 2 - 5y 2 2 + (1/20) y 3 2:

Նկատի ունեցեք, որ քառակուսի ձևի կանոնական ձևը որոշվում է երկիմաստորեն (միևնույն քառակուսի ձևը կարող է վերածվել կանոնական ձևի տարբեր ձևերով): Այնուամենայնիվ, տարբեր ձևերով ստացված կանոնական ձևերն ունեն մի շարք ընդհանուր հատկություններ. Մասնավորապես, քառակուսի ձևի դրական (բացասական) գործակիցներով տերմինների քանակը կախված չէ ձևը այս ձևին իջեցնելու մեթոդից (օրինակ, դիտարկված օրինակում միշտ կլինի երկու բացասական և մեկ դրական գործակից): . Այս հատկությունը կոչվում է քառակուսի ձևերի իներցիայի օրենք։

Եկեք ստուգենք դա՝ նույն քառակուսային ձևը այլ կերպ կրճատելով կանոնական ձևի վրա։ Սկսենք փոխակերպումը x 2 փոփոխականով.

f (x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3 (x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
= -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 = f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, որտեղ y 1 = - (2/3) x 1 + x 2 + (1/6) x 3, y 2 = (2/3) x 1 + (1/6) x 3 և y 3 = x 1: Այստեղ բացասական գործակից է -3 y 1-ի համար և երկու դրական գործակիցներ 3 և 2 y 2 և y 3-ի համար (իսկ մեկ այլ մեթոդ օգտագործելիս մենք ստացել ենք բացասական գործակից (-5) y 2-ի համար և երկու դրական գործակից. 2-ը y 1-ի համար: և 1/20 y 3-ի համար):

Հարկ է նաև նշել, որ քառակուսի ձևի մատրիցայի աստիճանը, որը կոչվում է քառակուսի ձևի աստիճանը, հավասար է կանոնական ձևի ոչ զրոյական գործակիցների թվին և չի փոխվում գծային փոխակերպումների դեպքում։

f (X) քառակուսի ձևը կոչվում է դրականորեն (բացասաբար) որոշակիեթե փոփոխականների բոլոր արժեքների համար, որոնք միաժամանակ հավասար չեն զրոյի, դա դրական է, այսինքն. f (X)> 0 (բացասական, այսինքն.
f (X)< 0).

Օրինակ՝ f 1 (X) = x 1 2 + x 2 2 քառակուսի ձևը դրական որոշակի է, քանի որ քառակուսիների գումարն է, իսկ f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 քառակուսի ձևը բացասական որոշակի է, քանի որ ներկայացնում է այն կարող է ներկայացվել որպես f 2 (X) = - (x 1 - x 2) 2:

Շատ գործնական իրավիճակներում քառակուսի ձևի որոշակիությունը որոշ չափով ավելի դժվար է հաստատել, հետևաբար դրա համար օգտագործվում է հետևյալ թեորեմներից մեկը (մենք կձևակերպենք դրանք առանց ապացույցների):

Թեորեմ... Քառակուսային ձևը դրական (բացասական) որոշակի է, եթե և միայն այն դեպքում, եթե նրա մատրիցայի բոլոր սեփական արժեքները դրական են (բացասական):

Թեորեմ(Սիլվեստրի չափանիշ): Քառակուսի ձևը դրական որոշակի է, եթե և միայն այն դեպքում, երբ այս ձևի մատրիցայի բոլոր հիմնական փոքրերը դրական են:

Մայոր (անկյունային) մինոր N-րդ կարգի A մատրիցի k-րդ կարգը կոչվում է մատրիցի որոշիչ, որը կազմված է A մատրիցի առաջին k տողերից և սյունակներից ():

Նկատի ունեցեք, որ բացասական հստակ քառակուսի ձևերի դեպքում մեծ փոքրերի նշանները փոխարինվում են, իսկ առաջին կարգի փոքրը պետք է լինի բացասական:

Օրինակ, եկեք ուսումնասիրենք քառակուսի f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 քառակուսի ձևը նշանի որոշակիության համար:

= (2 - լ) *
* (3 - լ) - 4 = (6 - 2լ - 3լ + լ 2) - 4 = լ 2 - 5լ + 2 = 0; D = 25 - 8 = 17;
... Հետևաբար, քառակուսի ձևը դրական որոշիչ է:

Մեթոդ 2. А D 1 = a 11 = 2> 0 մատրիցայի առաջին կարգի հիմնական մինորը D 2 = = 6 - 4 = 2> 0. Հետևաբար, ըստ Սիլվեստրի չափանիշի. քառակուսի ձևը դրական որոշիչ է:

Եկեք ուսումնասիրենք նշանի որոշակիության մեկ այլ քառակուսի ձև, f (x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2:

Մեթոդ 1. Կառուցենք A = քառակուսի ձևի մատրիցա: Բնութագրական հավասարումը կունենա ձև = (-2 - լ) *
* (- 3 - լ) - 4 = (6 + 2լ + 3լ + լ 2) - 4 = լ 2 + 5լ + 2 = 0; D = 25 - 8 = 17;
... Հետևաբար, քառակուսի ձևը բացասական որոշիչ է:

Մեթոդ 2. A D 1 = a 11 = մատրիցայի առաջին կարգի հիմնական մինորը
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Ուստի, ըստ Սիլվեստրի չափանիշի, քառակուսի ձևը բացասական որոշիչ է (մեծ փոքրերի նշանները հերթափոխվում են՝ սկսած մինուսից)։

Եվ որպես մեկ այլ օրինակ, եկեք ուսումնասիրենք քառակուսի f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 ձևը նշանի որոշակիության համար:

Մեթոդ 1. Կառուցենք A = քառակուսի ձևի մատրիցա: Բնութագրական հավասարումը կունենա ձև = (2 - լ) *
* (- 3 - լ) - 4 = (-6 - 2լ + 3լ + լ 2) - 4 = լ 2 + լ - 10 = 0; D = 1 + 40 = 41;
.

Այս թվերից մեկը բացասական է, մյուսը՝ դրական։ Սեփական արժեքների նշանները տարբեր են. Հետևաբար, քառակուսի ձևը չի կարող լինել ոչ բացասական, ոչ էլ դրական որոշիչ, այսինքն. այս քառակուսի ձևը որոշակի չէ (այն կարող է վերցնել ցանկացած նշանի արժեքներ):

Մեթոդ 2. Մատրիցի առաջին կարգի հիմնական մինորը A D 1 = a 11 = 2> 0. Երկրորդ կարգի հիմնական մինորը D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

Անկյունագծային մատրիցներն ամենապարզն են։ Հարց է առաջանում՝ հնարավո՞ր է գտնել հիմք, որի դեպքում գծային օպերատորի մատրիցը կունենա անկյունագծային ձև։ Նման հիմք կա.
Թող տրվի R n գծային տարածություն և դրանում գործող գծային A օպերատոր; այս դեպքում A օպերատորն իր մեջ վերցնում է R n, այսինքն՝ A: R n → R n:

Սահմանում. Ոչ զրոյական վեկտորը կոչվում է A օպերատորի սեփական վեկտոր, եթե A օպերատորը վերածվում է նրան համագիծ վեկտորի, այսինքն. λ թիվը կոչվում է A օպերատորի սեփական արժեք կամ սեփական արժեք, որը համապատասխանում է սեփական վեկտորին։
Եկեք նշենք սեփական արժեքների և սեփական վեկտորների որոշ հատկություններ:
1. Սեփական վեկտորների ցանկացած գծային համակցություն նույն սեփական արժեքին համապատասխանող A օպերատորի λ նույն սեփական արժեքով սեփական վեկտորն է:
2. Սեփական վեկտորներ A օպերատորի զույգ-զույգ տարբեր սեփական արժեքներով λ 1, λ 2,…, λ m են գծային անկախ:
3. Եթե սեփական արժեքները λ 1 = λ 2 = λ m = λ, ապա λ սեփական արժեքը համապատասխանում է առավելագույնը m գծային անկախ սեփական վեկտորներին:

Այսպիսով, եթե կան n գծային անկախ սեփական վեկտորներ համապատասխանում են տարբեր սեփական արժեքներին λ 1, λ 2,…, λ n, ապա դրանք գծային անկախ են, հետևաբար, դրանք կարելի է ընդունել որպես R n տարածության հիմք: Եկեք գտնենք A գծային օպերատորի մատրիցայի ձևը նրա սեփական վեկտորների հիման վրա, որի համար մենք գործում ենք A օպերատորի կողմից հիմքի վեկտորների վրա. ապա .
Այսպիսով, գծային A օպերատորի մատրիցը իր սեփական վեկտորների հիման վրա ունի անկյունագծային ձև, իսկ A օպերատորի սեփական արժեքները գտնվում են անկյունագծի վրա:
Կա՞ մեկ այլ հիմք, որի դեպքում մատրիցը անկյունագծային է: Այս հարցի պատասխանը տրվում է հետևյալ թեորեմով.

Թեորեմ. Գծային A օպերատորի մատրիցը հիմքում (i = 1..n) ունի անկյունագծային ձև, եթե և միայն այն դեպքում, եթե հիմքի բոլոր վեկտորները A օպերատորի սեփական վեկտորներն են:

Սեփական արժեքներ և սեփական վեկտորներ գտնելու կանոն

Թող տրվի վեկտոր , որտեղ x 1, x 2, ..., x n վեկտորի կոորդինատներն են հիմքի նկատմամբ և գծային A օպերատորի սեփական վեկտորն է, որը համապատասխանում է λ սեփական արժեքին, այսինքն. Այս հարաբերությունը կարելի է գրել մատրիցային տեսքով

. (*)

Հավասարումը (*) կարելի է համարել որպես գտնելու հավասարում, ընդ որում՝ մեզ հետաքրքրում են ոչ տրիվիալ լուծումները, քանի որ սեփական վեկտորը չի կարող զրո լինել։ Հայտնի է, որ գծային հավասարումների միատարր համակարգի ոչ տրիվիալ լուծումներ գոյություն ունեն, եթե և միայն այն դեպքում, եթե det (A - λE) = 0: Այսպիսով, որպեսզի λ լինի A օպերատորի սեփական արժեքը, անհրաժեշտ և բավարար է, որ det (A - λE) = 0:
Եթե ​​(*) հավասարումը մանրամասն գրված է կոորդինատային ձևով, ապա մենք ստանում ենք գծային միատարր հավասարումների համակարգ.

(1)
որտեղ գծային օպերատորի մատրիցն է։

Համակարգը (1) ունի ոչ զրոյական լուծում, եթե նրա որոշիչը D-ն հավասար է զրոյի

Ստացել է սեփական արժեքները գտնելու հավասարում:
Այս հավասարումը կոչվում է բնութագրիչ հավասարում, իսկ ձախ կողմը կոչվում է A մատրիցի բնորոշ բազմանդամը (օպերատոր): Եթե բնորոշ բազմանդամը չունի իրական արմատներ, ապա A մատրիցը չունի սեփական վեկտորներ և չի կարող վերածվել անկյունագծերի: .
Թող λ 1, λ 2,…, λ n լինեն բնորոշ հավասարման իրական արմատներ, և դրանց մեջ կարող են լինել բազմաթիվ արմատներ: Փոխարինելով այս արժեքներն իր հերթին (1) համակարգի՝ մենք գտնում ենք սեփական վեկտորները:

Օրինակ 12. Գծային A օպերատորը գործում է R 3-ում օրենքի համաձայն, որտեղ x 1, x 2, .., x n հիմքում ընկած վեկտորի կոորդինատներն են: , , ... Գտեք այս օպերատորի սեփական արժեքները և սեփական վեկտորները:
Լուծում. Մենք կառուցում ենք այս օպերատորի մատրիցը.
.
Մենք կազմում ենք սեփական վեկտորների կոորդինատների որոշման համակարգ.

Մենք կազմում ենք բնորոշ հավասարում և լուծում այն.

.
λ 1,2 = -1, λ 3 = 3:
Փոխարինելով λ = -1 համակարգում, մենք ունենք.
կամ
Որովհետեւ , ապա կան երկու կախյալ փոփոխականներ, և մեկ ազատ փոփոխական։
Թող x 1-ը լինի ազատ անհայտ, ուրեմն Մենք լուծում ենք այս համակարգը ցանկացած ձևով և գտնում ենք այս համակարգի ընդհանուր լուծումը. Լուծումների հիմնարար համակարգը բաղկացած է մեկ լուծումից, քանի որ n - r = 3 - 2 = 1:
λ = -1 սեփական արժեքին համապատասխանող սեփական վեկտորների բազմությունը ունի հետևյալ ձևը, որտեղ x 1-ը ցանկացած ոչ զրոյական թիվ է: Եկեք այս բազմությունից ընտրենք մեկ վեկտոր, օրինակ՝ դնելով x 1 = 1: .
Նմանապես վիճելով՝ մենք գտնում ենք սեփական վեկտորը, որը համապատասխանում է սեփական արժեքին λ = 3: .
R 3 տարածության մեջ հիմքը բաղկացած է երեք գծային անկախ վեկտորներից, բայց մենք ստացել ենք միայն երկու գծային անկախ սեփական վեկտոր, որոնցից R3-ում հիմքը չի կարող կազմվել։ Հետևաբար, գծային օպերատորի A մատրիցը չի կարող կրճատվել մինչև անկյունագծային ձև:

Օրինակ 13. Տրվում է մատրիցա .
1. Ապացուցեք, որ վեկտորը A մատրիցի սեփական վեկտորն է: Գտեք այս սեփական վեկտորին համապատասխան սեփական արժեքը:
2. Գտե՛ք հիմք, որում A մատրիցն ունի անկյունագծային ձև:
Լուծում.
1. Եթե, ապա - սեփական վեկտոր

.
Վեկտորը (1, 8, -1) սեփական վեկտոր է: Սեփական արժեք λ = -1:
Մատրիցը հիմքում ունի անկյունագծային ձև, որը բաղկացած է սեփական վեկտորներից: Նրանցից մեկը հայտնի է. Մնացածը գտնենք։
Մենք որոնում ենք սեփական վեկտորներ համակարգից.

Բնութագրական հավասարում. ;
(3 + λ) [- 2 (2-λ) (2 + λ) +3] = 0; (3 + λ) (λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1:
Եկեք գտնենք սեփական վեկտորը, որը համապատասխանում է λ = -3 սեփական արժեքին:

Այս համակարգի մատրիցայի աստիճանը հավասար է երկուսի և հավասար է անհայտների թվին, հետևաբար այս համակարգն ունի միայն զրոյական լուծում x 1 = x 3 = 0: x 2 այստեղ կարող է լինել ցանկացած ոչ զրո, օրինակ, x 2: = 1. Այսպիսով, վեկտորը (0 , 1,0) սեփական վեկտոր է, որը համապատասխանում է λ = -3: Եկեք ստուգենք.
.
Եթե ​​λ = 1, ապա մենք ստանում ենք համակարգը
Մատրիցայի աստիճանը երկու է: Մենք ջնջում ենք վերջին հավասարումը.
Թող x 3-ը լինի անվճար անհայտ: Այնուհետև x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3:
Սահմանելով x 3 = 1, մենք ունենք (-3, -9,1) - սեփական վեկտորը, որը համապատասխանում է սեփական արժեքին λ = 1. Ստուգում.

.
Քանի որ սեփական արժեքները իրական են և տարբեր, դրանց համապատասխան վեկտորները գծային անկախ են, ուստի դրանք կարող են հիմք ընդունել R 3-ում: Այսպիսով, հիմքում , , Ա մատրիցը ունի ձև.
.
Գծային A օպերատորի ոչ բոլոր մատրիցները՝ R n → R n-ը կարող են կրճատվել անկյունագծով, քանի որ որոշ գծային օպերատորների համար գծային անկախ սեփական վեկտորները կարող են փոքր լինել n-ից: Այնուամենայնիվ, եթե մատրիցը սիմետրիկ է, ապա ճշգրիտ m գծային անկախ վեկտորները համապատասխանում են m բազմակիության բնորոշ հավասարման արմատին:

Սահմանում. Սիմետրիկ մատրիցը քառակուսի մատրից է, որի հիմնական անկյունագծով սիմետրիկ տարրերը հավասար են, այսինքն, որում:
Դիտողություններ. 1. Սիմետրիկ մատրիցայի բոլոր սեփական արժեքները իրական են:
2. Զույգ տարբեր սեփական արժեքներին համապատասխանող սիմետրիկ մատրիցայի սեփական վեկտորները ուղղանկյուն են:
Որպես ուսումնասիրված ապարատի բազմաթիվ կիրառություններից մեկը՝ դիտարկենք երկրորդ կարգի կորի ձևի որոշման խնդիրը։