Zadaci sa izvodom na ispitu. Majstorska klasa „Izvod funkcije u zadacima ispita. geometrijsko i fizičko značenje izvoda; jednadžba tangente na graf funkcije; proučavanje funkcije pomoću izvoda

Derivat funkcije jedna je od najtežih tema u školskom programu. Neće svaki diplomac odgovoriti na pitanje šta je derivat.

Ovaj članak jednostavno i jasno objašnjava što je derivat i zašto je potreban.. Nećemo sada težiti matematičkoj strogosti prezentacije. Najvažnije je razumjeti značenje.

Prisjetimo se definicije:

Izvod je brzina promjene funkcije.

Na slici su prikazani grafikoni tri funkcije. Šta mislite koji najbrže raste?

Odgovor je očigledan - treći. Ima najveću stopu promjene, odnosno najveći derivat.

Evo još jednog primjera.

Kostya, Grisha i Matvey su dobili posao u isto vrijeme. Pogledajmo kako su se njihova primanja promijenila tokom godine:

Možete odmah vidjeti sve na grafikonu, zar ne? Kostjina primanja su se više nego udvostručila za šest meseci. I Grišini prihodi su također porasli, ali samo malo. A Matthewov prihod se smanjio na nulu. Početni uslovi su isti, ali brzina promjene funkcije, tj. derivat, - drugačije. Što se tiče Matveya, derivat njegovog prihoda je općenito negativan.

Intuitivno možemo lako procijeniti brzinu promjene funkcije. Ali kako da to uradimo?

Ono što zaista gledamo je koliko strmo graf funkcije ide gore (ili dolje). Drugim riječima, koliko se brzo y mijenja sa x. Očigledno, ista funkcija u različitim tačkama može imati različitu vrijednost derivacije – to jest, može se mijenjati brže ili sporije.

Derivat funkcije se označava sa .

Hajde da pokažemo kako pronaći koristeći graf.

Crta se graf neke funkcije. Uzmite tačku na njoj sa apscisom. Nacrtajte tangentu na graf funkcije u ovoj tački. Želimo procijeniti koliko strmo grafik funkcije ide gore. Zgodna vrijednost za ovo je tangenta nagiba tangente.

Derivat funkcije u tački jednak je tangenti nagiba tangente povučene na graf funkcije u toj tački.

Imajte na umu - kao ugao nagiba tangente uzimamo ugao između tangente i pozitivnog smera ose.

Ponekad učenici pitaju koja je tangenta na graf funkcije. Ovo je prava linija koja ima jedinu zajedničku tačku sa grafikom u ovom odeljku, štaviše, kao što je prikazano na našoj slici. Izgleda kao tangenta na kružnicu.

Hajde da nađemo. Sjećamo se da je tangenta oštrog ugla u pravokutnom trokutu jednaka omjeru suprotne katete i susjedne. Iz trougla:

Izvod smo pronašli koristeći graf, a da nismo ni znali formulu funkcije. Ovakvi zadaci se često nalaze na ispitu iz matematike pod brojem.

Postoji još jedna važna korelacija. Podsjetimo da je ravna linija data jednadžbom

Količina u ovoj jednačini se zove nagib prave linije. Jednaka je tangenti ugla nagiba prave linije prema osi.

Shvatili smo to

Prisjetimo se ove formule. Izražava geometrijsko značenje izvedenice.

Derivat funkcije u tački jednak je nagibu tangente povučene na graf funkcije u toj tački.

Drugim riječima, derivacija je jednaka tangenti nagiba tangente.

Već smo rekli da ista funkcija može imati različite izvode u različitim tačkama. Pogledajmo kako je derivacija povezana s ponašanjem funkcije.

Nacrtajmo graf neke funkcije. Neka se ova funkcija povećava u nekim područjima, a smanjuje u drugim, i to različitim brzinama. I neka ova funkcija ima maksimum i minimum bodova.

U jednom trenutku, funkcija se povećava. Tangenta na graf, nacrtana u tački, formira oštar ugao s pozitivnim smjerom ose. Dakle, izvod je pozitivan u tački.

U ovom trenutku, naša funkcija se smanjuje. Tangenta u ovoj tački formira tupi ugao s pozitivnim smjerom ose. Pošto je tangenta tupog ugla negativna, derivacija u tački je negativna.

Evo šta se dešava:

Ako je funkcija rastuća, njen izvod je pozitivan.

Ako se smanjuje, njegov izvod je negativan.

A šta će se dogoditi na maksimalnim i minimalnim tačkama? Vidimo da je u (maksimalna tačka) i (tačka minimuma) tangenta horizontalna. Prema tome, tangenta nagiba tangente u ovim tačkama je nula, a derivacija je takođe nula.

Tačka je maksimalna tačka. U ovom trenutku povećanje funkcije zamjenjuje se smanjenjem. Posljedično, predznak derivacije se mijenja u tački sa "plus" na "minus".

U tački - minimalnoj tački - derivacija je također jednaka nuli, ali joj se predznak mijenja sa "minus" na "plus".

Zaključak: uz pomoć izvoda možete saznati sve što nas zanima o ponašanju funkcije.

Ako je izvod pozitivan, tada se funkcija povećava.

Ako je izvod negativan, onda je funkcija opadajuća.

U tački maksimuma derivacija je nula i mijenja predznak sa plusa na minus.

U minimalnoj tački, derivacija je također nula i mijenja predznak sa minusa na plus.

Ove nalaze zapisujemo u obliku tabele:

	povećava	maksimalni poen	opadajući	minimalna tačka	povećava
+	0	-	0	+

Hajde da napravimo dva mala pojašnjenja. Jedan od njih će vam trebati kada rješavate ispitne zadatke. Drugi - na prvoj godini, sa ozbiljnijim proučavanjem funkcija i derivata.

Moguć je slučaj kada je derivacija funkcije u nekoj tački jednaka nuli, ali funkcija nema ni maksimum ni minimum u ovoj tački. Ova tzv :

U tački, tangenta na graf je horizontalna, a derivacija je nula. Međutim, prije točke funkcija se povećala - a nakon točke nastavlja rasti. Predznak derivacije se ne mijenja – ostao je pozitivan kakav je bio.

Takođe se dešava da u tački maksimuma ili minimuma izvod ne postoji. Na grafikonu to odgovara oštrom prekidu, kada je nemoguće nacrtati tangentu u datoj tački.

Ali kako pronaći izvod ako funkcija nije data grafom, već formulom? U ovom slučaju se primjenjuje

Derivat funkcije $y = f(x)$ u datoj tački $h_0$ je granica omjera prirasta funkcije i odgovarajućeg prirasta njenog argumenta, pod uslovom da potonji teži nuli:

$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$

Diferencijacija je operacija pronalaženja derivacije.

Tablica izvoda nekih elementarnih funkcija

Funkcija	Derivat
$c$	$0$
$x$	$1$
$x^n$	$nx^(n-1)$
$(1)/(x)$	$-(1)/(x^2)$
$√x$	$(1)/(2√x)$
$e^x$	$e^x$
$lnx$	$(1)/(x)$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	$(1)/(cos^2x)$
$ctgx$	$-(1)/(sin^2x)$

Osnovna pravila diferencijacije

1. Derivat zbira (razlike) jednak je zbiru (razlici) izvoda

$(f(x) ± g(x))"= f"(x)±g"(x)$

Pronađite izvod funkcije $f(x)=3x^5-cosx+(1)/(x)$

Izvod zbira (razlike) jednak je zbiru (razlici) izvoda.

$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + sinx - (1)/(x^2)$

2. Derivat proizvoda

$(f(x) g(x))"= f"(x) g(x)+ f(x) g(x)"$

Pronađite izvod $f(x)=4x cosx$

$f"(x)=(4x)" cosx+4x (cosx)"=4 cosx-4x sinx$

3. Derivat količnika

$((f(x))/(g(x)))"=(f"(x) g(x)-f(x) g(x)")/(g^2(x)) $

Pronađite izvod $f(x)=(5x^5)/(e^x)$

$f"(x)=((5x^5)" e^x-5x^5 (e^x)")/((e^x)^2)=(25x^4 e^x- 5x^5 e^x)/((e^x)^2)$

4. Derivat kompleksne funkcije jednak je umnošku izvoda eksterne funkcije i izvoda unutrašnje funkcije

$f(g(x))"=f"(g(x)) g"(x)$

$f"(x)=cos"(5x) (5x)"=-sin(5x) 5= -5sin(5x)$

Fizičko značenje izvedenice

Ako se materijalna tačka kreće pravolinijski i njena koordinata se mijenja ovisno o vremenu prema zakonu $x(t)$, tada je trenutna brzina ove tačke jednaka derivaciji funkcije.

Tačka se kreće duž koordinatne linije prema zakonu $x(t)= 1.5t^2-3t + 7$, gdje je $x(t)$ koordinata u trenutku $t$. U kom trenutku će brzina tačke biti jednaka 12$?

1. Brzina je derivacija od $x(t)$, pa hajde da nađemo derivaciju date funkcije

$v(t) = x"(t) = 1,5 2t -3 = 3t -3$

2. Da bismo pronašli u kom trenutku u vremenu $t$ je brzina bila jednaka $12$, sastavljamo i rješavamo jednačinu:

Geometrijsko značenje izvedenice

Podsjetimo da se jednačina prave linije koja nije paralelna sa koordinatnim osa može napisati kao $y = kx + b$, gdje je $k$ nagib prave linije. Koeficijent $k$ jednak je tangenti nagiba između prave i pozitivnog smjera $Ox$ ose.

Derivat funkcije $f(x)$ u tački $x_0$ jednak je nagibu $k$ tangente na graf u datoj tački:

Stoga možemo napraviti opštu jednakost:

$f"(x_0) = k = tgα$

Na slici se tangenta funkcije $f(x)$ povećava, pa je koeficijent $k > 0$. Pošto je $k > 0$, onda je $f"(x_0) = tgα > 0$. Ugao $α$ između tangente i pozitivnog smjera $Ox$ je oštar.

Na slici je tangenta na funkciju $f(x)$ opadajuća, pa stoga koeficijent $k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

Na slici je tangenta funkcije $f(x)$ paralelna sa $Oh$ osi, pa je koeficijent $k = 0$, dakle $f"(x_0) = tg α = 0$. Tačka $ x_0$ na kojem je $f "(x_0) = 0$, pozvan ekstrem.

Na slici je prikazan grafik funkcije $y=f(x)$ i tangenta na ovaj graf nacrtana u tački sa apscisom $x_0$. Pronađite vrijednost derivacije funkcije $f(x)$ u tački $x_0$.

Tangenta na graf raste, dakle, $f"(x_0) = tg α > 0$

Da bismo pronašli $f"(x_0)$, nalazimo tangentu nagiba između tangente i pozitivnog smjera ose $Ox$. Da bismo to učinili, kompletiramo tangentu na trokut $ABC$.

Pronađite tangentu ugla $BAC$. (Tangens oštrog ugla u pravokutnom trokutu je omjer suprotnog kraka i susjednog kraka.)

$tg BAC = (BC)/(AC) = (3)/(12)= (1)/(4)=0,25$

$f"(x_0) = tg VI = 0,25 $

Odgovor: $0,25

Izvod se također koristi za pronalaženje intervala rastućih i opadajućih funkcija:

Ako je $f"(x) > 0$ na intervalu, tada funkcija $f(x)$ raste na ovom intervalu.

Ako je $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

Na slici je prikazan graf funkcije $y = f(x)$. Pronađite među tačkama $h_1,h_2,h_3…h_7$ one tačke u kojima je derivacija funkcije negativna.

Kao odgovor, zapišite broj podataka.

VANNASTAVNI PRAKTIČNI RAD 2

Transformacija grafova funkcija.

Target

Iscrtajte grafove funkcija koristeći različite transformacije, odgovorite na pitanje problema.

Završetak radova

Smjernice

Rad je dizajniran za 10 opcija, broj opcije odgovara posljednjoj znamenki serijskog broja na listi. Na primjer, 1, 11, 21, 31 ... izvedite 1 opciju, 2,12, 22 ... - 2 opciju, itd.

Rad se sastoji iz dva dijela: prvi dio zadataka 1 - 5, to su zadaci koji se moraju završiti da bi dobili kredit, ako su ovi zadaci obavljeni sa greškom potrebno ih je ispraviti i ponovo predati rad na provjeru . Drugi dio sadrži zadatke, ispunjavanjem kojih možete dobiti dodatnu ocjenu: glavni dio +2 zadatka - "4", glavni dio +3 zadatka - "5".

Zadatak 1. Grafikon linearne funkcije je prava linija, za konstruiranje su dovoljne dvije tačke. (vrijednosti argumenta x uzimamo proizvoljno i razmatramo zamjenu vrijednosti funkcije y u formulu).

Da biste provjerili da li graf funkcije prolazi kroz navedenu tačku, trebate zamijeniti koordinate tačke umjesto x i y, ako dobijete tačnu jednakost, tada linija prolazi kroz navedenu tačku, inače ne prolazi .

Zadatak 2, 3, 4. Grafikoni naznačenih funkcija dobijaju se iz grafova funkcija , koristeći pomak duž x ili y ose.

, prvo nacrtajte funkciju ili , zatim ga pomjerimo za “a” jedinice udesno ili ulijevo (+ a - ulijevo, - a udesno), zatim ga pomaknemo za “b” jedinice gore ili dolje (+ u - gore, - u - dolje)

Slično s drugim funkcijama:

Zadatak 5 Da nacrtate graf funkcije: , potrebno je da: 1) izgradite graf funkcije , 2) dio grafika koji se nalazi iznad x ose ostaje nepromijenjen, 3) dio grafika koji je ispod x ose se preslikava.

Zadaci za samostalno rješavanje.

Obavezni dio

Zadatak 1. Nacrtajte graf linearne funkcije, odredite da li graf funkcije prolazi kroz navedenu tačku:

Zadatak 2. Nacrtajte graf kvadratne funkcije, navedite skup vrijednosti za ovu funkciju.

Zadatak 3. Napravite graf funkcije, odredite da li se navedena funkcija povećava ili smanjuje.

Zadatak 4. Napravi graf funkcije, odgovori na pitanje zadatka.

Zadatak 5. Napravi graf funkcije koji sadrži predznak modula.

Zadaci za dodatno ocjenjivanje.

Zadatak 6. Nacrtajte graf funkcije date po dijelovima, odredite ima li ova funkcija prijelomnu tačku:

Zadatak 7. Odrediti koliko rješenja ima sistem jednačina, obrazložiti odgovor. Izvucite zaključke odgovarajući na pitanja.

Koje ste grafove funkcija izgradili u ovom radu?

Kako se zove graf linearne funkcije?

Kako se zove graf kvadratne funkcije?

Koje transformacije grafikona znate?

Kako se graf parne funkcije nalazi u koordinatnom sistemu? Grafikon neparne funkcije?

U zadatku broj 13 Jedinstvenog državnog ispita iz matematike na osnovnom nivou, moraćete da pokažete veštine i znanje o jednom od koncepata ponašanja funkcije: izvode u tački ili stope povećanja ili smanjenja. Teorija za ovaj zadatak bit će dodana malo kasnije, ali to nas neće spriječiti da detaljno analiziramo nekoliko tipičnih opcija.

Analiza tipičnih opcija za zadatke br. 14 UPOTREBA iz matematike osnovnog nivoa

Opcija 14MB1

Grafikon prikazuje ovisnost temperature o vremenu u procesu zagrijavanja motora automobila. Horizontalna os pokazuje vrijeme u minutama koje je proteklo od pokretanja motora; na vertikalnoj osi je temperatura motora u stepenima Celzijusa.

Koristeći grafikon, uparite svaki vremenski interval sa karakteristikama procesa zagrijavanja motora u ovom intervalu.

U tabeli ispod svakog slova navedite odgovarajući broj.

Algoritam izvršenja:

Odaberite vremenski interval u kojem je temperatura pala.
Pričvrstite ravnalo na 30°C i odredite vremenski interval u kojem je temperatura bila ispod 30°C.

Odluka:

Odaberimo vremenski interval u kojem je temperatura opala. Ovaj dio je vidljiv golim okom, počinje 8 minuta od trenutka pokretanja motora.

Nanesite ravnalo na 30°C i odredite vremenski interval u kojem je temperatura bila ispod 30°C.

Ispod ravnala će se nalaziti dio koji odgovara vremenskom intervalu 0 - 1 min.

Uz pomoć olovke i ravnala nalazimo u kom vremenskom intervalu je temperatura bila u rasponu od 40°C do 80°C.

Iz tačaka koje odgovaraju 40°C i 80°C spuštamo okomice na grafik, a iz dobijenih tačaka spuštamo okomice na vremensku osu.

Vidimo da ovaj temperaturni interval odgovara vremenskom intervalu od 3 - 6,5 min. Odnosno od onih datih u stanju 3 - 6 min.

Odaberite odgovor koji nedostaje metodom eliminacije.

Opcija 14MB2

Odluka:

Analizirajmo graf funkcije A. Ako funkcija raste, onda je izvod pozitivan i obrnuto. Derivat funkcije je jednak nuli u tačkama ekstrema.

Prvo, funkcija A raste, tj. izvod je pozitivan. Ovo odgovara grafovima izvoda 2 i 3. U tački maksimuma funkcije x = -2, odnosno u ovoj tački, izvod bi trebao biti jednak nuli. Ovaj uslov odgovara grafikonu broj 3.

Prvo, funkcija B se smanjuje, tj. izvod je negativan. Ovo odgovara grafovima izvoda 1 i 4. Maksimalna tačka funkcije x = -2, odnosno u ovoj tački derivacija bi trebala biti jednaka nuli. Ovaj uslov odgovara grafikonu broj 4.

Prvo, funkcija B raste, tj. izvod je pozitivan. Ovo odgovara grafovima izvoda 2 i 3. Maksimalna tačka funkcije x = 1, odnosno u ovoj tački derivacija treba da bude jednaka nuli. Ovaj uslov odgovara grafikonu broj 2.

Metodom eliminacije možemo utvrditi da graf funkcije G odgovara grafu derivacije na broju 1.

Odgovor: 3421.

Opcija 14MB3

Algoritam izvršenja za svaku od funkcija:

Odrediti intervale rastućih i opadajućih funkcija.
Odredite maksimalnu i minimalnu tačku funkcije.
Izvucite zaključke, uskladite predložene rasporede.

Odluka:

Analizirajmo graf funkcije A.

Ako je funkcija rastuća, onda je derivacija pozitivna i obrnuto. Derivat funkcije je jednak nuli u tačkama ekstrema.

Ekstremna tačka je tačka u kojoj se postiže maksimalna ili minimalna vrednost funkcije.

Prvo, funkcija A raste, tj. izvod je pozitivan. Ovo odgovara grafovima izvoda 3 i 4. U tački maksimuma funkcije x=0, odnosno u ovoj tački, izvod bi trebao biti jednak nuli. Ovaj uslov odgovara grafikonu broj 4.

Analizirajmo graf funkcije B.

Prvo, funkcija B se smanjuje, tj. izvod je negativan. Ovo odgovara grafovima izvoda 1 i 2. Minimalna tačka funkcije x=-1, odnosno u ovoj tački izvod mora biti jednak nuli. Ovaj uslov odgovara grafikonu broj 2.

Analizirajmo graf funkcije B.

Prvo, funkcija B se smanjuje, tj. izvod je negativan. Ovo odgovara grafovima izvoda 1 i 2. Minimalna tačka funkcije x = 0, odnosno u ovoj tački derivacija bi trebala biti jednaka nuli. Ovaj uslov odgovara grafikonu broj 1.

Metodom eliminacije možemo utvrditi da graf funkcije G odgovara grafu derivacije na broju 3.

Odgovor: 4213.

Opcija 14MB4

Slika prikazuje graf funkcije i tangente povučene na nju u tačkama sa apscisama A, B, C i D.Desna kolona prikazuje vrijednosti izvoda u tačkama A, B, C i D. Koristeći graf, uparite svaku tačku sa vrijednošću izvoda funkcije u njoj.

POINTS
ALI
AT
With
D

VRIJEDNOSTI DERIVATA
1) –4
2) 3
3) 2/3
4) -1/2

Prisjetite se što derivacija znači, odnosno njegovu vrijednost u tački - vrijednost funkcije derivacije u tački jednaka je tangentu nagiba (koeficijentu) tangente.

U odgovorima imamo dvije pozitivne i dvije negativne opcije. Kao što se sjećamo, ako je koeficijent direktan (grafik y = kx + b) je pozitivna, tada je linija u porastu; ako je negativna, tada se linija smanjuje.

Imamo dvije rastuće prave - u tački A i D. Prisjetimo se sada šta znači vrijednost koeficijenta k?

Koeficijent k pokazuje koliko brzo se funkcija povećava ili smanjuje (u stvari, sam koeficijent k je izvod funkcije y = kx + b).

Stoga k = 2/3 odgovara nježnijoj pravoj liniji - D, a k = 3 - A.

Slično, u slučaju negativnih vrijednosti: tačka B odgovara strmijoj pravoj liniji sa k = -4, a tački C - -1/2.

Opcija 14MB5

Na slici, tačke pokazuju obim mjesečne prodaje grijača u prodavnici kućanskih aparata. Mjeseci su prikazani horizontalno, broj prodanih grijača je prikazan vertikalno. Radi jasnoće, tačke su povezane linijom.

Koristeći sliku, uparite svaki od navedenih vremenskih perioda sa karakteristikama prodaje grijača.

Algoritam izvršenja

Analiziramo dijelove grafikona koji odgovaraju različitim godišnjim dobima. Formuliramo situacije prikazane na grafikonu. Pronalazimo najprikladnije odgovore za njih.

Odluka:

Zimi je broj rasprodaja prelazio 120 komada/mjesečno, a stalno je u porastu. Ova situacija odgovara odgovoru 3. One. dobijamo: A-3.

U proljeće je prodaja postepeno pala sa 120 grijača mjesečno na 50. Opcija br. 2 je najbliža ovoj formulaciji. Imamo: B–2.

Ljeti se broj rasprodaja nije mijenjao i bio je minimalan. Drugi dio ove formulacije se ne odražava u odgovorima, a za prvi je pogodan samo broj 4. Dakle, imamo: U 4.

U jesen je prodaja rasla, ali njihov broj ni u jednom mjesecu nije prelazio 100 komada. Ova situacija je opisana u opciji #1. Dobijamo: G–1.

Opcija 14MB6

Grafikon prikazuje zavisnost brzine redovnog autobusa od vremena. Vertikalna osa prikazuje brzinu autobusa u km/h, horizontalna osa prikazuje vrijeme u minutama od pokretanja autobusa.

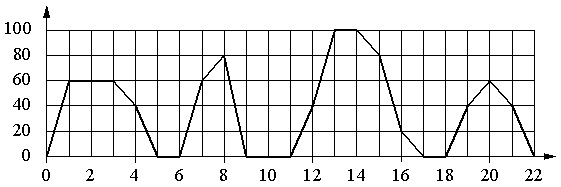
Koristeći graf, uparite svaki vremenski interval sa karakteristikom kretanja sabirnice u ovom intervalu.

Algoritam izvršenja

Određujemo cijenu podjele na horizontalnoj i vertikalnoj skali.
Analiziramo redom predložene iskaze 1–4 iz desne kolone („Karakteristike“). Upoređujemo ih sa vremenskim intervalima iz lijeve kolone tabele, nalazimo parove "slovo-broj" za odgovor.

Odluka:

Vrijednost podjele horizontalne skale je 1 s, vertikalne 20 km/h.

Kada se autobus zaustavi, njegova brzina je 0. 2 minute zaredom autobus je imao nultu brzinu samo od 9. do 11. minute. Ovo vrijeme spada u interval od 8-12 min. Dakle, imamo par za odgovor: B–1.
Autobus je imao brzinu od 20 km/h ili više u nekoliko vremenskih perioda. Štaviše, opcija A ovdje nije prikladna, jer je npr. u 7. minuti brzina bila 60 km/h, opcija B - jer je već primijenjena, opcija D - jer je na početku i na kraju intervala autobus imao nultu brzinu. U ovom slučaju, opcija B je prikladna (12-16 minuta); u tom intervalu autobus počinje da se kreće brzinom od 40 km/h, zatim ubrzava do 100 km/m i zatim postepeno smanjuje brzinu na 20 km/h. Dakle, imamo: U 2.
Ovdje se postavlja ograničenje brzine. Ne razmatramo opcije B i C. Preostali intervali A i G su prikladni. Stoga bi bilo ispravno prvo razmotriti 4. opciju, a zatim se ponovo vratiti na 3. opciju.
Od dva preostala intervala, samo 4-8 minuta je pogodno za karakteristiku br. 4, jer je u tom intervalu (u 6. minuti) došlo do zaustavljanja. U intervalu od 18-22 minuta nije bilo zaustavljanja. Dobijamo: A-4. Iz ovoga slijedi da je za karakteristiku br. 3 potrebno uzeti interval G, tj. ispada par G–3.

Opcija 14MB7

Tačkasta cifra pokazuje rast kineske populacije od 2004. do 2013. godine. Godina je prikazana horizontalno, rast stanovništva u procentima (povećanje stanovništva u odnosu na prethodnu godinu) je prikazan vertikalno. Radi jasnoće, tačke su povezane linijom.

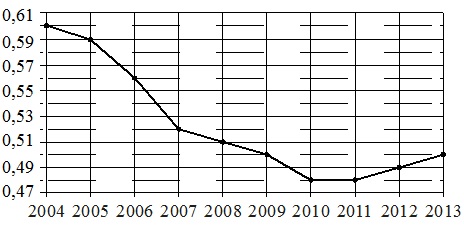
Koristeći dijagram, uparite svaki od naznačenih vremenskih perioda sa karakteristikom rasta kineske populacije tokom ovog perioda..

Algoritam izvršenja

Odredite vrijednost podjele vertikalne skale slike. Nalazi se kao razlika između para susednih vrednosti skale podeljenih sa 2 (jer postoje 2 podele između dve susedne vrednosti).
Analiziramo karakteristike 1–4 sekvencijalno date u uslovu (lijeva kolona tabele). Svaki od njih upoređujemo sa određenim vremenskim periodom (desna kolona tabele).

Odluka:

Vrijednost podjele vertikalne skale je 0,01%.

Pad rasta nastavio se kontinuirano od 2004. do 2010. godine. U periodu od 2010. do 2011. povećanje je bilo konstantno minimalno, a počevši od 2012. počelo je rasti. One. Rast je zaustavljen 2010. Ova godina je u periodu 2009-2011. Shodno tome, imamo: U 1.
Najveći pad rasta treba smatrati linijom grafikona sa „najstrmijim“ padanjem na slici. Pada na period 2006-2007. i iznosi 0,04% godišnje (0,59–0,56=0,04% u 2006. i 0,56–0,52=0,04% u 2007.). Odavde dobijamo: A-2.
Rast naznačen u karakteristici broj 3 započeo je 2007. godine, nastavio se 2008. godine i završio 2009. godine. Ovo odgovara vremenskom periodu B, tj. imamo: B–3.
Rast stanovništva počeo je rasti nakon 2011. godine, tj. u 2012–2013 Stoga dobijamo: G–4.

Opcija 14MB8

Slika prikazuje graf funkcije i tangente povučene na njega u tačkama sa apscisama A, B, C i D.

Desni stupac prikazuje vrijednosti izvoda funkcije u tačkama A, B, C i D. Koristeći graf, uparite svaku tačku sa vrijednošću derivacije funkcije u njoj.

Algoritam izvršenja

Razmatramo par tangenta koje imaju oštar ugao s pozitivnim smjerom x-ose. Uspoređujemo ih, pronalazimo podudaranje među parom odgovarajućih vrijednosti derivata.
Razmatramo par tangenti koje formiraju tupi ugao sa pozitivnim smjerom x-ose. Uspoređujemo ih po modulu, utvrđujemo korespondenciju njihovim vrijednostima izvoda između dva preostala u desnom stupcu.

Odluka:

Oštar ugao sa pozitivnim smjerom x-ose formiraju derivati u t.B i t.C. Ovi derivati imaju pozitivne vrijednosti. Dakle, ovdje treba birati između vrijednosti br. 1 i 3. Primjenjujući pravilo da ako je ugao manji od 45 0, onda je derivacija manja od 1, a ako je više, onda više od 1, zaključujemo: u t.B, modulo izvod je veći od 1 u t.C - manji od 1. To znači da možete napraviti parove za odgovor: U 3 i S-1.

Derivati u t.A i t.D formiraju tup ugao s pozitivnim smjerom x-ose. I ovdje primjenjujemo isto pravilo, malo ga parafrazirajući: što je tangenta u tački više "pritisnuta" na liniju ose apscise (u njenom negativnom smjeru), to je veća u apsolutnoj vrijednosti. Tada dobijamo: izvod u tački A je manji po apsolutnoj vrednosti od izvoda u tački D. Odavde imamo parove za odgovor: A-2 i D-4.

Opcija 14MB9

Tačke na slici prikazuju prosječnu dnevnu temperaturu zraka u Moskvi u januaru 2011. godine. Datumi u mjesecu su prikazani horizontalno, temperature u stepenima Celzijusa su prikazane vertikalno. Radi jasnoće, tačke su povezane linijom.

Koristeći sliku, uparite svaki od naznačenih vremenskih perioda sa karakteristikom promjene temperature.

Algoritam izvršenja

Analiziramo sekvencijalno karakteristike 1–4 (desni stupac), koristeći grafikon na slici. Svaku od njih stavljamo u liniju sa određenim vremenskim periodom (lijeva kolona).

Odluka:

Porast temperature uočen je tek na kraju perioda 22–28. januara. Ovdje je 27. i 28. porasla za 1 odnosno 2 stepena. Na kraju perioda 1–7. januara temperatura je bila stabilna (–10 stepeni), krajem 8–14. i 15–21. januara opala (sa –1 na –2 i sa –11 na –12 stepena, respektivno). Stoga dobijamo: G–1.
Pošto svaki vremenski period obuhvata 7 dana, temperaturu treba analizirati počevši od 4. dana svakog perioda. Temperatura je ostala nepromijenjena 3-4 dana samo od 4. do 7. januara. Tako dobijamo odgovor: A-2.
Mjesečna minimalna temperatura zabilježena je 17. januara. Ovaj broj spada u period od 15. do 21. januara. Odavde imamo par: U 3.
Temperaturni maksimum je pao 10. januara i iznosio je +1 stepen. Ovaj datum spada u period od 8. do 14. januara. Dakle, imamo: B-4.

Opcija 14MB10

Algoritam izvršenja

Vrijednost funkcije u tački je pozitivna ako se ova tačka nalazi iznad ose Ox.
Izvod u tački je veći od nule ako tangenta na tu tačku formira oštar ugao s pozitivnim smjerom x-ose.

Odluka:

Tačka A. Nalazi se ispod ose Ox, što znači da je vrijednost funkcije u njoj negativna. Ako u njemu povučemo tangentu, tada će ugao između nje i pozitivnog smjera Ox biti oko 90 0, tj. formira oštar ugao. Dakle, u ovom slučaju je prikladna karakteristika broj 3. One. imamo: A-3.

Tačka B. Nalazi se iznad ose Ox, tj. tačka ima pozitivnu vrijednost funkcije. Tangenta u ovoj tački će biti prilično blizu osi apscise, formirajući tupi ugao (nešto manji od 180 0) sa svojim pozitivnim smjerom. Prema tome, izvod je u ovom trenutku negativan. Dakle, ovdje je prikladna karakteristika 1. Dobijamo odgovor: U 1.

Tačka C. Tačka se nalazi ispod ose Ox, tangenta u njoj formira veliki tupi ugao sa pozitivnim smjerom ose apscise. One. u t.C, vrijednost i funkcije i derivacije je negativna, što odgovara karakteristici br. 2. odgovor: S-2.

Tačka D. Tačka se nalazi iznad ose Ox, a tangenta u njoj formira oštar ugao sa pozitivnim smjerom ose. Ovo sugerira da su i vrijednost funkcije i vrijednost derivacije ovdje veće od nule. odgovor: D-4.

Opcija 14MB11

Na slici, tačke pokazuju obim mjesečne prodaje frižidera u prodavnici kućanskih aparata. Meseci su prikazani horizontalno, broj prodatih frižidera je prikazan vertikalno. Radi jasnoće, tačke su povezane linijom.

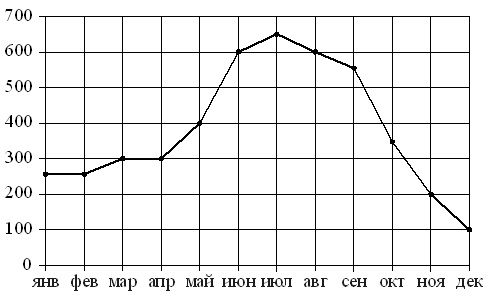
Koristeći sliku, uskladite svaki od navedenih vremenskih perioda sa karakteristikama prodaje frižidera.

Prvo pokušajte pronaći opseg funkcije:

Jeste li uspjeli? Uporedimo odgovore:

U redu? Dobro urađeno!

Pokušajmo sada pronaći raspon funkcije:

Pronađen? uporedi:

Je li se složilo? Dobro urađeno!

Idemo opet raditi s grafovima, samo što je sada malo teže - pronaći i domenu funkcije i opseg funkcije.

Kako pronaći i domenu i opseg funkcije (napredno)

Evo šta se dogodilo:

Što se tiče grafike, mislim da ste shvatili. Pokušajmo sada pronaći domenu funkcije u skladu s formulama (ako ne znate kako to učiniti, pročitajte odjeljak o):

Jeste li uspjeli? Provjeravam odgovori:

, budući da korijenski izraz mora biti veći ili jednak nuli.
, budući da je nemoguće podijeliti sa nulom i radikalni izraz ne može biti negativan.
, pošto, respektivno, za sve.
jer ne možete podijeliti sa nulom.

Ipak, ostaje nam još jedan trenutak koji nije sređen...

Dozvolite mi da ponovim definiciju i da se fokusiram na nju:

Primijećeno? Riječ "samo" je vrlo, vrlo važan element naše definicije. Pokušaću da ti na prste objasnim.

Recimo da imamo funkciju datu pravom linijom. . Kada, ovu vrijednost zamjenjujemo u naše "pravilo" i dobijamo to. Jedna vrijednost odgovara jednoj vrijednosti. Možemo čak napraviti tablicu različitih vrijednosti i nacrtati datu funkciju da to potvrdimo.

„Pogledaj! - kažete, - "" sastaje se dvaput!" Dakle, možda parabola nije funkcija? Ne, jeste!

Činjenica da se "" pojavljuje dva puta daleko je od razloga da se parabola optužuje za dvosmislenost!

Činjenica je da smo, računajući za, dobili jednu utakmicu. I kada se računa sa, dobili smo jednu utakmicu. Tako je, parabola je funkcija. Pogledajte grafikon:

Jasno? Ako ne, evo vam primjera iz stvarnog života, daleko od matematike!

Recimo da imamo grupu aplikanata koji su se sreli prilikom podnošenja dokumenata, od kojih je svaki u razgovoru rekao gdje živi:

Slažem se, sasvim je realno da nekoliko momaka živi u istom gradu, ali nemoguće je da jedna osoba živi u više gradova u isto vrijeme. Ovo je, takoreći, logičan prikaz naše "parabole" - Nekoliko različitih x odgovara istom y.

Hajde sada da smislimo primjer gdje ovisnost nije funkcija. Recimo da su ti isti momci ispričali za koje su se specijalnosti prijavili:

Ovdje imamo potpuno drugačiju situaciju: jedna osoba se lako može prijaviti za jedan ili više smjerova. tj jedan element setovi se dopisuju više elemenata setovi. odnosno to nije funkcija.

Provjerimo svoje znanje u praksi.

Odredite iz slika što je funkcija, a što nije:

Jasno? I evo ga odgovori:

Funkcija je - B,E.
Nije funkcija - A, B, D, D.

Pitate zašto? Da, evo zašto:

U svim brojkama osim AT) i E) ima nekoliko za jednog!

Siguran sam da sada možete lako razlikovati funkciju od ne-funkcije, reći šta je argument, a šta zavisna varijabla, kao i odrediti opseg argumenta i opseg funkcije. Pređimo na sljedeći odjeljak - kako definirati funkciju?

Načini postavljanja funkcije

Šta mislite šta znače riječi "postavi funkciju"? Tako je, znači objasniti svima o kojoj funkciji je riječ u ovom slučaju. Štaviše, objasnite na način da vas svi dobro razumiju i da su grafovi funkcija koje su ljudi nacrtali prema vašem objašnjenju bili isti.

Kako to mogu učiniti? Kako postaviti funkciju? Najlakši način, koji je već korišten više puta u ovom članku - koristeći formulu. Pišemo formulu i zamjenom vrijednosti u nju izračunavamo vrijednost. I kao što se sjećate, formula je zakon, pravilo prema kojem nama i drugoj osobi postaje jasno kako se X pretvara u Y.

Obično upravo to rade - u zadacima vidimo gotove funkcije definirane formulama, međutim, postoje i drugi načini postavljanja funkcije na koje svi zaboravljaju, a samim tim i pitanje "kako drugačije možete postaviti funkciju?" zbunjuje. Pogledajmo sve redom i počnimo s analitičkom metodom.

Analitički način definiranja funkcije

Analitička metoda je zadatak funkcije koja koristi formulu. Ovo je najuniverzalniji i najsveobuhvatniji i nedvosmislen način. Ako imate formulu, onda znate apsolutno sve o funkciji - možete napraviti tablicu vrijednosti na njoj, možete napraviti graf, odrediti gdje se funkcija povećava, a gdje smanjuje, općenito, istražite je u cijelosti.

Razmotrimo funkciju. šta to ima veze?

"Šta to znači?" - pitate. Sad ću objasniti.

Da vas podsjetim da se u notaciji izraz u zagradama naziva argumentom. A ovaj argument može biti bilo koji izraz, ne nužno jednostavan. Prema tome, bez obzira na argument (izraz u zagradama), umjesto toga ćemo ga napisati u izrazu.

U našem primjeru to će izgledati ovako:

Razmotrite još jedan zadatak koji se odnosi na analitičku metodu specificiranja funkcije koju ćete imati na ispitu.

Pronađite vrijednost izraza, at.

Sigurna sam da ste se u početku uplašili kada ste vidjeli takav izraz lica, ali u tome nema apsolutno ničeg strašnog!

Sve je isto kao u prethodnom primjeru: bez obzira na argument (izraz u zagradama), umjesto toga ćemo ga napisati u izrazu. Na primjer, za funkciju.

Šta bi trebalo učiniti u našem primjeru? Umjesto toga, trebate napisati, a umjesto -:

skratiti rezultirajući izraz:

To je sve!

Samostalan rad

Sada pokušajte sami pronaći značenje sljedećih izraza:

, ako
, ako

Jeste li uspjeli? Uporedimo naše odgovore: Navikli smo na činjenicu da funkcija ima oblik

Čak iu našim primjerima funkciju definiramo na ovaj način, ali je analitički moguće definirati funkciju implicitno, na primjer.

Pokušajte sami izgraditi ovu funkciju.

Jeste li uspjeli?

Evo kako sam ga napravio.

Sa kojom smo jednačinom završili?

Ispravno! Linearno, što znači da će graf biti prava linija. Napravimo tabelu da odredimo koje tačke pripadaju našoj liniji:

Upravo o tome smo pričali... Jedan odgovara nekoliko.

Pokušajmo nacrtati šta se dogodilo:

Je li ono što imamo funkcija?

Tako je, ne! Zašto? Pokušajte odgovoriti na ovo pitanje slikom. šta si dobio?

“Zato što jedna vrijednost odgovara nekoliko vrijednosti!”

Kakav zaključak možemo izvući iz ovoga?

Tako je, funkcija se ne može uvijek eksplicitno izraziti, a ono što je "prikriveno" u funkciju nije uvijek funkcija!

Tabelarni način definiranja funkcije

Kao što ime govori, ova metoda je jednostavna ploča. Da da. Kao onaj koji smo već napravili. Na primjer:

Ovdje ste odmah primijetili uzorak - Y je tri puta veći od X. A sada zadatak „vrlo dobro razmislite“: mislite li da je funkcija data u obliku tabele ekvivalentna funkciji?

Hajde da ne pričamo dugo, nego da crtamo!

Dakle. Crtamo funkciju datu na oba načina:

Vidite li razliku? Ne radi se o označenim tačkama! Pogledajte izbliza:

Jeste li ga sada vidjeli? Kada funkciju postavimo na tabelarni način, na grafu odražavamo samo one tačke koje imamo u tabeli i linija (kao u našem slučaju) prolazi samo kroz njih. Kada definiramo funkciju na analitički način, možemo uzeti bilo koje točke, a naša funkcija nije ograničena na njih. Evo takve karakteristike. Zapamtite!

Grafički način za izgradnju funkcije

Grafički način konstruisanja funkcije nije ništa manje zgodan. Nacrtamo našu funkciju, a druga zainteresirana osoba može pronaći koliko je y jednako pri određenom x, i tako dalje. Grafičke i analitičke metode su među najčešćim.

Međutim, ovdje se morate sjetiti o čemu smo pričali na samom početku - nije svaka „švergla“ nacrtana u koordinatnom sistemu funkcija! Zapamtite? Za svaki slučaj, kopiraću ovde definiciju šta je funkcija:

U pravilu ljudi obično imenuju upravo ona tri načina specificiranja funkcije koje smo analizirali - analitički (pomoću formule), tabelarni i grafički, potpuno zaboravljajući da se funkcija može opisati verbalno. Volim ovo? Da, vrlo lako!

Verbalni opis funkcije

Kako verbalno opisati funkciju? Uzmimo naš nedavni primjer - . Ova funkcija se može opisati kao "svaka realna vrijednost x odgovara njenoj trostrukoj vrijednosti." To je sve. Ništa komplikovano. Naravno, prigovorit ćete - "postoje tako složene funkcije koje je jednostavno nemoguće verbalno postaviti!" Da, ima ih, ali postoje funkcije koje je lakše opisati verbalno nego postaviti formulom. Na primjer: "svaka prirodna vrijednost x odgovara razlici između cifara od kojih se sastoji, dok se najveća cifra sadržana u unosu broja uzima kao minus." Sada razmotrite kako se naš verbalni opis funkcije implementira u praksi:

Najveća znamenka u datom broju - odnosno - se smanjuje, tada:

Glavne vrste funkcija

Sada pređimo na ono najzanimljivije - razmotrit ćemo glavne vrste funkcija s kojima ste radili/radili i radit ćete u toku školske i institutske matematike, odnosno upoznaćemo ih, da tako kažem, i dajte im kratak opis. Pročitajte više o svakoj funkciji u odgovarajućem odjeljku.

Linearna funkcija

Funkcija oblika, gdje su realni brojevi.

Graf ove funkcije je prava linija, pa se konstrukcija linearne funkcije svodi na pronalaženje koordinata dvije tačke.

Položaj prave linije na koordinatnoj ravni zavisi od nagiba.

Opseg funkcije (aka raspon argumenata) - .

Raspon vrijednosti je .

kvadratna funkcija

Funkcija forme, gdje

Graf funkcije je parabola, kada su grane parabole usmjerene prema dolje, kada - prema gore.

Mnoga svojstva kvadratne funkcije zavise od vrijednosti diskriminanta. Diskriminanta se izračunava po formuli

Položaj parabole na koordinatnoj ravni u odnosu na vrijednost i koeficijent prikazan je na slici:

Domain

Raspon vrijednosti ovisi o ekstremumu date funkcije (vrh parabole) i koeficijentu (smjer grana parabole)

Inverzna proporcionalnost

Funkcija data formulom, gdje

Broj se naziva faktor inverzne proporcionalnosti. Ovisno o kojoj vrijednosti, grane hiperbole su u različitim kvadratima:

Domena - .

Raspon vrijednosti je .

SAŽETAK I OSNOVNA FORMULA

1. Funkcija je pravilo prema kojem se svakom elementu skupa dodjeljuje jedinstveni element skupa.

- ovo je formula koja označava funkciju, odnosno zavisnost jedne varijable od druge;
- varijabla ili argument;
- zavisna vrijednost - mijenja se kada se argument promijeni, odnosno prema nekoj specifičnoj formuli koja odražava ovisnost jedne vrijednosti od druge.

2. Važeće vrijednosti argumenata, ili opseg funkcije, je ono što se odnosi na moguće mogućnosti pod kojima funkcija ima smisla.

3. Raspon vrijednosti funkcije- to su vrijednosti koje uzima, sa važećim vrijednostima.

4. Postoje 4 načina za postavljanje funkcije:

analitički (koristeći formule);
tabelarni;
grafički
verbalni opis.

5. Glavne vrste funkcija:

: , gdje su realni brojevi;
: , gdje;
: , gdje.